Controlled Release Using Gas Detonation in Needle-Free Liquid Jet Injections for Drug Delivery
Abstract
:1. Introduction
2. Fundamentals and Methods
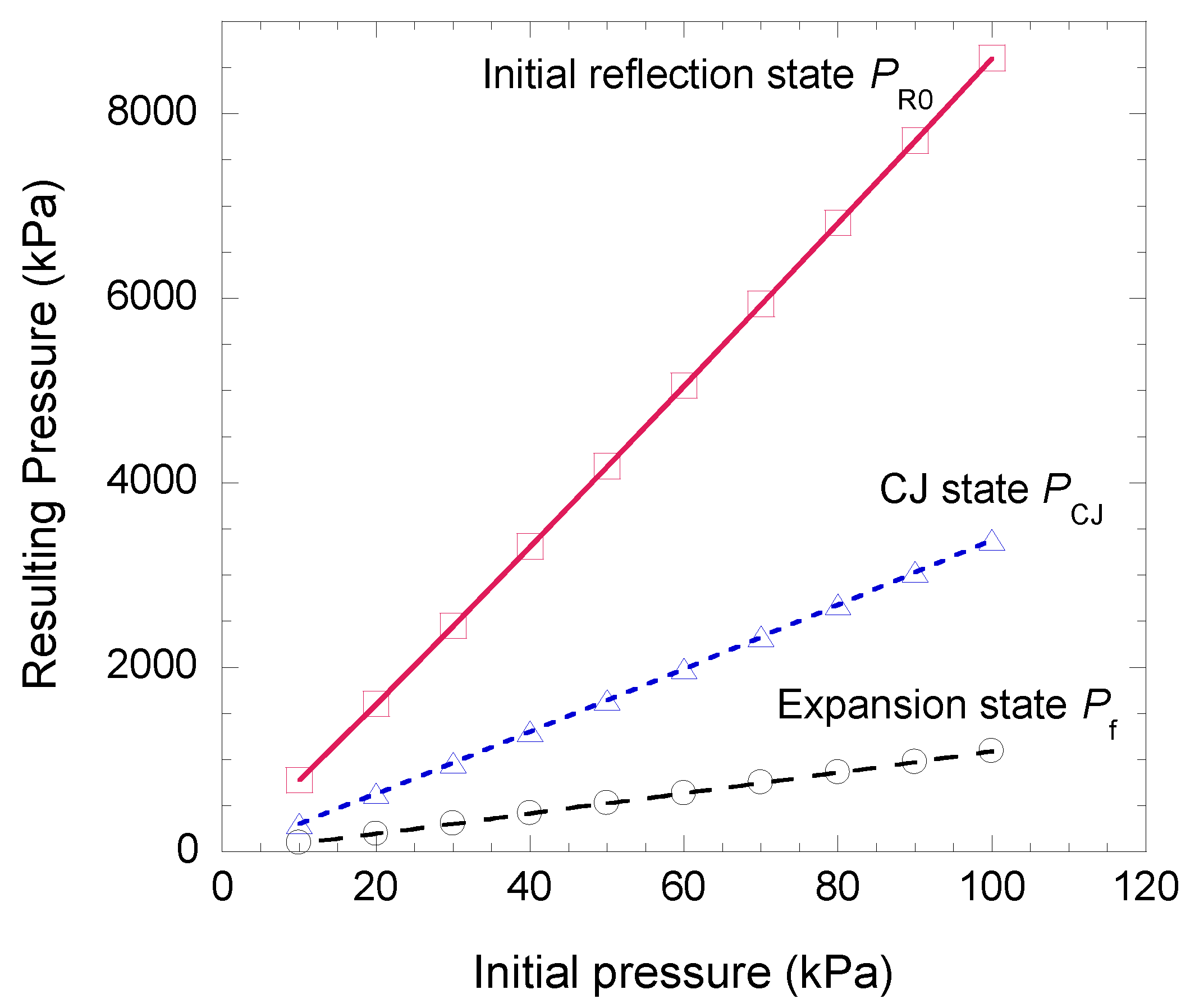
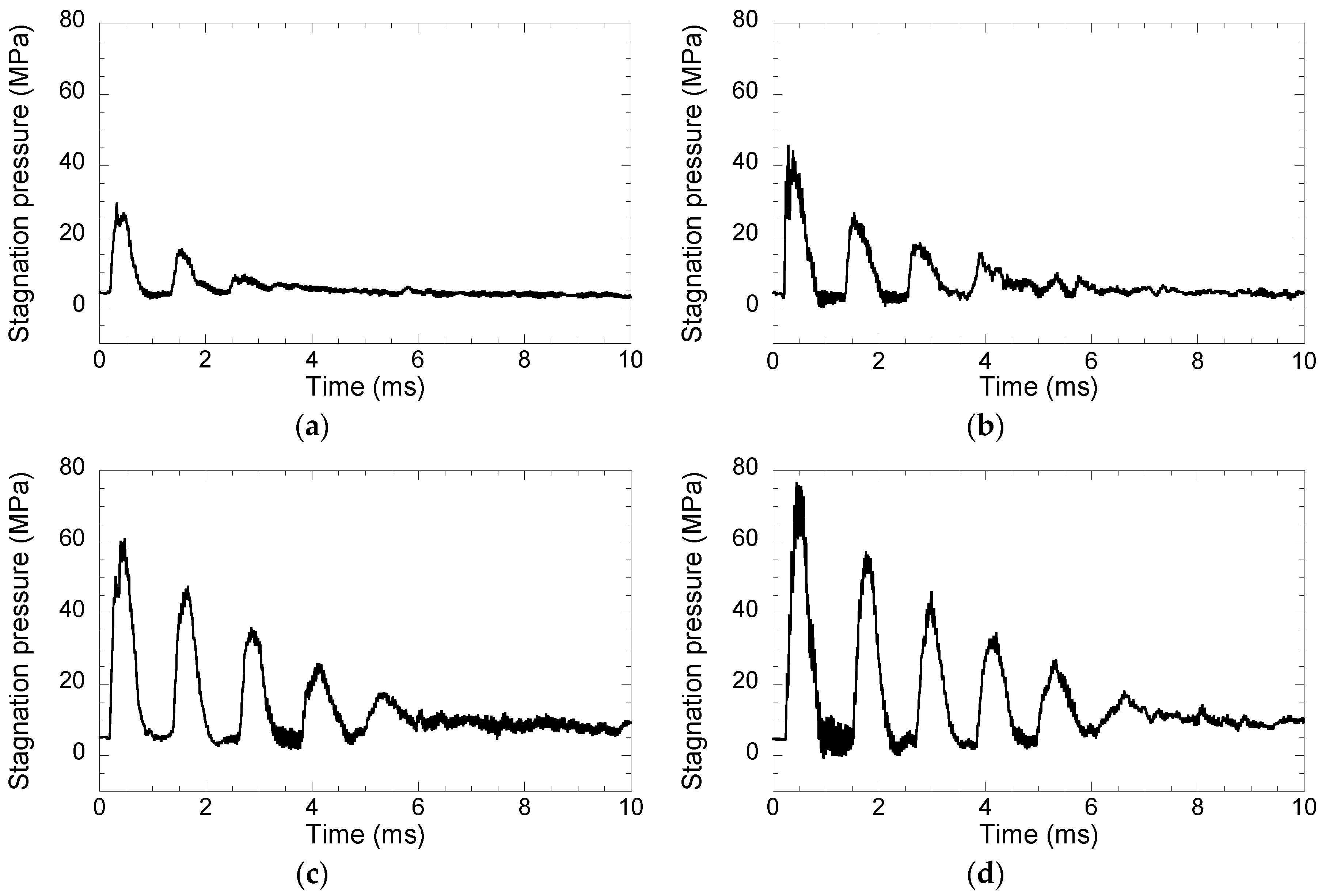
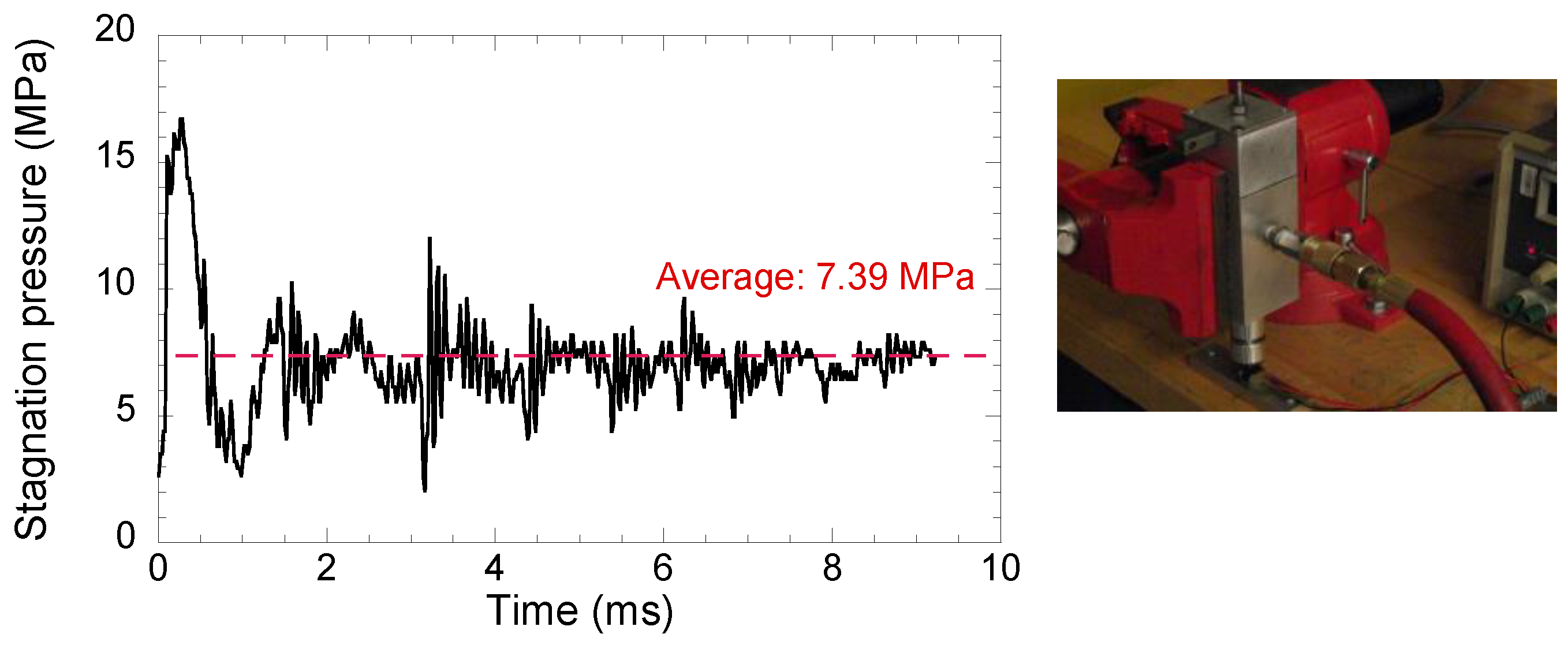
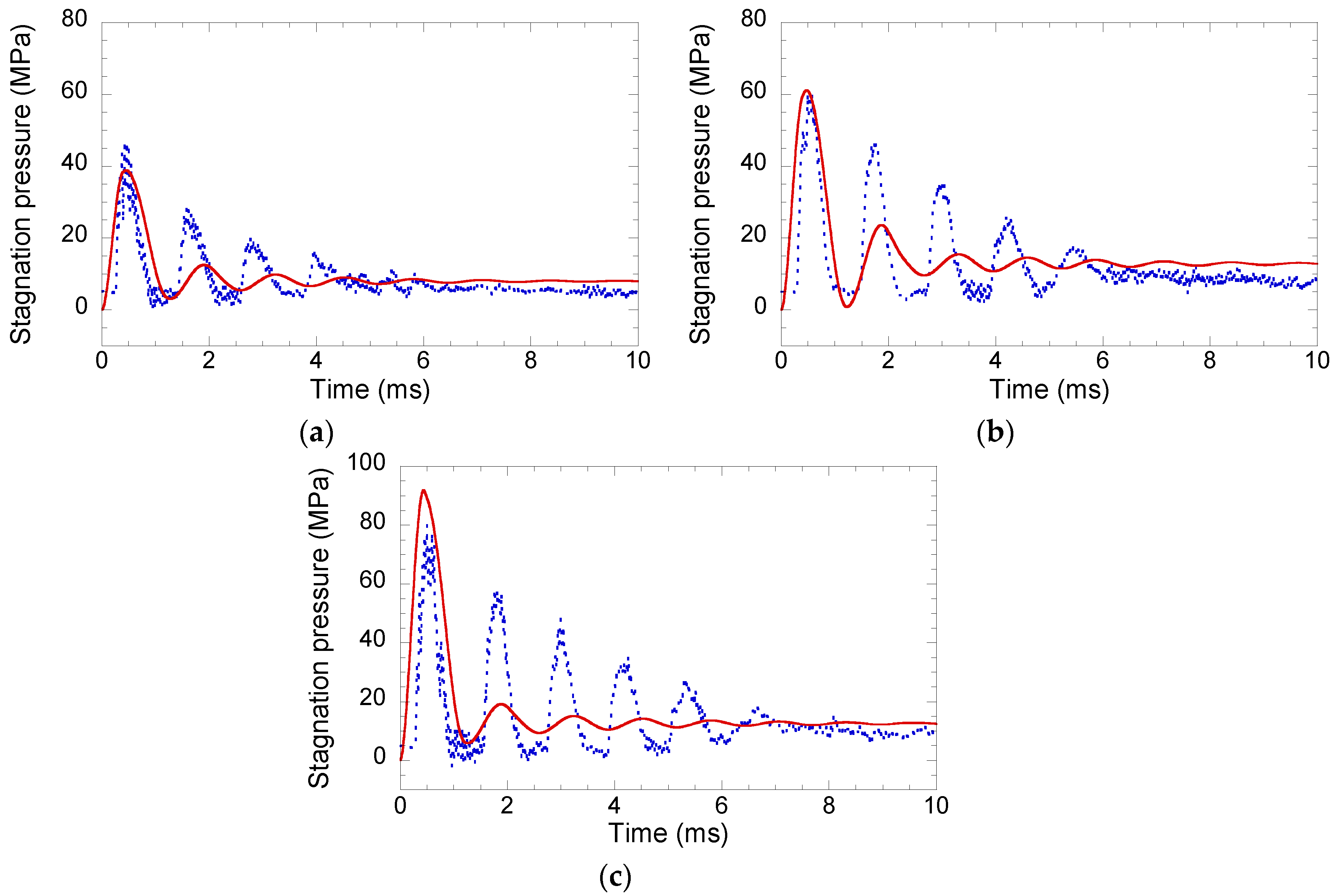
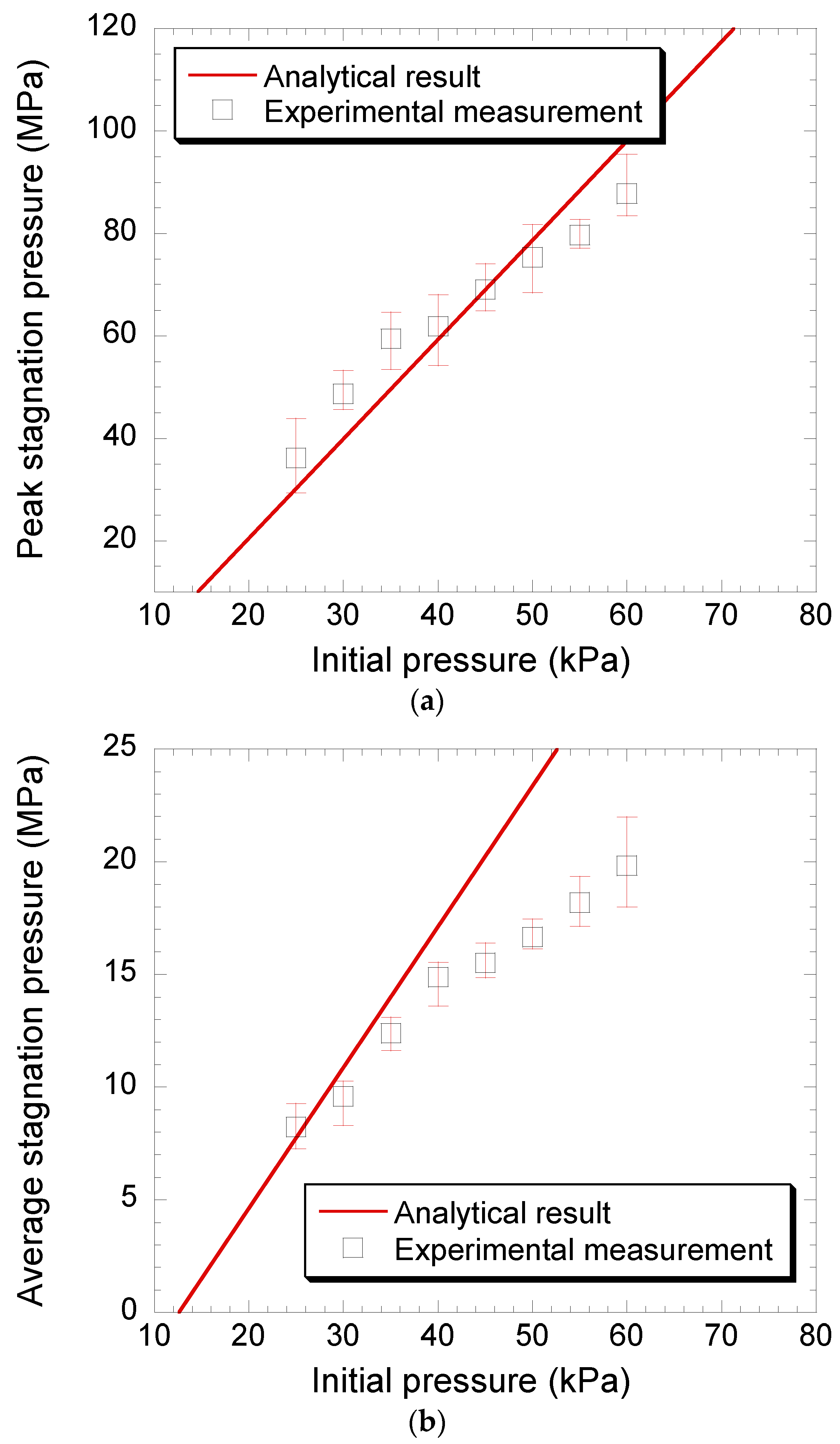
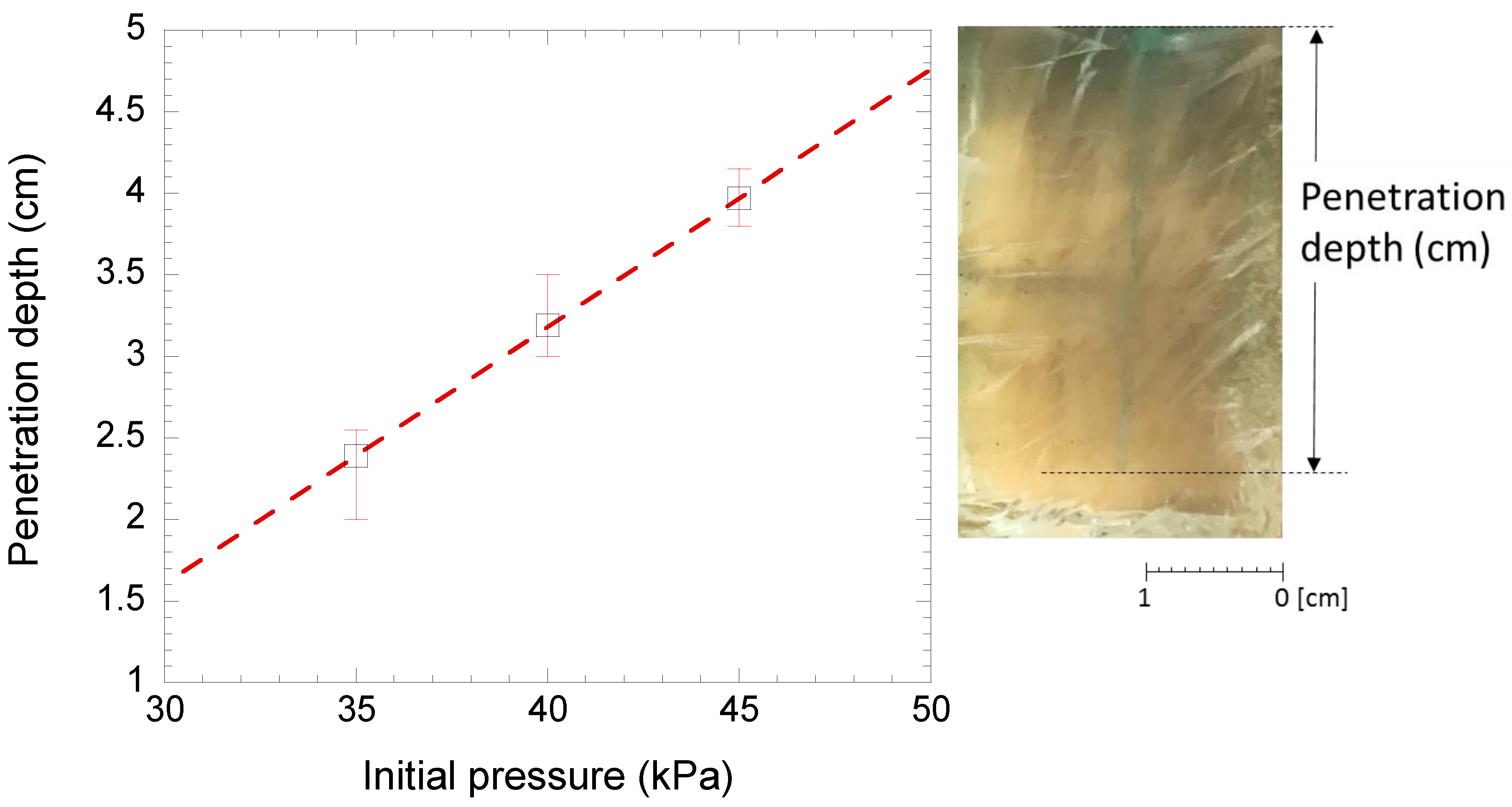
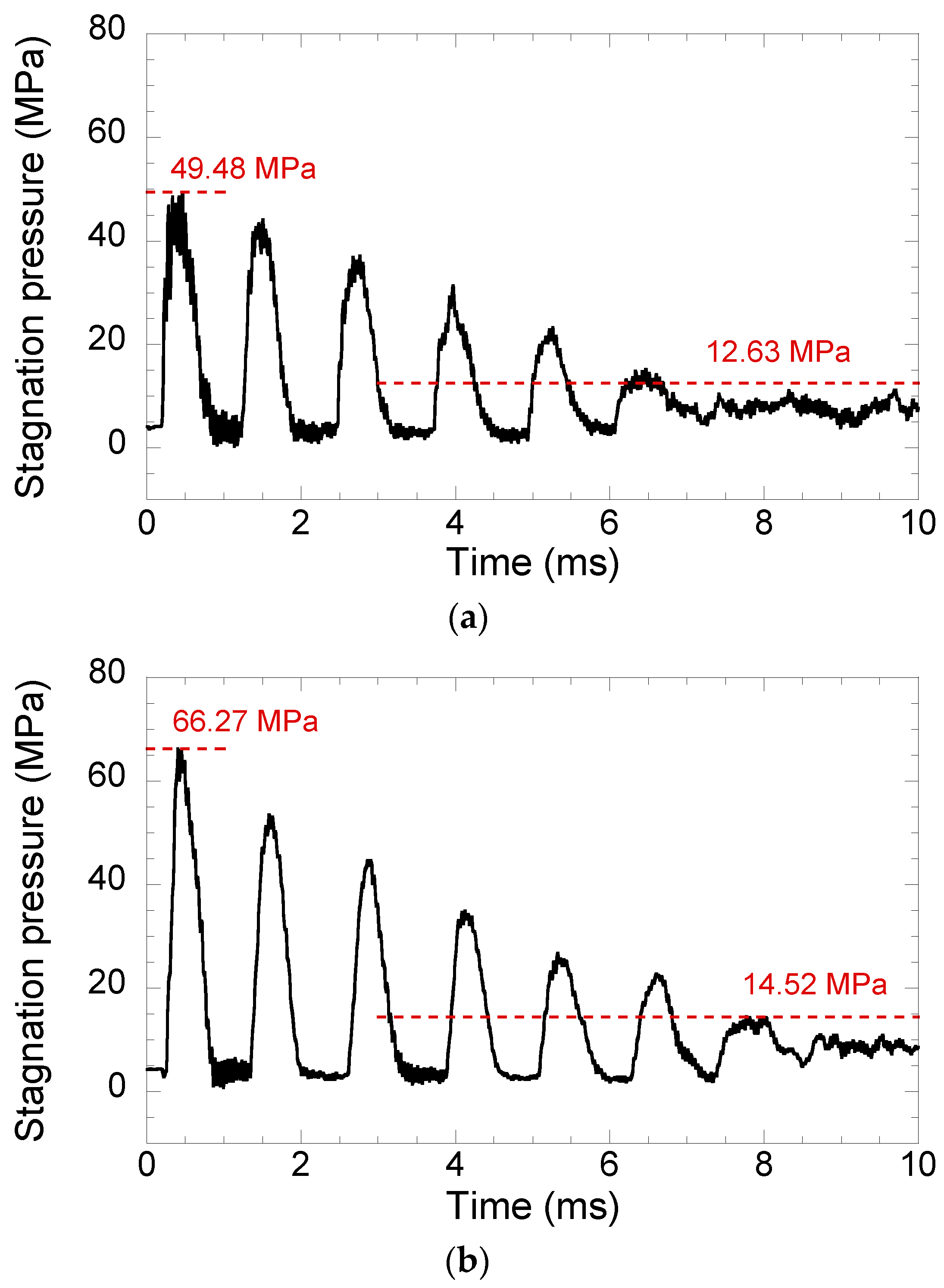
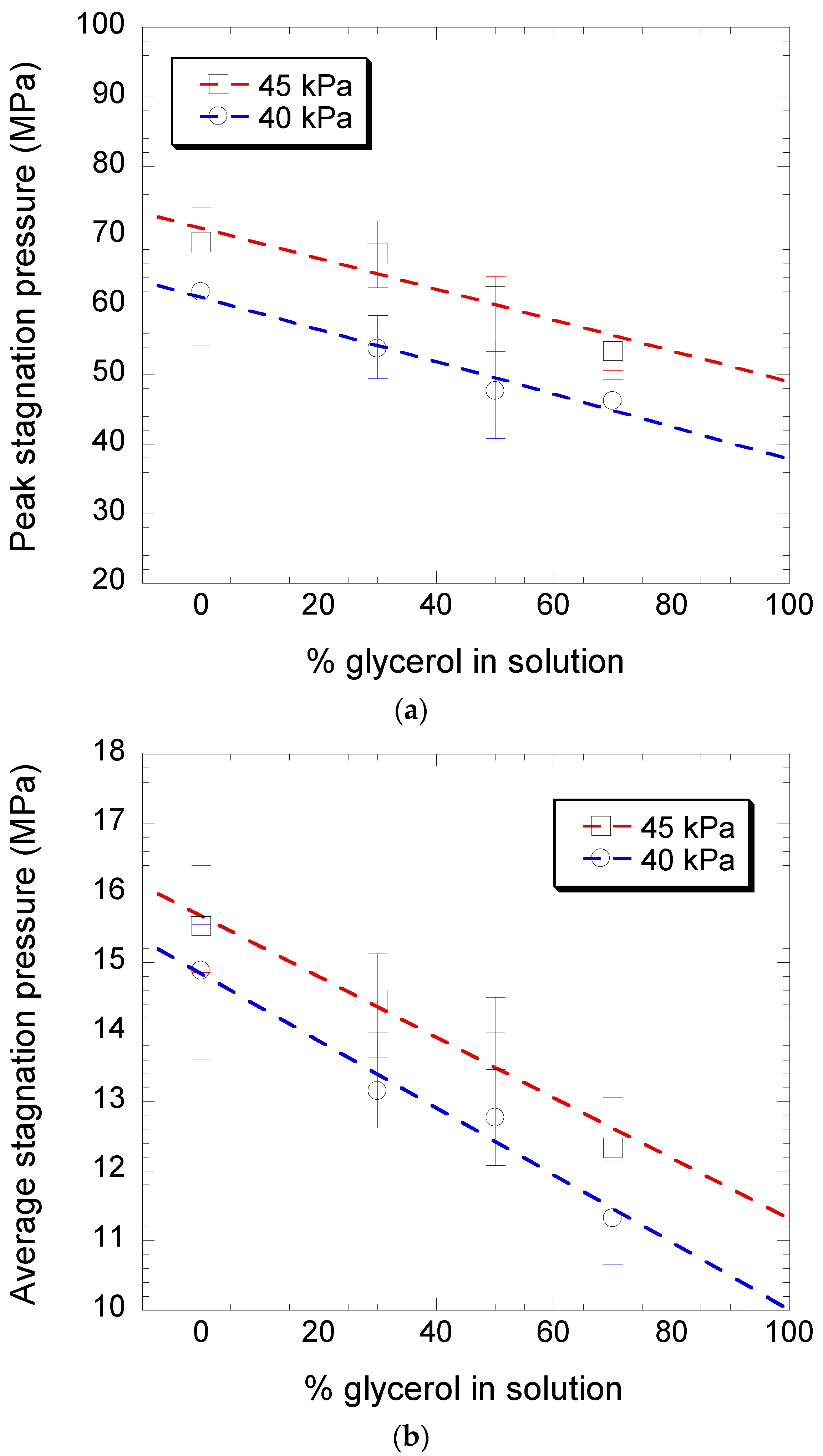
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mitragotri, S. Immunization without needles. Nat. Rev. Immunol. 2005, 5, 905–917. [Google Scholar] [CrossRef] [PubMed]
- Baxter, J.; Mitragotri, S. Needle-free liquid jet injections: Mechanisms and applications. Expert Rev. Med. Devices 2006, 3, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Mitragotri, S. Current status and future prospects of needle free liquid jet injectors. Nat. Rev. Drug Discov. 2006, 5, 543–548. [Google Scholar] [CrossRef] [PubMed]
- Hingson, R.A.; Davis, H.S.; Rosen, M. Historical development of jet injection and envisioned uses in mass immunization and mass therapy based upon 2 decades experience. Mil. Med. 1963, 128, 516–524. [Google Scholar] [CrossRef]
- Wijsmuller, G.; Snider, D.E., Jr. Skin testing: A comparison of the jet injector with the Mantoux method. Am. Rev. Respir. Dis. 1975, 112, 789–798. [Google Scholar] [PubMed]
- Schneider, U.; Birnbacher, R.; Schober, E. Painfulness of needle and jet injection in children with diabetes mellitus. Eur. J. Pediatr. 1994, 153, 409–410. [Google Scholar] [CrossRef] [PubMed]
- Raviprakash, K.; Porter, K.R. Needle-free injection of DNA vaccines: A brief overview and methodology. Methods. Mol. Med. 2006, 127, 83–89. [Google Scholar] [PubMed]
- Fargnoli, A.S.; Katz, M.G.; Williams, R.D.; Marguilles, K.B.; Bridges, C.R. A needleless liquid jet injection delivery method for cardiac gene therapy: A comparative evaluation versus standard routes of delivery reveals enhanced therapeutic retention and cardiac specific gene expression. J. Cardiovasc. Trans. Res. 2014, 7, 756–767. [Google Scholar] [CrossRef]
- Kendall, M. Engineering of needle-free physical methods to target epidermal cells for DNA vaccination. Vaccine 2006, 24, 4651–4656. [Google Scholar] [CrossRef]
- Baker, A.B.; Sanders, J.E. Fluid mechanics analysis of a spring-loaded jet injector. IEEE Trans. Biomed. Eng. 1999, 46, 235–242. [Google Scholar] [CrossRef]
- Schramm, J.R.; Mitragotri, S. Transdermal drug delivery by jet injectors: Energetics of jet formation and penetration. Pharm. Res. 2002, 19, 1673–1679. [Google Scholar] [CrossRef] [PubMed]
- Schramm-Baxter, J.; Mitragotri, S. Needle-free jet injections: Dependence of jet penetration and dispersion in the skin on jet power. J. Control. Release 2004, 97, 527–535. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.B.; Martin, G.P.; Jones, S.A.; Akomeah, F.K. Dermal and transdermal drug delivery systems: Current and future prospects. Drug Deliv. 2006, 13, 175–187. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Zhou, H.; Li, J.; Cheng, G.J. A model on liquid penetration into soft material with application to needle-free jet injection. Asme J. Biomech. Eng. 2010, 132, 101005. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Zhou, H.; Li, J.; Cheng, G. Stagnation pressure in liquid needle-free injection: Modeling and experimental validation. J. Drug Deliv. Lett. 2011, 1, 97–104. [Google Scholar]
- Baxter, J.; Mitragotri, S. Jet-induced skin puncture and its impact on needle-free jet injections: Experimental studies and a predictive model. J. Control. Release 2005, 106, 361–373. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, C.; Mannavathy, C.; Srikanth, D.; Tabassum, R. Needle free drug delivery systems: A review. Int. J. Pharm. Res. Dev. Ijprd 2011, 3, 7–15. [Google Scholar]
- Portaro, R.; Ng, H.D. Experiments and modeling of air-powered needle free liquid injectors. J. Med. Biol. Eng. 2015, 35, 685–695. [Google Scholar] [CrossRef]
- Nakayama, H.; Portaro, R.; Kiyanda, C.B.; Ng, H.D. CFD modeling and validation of high speed liquid jets from an air-powered needle-free injection system. J. Mech. Med. Biol. 2015, 16, 1650045. [Google Scholar] [CrossRef]
- Taberner, A.; Hogan, N.C.; Hunter, I.W. Needle-free jet injection using real-time controlled linear Lorentz-force actuators. Med. Eng. Phys. 2012, 34, 1228–1235. [Google Scholar] [CrossRef]
- Li, X.; Ruddy, B.; Taberner, A. Characterization of needle-assisted jet injections. J. Control. Release 2016, 243, 195–203. [Google Scholar] [CrossRef] [PubMed]
- Ruddy, B.; Dixon, A.; Williams, R.; Taberner, A. Optimization of portable electronically-controlled needle-free jet injection systems. IEEE/Asme Trans. Mechatron. 2017, 22, 2013–2021. [Google Scholar] [CrossRef]
- Fletcher, D.A.; Palanker, D.V. Pulsed liquid microjet for microsurgery. Appl. Phys. Lett. 2001, 78, 1933–1935. [Google Scholar] [CrossRef] [Green Version]
- Tagawa, Y.; Oudalov, N.; Visser, C.W.; Peters, I.R.; van der Meer, D.; Sun, C.; Prosperetti, A.; Lohse, D. Highly focused supersonic microjets. Phys. Rev. X 2012, 2, 031002. [Google Scholar] [CrossRef]
- Menezes, V.; Nakagawa, A.; Takayama, K. Laser-based pulsed liquid microjet for surgery. J. Indian Inst. Sci. 2006, 86, 207–214. [Google Scholar]
- Berrospe-Rodriguez, C.; Visser, C.W.; Schlautmann, S.; Ramos-Garcia, R.; Fernandez Rivas, D. Continuous-wave laser generated jets for needle free applications. Biomicrofluidics 2016, 10, 014104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKeage, J.W.; Ruddy, B.P.; Nielsen, P.M.F.; Taberner, A.J. The effect of jet speed on large volume jet injection. J. Control. Release 2018, 280, 51–57. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.M.J.; Ruddy, B.P.; Hogan, N.C.; Hunter, I.W.; Nielsen, P.M.F.; Taberner, A.J. Analysis of moving-coil actuator jet injectors for viscous fluids. IEEE Trans. Biomed. Eng. 2016, 63, 1099–1106. [Google Scholar] [CrossRef]
- Rao, S.S.; Gomez, P.; Mascola, J.R.; Dang, V.; Krivulka, G.R.; Yu, F.; Lord, C.I.; Shen, L.; Bailer, R.; Nabel, G.J.; et al. Comparative evaluation of three different intramuscular delivery methods for DNA immunization in a nonhuman primate animal model. Vaccine 2006, 24, 367–373. [Google Scholar] [CrossRef]
- Chase, C.C.; Daniels, C.S.; Garcia, R. Needle-free injection technology in swine: Progress toward vaccine efficacy and pork quality. J. Swine Health Prod. 2008, 16, 254–261. [Google Scholar]
- Mousel, M.R.; Leeds, T.D.; White, S.N.; Herrmann-Hoesing, L.M. Technical note: Comparison of traditional needle vaccination with pneumatic, needle-free vaccination for sheep. J. Anim. Sci. 2008, 86, 1468–1471. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Pan, M.; Liu, T. Design and analysis of a continuous split typed needle-free injection system for animal vaccination. Open Biomed. Eng. J. 2017, 11, 59–71. [Google Scholar] [CrossRef] [PubMed]
- Wolanski, P. Detonative propulsion. Proc. Combust. Inst. 2013, 34, 125–158. [Google Scholar] [CrossRef]
- Vasil’ev, V.V. The principle aspects of application of detonation in propulsion systems. J. Combust. 2013, 945161. [Google Scholar]
- Golub, V.V.; Bazhenova, T.V.; Baklanov, D.I.; Ivanov, K.V.; Kirvokorytov, M.S. Using of hydrogen-air mixture detonation in needle-free injection devices. High Temp. 2013, 51, 138–140. [Google Scholar] [CrossRef]
- Krivokoritov, M.; Baklanov, D.; Golub, V.; Ivanov, K. Application of Gas Detonation for a Needleless Device Development. In Proceedings of the 28th International Symposium on Shock Waves, Manchester, UK, 17–22 July 2012; Kontis, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 403–407. [Google Scholar]
- Gordon, S.; McBride, B.J. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications, Technical Report 1311; NASA Reference Publication; NASA: Washington, DC, USA, 1994.
- Stanyukovich, K.P. Unsteady Motion of Continuous Media; Pergamon Press: New York, NY, USA, 1960. [Google Scholar]
- Shepherd, J.E.; Teodorczyk, A.; Knystautas, R.; Lee, J.H.S. Shock waves produced by reflected detonations. Prog. Astro. Aero. 1991, 134, 244–264. [Google Scholar]
- Beltman, W.M.; Shepherd, J.E. Linear elastic response of tubes to internal detonation loading. J. Sound Vib. 2002, 252, 617–655. [Google Scholar] [CrossRef]
- Karnesky, J.; Damazo, J.; Chow-Yee, K.; Rusinek, A.; Shepherd, J. Plastic deformation due to reflected detonation. Int. J. Solids Struct. 2013, 50, 97–110. [Google Scholar] [CrossRef] [Green Version]
- Damazo, J.; Shepherd, J.E. Observations on the normal reflection of gaseous detonations. Shock Waves 2017, 27, 795–810. [Google Scholar] [CrossRef]
- Arora, A.; Hakim, I.; Baxter, J.; Rathnasingham, R.; Srinivasan, R.; Mitragotri, S. Needle free delivery of macromolecules across the skin by nanolitre-volume pulsed microjets. Proc. Nat. Acad. Sci. USA 2007, 104, 4255–4260. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Kumar, A.; Prasad, P.S.; Rao, M.R. Experimental studies of water hammer in propellant feed system of reaction control system. Propul. Power Res. 2018, 7, 52–59. [Google Scholar] [CrossRef]
- Portaro, R.; Nakayama, H.; Ng, H.D. Optimization of drug viscosity used in gas-powered liquid jet injectors. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar]
- Shergold, O.A.; Fleck, N.A. Mechanisms of deep penetration of soft solids, with application to the injection and wounding of skin. Proc. Roy. Soc. Lond. A 2004, 460, 3037–3058. [Google Scholar] [CrossRef]
- Wu, M.H.; Burke, M.P.; Son, S.F.; Yetter, R.A. Flame acceleration and the transition to detonation of stoichiometric ethylene/oxygen in microscale tubes. Proc. Combust. Inst. 2007, 31, 2429–2436. [Google Scholar] [CrossRef]
- Wu, M.H.; Wang, C.Y. Reaction propagation modes in millimeter-scale tubes for ethylene/oxygen mixtures. Proc. Combust. Inst. 2011, 33, 2287–2293. [Google Scholar] [CrossRef]
- Han, W.; Yang, G.; Law, C.K. Flame acceleration and deflagration-to-detonation transition in micro- and macrochannels: An integrated mechanistic study. Combust. Flame 2017, 176, 285–298. [Google Scholar] [CrossRef]



| Injector Parameters | |
|---|---|
| Orifice nozzle diameter, Do | 200 μm |
| Driver diameter, Dd | 44.4 mm |
| Piston diameter, Dp | 6.35 mm |
| Mass of the piston, Mp | 150 g |
| Liquid column, L | 20 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portaro, R.; Sadek, J.; Xu, H.; Ng, H.D. Controlled Release Using Gas Detonation in Needle-Free Liquid Jet Injections for Drug Delivery. Appl. Sci. 2019, 9, 2712. https://doi.org/10.3390/app9132712
Portaro R, Sadek J, Xu H, Ng HD. Controlled Release Using Gas Detonation in Needle-Free Liquid Jet Injections for Drug Delivery. Applied Sciences. 2019; 9(13):2712. https://doi.org/10.3390/app9132712
Chicago/Turabian StylePortaro, Rocco, Jad Sadek, Han Xu, and Hoi Dick Ng. 2019. "Controlled Release Using Gas Detonation in Needle-Free Liquid Jet Injections for Drug Delivery" Applied Sciences 9, no. 13: 2712. https://doi.org/10.3390/app9132712
APA StylePortaro, R., Sadek, J., Xu, H., & Ng, H. D. (2019). Controlled Release Using Gas Detonation in Needle-Free Liquid Jet Injections for Drug Delivery. Applied Sciences, 9(13), 2712. https://doi.org/10.3390/app9132712






