Aerodynamic Performance of Quadrotor UAV with Non-Planar Rotors
Abstract
:1. Introduction
2. Aerodynamics of the Quadrotor
2.1. Aerodynamics of the Isolated Rotor
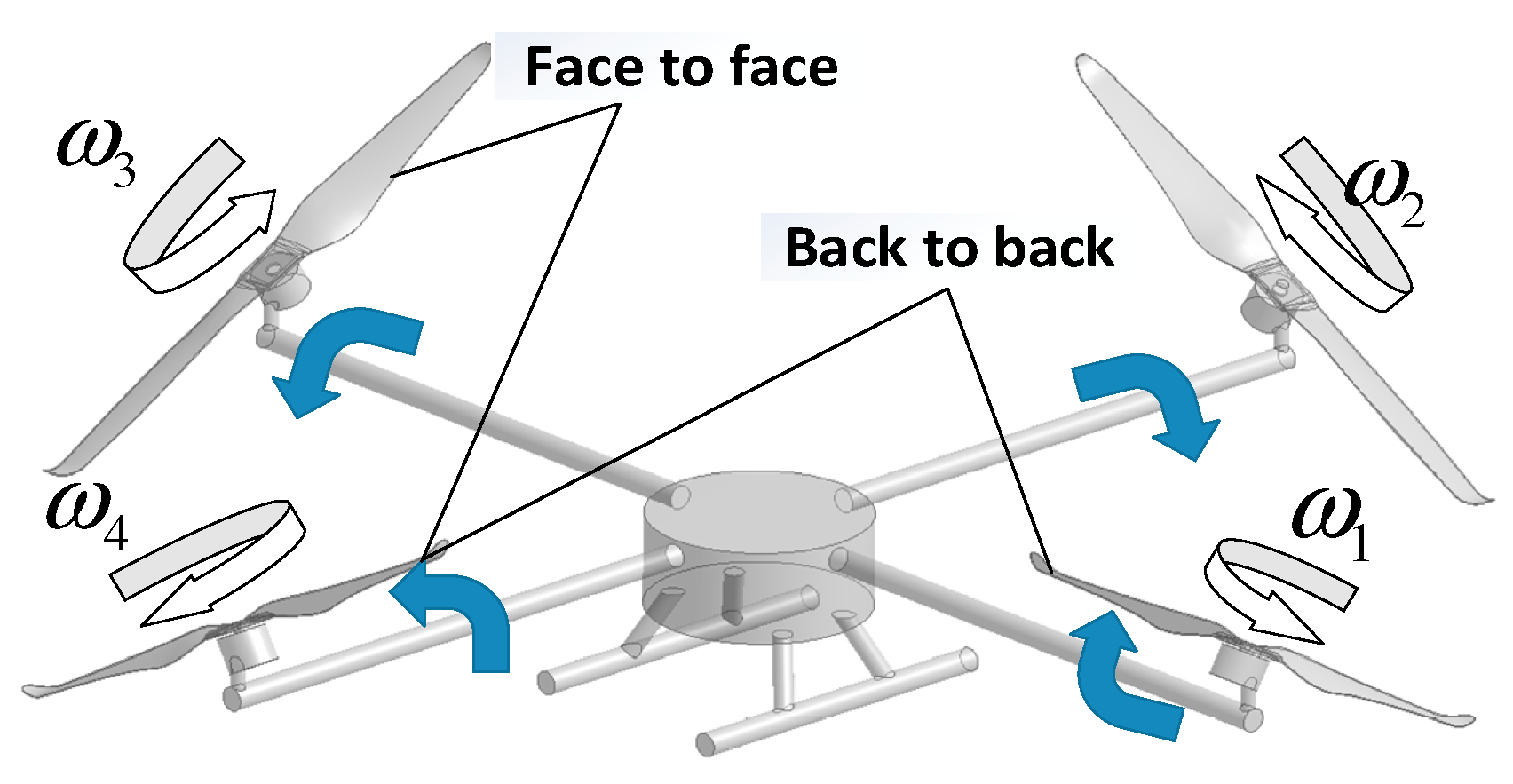
2.2. Aerodynamic Model of a Non-Planar Quadrotor Considering Rotor Interference
2.3. Power Model of a Non-Planar Quadrotor
3. Computational-Fluid-Dynamics Analysis
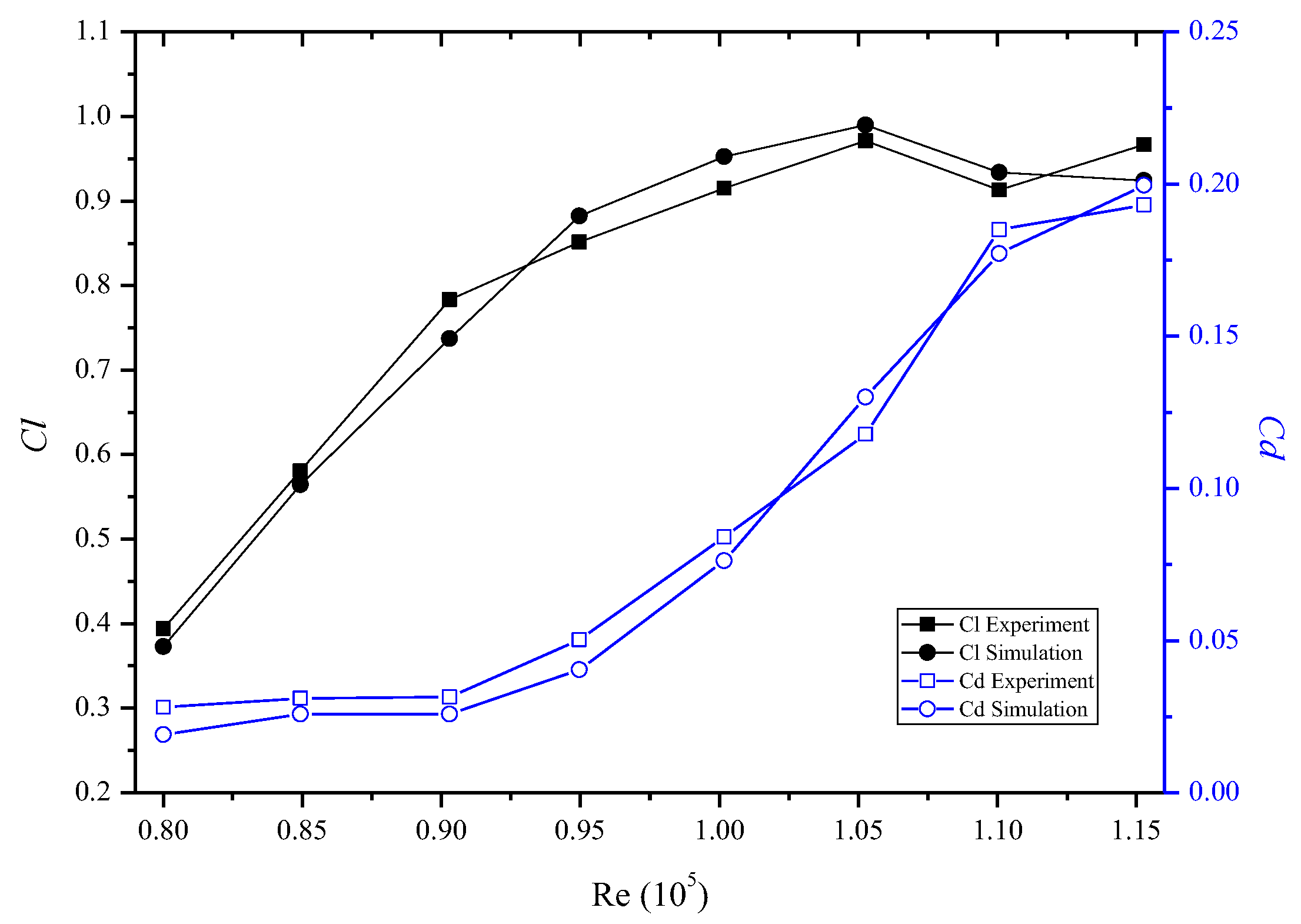
3.1. CFD Simulations for the Isolated Single Rotor
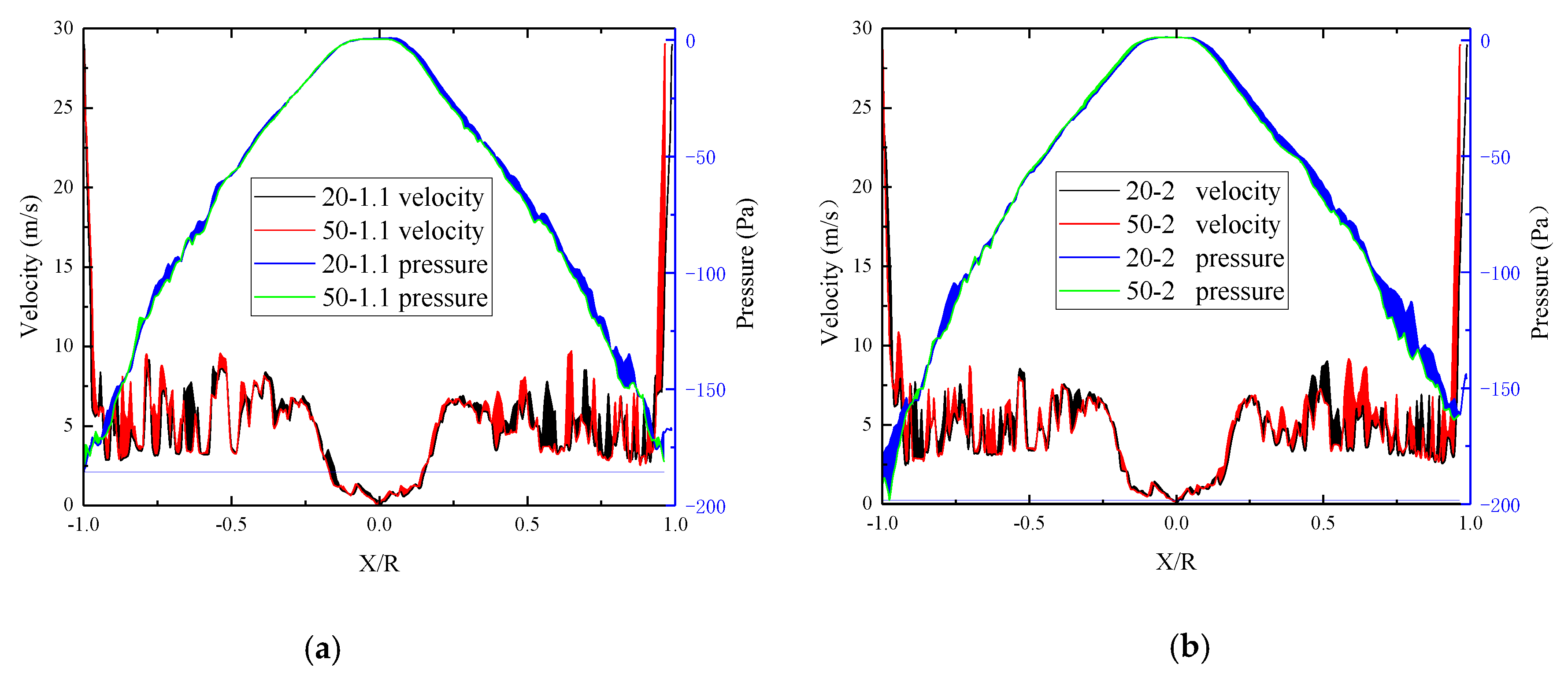
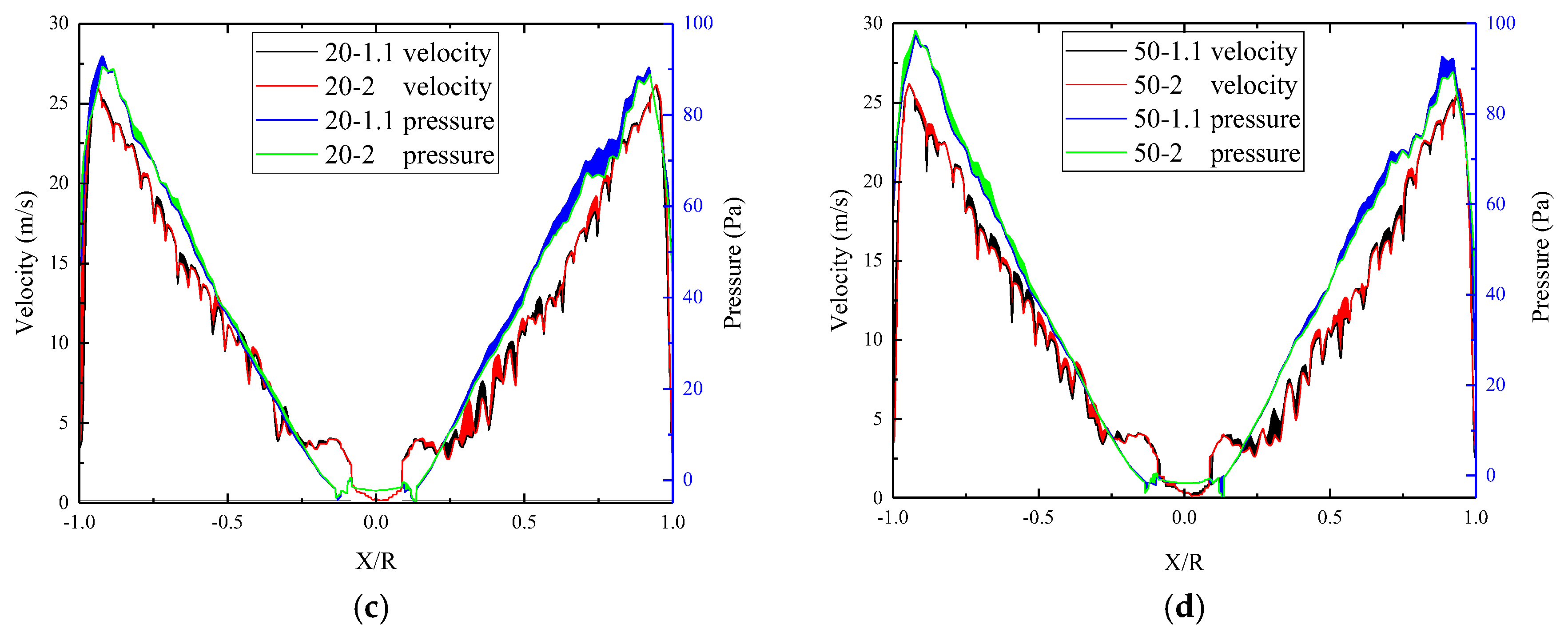
3.2. Simulation Results of Non-Planar Quadrotor
4. Experimental Study
5. Conclusions
- (1)
- The non-planar quadrotor rotor thrust will increase by 5–6% compared to the isolated rotor without interference. The tilt angle increased the actual induced velocity and outflow to increase the thrust of rotor;
- (2)
- The thrust becomes stable when the spacing is larger 1.4 d and the power is also significantly affected by the high-intensity vortex attached to the surface of the rotor and the tip vortex;
- (3)
- The flow field of the non-planar quadrotor is extremely complex, mainly based on unsteady flow caused by the intense outflow. There is a large pressure gradient in the vortex due to the periodic unsteady airflow pulsation generated by the rotor itself and the wake diffusion. Each vortex is a distorted sub-zone that causes the pressure distribution pulsations;
- (4)
- Power consumption of the non-planar quadrotor increases with the thrust which will cause a substantially balanced power loading. Moreover, the power loading of the non-planar quadrotor is less than the isolated rotors showed a better performance compared with the traditional planar rotors;
- (5)
- The unique aerodynamic performance of the non-planar quadrotor is significantly improved at a larger tilt angle with smaller spacing where the tip vortex is relatively strong, which is beneficial to optimize the multi-rotor system for the further studies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ryll, M.; Bülthoff, H.H.; Giordano, P.R. Modeling and control of a quadrotor UAV with tilting propellers. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4606–4613. [Google Scholar]
- Efraim, H.; Shapiro, A.; Weiss, G. Quadrotor with a Dihedral Angle: On the Effects of Tilting the Rotors Inwards. Int. J. Intell. Syst. 2015, 80, 313–324. [Google Scholar] [CrossRef]
- Elfeky, M.; Elshafei, M.; Saif, A.W.A.; Al-Malki, M.F. Quadrotor helicopter with tilting rotors: Modeling and simulation. In Proceedings of the 2013 World Congress on Computer and Information Technology (WCCIT), Sousse, Tunisia, 22–24 June 2013; pp. 1–5. [Google Scholar]
- Şenkul, A.F.; Altug, E. System Design of a Novel Tilt-Roll Rotor Quadrotor UAV. Int. J. Intell. Syst. 2015, 84, 1–25. [Google Scholar] [CrossRef]
- Senkul, A.F.; Altug, E. Modeling and control of a novel tilt-Roll rotor quadrotor UAV. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems, Atlanta, GA, USA, 28–31 May 2013; pp. 1071–1076. [Google Scholar]
- Ryll, M.; Bülthoff, H.H.; Giordano, P.R. A Novel Overactuated Quadrotor Unmanned Aerial Vehicle: Modeling, Control, and Experimental Validation. IEEE Trans. Control Syst. Technol. 2015, 23, 540–556. [Google Scholar] [CrossRef]
- Meng, J.D.; Zhao, Z.G. Modeling and Simulation of Microquadrotor UAV. J. Lanzhou Jiaotong Univ. 2013, 32, 63–67. [Google Scholar]
- Ferrarese, G.; Giulietti, F.; Avanzini, G. Modeling and Simulation of a Quad-Tilt Rotor Aircraft. IFAC Proc. Vol. 2013, 46, 64–70. [Google Scholar] [CrossRef]
- Salih, A.L.; Moghavvemi, M.; Mohamed, H.A.F.; Gaeid, K.S. Flight PID Controller Design for a UAV Quadrotor. Sci. Res. Essays 2010, 5, 3660–3667. [Google Scholar]
- Salih, A.L.; Moghavvemi, M.; Mohamed, H.A.F.; Gaeid, K.S. Modelling and PID Controller Design for a Quadrotor Unmanned Air Vehicle. In Proceedings of the 2010 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 28–30 May 2010; pp. 1–5. [Google Scholar]
- Li, J.; Li, Y. Dynamic Analysis and PID Control for a Quadrotor. In Proceedings of the International Conference on Mechatronics and Automation (ICMA), Beijing, China, 7–10 August 2011; pp. 573–578. [Google Scholar]
- Bouabdallah, S.; Siegwart, R. Backstepping and Sliding-Mode Techniques Applied to an Indoor Micro Quadrotor. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2247–2252. [Google Scholar]
- Madani, T.; Benallegue, A. Backstepping Control for a Quadrotor Helicopter. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3255–3260. [Google Scholar]
- Madani, T.; Benallegue, A. Backstepping Sliding Mode Control Applied to a Miniature Quadrotor Flying Robot. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 700–705. [Google Scholar]
- Turpin, M.; Michael, N.; Kumar, V. Trajectory Design and Control for Aggressive Formation Flight with Quadrotors. Auton. Robots 2012, 33, 143–156. [Google Scholar] [CrossRef]
- Huang, H.; Hoffmann, G.M.; Waslander, S.L.; Tomlin, C.J. Aerodynamics and Control of Autonomous Quadrotor Helicopters in Aggressive Maneuvering. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3277–3282. [Google Scholar]
- Yasuda, H.; Keiichi, K.; Yoshiaki, N. Numerical Analysis of Flow Field and Aerodynamic Characteristics of a Quadrotor. Trans. Jpn. Soc. Aeronaut. Space Sci. 2013, 11, 61–70. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, L.; Yan, G. Novel Quadrotor Forward-Flight Model Based on Wake Interference. AIAA J. 2015, 53, 3522–3533. [Google Scholar] [CrossRef]
- Powers, C.; Mellinger, D.; Kushleyev, A.; Kothmann, B.; Kumar, V. Influence of Aerodynamics and Proximity Effects in Quadrotor Flight. Exp. Robot. 2013, 88, 289–302. [Google Scholar]
- Nguyen, H.; Liu, Y.; Koichi, M. Experimental Study for Aerodynamic Performance of Quadrotor Helicopter. Trans. Jpn. Soc. Aeronaut. Space Sci. 2018, 61, 29–39. [Google Scholar] [CrossRef] [Green Version]
- Kaya, D.; Kutay, T. Aerodynamic Modeling and Parameter Estimation of a Quadrotor Helicopter. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Yeong, S.P.; Dol, S.S. Aerodynamic Optimization of Micro Aerial Vehicle. J. Appl. Fluid Mech. 2016, 9, 2111–2121. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Min, K.J.; Kwon, O.J. Numerical Study of Aerodynamic Performance of a Multirotor Unmanned-Aerial-Vehicle Configuration. J. Aircr. 2014, 52, 839–846. [Google Scholar] [CrossRef]
- Leishman, J.G. Momentum Analysis in Forward Flight: Principles of Helicopter Aerodynamics, Fundamentals of Rotor Aerodynamics; Cambridge University Press: New York, NY, USA, 2006; p. 94. [Google Scholar]
- Seddon, J.; Newman, S. Basic Helicopter Aerodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Naidoo, Y.; Riaan, S.; Glen, B. Rotor aerodynamic analysis of a quadrotor for thrust critical applications. In Proceedings of the 4th Robotics and Mechatronics Conference of South Africa (ROBMECH 2011), Gauteng, South Africa, 23–25 November 2011. [Google Scholar]
- Johnson, W. Twin Rotor Interference in Forward Flight. In Helicopter Theory; Dover: New York, NY, USA, 1994; p. 142. [Google Scholar]
- Bohorquez, F.; Samuel, P.; Sirohi, J.; Pines, D.; Rudd, L.; Perel, R. Design, Analysis and Hover Performance of a Rotary Wing Micro Air Vehicle. J. Am. Helicopter Soc. 2003, 48, 80–81. [Google Scholar] [CrossRef]
- Jang, J.; Yang, G. Design of Wing Root Rotation Mechanism for Dragonfly-Inspired Micro Air Vehicle. Appl. Sci. 2018, 8, 1868. [Google Scholar] [CrossRef]
- Lei, Y.; Ji, Y.; Wang, C.; Bai, Y.; Xu, Z. Full-scale measurement on the aerodynamics of non-planar rotor pairs in a Hexacopter. J. Mech. Robot. 2017, 9, 064502. [Google Scholar] [CrossRef]
















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; Wang, J. Aerodynamic Performance of Quadrotor UAV with Non-Planar Rotors. Appl. Sci. 2019, 9, 2779. https://doi.org/10.3390/app9142779
Lei Y, Wang J. Aerodynamic Performance of Quadrotor UAV with Non-Planar Rotors. Applied Sciences. 2019; 9(14):2779. https://doi.org/10.3390/app9142779
Chicago/Turabian StyleLei, Yao, and Jinli Wang. 2019. "Aerodynamic Performance of Quadrotor UAV with Non-Planar Rotors" Applied Sciences 9, no. 14: 2779. https://doi.org/10.3390/app9142779
APA StyleLei, Y., & Wang, J. (2019). Aerodynamic Performance of Quadrotor UAV with Non-Planar Rotors. Applied Sciences, 9(14), 2779. https://doi.org/10.3390/app9142779




