Design and Analysis of a Robust UAV Flight Guidance and Control System Based on a Modified Nonlinear Dynamic Inversion
Abstract
:1. Introduction
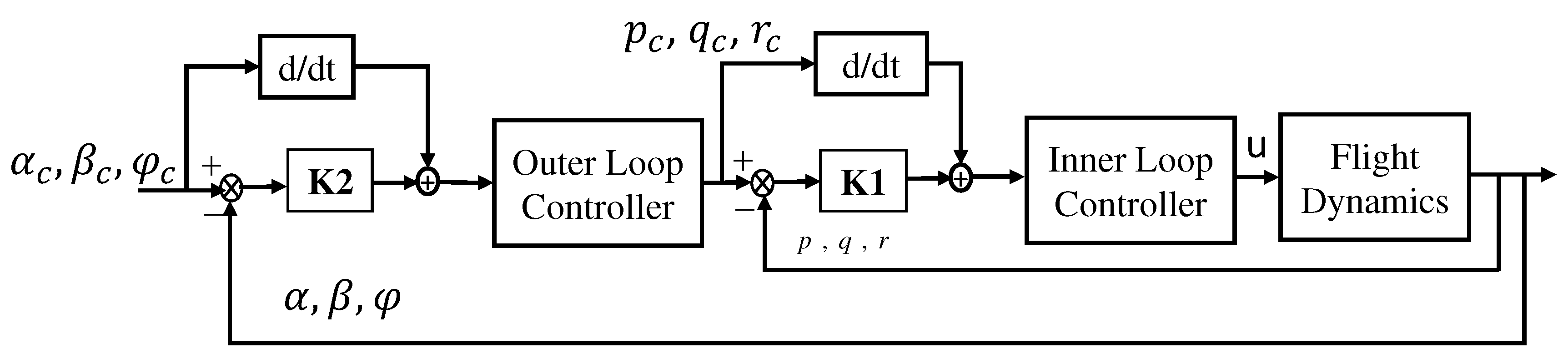
- Feedback linearization approach is employed to achieve the best UAV maneuvers. The most inner loop is the fastest dynamics corresponding to the angular rate states p, q, and r, which are controlled by three inputs: aileron, elevator, and rudder deflections. The consequent outer states , , and are slower than the previous loop, which are controlled by angular rate states p, q, and r. The designed control law guarantees asymptotic stability of the error between the desired states and the current one. The premise of this approach is that there is a significant execution time between the inner fast states and the outer slow states in the open-loop plant.
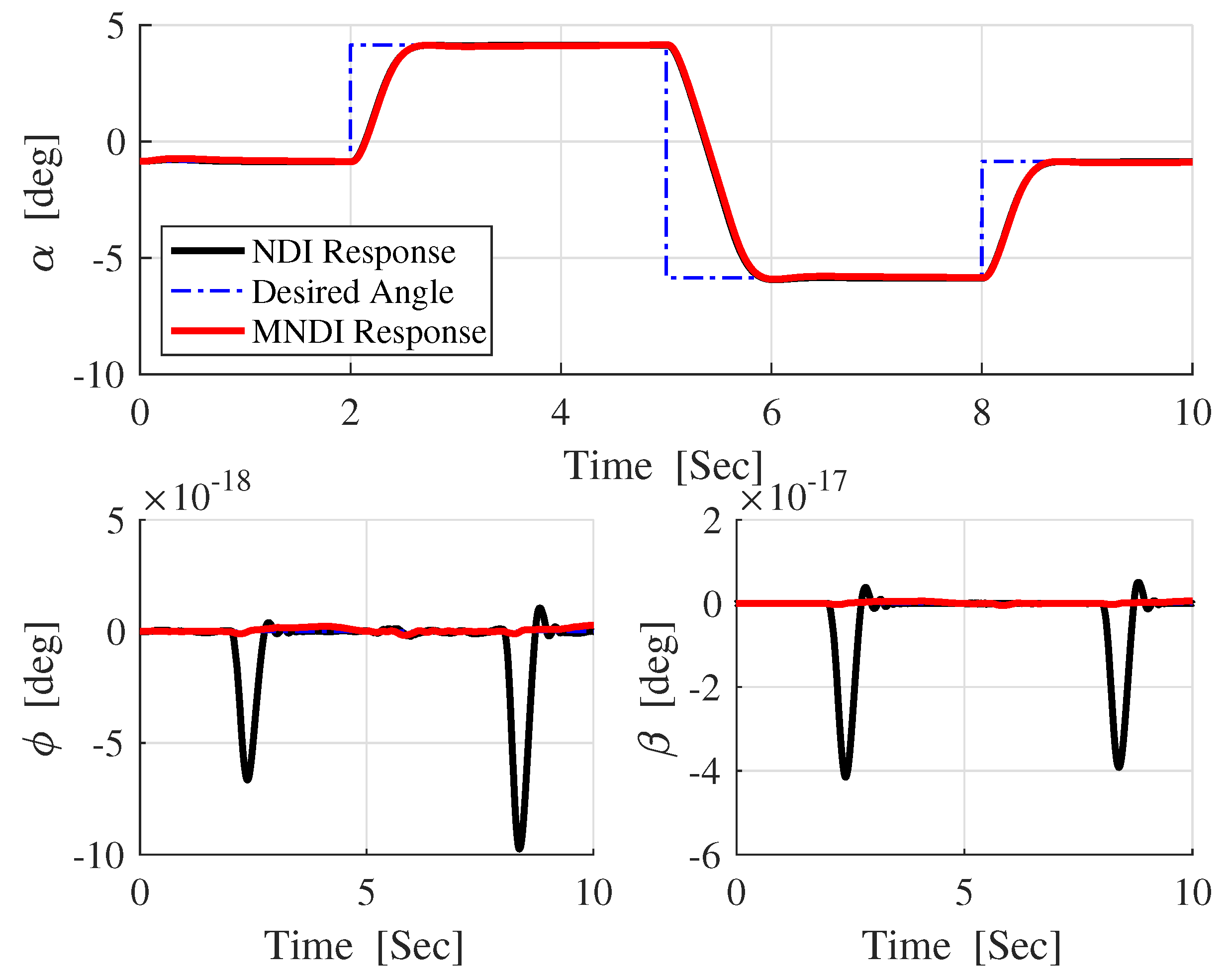
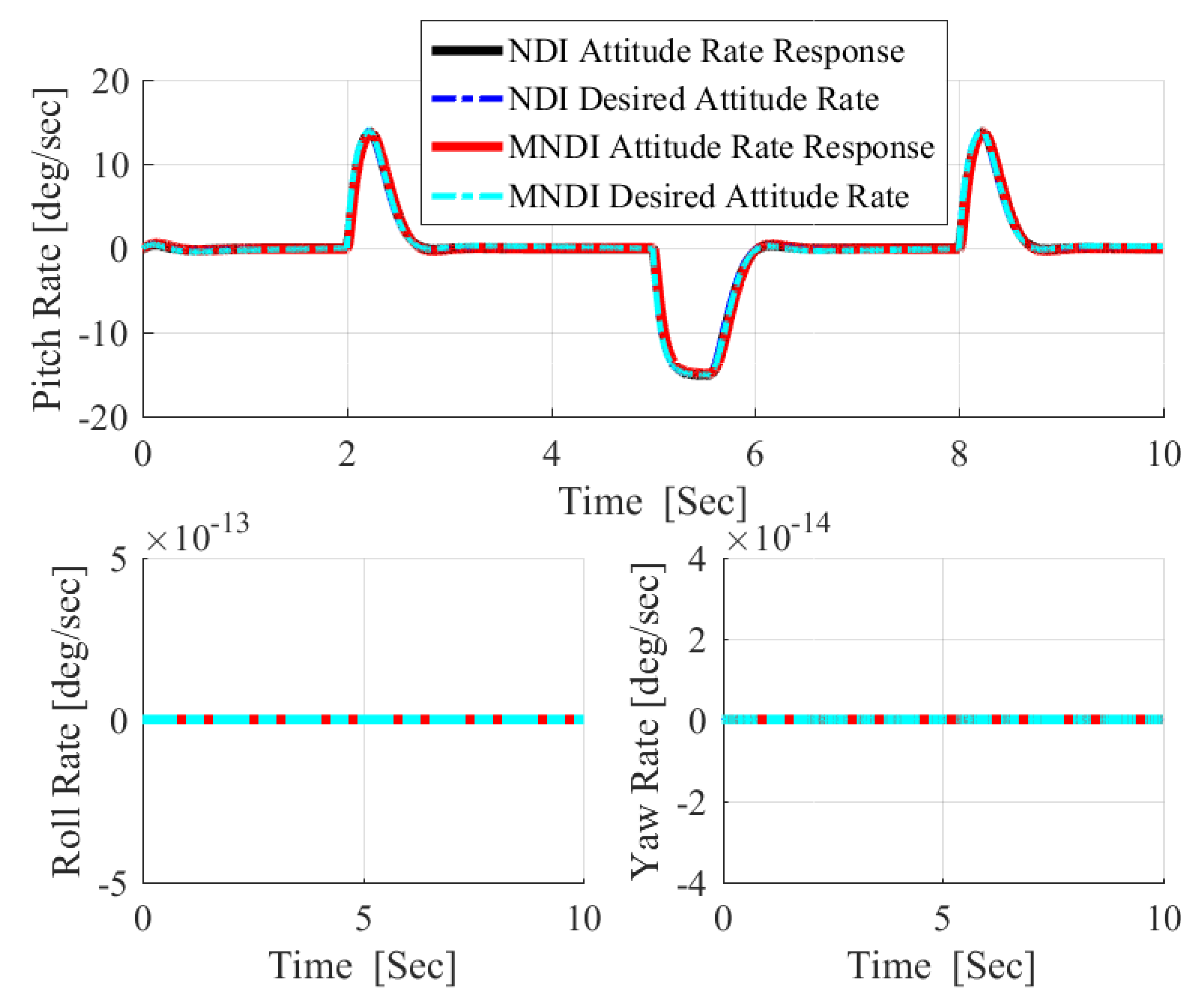
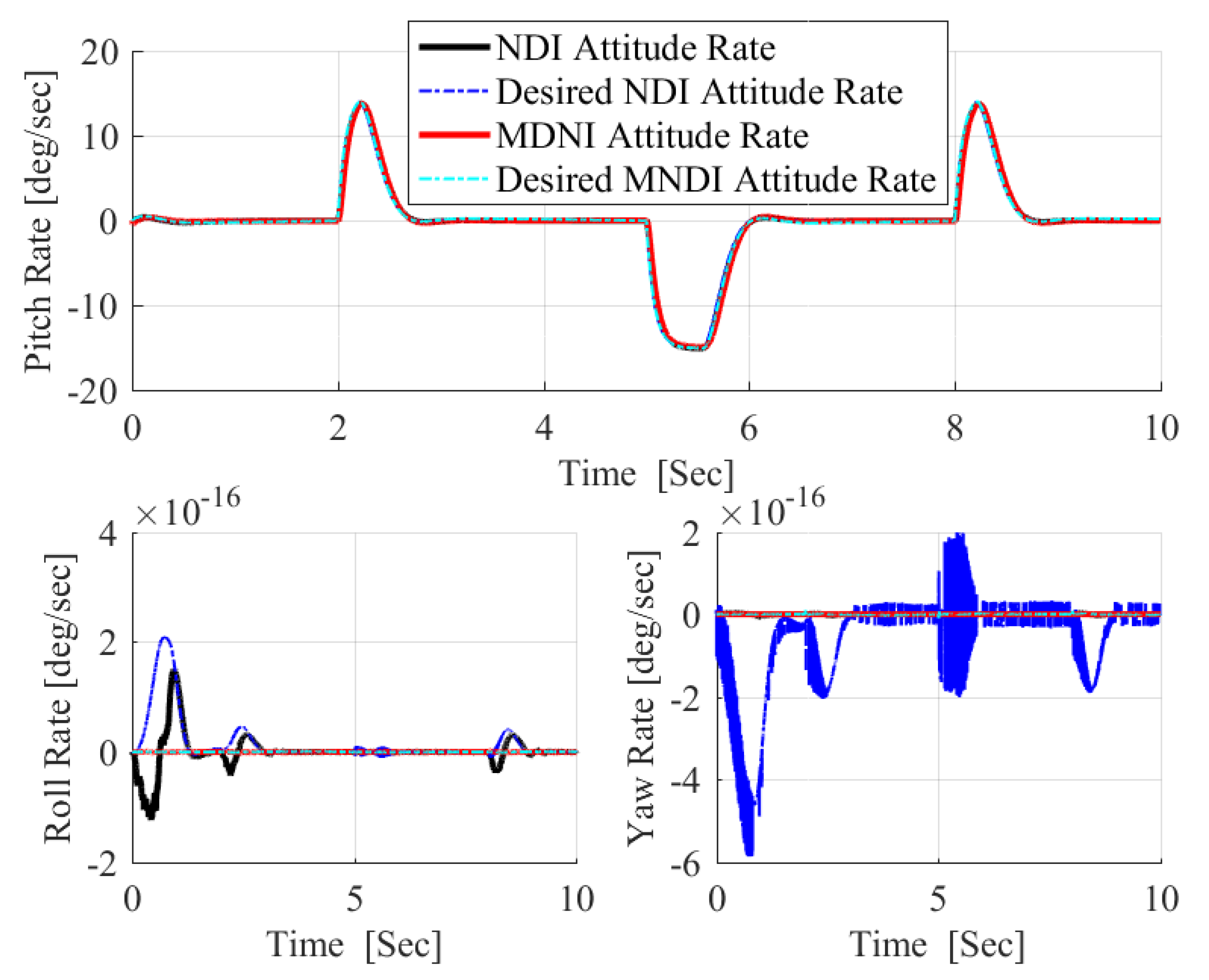
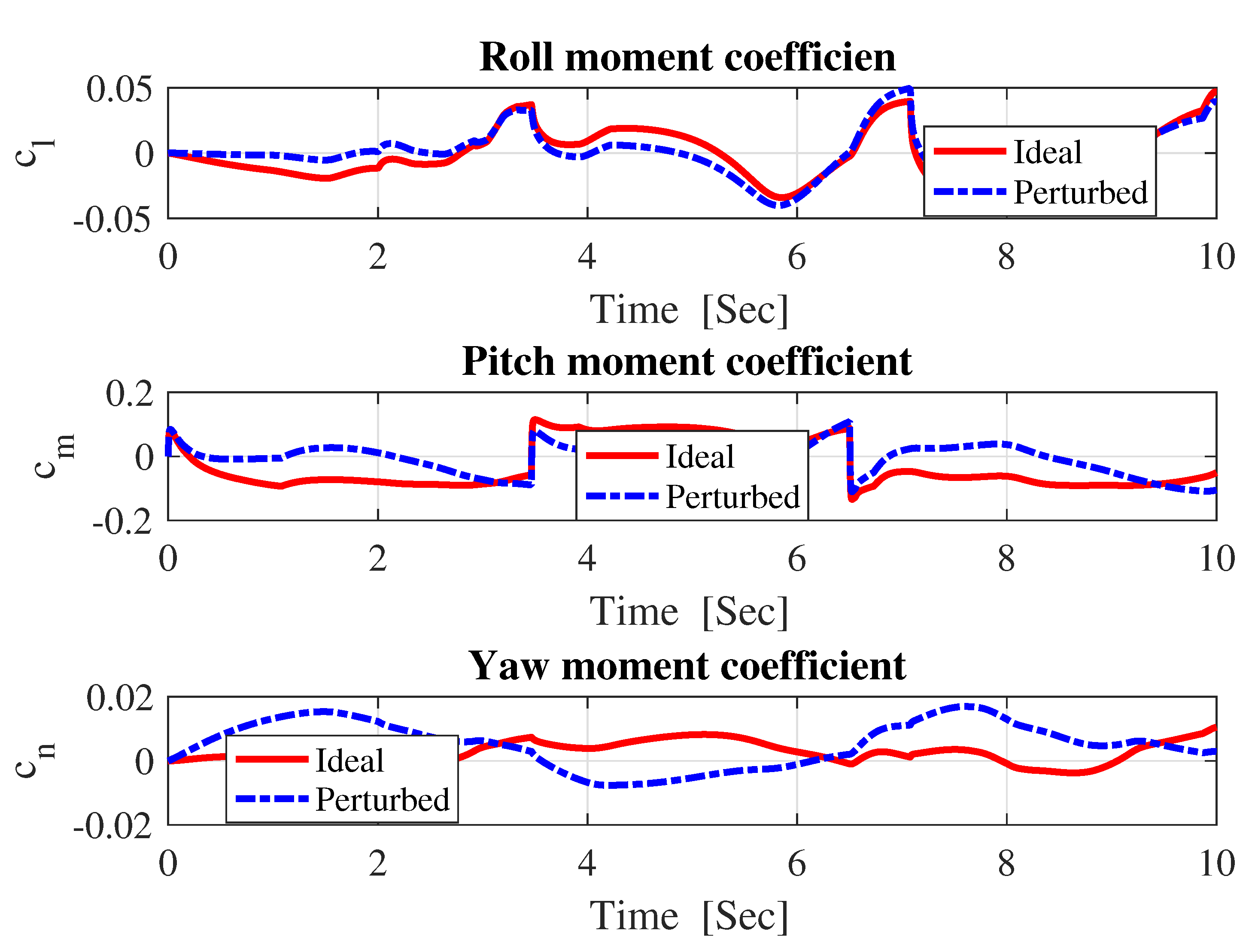
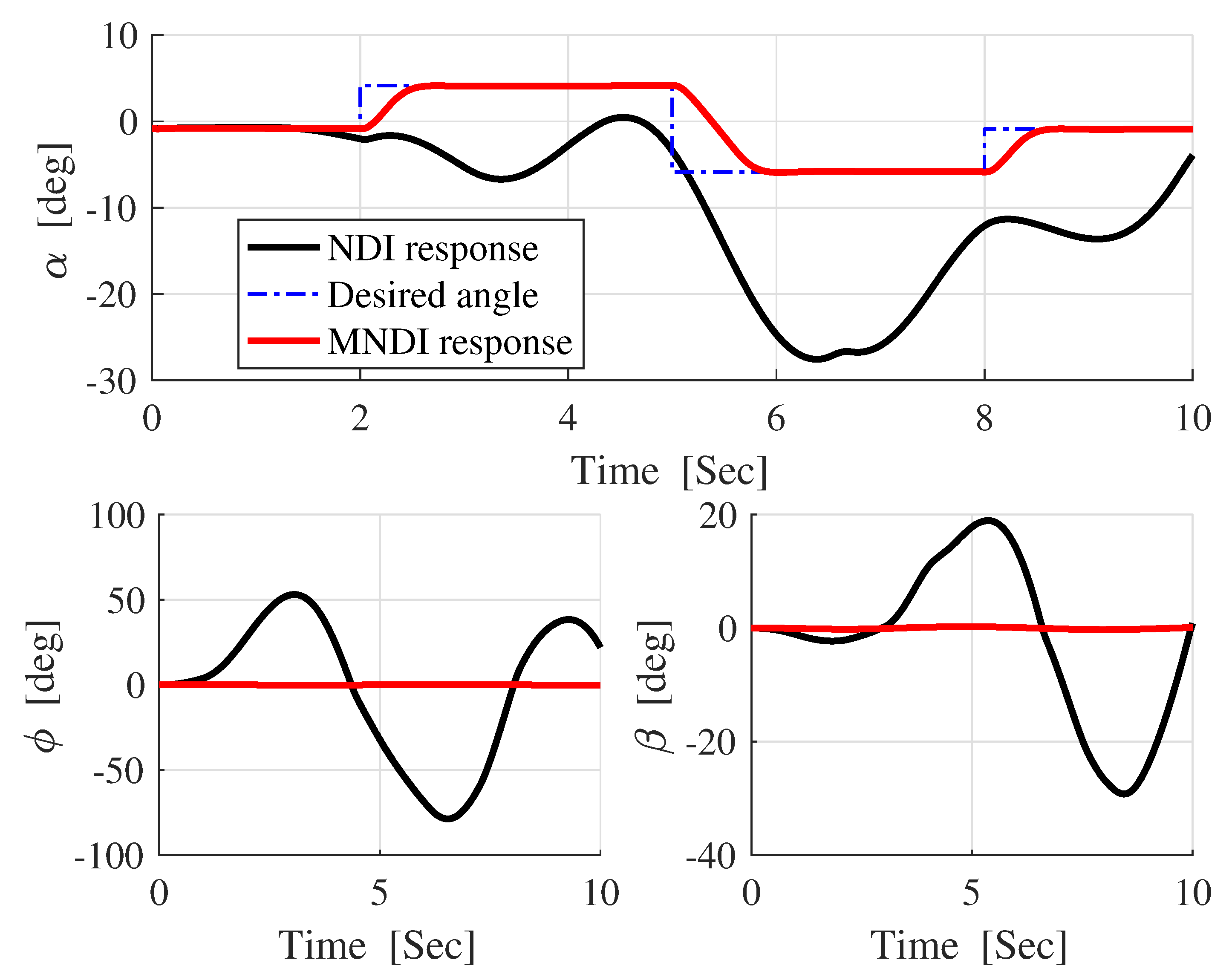
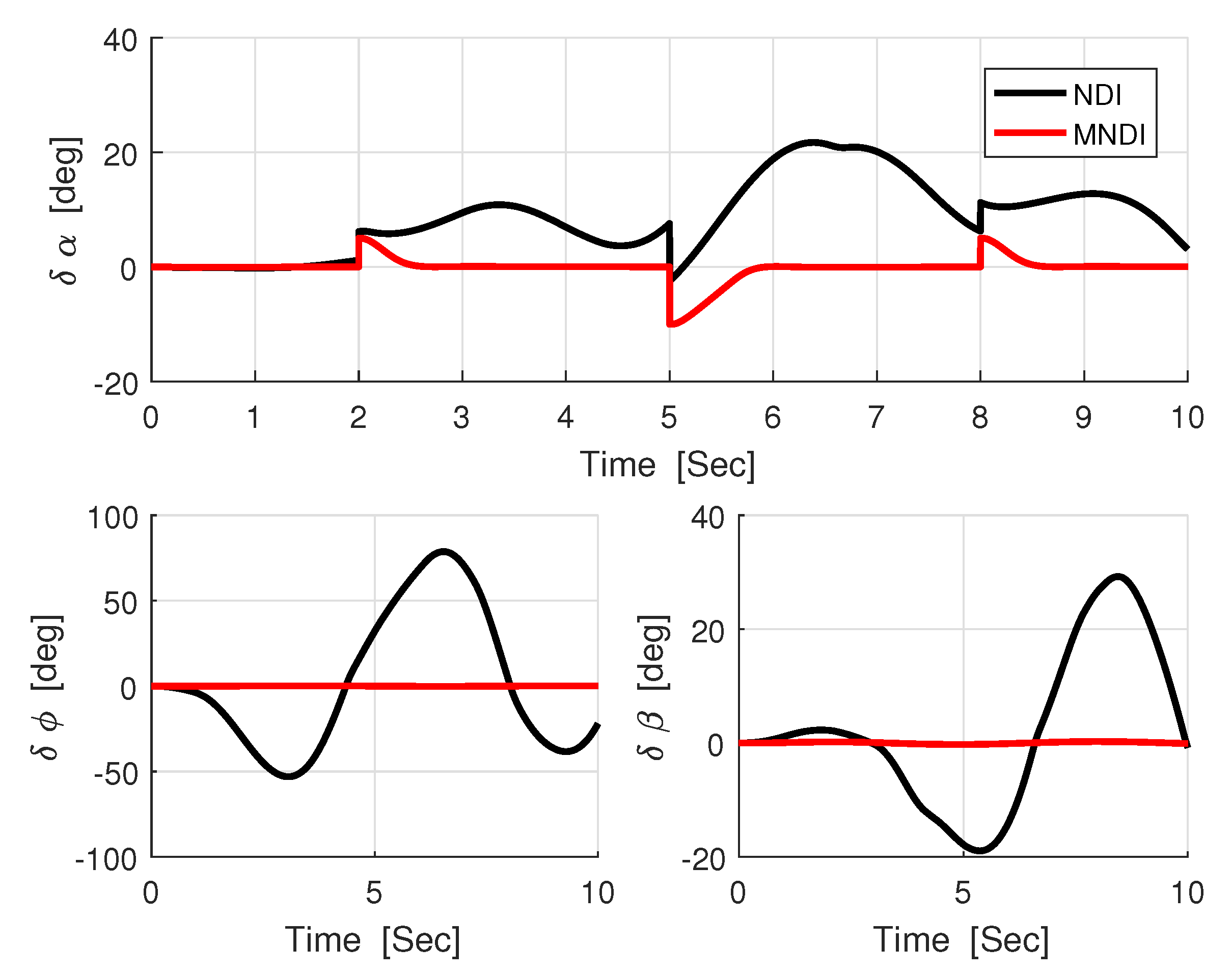
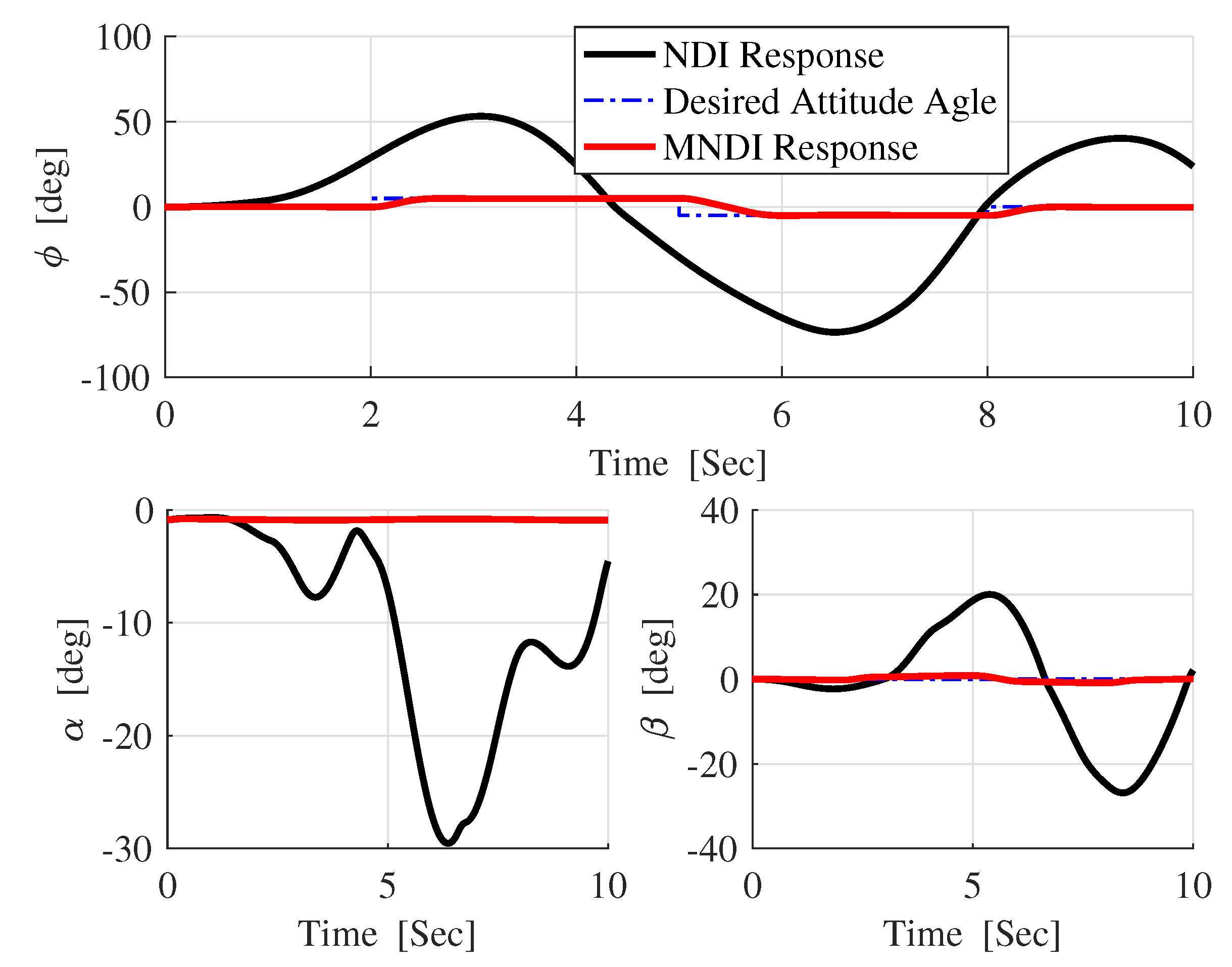
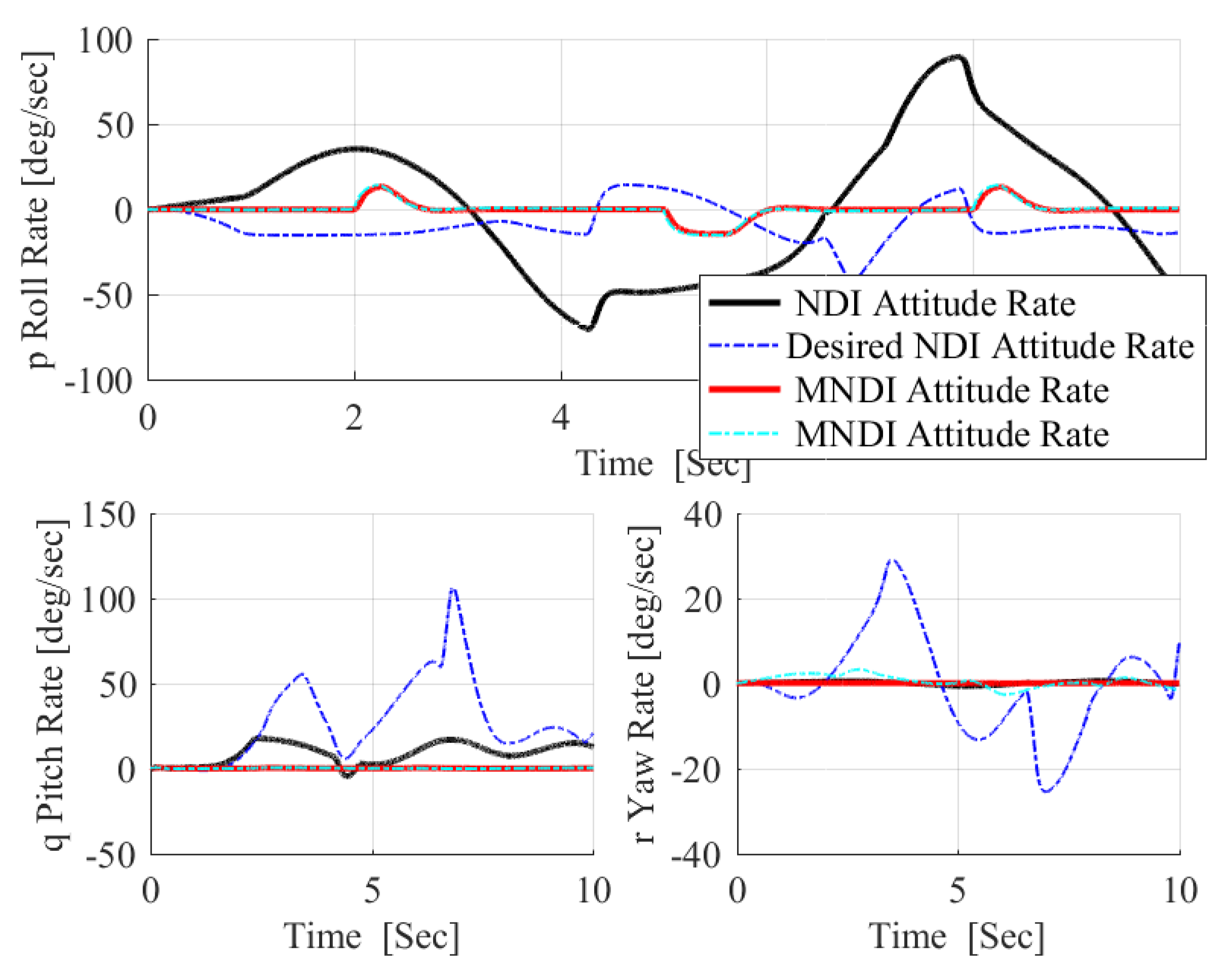
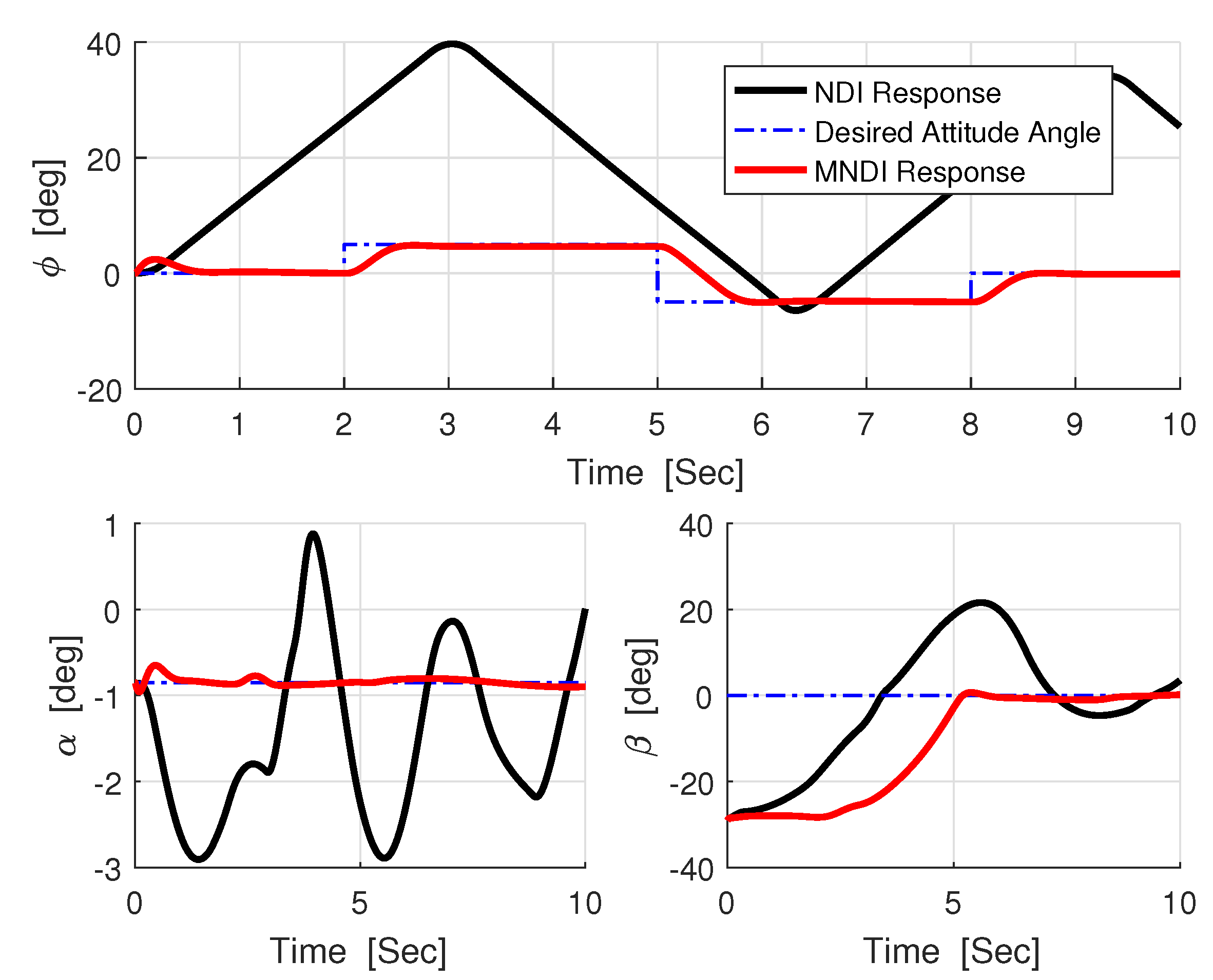
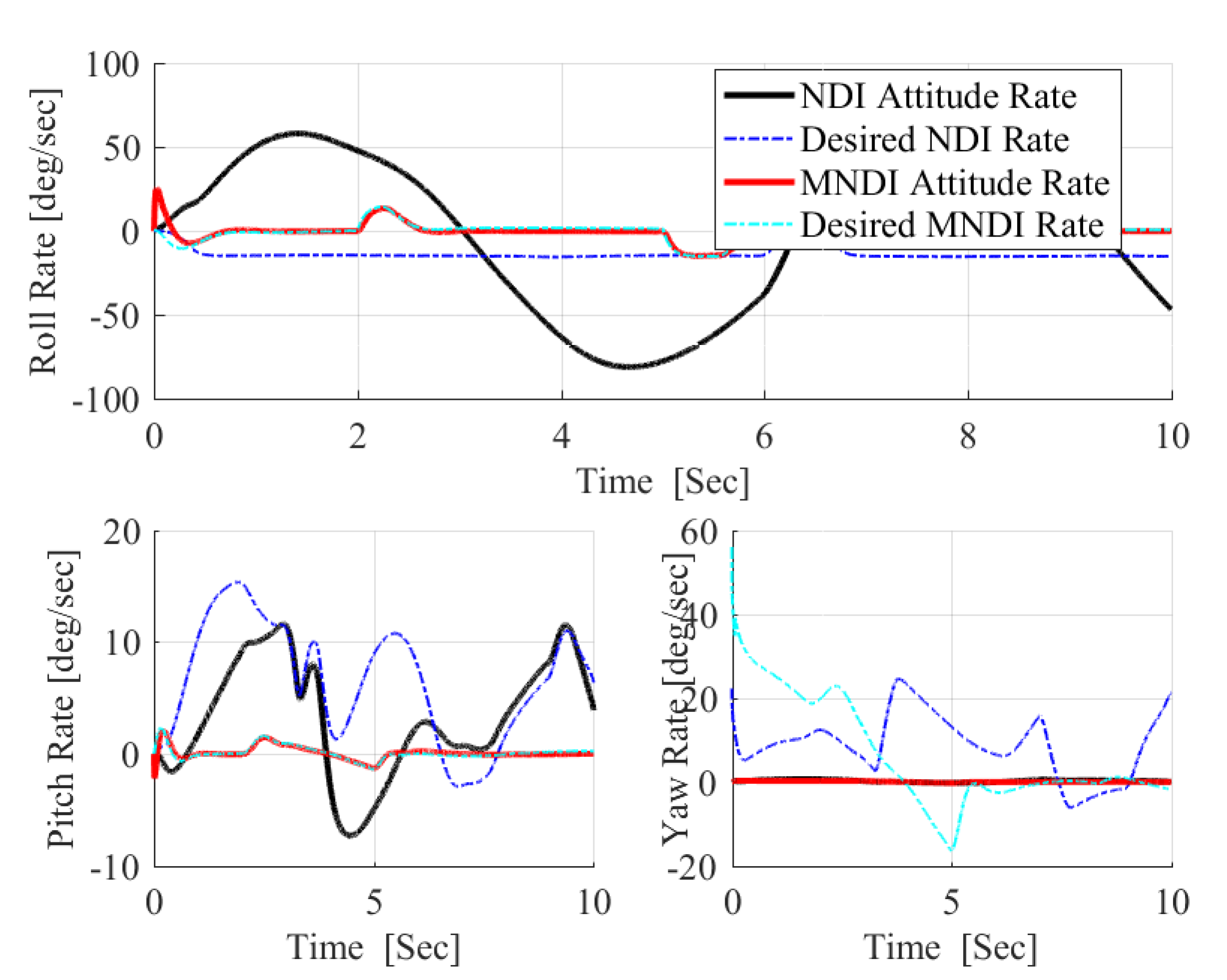
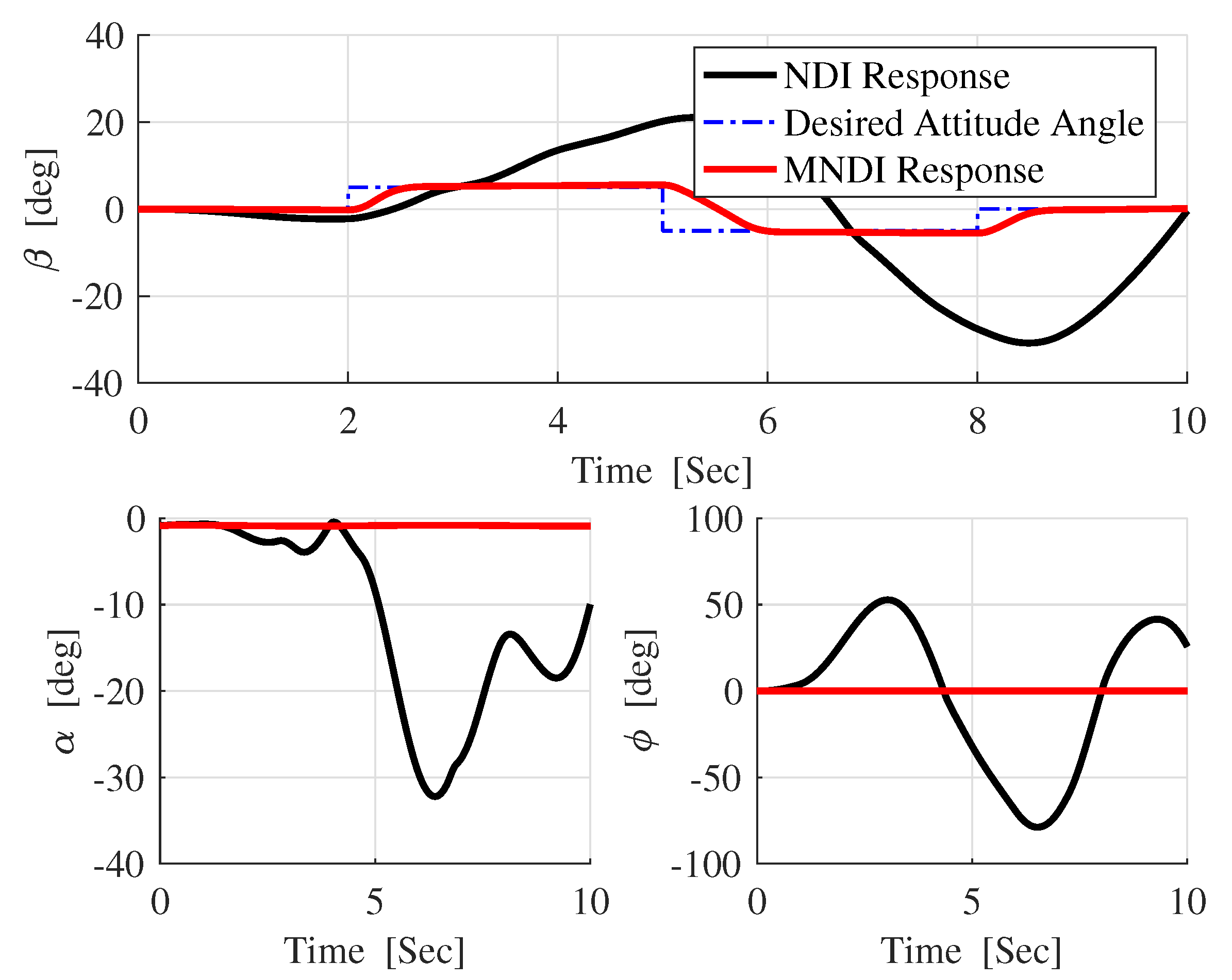
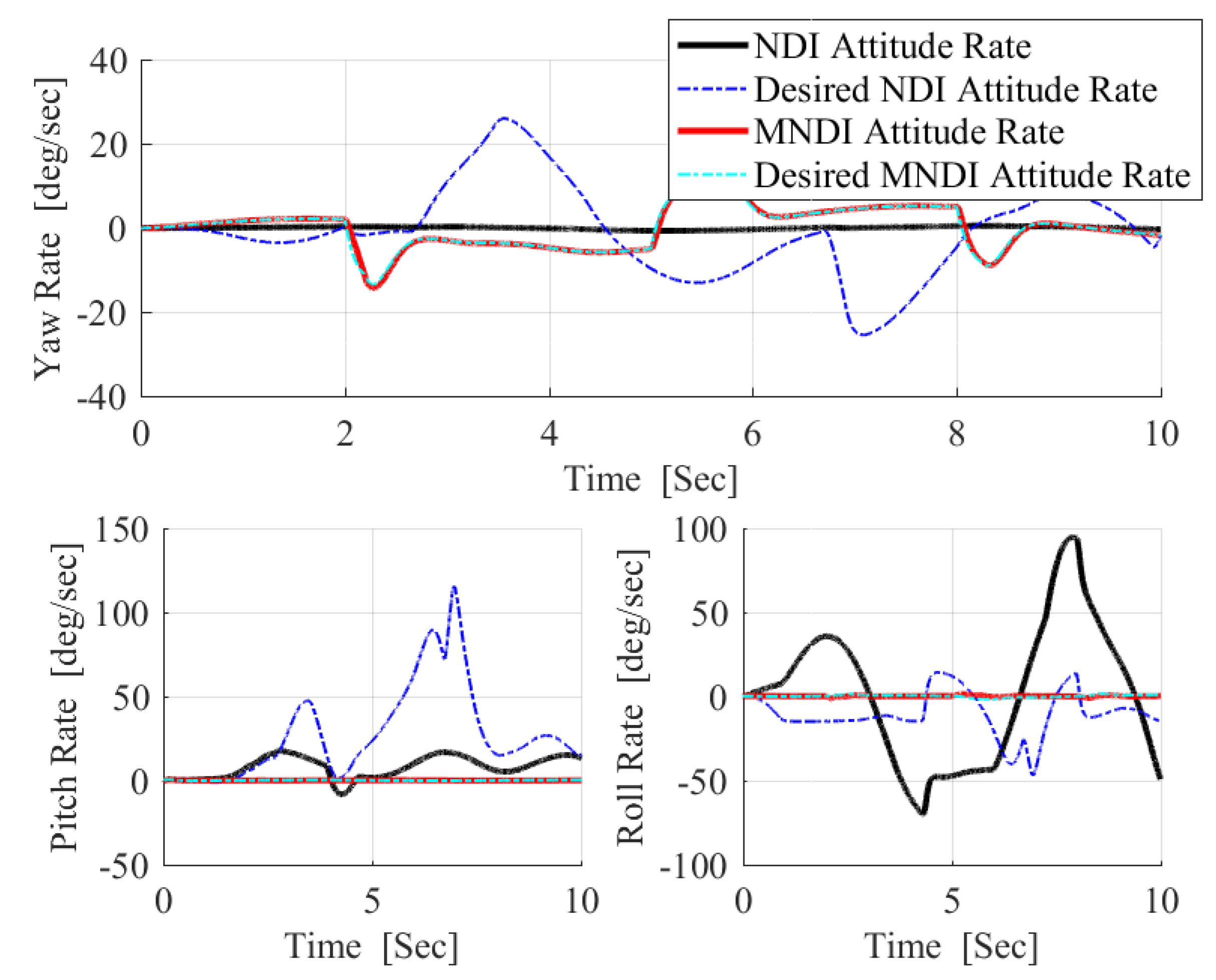
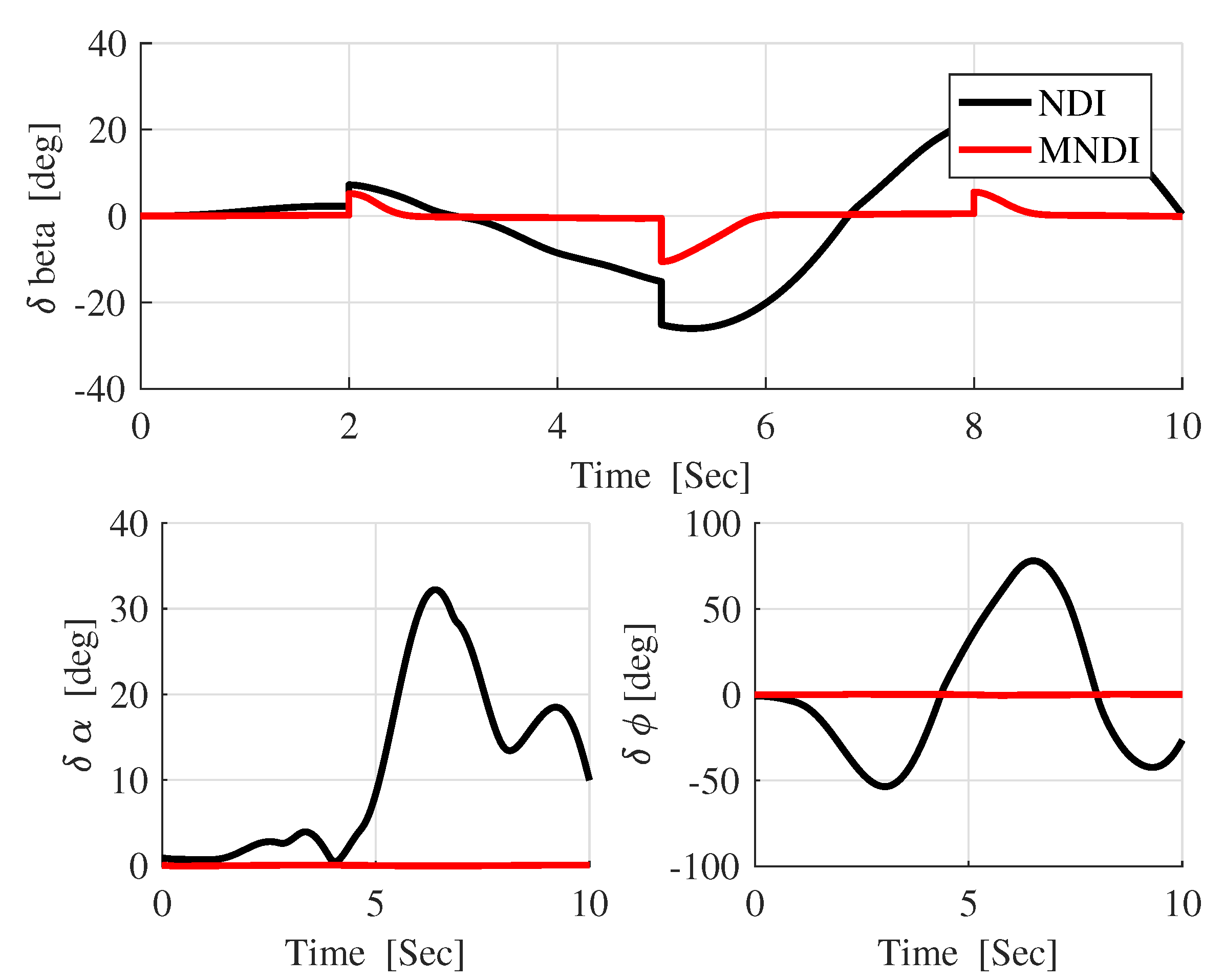
- The most critical task for the flight control system is to maintain flight stability under uncertainties and perturbed conditions. In fixed-wing UAV system, altitude and attitude angles , , and are playing a vital role for flight stabilization. However, NLDI is a model-dependent flight controller, which means it is prone to any small system variations. In this paper, a new modification on NLDI incorporates all uncertainties that increases the system robustness against the model mismatch.
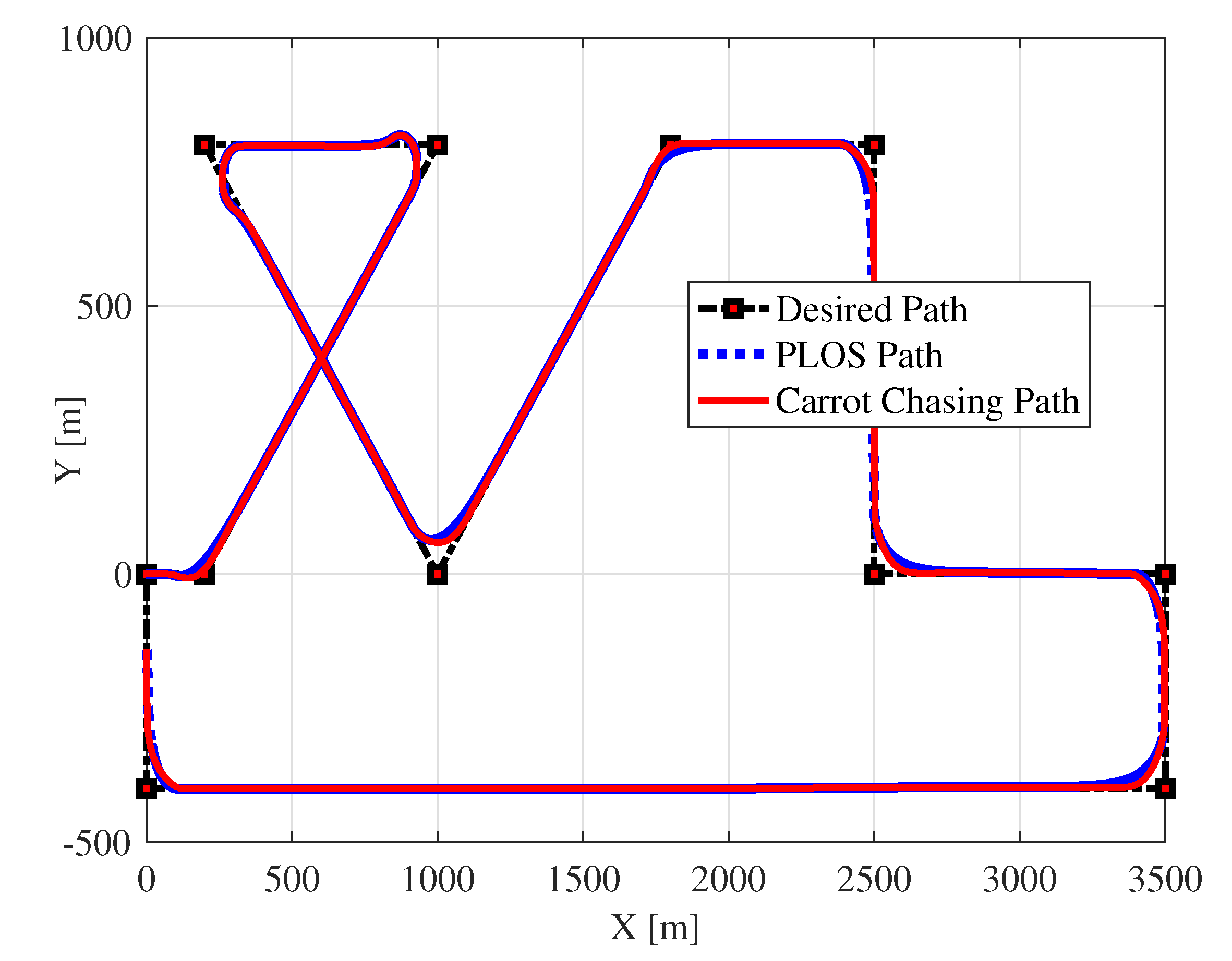
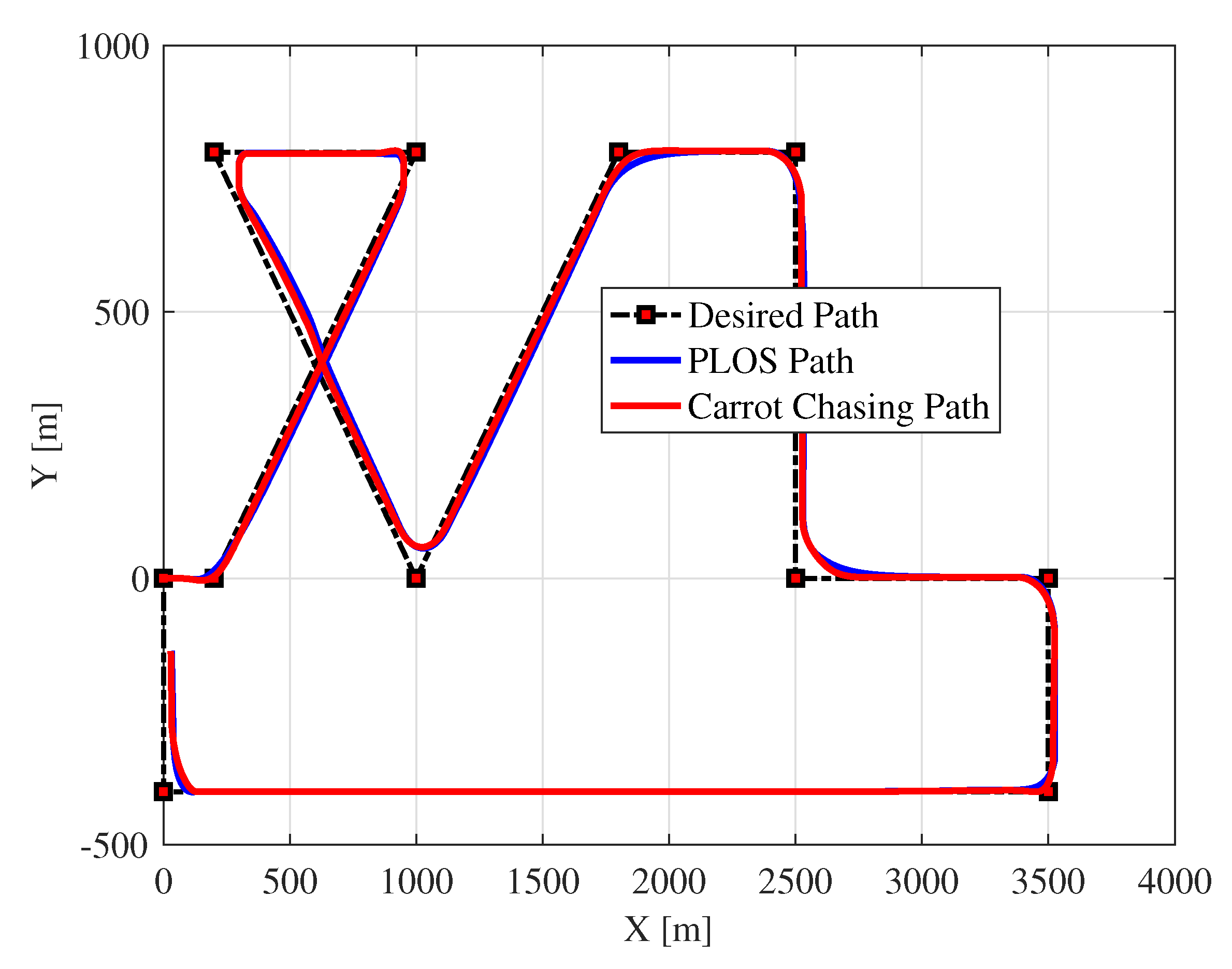
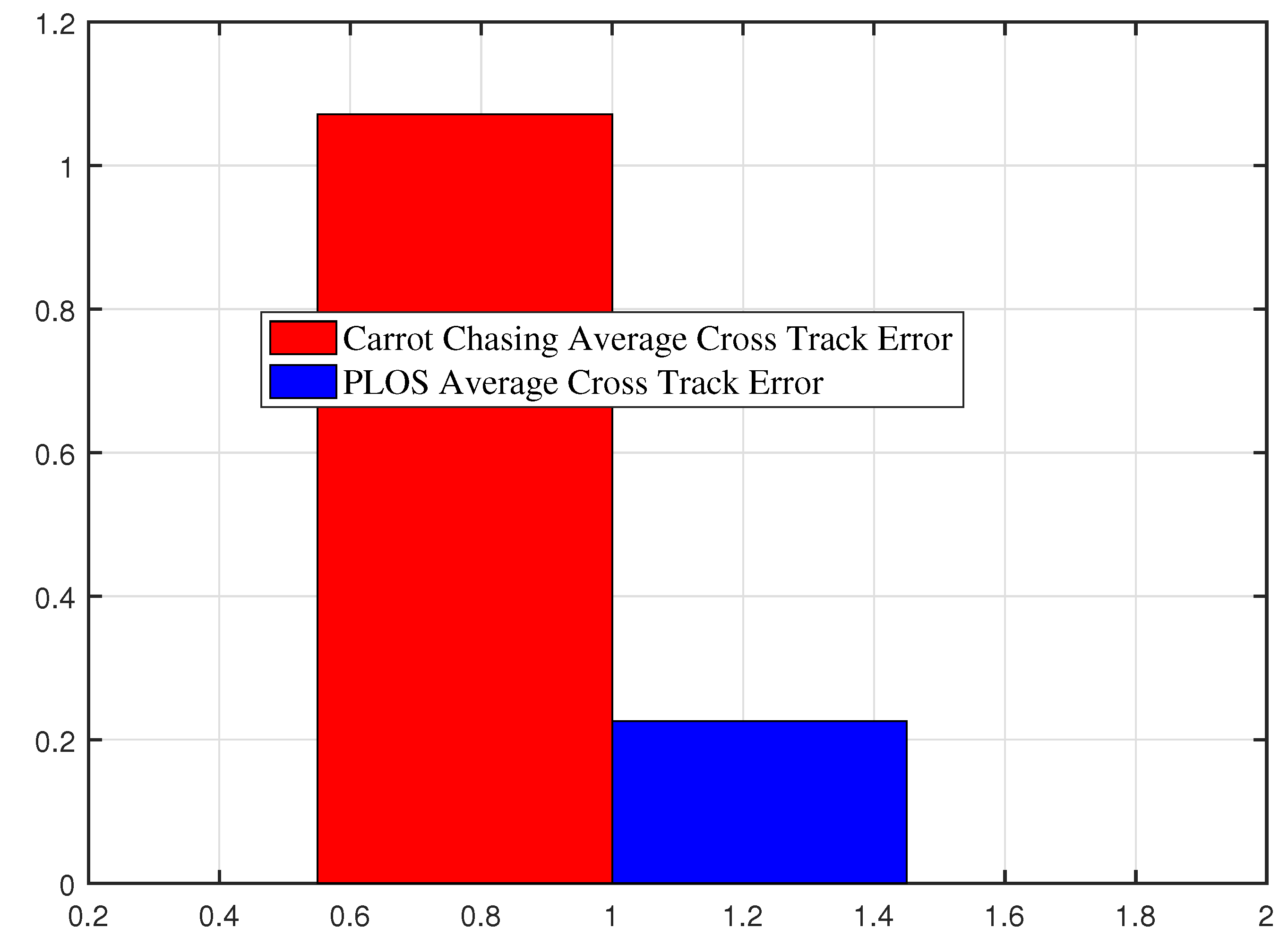
- The study presented in this research is to compare and analyze two common paths following algorithms for UAV. The concept of path following based on carrot chasing is to track a virtual target point sliding along the line of sight between two consequent waypoints. After each time updating, the UAV gets closer to the path and asymptotically follows the path. On the other hand, the concept of Pure pursuit and line-of-sight (PLOS) path following algorithm vanishes the cross-track error distance using LOS control law, in addition to eliminating the LOS angle error using pure pursuit guidance law.
2. Guidance Law Formulation
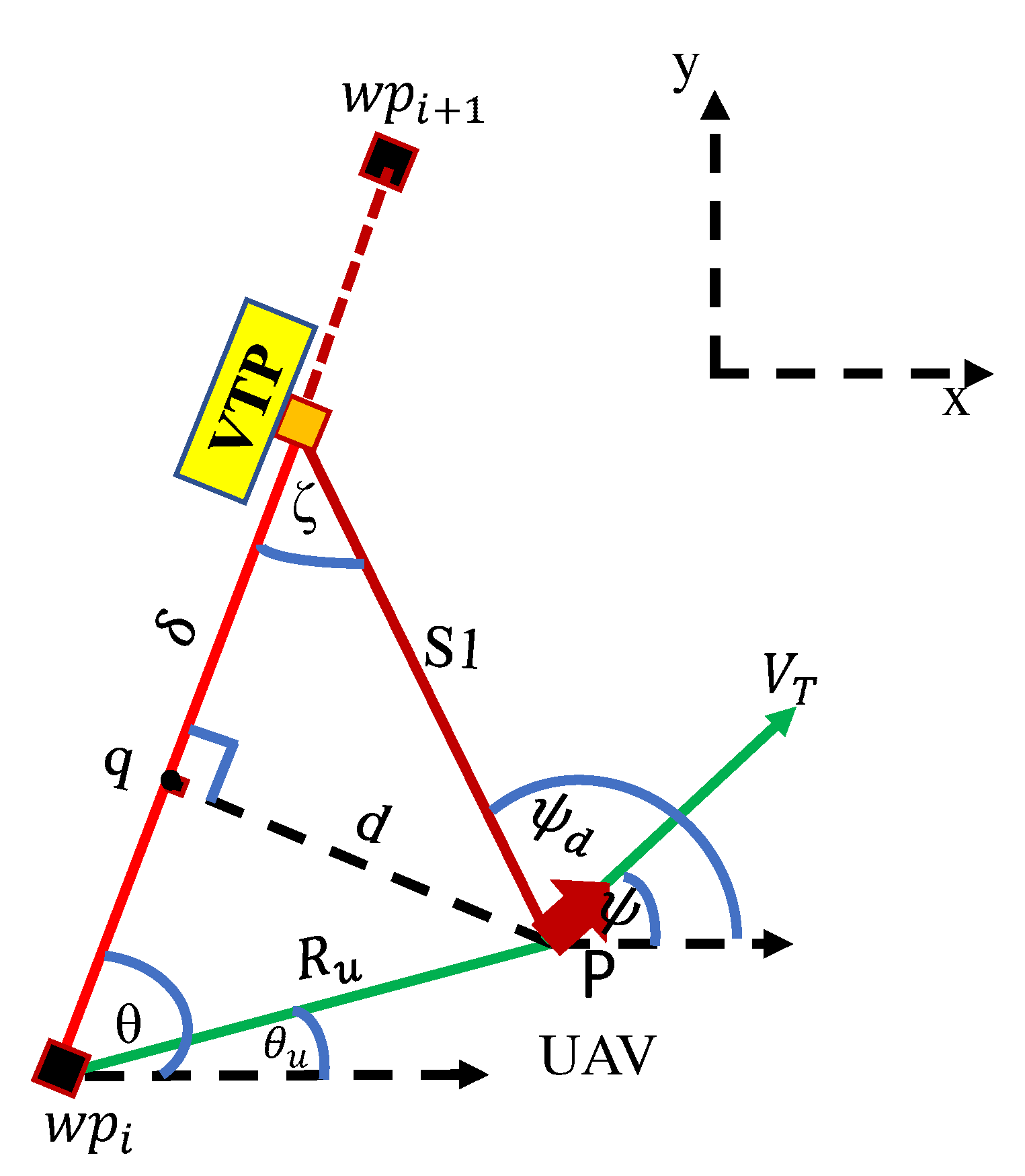
2.1. Problem Description
2.2. Carrot Chasing Guidance Algorithm
- Initialize the waypoints , , UAV current position , and the path parameter .
- Calculate the LOS angle .
- Calculate the angle between the current position p and the previous waypoint .
- Calculate the distance between the current position p and the next waypoint .
- Calculate the distance between the UAV current position p and the VTP .
- Calculate the cross-track error angle .
- Calculate the desired heading angle .
- Calculate the current miss distance S according to desired waypoint radius r.
- Calculate the desired guidance law , which represents the desired bank angle for UAV with airspeed .
2.3. Pure Pursuit and LOS Guidance Algorithm
- Initialize the waypoints vector , , UAV current position , and the path parameter .
- Calculate the LOS angle .
- Calculate the distance between the current position p and the next waypoint .
- Calculate the cross-track error distance .
- Calculate the current miss distance S according to desired waypoint radius r.
- Calculate the desired guidance law , which represents the desired bank angle.
3. Nonlinear Dynamic Inversion Control Law
3.1. Inner Fast Loop
3.2. Outer Slow Loop
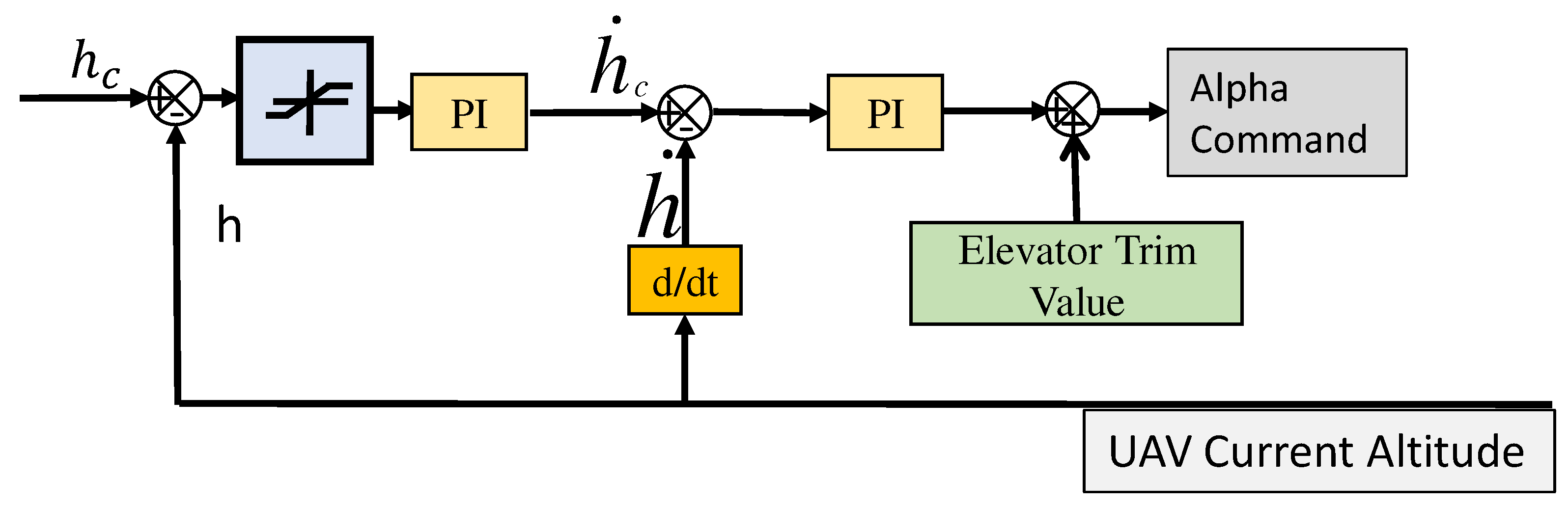
3.3. Altitude Control Loop
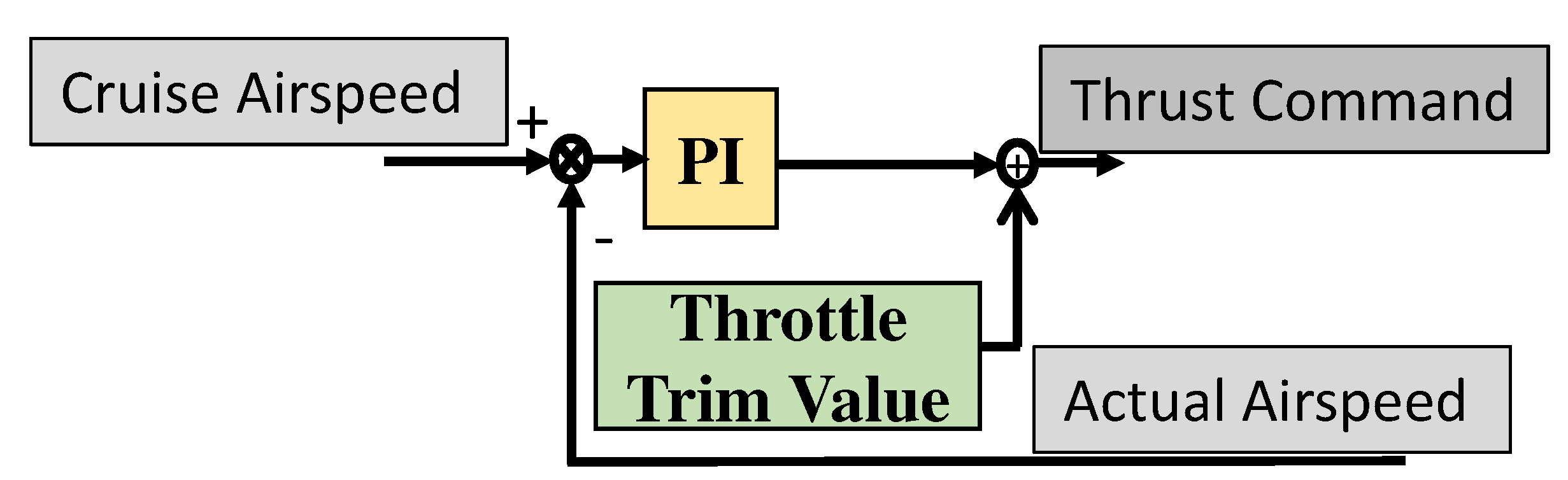
3.4. UAV Speed Control Loop
4. Modified NLDI
5. Results and Discussion
5.1. Robustness Analysis with NLDI and MNLDI
5.2. Evaluation of Two UAV Path Following Algorithms
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nelson, D.R.; Barber, D.B.; McLain, T.W.; Beard, R.W. Vector Field Path Following for Miniature Air Vehicles. IEEE Trans. Robot. 2007, 23, 519–529. [Google Scholar] [CrossRef] [Green Version]
- Patel, M.; Jernigan, S.; Richardson, R.; Ferguson, S.; Buckner, G. Autonomous Robotics for Identification and Management of Invasive Aquatic Plant Species. Appl. Sci. 2019, 9, 2410. [Google Scholar] [CrossRef]
- Kaminer, I.; Pascoal, A.; Hallberg, E.; Silvestre, C. Trajectory tracking for autonomous vehicles: An integrated approach to guidance and control. J. Guid. Control. Dyn. A Publ. Am. Inst. Aeronaut. Astronaut. Devoted Technol. Dyn. Control 1998, 21, 29–38. [Google Scholar] [CrossRef]
- Sujit, P.B.; Saripalli, S.; Sousa, J.B. Unmanned Aerial Vehicle Path Following: A Survey and Analysis of Algorithms for Fixed-Wing Unmanned Aerial Vehicless. IEEE Control Syst. 2014, 34, 42–59. [Google Scholar]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive Sliding Mode Trajectory Tracking Control for Unmanned Surface Vehicle with Modeling Uncertainties and Input Saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Enomoto, K.; Yamasaki, T.; Takano, H.; Baba, Y. Guidance and Control System Design for Chase UAV. AIAA Guid. Navig. Control Conf. Exhib. 2013, 976–984. [Google Scholar] [CrossRef]
- Ambrosino, G.; Ariola, M.; Ciniglio, U.; Corraro, F.; De Lellis, E.; Pironti, A. Path Generation and Tracking in 3-D for UAVs. IEEE Trans. Control Syst. Technol. 2009, 17, 980–988. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J.P. Performance and lyapunov stability of a nonlinear path-following guidance method. IEEE J. Guid. Control Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Sujit, P.B.; Saripalli, S.; Sousa, J.B. An evaluation of UAV path following algorithms. In Proceedings of the 2013 European Control Conference, Zurich, Switzerland, 17–19 July 2013; pp. 3332–3337. [Google Scholar]
- Mori, K.; Takahashi, M. Minimum-Time Attitude Maneuver and Robust Attitude Control of Small Satellite Mounted with Data Relay Communication Antenna. Appl. Sci. 2019, 9, 1001. [Google Scholar] [CrossRef]
- Sun, M.; Zhu, R.; Yang, X. UAV Path Generation, Path Following and Gimbal Control. In Proceedings of the 2008 IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 870–873. [Google Scholar]
- Rhee, I.; Park, S.; Ryoo, C.-K. A tight path following algorithm of an UAS based on PID control. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010. [Google Scholar]
- Cunha, R.; Silvestre, C.; Pascoal, A. A path following controller for model-scale helicopters. In Proceedings of the European Control Conference (ECC), Cambridge, UK, 1–4 September 2003; pp. 2248–2253. [Google Scholar]
- Ratnoo, A.; Sujit, P.B.; Kothari, M. Adaptive Optimal Path Following for High Wind Flights. IFAC Proc. Vol. 2011, 44, 12985–12990. [Google Scholar] [CrossRef] [Green Version]
- Niu, H.; Lu, Y.; Savvaris, A.; Tsourdos, A. Efficient path following algorithm for unmanned surface vehicle. Oceans 2016. [Google Scholar] [CrossRef]
- Kothari, M.; Postlethwaite, I. A Probabilistically Robust Path Planning Algorithm for UAVs Using Rapidly-Exploring Random Trees. J. Intell. Robot. Syst. 2013, 71, 231–253. [Google Scholar] [CrossRef]
- Slotine, J.-J.E.; Li, W.P. Applied Nonlinear Control; United States Edition; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Tran, D.-T.; Truong, H.-V.-A.; Ahn, K.K. Adaptive Backstepping Sliding Mode Control Based RBFNN for a Hydraulic Manipulator Including Actuator Dynamics. Appl. Sci. 2019, 6, 1265. [Google Scholar] [CrossRef]
- Snell, S.A.; Nns, D.F.; Arrard, W.L. Nonlinear inversion flight control for a supermaneuverable aircraft. J. Guid. Control. Dyn. 1992, 15, 976–984. [Google Scholar] [CrossRef]
- Kamal, A.M.; Bayoumy, A.M.; Elshabka, A.M. Modeling and flight simulation of unmanned aerial vehicle enhanced with fine tuning. Aerosp. Sci. Technol. 2016, 51, 106–117. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safwat, E.; Zhang, W.; Mohsen, A.; Kassem, M. Design and Analysis of a Robust UAV Flight Guidance and Control System Based on a Modified Nonlinear Dynamic Inversion. Appl. Sci. 2019, 9, 3600. https://doi.org/10.3390/app9173600
Safwat E, Zhang W, Mohsen A, Kassem M. Design and Analysis of a Robust UAV Flight Guidance and Control System Based on a Modified Nonlinear Dynamic Inversion. Applied Sciences. 2019; 9(17):3600. https://doi.org/10.3390/app9173600
Chicago/Turabian StyleSafwat, Ehab, Weiguo Zhang, Ahmed Mohsen, and Mohamed Kassem. 2019. "Design and Analysis of a Robust UAV Flight Guidance and Control System Based on a Modified Nonlinear Dynamic Inversion" Applied Sciences 9, no. 17: 3600. https://doi.org/10.3390/app9173600
APA StyleSafwat, E., Zhang, W., Mohsen, A., & Kassem, M. (2019). Design and Analysis of a Robust UAV Flight Guidance and Control System Based on a Modified Nonlinear Dynamic Inversion. Applied Sciences, 9(17), 3600. https://doi.org/10.3390/app9173600




