Reliable Method to Detect Alloy Soldering Fractures under Accelerated Life Test
Abstract
:1. Introduction
Objective
2. Soldering Alloy
3. Accelerated Life Test (ALT)
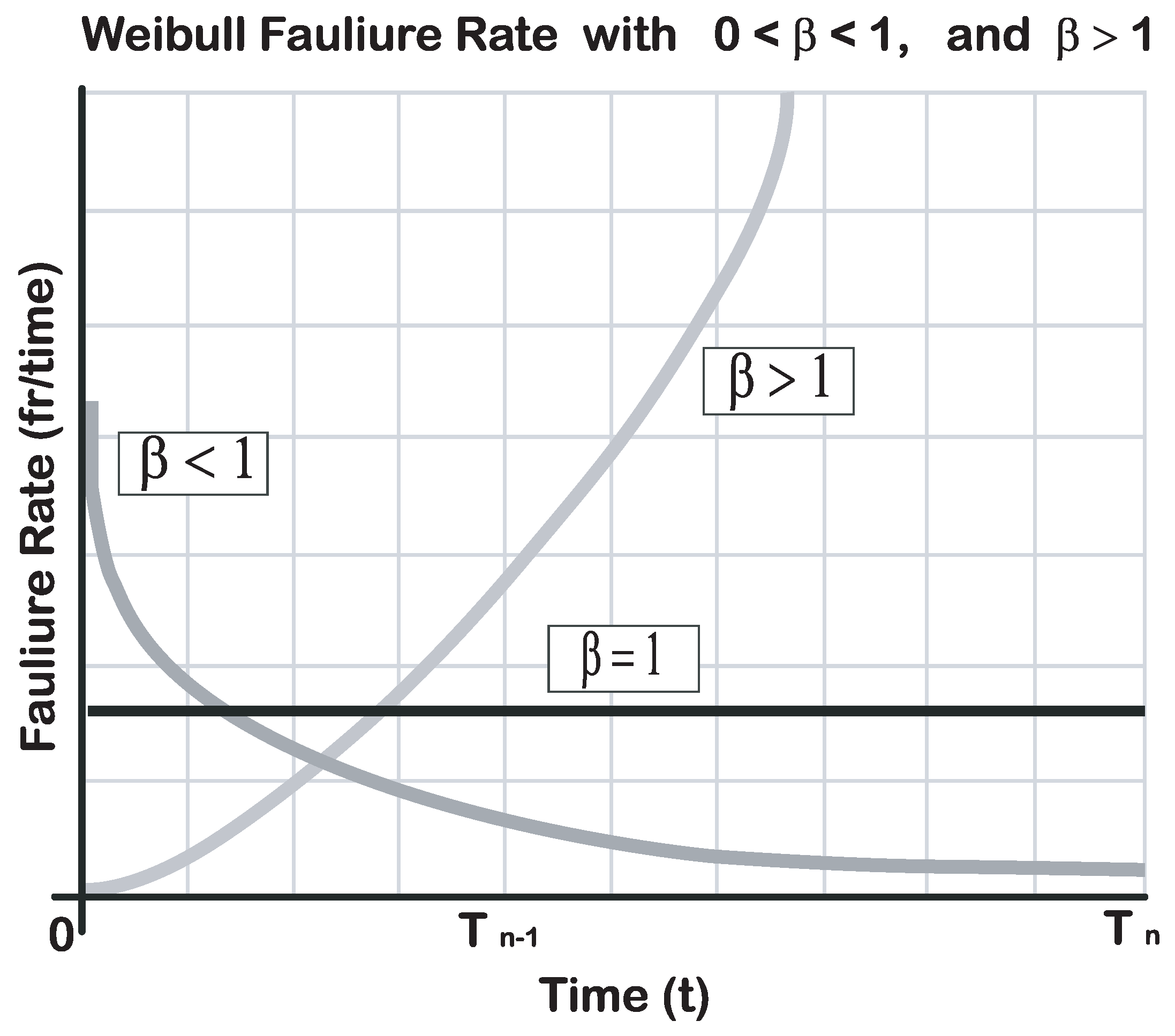
4. Reliability Model
- = Failure rate
- = Instantaneous failure speed function
- = Failure rate.
- = Average of units examined.
- is the risk rate decrease.
- is the remaining life of a stable system, and the failures are random.
- the risk rate increase indicating that the product is in the wear region.
5. Methodology
- = pre-exponential factor or frequency factor.
- k = kinetic constant Boltzmann’s constant (physical constant that relates absolute temperature and energy).
- = activation energy.
- = Field-use temperature
- = Accelerated test temperature.
6. Results
- = Degrees of freedom. Number of values that can be assigned arbitrarily, before the rest of the variables automatically take a value.
- = Sum of squares, represents a measure of variation or deviation with respect to the mean.
- = Square Medium, are used to determine if the terms of a model are significant.
- = probability corresponding to the test statistic.
- = is a value you get when you run an ANOVA test or a regression analysis to find out if the means between two populations are significantly different.
- = Adjusted Value, indicates which comparisons between the levels of the factors within a family of comparisons are significantly different.
- S = Standard deviation.
- = Coefficient of determination.
- = Adjusted coefficient of determination. Is the percentage of variation in the response variable that is explained by its relation to one or predictor variables, adjusted for the number of predictors in the model.
- = Predetermined coefficient of determination. Adjustments in model looking for an approach in the desired values.
- = There is a main effect when different levels of a factor affect the response differently.
- = Coefficient of determination.
- = The standard error of the coefficient estimates the variability between the coefficient estimates that would be obtained if the samples were taken from the same population repeatedly. The calculation assumes that the size of the sample and the coefficients to be estimated would remain the same if the sample were taken repeatedly.
- = Measure the relationship between the coefficient and its standard error.
- = probability corresponding to the test statistic.
- = The variance inflation factor indicates how much the variance of a coefficient is inflated due to the correlations among the predictors in the model. Use the VIF to describe how much multicollinearity (which is correlation between predictors) exists in a regression analysis. Multicollinearity is problematic because it can increase the variance of the regression coefficients, making it difficult to evaluate the individual impact that each of the correlated predictors has on the response.
7. Discussion and Conclusions
7.1. Discussion
- The observed degradation (change) is not reversible when tension is removed.
- There is a unique or dominant degradation process that can be studied (POF).
- Any degradation before the start of the accelerated test.
- The determination of the probability of failure, the product under conditions of use, means low life.
- Conditions of use and projected returns and guarantees.
- Costs can also be used to help in the detection of faults and process improvement
- Carrying out risk assessments, design, comparisons, etc.
- Application of Planned Statistical Techniques to expand the designer’s ability to draw conclusions from an ALT;
- Study of strengths and weaknesses in each ALT model presented and cross this study with current practices to determine the best test strategies;
- Reliability management practices, with definition of sequence, importance, allocation of resources and impact of ALT procedures in the product development cycle.
7.2. Conclusions
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| ALT | Accelerated Life Test. |
| MTBF | Mean time between failure. |
| TF | Failure rate. |
| Pre-exponential factor or frequency factor. | |
| Activation energy. | |
| Instantaneous failure speed function | |
| Failure rate | |
| Reliability function or survival function. | |
| Failure rate. | |
| k | Boltzmann’s constant (physical constant that relates absolute temperature and energy. Commonly for an LED 0.7 V is required). |
| Field-use temperature | |
| Accelerated test temperature. | |
| Weibull distribution form parameter | |
| Scale parameter or Weibull distribution life parameter |
References
- McLean, R.S.; Antony, J.; Dahlgaard, J.J. Failure of continuous improvement initiatives in manufacturing environments: A systematic review of the evidence. Total Qual. Manag. Bus. Excell. 2017, 28, 219–237. [Google Scholar] [CrossRef]
- Karppinen, J.; Li, J.; Paulasto-Krockel, M. The effects of concurrent power and vibration loads on the reliability of board-level interconnections in power electronic assemblies. IEEE Trans. Device Mater. Reliab. 2012, 13, 167–176. [Google Scholar] [CrossRef]
- Mattila, T.T.; Li, J.; Kivilahti, J.K. On the effects of temperature on the drop reliability of electronic component boards. Microelectron. Reliab. 2012, 52, 165–179. [Google Scholar] [CrossRef]
- Coit, D.W.; Evans, J.L.; Vogt, N.T.; Thompson, J.R. A method for correlating field life degradation with reliability prediction for electronic modules. Qual. Reliab. Eng. Int. 2005, 21, 715–726. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Sangwongwanich, A.; Blaabjerg, F. Design for reliability of power electronic systems. In Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2018; pp. 1423–1440. [Google Scholar]
- Parish, C.M.; Kumar, N.K.; Snead, L.L.; Edmondson, P.D.; Field, K.G.; Silva, C.; Williams, A.M.; Linton, K.; Leonard, K.J. LAMDA: Irradiated-materials microscopy at Oak Ridge National Laboratory. Microsc. Microanal. 2015, 21, 1003–1004. [Google Scholar] [CrossRef]
- Li, Y.; Xie, Y.; Chen, R.; Han, L.; Chen, D.; Su, H. A multilayer power inductor fabricated by cofirable ceramic/ferrite materials with LTCC technology. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1402–1409. [Google Scholar] [CrossRef]
- Wu, P.; Guo, L.; Lou, S.; Gao, J. Local and Global Randomized Principal Component Analysis for Nonlinear Process Monitoring. IEEE Access 2019, 7, 25547–25562. [Google Scholar] [CrossRef]
- Kadanoff, L.P. Quantum Statistical Mechanics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ruiz, C.; Liao, H.; Pohl, E.; Sullivan, K.M. Bayesian accelerated reliability growth of complex systems. In Proceedings of the 2018 Annual Reliability and Maintainability Symposium (RAMS), Reno, NV, USA, 22–25 January 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Canakci, A.; Erdemir, F.; Varol, T.; Patir, A. Determining the effect of process parameters on particle size in mechanical milling using the Taguchi method: Measurement and analysis. Measurement 2013, 46, 3532–3540. [Google Scholar] [CrossRef]
- Acevedo, P.E.; Jackson, D.S.; Kotlowitz, R.W. Reliability growth and forecasting for critical hardware through accelerated life testing. Bell Labs Tech. J. 2006, 11, 121–135. [Google Scholar] [CrossRef]
- Regattieri, A.; Casto, A.; Piana, F.; Faccio, M.; Ferrari, E. Reliability prediction of a mechanical component through accelerated life testing. In Proceedings of the 24th International Conference on Production Research (ICPR 2017), Posnan, Poland, 30 July–3 August 2017; p. 10. [Google Scholar]
- Cheng, S.; Huang, C.M.; Pecht, M. A review of lead-free solders for electronics applications. Microelectron. Reliab. 2017, 75, 77–95. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design of Experiments. Stat. Dig. Newsl. ASQ Stat. Div. 2017, 36, 17–22. [Google Scholar]
- Bickford, J.P.; Habib, N.; Li, B.; Nsame, P.A. Semiconductor Device Reliability Model and Methodologies for Use Thereof. U.S. Patent 9,064,087, 23 June 2015. [Google Scholar]
- Su, C.T.; Chou, C.J.; Chen, L.F. Application of six sigma methodology to optimize the performance of the inter-metal dielectric process. IEEE Trans. Semicond. Manuf. 2009, 22, 297–304. [Google Scholar] [CrossRef]
- Albliwi, S.A.; Antony, J.; Lim, S.A.H. A systematic review of Lean Six Sigma for the manufacturing industry. Bus. Process Manag. J. 2015, 21, 665–691. [Google Scholar] [CrossRef]
- Bain, L. Statistical Analysis of Reliability and Life-Testing Models: Theory and Methods; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Chen, H.; Wang, L.; Han, J.; Li, M.; Liu, H. Microstructure, orientation and damage evolution in SnPb, SnAgCu, and mixed solder interconnects under thermomechanical stress. Microelectron. Eng. 2012, 96, 82–91. [Google Scholar] [CrossRef]
- Lou, P.; Yuan, L.; Hu, J.; Yan, J.; Fu, J. A Comprehensive assessment approach to evaluate the trustworthiness of manufacturing services in cloud manufacturing environment. IEEE Access 2018, 6, 30819–30828. [Google Scholar] [CrossRef]
- Lionetto, F.; Mele, C.; Leo, P.; D’Ostuni, S.; Balle, F.; Maffezzoli, A. Ultrasonic spot welding of carbon fiber reinforced epoxy composites to aluminum: Mechanical and electrochemical characterization. Compos. Part B Eng. 2018, 144, 134–142. [Google Scholar] [CrossRef]
- Scrivener, K.; Snellings, R.; Lothenbach, B. A Practical Guide to Microstructural Analysis of Cementitious Materials; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Minitab, Inc. MINITAB. [Computer Program Manual]; Minitab, Inc.: State College, PA, USA, 2014. [Google Scholar]
- Shao, C.; Zhang, P.; Zhu, Y.; Zhang, Z.; Tian, Y.; Zhang, Z. Simultaneous improvement of strength and plasticity: Additional work-hardening from gradient microstructure. Acta Mater. 2018, 145, 413–428. [Google Scholar] [CrossRef]
- West, D.R.F. Ternary Phase Diagrams in Materials Science; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Holder, A.M.; Siol, S.; Ndione, P.F.; Peng, H.; Deml, A.M.; Matthews, B.E.; Schelhas, L.T.; Toney, M.F.; Gordon, R.G.; Tumas, W.; et al. Novel phase diagram behavior and materials design in heterostructural semiconductor alloys. Sci. Adv. 2017, 3, e1700270. [Google Scholar] [CrossRef]
- Matthews, B.E.; Holder, A.M.; Schelhas, L.T.; Siol, S.; May, J.W.; Forkner, M.R.; Vigil-Fowler, D.; Toney, M.F.; Perkins, J.D.; Gorman, B.P.; et al. Using heterostructural alloying to tune the structure and properties of the thermoelectric Sn1−x Cax Se. J. Mater. Chem. A 2017, 5, 16873–16882. [Google Scholar] [CrossRef]
- Siol, S.; Holder, A.; Steffes, J.; Schelhas, L.T.; Stone, K.H.; Garten, L.; Perkins, J.D.; Parilla, P.A.; Toney, M.F.; Huey, B.D.; et al. Negative-pressure polymorphs made by heterostructural alloying. Sci. Adv. 2018, 4, eaaq1442. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Hua, X.; Wu, D. Relationship between the weld pool convection and metallurgical and mechanical properties in hybrid welding for butt joint of 10-mm-thick aluminum alloy plate. Weld. World 2018, 62, 895–903. [Google Scholar] [CrossRef]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 1–131. [Google Scholar]
- Chidambaram, V.; Hattel, J.; Hald, J. Design of lead-free candidate alloys for high-temperature soldering based on the Au–Sn system. Mater. Des. 2010, 31, 4638–4645. [Google Scholar] [CrossRef]
- Al Ahmar, J.; Wiss, E.; Wiese, S. Four-point-bending experiments on multilayer ceramic capacitors: Microstructural details on crack initiation and propagation. In Proceedings of the 2018 19th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Toulouse, France, 15–18 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Nelson, W. Weibull percentile estimates and confidence limits from singly censored data by maximum likelihood. IEEE Trans. Reliab. 1976, 25, 20–24. [Google Scholar] [CrossRef]
- Bai, D.S.; Chung, S.; Chun, Y. Optimal design of partially accelerated life tests for the lognormal distribution under type I censoring. Reliab. Eng. Syst. Saf. 1993, 40, 85–92. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Kim, C.H.; Kim, J.M. Effective Prediction of Bearing Fault Degradation under Different Crack Sizes Using a Deep Neural Network. Appl. Sci. 2018, 8, 2332. [Google Scholar] [CrossRef]
- Chebat, F.; Peron, M.; Viespoli, L.; Welo, T.; Berto, F. Fatigue strength assessment of steel rollers: On the reliability of the strain energy density approach on real components. Appl. Sci. 2018, 8, 1015. [Google Scholar] [CrossRef]
- Wang, C.; Xie, H.; Zhang, L.; Gong, Y.; Pastel, G.; Dai, J.; Liu, B.; Wachsman, E.D.; Hu, L. Universal soldering of lithium and sodium alloys on various substrates for batteries. Adv. Energy Mater. 2018, 8, 1701963. [Google Scholar] [CrossRef]
- Ping, Y.; Jie, Z.; Dongyang, W.; Binghao, B. Research on parametric analysis for stress of Plastic Ball Grid Array solder joint under shock load. Int. J. Mater. Prod. Technol. 2008, 31, 293–304. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z. A novel time-variant reliability analysis method based on failure processes decomposition for dynamic uncertain structures. J. Mech. Des. 2018, 140, 051401. [Google Scholar] [CrossRef]
- Xiao, N.C.; Zuo, M.J.; Zhou, C. A new adaptive sequential sampling method to construct surrogate models for efficient reliability analysis. Reliab. Eng. Syst. Saf. 2018, 169, 330–338. [Google Scholar] [CrossRef]
- Fang, W.; Hu, L.; He, W.; Wang, E.; Li, X. Microstructure and properties of a TiAl alloy prepared by mechanical milling and subsequent reactive sintering. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2005, 403, 186–190. [Google Scholar] [CrossRef]





| No. | Solder Alloy | Path | Temperature | Pret | Vibration |
|---|---|---|---|---|---|
| 3 | −1 | −1 | 1 | −1 | −1 |
| 4 | −1 | 1 | 1 | 1 | −1 |
| 5 | −1 | 1 | −1 | −1 | −1 |
| 8 | 1 | −1 | 1 | 1 | −1 |
| 11 | −1 | −1 | −1 | −1 | 1 |
| 12 | −1 | 1 | −1 | 1 | 1 |
| 13 | 1 | 1 | 1 | −1 | −1 |
| 15 | −1 | 1 | 1 | −1 | 1 |
| 17 | −1 | −1 | −1 | 1 | −1 |
| 18 | −1 | −1 | 1 | 1 | 1 |
| 19 | −1 | −1 | −1 | −1 | 1 |
| 26 | 1 | −1 | −1 | 1 | 1 |
| 28 | 1 | −1 | −1 | −1 | −1 |
| 31 | 1 | 1 | 1 | 1 | 1 |
| 33 | 1 | 1 | −1 | −1 | 1 |
| 39 | 1 | −1 | 1 | −1 | 1 |
| 45 | 1 | 1 | −1 | 1 | −1 |
| GL | SC Adjust. | MC Adjust. | |||
|---|---|---|---|---|---|
| Source | 5 | 726,392 | 145,278 | 27.39 | 0 |
| Model | 4 | 699,736 | 174,934 | 32.98 | 0 |
| Lineal | 1 | 531,227 | 531,227 | 100.15 | 0 |
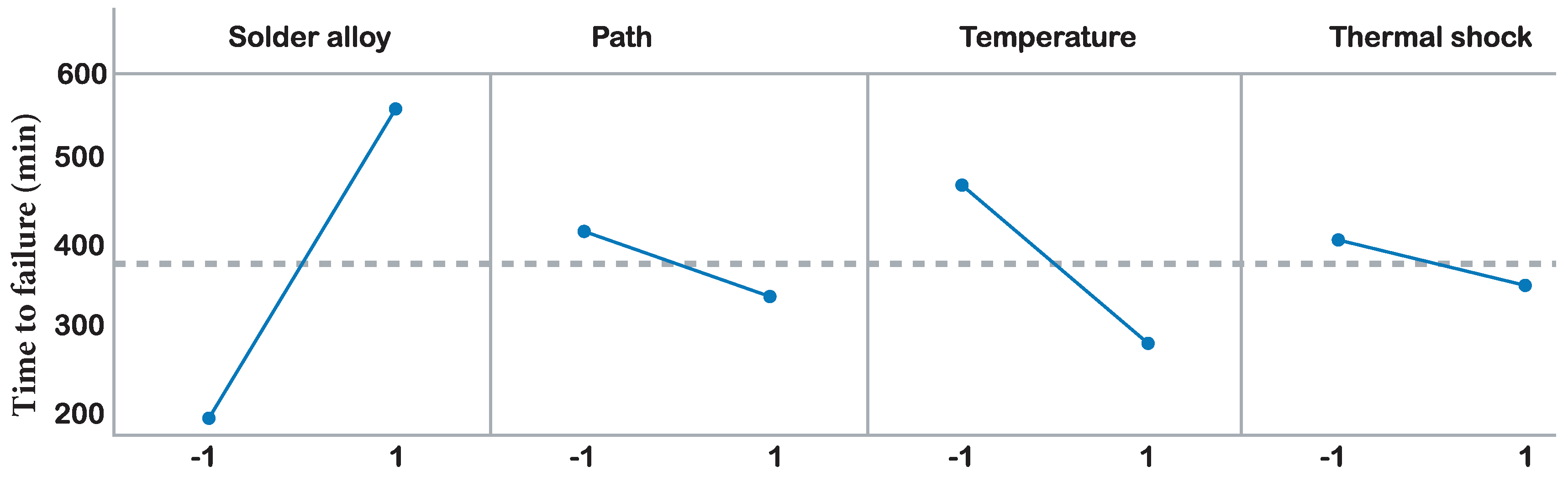
| Soldering alloy | 1 | 21,415 | 21,415 | 4.04 | 0.07 |
| Temperature | 1 | 137,972 | 137,972 | 26.01 | 0 |
| Thermal Shock | 1 | 10,158 | 10,158 | 1.92 | 0.194 |
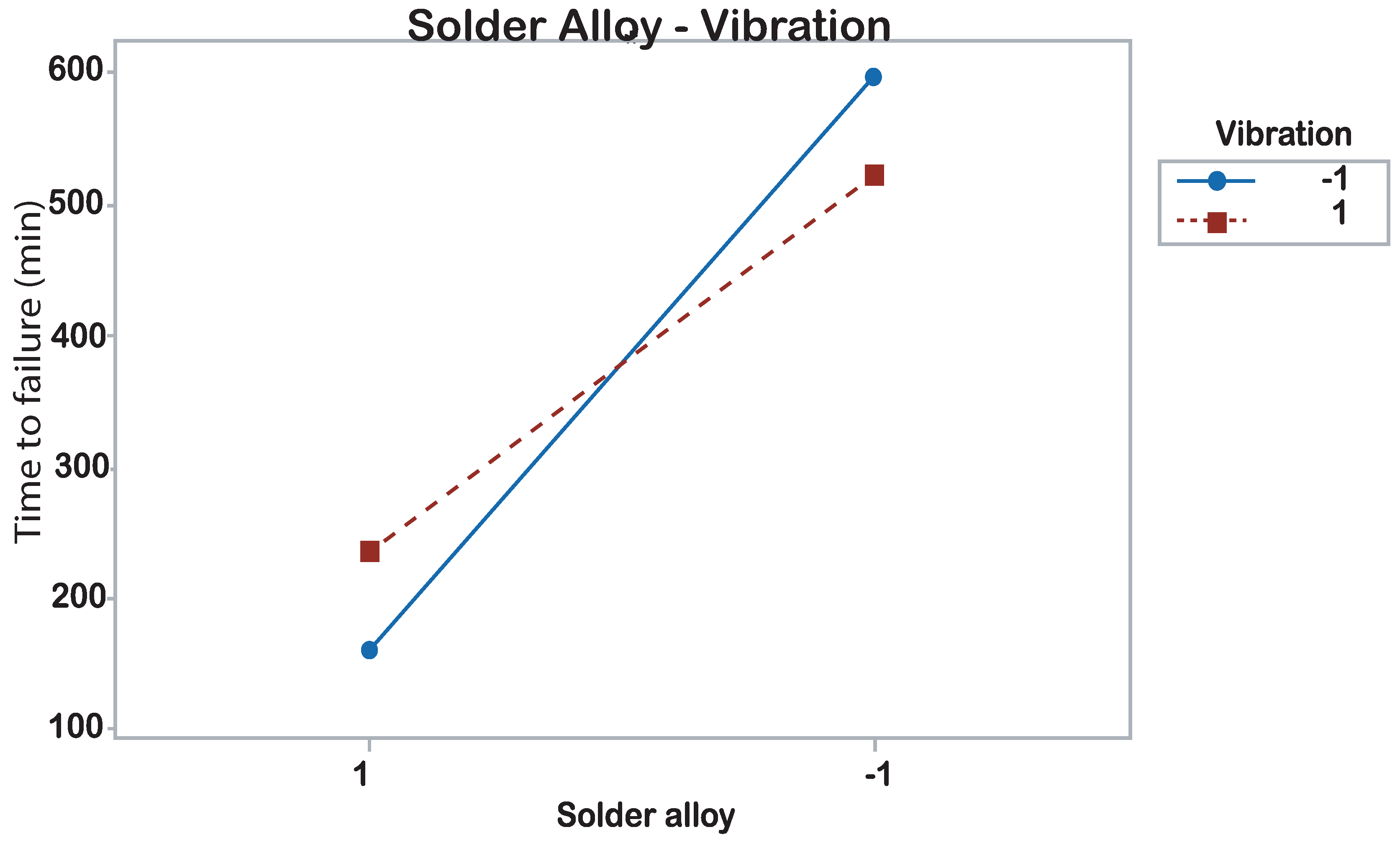
| Interactions with 2 terms | 1 | 24,321 | 24,321 | 4.59 | 0.055 |
| Soldering alloy*vibration | 1 | 24,321 | 24,321 | 4.59 | 0.055 |
| Error | 11 | 58,346 | 5304 | ||
| Lack of adjustment | 10 | 53,246 | 5325 | 1.04 | 0.649 |
| Pure error | 1 | 5101 | 5101 | ||
| Total | 16 | 784,738 |
| S | R | R-(Adjust) | R(Pred) |
|---|---|---|---|
| 72.8301 | 92.56% | 89.19% | 82.52% |
| Term | Effect | Coef | SE Coef. | VIF | |||
|---|---|---|---|---|---|---|---|
| Constant | 378.8 | 17.8 | 21.24 | 0 | |||
| Soldering alloy | 361 | 180.5 | 18 | 10.01 | 0 | 1.04 | |
| Path | −72.5 | −36.2 | 18 | −2.01 | 0.07 | 1.04 | |
| Temperature | −184 | −92 | 18 | −5.1 | 0 | 1.04 | |
| Thermal Shock | −51.5 | −25.7 | 18.6 | −1.38 | 0.194 | 1.1 | |
| Solder alloy-vibration | −76.4 | −38.2 | 17.8 | −2.14 | 0.055 | 1.02 | |
| Soldering Alloy | Parameters |
|---|---|
| SnPb | Beta: 2.2923 |
| SnPb | Eta: 319.4363 |
| SnPb | Failure rate: 0.5364 |
| SnPb | Mean Life: 282.9822 |
| SnAgCu | Beta: 7.7790 |
| SnAgCu | Eta: 665.2968 |
| SnAgCu | Failure rate: 5.4508 × |
| SnAgCu | Mean life: 625.6784 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamora-Antuñano, M.A.; Mendoza-Herbert, O.; Culebro-Pérez, M.; Rodríguez-Morales, A.; Rodríguez-Reséndiz, J.; Gonzalez-Duran, J.E.E.; Mendez-Lozano, N.; Gonzalez-Gutierrez, C.A. Reliable Method to Detect Alloy Soldering Fractures under Accelerated Life Test. Appl. Sci. 2019, 9, 3208. https://doi.org/10.3390/app9163208
Zamora-Antuñano MA, Mendoza-Herbert O, Culebro-Pérez M, Rodríguez-Morales A, Rodríguez-Reséndiz J, Gonzalez-Duran JEE, Mendez-Lozano N, Gonzalez-Gutierrez CA. Reliable Method to Detect Alloy Soldering Fractures under Accelerated Life Test. Applied Sciences. 2019; 9(16):3208. https://doi.org/10.3390/app9163208
Chicago/Turabian StyleZamora-Antuñano, M.A., O. Mendoza-Herbert, M. Culebro-Pérez, A. Rodríguez-Morales, Juvenal Rodríguez-Reséndiz, J.E.E. Gonzalez-Duran, N. Mendez-Lozano, and C.A. Gonzalez-Gutierrez. 2019. "Reliable Method to Detect Alloy Soldering Fractures under Accelerated Life Test" Applied Sciences 9, no. 16: 3208. https://doi.org/10.3390/app9163208
APA StyleZamora-Antuñano, M. A., Mendoza-Herbert, O., Culebro-Pérez, M., Rodríguez-Morales, A., Rodríguez-Reséndiz, J., Gonzalez-Duran, J. E. E., Mendez-Lozano, N., & Gonzalez-Gutierrez, C. A. (2019). Reliable Method to Detect Alloy Soldering Fractures under Accelerated Life Test. Applied Sciences, 9(16), 3208. https://doi.org/10.3390/app9163208






