Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids
Abstract
:1. Introduction
2. Non-Integer Order Calculus
3. Description of an Isolated Fractional-Order Microgrid Model
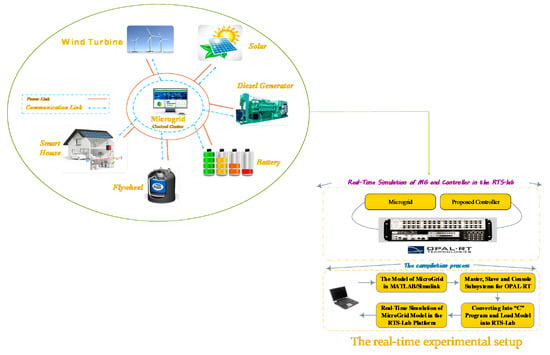
3.1. An Isolated Microgrid
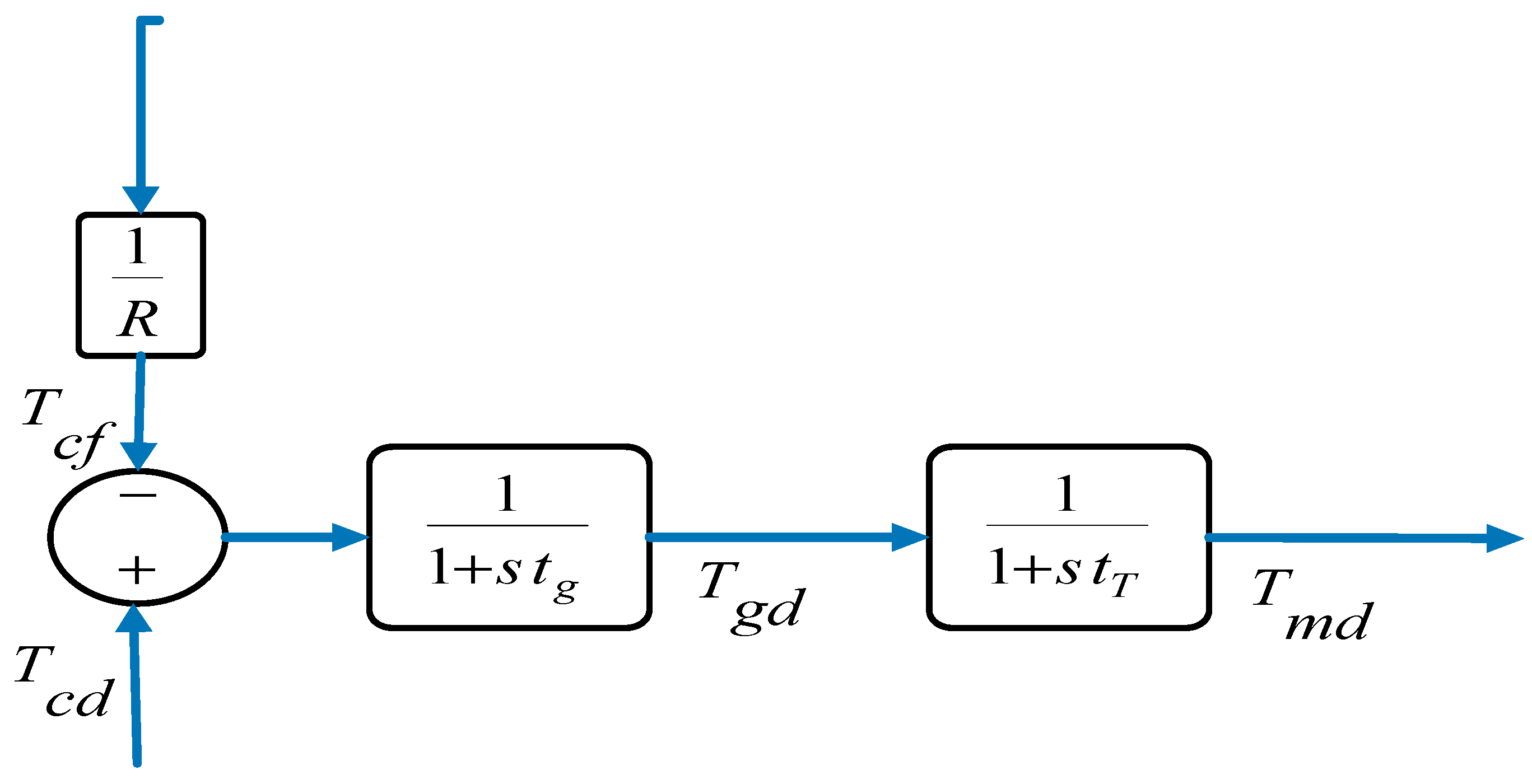
3.2. The Diesel Engine Generator Model
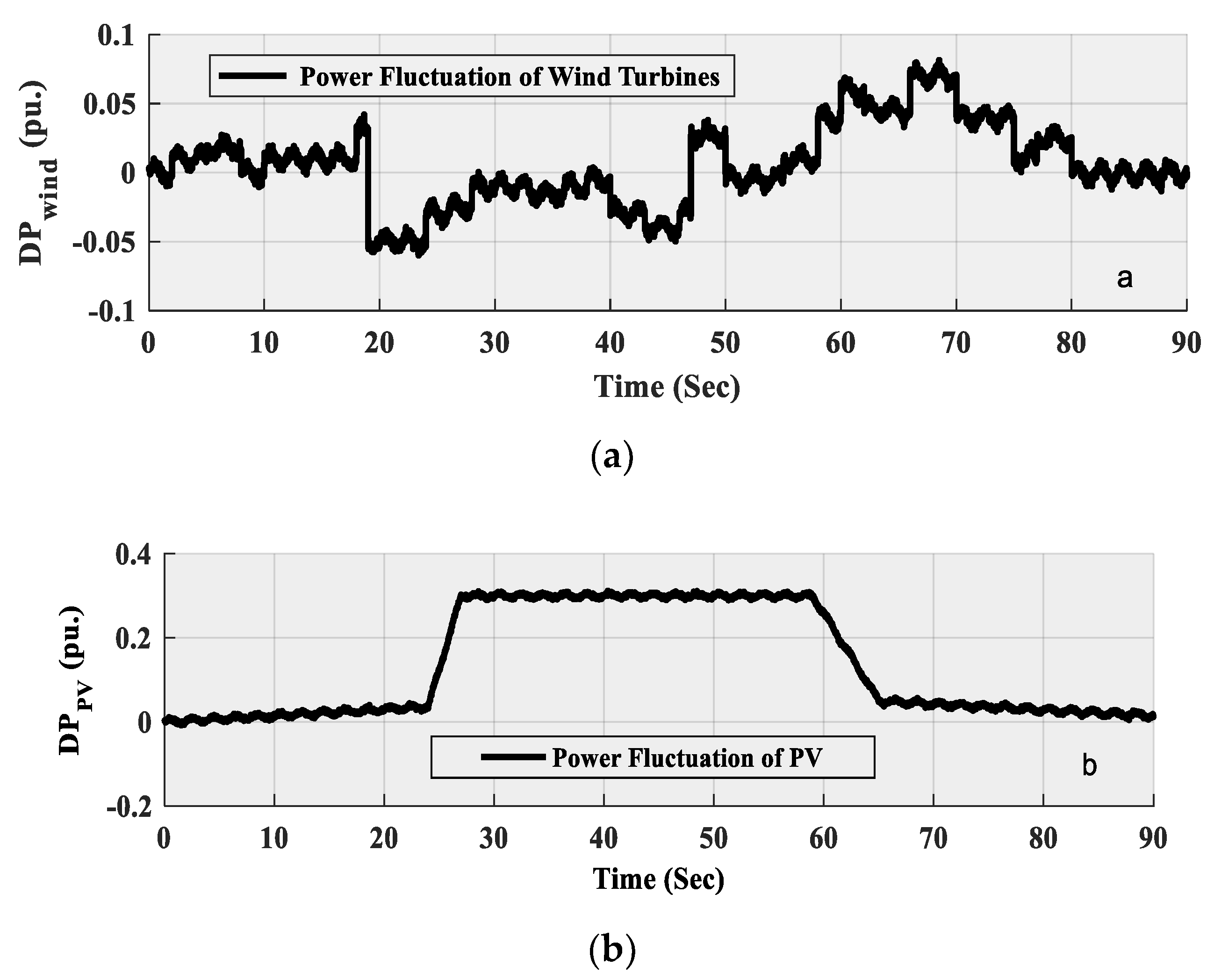
3.3. Wind Turbine Generator
3.4. Model of a Photovoltaic (PV) Generation
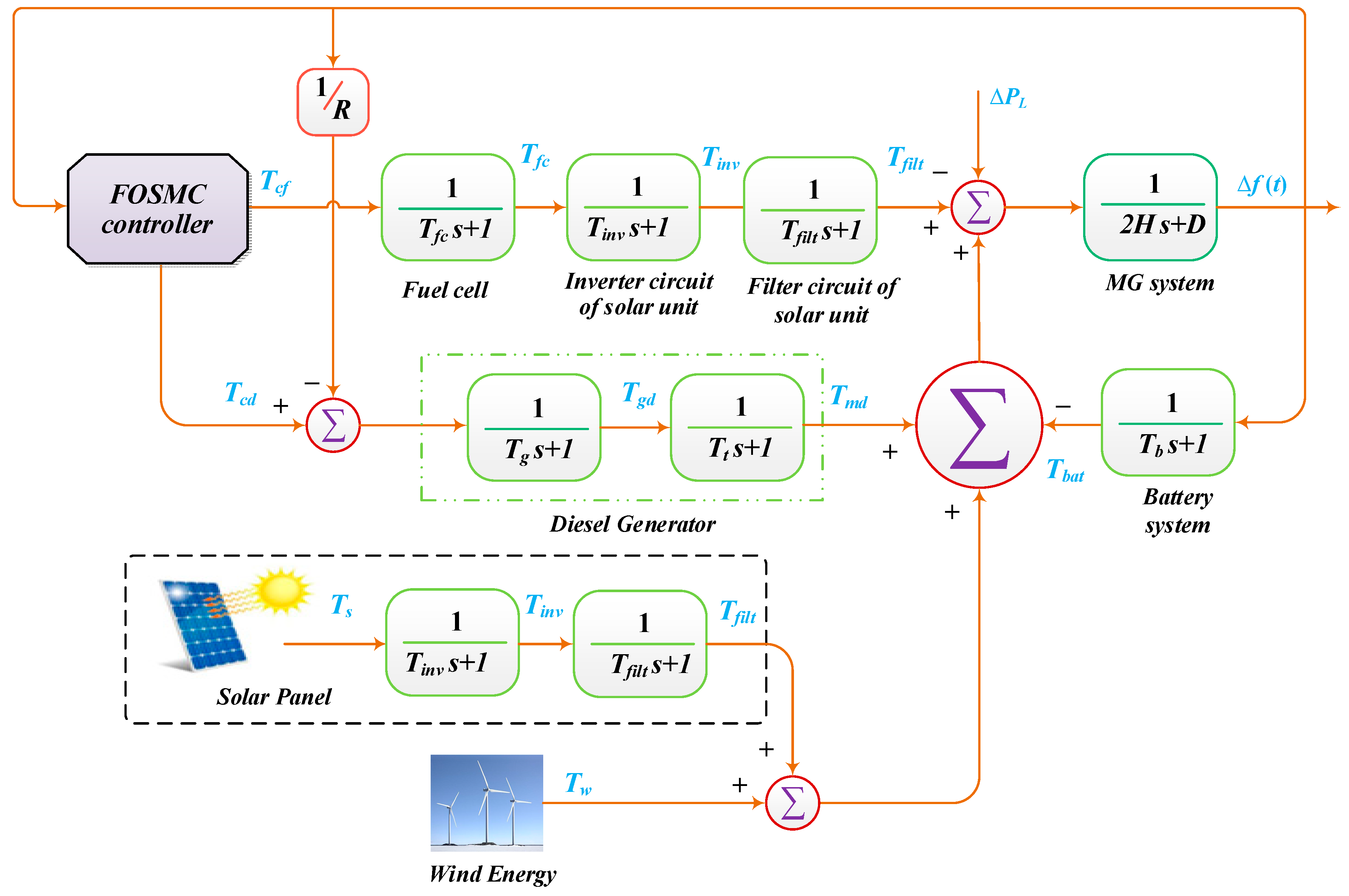
3.5. Structure of the LFC-Based MG System
4. Proposed Fractional-Order Sliding Mode Control Scheme
5. Overview of the Original SCA
The Hybrid SCA and HS
6. Simulation and Real-Time Results
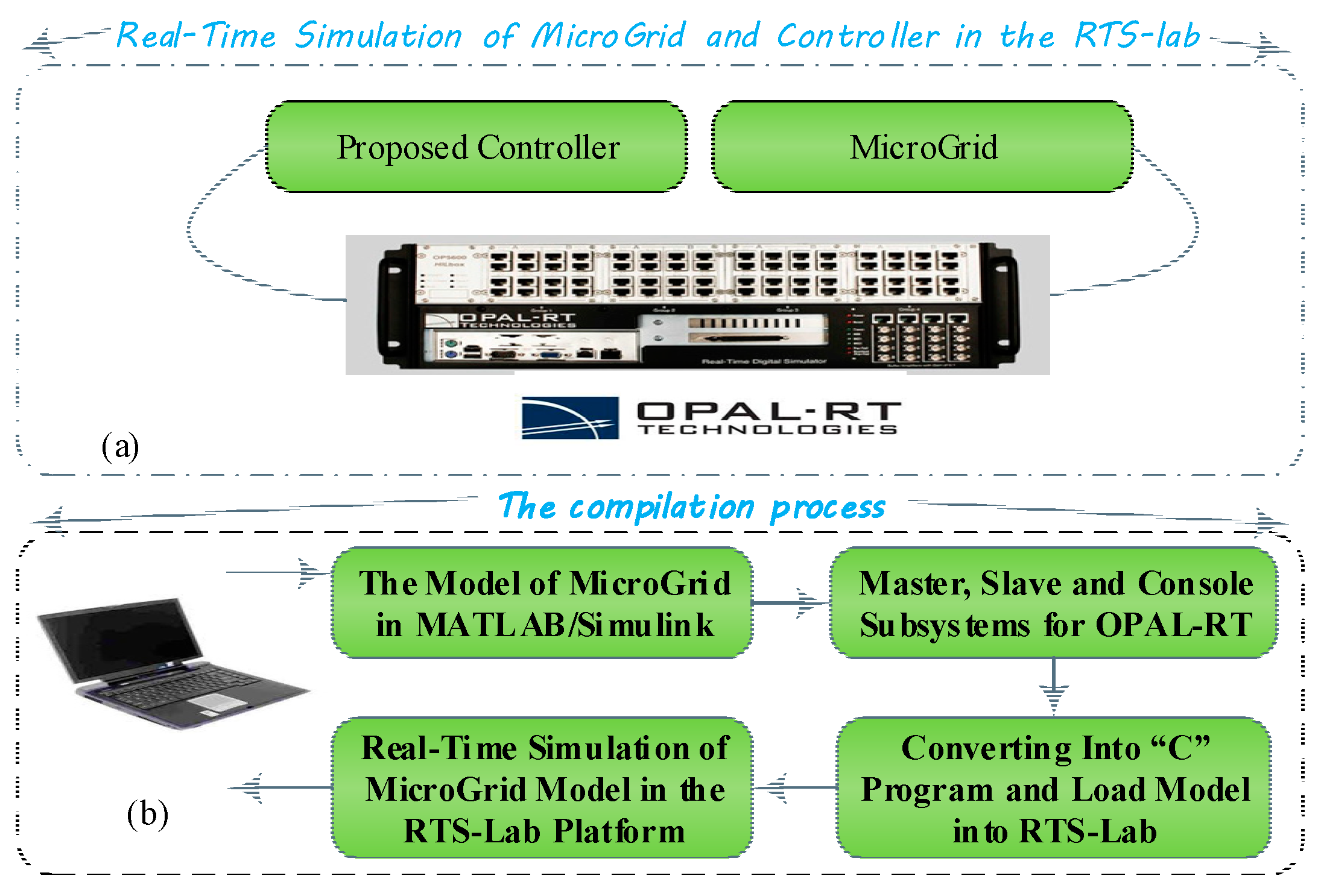
- (i)
- A real-time OPAL-RT simulator is used which simulates the studied MG shown in Figure 3;
- (ii)
- For the programming host, a PC is used as the command station to execute the MATLAB/Simulink based-code on the OPAL-RT;
- (iii)
- A router is established to connect all the setup devices in the same sub-network. In this application, the OPAL-RT is connected to the DK60 board by Ethernet ports.
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| LFC | Load Frequency Control |
| SMC | Sliding Mode Control |
| MPC | Model Predictive Control |
| SCA | Sine Cosine Algorithm |
| HS | Harmony Search |
| HMCR | Harmony Memory Consideration Rate |
| PAR | Pitch Adjustment Rate |
| RES | Renewable Energy Source |
| DG | Distributed Generator |
| DEG | Diesel Engine Generator |
| RES | Renewable Energy Source |
| PV | Photovoltaic |
| WTG | Wind Turbine Generator |
| ESS | Energy Storage System |
| FC | Fuel Cell |
| FESS | Flywheel Energy Storage System |
| BESS | Battery Energy Storage System |
| PHEV | Plug-In Hybrid Electric Vehicle |
| MGDS | Microgrid Dispatch System |
| DMS | Distribution Management System |
| HIL | Hardware-in-the-Loop |
References
- Chowdhury, S.; Chowdhury, S.P.; Crossley, P. Microgrids and Active Distribution Networks; Institution of Engineering and Technology: London, UK, 2009. [Google Scholar]
- Gheisarnejad, M.; Khooban, M.H.; Dragicevic, T. The Future 5G Network Based Secondary Load Frequency Control in Maritime Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. Secondary load frequency control for multi-microgrids: HiL real-time simulation. Soft Comput. 2019, 23, 5785–5798. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García, P.; Fernández, L.M.; Jurado, F. Energy dispatching based on predictive controller of an off-grid wind turbine/photovoltaic/hydrogen/battery hybrid system. Renew. Energy 2015, 74, 326–336. [Google Scholar] [CrossRef]
- Serban, I.; Teodorescu, R.; Marinescu, C. Energy storage systems impact on the short-term frequency stability of distributed autonomous microgrids, an analysis using aggregate models. IET Renew. Power Gener. 2013, 7, 531–539. [Google Scholar] [CrossRef]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust Frequency Control in an Islanded Microgrid: H∞ and μ -Synthesis Approaches. IEEE Trans. Smart Grid 2015, 7, 706–717. [Google Scholar] [CrossRef]
- Khalghani, M.R.; Khooban, M.H.; Mahboubi-Moghaddam, E.; Vafamand, N.; Goodarzi, M. A self-tuning load frequency control strategy for microgrids: Human brain emotional learning. Int. J. Electr. Power Energy Syst. 2016, 75, 311–319. [Google Scholar] [CrossRef]
- Jiayi, H.; Chuanwen, J.; Rong, X. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Moghadam, M.; Boudjadar, J.; Khooban, M.H. Active Power Sharing and Frequency Recovery Control in an Islanded Microgrid with Nonlinear load and Non-Dispatchable DG. IEEE Syst. J. 2019, 5, 1–11. [Google Scholar] [CrossRef]
- Heydari, R.; Gheisarnejad, M.; Khooban, M.H.; Dragicevic, T.; Blaabjerg, F. Robust and fast voltage-source-converter (vsc) control for naval shipboard microgrids. IEEE Trans. Power Electron. 2019, 34, 8299–8303. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Kriging Based Surrogate Modeling for Fractional Order Control of Microgrids. IEEE Trans. Smart Grid 2015, 6, 36–44. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional order fuzzy control of hybrid power system with renewable generation using chaotic PSO. ISA Trans. 2016, 62, 19–29. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Shasadeghi, M.; Dragicevic, T.; Blaabjerg, F. Load frequency control in microgrids based on a stochastic noninteger controller. IEEE Trans. Sustain. Energy 2017, 9, 853–861. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Fractional order AGC for distributed energy resources using robust optimization. IEEE Trans. Smart Grid 2015, 7, 2175–2186. [Google Scholar] [CrossRef]
- Pahasa, J.; Ngamroo, I. Coordinated control of wind turbine blade pitch angle and PHEVs using MPCs for load frequency control of microgrid. IEEE Syst. J. 2014, 10, 97–105. [Google Scholar] [CrossRef]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N.; Catalão, J.P.S. Frequency regulation in hybrid power systems using particle swarm optimization and linear matrix inequalities based robust controller design. Int. J. Electr. Power Energy Syst. 2014, 63, 887–900. [Google Scholar] [CrossRef]
- Bevrani, H.; Habibi, F.; Babahajyani, P.; Watanabe, M.; Mitani, Y. Intelligent frequency control in an AC microgrid: Online PSO-based fuzzy tuning approach. IEEE Trans. Smart Grid 2012, 3, 1935–1944. [Google Scholar] [CrossRef]
- Ghafouri, A.; Milimonfared, J.; Gharehpetian, G.B. Fuzzy-adaptive frequency control of power system including microgrids, wind farms, and conventional power plants. IEEE Syst. J. 2014, 12, 2772–2781. [Google Scholar] [CrossRef]
- Qu, Q.; Zhang, H.; Yu, R.; Liu, Y. Neural network-based H∞ sliding mode control for nonlinear systems with actuator faults and unmatched disturbances. Neurocomputing 2018, 275, 2009–2018. [Google Scholar] [CrossRef]
- Ngo, Q.H.; Nguyen, N.P.; Nguyen, C.N.; Tran, T.H.; Ha, Q.P. Fuzzy sliding mode control of an offshore container crane. Ocean Eng. 2017, 140, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Sun, F.; Li, H.; He, B. Neural-network-based sliding-mode control for multiple rigid-body attitude tracking with inertial information completely unknown. Inf. Sci. 2017, 400, 91–104. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. Design an optimal fuzzy fractional proportional integral derivative controller with derivative filter for load frequency control in power systems. Trans. Inst. Meas. Control. 2019, 41, 2563–2581. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M.; Vafamand, N.; Boudjadar, J. Electric Vehicle Power Propulsion System Control Based on Time-Varying Fractional Calculus: Implementation and Experimental Results. IEEE Trans. Intell. Veh. 2019, 4, 255–264. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, J.; Mi, X.; Khan, M.W. Fractional order sliding mode based direct power control of grid-connected DFIG. IEEE Trans. Power Syst. 2017, 33, 3087–3096. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 367–377. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Wang, B.; Ding, J.; Wu, F.; Zhu, D. Robust finite-time control of fractional-order nonlinear systems via frequency distributed model. Nonlinear Dyn. 2016, 85, 2133–2142. [Google Scholar] [CrossRef]
- Khooban, M.-H.; Niknam, T.; Blaabjerg, F.; Davari, P.; Dragicevic, T. A robust adaptive load frequency control for micro-grids. ISA Trans. 2016, 65, 220–229. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Blaabjerg, F.; Dragičević, T. A new load frequency control strategy for micro-grids with considering electrical vehicles. Electr. Power Syst. Res. 2017, 143, 585–598. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Khooban, M.H.; Gheisarnejad, M.; Vafamand, N.; Jafari, M.; Mobayen, S.; Dragicevic, T. Robust Frequency Regulation in Mobile Microgrids: HIL Implementation. IEEE Syst. J. 2019. [Google Scholar] [CrossRef]
- Xiang, W.L.; An, M.Q.; Li, Y.Z.; He, R.C.; Zhang, J.F. An improved global-best harmony search algorithm for faster optimization. Expert Syst. Appl. 2014, 41, 5788–5803. [Google Scholar] [CrossRef]
- Khooban, M.H.; Dragicevic, T.; Blaabjerg, F.; Delimar, M. Shipboard microgrids: A novel approach to load frequency control. IEEE Trans. Sustain. Energy 2017, 9, 843–852. [Google Scholar] [CrossRef]
- Database of Wind Characteristics. Available online: www.winddata.com (accessed on 10 October 2014).
- Solar Radiation Modeling. Available online: www.solargis.info/doc/solar-and-pv-data (accessed on 10 October 2014).



| Symbol and Abbreviation | Values | Symbol and Abbreviation | Values |
|---|---|---|---|
| (change in load power) | 0.02 s | (governor time constant) | 0.08 s |
| (time constant of inverter circuit of solar unit) | 0.04 s | (battery power time constant) | 0.1 s |
| (time constant of fuel cell) | 0.26 s | 2H (inertia constant) | 0.1667 |
| (time constant of filter circuit of solar unit) | 0.004 s | D (damping coefficient) | 0.015 |
| (diesel generator time constant) | 2.00 s | R (DG speed regulation) | 3 |
| Parameters | Variation Range |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esfahani, Z.; Roohi, M.; Gheisarnejad, M.; Dragičević, T.; Khooban, M.-H. Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids. Appl. Sci. 2019, 9, 3411. https://doi.org/10.3390/app9163411
Esfahani Z, Roohi M, Gheisarnejad M, Dragičević T, Khooban M-H. Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids. Applied Sciences. 2019; 9(16):3411. https://doi.org/10.3390/app9163411
Chicago/Turabian StyleEsfahani, Zahra, Majid Roohi, Meysam Gheisarnejad, Tomislav Dragičević, and Mohammad-Hassan Khooban. 2019. "Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids" Applied Sciences 9, no. 16: 3411. https://doi.org/10.3390/app9163411
APA StyleEsfahani, Z., Roohi, M., Gheisarnejad, M., Dragičević, T., & Khooban, M.-H. (2019). Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids. Applied Sciences, 9(16), 3411. https://doi.org/10.3390/app9163411