Moisture Buffering of Multilayer Internal Wall Assemblies at the Micro Scale: Experimental Study and Numerical Modelling
Abstract
:1. Introduction
2. Methodology
2.1. Sample Compositions and Material Properties
2.2. Hygrothermal Tests
3. Results and Discussion
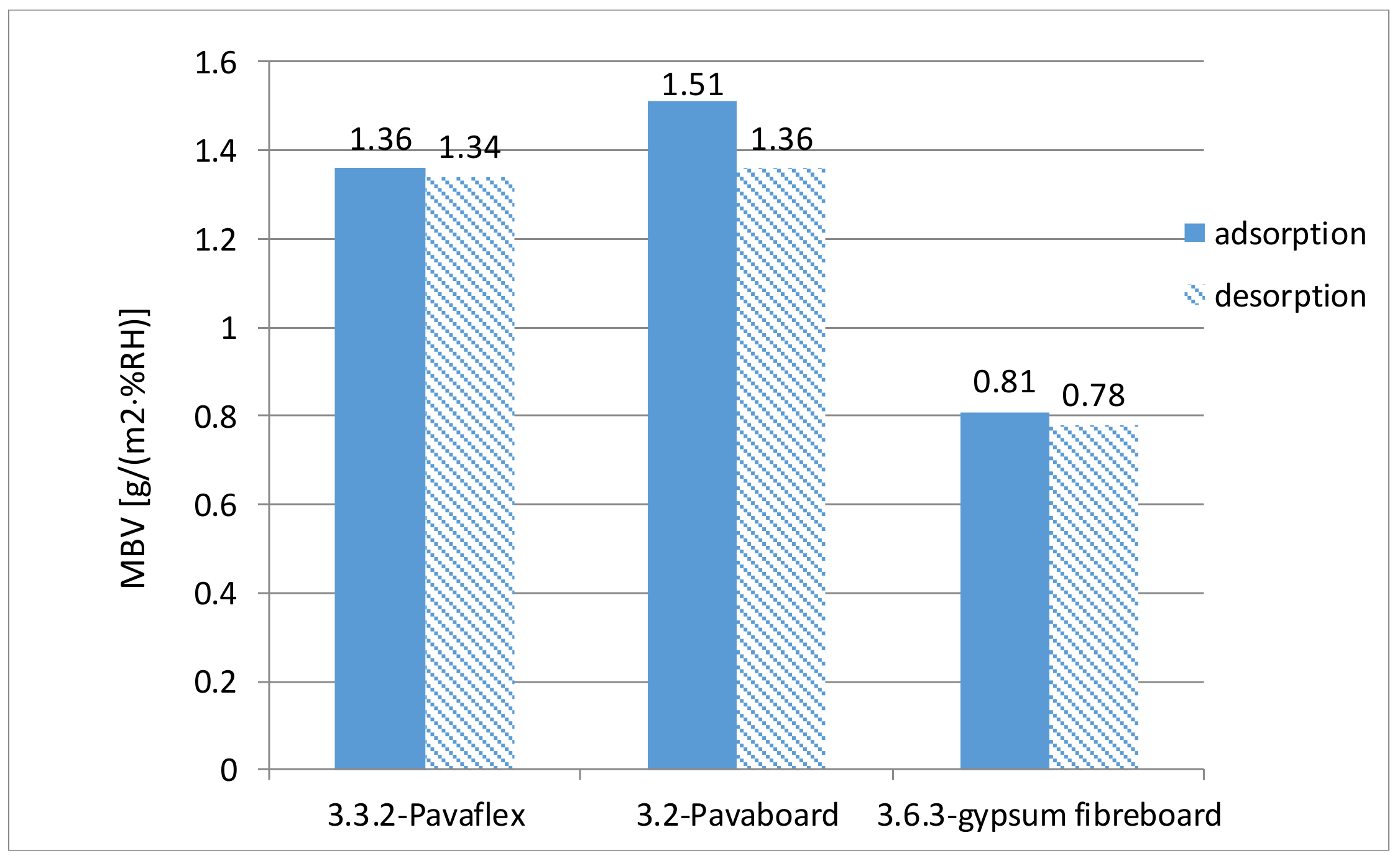
3.1. Sorption/Desorption Kinetic
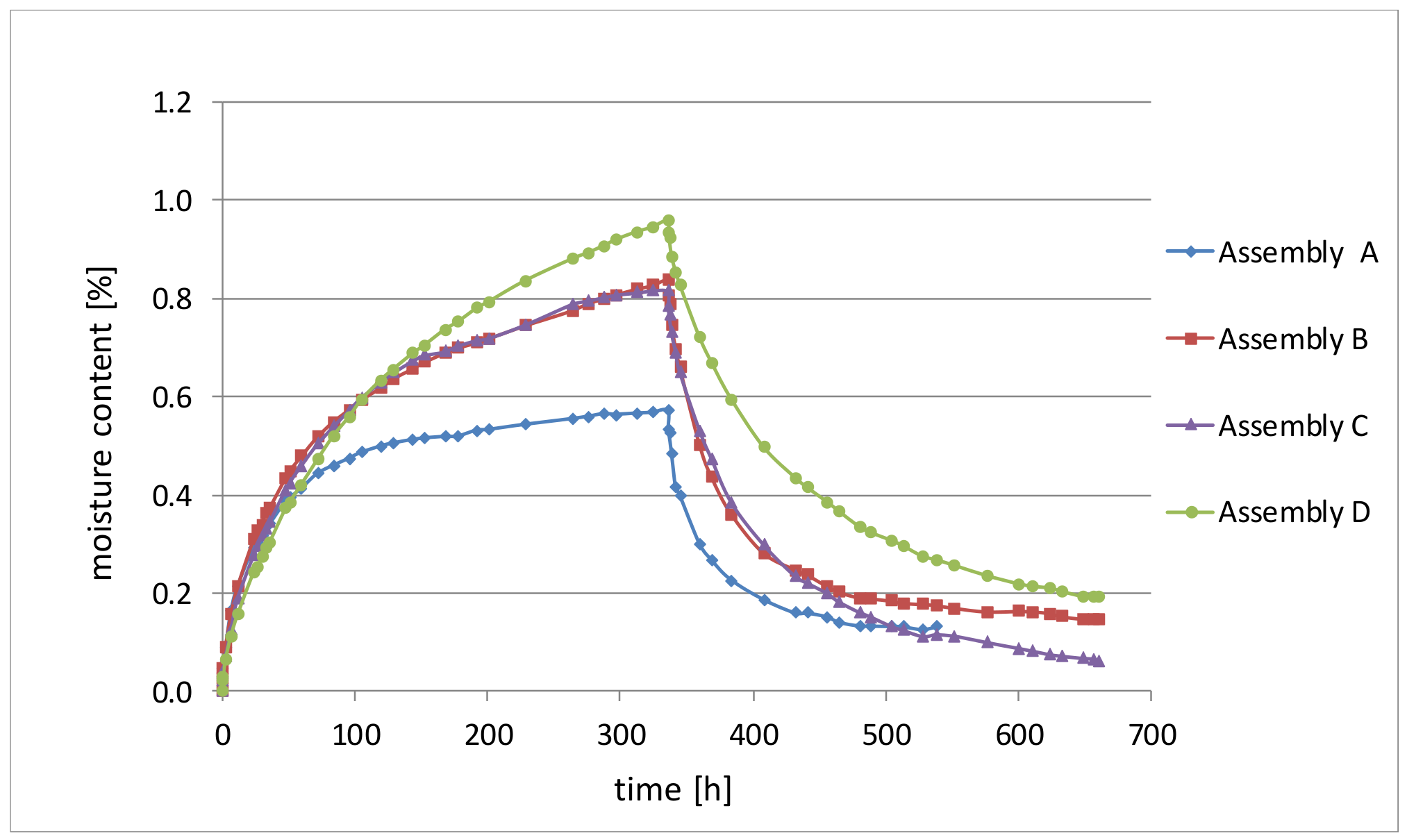
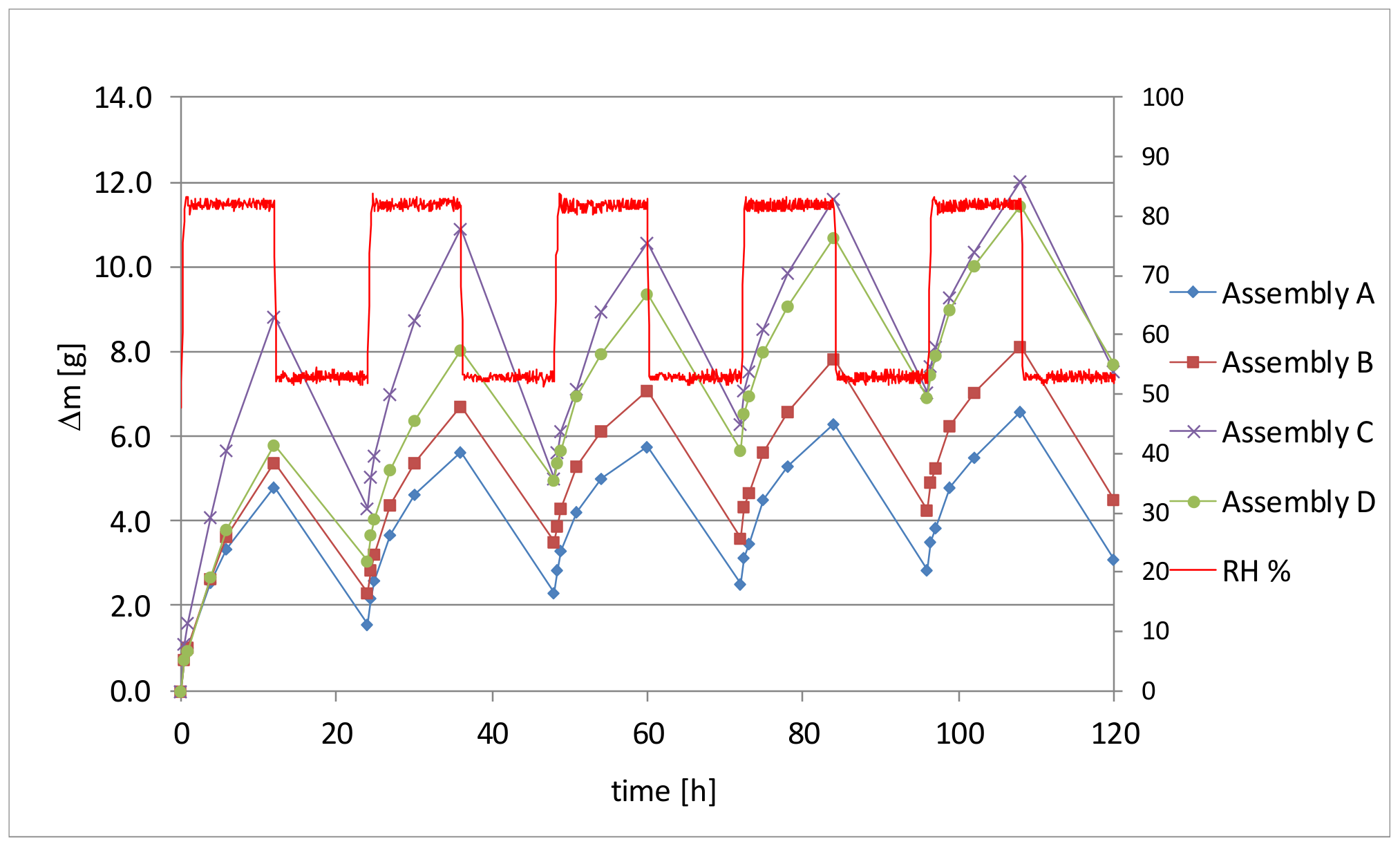
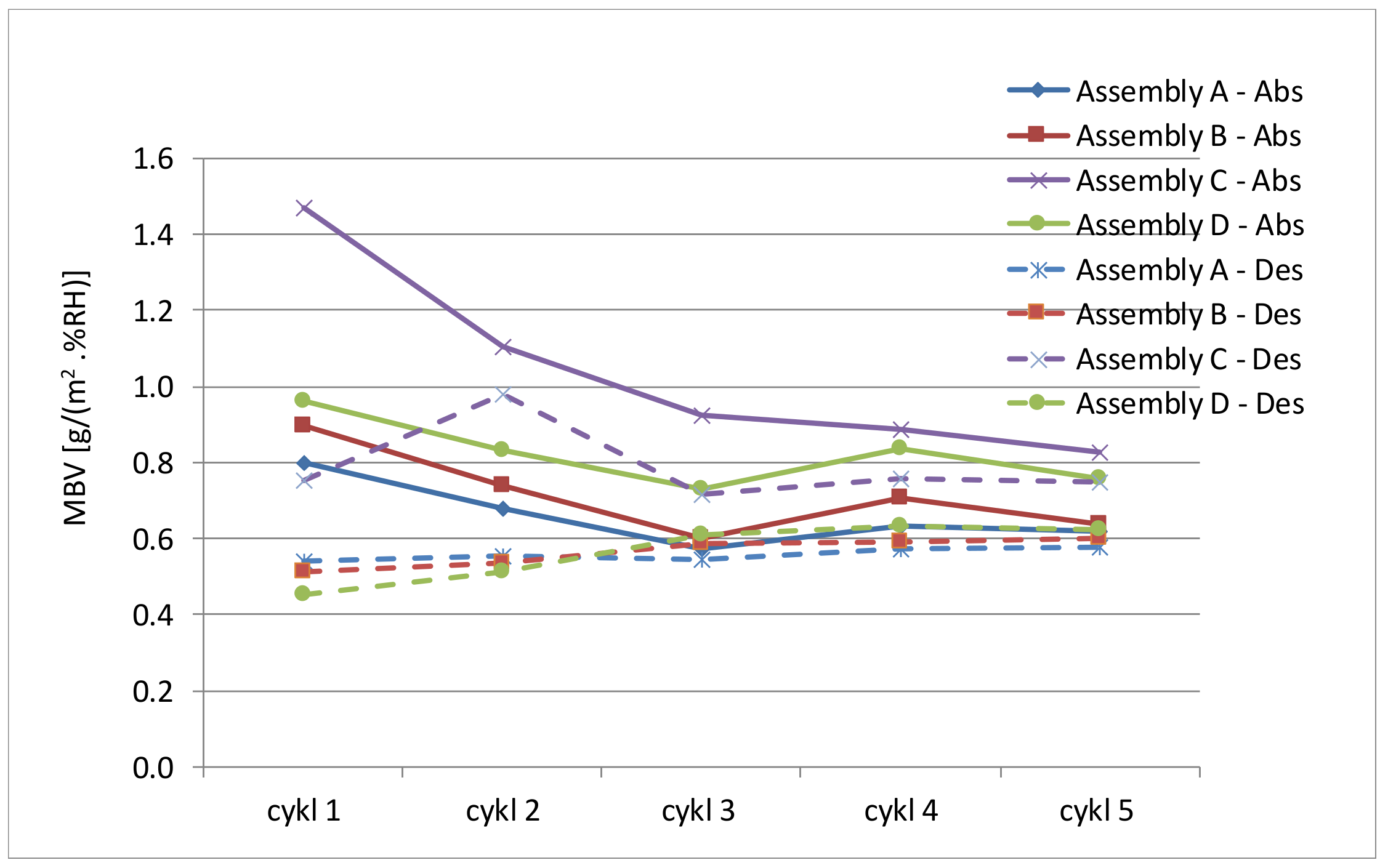
3.2. Moisture Buffering Test
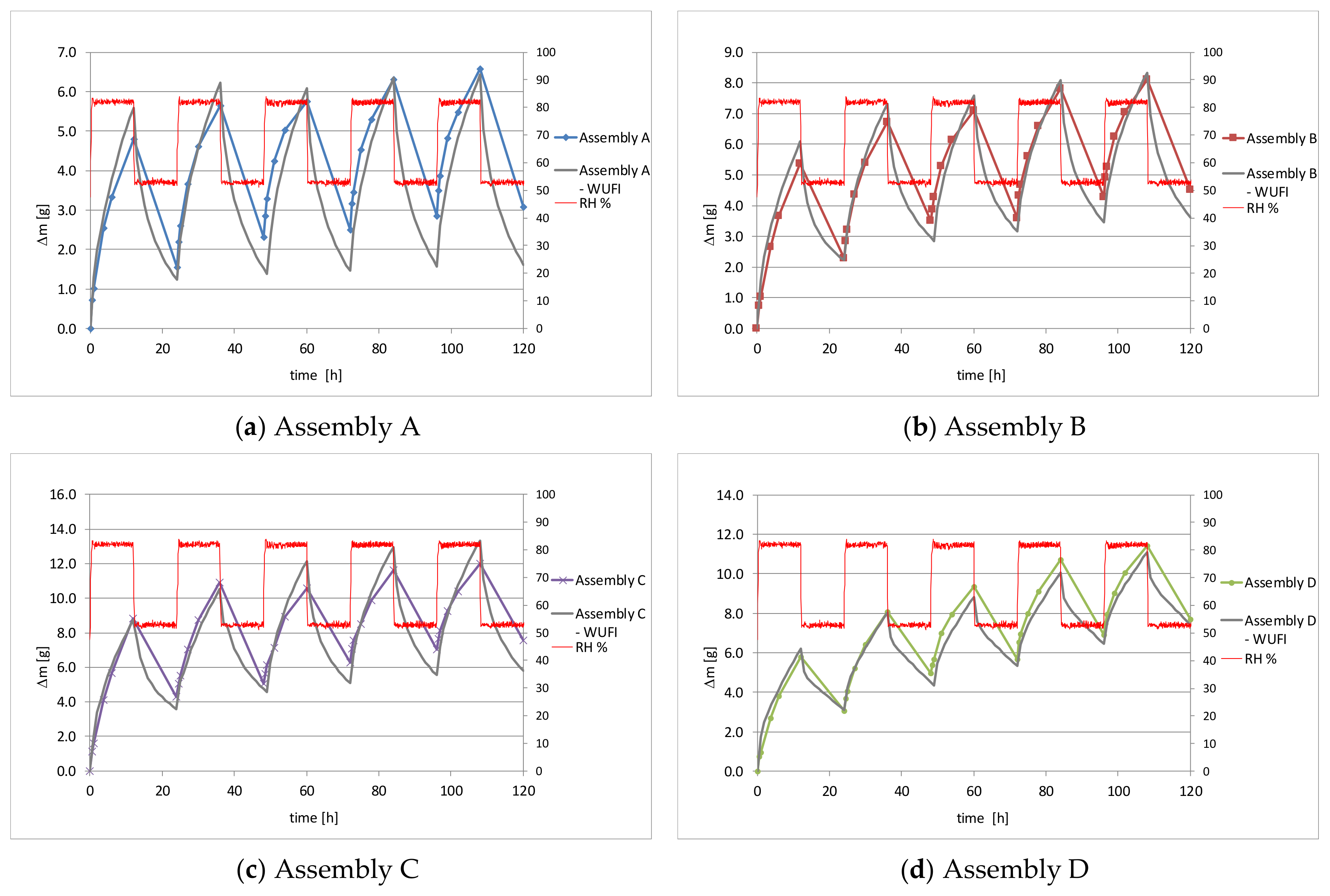
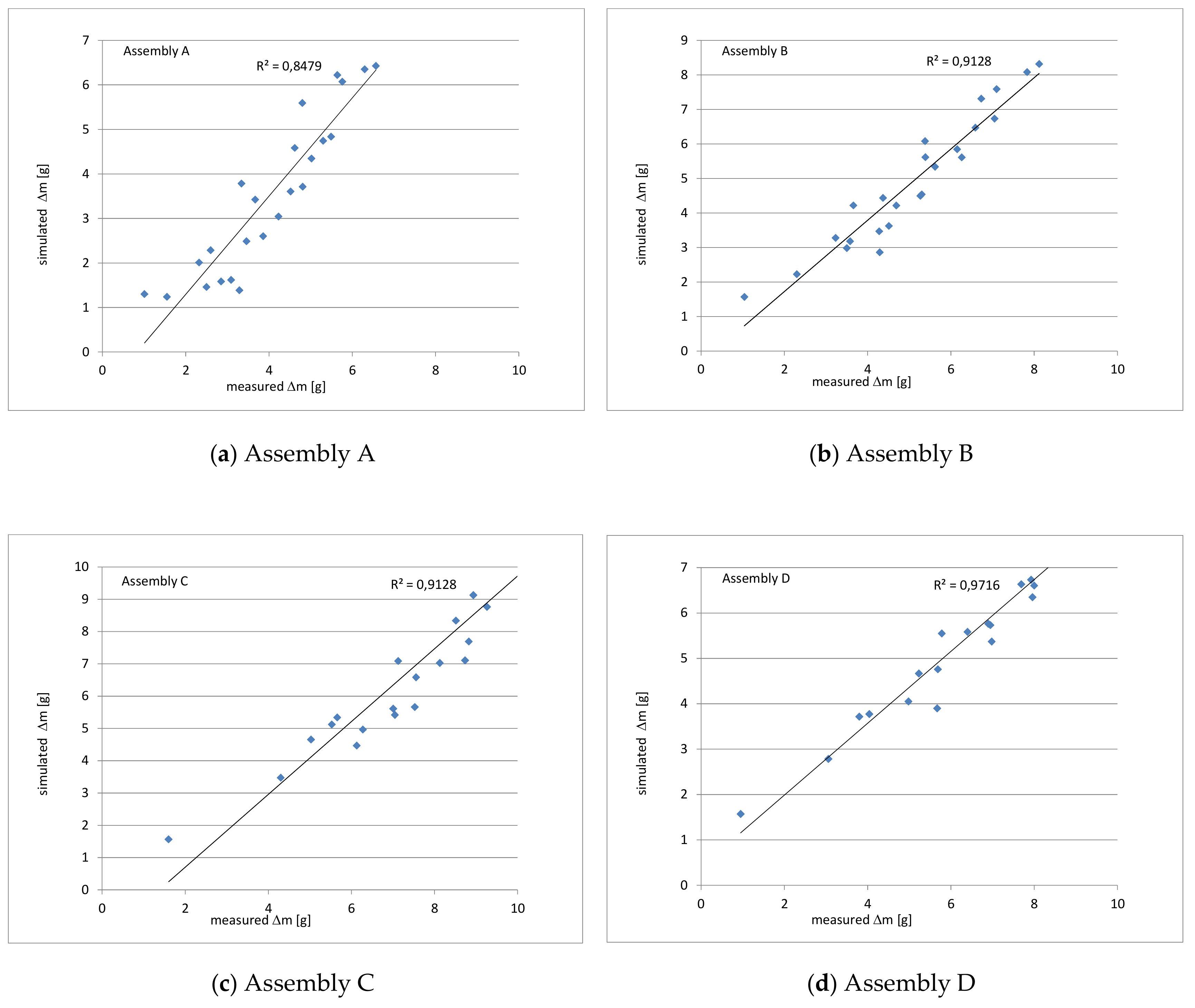
4. Comparison between Simulation and Experiments
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018 Amending Directive 2010/31/EU on the Energy Performance of Buildings and Directive 2012/27/EU on Energy Efficiency. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv%3AOJ.L_.2018.156.01.0075.01.ENG (accessed on 12 April 2018).
- Korjenic, A.; Zach, J.; Hroudová, J. The use of insulating materials based on natural fibers in combination with plant facades in building constructions. Energy Build. 2016, 116, 45–58. [Google Scholar] [CrossRef]
- Limam, A.; Zerizer, A.; Quenard, D.; Sallee, H.; Chenak, A. Experimental thermal characterization of bio-based materials (Aleppo Pine wood, cork and their composites) for building insulation. Energy Build. 2016, 116, 89–95. [Google Scholar] [CrossRef]
- Madhumathi, A.; Sundarraja, M.C.; Shanthipriya, R. A comparative study of the thermal comfort of different building materials in Madurai. Int. J. Earth Sci. Eng. 2014, 7, 1004–1018. [Google Scholar]
- Salonvaara, M.; Ojanen, T.; Holm, A.; Künzel, H.M.; Karagiozis, A.N. Moisture Buffering Effects on Indoor Air Quality-experimental and Simulation Results. In Proceedings of the Performance of Exterior Envelopes of Whole Buildings IX International Conference, Clearwater Beach, FL, USA, 5 December 2004. [Google Scholar]
- Simonson, C. Energy consumption and ventilation performance of a naturally ventilated ecological house in a cold climate. Energy Build. 2005, 37, 23–35. [Google Scholar] [CrossRef]
- Woloszyn, M.; Kalamees, T.; Abadie, M.O.; Steeman, M.; Kalagasidis, A.S. The effect of combining a relative-humidity-sensitive ventilation system with the moisture-buffering capacity of materials on indoor climate and energy efficiency of buildings. Build. Environ. 2009, 44, 515–524. [Google Scholar] [CrossRef]
- Osanyintola, O.F.; Simonson, C.J. Moisture buffering capacity of hygroscopic building materials: Experimental facilities and energy impact. Energy Build. 2006, 38, 1270–1282. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, M.; Rode, C.; Chen, Z. Moisture buffering phenomenon and its impact on building energy consumption. Appl. Therm. Eng. 2017, 124, 337–345. [Google Scholar] [CrossRef]
- Rode, C.; Peuhkuri, R.H.; Mortensen, L.H.; Hansen, K.K. Moisture Buffering of Building Materials. 2005 Final Report. Technical University of Denmark. Available online: https://core.ac.uk/download/pdf/60659981.pdf (accessed on 5 January 2019).
- Padfied, T. The Role of Absorbent Building Materials. In Moderating Changes of Relative Humidity in Department of Structural Engineering and Materials. Ph. D. Thesis, The Technical University of Denmark, Lyngby, Denmark, 1998. [Google Scholar]
- McGregor, F.; Heath, A.; Fodde, E.; Shea, A. Conditions affecting the moisture buffering measurement performed on compressed earth blocks. Build. Environ. 2014, 75, 11–18. [Google Scholar] [CrossRef] [Green Version]
- Dubois, S.; McGregor, F.; Evrard, A.; Heath, A.; Lebeau, F. An inverse modelling approach to estimate the hygric parameters of clay-based masonry during a Moisture Buffer Value test. Build. Environ. 2014, 81, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Laborel-Préneron, A.; Magniont, C.; Aubert, J.E. Hygrothermal properties of unfired earth bricks: Effect of barley straw, hemp shiv and corn cob addition. Energy Build. 2018, 178, 265–278. [Google Scholar] [CrossRef]
- Palumbo, M.; Lacasta, A.M.; Holcroft, N.; Shea, A.; Walker, P. Determination of hygrothermal parameters of experimental and commercial bio-based insulation materials. Constr. Build. Mater. 2016, 124, 269–275. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, D.M.; Grillet, A.-C.; Diep, T.M.H.; Thuc, C.N.H.; Woloszyn, M. Hygrothermal properties of bio-insulation building materials based on bamboo fibers and bio-glues. Constr. Build. Mater. 2017, 155, 852–866. [Google Scholar] [CrossRef]
- Evrard, A.; Herde, D. Hygrothermal performance of lime hemp wall assemblies. J. Build. Phys. 2010, 34, 15–25. [Google Scholar] [CrossRef]
- Mortensen, L.H.; Rode, C.; Peuhkuri, R.H. Full Scale Tests of Moisture Buffer Capacity of Wall Materials. In Proceedings of the 7th Symposium on Building Physics in the Nordic Countries, Reykjavik, Iceland, 13–15 June 2005; The Icelandic Building Research Institute, IBRI, 2005. Available online: https://orbit.dtu.dk/files/122242065/Paper_NBPS2005_passys_ver.1.1_w_header.pdf (accessed on 25 January 2019).
- Colinart, T.; Lelievre, D.; Glouannec, P. Experimental and numerical analysis of the transient hygrothermal behavior of multilayered hemp concrete wall. Energy Build. 2016, 112, 1–11. [Google Scholar] [CrossRef]
- Latif, E.; Lawrence, M.; Shea, A.; Walker, P.; Walker, P. Moisture buffer potential of experimental wall assemblies incorporating formulated hemp-lime. Build. Environ. 2015, 93, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Ojanen, T.; Salonvaara, M. A Method to Determine the Moisture Buffering Effect of Structures During Diurnal Cycles of Indoor Air Moisture Loads. In Proceeding of the 2nd International Building Physics Conference, Leuven, Belgium, 14–18 September 2003. [Google Scholar]
- Busser, T.; Berger, J.; Piot, A.; Pailha, M.; Woloszyn, M. Experimental Validation of Hygrothermal Models for Building Materials and Walls: An Analysis of Recent Trends. 2018. Available online: https://hal.archives-ouvertes.fr/hal-01678857/document (accessed on 15 April 2019).
- IBP. WUFI® Pro Version 5.3; Fraunhofer Institute for Building Physics: Holzkirchen, Germany, 2015. [Google Scholar]
- EN 12664. Thermal Performance of Building Materials and Products. Determination of Thermal Resistance by Means of Guarded Hot Plate and Heat Flow Meter Methods. Dry and Moist Products of Medium and Low Thermal Resistance; CEN: Brussels, Belgium, 2002. [Google Scholar]
- ISO 12571. Hygrothermal Performance of Building Materials and Products. Determination of Hydroscopic Sorption Properties; International Organization for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- ISO 12572. Hygrothermal Performance of Building Materials and Products. Determination of Water Vapour Transmission Properties-Cup Method; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- EN 1602. Thermal Insulating Products for Building Applications. Determination of the Apparent Density; CEN: Brussels, Belgium, 2013. [Google Scholar]
- JISA 1470-1. Test Method of Adsorption/desorption Efficiency for Building Materials to Regulate an Indoor Humidity–Part 1: Response method of Humidity Japan; Japanese Standards Association: Tokyo, Japan, 2002. [Google Scholar]
- ISO 24353. Hygrothermal Performance of Building Materials and Products. Determination of Moisture Adsorption/Desorption Properties in Response to Humidity Variation; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Padfied, T.; Jeansen, L. Humidity Buffering by Absorbent Materials. 2010. Available online: https://www.conservationphysics.org/ppubs/humidity_buffering_building_interiors_nsb2011.pdf (accessed on 22 November 2018).
- Wu, Y.; Gong, G.; Yu, C.W.; Huang, Z. Proposing ultimate moisture buffering value (UMBV) for characterization of composite porous mortars. Constr. Build. Mater. 2015, 82, 81–88. [Google Scholar] [CrossRef]
- DIN 18947. Earth Plasters–Terms and Definitions, Requirements, Test Methods; NABau: Berlin, Germany, 2013. (In German) [Google Scholar]
- Busser, T.; Piot, A.; Pailha, M.; Bejat, T.; Woloszyn, M. From Materials Properties to Modelling Hygrothermal Transfers of Highly Hygroscopic Walls; CESBP: Dresden, Germany, 2016; Available online: https://www.researchgate.net/publication/308266233_from_materials_properties_to_modelling_hygrothermal_transfers_of_highly_hygroscopic_walls (accessed on 15 March 2019).
- Ge, H.; Yang, X.; Fazio, P.; Rao, J. Influence of moisture load profiles on moisture buffering potential and moisture residuals of three groups of hygroscopic materials. Build. Environ. 2014, 81, 162–171. [Google Scholar] [CrossRef]
- Abadie, M.O.; Mendonça, K.C. Moisture performance of building materials: From material characterization to building simulation using the Moisture Buffer Value concept. Build. Environ. 2009, 44, 388–401. [Google Scholar] [CrossRef]
- McGregor, F.; Heath, A.; Shea, A.; Lawrence, M. The moisture buffering capacity of unfired clay masonry. Build. Environ. 2014, 82, 599–607. [Google Scholar] [CrossRef] [Green Version]
- Rahim, M.; Douzane, O.; Le, A.T.; Promis, G.; Laidoudi, B.; Crigny, A.; Dupre, B.; Langlet, T. Characterization of flax lime and hemp lime concretes: Hygric properties and moisture buffer capacity. Energy Build. 2015, 88, 91–99. [Google Scholar] [CrossRef]
- Belakroum, R.; Gherfi, A.; Kadja, M.; Maalouf, C.; Lachi, M.; El Wakil, N.; Mai, T. Design and properties of a new sustainable construction material based on date palm fibers and lime. Constr. Build. Mater. 2018, 184, 330–343. [Google Scholar] [CrossRef]
- Kalamees, T.; Vinha, J. Hygrothermal calculations and laboratory tests on timber-framed wall structures. Build. Environ. 2003, 38, 689–697. [Google Scholar] [CrossRef]
- EN 15026. Hygrothermal Performance of Building Components and Building Elements—Assessment of Moisture Transfer by Numerical Simulation; CEN: Brussels, Belgium, 2007. [Google Scholar]
- James, C.; Simonson, C.J.; Talukdar, P.; Roels, S. Numerical and experimental data set for benchmarking hygroscopic buffering models. Int. J. Heat Mass Transf. 2010, 53, 3638–3654. [Google Scholar] [CrossRef]
- Talukdar, P.; Osanyintola, O.F.; Olutimayin, S.O.; Simonson, C.J. An experimental data set for benchmarking 1-D, transient heat and moisture transfer models of hygroscopic building materials. Part II: Experimental, numerical and analytical data. Int. J. Heat Mass Transf. 2007, 50, 4915–4926. [Google Scholar] [CrossRef]
- Busser, T.; Berger, J.; Piot, A.; Pailha, M.; Woloszyn, M. Dynamic experimental method for identification of hygric parameters of a hygroscopic material. Build. Environ. 2018, 131, 197–209. [Google Scholar] [CrossRef]
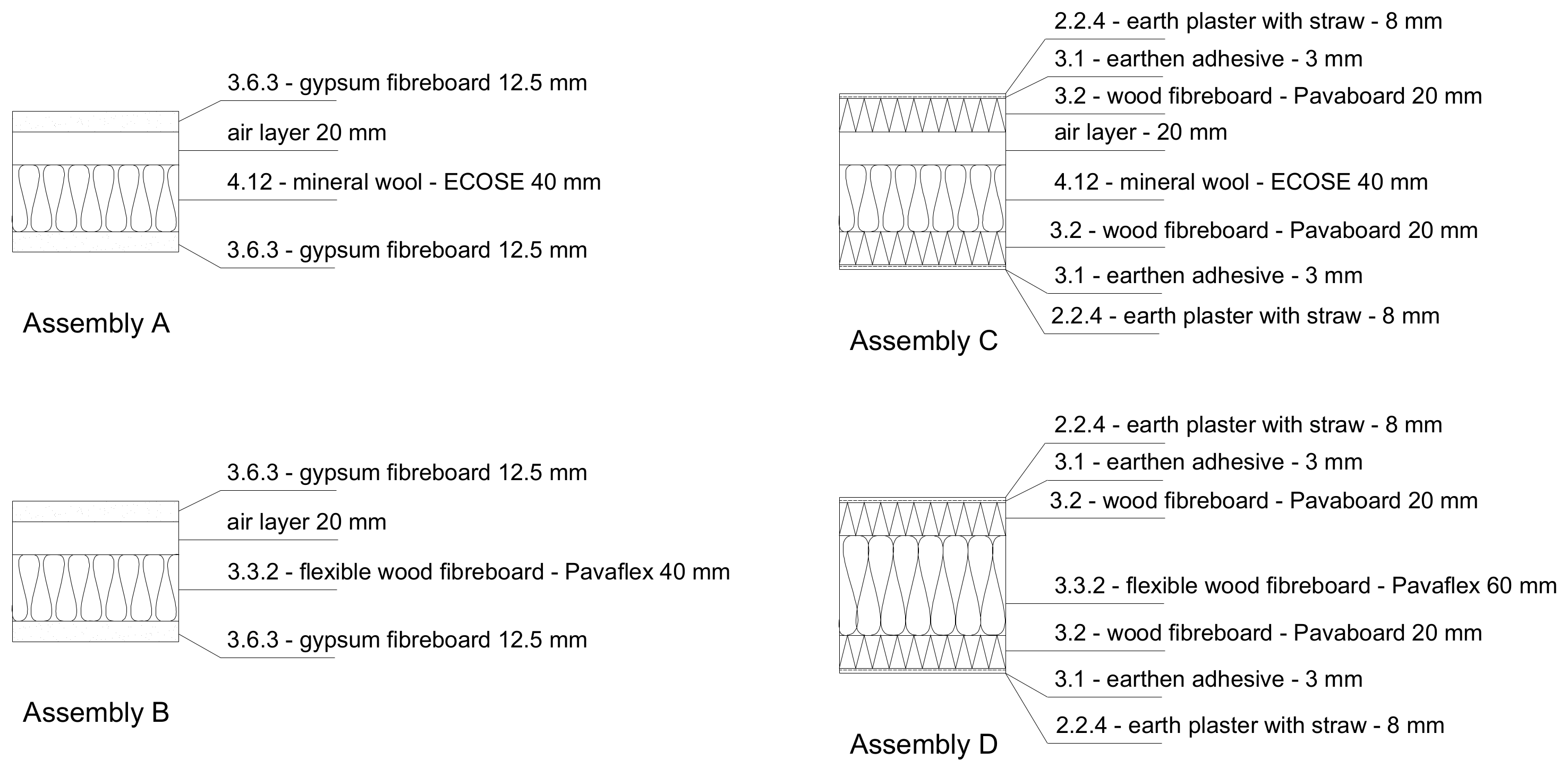
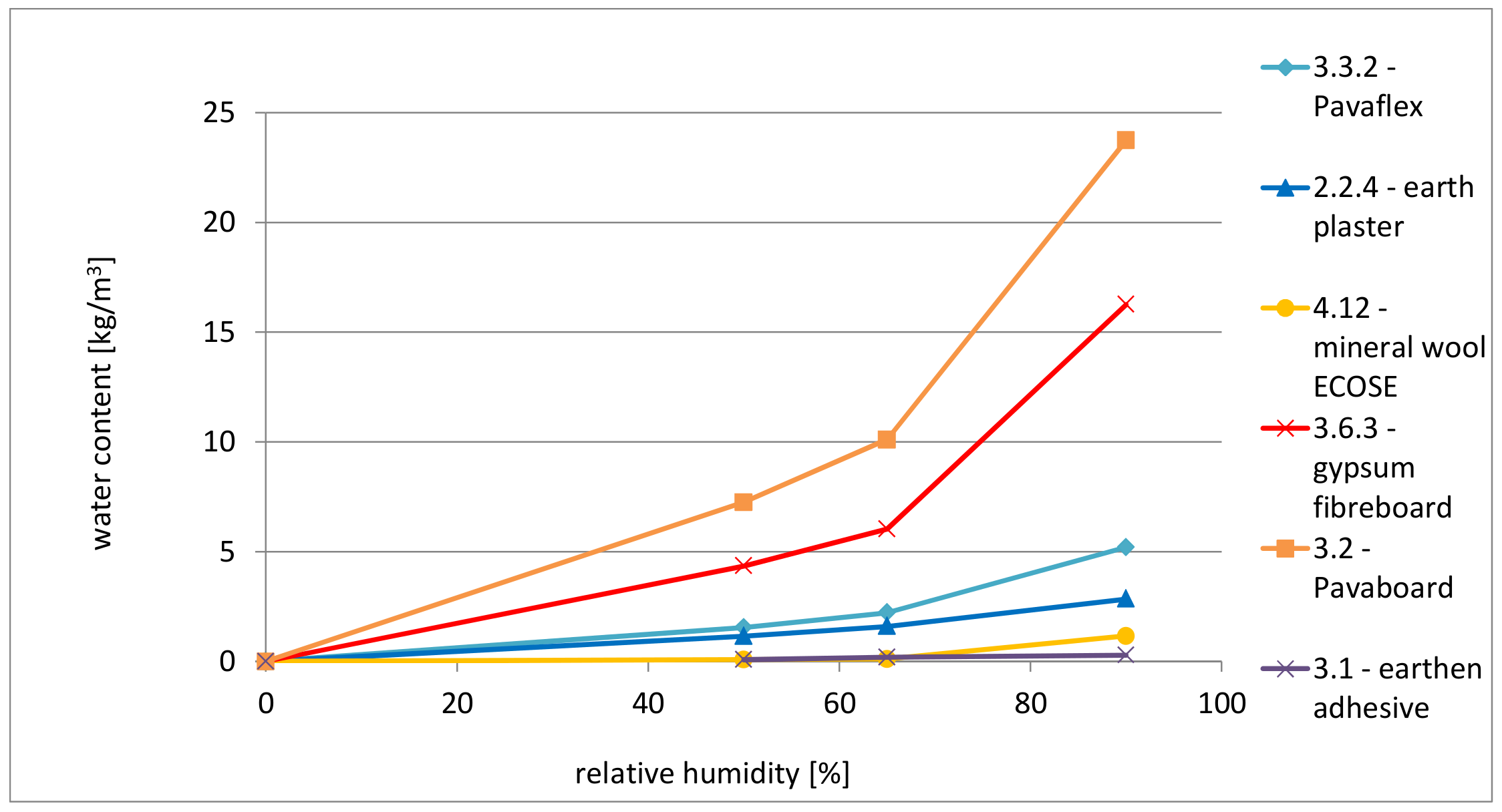


| Materials | Thickness | Density | Water-Vapour Resistance Factor | Conductivity 1 | Specific Heat | Porosity | ||
|---|---|---|---|---|---|---|---|---|
| (mm) | (kg/m3) | (-) | (W·m−1·K−1) | (J·kg−1·K−1) | (m3/m3) | |||
| 20% | 50% | 80% | ||||||
| 2.2.4 earth plaster with straw | 0.008 | 1456 | 18 | 0.71 | 0.75 | 0.94 | 880 | 0.85 |
| 3.1 earthen adhesive | 0.003 | 45 | 67 | 0.34 | 0.344 | 0.404 | 880 | 0.9 |
| 3.2 wood fibreboard Pavaboard | 0.020 | 232 | 6 | 0.047 | 0.048 | 0.051 | 1200 | 0.91 |
| 3.3.2 flexible wood fibreboard Pavaflex | 0.040 | 70 | 5 | 0.037 | 0.038 | 0.052 | 2100 | 0.96 |
| 3.6.3 gypsum fibreboard | 0.125 | 1200 | 15 | 0.22 | 0.23 | 0.24 | 800 | 0.53 |
| 4.12 mineral wool ECOSE | 0.40 | 15 | 3 | 0.037 | 0.038 | 0.041 | 850 | 0.9 |
| Sample | ΔMC Uptake at 80% RH (%) | ΔMC Release at 50% RH (%) |
|---|---|---|
| Assembly D | 0.96 | 0.77 |
| Assembly C | 0.84 | 0.69 |
| Assembly B | 0.82 | 0.75 |
| Assembly A | 0.57 | 0.42 |
| Material | ξ | δa (10−11) | dp,1% |
|---|---|---|---|
| (kg·m−1·s−1·Pa−1) | (mm) | ||
| 2.2.4 earth plaster with straw | 0.035 | 1.11 | 18.9 |
| 3.1 earthen adhesive | 0.003 | 0.28 | 174.3 |
| 3.2 wood fibreboard—Pavaboard | 0.417 | 3.33 | 23.8 |
| 3.3.2 flexible wood fibreboard—Pavaflex | 0.082 | 4.17 | 109.4 |
| 3.6.3 gypsum fibreboard | 0.417 | 3.33 | 10.2 |
| 4.12 mineral wool—ECOSE | 0.022 | 7.5 | 610.8 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczorek, D. Moisture Buffering of Multilayer Internal Wall Assemblies at the Micro Scale: Experimental Study and Numerical Modelling. Appl. Sci. 2019, 9, 3438. https://doi.org/10.3390/app9163438
Kaczorek D. Moisture Buffering of Multilayer Internal Wall Assemblies at the Micro Scale: Experimental Study and Numerical Modelling. Applied Sciences. 2019; 9(16):3438. https://doi.org/10.3390/app9163438
Chicago/Turabian StyleKaczorek, Dobrosława. 2019. "Moisture Buffering of Multilayer Internal Wall Assemblies at the Micro Scale: Experimental Study and Numerical Modelling" Applied Sciences 9, no. 16: 3438. https://doi.org/10.3390/app9163438
APA StyleKaczorek, D. (2019). Moisture Buffering of Multilayer Internal Wall Assemblies at the Micro Scale: Experimental Study and Numerical Modelling. Applied Sciences, 9(16), 3438. https://doi.org/10.3390/app9163438




