1. Introduction
Lean production as a production strategy is one of important paradigms of the 21st century which has been introduced in various variants practically in all companies in the world. A lean environment can minimise waste by elimination, merging or simplification of technologically unnecessary operations (stock, transport) and unnecessary elements of the work process (auxiliary and extra activities), that do not give any added value. Analyses [
1] have shown that merely 20% of activities in a production process directly add added value, 20% of activities do not directly give any added value, but are needed in order to carry out activities that add added value, while the rest (60%) are the activities which do not add added value and are, therefore, indicated as waste.
If a technological operation is observed as a fundamental element of a lead time for the production of a component, it is determined that the lead time of an operation consists of: (1) transition time calculated as completion of the preceding operation until the beginning of performance of the observed operation; it represents as much as 90% of the time in the structure of the lead time of an operation, and (2) operation performance time which represents only a 10% share in the structure of the lead time [
2].
Based on the above, the transition time is by far the most important in the structure of the lead time of an operation and it consists of a waiting time after a preceding operation, a transport time, and a waiting time before the observed operation [
3].
Each production-based company has a certain arrangement of sectors and workplaces, which can vary in its optimal layout. A great potential in terms of reducing losses and consequently in raising competitiveness can be hidden in a sub-optimal layout. It is common that smaller companies add newly bought machinery to places where space was sufficient, despite the sub-optimal layout.
This finding calls for a need to reorganise the material flow within a production system in a way to have minimum [
4] transition time between operations. This has a direct impact on the cost of a company’s internal transport [
5]. Francis, McGinnis and White [
6] maintain, that 20% to 50% of direct costs can be attributed to the costs of material manipulation [
7], wherein innovative organisational concepts have a decisive impact [
8].
The material flow can be defined as a structured and organised movement of a material from point A to point B through a production system in compliance with a prescribed technological method under consideration of efficient use of space, savings in energy and human resources [
5]. Material flow is a complex process of each production system and can be optimised without adequate tools for planning a material flow. Before optimising a material flow, the inventory must first be taken (the current situation assessed). A material flow usually consists of a huge number of elements (each with its own technological method) that are not identical but are similar in certain criteria. This is why families need to be formed on the basis of selection of representative elements. The quantity of data to be inventoried and analysed can thus be considerably reduced.
Bhosale and Pawar [
9] have modified a mathematical model to optimise material flow optimisation of a flexible manufacturing system with a real coded genetic algorithm. In their article [
10], the authors showed application of a statistical analysis and use of a group technology for the introduction of lean concepts into production systems in order to reach better leanness and consequently effectiveness of production systems. The group technology is also used for the analysis of a material flow in the process of converting a company having mass production and shop-floor configuration of workplaces into a cellular organisation of workplaces [
11].
Due to a diversity of elements the conventional ABC analysis and the multi-criteria ABC analysis, such as [
12,
13], are no longer sufficient in our case to inventory the material flow.
Based on a literature review a new model called the methodology for searching representative elements (MIRE) was designed which assists us in processing huge quantities of data.
The result of the method is an approximation of the real situation, while deviations are checked by feedback. All five steps of the MIRE are repeated as necessary, until a satisfactory ratio between the approximation accuracy and time savings is obtained in the processing of data.
2. Methods
2.1. Literature Review
Group technology (GT) is an approach of production management, in which part families are formed from a plurality of various parts that are manufactured in a treated production system and that use the same group of machines to be transformed from an input material into the required final shape and property of the product.
The methods designed to search families of parts and the group of machines they belong to are treated in the literature as cell formation techniques. Based on a proposal of various authors Selim et al. [
14] proposes the following overview of the cell formation technique:
- (1)
Descriptive procedures (part family identification, machine group identification, part families/machine grouping simultaneously);
- (2)
Cluster analysis;
- (3)
Graph partitioning;
- (4)
Artificial intelligence;
- (5)
Mathematical programming (linear programming, linear and quadratic integer programming, dynamic programming, goal programming).
Descriptive procedures part families/machine grouping were first represented by Burbidge as a Production flow analysis [
15]. Dekleva et al. [
16] extended the Burbridge’s production flow analysis and called it the extended production flow analysis. The extended material flow analysis included two steps:
- (1)
Macroanalysis is analysing the material flow (flow of parts) on a macro level, i.e., between departments of a company. The goals of these analysis were: identification of extra paths between the departments of the company and their elimination (usually by changing a technological method) and determination of a standard material flow between the departments of the company.
- (2)
Microanalysis is included in a material flow analysis within an individual department. The goals of this analysis were: simultaneous identification of part families and groups of needed machines for their manufacturing and formation of production cells for the part families. A cluster analysis method and an incidence matrix method were proposed for the formation of cells.
Nouri et al. [
17] propose, in particular, metaheuristic techniques such as: genetic algorithm, artificial neural networks, fuzzy set theory, colony systems, tabu search, branch and bound method, simulated annealing.
Nowadays, the goals of group technology and formation of various shapes of production systems (cells) need to be connected, especially with the goals of leanness, flexibility and agility of production. Due to market demands, a large number of different, yet mutually similar parts appear in the production process. That means that the production program contains a large number of different products that are similar to each other, as the companies emphasizes the possibility of making a tailored products for each customer to maintain its competitiveness in global markets. It is quite common in smaller companies that the record of material flow has never been made. They simply lack the time and the human resources, while trying to maintain acceptable production and make profit. With time and production line updates, the layout becomes increasingly non-optimal and the diversity of products only increases this problem.
So, it is not reasonable to analyse a material flow and a value flow on the entire amount of available data. Within thousands of pieces, representative parts (hereinafter representative elements) need to be selected. This is made possible by the methodology for searching representative elements, MIRE, which can relatively quickly give us a sufficient approximation of the material flow, which serves as the basis and the first step towards lean production, consequently increasing the company’s competitiveness in the global market.
The methodology is most suitable for smaller companies that throughout their growth and development simply did not have the time, resources and competences to create a material flow inventory because their priorities were mainly focused on delivering the products and keeping up to date with the latest technological trends.
2.2. Methodology for Searching Representative Elements (MIRE)
Basic data for the implementation of the MIRE can differ, yet they usually refer to one selected influencing variable, e.g., mass, dimension, volume, size, material value, production time, added value. It is important that a selected variable is used throughout the methodology from its very beginning.
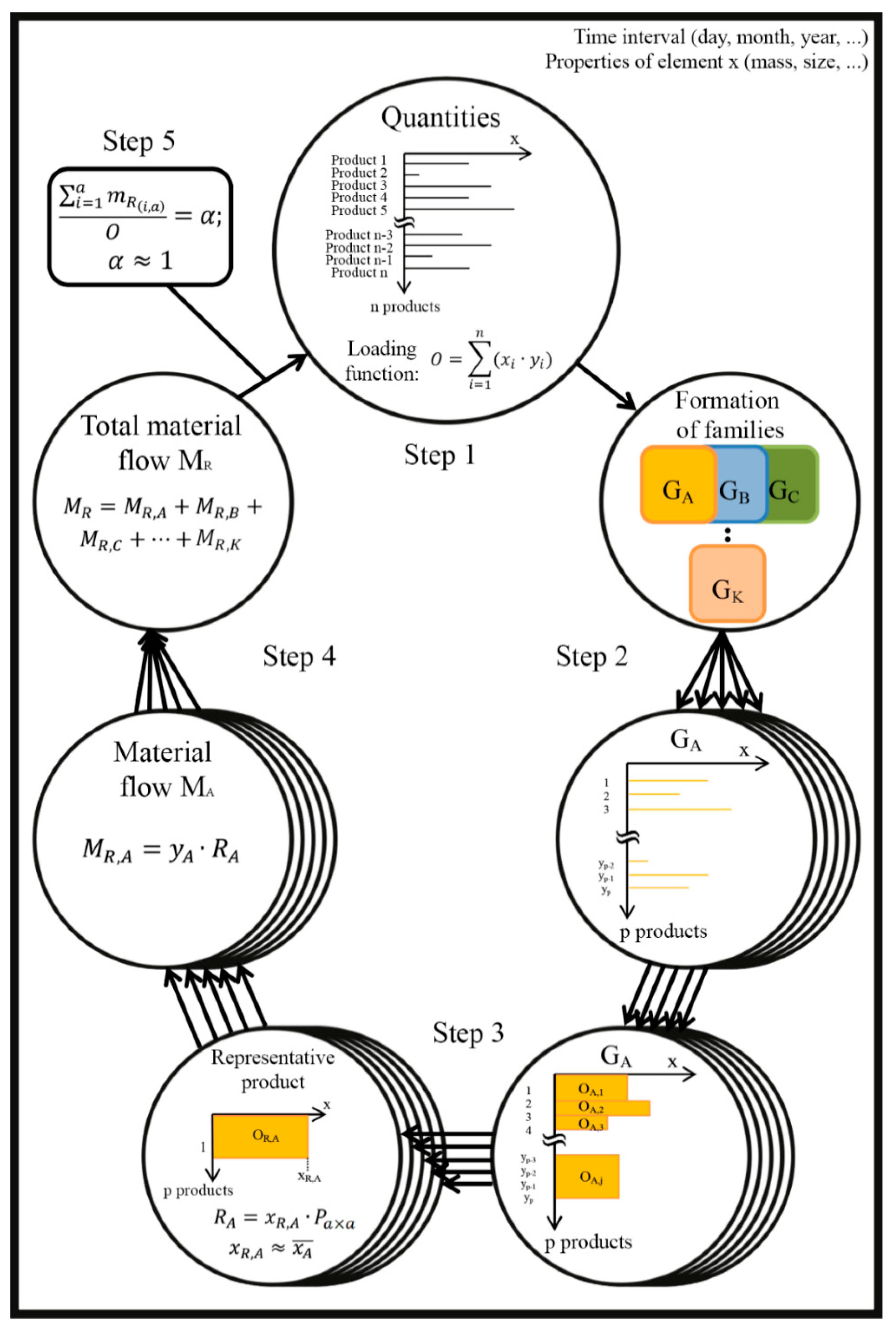
The MIRE methodology follows five steps represented in
Figure 1. First, a time interval for data gathering and a creating criterion(s) are selected, which are then considered through the entire analysis process.
2.2.1. Step 1: Quantities
In a first step, an influential variable is selected that will serve as the basis for searching representative elements.
A production of n number of products is anticipated for the selected time interval, each of them having value x.
The loading function is defined as a product of the variable of one product with their own quantity and functions as a weight function (
Figure 2). The total load in the selected time interval is:
2.2.2. Step 2: Formation of Families
The products having a similar sequence of technological operations are grouped into families (
Figure 3), where the selected variable is not yet taken into consideration. The larger the number of families, the more precisely the material flow will be inventoried.
Gl—indication of family l
K—number of families; where: K ≤ n
p—number of products in a family
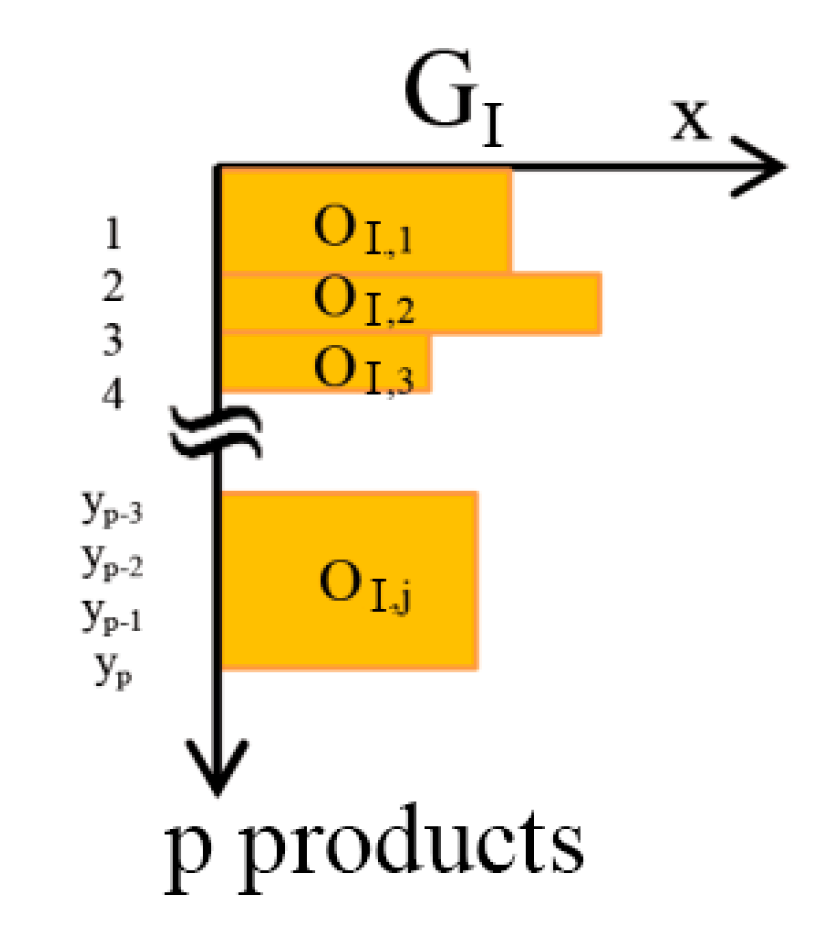
2.2.3. Step 3: Selection of a Representative Product of the Family
The family joins products with different values
x, which have an identical or similar sequence of technological operations. The variables selected with an identical or similar value are grouped (
Figure 4). The accuracy of grouping impacts the accuracy of material flow inventory. The more groups that are formed, the more accurate the inventory will be.
So,
j groups are obtained and each group has a load
OI,i.
Ol,i—load of the ith group of products having an identical or similar value of the selected variable within family l
xl,i—value of the selected variable of a product in the ith group of family l
yl,i—number of products in the ith group of family l
—average value of the selected variable of a product of family l
Ol—total load of family l
yl—number of all products of family l
The obtained is used to search for such a product within family l, to which the value of variable x gets closest. In this way a representative product of family l, Rl, is selected.
The representative product should be assigned a path through the production and a sequence of treatment processes. This path should be written in a square FROM–TO matrix
Pa×a, where
a is the number of workplaces. Column or row
a should represent the last workplace in the production (assembly, warehouse, takeover, etc.).
The representative product of the
Ith family thus has the value of the selected variable
xR,l and path
P.
2.2.4. Step 4: Material Flow
The calculation of representative products of individual families allows us to define their material flow:
The total material flow of all families in this case is:
2.2.5. Step 5: Checking Material Flow Approximation Accuracy
All representative products have been obtained and used to calculate an approximation of the total material flow. Since its accuracy is of interest, the equation below is used:
mR(i,a)—
ith element of the
ath column in matrix M
R.
The closest
α comes to value 1, the more accurate the material flow
MR inventory is.
M—actual material flow.
The actual material flow or 100% accuracy of inventory of material flow
MR is obtained with the proviso that the number of families equals the number of all products in the selected time interval (
K =
n). In such a case, exactly one product is present within each family and this automatically means:
As there are no deviations in the values of the selected variable and FROM–TO matrices of representative products, the material flow is inventoried with 100% accuracy.
The essence of this methodology to reduce the quantity of data to be processed in order to obtain a satisfactory material flow inventory. Therefore it is not reasonable, that K = n.
To obtain credible results consistency is needed:
In classifying the products into families based on a criterion of sequence of treatment processes;
In grouping the products within families based on the criterion (selected variable); and
In selecting a representative product based on .
As described, MIRE helps us process large amounts of data and it is especially useful for cases where the elements are different and similar at the same time, depending on the criteria (size, weight, cost, etc.). By creating families and selecting their representative elements, the amount of data, that needs to be processed is significantly reduced. In this case, due to the variety of elements, the classic ABC analysis is not sufficient [
17]. The result of the process is an approximation of the real material flow, and the deviations are checked by a feedback loop. All five MIRE steps are repeated as needed, until a satisfactory ratio between the accuracy of the approximation and the saved time is achieved.
MIRE can also be used by companies that already had their material flow recorded, but need to quickly check how optimal their layout is. This is suitable after adding or updating the machinery or presenting a new product into the production line. In cases where the company never had their material flow recorded, MIRE can significantly shorten the time needed by reducing the quantity of data to be inventoried and analysed, because we do not need to consider all the material flow data, but only the elements, based on which we can satisfactorily describe the material flow. Needed input can be accumulated through positions of assembly drawings or any other source, that contains information about product parts, technological operations, etc.
3. Case Study
A Slovene company having 80 employees counts on adaptability and the possibility of manufacturing custom-made products, which provides an opportunity for being competitive on the global market.
Since the company does not have an Enterprise Resource Planning system (ERP system) or does rather not use it for production management, there is no material flow traceability. The company has a material flow inventory for positions of an assembly drawing; however, there is no material flow overview through the production to the assembly. So, there is no overview, through which processing phases blanks are transferred when leaving the main warehouse. Since a material flow inventory is needed to prepare a layout, this was a major problem. There was a huge quantity of data in the form of launching orders and structural product tallies. This is why a methodology had to be found, with which an accurate material flow inventory could be obtained in the simplest possible way.
An analysis of production assortments of companies in Slovenia has shown that data on masses of parts are the easiest to obtain; it was used in this paper as the main influencing variable x.
3.1. Application of the MIRE Methodology
The main advantage of the MIRE methodology is the reduction of the number of products, for which a path through the production needs to be traced in order to achieve a satisfactory inventory of the total material flow.
The period from 2012 to 2015 was selected for the analysis. Only the last year could have been included in the material flow inventory, which would reduce the quantity of data, however, a possibility of influence of potential fluctuation in orders would be increased. Inclusion of a longer period of time provides for a more precise annual sales average and more reliable anticipation of production load for the years to come.
The company produced approximately 3300 products in the past four years.
3.2. Selection of Representative Products
By using the clustering technology, the products were classified pursuant to their production mode into 96 groups. A two-dimensional ABC analysis was used [
18] on criteria of product size and frequency of production. With the help of the employees, the products were divided into three main families and designated:
The products were classified into 18 groups based on the quantity of produced products.
Table 1 shows the data on the quantities produced in the period from 2012 to 2015.
For a further analysis, five families were selected from the entire family of products (18 products) The selection was based on experience and the quantities of products these families cover: Product 1, Product 5, Product 6, Product 7 and Product 10.
Suppliers supply a large quantity of various products (supplier products—77 families) for the analysed final product, yet many of them appear rarely.
Table 2 shows the 10 most frequent products from suppliers, which are used for the analysis.
Additionally, a module was selected that is integrated into all products (products from suppliers excluded). The modules differ only in size but are treated separately, because a buyer does sometimes not need it or orders it separately. As they are all practically only scaled versions of Module 1, weights were introduced on the basis of size/mass. A representative product of the module family was determined, which is shown in
Table 3.
As a representative product, only one module is selected, the weight of which comes closest to the average weight of the module. In this case, Module 7 with weight 20 came closest to the average weight of the module which amounts to 18.3. A weight function method was used to determine all representative products of the selected families.
4. Simulation
A production line with 356 different product groups was simulated, creating more than 44,000 individual products. The properties of each were: produced quantity, mass, the sequence of technological operations, size, cost and production time. This represented a common year of production in a smaller company. Data was written in a spreadsheet, then read and handled with a code written in MATLAB (Matlab 2018a, The MathWorks Inc., Natick, MA, USA). The presented simulation shows how we can choose a small fraction of products according to desired variables and still achieve a sufficient portion of the whole material flow.
A simulation by all steps of the MIRE methodology for the selected production will be shown below. In a first step, an influencing variable needs to be selected, which is a product mass in our case.
Figure 5 graphically illustrates all products of the production as a function of mass.
Figure 5 shows an entire population of products of the selected production at the selected influencing variable (mass). The arrangement in
Figure 5 is not ordered by size, it is random. There is huge dissemination of a number of products based on the criterion of product mass since the mass ranges from several kilos to more than two tons. The illustrated case represents a typical production assortment of a company that produces custom-made products.
This step is followed by grouping of products within a family (
Figure 6) and selection of a representative of the family that will make the best inventory of the products within a family (
Figure 7) as the representative of this family.
Figure 6 illustrates a distribution of products by mass within a certain family that was formed based on the sequence of treatment processes. More than 500 products are classified in 25 groups.
If a closer look is taken at each group, an average mass of one product of the entire family can be determined (
Figure 7).
The representatives of groups within a family and their mass are shown in
Figure 7. The red line represents an average mass of a product in a family. A representative of group 13 comes closest to this value and this is why it is selected as the representative of the family.
Then follows simulation of descending distribution of representatives by share under consideration of the criterion of the mass (
Figure 8).
The graph in
Figure 8 can be used to determine how many representatives will be selected and their material flow inventoried to include a satisfactory share of the entire production assortment. The criteria of size, price and production time are also shown.
An increase in the share of production time and size is noticed with the twelfth heaviest representative, and it will therefore be the most reasonable to select the 12 heaviest representatives and define their material flow. In this way, more than 80% share of the mass of all products, almost 60% share of the size of all products, approximately 50% share of the total production time, and approximately 45% share of the price of all products would be captured.
Figure 9 shows a graph of selection of a number of representatives in a multi-criteria selection. The important variables are the mass and size of a product in a ratio of 3:2, which serves as an example of approximation of criteria importance regarding transport and stock. As evident from the figure, the reasonable number of representatives to be selected could be 6, 11 or 17, as the processing time/share of the inventory ratio is the most beneficial. This depends on the share of the inventory of all variables, with which we are satisfied. The larger the number of selected representatives, the higher share of the production assortment will be included. If the first 11 most important representatives are taken as an example based on the mass and size (in a 3:2 ratio), an approximately 80% share of the total mass of all products, an almost 60% share of the size and some 30% share of the price and production time of all products are inventoried.
The black line represents an order of the representatives which are distributed from the most important to the least important one based on both criteria: mass and size in a 3:2 ratio. If these two criteria would be equally important, the black curve would be a line of symmetry of the red and blue lines or a centroidal axis of the hatched area, but we see that it comes closer to the curve of the mass.
5. Results
The methodology for searching representative elements provides a satisfactory material flow inventory. In fact, it proves to be a very efficient way for the processing of a large quantity of mutually similar data. The simulation shows how MIRE manipulates product information through each step. The generated data represents a typical production assortment of a company that produces custom-made products.
Figure 8 and
Figure 9 describe how the share of selected variable increases together with the number of representatives of each product family. The increase of the share of other variables can be seen, too, and an example of one and two criteria simulation is illustrated.
Out case study did not include any pre-recorded material flow, thus only an approximation of the material flow share could be done with MIRE. Sufficient data had to be obtained manually from assembly drawings and it would be very time consuming to gather all the information needed to calculate the entire material flow. A solution was needed quickly, which led to the creation of MIRE methodology.
Table 4 shows that the representative products inventory almost a half of the total material flow. There may be certain deviation, yet it can be neglected if we bear in mind that only 0.5% of all products were selected for the 44% share of the inventory. The work is reduced by almost a factor of 100, while the obtained material flow is more than sufficient to design a new layout because it includes the most frequent, the largest and the most important products of the company.
MIRE is estimated to speed up the process of creating the material flow inventory up to 10 times. It can be also be used to check how optimal is the current layout. Instead of weeks, the material flow can be calculated in hours, saving time and consequently money. Although the output does not cover 100% of the material flow, the final share of it is sufficient as we can choose and adjust and multiple variables and its weights until they meet our needs and achieve high enough certainty of the result.
6. Conclusions
There are many efficient methods designed to search families of parts. They vary from relatively simple to very sophisticated, but they all have one thing in common: a large amount of data. In our case, the company did not have a pre-recorded material flow. There was no ERP system, so we had to be creative in our search for relevant product information. We gathered the necessary data from assembly drawings manually. With MIRE methodology we were able to find the sufficient data for the calculation of an approximation of the total material flow.
The MIRE saves plenty of time in processing a huge quantity of data. It is mostly applicable for cases, where the elements differ from each other based on some criteria and are similar to each other based on others. It can be of great help to the companies that do not have a digital observer of inventory of material flow in the ERP system, because it can give a sufficient approximation of the actual situation. The MIRE result helped in conceiving a suboptimal production layout that will serve as a basis for re-organisation of the production of the company.
Having proved that the MIRE is applicable and efficient, it is reasonable to develop it further. The steps, in which weight functions are used, can be even more precisely defined.
Simulations would help us detect the influence of deviation of a representative product from an average product, the influence of the number of families which is inversely proportional to the number of elements in an individual family, and the influence of accuracy of grouping of products within a family. Input data, such as number of workplaces, number of families, and number of all products would additionally be changed and their correlation with other factors could be monitored.
Ideally, a mathematical model could create graphs and tables that will be easy to use and from which it would be easy to deduct what share and reliability of a material flow inventory can be anticipated based on known input parameters. Simultaneously with simulations, the MIRE would be used on the data in the companies which have an accurate material flow inventory as an upgrade to the ERP system. The simulated and real results could be compared for an even more thorough understanding of MIRE’s advantages. This could be done in a company that has a complete overview and tracking of its material flow. In that case, many other methods have already been developed, but all of them require an organised database. The MIRE method was developed for a specific and practical case, where there is essentially minimal information of the company’s material flow. Therefore, comparison to other methods is a little difficult and unwarranted. Regarding further development of MIRE methodology, some programming knowledge could convert the final product into computer software, into which a person could enter input parameters, select the desired material flow, and share its accuracy. This would result in instructions that would suggest which families should be selected and what should the representative products be, to which the FROM–TO matrix would need to be assigned.