Feedback Stabilization of First Order Neutral Delay Systems Using the Lambert W Function

Abstract

This paper presents a new approach to stabilize the first order neutral delay differential systems with two time delays. First, we provided a few oscillation and non-oscillation criteria for the neutral delay differential equations using spectrum analysis and the Lambert W function. These conditions were explicit and the real roots were analytically expressed in terms of the Lambert W function in the case of non-oscillation. Second, we designed a stabilizing state feedback controller for the neutral delay differential systems with two time delays, wherein the proportional and derivative gains were analytically determined using the results of the non-oscillation criteria. A few examples are given to illustrate the main results.

1. Introduction

Many practical problems can be described using delay differential equations (DDE), as time delays are intrinsic to many real systems. Additionally, multiple sensors, actuators, controllers, shared communication networks, and haptics introduce multiple time delays [1,2,3,4]. The delays, which are either fixed constants or distributed delays, play an important role in real systems. Neutral delay differential equations (NDDE) are dynamic systems, wherein the delays appear in both the state variables and their time derivatives. Practical applications of NDDE can be seen in circuit theory [5], mechanical systems [6,7,8], neural networks [9], bioengineering [10], economics [11], and control engineering [12,13,14]. Recent research topics in the field of delay differential systems are stability analysis, bifurcation analysis, control theory and application, numerical computation, and periodic solutions analysis.

Stability analysis and stabilization of neutral delay differential systems (NDDS) is a subject of great practical and theoretical importance. This field has received considerable attention over the decades because a time delay might change the performance and stability of a control system considerably. Moreover, the NDDS exhibit drastic differences in their characteristic behavior as compared to the retarded delay differential equation (RDDE), wherein the delay argument does not occur in the highest order derivative term. Comprehensive research on this subject can be found in the literature [14,15]. However, the solution of delay differential systems is complex due to the presence of exponential type transcendental terms in the system characteristic equation. Conventional approaches used for the stability analysis of NDDS are based on the Lyapunov function. These techniques seek to determine the solution of a linear matrix inequality problem. The spectrum approach used to solve the stability problem is mainly based on the solution of an eigenvalue problem. This provides a more accurate stability analysis with less computational burden. The authors in [16], have investigated the stability of the first order RDDE using the Lambert W function, which has been implemented in all major mathematical software packages (for example, MATLAB, Mathematica, Maple, and R).

Blyuss [17] has developed a time-delayed proportional control law that stabilizes the unstable second order neutral delay systems using the parameter space approach. A delayed proportional derivative (PD) controller with a single constant delay for the second-order undamped system has been presented in [18]. In the study described in [19], the authors showed that a non-descriptor type neutral time delay system could be µ-stabilized using derivative feedback under certain conditions. The authors in [20], have designed a proportional state feedback controller for the NDDS with multiple time-delays by the pole placement method. The radius of the essential spectrum of the neural equation solution operator was computed, and the stabilization problem of the neutral equation was reduced to a problem involving only a finite number of characteristic roots. A Lyapunov function-based stability criterion for the scalar NDDE with a single delay has been presented in [21].

In the last few decades, there has been considerable interest in deriving new sufficient conditions for the oscillation or non-oscillation of various types of first-order NDDE solutions [22,23,24,25,26]. This has been the case due to its theoretical interest and important applications. A few sufficient conditions for NDDE with constant coefficients have been presented in [22,23,24]. A number of authors have established a few sufficient conditions for oscillation and non-oscillation using an auxiliary solution [25,26].

In this study, we developed a new stabilization method for first order NDDS with two time-delays. The proposed method consists of two parts: (1) sufficient conditions for the oscillation and non-oscillation of solutions of the NDDE using the geometric approach, and (2) a stabilization method using a state feedback controller. The Lambert W function is well applicable to the DDE with a single delay. Furthermore, the roots of its corresponding characteristic equation can be expressed in terms of the Lambert W function. An outline of the first part of the method is that firstly we define two functions $f(\lambda )$ and $g(\lambda )$, which are transcendental equations, such that the characteristic equation $p(\lambda )$ is the difference of two functions, i.e., $p(\lambda )=f(\lambda )-g(\lambda )$. The solution sets of $f(\lambda )=g(\lambda )$ are then equal to the roots of the characteristic equation. Secondly, the geometric properties of the introduced functions are obtained using the Lambert W function. The solutions of the characteristic equations are the intersection points (or tangent points), of the two defined functions. This enables us to easily derive the sufficient oscillation conditions, and the sufficient conditions for the existence of non-oscillations of the characteristic equation using the Lambert W function. Therefore, the solutions of the NDDE are analytically expressed in terms of the Lambert W function. In the second part of the method, we designed a stabilizing state feedback controller for NDDS with two time-delays, where the proportional and derivative gains were analytically determined using the results from part one.

This paper is organized as follows: In Section 2, the problem is formulated and a few preliminary concepts are detailed. In Section 3, we present the oscillation and non-oscillation criteria for the NDDE and design a stabilizing state feedback controller. In Section 4, some illustrative examples are given to show the effectiveness of the proposed method. This paper ends with a few concluding remarks.

2. Preliminary and Problem Formulation

The Lambert W function (hereafter denoted as $W(\cdot )$), is a multivalued complex function defined as the solution of the following equation:

$$W(z)e^{W(z)}=z,$$

(1)

where, $z$ is a complex number. The Lambert W function has infinitely many complex branches when $z$ is a complex number [27]. If $z$ is a real number and $z\ge -e^{-1}$, then $W(z)$ becomes a real function with two possible real branches. By convention, the branch satisfying $W(z)\ge -1$ is considered to be the principal branch ($W_0(z)$), while that satisfying $W(z)<-1$ is the negative branch ($W_{-1}(z)$). Several function values of $W(z)$ are $W(-e^{-1})=-1$, $W(0)=0$, and $W(e)=1$.

In this paper, we consider the first order NDDS with two time delays of the form:

$$\dot{x}(t)+a\dot{x}(t-{\tau }_1)+bx(t-{\tau }_2)=u(t),$$

(2)

where $b,{\tau }_1,{\tau }_2$ are positive constants, $a$ is a negative parameter, and $u(t)$ is a control input. The autonomous NDDE is given by:

$$\dot{x}(t)+a\dot{x}(t-{\tau }_1)+bx(t-{\tau }_2)=0.$$

(3)

The characteristic equation associated with Equation (3) is given by:

$$p(\lambda )=\lambda +a\lambda e^{-{\tau }_1\lambda }+b{e}^{-{\tau }_2\lambda },$$

(4)

where, $\lambda \in C$ are the characteristic roots. All solutions of Equation (4) are oscillatory if and only if the corresponding characteristic equation has no real roots [24].

Here, we define two functions as follows:

$$f(\lambda )=\lambda +a\lambda e^{-{\tau }_1\lambda },$$

(5)

$$g(\lambda )=-b{e}^{-{\tau }_2\lambda }.$$

(6)

Using Equations (5) and (6) we can rewrite the characteristic equation as:

$$p(\lambda )=f(\lambda )-g(\lambda ).$$

(7)

Thereafter, $p(\lambda )=0$ results in the following equation:

$$f(\lambda )=g(\lambda ).$$

(8)

Hence, the solution set of Equation (8) is equal to the roots of Equation (4).

Throughout this paper, we assume that $b,{\tau }_1,{\tau }_2$ are positive constants and $\mathrm{Re}(\lambda )$ denotes the real part of a complex variable $\lambda$.

3. Main Results

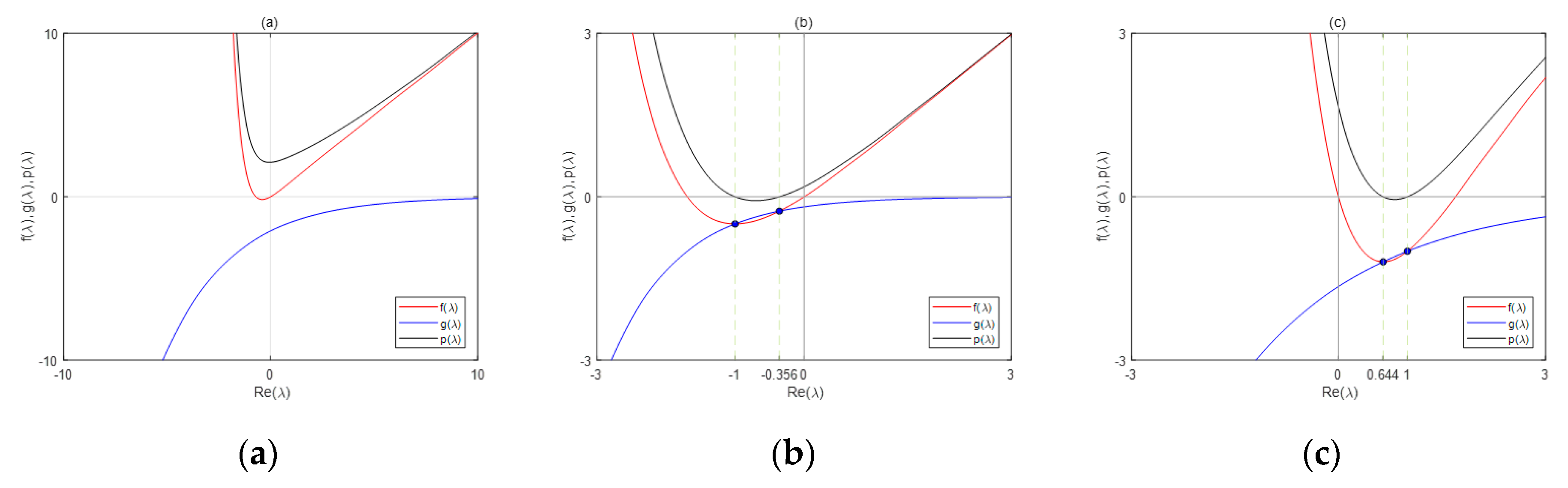
3.1. Oscillation and Non-Oscillation Criteria

In this section, we discuss the oscillation and non-oscillation criteria for Equation (4). The non-oscillation criteria indicate the definite existence of some real roots.

Lemma 1.

If$a<0$, then the following are true:

(i) 

The global minimum value of$f(\lambda )$is nonpositive.

(ii) 

$f(\lambda )$is strictly decreasing on$(-\infty ,{\lambda }_m)$, strictly increasing on$({\lambda }_m,\infty )$and has a global minimum point at ${\lambda }_m$.

Proof. 

In Equation (5), $f(0)=0$ and the extreme values of $f(\lambda )$ are obtained by applying L’Hopital’s rule. Subsequently, $f(-\infty )=\infty$, and $f(\infty )=\infty$. Hence, the graph of Equation (5) opens upwards. Therefore, the global minimum can be found by setting its first derivative to zero.

$$f^{\prime }(\lambda )=1+a{e}^{-{\tau }_1\lambda }-a{\tau }_1\lambda e^{-{\tau }_1\lambda }=0.$$

(9)

Multiplying both sides of Equation (9) by $\frac{e}{a}$, we get:

$$\left(1-{\tau }_1\lambda \right)e^{1-{\tau }_1\lambda }=-e{a}^{-1}.$$

(10)

Using the Lambert W function, the above equation can be rewritten as:

$$W(-e{a}^{-1})e^{W(-e{a}^{-1})}=-e{a}^{-1}.$$

(11)

From Equations (10) and (11) we obtain:

$$1-{\tau }_1\lambda =W(-e{a}^{-1}).$$

(12)

Hence, the zero (denoted by ${\lambda }_m$) of Equation (9) can be written in terms of the Lambert W function as:

$${\lambda }_m=\frac{1}{{\tau }_1}\left(1-W(-e{a}^{-1})\right).$$

(13)

As $a<0$, ${\lambda }_m$ is a real value. When $a=-1$, then ${\lambda }_m=0$ and $f(0)=0$. Substituting Equation (13) into Equation (5), we obtain the following equation:

$$\begin{array}{c}f({\lambda }_m)=\frac{1}{{\tau }_1}\left(1-W(-e{a}^{-1})\right)+\frac{1}{{\tau }_1}\left(1+a{e}^{W(-e{a}^{-1})-1}\right),\\ =\frac{1}{{\tau }_1}\left(2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}\right).\end{array}$$

(14)

To simplify, let:

$$\gamma =2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}.$$

(15)

Multiplying both sides of Equation (15) by $W(-e{a}^{-1})$, we obtain:

$$\gamma W(-e{a}^{-1})=2W(-e{a}^{-1})-W^2(-e{a}^{-1})+aW(-e{a}^{-1})e^{W(-e{a}^{-1})}{e}^{-1}.$$

(16)

From Equation (1), $W(-e{a}^{-1})e^{W(-e{a}^{-1})}=-e{a}^{-1}$. Hence, Equation (16) can be rewritten as:

$$\gamma W(-e{a}^{-1})=2W(-e{a}^{-1})-W^2(-e{a}^{-1})-1.$$

(17)

We obtain the following inequality for $W(-e{a}^{-1})>0$:

$$\gamma =-\frac{{\left(W(-e{a}^{-1})-1\right)}^2}{W(-e{a}^{-1})}<0.$$

(18)

This implies that $f({\lambda }_m)\le 0$, where the equality holds when $a=-1$. Now, we will prove (ii). Let ${\lambda }_r={\lambda }_m+r$, $r\in R$. Then Equation (9) yields:

$$\begin{array}{c}{f}^{\prime }({\lambda }_r)=1+a{e}^{-{\tau }_1{\lambda }_m}{e}^{-{\tau }_{1}r}-a{\tau }_1{\lambda }_m{e}^{-{\tau }_1{\lambda }_m}{e}^{-{\tau }_{1}r}-a{\tau }_{1}r{e}^{-{\tau }_1{\lambda }_m}{e}^{-{\tau }_{1}r},\\ =\left(1+a{e}^{-{\tau }_1{\lambda }_m}-a{\tau }_1{\lambda }_m{e}^{-{\tau }_1{\lambda }_m}\right)e^{-{\tau }_{1}r}+1-e^{-{\tau }_{1}r}-a{\tau }_{1}r{e}^{-{\tau }_1{\lambda }_m}{e}^{-{\tau }_{1}r}.\end{array}$$

(19)

Using Equation (9), Equation (19) yields:

$$f^{\prime }({\lambda }_r)=1-e^{-{\tau }_{1}r}-a{\tau }_{1}r{e}^{-{\tau }_1{\lambda }_m}{e}^{-{\tau }_{1}r}.$$

(20)

If $r>0$, then $0<e^{-{\tau }_{1}r}<1$, and this results in $f^{\prime }({\lambda }_r)>0$. This implies that $f(\lambda )$ is strictly increasing on the interval $\left({\lambda }_m,\infty \right)$. If $r<0$, then $e^{-{\tau }_{1}r}>1$, and this results in $f^{\prime }({\lambda }_r)<0$. This also implies that $f(\lambda )$ is strictly decreasing on the interval $\left(-\infty ,{\lambda }_m\right)$. □

We can rewrite Equation (5) as follows:

$$f(\lambda )=\lambda \left(1+a{e}^{-{\tau }_1\lambda }\right).$$

(21)

The roots of Equation (21) are $\lambda =0$ and $\lambda =\frac{1}{{\tau }_1}\ln (-a)$. Since $\ln (-a)>0$ for $a<-1$ and $\ln (-a)<0$ for $-1<a<0$, we consider the following three cases: (i) $-1<a<0$, (ii) $a=-1$, and (iii) $a<-1$.

Lemma 2.

If$-1<a<0$and$\lambda \le \frac{1}{{\tau }_1}$, then$f(\lambda )$is convex on the interval$[\frac{1}{{\tau }_1}\ln (-a),\frac{1}{{\tau }_1}]$.

Proof. 

The second derivative of $f(\lambda )$ is given by:

$$f^{″}(\lambda )=-{\tau }_{1}a{e}^{-{\tau }_1\lambda }-a{\tau }_1{e}^{-{\tau }_1\lambda }\left(1-{\tau }_1^{}\lambda \right).$$

(22)

Because $a<0$, then $f^{″}(\lambda )>0$ if $\lambda \le \frac{1}{{\tau }_1}$. □

Lemma 3.

If$a<-1$and$\lambda \le \frac{1}{{\tau }_1}$, then$f(\lambda )$is convex on the interval$[0,\frac{1}{{\tau }_1}]$.

Proof. 

The proof is similar to that of Lemma 2. □

Remark 1.

The above lemmas show that$f(\lambda )$is not a convex function on$\mathrm{Re}\left(\lambda \right)$. As$g(\lambda )$is infinitely differentiable and its second derivative is positive,$g(\lambda )$is a concave function for all$\mathrm{Re}\left(\lambda \right)$.

The solutions of Equation (4) are the intersection points (or tangent points) of the functions $f(\lambda )$ and $g(\lambda )$. For $-1<a<0$, $f(\lambda )<0$ for all $\lambda \in \left(\frac{1}{{\tau }_1}\ln (-a),0\right)$ and $g(\lambda )$ is a concave function. If the global minimum value, $f({\lambda }_m)$, is greater than $-b={\sup }_{\lambda \in (-\infty ,0)}g(\lambda )$, then they do not intersect at any point. This implies that Equation (3) has no real solution.

Theorem 1.

If$-1<a<0$ and

$$2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}+\mathrm{b}{\tau }_1>0,$$

(23)

then every solution of Equation (3) oscillates.

Proof. 

We obtain from Equation (14), in several steps, the following mutually equivalent inequalities:

$$f({\lambda }_m)>-\mathrm{b}\iff \frac{1}{{\tau }_1}\left(2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}\right)>-\mathrm{b},$$

$$\iff 2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}>-\mathrm{b}{\tau }_1,$$

$$\iff 2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}+\mathrm{b}{\tau }_1>0.$$

This completes the proof. □

Theorem 2

[24] (Theorem 2). If $a=-1$, then every solution of Equation (3) oscillates.

Proof. 

If $a=-1$, then $f(\lambda )\ge 0$ for all $\mathrm{Re}(\lambda )$. As $g(\lambda )<0$ for all $\mathrm{Re}(\lambda )$, they do not intersect at any point. This implies that $p(\lambda )$ has no real roots. Another proof can be formulated as follows, if $a=-1$, the Equation (4) becomes:

$$p(\lambda )=\lambda -\lambda e^{-{\tau }_1\lambda }+b{e}^{-{\tau }_2\lambda }=\lambda \left(1-e^{-{\tau }_1\lambda }\right)+b{e}^{-{\tau }_2\lambda }.$$

(24)

For all $\mathrm{Re}(\lambda )$, $p(\lambda )\ge b>0$. □

Theorem 3.

If$a<-1$ and

$$2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}+{\tau }_{1}b{\left(-a\right)}^{-\frac{{\tau }_2}{{\tau }_1}}>0,$$

(25)

then every solution of Equation (3) oscillates.

Proof. 

The proof is similar to that of Theorem 1. The maximum value of $g(\lambda )$ on the interval $\left(0,\frac{1}{{\tau }_1}\ln (-a)\right)$ is $g(\frac{1}{{\tau }_1}\ln (-a))$ as $g(\lambda )$ is a concave function. If $f({\lambda }_m)$ is greater than $g(\frac{1}{{\tau }_1}\ln (-a))$, then they do not intersect at any point. We proceed as in the proof of Theorem 1 to immediately obtain the following result:

$$f({\lambda }_m)>g(\frac{1}{{\tau }_1}\ln (-a))\iff \frac{1}{{\tau }_1}\left(2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}\right)-b{e}^{-\frac{{\tau }_2}{{\tau }_1}\ln (-a)}$$

$$\iff 2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}>-{\tau }_{1}b{\left(-a\right)}^{-\frac{{\tau }_2}{{\tau }_1}}.$$

 □

Theorem 4.

Assume that$-1<a<0$. If

$$2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}+b{\tau }_1<0,$$

(26)

then Equation (3) has two negative real roots.

Proof. 

First, we determine the maximal number of real roots of the quasi-polynomial function (Equation (4)). From the Pólya-Szegö bound (see Theorem A1), setting $\xi =\theta =0$ gives a bound on the number of real roots for (4). Here, $d_1=2$ and $d_2=1$, therefore, the maximal number of real roots is 2. Next, two functions $f(\lambda )$ and $g(\lambda )$ intersect in the third quadrant of the complex plane if Equation (26) is satisfied. As $g(\lambda )$ is a strictly increasing function, and $f(\lambda )$ strictly decreases on the interval $\left(\frac{1}{{\tau }_1}\ln (-a),{\lambda }_m\right)$ and strictly increases on the interval $\left({\lambda }_m,0\right)$, then $g(\lambda )$ intersects two points of $f(\lambda )$ if $f({\lambda }_m)<g({\lambda }_m)$. This completes the proof. □

Theorem 5.

Assume that$a<-1$. If

$$2-W(-e{a}^{-1})+a{e}^{W(-e{a}^{-1})-1}+{\tau }_{1}b{\left(-a\right)}^{-\frac{{\tau }_2}{{\tau }_1}}<0,$$

(27)

then Equation (3) has two positive real roots.

Proof. 

The proof is similar to that derived for Theorem 4. □

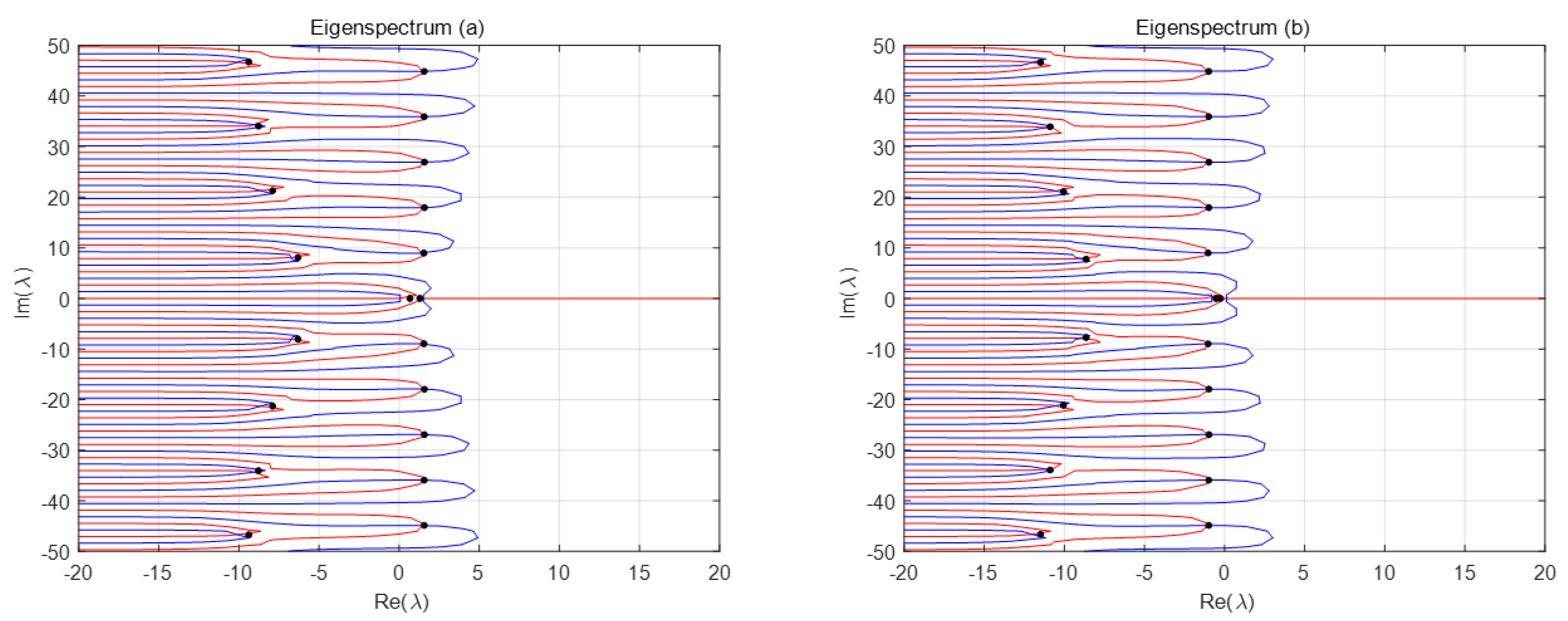
3.2. Stabilization of the NDDS

In this section, we consider a state feedback controller of the form:

$$u(t)=k_d\dot{x}(t-{\tau }_1)+k_{p}x(t-{\tau }_2),$$

(28)

where, $k_p$ and $k_d$ are the proportional and derivative gains, respectively. Our objective was to analytically determine the set of controller parameters that makes the NDDS (2) exponentially stable. Including the state feedback controller (28), the NDDS (2) can be written as:

$$\dot{x}(t)+(a-k_d)\dot{x}(t-{\tau }_1)+(b-k_p)x(t-{\tau }_2)=0,$$

(29)

Therefore, the characteristic equation of the NDDS (29) is expressed as follows:

$$q(\lambda )=\lambda +a_f\lambda e^{-{\tau }_1\lambda }+b_f{e}^{-{\tau }_2\lambda },$$

(30)

where, $a_f=a-k_d$ and $b_f=b-k_p$. Using Theorem 4, we first determine $k_d$ such that $-1<a_f<0$ and subsequently, we find $k_p$ from Equations (8) and (13). The main results of this section are summarized in the following theorem.

Theorem 6.

If$a<k_d<a+1$and

$$k_p=b+\frac{1}{{\tau }_1}(1-W(-e{a}_f^{-1}))\left(1+a_f{e}^{W(-e{a}_f^{-1})-1}\right)e^{{\tau }_2{\lambda }_m},$$

(31)

where,${\lambda }_m=\frac{1}{{\tau }_1}\left(1-W(-e{a}_f^{-1})\right)$, then the state feedback controller (28) makes the NDDS (2) exponentially stable.

4. Examples

A few examples and numerical simulation results have been presented here to validate the analytical results of the previous section.

Example 1.

Consider the NDDE

$$\dot{x}(t)-0.3\dot{x}(t-1.7)+2.1x(t-0.3)=0,$$

(32)

where,$a=-0.3,b=2.1,{\tau }_1=1.7,{\tau }_2=0.3$. Because$-1<a<0$, from Theorem 1 we get:

$$2-W(-a{e}^{-1})+a{e}^{W(-a{e}^{-1})-1}+b{\tau }_1=3.29266.$$

Equation (32) satisfies the condition of Theorem 1. Hence, every solution of this NDDE is oscillatory. The results are depicted in Figure 1a.

Figure 1. Graphs of the characteristic equation and two functions in Equations (5) and (6). (a) Example 1. a = −0.3, b = 2.1, ${\tau }_1=1.7$, ${\tau }_2=0.3$, (b) Example 2. a = −0.18394, b = 0.18394, ${\tau }_1=1$, ${\tau }_2=1$, (c) Example 3. a = −5.4366, b = 1.6487, ${\tau }_1=1$, ${\tau }_2=0.5$.

Example 2.

Consider the NDDE [24]

$$\dot{x}(t)-\frac{1}{2e}\dot{x}(t-1)+\frac{1}{2e}x(t-2)=0,$$

(33)

where,$a=-\frac{1}{2e},b=\frac{1}{2e},{\tau }_1=1,{\tau }_2=1$. As$-1<a<0$, from Theorem 1 we have:

$$2-W(-a{e}^{-1})+a{e}^{W(-a{e}^{-1})-1}+b{\tau }_1=-0.31606.$$

Equation (33) does not satisfy the condition of Theorem 1, but satisfies the condition of Theorem 4. Therefore, there are two negative real roots. The results are depicted in Figure 1b.

Example 3.

Consider the NDDE [28]

$$\dot{x}(t)-2e\dot{x}(t-1)+\sqrt{e}x(t-0.5)=0,$$

(34)

where,$a=-2e,b=\sqrt{e},{\tau }_1=1,{\tau }_2=0.5$. As$a<-1$, from Theorem 3 we obtain:

$$2-W(-a{e}^{-1})+a{e}^{W(-a{e}^{-1})-1}+{\tau }_{1}b{\left(-a\right)}^{-\frac{{\tau }_2}{{\tau }_1}}=-5.4366.$$

Equation (34) does not satisfy the condition of Theorem 3, but satisfies the condition of Theorem 5. Thus, there are two positive real roots. The results are shown in Figure 1c.

The solid red, blue and black lines in Figure 1 represent $f(\lambda )$, $g(\lambda )$, and the characteristic equation $p(\lambda )$, respectively. The intersections of the two functions (red and blue lines), denoted by the blue dots, are the real roots of the corresponding equation. The intersection points between the characteristic equation and the real axis exactly equal the blue dots. Figure 1a shows that there is actually no intersection between $p(\lambda )$ and the real axis, which implies that every solution of Equation (3) oscillates. Figure 1b,c establishes the existence of real roots.

Example 4.

Consider a NDDS with state feedback:

$$\dot{x}(t)+a\dot{x}(t-{\tau }_1)+bx(t-{\tau }_2)=u(t),$$

(35)

and$u(t)=k_d\dot{x}(t-{\tau }_1)+k_{p}x(t-{\tau }_2)$, where$a=-3,b=1.31014,{\tau }_1=0.7,{\tau }_1=1.2$and the continuous initial history is given by$x(t)=-1$.

The characteristic equation of Equation (35) in the absence of control becomes a simple quasi-polynomial:

$$\lambda -3\lambda e^{-0.7\lambda }+1.31014e^{-1.2\lambda }=0.$$

(36)

Applying Equation (27) to Equation (36), we obtain −0.271786. This indicates that there are two positive real roots based on Theorem 5. Applying the QPmR (Quasi-Polynomial Mapping based Root-finder [29]) algorithm to Equation (36), the rightmost spectrum of the characteristic equation (36) is depicted in Figure 2a. Here, the four rightmost roots are 1.2902, 0.6683, 1.5766 + i7.9386, and 1.5766 − i7.9386. Figure 3a shows the time response in the absence of feedback control.

Figure 2. Rightmost spectrum of the characteristic equation. The spectrum values are denoted as black dots. The blue and red lines are the isolines of the real and imaginary parts of the characteristic equation to zero, respectively. (a) Without state feedback. A few eigenvalues are located in the right-half plane of the imaginary axis. (b) With a state feedback controller. All eigenvalues are located in the open left-half plane of the imaginary axis.

Figure 3. System response (a) without state feedback, and (b) with a state feedback controller for $k_p=1.23336$ and $k_d=-2.5$. The chosen state feedback controller gain exponentially stabilizes the NDDS.

We used a state feedback controller where the controller gains were analytically determined from Theorem 6, as one of the goals of this study was to stabilize the NDDS (35). First, we selected the derivative gain $k_d=-2.5$ that satisfies the condition $a<k_d<a+1$, such that $-1<a_f(=a-k_d)<0$. Next, we can obtain ${\lambda }_m=\frac{1}{{\tau }_1}(1-W(-e{a}_f^{-1}))=-0.5355$ from Equation (13), and finally the proportional gain was determined using Equation (31). Figure 2b and Figure 3b show the rightmost spectrum and time response, respectively of the NDDS with the state feedback controller. Applying the QPmR to the NDDS with a feedback system, the four rightmost roots were determined to be −0.2652, −0.5355, −0.9979 + i35.9105, and −0.9979 − i35.9105, which indicates that all the roots of its characteristic equation are located to the left of the imaginary axis. The characteristic equation of Equation (35), with the state feedback controller, becomes $\lambda -0.5\lambda e^{-0.7\lambda }+0.0768e^{-1.2\lambda }=0$, and the condition described by Equation (26) gives a value of $-0.0645668$. Based on Theorem 4, the NDDS with the above state feedback controller has two negative real roots. It should be noted that the calculated root ${\lambda }_m$ equals one of the rightmost roots produced by the QPmR. Therefore, we can assign a pole of the NDDS by adjusting the controller gains.

Example 5.

Consider the following single-species population growth with time delay and feedback control [30]:

$$\dot{N}(t)=rN(t)\left(1-\frac{1}{K}\left(N(t-\tau )+c\dot{N}(t-\tau )\right)\right)-q\left(N(t-\tau ),\dot{N}(t-\tau )\right),$$

(37)

where$N(t)$is the population,$r$is the intrinsic growth rate,$\tau$is the recovering time,$c$is the growth rate associated with the growth rate at time$t-\tau$, and$K$is the environmental carrying capacity. Parameters$r,\tau ,c,K$are positive. In Equation (37), if$q(\cdot )=0$, it is sometimes called a dynamic food-limited population model [31].

Equation (37) can be rewritten as:

$$\dot{N}(t)=rN(t)\left(\left(1-\frac{1}{K}N(t-\tau )\right)+c\frac{d}{dt}\left(1-\frac{1}{K}N(t-\tau )\right)\right)-q\left(N(t-\tau ),\dot{N}(t-\tau )\right).$$

(38)

Let $z(t)=1-\frac{1}{K}N(t)$, then $N(t)=K\left(1-z(t)\right)$, and

$$\dot{z}(t)=-r\left(1-z(t)\right)\left(z(t-\tau )+c\dot{z}(t-\tau )\right)+Kq\left(z(t-\tau ),\dot{z}(t-\tau )\right).$$

(39)

The variational equation of Equation (39) about the trivial solution, $z(t)=0$, takes the form:

$$\dot{z}(t)=-rz(t-\tau )-rc\dot{z}(t-\tau )+\frac{1}{K}q\left(z(t-\tau ),\dot{z}(t-\tau )\right).$$

(40)

Compare Equation (40) with Equation (4), we see in this case, $a=rc$, $b=r$, ${\tau }_1={\tau }_2=\tau$.

We assume that the feedback controller is in the following form:

$$q(t)=k_d\dot{z}(t-\tau )+k_{p}z(t-\tau ).$$

(41)

A dynamic bacteria population model which is represented by an autonomous system of Equation (37), was introduced and discussed in [31]. According to [24], if $r,c,\tau$ are positive constants, then every non-oscillation solution of the autonomous system of Equation (37) tends to zero as $t\to \infty$. However, the real root is not guaranteed to be the rightmost pole.

Table 1 shows the five rightmost poles as a function of $r,c$, and assuming $K=1$ and $\tau =0.1$. The odd columns are without feedback control, and the even columns are with feedback control. In the second and third cases, without feedback control, some complex-conjugated roots are found on the right-hand side of the complex plane and they make the system unstable. With a state feedback controller designed by Theorem 6, all roots are located on the left-hand side of the complex plane. Based on Theorem 4, Equation (40) with the state feedback controller has two negative real roots, and these roots are the rightmost.

Table 1. Dominant poles of population model (Equation (40)) with different $c$.

$\mathit{r}=\frac{\mathit{\pi }}{\sqrt{3}}+\frac{1}{20},\mathit{c}=\frac{\sqrt{3}}{2\mathit{\pi }}-\frac{1}{25}=0.2356$ [31]		$\mathit{r}=\frac{\mathit{\pi }}{\sqrt{3}}+\frac{1}{20},\mathit{c}=0.56$		$\mathit{r}=\frac{\mathit{\pi }}{\sqrt{3}}+\frac{1}{20},\mathit{c}=0.63$
without Feedback	with Feedback	without Feedback	with Feedback	without Feedback	with Feedback
−0.1656	−2.5687	−0.2777	−2.6174	−0.2936	−2.5194
−8.2685 − i31.2548	−3.7482	0.4315 − i31.2442	−3.8654	1.6161 − i31.2448	−3.6338
−8.2685 + i31.2548	−6.9049 + i0.6305	0.4315 + i31.2442	−7.1044 − i63.0651	1.6161 + i31.2448	−6.7092 + i63.0384
−8.2321 + i94.1912	−6.9049 − i0.6305	0.4281 − i94.1908	−7.1044 + i63.0651	1.6070 + i94.1908	−6.7092 − i63.0384
−8.2321 − i94.1912	−6.9247 + i1.2577	0.4281 + i94.1908	−7.1260 + i125.7820	1.6070 − i94.1908	−6.7272 + i125.7683

The simulation results show that the designed state feedback controller makes the NDDS exponentially stable.