Thermal-Performance Evaluation of Bicycle Helmets for Convective and Evaporative Heat Loss at Low and Moderate Cycling Speeds
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Helmets
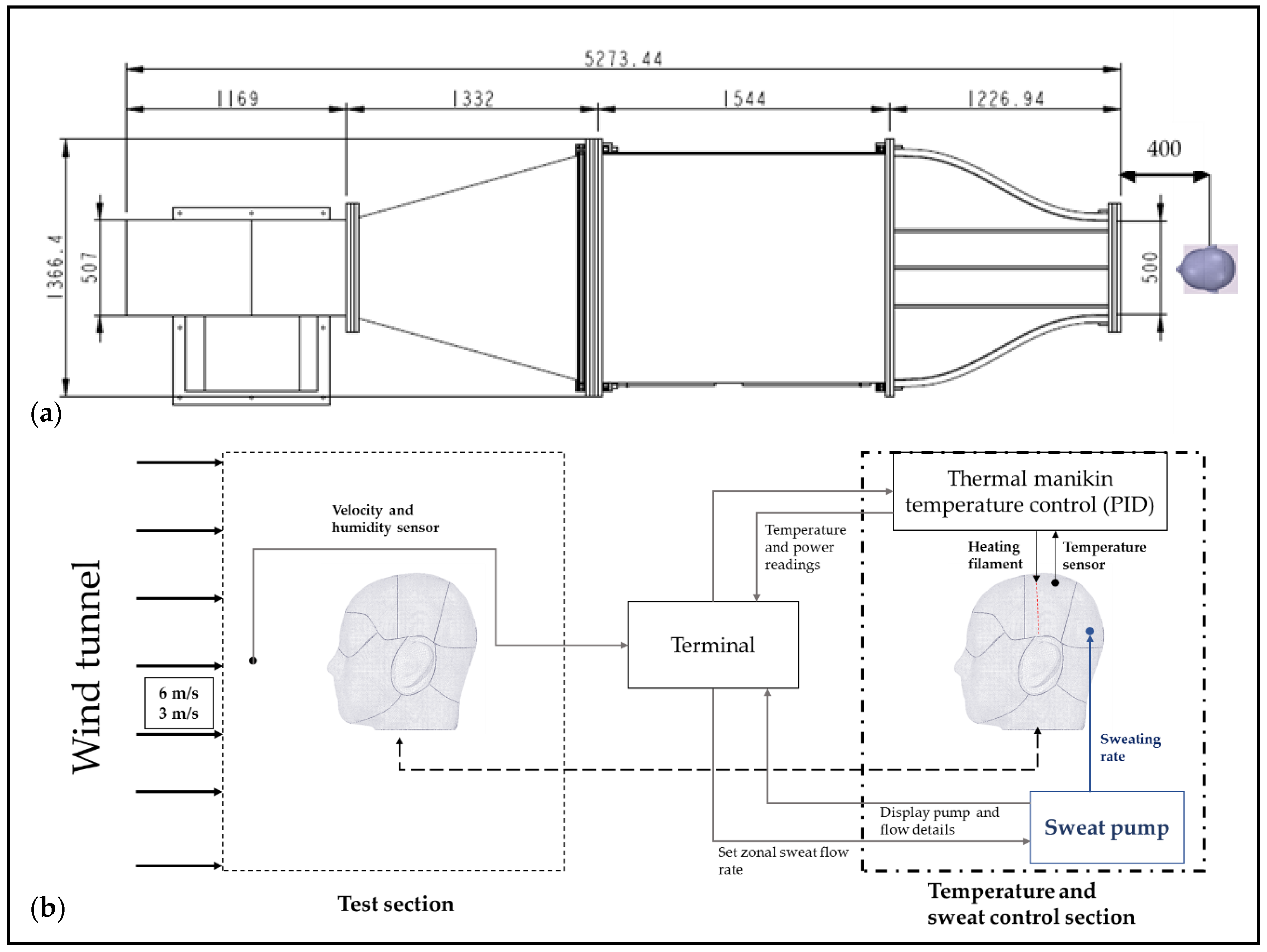
2.2. Thermal Manikin
2.3. Experiment Procedure
2.3.1. Convective Heat-Loss Tests
2.3.2. Latent Heat-Loss Tests
2.4. Methods—Theoretical Background
2.4.1. Body and Environment
2.4.2. Thermal Resistance (Rct)
2.4.3. Statistical Analysis
2.5. Limitations and Considerations
3. Results and Discussion
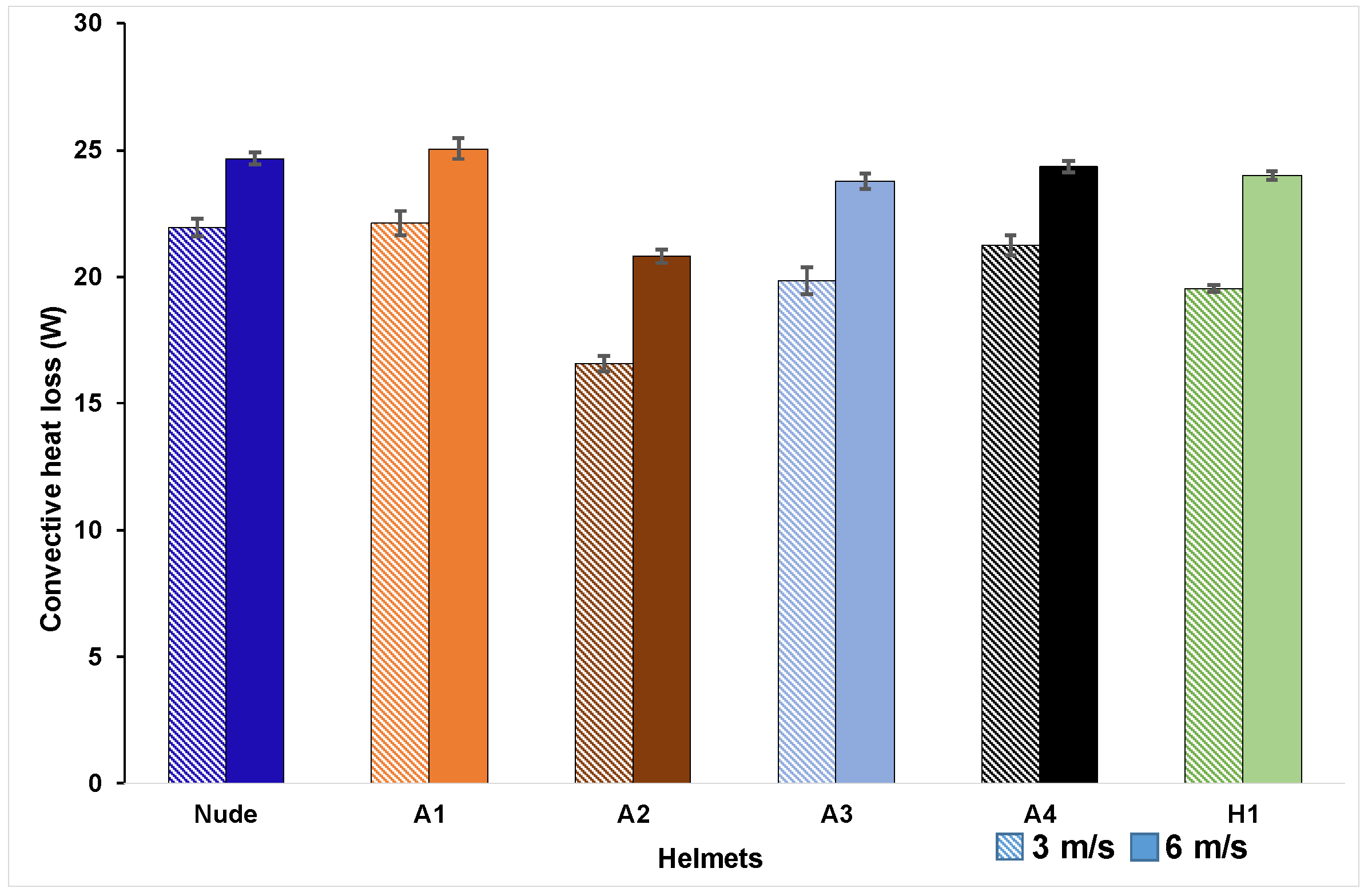
3.1. Convective Heat-Transfer Characteristics of Head-Helmet Ensembles
Zonal Heat Transfer Characteristics
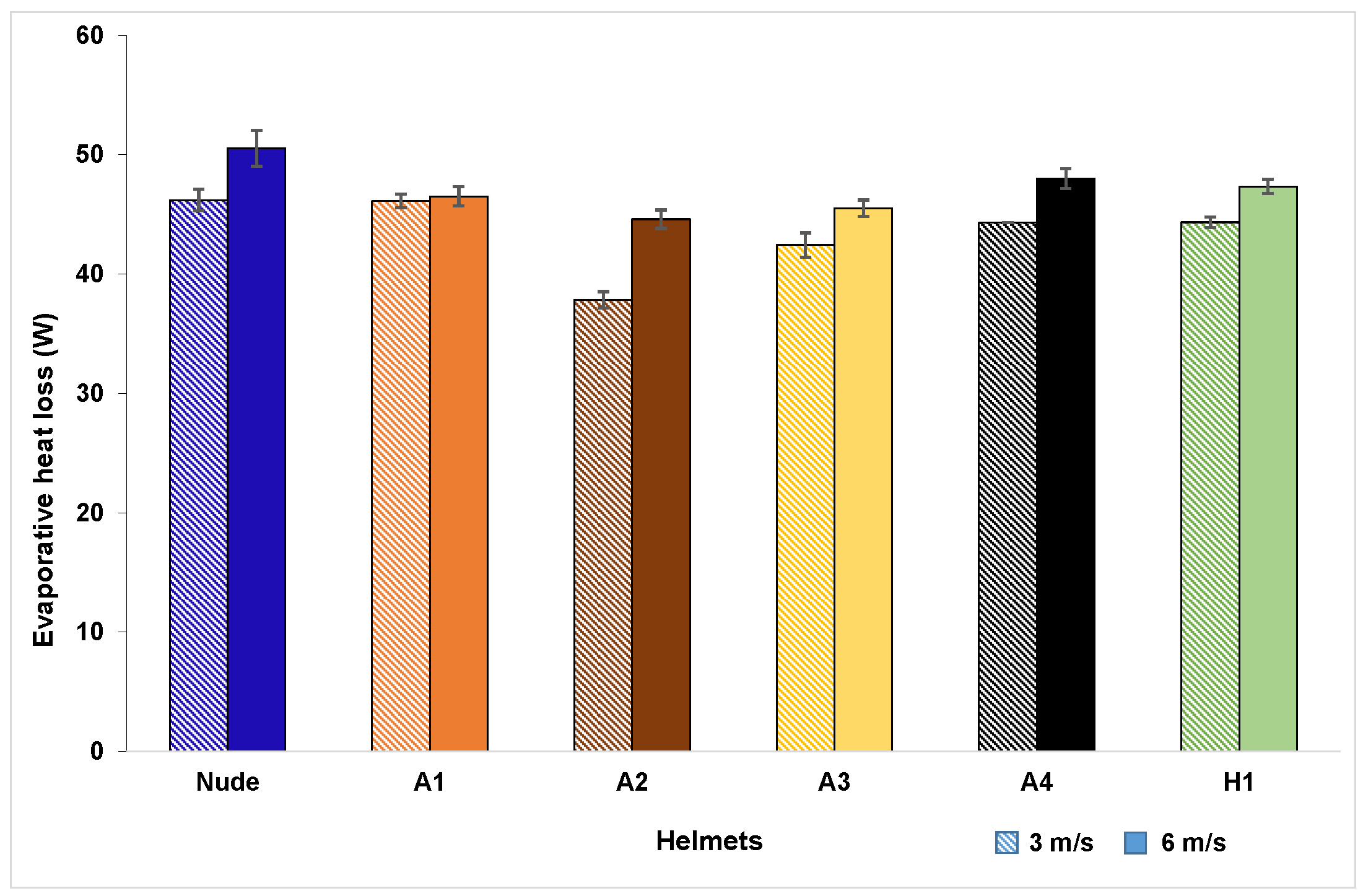
3.2. Evaporative-Heat-Transfer Characteristics of Helmet Ensembles
Zonal Heat Transfer Characteristics
4. Conclusions
- Evaporative heat-transfer mode accounts for 51%–53% of total heat transferred from the nude head, demonstrating the significant role played by sweat in heat transfer and thermal performance.
- At low velocity (3 m/s), open Helmet A1 showed the highest overall cooling efficiency due to high heat transfer from parietal and facial zones and closed Helmet A2 showed the lowest overall cooling efficiency due to low heat transfer from all the zones for both convective and evaporative heat transfer.
- At moderate velocity (6 m/s), for convection, open Helmet A1 recorded the highest cooling efficiency due to high heat transfer from parietal zone and closed Helmet A2 showed lowest cooling efficiency due to low heat transfer from all the zones as a result of it shell-like design. For evaporation, open Helmet A4 recorded the highest cooling efficiency as a result of high parietal zone heat transfer.
- Overall cooling efficiency of closed helmet with prominent internal channels and outlets (H1) was better than the closed helmets with inlets and outlets (A2) depicting the influence of internal channels on heat transfer.
- Among the zonal heat flux values for the zones under the helmet, frontal zones recorded the highest heat transfer and the parietal zone recorded the lowest heat transfer for all the tested helmets. Further research into the parameters influencing these zonal heat transfer characteristics would provide valuable insight on improving the zonal thermal performance of helmets.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wood, T.; Milne, P. Head-injuries to pedal cyclists and the promotion of helmet use in Victoria, Australia. Accid. Anal. Prev. 1988, 20, 177–185. [Google Scholar] [CrossRef]
- Hoye, A. Bicycle helmets—To wear or not to wear? A meta-analysis of the effects of bicycle helmets on injuries. Accid. Anal. Prev. 2018, 117, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Joseph, B.; Azim, A.; Haider, A.A.; Kulvatunyou, N.; O’Keeffe, T.; Hassan, A.; Gries, L.; Tran, E.; Latifi, R.; Rhee, P. Bicycle helmets work when it matters the most. Am. J. Surg. 2017, 213, 413–417. [Google Scholar] [CrossRef]
- Burke, E.R. Safety standards for bicycle helmets. Physician Sportsmed. 1988, 16, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Olivier, J.; Creighton, P. Bicycle injuries and helmet use: A systematic review and meta-analysis. Int. J. Epidemiol. 2017, 46, 372. [Google Scholar] [CrossRef] [PubMed]
- Cripton, P.A.; Dressler, D.M.; Stuart, C.A.; Dennison, C.R.; Richards, D. Bicycle helmets are highly effective at preventing head injury during head impact: Head-form accelerations and injury criteria for helmeted and unhelmeted impacts. Accid. Anal. Prev. 2014, 70, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Mills, N.J.; Gilchrist, A. Oblique impact testing of bicycle helmets. Int. J. Impact Eng. 2008, 35, 1075–1086. [Google Scholar] [CrossRef]
- Bliven, E.; Rouhier, A.; Tsai, S.; Willinger, R.; Bourdet, N.; Deck, C.; Madey, S.M.; Bottlang, M. Evaluation of a novel bicycle helmet concept in oblique impact testing. Accid. Anal. Prev. 2019, 124, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.; Dau, N.; Feist, F.; Deck, C.; Willinger, R.; Madey, S.M.; Bottlang, M. Angular Impact Mitigation system for bicycle helmets to reduce head acceleration and risk of traumatic brain injury. Accid. Anal. Prev. 2013, 59, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.; Mohan, D. An improved motorcycle helmet design for tropical climates. Appl. Ergon. 1993, 24, 427–431. [Google Scholar] [CrossRef]
- Li, G.-L.; Li, L.-P.; Cai, Q.-E. Motorcycle helmet use in southern china: An observational study. Traffic Inj. Prev. 2008, 9, 125–128. [Google Scholar] [CrossRef]
- Skalkidou, A.; Petridou, E.; Papadopoulos, F.C.; Dessypris, N.; Trichopoulos, D. Factors affecting motorcycle helmet use in the population of Greater Athens, Greece. Inj. Prev. 1999, 5, 264–267. [Google Scholar] [CrossRef] [PubMed]
- Servadei, F.; Begliomini, C.; Gardini, E.; Giustini, M.; Taggi, F.; Kraus, J. Effect of Italy’s motorcycle helmet law on traumatic brain injuries. Inj. Prev. 2003, 9, 257–260. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE. ANSI/ASHRAE Standard 55 2010—Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2010. [Google Scholar]
- Reardon, F.D.; Leppik, K.E.; Wegmann, R.; Webb, P.; Ducharme, M.B.; Kenny, G.P. The Snellen human calorimeter revisited, re-engineered and upgraded: Design and performance characteristics. Med. Biol. Eng. Comput. 2006, 44, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Hambraeus, L.; Sjodin, A.; Webb, P.; Forslund, A.; Hambraeus, K.; Hambraeus, T. A suit calorimeter for energy-balance studies on humans during heavy exercise. Eur. J. Appl. Physiol. Occup. Physiol. 1994, 68, 68–73. [Google Scholar] [CrossRef] [PubMed]
- Hartley, G.L.; Flouris, A.D.; Plyley, M.J.; Cheung, S.S. The effect of a covert manipulation of ambient temperature on heat storage and voluntary exercise intensity. Physiol. Behav. 2012, 105, 1194–1201. [Google Scholar] [CrossRef] [PubMed]
- De Bruyne, G.; Aerts, J.M.; Van Der Perre, G.; Goffin, J.; Verpoest, I.; Berckmans, D. Spatial differences in sensible and latent heat losses under a bicycle helmet. Eur. J. Appl. Physiol. 2008, 104, 719–726. [Google Scholar] [CrossRef]
- Bruhwiler, P.A. Heated, perspiring manikin headform for the measurement of headgear ventilation characteristics. Meas. Sci. Technol. 2003, 14, 217–227. [Google Scholar] [CrossRef]
- Hsu, Y.; Tai, C.; Chen, T. Improving thermal properties of industrial safety helmets. Int. J. Ind. Ergon. 2000, 26, 109–117. [Google Scholar] [CrossRef]
- Abeysekera, J.D.A.; Holmer, I.; Dupuis, C. Heat-transfer characteristics of industrial safety helmets. In Towards Human Work. Solutions to Problems in Occupational Health and Safety; Taylor and Francis Group: London, UK, 1991; pp. 297–303. [Google Scholar]
- Osczevski, R.J. Design and Evaluation of a Three-Zone Thermal Manikin Head; Defense and Civil Institute of Environmental Medicine: Toronto, ON, Canada, 1996; p. 20. [Google Scholar]
- Liu, X.X.; Holmer, I. Evaporative heat-transfer characteristics of industrial safety helmets. Appl. Ergon. 1995, 26, 135–140. [Google Scholar] [CrossRef]
- Reid, J.; Wang, E.L. A system for quantifying the cooling effectiveness of bicycle helmets. J. Biomech. Eng.-Trans. Asme 2000, 122, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Ghani, S.; Elbialy, E.M.A.A.; Bakochristou, F.; Gamaledin, S.M.A.; Rashwan, M.M. The effect of forced convection and PCM on helmets’ thermal performance in hot and arid environments. Appl. Therm. Eng. 2017, 111, 624–637. [Google Scholar] [CrossRef]
- Martinez, N.; Psikuta, A.; Corberan, J.M.; Rossi, R.M.; Annaheim, S. Multi-sector thermo-physiological head simulator for headgear research. Int. J. Biometeorol. 2017, 61, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Ueno, S.; Sawada, S. Effects of ventilation openings in industrial safety helmets on evaporative heat dissipation. J. Occup. Health 2019, 61, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Underwood, L.; Vircondelet, C.; Jermy, M. Thermal comfort and drag of a streamlined cycling helmet as a function of ventilation hole placement. Proc. Inst. Mech. Eng. Part P-J. Sports Eng. Technol. 2018, 232, 15–21. [Google Scholar] [CrossRef]
- Bogerd, C.P.; Aerts, J.-M.; Annaheim, S.; Bröde, P.; De Bruyne, G.; Flouris, A.D.; Kuklane, K.; Sotto Mayor, T.; Rossi, R.M. A review on ergonomics of headgear: Thermal effects. Int. J. Ind. Ergon. 2015, 45, 1–12. [Google Scholar] [CrossRef]
- Bruhwiler, P.A.; Ducas, C.; Huber, R.; Bishop, P.A. Bicycle helmet ventilation and comfort angle dependence. Eur. J. Appl. Physiol. 2004, 92, 698–701. [Google Scholar] [CrossRef]
- Martinez, N.; Psikuta, A.; Rossi, R.M.; Corberan, J.M.; Annaheim, S. Global and local heat transfer analysis for bicycle helmets using thermal head manikins. Int. J. Ind. Ergon. 2016, 53, 157–166. [Google Scholar] [CrossRef]
- Bruhwiler, P.A. Role of the visor in forced convective heat loss with bicycle helmets. Int. J. Ind. Ergon. 2009, 39, 255–259. [Google Scholar] [CrossRef]
- Bogerd, C.P.; Bruhwiler, P.A.; Heus, R. The effect of rowing headgear on forced convective heat loss and radiant heat gain on a thermal manikin headform. J. Sport Sci. 2008, 26, 733–741. [Google Scholar] [CrossRef]
- De Bruyne, G.; Aerts, J.M.; Vander Sloten, J.; Goffin, J.; Verpoest, I.; Berckmans, D. Quantification of local ventilation efficiency under bicycle helmets. Int. J. Ind. Ergon. 2012, 42, 278–286. [Google Scholar] [CrossRef]
- Bruhwiler, P.A.; Buyan, M.; Huber, R.; Bogerd, C.P.; Sznitman, J.; Graf, S.F.; Rosgen, T. Heat transfer variations of bicycle helmets. J. Sport Sci. 2006, 24, 999–1011. [Google Scholar] [CrossRef] [PubMed]
- Pang, T.Y.; Subic, A.; Takla, M.; Pang, T.Y.; Subic, A.; Takla, M. Evaluation of thermal and evaporative resistances in cricket helmets using a sweating manikin. Appl. Ergon. 2014, 45, 300–307. [Google Scholar] [CrossRef] [PubMed]
- Bogerd, C.P.; Bruhwiler, P.A. Heat loss variations of full-face motorcycle helmets. Appl. Ergon. 2009, 40, 161–164. [Google Scholar] [CrossRef] [PubMed]
- Bruhwiler, P.A. Radiant heat transfer of bicycle helmets and visors. J. Sport Sci. 2008, 26, 1025–1031. [Google Scholar] [CrossRef] [PubMed]
- Aljaste, H.; Kuklane, K.; Heidmets, S. Better bicycle helmets for commuters—Evaluation of ventilation. In Proceedings of the International Cycling Safety Conference 2014, Gothenburg, Sweden, 18–19 November 2014. [Google Scholar]
- Danckaers, F.; Lacko, D.; Verwulgen, S.; De Bruyne, G.; Huysmans, T.; Sijbers, J. A combined statistical shape model of the scalp and skull of the human head. Adv. Intell. Syst. 2018, 591, 538–548. [Google Scholar]
- ASTM. ASTM F1291-16. Standard Test Method for Measuring the Thermal Insulation of Clothing Using a Heated Manikin; ASTM: West Conshohocken, PA, USA, 2016. [Google Scholar]
- ASTM. ASTM F2370-16. Standard Test Method for Measuring the Evaporative Resistance of Clothing Using a Sweating Manikin; ASTM: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Mukunthan, S.; Kuklane, K.; Huysmans, T.; De Bruyne, G. A comparison between physical and virtual experiments of convective heat transfer between head and bicycle helmet. Adv. Intell. Syst. 2018, 591, 517–527. [Google Scholar]
- Weiner, J.S. The regional distribution of sweating. J. Physiol. 1945, 104, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Nadel, E.R.; Mitchell, J.W.; Stolwijk, J.A.J. Control of local and total sweating during exercise transients. Int. J. Biometeorol. 1971, 15, 201–206. [Google Scholar] [CrossRef] [PubMed]
- IUPS. Glossary of terms for thermal physiology. Jpn. J. Physiol. 2001, 51, 245–280. [Google Scholar]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill Book Co.: New York, NY, USA, 1972. [Google Scholar]
- Clark, R.E.; Edholm, O.G. Man and his thermal environment. J. Am. Soc. Nav. Eng. 1958, 70, 331–340. [Google Scholar]
- Song, G.W.; Paskaluk, S.; Sati, R.; Crown, E.M.; Dale, J.D.; Ackerman, M. Thermal protective performance of protective clothing used for low radiant heat protection. Text. Res. J. 2011, 81, 311–323. [Google Scholar] [CrossRef]
- Mccullough, E.A. Factors Affecting the resistance to heat-transfer provided by clothing. J. Therm. Biol. 1993, 18, 405–407. [Google Scholar] [CrossRef]
- Havenith, G.; Holmer, I.; Parsons, K. Personal factors in thermal comfort assessment: Clothing properties and metabolic heat production. Energy Build. 2002, 34, 581–591. [Google Scholar] [CrossRef]
- Qian, X.M.; Fan, J.T. Interactions of the surface heat and moisture transfer from the human body under varying climatic conditions and walking speeds. Appl. Ergon. 2006, 37, 685–693. [Google Scholar] [CrossRef] [PubMed]
- Osczevski, R.J. The Basis of Wind Chill. Arctic 1995, 48, 313–405. [Google Scholar] [CrossRef]
- Shishodia, B.S.; Sanghi, S.; Mahajan, P. Computational and subjective assessment of ventilated helmet with venturi effect and backvent. Int. J. Ind. Ergon. 2018, 68, 186–198. [Google Scholar] [CrossRef]




| No. | A1-Z1 | A2-Armor | A3-Blade | A4-Century | H1 | |
|---|---|---|---|---|---|---|
| Type/Size | Open/M | Closed/M | Open/M | Open/M | Closed | |
| 1 | Weight (g) | 190 | 250 | 230 | 277 | 150 |
| 2 | Material | Polycarbonate outer shell with expanded polystyrene (EPS) foam inner layer and padding | Plaster shell with padding | |||
| 3 | No. of vents | 31 | 16 | 22 | 18 | 4 |
| 4 | Surface area (m2) | 0.270 | 0.263 | 0.255 | 0.240 | 0.196 |
| 5 | Remarks | Padding: 5 x 3 mm. | Padding: 8 mm thick on the sides | Multidirectional impact protection system (MIPS) layer below inner layer | Twist cap technology for better aerodynamics and ventilation | Prototype design, 3 mm thick padding [39] |
| 6 | Homologation | EN 1078 | Not available | |||
 |  |  |  |  | ||
| S. No. | Zone | Surface Area (m2) |
|---|---|---|
| 1 | Frontal (scalp1) | 0.017 |
| 2 | Parietal (scalp2) | 0.017 |
| 3 | Superior occipital (scalp-rear1) | 0.015 |
| 4 | Inferior occipital (scalp-rear2) | 0.015 |
| 5 | Ocular (forehead) | 0.010 |
| 6 | Facial (face) | 0.026 |
| 7 | Left temporal (ear–left) | 0.007 |
| 8 | Right temporal (ear–right) | 0.007 |
| 9 | Neck | 0.030 |
| Total | 0.144 |
| (a) | ||||
| Helmet | Convective Heat Loss (W) | Thermal Resistance Rct (°C.m2/W) | Cooling Efficiency (%) | |
| Mean | SD | |||
| Nude | 21.9 | 0.30 | 0.052 | |
| A1 | 22.1 | 0.42 | 0.051 | 100.9 |
| A2 | 16.6 | 0.28 | 0.069 | 75.6 |
| A3 | 19.8 | 0.48 | 0.057 | 90.5 |
| A4 | 21.3 | 0.35 | 0.054 | 96.9 |
| H1 | 19.5 | 0.12 | 0.058 | 89.0 |
| (b) | ||||
| Helmet | Convective Heat Loss (W) | Thermal Resistance Rct (°C.m2/W) | Cooling Efficiency (%) | |
| Mean | SD | |||
| Nude | 24.7 | 0.3 | 0.046 | |
| A1 | 25.1 | 0.4 | 0.046 | 101.6 |
| A2 | 20.8 | 0.2 | 0.055 | 84.4 |
| A3 | 23.8 | 0.3 | 0.049 | 96.4 |
| A4 | 24.4 | 0.2 | 0.047 | 98.7 |
| H1 | 24.0 | 0.2 | 0.048 | 97.3 |
| (a) | |||
| Helmet | Apparent Evaporative Heat Loss (W) | Cooling Efficiency (%) | |
| Mean | SD | ||
| Nude | 47.4 | 2.2 | |
| A1 | 46.1 | 0.6 | 97.3 |
| A2 | 37.8 | 0.7 | 79.8 |
| A3 | 42.4 | 1.0 | 89.5 |
| A4 | 44.3 | 0.0 | 93.4 |
| H1 | 44.3 | 0.4 | 93.5 |
| (b) | |||
| Helmet | Apparent Evaporative Heat Loss (W) | Cooling Efficiency (%) | |
| Mean | SD | ||
| Nude | 50.4 | 0.5 | |
| A1 | 47.3 | 0.8 | 95.4 |
| A2 | 44.6 | 0.8 | 89.9 |
| A3 | 45.5 | 0.7 | 91.7 |
| A4 | 48.0 | 0.8 | 96.7 |
| H1 | 47.4 | 0.6 | 95.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukunthan, S.; Vleugels, J.; Huysmans, T.; Kuklane, K.; Mayor, T.S.; De Bruyne, G. Thermal-Performance Evaluation of Bicycle Helmets for Convective and Evaporative Heat Loss at Low and Moderate Cycling Speeds. Appl. Sci. 2019, 9, 3672. https://doi.org/10.3390/app9183672
Mukunthan S, Vleugels J, Huysmans T, Kuklane K, Mayor TS, De Bruyne G. Thermal-Performance Evaluation of Bicycle Helmets for Convective and Evaporative Heat Loss at Low and Moderate Cycling Speeds. Applied Sciences. 2019; 9(18):3672. https://doi.org/10.3390/app9183672
Chicago/Turabian StyleMukunthan, Shriram, Jochen Vleugels, Toon Huysmans, Kalev Kuklane, Tiago Sotto Mayor, and Guido De Bruyne. 2019. "Thermal-Performance Evaluation of Bicycle Helmets for Convective and Evaporative Heat Loss at Low and Moderate Cycling Speeds" Applied Sciences 9, no. 18: 3672. https://doi.org/10.3390/app9183672
APA StyleMukunthan, S., Vleugels, J., Huysmans, T., Kuklane, K., Mayor, T. S., & De Bruyne, G. (2019). Thermal-Performance Evaluation of Bicycle Helmets for Convective and Evaporative Heat Loss at Low and Moderate Cycling Speeds. Applied Sciences, 9(18), 3672. https://doi.org/10.3390/app9183672





