Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis
Abstract
:Featured Application
Abstract
1. Introduction
2. Traditional Matrix Structural Analysis (MSA)
3. Matrix Structural Analysis for Exact Solutions of Shear Deformable Beams
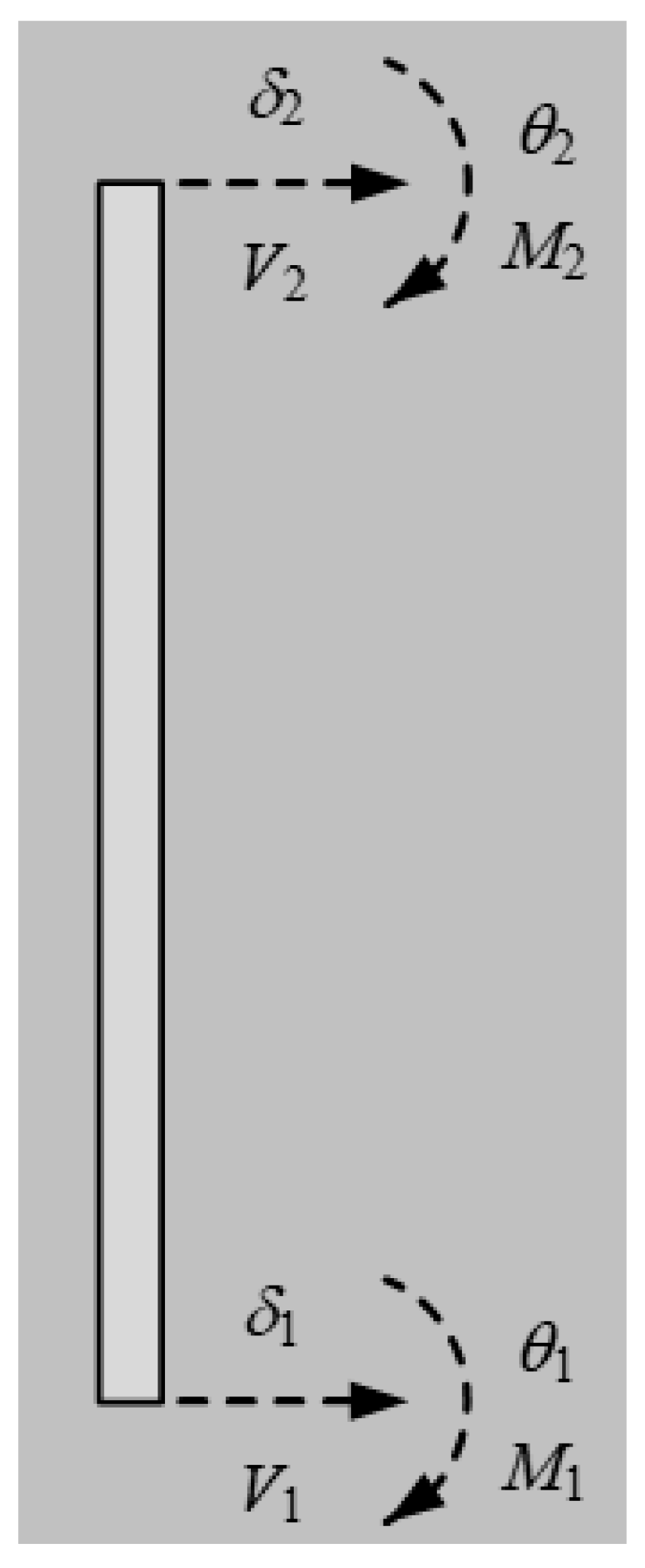
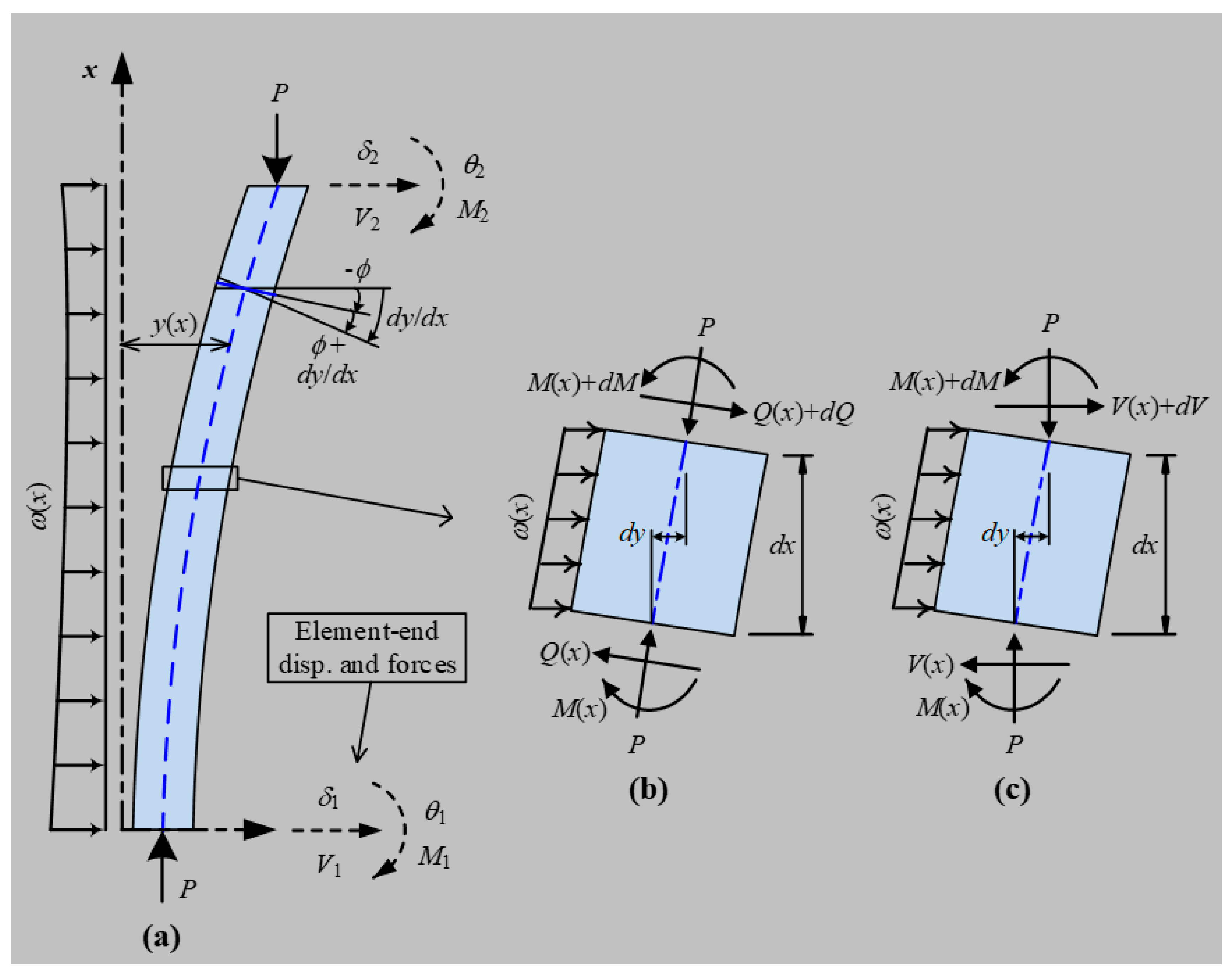
3.1. Relationship between Element-End Displacements and Forces
3.2. Second-Order MSA for Exact Buckling Solutions of Shear Deformable Beams
4. Applications and Discussions
4.1. Elastic Buckling Analysis of Shear Deformable Columns
4.2. Obtaining First-Order Stiffness Matrix
4.3. Comparison with the Simplified Expression by Ekhande et al.
5. Summary and Conclusions
- Equilibrium analysis of an axial-loaded Timoshenko beam–column is conducted based on the equilibrium conditions of shear force and bending moment of an element short segment, and a fourth-order governing differential equation is established. The solution of the differential equation can be used to analyze the element deformations and forces. Then, the element stability stiffness matrix is formulated, showing the relationship between the element-end flexural deformations and the corresponding forces.
- Based on the element stability stiffness matrix, a matrix structural analysis approach for the elastic buckling analysis of axial-loaded Timoshenko beam–columns is established. First, the structural stiffness matrix is assembled from the element stiffness matrix to show global structural responses. The eigenproblem for an elastic buckling analysis is then solved by setting the determinant of the structural stiffness matrix to zero. The established matrix analysis approach is demonstrated using classical elastic buckling analysis examples of the Timoshenko column with typical element-end boundary conditions.
- The simplified form for the element stability stiffness matrix of Timoshenko beam–columns by Ekhande et al. [18] could lead to large errors because it is defined considering the conditions that it gives the same result as the exact solution for zero shear deformation effect or zero axial force effect. However, for the condition of a relatively large axial force factor, the exact element stability stiffness matrix derived in this paper should be used.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Equilibrium Analysis of Shear Deformable Timoshenko Beam–Column
References
- Galambos, T.V.; Surovek, A.E. Structural Stability of Steel: Concepts and Applications for Structural Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Trahair, N.S.; Bradford, M.A.; Nethercot, D.A.; Gardner, L. The Behaviour and Design of Steel Structures to EC3, 4th ed.; Taylor & Francis: Abingdon, UK, 2008. [Google Scholar]
- Wang, C.M.; Wang, C.Y.; Reddy, J.N. Exact Solutions for Buckling of Structural Members; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chen, J. Stability of Steel Structures: Theory and Design, 5th ed.; Science Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Chen, W.F.; Atsuta, T. In-plane behavior and design. In Theory of Beam-Columns; J. Ross Publishing: Plantation, FL, USA, 2007; Volume 1. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw Hill: New York, NY, USA, 1961. [Google Scholar]
- McGuire, W.; Gallagher, R.H.; Ziemian, R.D. Matrix Structural Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Beaufait, F.W.; Rowan, W.H., Jr.; Hoadley, P.G.; Hackett, R.M. Computer Methods of Structural Analysis; Prentice-Hall: Upper Saddle River, NJ, USA, 1970. [Google Scholar]
- Yang, Y.B.; McGuire, W. Stiffness matrix for geometric nonlinear analysis. J. Struct. Eng. 1986, 112, 853–877. [Google Scholar] [CrossRef]
- Munoz, H.R. Elastic Second-Order Computer Analysis of Beam–Columns and Frames. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 1991. [Google Scholar]
- Colorado-Urrea, G.J.; Aristizabal-Ochoa, J.D. Second-order stiffness matrix and load vector of an imperfect beam–column with generalized end conditions on a two-parameter elastic foundation. Eng. Struct. 2014, 70, 260–270. [Google Scholar] [CrossRef]
- Yuan, S. Programming Structural Mechanics, 2nd ed.; Higher Education Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Pan, W.H.; Eatherton, M.R.; Tao, M.X.; Yang, Y.; Nie, X. Design of single-level guyed towers considering interrelationship between bracing strength and rigidity requirements. J. Struct. Eng. 2017, 143, 04017128. [Google Scholar] [CrossRef]
- Pan, W.H.; Eatherton, M.R.; Nie, X.; Fan, J.S. Stability and adequate bracing design of pre-tensioned cable braced inverted-Y-shaped Ferris wheel support system using matrix structural second-order analysis approach. J. Struct. Eng. 2018, 144, 04018194. [Google Scholar] [CrossRef]
- Hibbeler, R.C. Structural Analysis, 8th ed.; Pearson: London, UK, 2009. [Google Scholar]
- Long, Y.Q.; Bao, S.H.; Kuang, W.Q.; Yuan, S. Structural Mechanics, 2nd ed.; Higher Education Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Ekhande, S.G.; Selvappalam, M.; Madugula, M.K.S. Stability functions for three-dimensional beam–columns. J. Struct. Eng. 1989, 115, 467–479. [Google Scholar] [CrossRef]
- Wang, C.M.; Reddy, J.N.; Lee, K.H. Shear Deformable Beams and Plates: Relationships with Classical Solutions; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]

| Case | Boundary Conditions | Conditions for Buckling | Axial Force Factor at Buckling State (λcr) | Buckling Axial Force (Pcr) |
|---|---|---|---|---|
| 1 | Pinned–pinned | STB − CTB = 0 | λcr = π | |
| 2 | Fixed–free | TTBSTB − QTB2 = 0 | λcr = π/2 | |
| 3 | Fixed–clamped | TTB = 0 | λcr = π | |
| 4 | Fixed–pinned | STB = 0 | ||
| 5 | Fixed–fixed | ϕTB = 0 | λcr = 2π |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.-P.; Pan, W.-H.; Tong, J.-Z. Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis. Appl. Sci. 2019, 9, 3814. https://doi.org/10.3390/app9183814
Hu Z-P, Pan W-H, Tong J-Z. Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis. Applied Sciences. 2019; 9(18):3814. https://doi.org/10.3390/app9183814
Chicago/Turabian StyleHu, Zheng-Ping, Wen-Hao Pan, and Jing-Zhong Tong. 2019. "Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis" Applied Sciences 9, no. 18: 3814. https://doi.org/10.3390/app9183814




