Deflection Reduction Shaping Commands with Asymmetric First-Order Actuators
Abstract
:1. Introduction
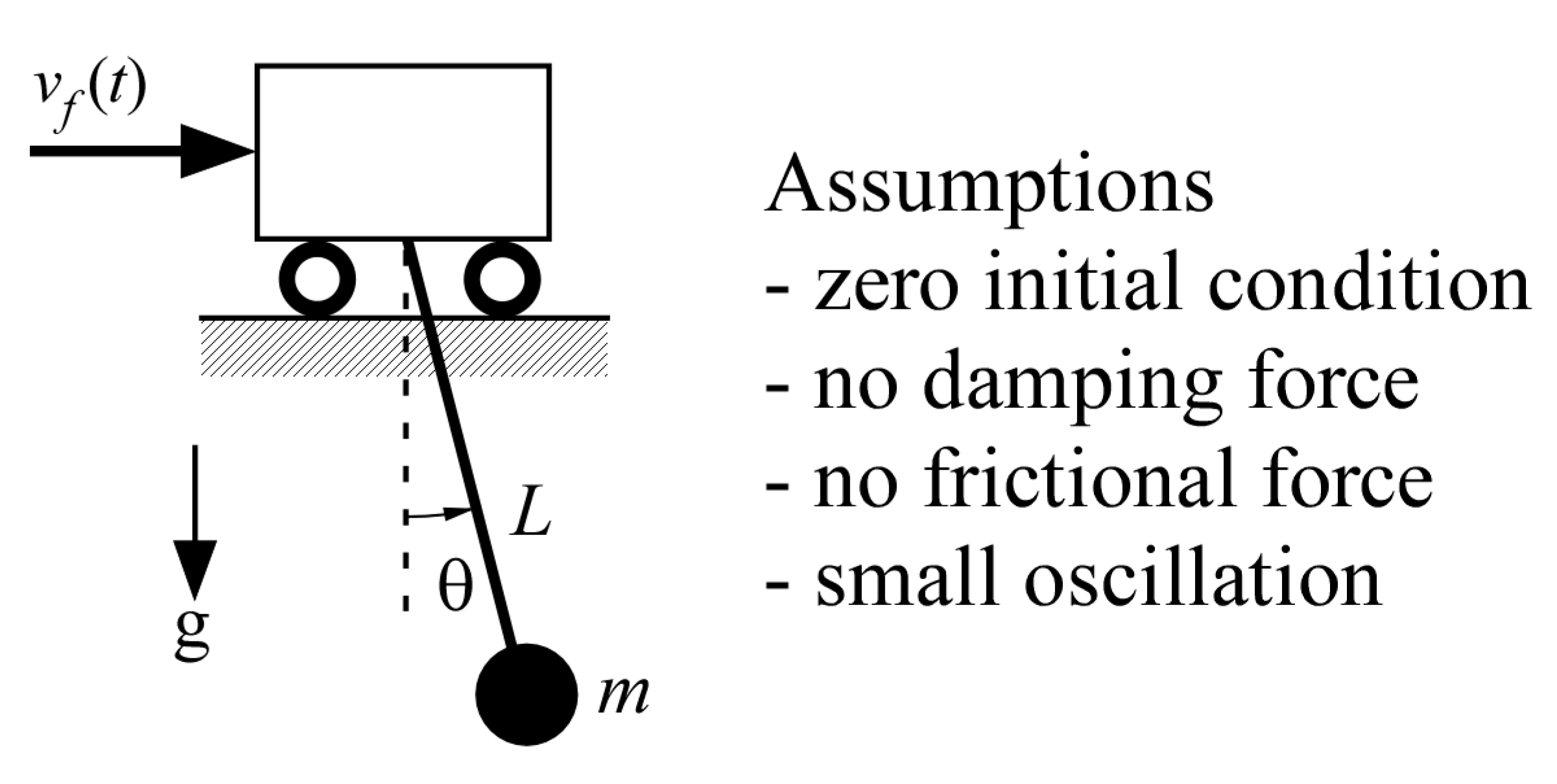
2. Materials and Methods
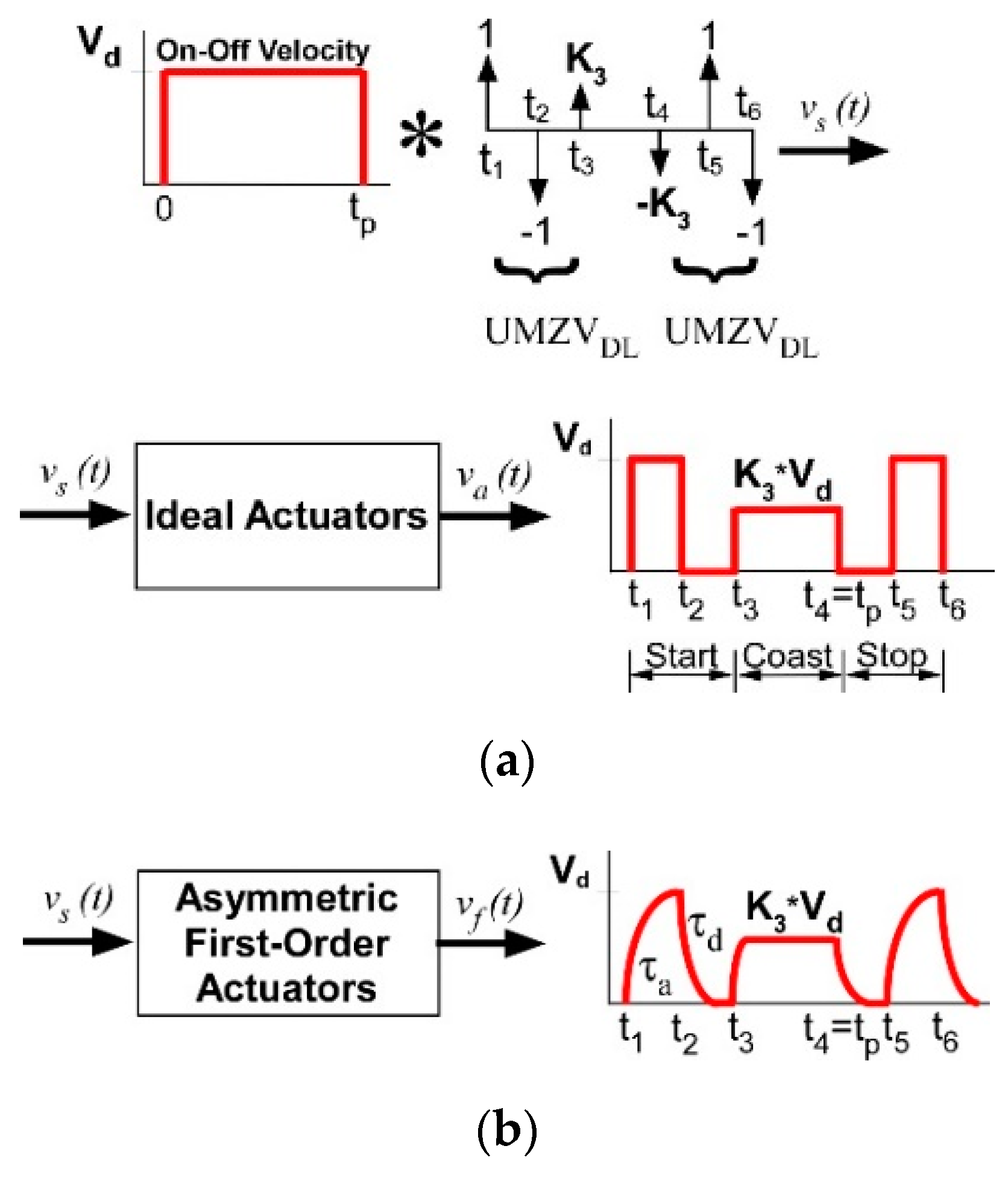
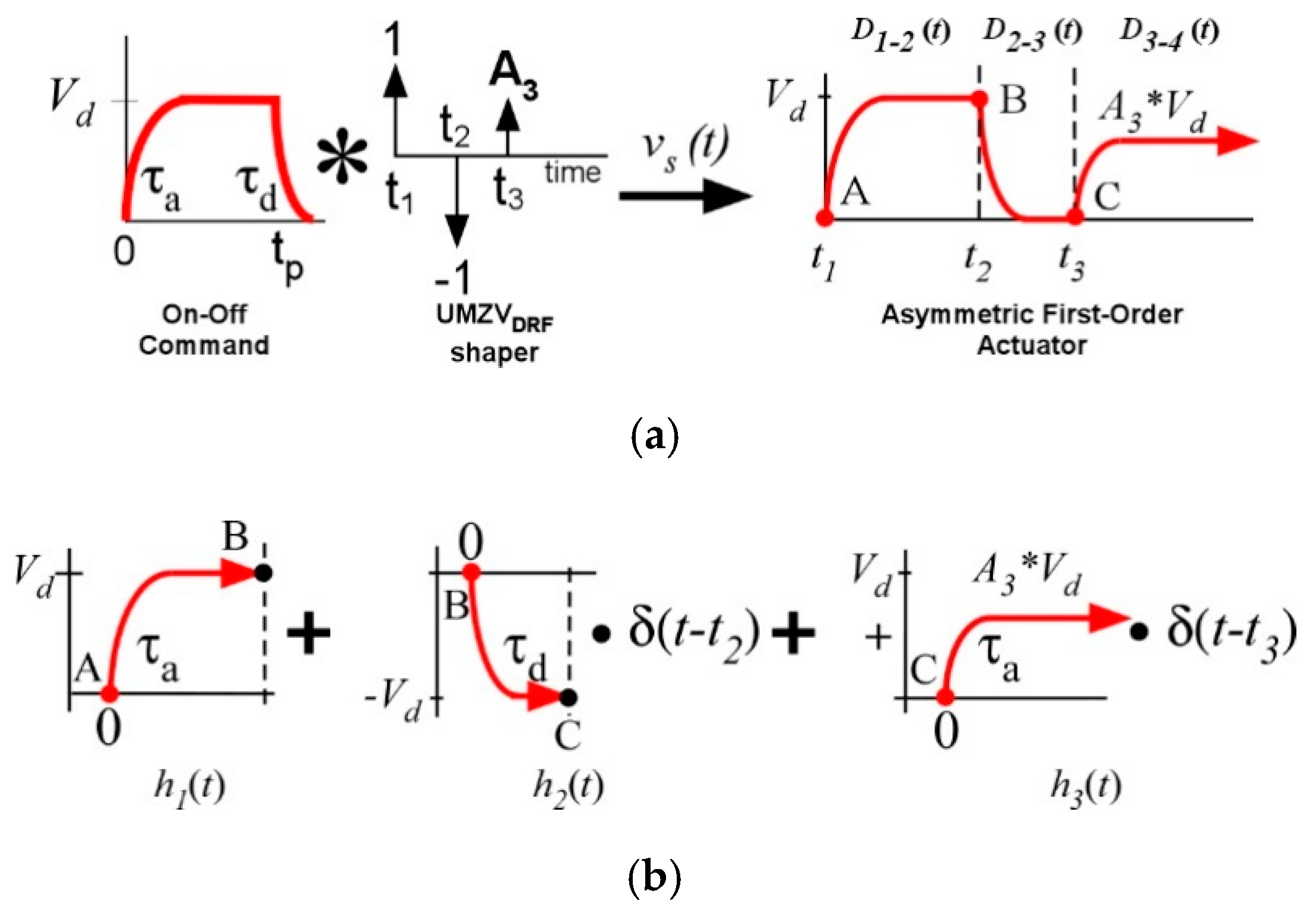
2.1. Analytical Deflection Reduction Shaping Command
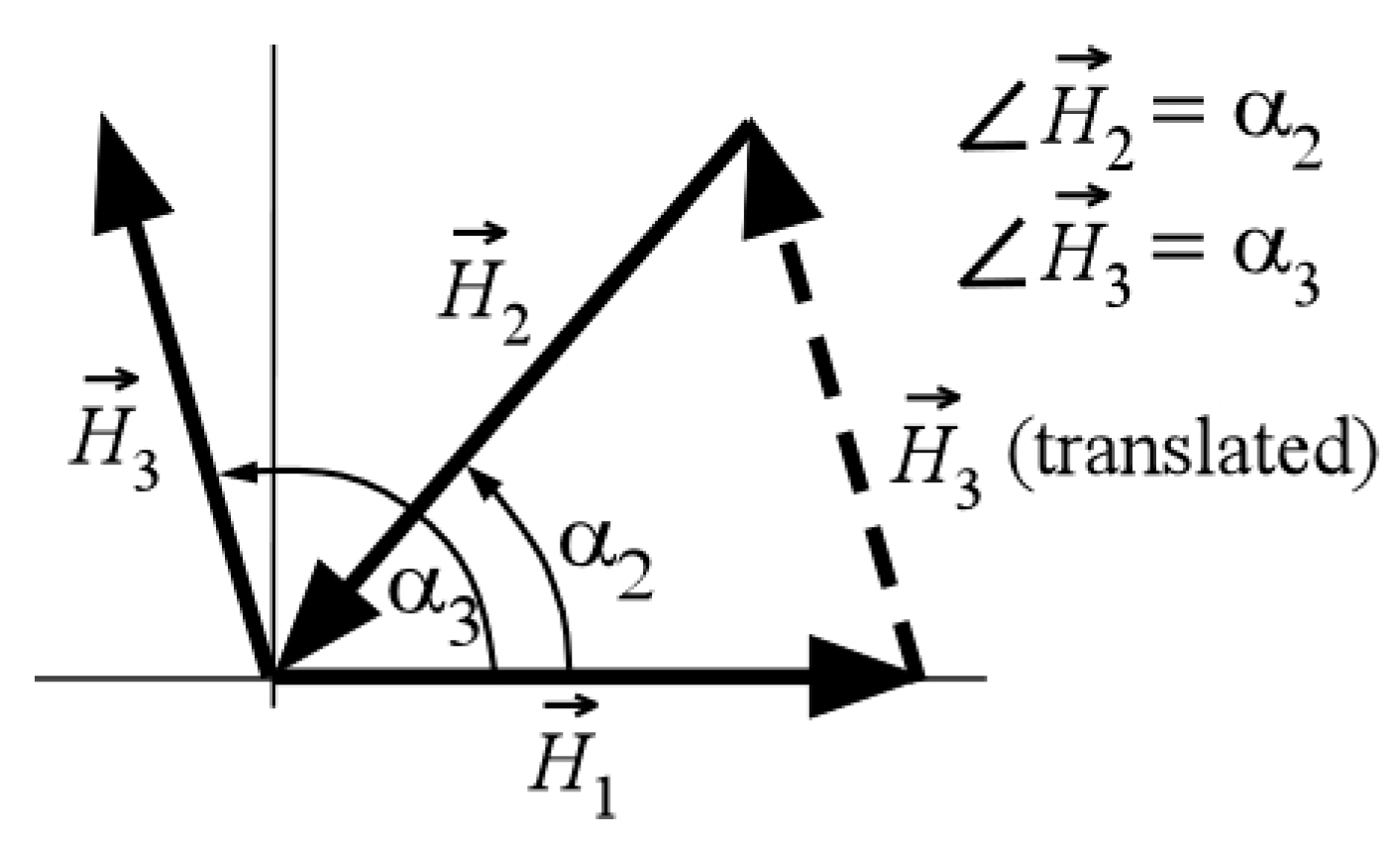
2.2. Optimized Deflection Reduction Shaping Commands
- step 1.
- Find the maximum deflection computed by Equation (22) at and .
- step 2.
- As an initial guess of the UMZVDRFO shaper, set up , and obtained by the UMZVDL shaper of Equation (1) with a desired ratio .
- step 3.
- Minimize the cost function Equation (28) with constraint Equations (23), (25)–(27). At every constraint evaluation of Equation (23), is computed by utilizing Equations (22) and (24).
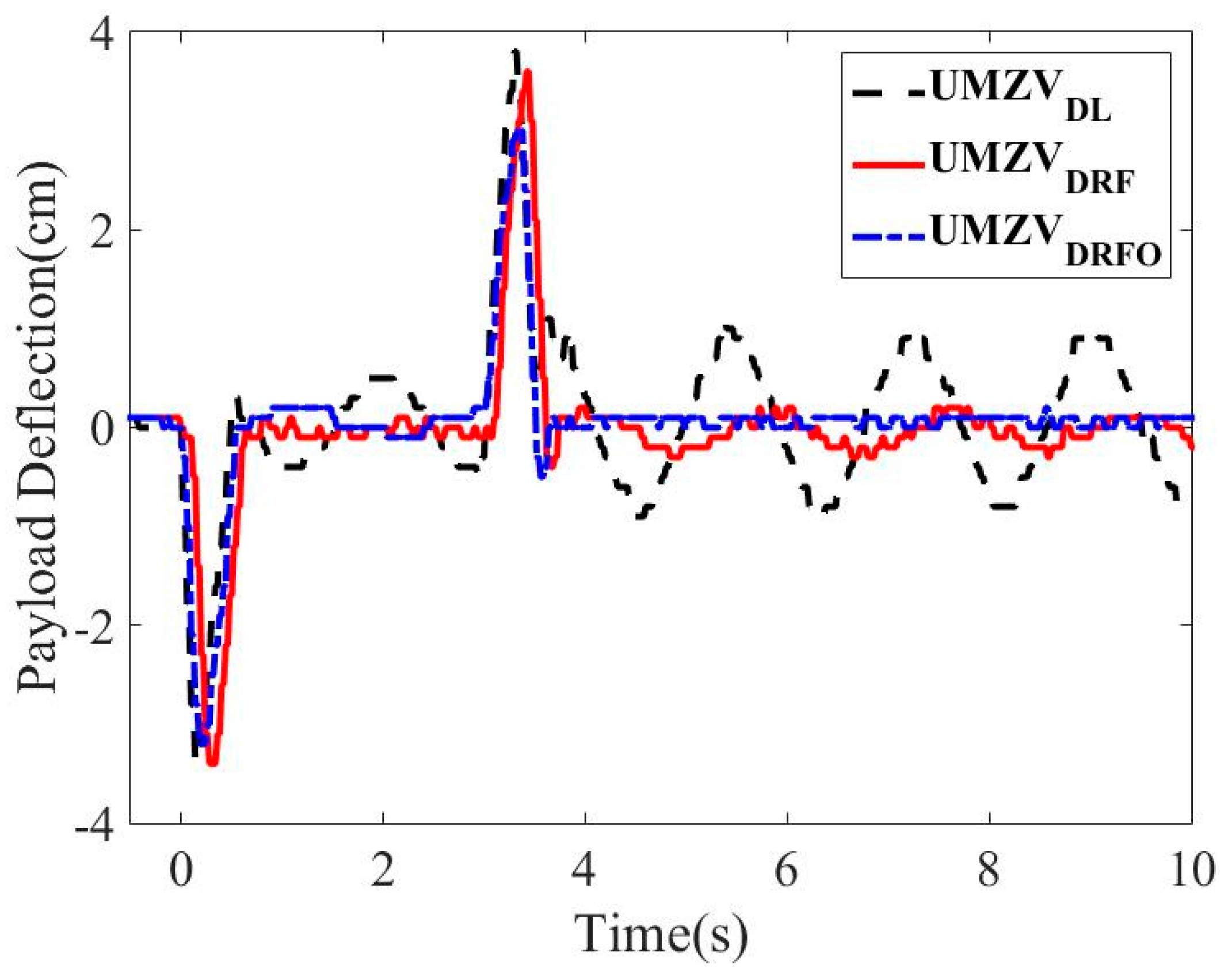
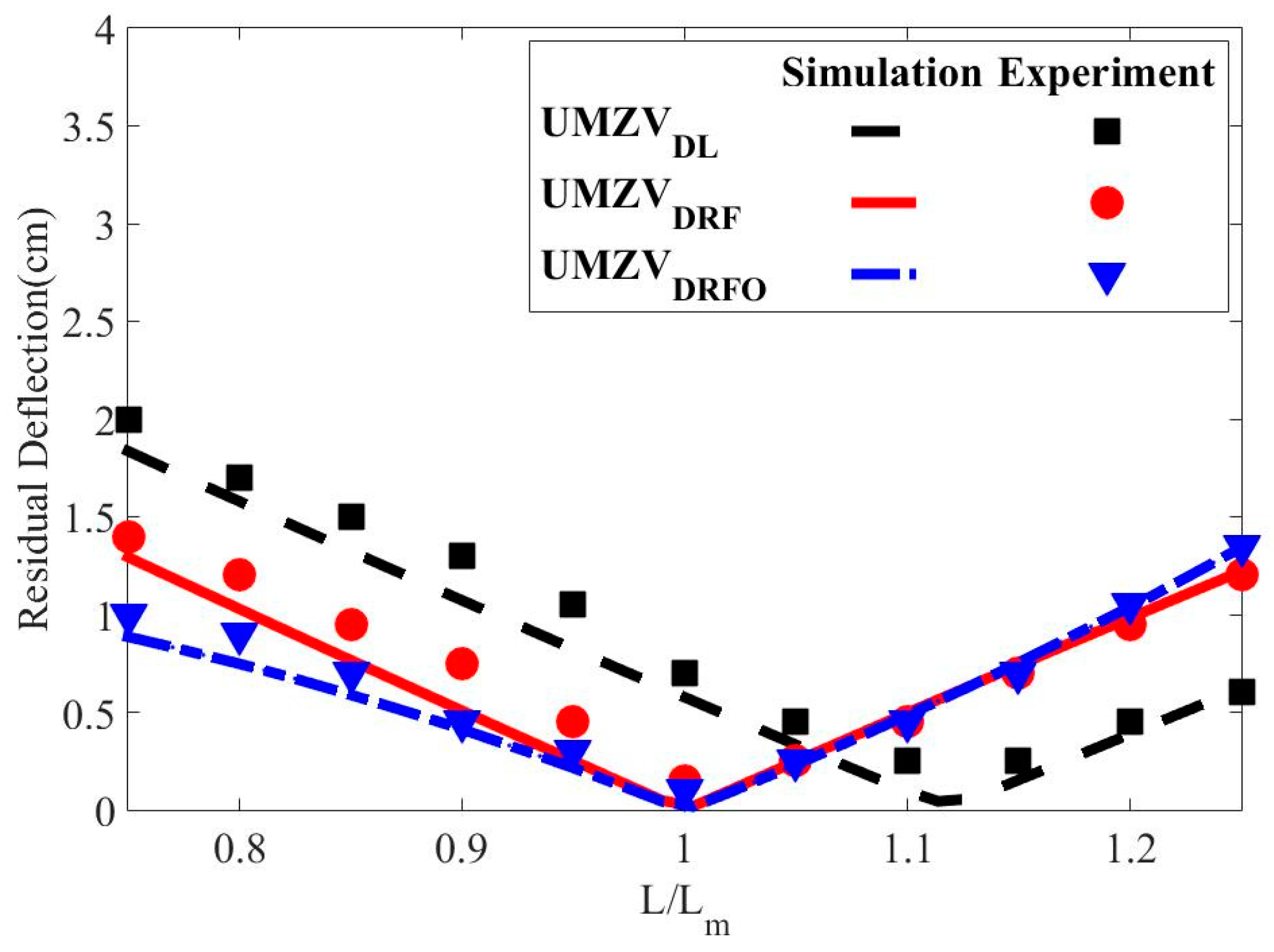
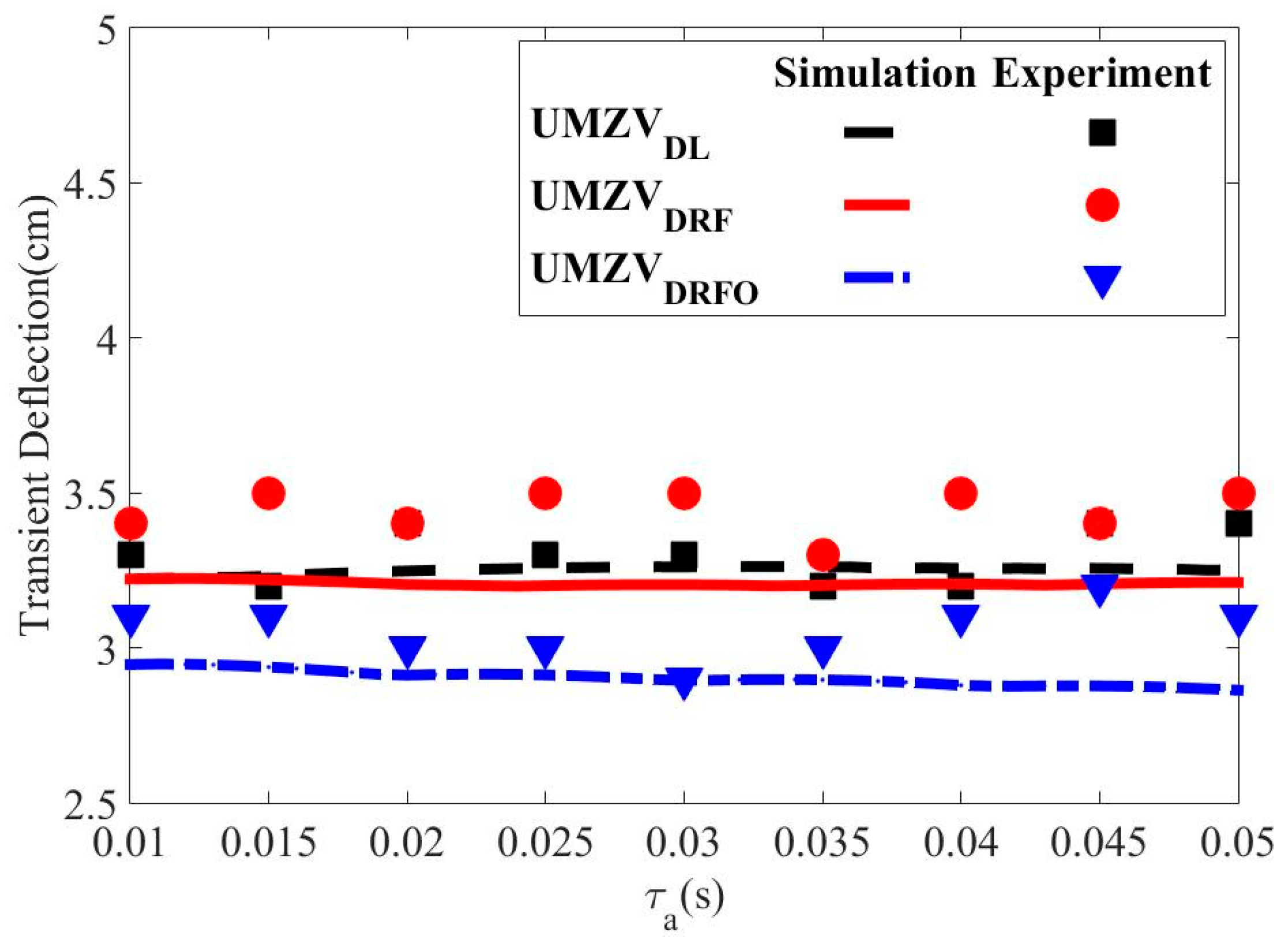
3. Numerical Results
4. Experimental Results
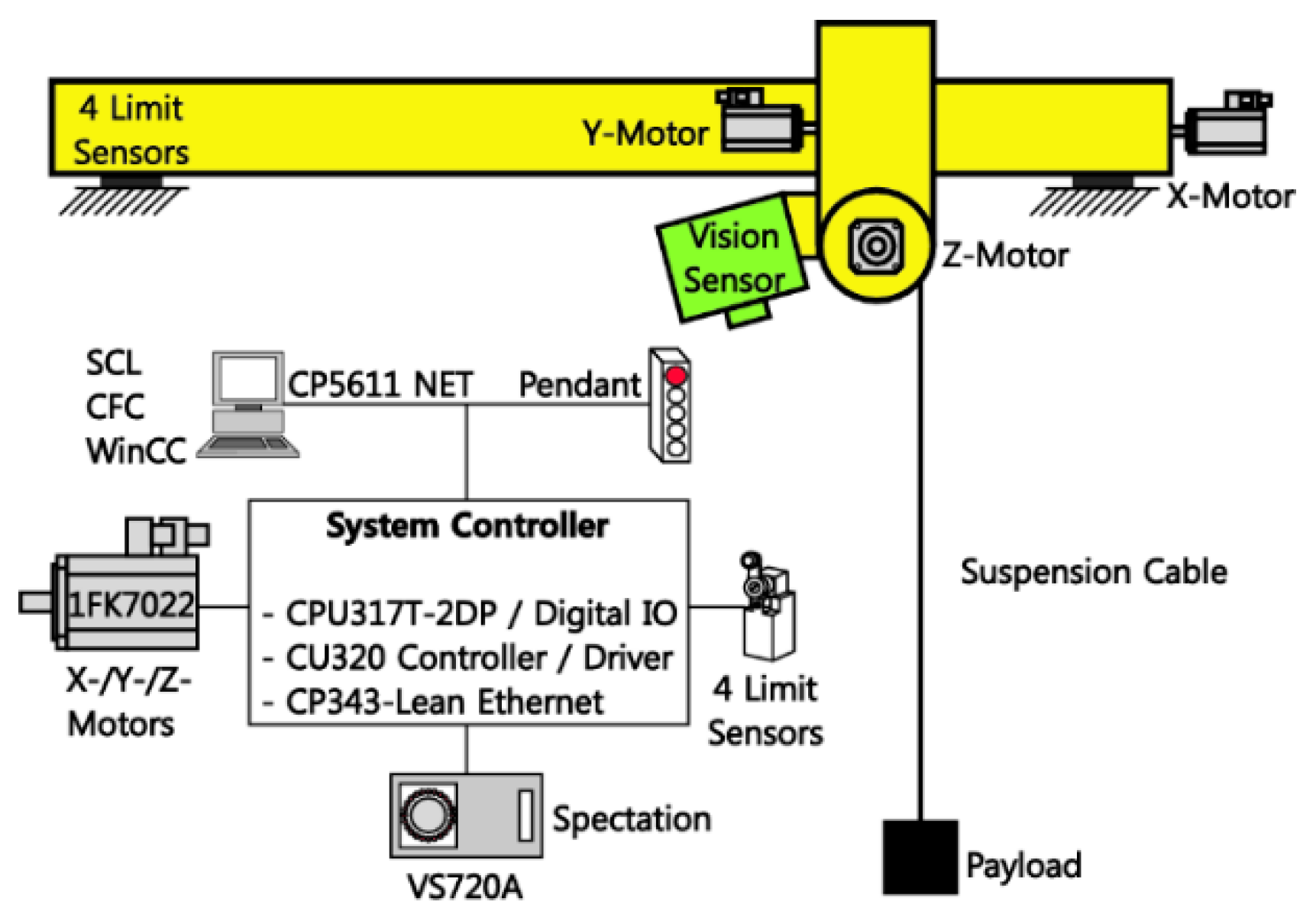
4.1. Experimental Set-Up
4.2. Experimental Assessment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sakawa, Y.; Shindo, Y. Optimal control of container cranes. Automatica 1982, 18, 257–266. [Google Scholar] [CrossRef]
- Shan, J.; Liu, H.-T.; Sun, D. Modified input shaping for a rotating single-link flexible manipulator. J. Sound Vib. 2005, 285, 187–207. [Google Scholar] [CrossRef]
- Lu, G.-Q.; Cereska, A.; Augustinavicius, G.; Maskeliunas, R.; Ragulskis, M. Intelligent Control and Performance Evaluation of a Novel Precise Positioning Stage. J. Intell. Fuzzy Syst. 2019, 36, 1205–1214. [Google Scholar] [CrossRef]
- Gorinevsky, D.; Vukovich, G. Nonlinear input shaping control of flexible spacecraft reorientation maneuver. J. Guid. Control Dyn. 1998, 21, 264–270. [Google Scholar] [CrossRef]
- Singer, N.C.; Seering, W.P. Preshaping Command Inputs to Reduce System Vibration. J. Dyn. Syst. Meas. Control 1990, 112, 76–82. [Google Scholar] [CrossRef]
- Singhose, W.; Singer, N.; Seering, W. Time-Optimal Negative Input Shapers. J. Dyn. Syst. Meas Control 1997, 119, 198–205. [Google Scholar] [CrossRef]
- Singhose, W.; Mills, B.; Seering, W. Closed-Form Methods for Generating On-Off Commands for Undamped Flexible Structures. J. Guid. Control Dyn. 1999, 22, 378–382. [Google Scholar] [CrossRef]
- Liu, Q.; Wie, B. Robust Time-Optimal Control of Uncertain Flexible Spacecraft. J. Guid. Control Dyn. 1992, 15, 597–604. [Google Scholar] [CrossRef]
- Ben-Asher, J.; Burns, J.A.; Cliff, E.M. Time-Optimal Slewing of Flexible Spacecraft. J. Guid. Control Dyn. 1992, 15, 360–367. [Google Scholar] [CrossRef]
- Singh, T.; Vadali, S.R. Robust Time-Optimal Control: A Frequency Domain Approach. J. Guid. Control Dyn. 1994, 17, 346–353. [Google Scholar] [CrossRef]
- Tuttle, T.; Seering, W. Experimental Verification of Vibration Reduction in Flexible Spacecraft Using Input Shaping. J. Guid. Control Dyn. 1997, 20, 658–664. [Google Scholar] [CrossRef]
- Singhose, W.; Banerjee, A.; Seering, W. Slewing Flexible Spacecraft with Deflection-Limiting Input Shaping. J. Guid. Control Dyn. 1997, 20, 291–298. [Google Scholar] [CrossRef]
- Wie, B.; Sinha, R.; Sunkel, J.; Cox, K. Robust Fuel- and Time-Optimal Control of Uncertain Flexible Space Structures. Am. Control Conf. 1993, 2475–2479. [Google Scholar]
- Singh, T. Fuel/Time Optimal Control of the Benchmark Problem. J. Guid. Control Dyn. 1995, 18, 1225–1231. [Google Scholar] [CrossRef]
- Singhose, W.; Derezinski, S.; Singer, N. Extra-Insensitive Input Shapers for Controlling Flexible Spacecraft. J. Guid. Control Dyn. 1996, 19, 385–391. [Google Scholar] [CrossRef]
- Kojima, H.; Singhose, W. Adaptive Deflection-Limiting Control for Slewing Flexible Space Structures. J. Guid. Control Dyn. 2007, 30, 61–67. [Google Scholar] [CrossRef] [Green Version]
- Sung, Y.-G.; Singhose, W. Closed-Form Specified-Fuel Commands for Two-Mode Systems. J. Guid. Control Dyn. 2007, 30, 1590–1596. [Google Scholar] [CrossRef]
- Robertson, M.J.; Singhose, W. Closed-Form Deflection-Limiting Commands. Am. Control Conf. 2005, 2104–2109. [Google Scholar]
- Robertson, M.J.; Singhose, W. Robust Analytic Deflection-Limiting Commands. Am. Control Conf. 2006, 363–368. [Google Scholar]
- Sung, Y.-G.; Singhose, W. Deflection-Limiting Commands for Systems with Velocity Limits. J. Guid. Control Dyn. 2008, 31, 472–478. [Google Scholar] [CrossRef]
- Vossller, M.; Singh, T. Characteristics of Deflection-Limited Time Optimal Control of the Benchmark Problem. In Proceedings of the 2008 International Symposium on Flexible Automation, Atlanta, GA, USA, 23–26 June 2008. [Google Scholar]
- Danielson, J.; Lawrence, J.; Singhose, W. Command Shaping for Flexible Systems subject to Constant Acceleration Limits. J. Dyn. Syst. Meas. Control 2008, 130, 051011. [Google Scholar] [CrossRef]
- Sung, Y.-G.; Jang, W.-S.; Kim, J.-Y. Negative Input Shaped Commands for Unequal Acceleration and Braking Delays of Actuators. J. Dyn. Syst. Meas. Control 2018, 140, 094501. [Google Scholar] [CrossRef]
- Lawrence, J.; Falkenberg, M.; Singhose, W. Input Shaping for a Flexible Nonlinear One-Link Robotic Arm with Backlash. In Proceedings of the Japan-USA Symposium on Flexible Automation, Denver, CO, USA, 19–21 July 2004. [Google Scholar]
- Lawrence, J.; Singhose, W.; Hekman, K. Friction-Compensating Command Shaping for Vibration Reduction. J. Vib. Acoust. 2005, 127, 307–314. [Google Scholar] [CrossRef]
- Kim, J.-J.; Kased, R.; Singh, T. Time-Optimal Control of Flexible Systems subject to Friction. Optim. Control Appl. Methods 2008, 29, 257–277. [Google Scholar] [CrossRef]
- Bradley, T.H.; Danielson, D.; Lawrenc, J.E.; Singhose, W. Command Shaping Under Nonsysmetrical Acceleration and Braking Dynamic. J. Vib. Acoust. 2008, 130, 054503. [Google Scholar] [CrossRef]
- Sung, Y.-G.; Ryu, B.-J. On-Off Shaping Commands for Asymmetrically Delayed Second-Order Actuators. J. Electr. Eng. Technol. 2019, 14, 2205–2216. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emani-Naeini, A. Feedback Control of Dynamic Systems, 4th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]



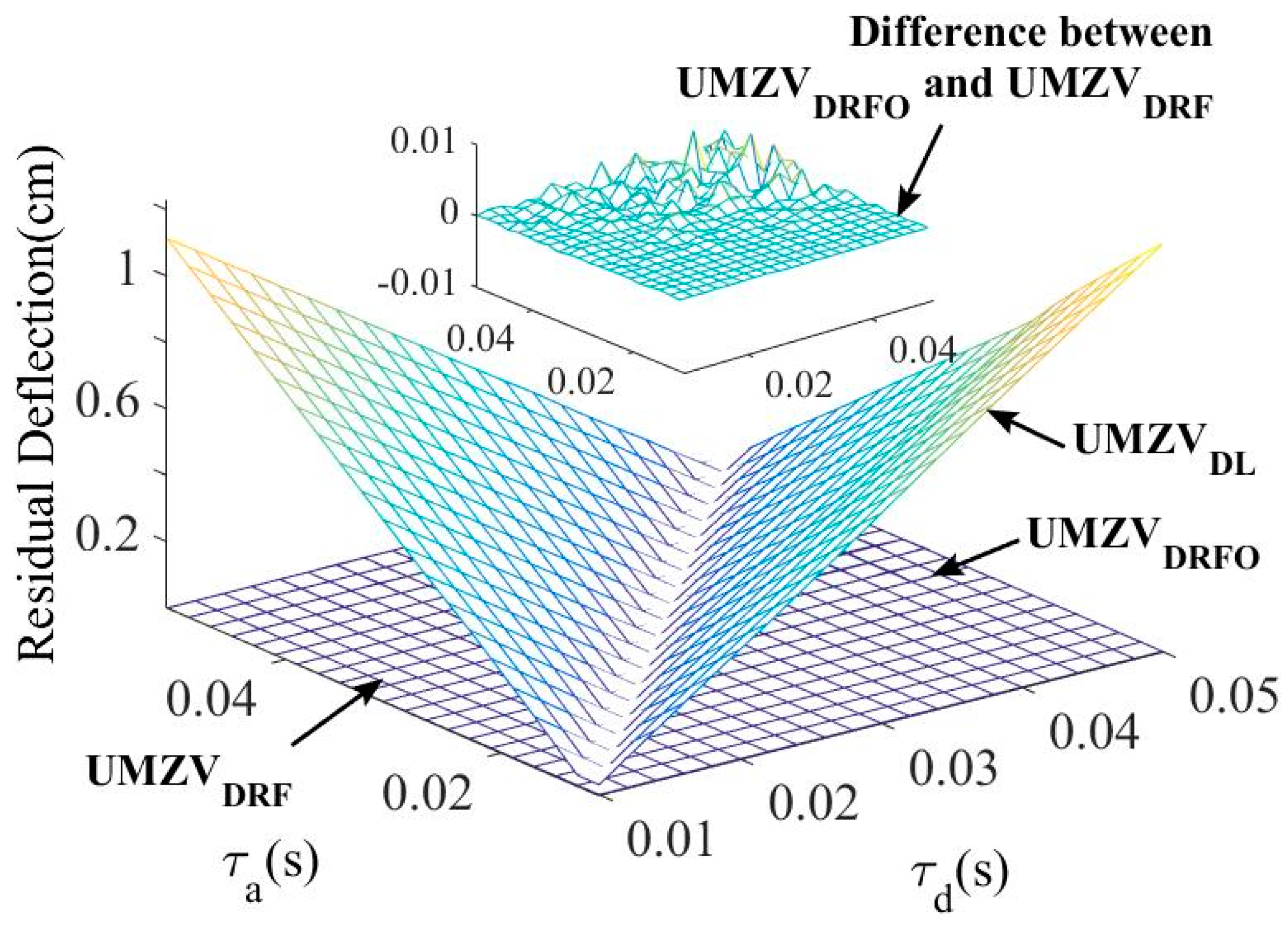
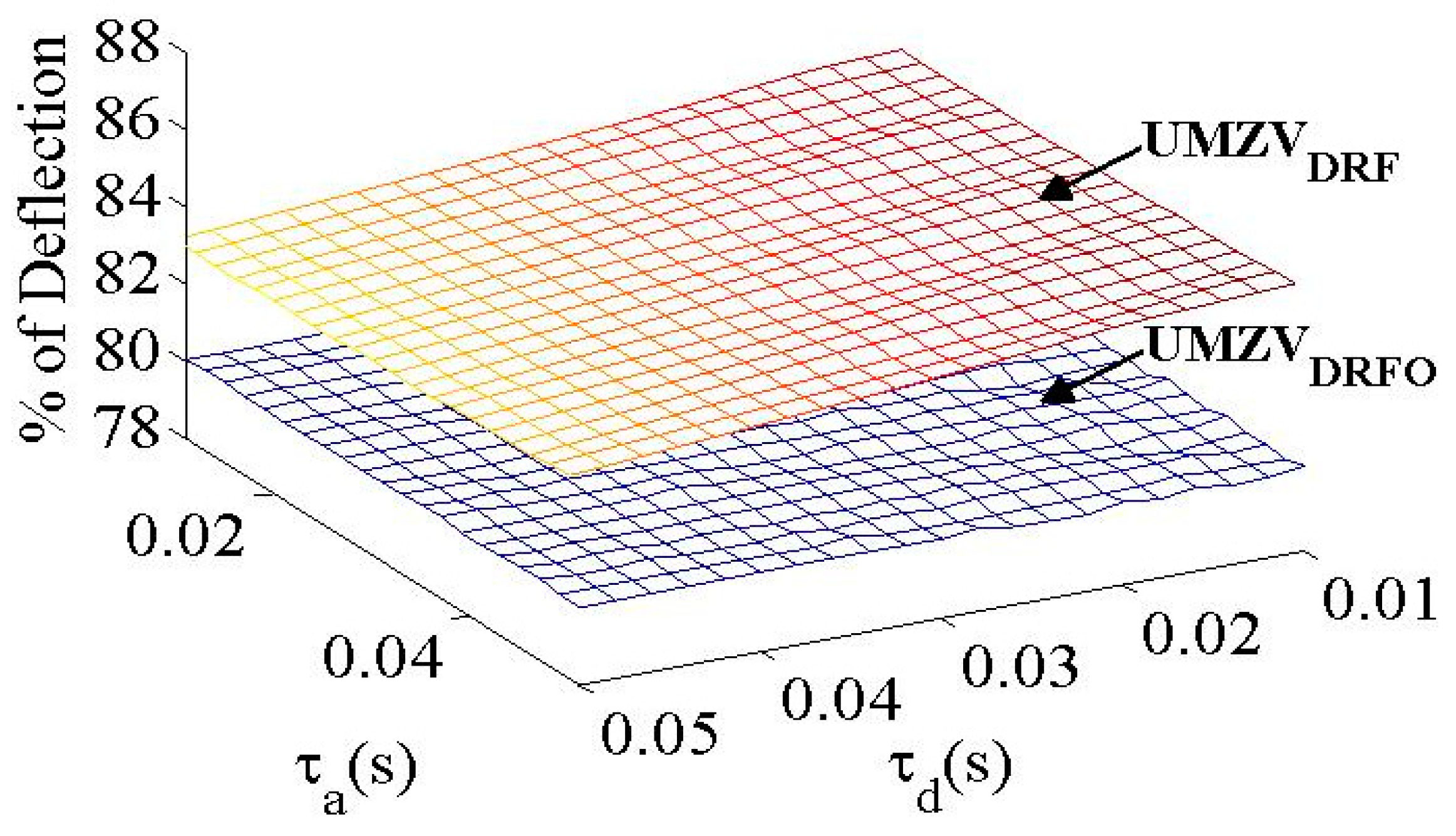
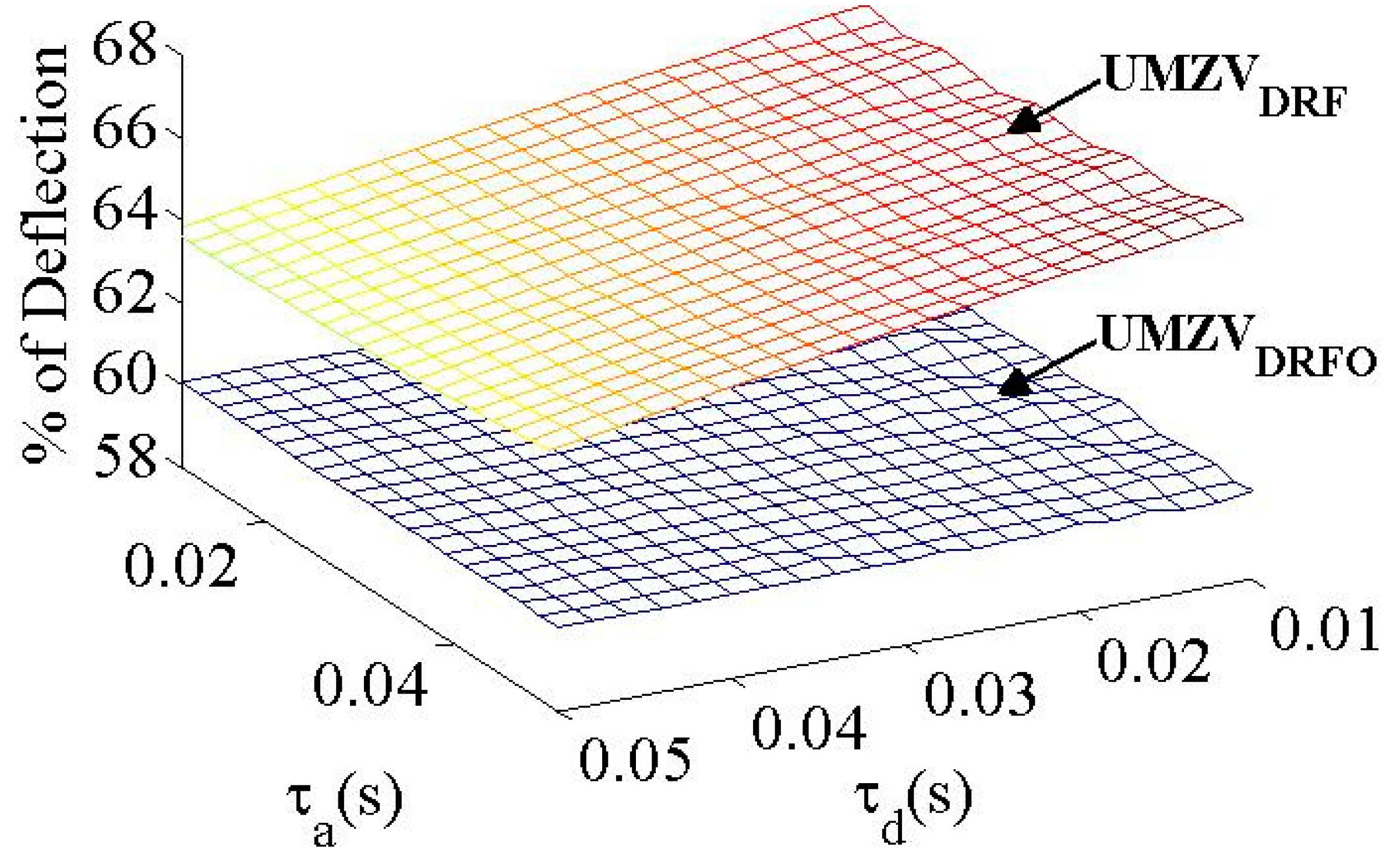

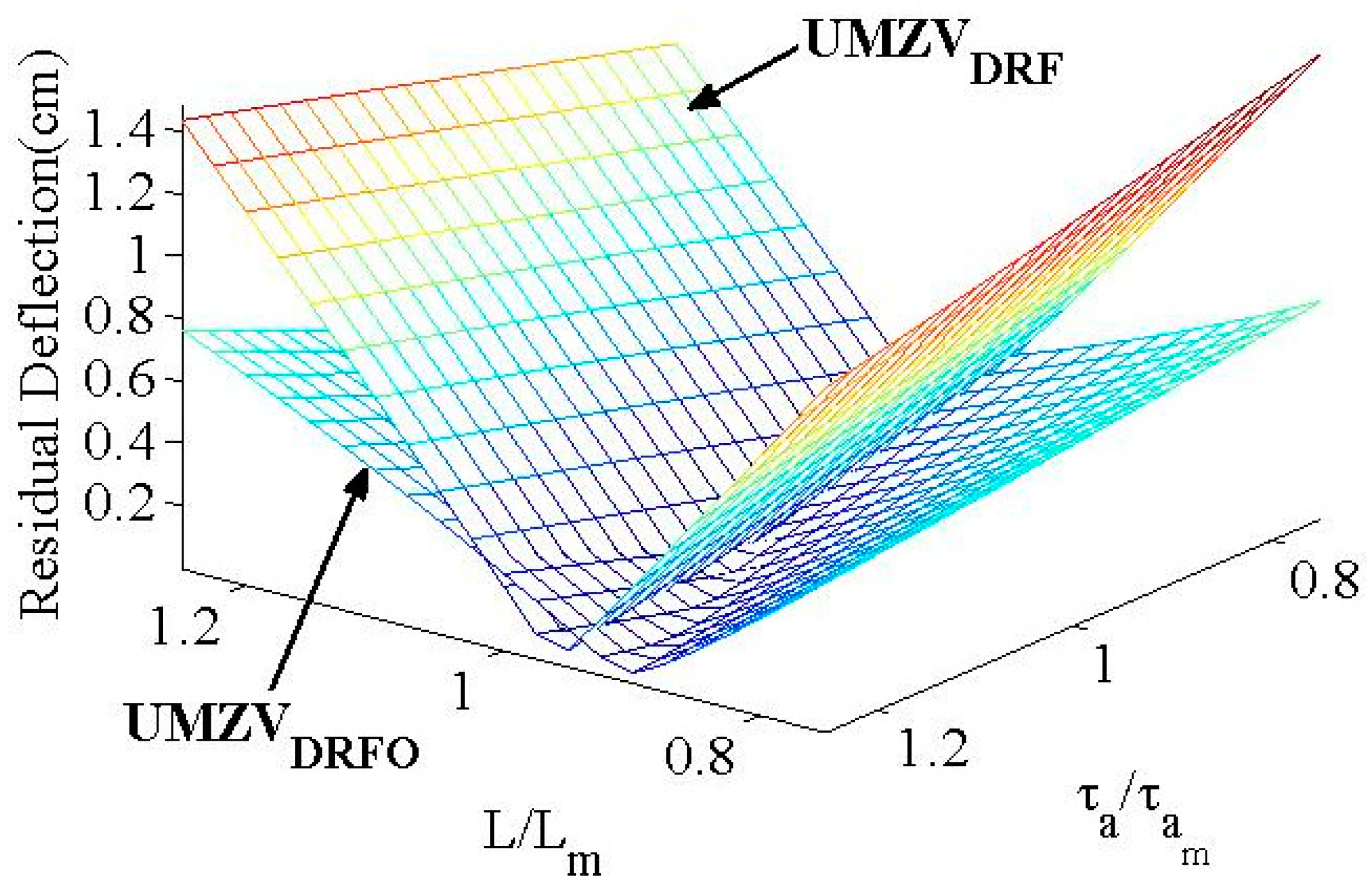




| τa | τd | L | Vd | tp | Dlim | Dflim |
|---|---|---|---|---|---|---|
| 0.03 s | 0.01 s | 0.8 m | 0.2 m/s | 3 s | 0.3 | 0.6 |
| Type | Input Shaper |
|---|---|
| UMZVDL | |
| UMZVDRF | |
| UMZVDRFO |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, Y.-G.; Kim, C.-L. Deflection Reduction Shaping Commands with Asymmetric First-Order Actuators. Appl. Sci. 2019, 9, 3982. https://doi.org/10.3390/app9193982
Sung Y-G, Kim C-L. Deflection Reduction Shaping Commands with Asymmetric First-Order Actuators. Applied Sciences. 2019; 9(19):3982. https://doi.org/10.3390/app9193982
Chicago/Turabian StyleSung, Yoon-Gyung, and Chang-Lae Kim. 2019. "Deflection Reduction Shaping Commands with Asymmetric First-Order Actuators" Applied Sciences 9, no. 19: 3982. https://doi.org/10.3390/app9193982
APA StyleSung, Y.-G., & Kim, C.-L. (2019). Deflection Reduction Shaping Commands with Asymmetric First-Order Actuators. Applied Sciences, 9(19), 3982. https://doi.org/10.3390/app9193982






