Abstract
We investigate the topological bound modes of surface plasmon polaritons (SPPs) in a graphene pair waveguide array. The arrays are with uniform inter-layer and intra-layer spacings but the chemical potential of two graphene in each pair are different. The topological bound modes emerge when two arrays with opposite sequences of chemical potential are interfaced, which are analogous to Jackiw-Rebbi modes with opposite mass. We show the topological bound modes can be dynamically controlled by tuning the chemical potential, and the propagation loss of topological bound modes can be remarkably reduced by decreasing the chemical potential. Thanks to the strong confinement of graphene SPPs, the modal wavelength of topological bound modes can be squeezed as small as 1/70 of incident wavelength. The study provides a promising approach to realizing robust light transport beyond diffraction limit.
1. Introduction
Surface plasmon polaritons (SPPs), the surface waves supported at the interface of metal and dielectric, have attracted enormous attention as they are able to propagate beyond diffraction limit and realize strong field enhancement [1,2,3,4]. In searching for new plasmonic material, graphene, a two-dimensional material composed of carbon atoms, has emerged as a promising candidate instead of noble metal [5,6,7,8,9,10]. Graphene shows stable mechanical properties thanks to the stability of the sp2 bonds that form the hexagonal lattice and oppose a variety of in-plane deformations [5,11]. The chemical properties of graphene are quite stable and will not be easily oxidized. The optical properties of graphene change with the change of the dielectric environment in contact with it. For example, air components such as different concentrations of oxygen and water vapor may affect the chemical potential of graphene [5]. The unique electronic, thermal, mechanical, and chemical characteristics of graphene, along with the intrinsic benefits of a carbon material, make it a promising candidate for many applications, such as supercapacitor [11,12,13,14]. Graphene based plasmonic devices have many new advantages when compared with metal. The SPPs in graphene are confined more than two orders smaller than that of free-space wavelength [8]. The surface conductivity of graphene can be dynamically controlled by tuning chemical potential via electrostatic and chemical doping [5]. The high carrier mobility in graphene makes it suitable for ultra-fast switching [15,16,17,18]. Graphene is also convenient to integrate with other optical nanodevices thanks to its dimensionless and flexible properties [6]. Moreover, graphene is utilized to investigate nonlinear optics due to its high nonlinear coefficient [19,20,21,22,23]. Many schemes are proposed to manipulate the optical property and control the propagation of SPPs, such as coupled graphene waveguides [24,25,26], graphene metamaterials [7,27], and dynamic modulation [28,29,30,31]. The graphene waveguide arrays have also been utilized to demonstrate optical analogues of semiclassical electron dynamics [32,33,34].
On the other hand, topology, a new freedom that characterizes the collective behavior of the wave functions on the photonic band structure, is demonstrated to reveal new states of light and provide robust way to control light flows [35,36,37,38]. One important feature of topological theory is that topologically-protected bound states emerge when two structures with different topologies are interfaced [35,39,40]. Such topological bound modes are usually located at the middle of band gap and rather robust against certain structure disorder. For example, the Su–Schriffer–Heeger (SSH) model, which studies the topology of a binary periodic array, can possess two distinct topological phases determined by the relative strength of inter-layer and intra-layer couplings [41,42,43,44]. The structure is topologically nontrivial as inter-layer coupling is stronger than intra-layer coupling, while it is topologically trivial as inter-layer coupling is weaker than intra-layer coupling [41]. The SSH model is demonstrated using graphene sheets [45,46,47,48,49]. However, the optical properties of topological bound modes in these systems are mostly determined by the spatial spacing between different graphene sheets, which cannot be flexibly adjusted after manufacturing.
In this work, we propose another scheme to investigate the topological bound modes in the binary graphene sheet arrays. The arrays are with uniform inter-layer and intra-layer spacings but the chemical potential of two graphene in each unit cell is different. The topological bound mode emerges when two arrays with opposite sequence of chemical potential are interfaced, which is analogous to Jackiw-Rebbi mode at the interface where the mass term changes sign in a Dirac equation with position dependent mass [50,51,52,53,54]. The Jackiw-Rebbi model is a type of topological bound state and firstly proposed in [50]. Such modes are recently discovered in other photonic systems, such as optical waveguides [51,52] and nano particles [53,54]. Here, we show the plasmonic Jackiw-Rebbi modes exist in graphene sheet arrays. As a result of strong confinement and tunable optical response of graphene SPPs, the Jackiw-Rebbi modes can be squeezed into deep subwavelength scale and dynamically controlled by tuning the chemical potential. The influence of chemical potential on propagation loss is also discussed.
2. Materials and Methods
2.1. Coupled-Mode Equations
The Jackiw-Rebbi modes can be solved from a tight bounding model, which is also known as coupled mode theory in optical waveguides. We consider the interface of two arrays with different masses, that is, different detuning of propagation constants. Then, the coupled mode equation can be given as
where an represents the field amplitude at nth waveguide, z denotes coordinate along the wave propagation direction, c is the coupling strength between adjacent waveguides, and σ is the mismatch of propagation constant. For left arrays (n < 0), the detuning of propagation constant is σ = σ1, while we set σ = σ2 for right waveguide array. The eigenvalues β and related bound modes of Equation (1) is can be solved by setting −idan/dz = βan = c(an+1+an-1)−(−1)nσan.
−idan/dz = c(an+1+an-1)−(−1)nσan,
According to [51], the solution of Jackiw-Rebbi modes at the interface can be divided into two cases. If −σ1 = σ2 = σ0 > 0, one has:
the amplitudes satisfy the relation a2n-1 = a2n. For the right sites, that is, n ≥ 0, the amplitudes fulfill the relation a2n/a2n+1 = −[σ0/c + (1 + /c2)1/2]. For the left sites, that is, n < 0, the amplitudes fulfill the relation a2n+1/a2n = −[σ0/c + (1 + /c2)1/2].
If σ1 = −σ2 = σ0 > 0, one has:
at the same time, the amplitudes satisfy the relation a2n-1 = a2n. For the right sites, that is, n ≥ 0, the amplitude fulfills the relation a2n/a2n+1 = [σ0/c + (1 + /c2)1/2]. For the left sites, that is, n < 0, the amplitude fulfills the relation a2n+1/a2n = [σ0/c + (1 + /c2)1/2].
2.2. Graphene Waveguide Arrays
Now we consider the realization of Jackiw-Rebbi modes in graphene sheet arrays. Figure 1 depicts the geometry of graphene pair arrays under consideration. The SPPs propagate along the z axis. The structure is composed of two different arrays. For each array, there are two graphene sheets in each unit cell with alternating chemical potential. The middle of the structure is a defect as the sequences of chemical potential at left and right arrays are different.
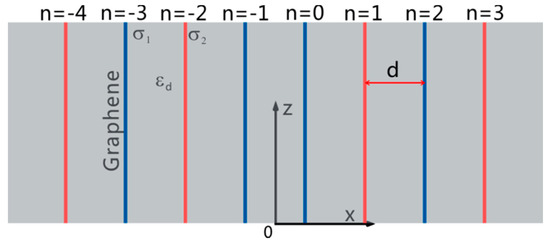
Figure 1.
The geometric scheme of graphene waveguide arrays. The red and blue colors represent graphene sheets with different chemical potentials. The center of the structure is a defect. n denotes the waveguide number.
The propagation constants of SPPs are different with different chemical potentials. In such an arrangement, the center defect will support Jackiw-Rebbi modes. The arrays are embedded in the dielectrics with permittivity denoted as εd. Here they are initially assumed to be freestanding in air with εd = 1. The intra- and inter-layer spacings are uniform and denoted as d. The surface conductivities are represented by σ1 and σ2, which are related to temperature T, chemical potential μ, momentum relaxation time τ, and photon frequency ω. The surface conductivity of graphene can be determined by the Kubo formula [6]
where e is the electron charge, ℏ is the reduced Planck’s constant, and kB is Boltzmann constant. In this work, the room temperature (T = 300 K) is assumed. The spatial spacing, momentum relaxation time, and incident wavelength are fixed at d = 70 nm, τ = 1 ps, and λ = 10 μm. The chemical potential of graphene sheet is kept at μ1 = 0.15 eV and chemical potential of the other sheets μ2 is changed. The parameters of graphene are typically used for simulation [24], which coincides with the current experiment. Under these parameters, the graphene sheets are weakly coupled.
We only focus on the TM polarized SPPs propagating along z axis. The propagation constants and mode profiles of supermodes in waveguide arrays can be figured out by transfer matrix method [1,55], which is based on the boundary condition of the electromagnetic field. Moreover, we also calculate the wave propagation in the structure performed based on the finite element method. The graphene is modeled by using the surface current boundary condition. The domain has been discretized by using homogeneous mesh with the maximal element size being less than 1/12 of the graphene SPP wavelength.
3. Results
Figure 2 shows the effective refractive index neff of eigenmodes in the limited graphene sheet arrays for two different cases. The total number of graphene sheets is N = 40. For a single graphene sheet, there is only one TM polarized SPP mode. As a result, the system composed of 40 graphene sheets will support 40 supermodes. Figure 2a,b plot the real part and imaginary part of effective refractive index with μ1 = μ2 = 0.15 eV. In this case, the structure is with uniform graphene sheet and no interface is formed at the middle of the structure. Both the spectra of Re (neff) and Im (neff) are continuously varied and no gap is found in the spectra. As a result, no bound modes are supported in the system.
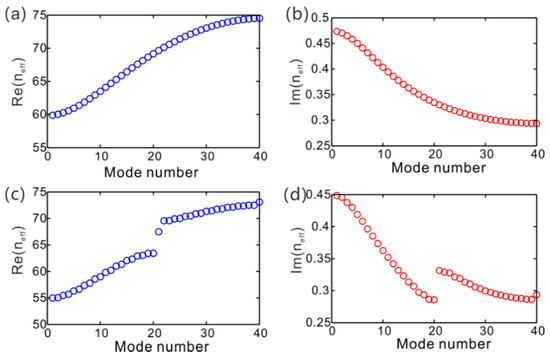
Figure 2.
The effective refractive index of supermodes for two different structures. (a,b) are the real and imaginary parts of refractive index for μ2 = 0.15 eV, respectively. (c,d) are Re (neff) and Im (neff) for μ2 = 0.18 eV, respectively. In all cases, μ1 = 0.15 eV.
The case is different if we tune chemical potential μ2 of some graphene sheets. Figure 2c,d plot the real and imaginary parts of effective refractive index with μ1 = 0.15 eV and μ2 = 0.18 eV. In this case, the structure now can be regarded as two arrays with different sequences of chemical potential connected, and the center of the structure is the interface. The results show that there is evidently a SPP mode in the band gap of Re (neff) with effective refractive index being neff = 68 + 0.3i. The wavelength of SPPs is figured out as λSPP = λ/neff = 1/68. On the other hand, there is also another trivial defect mode with largest real part of effective refractive index as shown in Figure 2c.
Figure 3a,b plot the mode profile (|H|) of topological and trivial defect modes, respectively. The dotted lines indicate the location of graphene sheet. Both modes are located at the center defect, but their field distributions are different. For the topological mode, the field at the center of two graphene sheets is almost vanished, while the field for the trivial defect mode is not vanished. As explained above, the topological bound mode emerges because the sequence of chemical potential of two graphene sheet arrays is different. The trivial defect mode is formed as the two graphene sheets around the defect constitute a region of different effective refractive index than the rest of the structure.
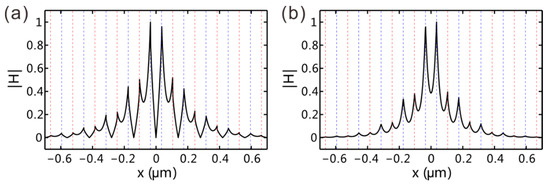
Figure 3.
The field distributions for (a) topological bound mode and (b) trivial defect mode.
Figure 4 shows the wave propagation of SPPs for two different structures with different chemical potentials. In both cases, the wave is launched from a single graphene sheet at the center waveguide. In Figure 4a, the graphene sheets are uniform with the chemical potential of graphene μ1 = μ2 = 0.15 eV. In this case, there is no bound mode supported in the system and the SPPs spread during the propagation, which is known as discrete diffraction. In Figure 4b, the chemical potential is μ1 = 0.15 eV and μ2 = 0.18 eV. As the SPPs are incident from the single graphene sheet at the center defect, most energy is confined at the center of the structure. Moreover, the intensity of light shows a beating pattern during the propagation. This is because the trivial and non-trivial defect modes are excited simultaneously.
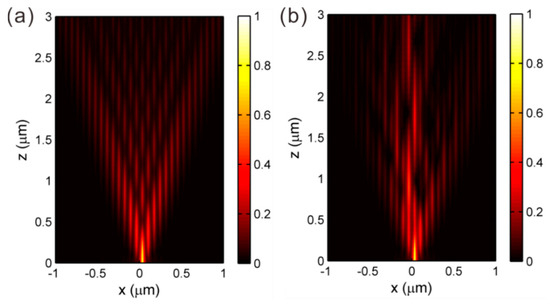
Figure 4.
The propagation of surface plasmon polaritons (SPPs) for a single-waveguide excitation. (a) μ1 = μ2 = 0.15 eV. (b) μ1 = 0.15 eV and μ2 = 0.18 eV.
The surface conductivity of graphene relates largely to the chemical potential, which can be controlled by electrostatic and chemical doping [5]. Figure 5 plots the numerically calculated effective refractive index as chemical potential μ2 changes form 0.13 eV to 0.17 eV. The chemical potential μ1 is fixed at 0.15 eV. In Figure 5a, we plot the real part of refractive index. As μ2 = μ1, there are no bandgap or topological bound modes. The bandgap broadens when chemical potential is tuned away from 0.15 eV. The topological bound modes appear in the bandgap with effective refractive index approaching Re (neff) = 70. The real part of effective refractive index shows a slight decrease with the increase of chemical potential. On the other hand, the system also supports trivial defect modes. For small μ2, the real part of the effective refractive index of the trivial defect mode is the smallest. In contrast, Re (neff) of trivial defect mode becomes largest as chemical potential μ2 increases. Figure 5b plots the imaginary part of effective refractive index. The red dots represent the imaginary part of refractive index. For small chemical potentials, the topological bound modes have the smallest imaginary modes among all supermodes; that is, the lowest propagation loss. As a result, the topological modes will dominate for a single-waveguide excitation after enough propagation distances.
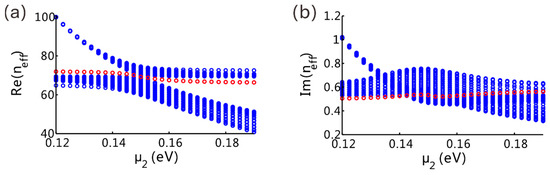
Figure 5.
The eigenvalue spectra for different chemical potentials. (a) Real part and (b) imaginary part. The red dots represent the topological bound modes.
The topological bound modes are extremely robust against structural disorder. To test the robustness of Jackiw-Rebbi modes, we consider the chemical potential of original graphene sheet arrays to be μ1 = 0.15 eV and μ2 = 0.18 eV, and the corresponding surface conductivity are σ1 and σ2, respectively. We further introduce disorder into them by defining a random fluctuation of the surface conductivity. The additional surface conductivity of nth graphene sheet is set to be a random value δn, which is smaller than (σ2 − σ1)/4. Figure 6a,b plot the real and imaginary part of effective refractive index for one disordered structure. The results show that the band gap still does not close and the Jackiw-Rebbi persists in the gap.
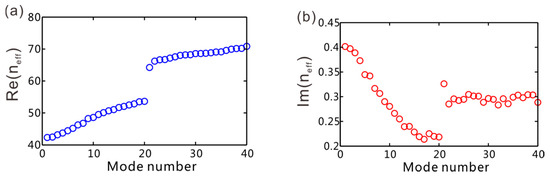
Figure 6.
Robustness of the Jackiw-Rebbi against perturbation. The chemical potential (a) real part and (b) imaginary part of effective refractive index.
4. Conclusions
In conclusion, we have studied the topological plasmonic modes in a graphene pair waveguide array based on Jackiw-Rebbi modes. The interlayer and intralayer spacing of the arrays is uniform but the chemical potential of two graphene in each pair are different. We show the topological bound modes take place with changing the chemical potential of graphene such that two arrays with opposite sequences of chemical potential are interfaced. Such topological bound modes are analogous to Jackiw-Rebbi modes in a Dirac equation. Due to the strong confinement of graphene SPPs, the modal wavelength of the topological bound mode can reach as small as 1/70 of incident wavelength. As the emerging condition of topological bound modes is determined by the chemical potential, the topological bound modes can be dynamically controlled. Moreover, the imaginary part of the effective index of topological bound mode can be smaller than other modes by decreasing the chemical potential. We also show the trivial defect modes emerge in the system, which can be reflected from the wave propagation. Further studies can be carried out from the following three aspects. The first is the structure design by using graphene ribbons, which are easier to be fabricated in experiments than the planar graphene sheets. Secondly, whether the suitably-distributed loss can generate Jackiw-Rebbi modes is also an interesting topic. Thirdly, one may extend the study to higher dimensions, such as the two-dimensional graphene-coated nanowire arrays.
Author Contributions
Conceptualization, D.Z. and S.K.; methodology, C.X.; software, P.Z. and D.Z.; validation, S.K.; formal analysis, C.X.; investigation, S.K.; resources, P.Z.; data curation, C.X.; writing—original draft preparation, D.Z.; writing—review and editing, H.G., M.H. and S.K.; visualization, C.X. and P.Z.; supervision, S.K.; project administration, S.K.; funding acquisition, S.K. and D.Z.
Funding
This research was funded by National Natural Science Foundation of China (NSFC) (11804259), Program for Distinguished Middle-aged and Young Innovative Research Team in Higher Education of Hubei, China (T201806), the Campus Science Foundation Research Project of Wuhan Institute of Technology (K201821), the Colleges and Universities of National Innovation and Entrepreneurship Training Plan (S201910927024), Science and Technology Plan Research Project of Hubei Education Department (B2019162).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin, Germany, 2007. [Google Scholar]
- Ding, F.; Bozhevolnyi, S.I. A Review of Unidirectional Surface Plasmon Polariton Metacouplers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 4600611. [Google Scholar] [CrossRef]
- Ke, S.; Liu, J.; Liu, Q.; Zhao, D.; Liu, W. Strong absorption near exceptional points in plasmonic waveguide arrays. Opt. Quantum Electron. 2018, 50, 318. [Google Scholar] [CrossRef]
- Ding, F.; Deshpande, R.; Bozhevolnyi, S.I. Bifunctional Gap-Plasmon Metasurfaces for Visible Light: Polarization-Controlled Unidirectional Surface Plasmon Excitation and Beam Steering at Normal Incidence. Light Sci. Appl. 2018, 7, 17178. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Loh, K.P. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.Y.; Al, A. Atomically thin surface cloak using graphene monolayers. ACS Nano 2011, 5, 5855–5863. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Ke, S.; Wang, B.; Long, H.; Wang, K.; Lu, P. Numerical study on plasmonic absorption enhancement by a rippled graphene sheet. J. Lightwave Technol. 2017, 35, 320–324. [Google Scholar] [CrossRef]
- Deng, H.; Ye, F.; Malomed, B.A.; Chen, X.; Panoiu, N.C. Optically and electrically tunable Dirac points and Zitterbewegung in graphene-based photonic superlattices. Phys. Rev. B 2015, 91, 201402. [Google Scholar] [CrossRef]
- Liu, J.X.; Park, S.; Nowak, D.; Tian, M.C.; Wu, Y.; Long, H.; Wang, K.; Wang, B.; Lu, P. Near-Field Characterization of Graphene Plasmons by Photo-Induced Force Microscopy. Laser Photonics Rev. 2018, 12, 1800040. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Liu, W. Adiabatic transfer of surface plasmons in non-Hermitian graphene waveguides. Opt. Quantum Electron. 2018, 50, 393. [Google Scholar] [CrossRef]
- Salunkhe, R.R.; Lee, Y.H.; Chang, K.H.; Li, J.M.; Simon, P.; Tang, J.; Torad, N.L.; Hu, C.C.; Yamauchi, Y. Nanoarchitectured graphene-based supercapacitors for next-generation energy-storage applications. Chem. Eur. J. 2014, 20, 13838–13852. [Google Scholar] [CrossRef]
- Tang, J.; Yamauchi, Y. MOF morphologies in control. Nat. Chem. 2016, 8, 638–639. [Google Scholar] [CrossRef] [PubMed]
- Salunkhe, R.R.; Hsu, S.; Wu, K.C.W.; Yamauchi, Y. Large-Scale Synthesis of Reduced Graphene Oxides with.Uniformly Coated Polyaniline for Supercapacitor Applications. ChemSusChem 2014, 7, 1551–1556. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.; Tang, J.; Henzie, J.; Li, Y.; Xu, X.; Chen, T.; Wang, Z.; Wang, J.; Ide, Y.; Bando, Y.; et al. Assembly of Hollow Carbon Nanospheres on Graphene Nanosheets and Creation of Iron−Nitrogen-Doped Porous Carbon for Oxygen Reduction. ACS Nano 2018, 12, 5674–5683. [Google Scholar] [CrossRef] [PubMed]
- Ni, G.X.; Wang, L.; Goldflam, M.D.; Wagner, M.; Fe, Z.; McLeo, A.S.; Liu, M.K.; Keilman, F.; Özyilmaz, B.; Castro, A.H.; et al. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photonics 2016, 10, 244–247. [Google Scholar] [CrossRef]
- Li, M.; Xie, H.; Cao, W.; Luo, S.; Tan, J.; Feng, Y.; Du, B.; Zhang, W.; Li, Y.; Zhang, Q.; et al. Photoelectron Holographic Interferometry to Probe the Longitudinal Momentum Offset at the Tunnel Exit. Phys. Rev. Lett. 2019, 122, 183202. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Zhou, Y.; He, M.; Chen, Y.; Ke, Q.; Liang, J.; Zhu, X.; Li, M.; Lu, P. Determination of the Ionization Time Using Attosecond Photoelectron Interferometry. Phys. Rev. Lett. 2018, 121, 253203. [Google Scholar] [CrossRef] [PubMed]
- Zhai, C.; Zhang, Y.; Zhang, Q. Characterizing the ellipticity of an isolated attosecond pulse. Opt. Commun. 2019, 437, 104–109. [Google Scholar] [CrossRef]
- Kou, Y.; Förstner, J. Discrete plasmonic solitons in graphene-coated nanowire arrays. Opt. Express 2016, 24, 4714–4721. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, Z.; Wang, B.; Long, H.; Wang, K.; Lu, P. Surface plasmonic lattice solitons in semi-infinite graphene sheet arrays. J. Lightwave Technol. 2017, 35, 2960–2965. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Z.; Long, H.; Wang, K.; Wang, B.; Lu, P. Optical bistability in defective photonic multilayers doped by graphene. Opt. Quantum Electron. 2017, 49, 163. [Google Scholar] [CrossRef]
- Li, L.; Lan, P.; Zhu, X.; Huang, T.; Zhang, Q.; Lein, M.; Lu, P. Reciprocal-Space-Trajectory Perspective on High-Harmonic Generation in Solids. Phys. Rev. Lett. 2019, 122, 193901. [Google Scholar] [CrossRef] [PubMed]
- Kinyua, D.M.; Niu, L.; Long, H.; Wang, K.; Wang, B. Tuning the photoinduced charge transfer from CdTe quantum dots to ZnO nanofilms through Ga doping. Opt. Mater. 2019, 96, 109311. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Garcı´a-Vidal, F.J.; Yuan, X.; Teng, J. Strong Coupling of Surface Plasmon Polaritons in Monolayer Graphene Sheet Arrays. Phy. Rev. Lett. 2012, 109, 073901. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Wang, B.; Qin, C.; Long, H.; Wang, K.; Lu, P. Exceptional points and asymmetric mode switching in plasmonic waveguides. J. Lightwave Technol. 2016, 34, 5258–5262. [Google Scholar] [CrossRef]
- Ke, S.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological mode switching in a graphene doublet with exceptional points. Opt. Quantum Electron. 2017, 49, 224. [Google Scholar] [CrossRef]
- Li, J.; Fu, J.; Liao, Q.; Ke, S. Exceptional points in chiral metasurface based on graphene strip arrays. J. Opt. Soc. Am. B 2019, 36, 2492–2498. [Google Scholar] [CrossRef]
- Qin, C.; Wang, B.; Long, H.; Wang, K.; Lu, P. Nonreciprocal phase shift and mode modulation in dynamic graphene waveguides. J. Lightwave Technol. 2016, 34, 3877–3883. [Google Scholar]
- Zhao, D.; Liu, F.; Meng, P.; Wen, J.; Xu, S.; Li, Z.; Zhong, D. Reflection Enhancement and Giant Lateral Shift in Defective Photonic Crystals with Graphene. Appl. Sci. 2019, 9, 2141. [Google Scholar] [CrossRef]
- Liu, Q.; Ke, S.; Liu, W. Mode conversion and absorption in an optical waveguide under cascaded complex modulations. Opt. Quantum Electron. 2018, 50, 356. [Google Scholar] [CrossRef]
- Zhao, D.; Zhong, D.; Hu, Y.; Ke, S.; Liu, W. Imaginary modulation inducing giant spatial Goos–Hänchen shifts in one-dimensional defective photonic lattices. Opt. Quantum Electron. 2019, 51, 113. [Google Scholar] [CrossRef]
- Wang, F.; Qin, C.Z.; Wang, B.; Long, H.; Wang, K.; Lu, P.X. Rabi oscillations of plasmonic supermodes in graphene multilayer arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 4600105. [Google Scholar] [CrossRef]
- Wang, S.; Wang, B.; Qin, C.; Wang, K.; Long, H. Rabi oscillations of optical modes in a waveguide with dynamic modulation. Opt. Quantum Electron. 2017, 49, 389. [Google Scholar] [CrossRef]
- Qin, C.; Zhou, F.; Peng, Y.; Sounas, D.; Zhu, X.; Wang, B.; Dong, J.; Zhang, X.; Alù, A.; Lu, P. Spectrum Control through Discrete Frequency Diffraction in the Presence of Photonic Gauge Potentials. Phys. Rev. Lett. 2018, 120, 133901. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Peng, Y.G.; Qin, C.Z.; Zhao, D.G.; Shen, Y.X.; Xu, X.Y.; Bao, M.; Jia, H.; Zhu, X.F. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 2016, 7, 13368. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Zhao, D.; Liu, Q.; Wu, S.; Wang, B.; Lu, P. Optical imaginary directional couplers. J. Lightwave Technol. 2018, 36, 2510–2516. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, J.; Liu, Q.; Liao, Q.; Wang, B.; Lu, P. Topological bound modes in anti-PT-symmetric optical waveguide arrays. Opt. Express 2019, 27, 13858–13870. [Google Scholar] [CrossRef]
- Deng, H.; Chen, X.; Panoiu, N.C.; Ye, F. Topological surface plasmons in superlattices with changing sign of the average permittivity. Opt. Lett. 2016, 41, 4281–4284. [Google Scholar] [CrossRef]
- Deng, H.; Chen, Y.; Panoiu, N.C.; Malomed, B.A.; Ye, F. Surface modes in plasmonic Bragg fibers with negative average permittivity. Opt. Express 2018, 26, 2559–2568. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Andrea, I.; Collins, M.J.; Harari, G.; Lumer, Y.; Rechtsman, M.C.; Eggleton, B.J.; Segev, M. Topological optical waveguiding in silicon and the transition between topological and trivial defect states. Phys. Rev. Lett. 2016, 116, 163901. [Google Scholar] [CrossRef]
- Cheng, Q.; Pan, Y.; Wang, Q.; Li, T.; Zhu, S. Topologically protected interface mode in plasmonic waveguide arrays. Laser Photonics Rev. 2015, 9, 392–398. [Google Scholar] [CrossRef]
- Pocock, S.R.; Xiao, X.; Huidobro, P.A.; Giannini, V. Topological plasmonic chain with retardation and radiative effects. ACS Photonics 2018, 5, 2271–2279. [Google Scholar] [CrossRef]
- Ling, C.W.; Xiao, M.; Chan, C.T.; Yu, S.F.; Fung, K.H. Topological edge plasmon modes between diatomic chains of plasmonic nanoparticles. Opt. Express 2015, 23, 2021–2031. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Wang, L.; Xiao, M.; Wen, W.; Chan, C.T.; Han, D. Topological edge modes in multilayer graphene systems. Opt. Express 2015, 23, 21585–21595. [Google Scholar] [CrossRef] [PubMed]
- Ke, S.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological edge modes in non-Hermitian plasmonic waveguide arrays. Opt. Express 2017, 25, 11132–11143. [Google Scholar] [CrossRef] [PubMed]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quantum Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Wang, F.; Ke, S.; Qin, C.; Wang, B.; Long, H.; Wang, K.; Lu, P. Topological interface modes in graphene multilayer arrays. Opt. Laser Technol. 2018, 103, 272–278. [Google Scholar] [CrossRef]
- Ge, L.; Liu, L.; Xiao, M.; Du, G.; Shi, L.; Han, D.; Chan, C.T.; Zi, J. Topological phase transition and interface states in hybrid plasmonic-photonic systems. J. Opt. 2017, 19, 06LT02. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Solitons with fermion number ½. Phys. Rev. D 1976, 13, 3398. [Google Scholar] [CrossRef]
- Truong, X.T.; Biancalana, F. Linear and nonlinear photonic Jackiw-Rebbi states in waveguide arrays. Phys. Rev. A 2017, 96, 013831. [Google Scholar]
- Tran, T.X.; Duong, D.C.; Fabio, B. Interaction Between Dirac Solitons and Jackiw–Rebbi States in Binary Waveguide Arrays. J. Lightwave Technol. 2017, 35, 5092–5097. [Google Scholar] [CrossRef]
- Alexey, A.G.; Dmitry, V.Z.; Alexey, P.S.; Alexander, B.K.; Maxim, A.G. Photonic Jackiw-Rebbi states in all-dielectric structures controlled by bianisotropy. Phys. Rev. B 2019, 99, 205122. [Google Scholar]
- Charles, A.D.; Guillaume, W. Topological collective plasmons in bipartite chains of metallic nanoparticles. Phys. Rev. B 2017, 95, 125426. [Google Scholar]
- Wang, H.; Kong, W.; Zhang, P.; Li, Z.; Zhong, D. Coherent Perfect Absorption Laser Points in One-Dimensional Anti-Parity–Time-Symmetric Photonic Crystals. Appl. Sci. 2019, 9, 2738. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).