A Novel Model of Pressure Decay in Pressure-Driven Membrane Integrity Tests Based on the Bubble Dynamic Process

Abstract

The membrane integrity is estimated using a pressure decay test based on the bubble dynamic process of membrane defects. The present work builds a schematic diagram for a bubble formation model of a pressure decay test, proposes a simulation model of pressure decay rate (PDR) in the membrane gas chamber by means of numerical simulation using microdefect bubble dynamic behavior, and tries to establish the main factors influencing the back-calculated defect size resolution. Results obtained from the variations in the membrane gas chamber pressure and the PDR allowed for accurate determination of the membrane defect size, and the PDR was found to be relatively dependent on the gas chamber volume and the initial applied test pressure. The measured data about PDR using controlled experimental parameters was in good agreement with the trend found in the prediction model, proving that the pressure decay test process is in essence a bubble dynamic process. Furthermore, the back-calculated defect size resolution was found to decrease with the increase in gas chamber volume and PDR as well as with the decrease in applied pressure.

1. Introduction

Intact, low-pressure ultrafiltration membranes can completely remove particulates and pathogens and thus produce drinking water that meets the stringent regulations on water quality [1]. For this, accurate and efficient integrity monitoring of the membrane system is fundamental to guarantee the quality of filtered products and detect the presence of oversized pores or defects that can compromise the retention capability of the filter [2]. Integrity tests should be sensitive to defects as small as 3 μm, which is based on the lower size range of Cryptosporidium oocysts, so that the tests can make sure any defect that is large enough for oocysts to pass will prompt a response from the integrity test being used [1,3,4]. In such a context, the detection method should be highly sensitive, quick and easy, have a signal that can be interpreted by programmable logic controller (PCL), and should be able to be carried out as frequently as possible. Generally, conventional membrane integrity monitoring techniques, including direct and indirect methods, have been reported [2].

Among the various integrity monitoring methods, the pressure decay test (PDT), a direct method, appears to be a reliable and common method. The generic protocol for a pressure decay test described in the United States Environmental Protection Agency (USEPA) guidelines is as follows: (1) drain the water from one side of the membrane, (2) pressurize the drained side of the fully wetted membrane, and (3) isolate the pressure source and monitor the decay for a designated period of time. This method is very sensitive in detecting leaks and integrity breaches and takes advantage of existing equipment, such as pressure and flow meters, to test the integrity over a large number of membranes. However, the method still has some weaknesses, including the inability to continuously monitor integrity, the inability to measure the pressurized air volume for calculation, the potential false positive results if the membrane is not fully wetted, and the difficulty in detecting horizontally oriented membranes due to potential draining and air venting problems [2,5,6]. The log removal value (LRV) can be calculated to express the membrane integrity, but the effectiveness of PDT in detecting membrane integrity changes is affected by the characteristics of the membrane surface. Correct LRV calculations require accurate inputs obtained under representative conditions, such as filtrate flow capacity, air–liquid conversion ratio, volumetric concentration factor, smallest verifiable decay rate, and volume of pressurized air in the system during the test. Moreover, the timing of the PDT has an impact on the calculated LRV, which can be counterintuitive in certain circumstances [2,6]. The calculation of the sensitivity of the test method requires an accurate measurement of the volume of pressurized air in the system, and an important concern associated with the pressure decay test is the potential for larger decay rates, even within the upper control limit, to affect the accuracy of the test. For example, if the total pressure decay over the duration of the test reduces the applied pressure on the membrane to a level below what is sufficient to meet the resolution criterion, the test would not comply with the requirements of the rule [1]. Therefore, changes in the pressure and the pressure decay rate (PDR) in the membrane gas chamber needs to be analyzed.

Brehant et al. [7] developed a decision-aid tool to comply with the USEPA rule that requires a resolution of 3 μm when the pressure is higher than 500 mbar, although the model needs to be calibrated on each full-scale membrane system to refine the prediction of LRV. Minnery et al. [8] conducted a sensitivity analysis of pressure-based integrity test and solved the defect size resolution using Monte Carlo and probability bounds analysis for five commercial membrane designs. The authors found that the resolution in some tests was insufficient to verify the presence of a barrier for oocysts of Cryptosporidium. Here, the pressure decay test process was considered as a static process, which only took into account the test pressure at test completion, the maximum hydraulic head, the pore shape correction factor, and the material-specific contact angle.

In gas–liquid fluidization systems, bubble dynamics plays a key role in dictating the transport phenomena, and the pressure affects the physical properties of the gas and liquid phases and hence the bubble behavior [9]. The dynamics of bubble flow is relatively complicated and is affected by many parameters, such as the defect diameter, gas flow rate, liquid height, wettability, and physical properties of the dispersed and continuous phases [10]. According to the bubble dynamics theory, the pressure decay test process, which involves gas entering wet microdefects and balancing the resistance, bubble formation and detachment, and then gas chamber pressure decay, would be a bubble dynamic process. The bubble dynamic behavior of membrane defects has a significant effect on the pressure decay characteristics and identification of membrane integrity. In addition, the membrane is well characterized with regard to its elastic properties, which are responsible for the gas pressure decay. Therefore, we can better understand the mechanisms in pressure decay tests from studies on the dynamic behaviors of bubbles and the air flow from the defect or breach on the membrane.

Bubbling behaviors, including bubble formation, movement, and interaction, play an important role in the practical operation of many industry reactors. As a result, bubbling behavior has been a widespread topic of interest for a long time. Zhu et al. [11,12] investigated the dynamic behavior of bubbles emerging from different micro-orifices on a plate in a stagnant and isothermal liquid and found that, with the increase in the height, the bubble velocity reduced first and then increased, while the bubble radius and aspect ratio appeared as a bifurcation structure. Loubière et al. [13] analyzed locally the dynamics of bubble growth and detachment from a rigid orifice and a flexible orifice and found that the differences in orifice nature and properties had a strong impact on the associated bubble formation phenomena. In a full-scale gas–liquid reactor, the different bubble generations was found to have a strong impact on the gas hold-up, the interfacial area, and the mass transfer. Furthermore, Loubiere et al. [14] proposed an analytical model to describe the dynamics of bubble growth and its detachment process generated from a flexible rubber membrane orifice submerged in water, taking into account the rubber membrane features (elastic behavior and wettability). The predicted bubble diameters at detachment were in agreement with the experimental measurements, and the orifice coefficient, the elastic pressure, and the surface tension force appeared to be key parameters. The main characteristic considered nonspherical bubble formations from a flexible membrane sparger orifice. Dietrich et al. [15] investigated the formation of bubbles in micro- and macroreactors and proposed a method to reveal the various mechanisms governing the formation from micro- to macroscale.

Based on these previous studies, the objective of the present work was to study bubble formation on submerged defects on ultrafiltration membranes under exactly defined conditions and develop an analytical model to describe the pressure decay generated from membrane damage in the membrane gas chamber using bubble dynamic behaviors. The aim was to better understand the parameters that govern the pressure decay rate. By comparing the predicted pressure decay rates with the experimental data, this study presents the development and experimental validation of a theoretical model that describes changes in the pressure and the PDR in the membrane gas chamber during pressure decay tests.

2. Theoretical Model

2.1. Model Assumption

During a pressure decay test, gas replaces water on one side of the membrane, i.e., the permeate side or the feed side. The pressure decay test occurs with one side of the membrane in gas and the other in water, creating a hydrodynamic gradient across the membrane that varies vertically along the height of the membrane. When the increase in the pressure in the gas chamber balances the sum of resistances due to hydrostatic pressure, surface tension, and membrane elastic pressure, gas flows across the defect and a bubble begins its growth process. The bubble surface moves as a result of the difference in pressure between the inside and the outside of the bubble. The bubble rises during bubble growth, and the neck is formed in the final period. The bubble detaches itself when the bubble neck is closed. As a result, the pressure in the gas chamber declines, leading to pressure decay.

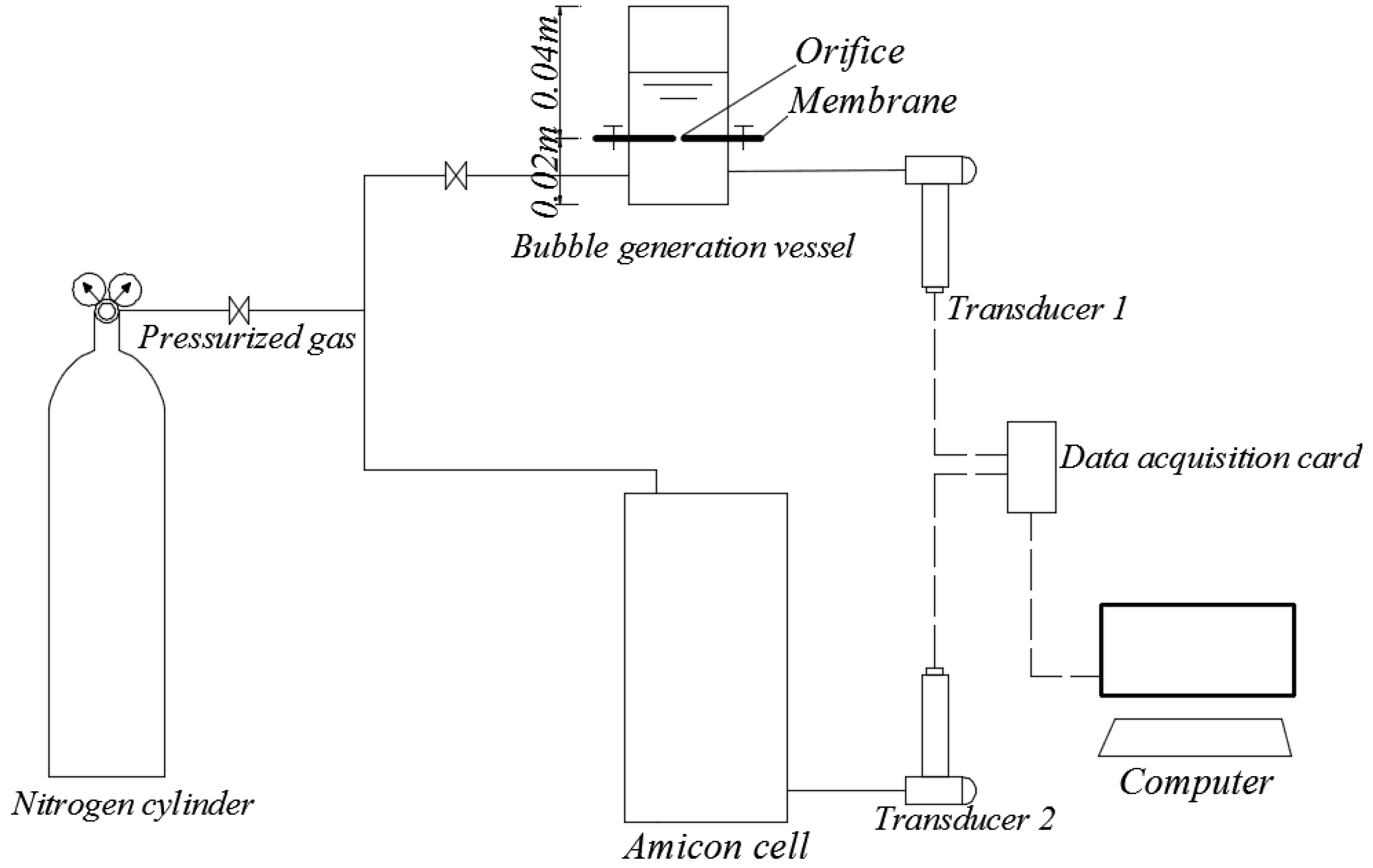
Figure 1 shows the bubble formation model of a pressure decay test setup for a membrane system. It assumes the following: (1) The air in the pressurized volume of the membrane system is in the quasi-equilibrium state. (2) The gas pressures inside the bubble and in the membrane gas chamber are both uniform within their respective volumes. (3) The liquid is incompressible. (4) The air flowing through thin-walled orifice is an unsteady isothermal flow process for high-pressure air flow. For a specific moment, the flow can be seen as a steady flow, and the flow loss can only be a local loss. (5) As has been developed by Farahbakhsh et al. [16], once the diffusive airflow rate is known for a given integral membrane, and assuming ideal gas behavior for air, the pressure change and the pressure decay rate due to diffusion can be estimated. For this model, once the membrane has defects, the flow through the defect is many times more than the diffusion flow through the pore; the effect of diffusive flow on the pressure change and the pressure decay rate can be neglected.

2.2. Gas Equation

When the pressure in the membrane gas chamber is increased to equilibrate the sum of resistances due to hydrostatic pressure, surface tension, and membrane elastic pressure, gas flows across the damage, and a bubble starts its growth process. The gas flow rate through the defect is dependent on the difference in pressure between the gas chamber and the bubble. The bubble rises during bubble growth, and the neck is formed in the final period. The bubble detaches itself when the bubble neck is closed.

The ideal gas equation based on assumption (1) is as follows:

$$PV=\frac{mRT}{M}$$

(1a)

where P is the pressure of the gas, V is the volume of the gas, R is the ideal gas constant, T is the absolute temperature of the gas, m is the mass, and M is the molar mass.

The thermodynamic system is defined as the sum of the gas in the bubble and in the membrane chamber. The continuity equation of the control box can be expressed as follows:

$$\frac{dm}{dt}=\frac{M}{RT}\left(V\frac{dP}{dt}+P\frac{dV}{dt}\right)=\frac{M}{RT}\left(V_g\frac{d{P}_g}{dt}+P_g\frac{d{V}_g}{dt}+V_b\frac{d{P}_b}{dt}+P_b\frac{d{V}_b}{dt}\right)$$

(1b)

where P_g is the pressure of the gas in the membrane gas chamber, V_g is the volume of the membrane gas chamber, P_b is the pressure of the gas in the bubble, and V_b is the volume of the bubble.

2.3. Damage Equation

The gas defect flow equation can be established as follows:

$$u_0=\mu \sqrt{\frac{2\left(P_g-P_b\right)}{{\rho }_g}}$$

(2)

where u₀ is the air flow rate through the defect, μ is the defect-metering coefficient, and ρ_g is the gas density.

2.4. Pressure Change in the Gas Chamber

The increment of bubble mass is the gas mass flowing through the damage. The mass conservation equation can be expressed as follows:

$$\frac{\pi }{4}{d}_{OR}^2{\rho }_g{u}_0=\frac{M}{RT}\left(V_b\frac{d{P}_b}{dt}+P_b\frac{d{V}_b}{dt}\right)$$

(3a)

In addition, assuming a polytropic behavior of gas in the membrane gas chamber, the mass conservation equation can be expressed as follows:

$$\frac{d{P}_g}{dt}=\frac{\chi P_g}{V_g}\left(-\frac{\pi }{4}{d}_{OR}^2{u}_0\right)=\frac{\chi P_g}{V_g}\left(-\frac{d{V}_b}{dt}\right)$$

(3b)

The gas chamber volume V_g is measured experimentally. In the literature, the polytropic coefficient χ is defined between 1 for isothermal change [17] and 1.4 for adiabatic change [18]. Even though the thermodynamic behavior of the membrane gas chamber is not usual, the pressure decay time can be assumed to be enough to balance the temperature both inside and outside; the polytropic coefficient is assumed to be equal to 1.

2.5. Change in Damage Size

Making reference to the dynamic rubber membrane behavior studied experimentally by Loubiere et al. [14], equivalent diameters corresponding to the diameters can be determined from the hole area (Ha), assuming a circular hole, and can be given by the following expression:

$$d_{OR}={\left[\frac{4\left(Ha\right)}{\pi }\right]}^{\frac{1}{2}}$$

(4a)

These equivalent hole diameters are calculated from an area that is determined from the image considered, so it is uncertain whether the measured area is the same throughout the entire membrane thickness and whether the equivalent diameter is the effective one [14]. As soon as gas pressure is applied, the membrane bulges, and the defect size increases. Using the model developed by Loubière at al. [14] which showed the connection between membrane deflection and pressure drop, the orifice diameters correspond to the applied pressure in the gas chamber and can be assumed and expressed as follows:

$$d_{OR}=D_0{\left(\frac{P_g}{P_{atm}}\right)}^{\omega }$$

(4b)

where ω is the modified coefficient. The equivalent defect diameter can be calculated from an area that is defined from the treated images.

2.6. Initial and Boundary Conditions

2.6.1. Initial Conditions

The bubble is initially assumed to be a hemisphere with diameter equal to the real surface/bubble contact surface diameter d_w (which may be equal to d_OR, depending on the membrane wettability) in static equilibrium with the surrounding liquid. The reality is somewhat more complex because the liquid flow field is affected by the preceding bubble wake. As these effects are difficult to determine, the actual initial conditions are generally unknown, and the initial bubble shape chosen represents a compromise. The velocities and accelerations of all elements are initially taken as zero. The initial pressure in the gas chamber is taken as the sum of the hydrostatic pressure at the defect, the surface tension pressure, and the elastic pressure as follows:

$$t=0:P_{g|0}=P_{atm}+{\rho }_{l}g\left(H-\frac{d_W}{2}\right)+\frac{4\sigma }{d_W}+P_e=P_{b|0},V_b=\frac{\pi }{12D_0^3},u_0=0$$

(5)

where H is the water depth on the membrane, ρ_l is the water density, and P_e is the elastic pressure that should be determined experimentally for each flexible membrane according to Reference [14].

2.6.2. Boundary Conditions

When the pressure in the gas chamber starts to decline, a bubble begins to form, and the pressure in the bubble increases as a result of a decrease in pressure in the gas chamber. When the balance is established in two sides of the membrane, in the bubble growth detachment stage, the neck is formed, and the old bubble then detaches itself while the new bubble enters the expansion stage [19]. As a result, a circulation is formed for the decay in the gas chamber.

2.7. Numerical Resolution

Equations (1b), (2), (3b), (4b) and (5), coupled with the initial and boundary conditions, describe the dynamics of the bubble formation process. They can be solved by means of a finite-difference method.

To solve the nonspherical bubble formation model numerically, the following algorithm of the finite-difference procedure is used:

(a)

The operating conditions, the initial time step, and the initial surface point number are defined to form the parameter initialization.

(a)

Provided that the bubble does not detach and the gas chamber volume does not change, the air flow rate through the orifice v at time t can be given by the following expression:

$${v|}_t=\mu \sqrt{\frac{2\left({P_g|}_t{-P_b|}_t\right)}{{\rho }_g}}$$

(6)

The pressure in the gas chamber at time t is obtained from an integral equation:

$$\frac{{dP}_g}{dt}=-\frac{\pi P_g{D}^{2}v}{4V}$$

(7)

$${P_g|}_t=\frac{{P_g|}_{t-\Delta t}-\Delta t\ast \pi D^2\ast {P_g|}_{t-\Delta t}\ast {v|}_{t-\Delta t}}{4V}$$

(8)

The pressure inside the bubble at time t can be given by the following expression:

$$\frac{d{P}_b}{dt}=\frac{\pi D^{2}v}{4}$$

(9)

$${P_b|}_t=\frac{{P_b|}_{t-\Delta t}+\Delta t\ast \pi D^2\ast {v|}_{t-\Delta t}}{4}$$

(10)

The volume inside the bubble can be expressed as follows:

$$\frac{{dV}_b}{dt}=\frac{\left(P_g-P_b\right)\pi D^{2}v}{{4P}_b}$$

(11)

$${V_b|}_t=\frac{{V_b|}_{t-\Delta t}+\Delta t\ast \left({P_g|}_{t-\Delta t}-{P_b|}_{t-\Delta t}\right)\ast \pi D^2\ast {v|}_{t-\Delta t}}{4{P_b|}_{t-\Delta t}}$$

(12)

(c)

The pressure in the gas chamber is compared with the pressure in the bubble at time t calculated in step (b). If the error is more than 10 Pa, it can be considered that the bubble does not detach, and the procedure begins again at step (a) with t + ∆t; otherwise, the bubble detaches, and the procedure continues on to step (d).

(d)

The bubble detaches. The variation in all parameters as a function of growth time are given and recorded.

In this calculation, the experimental values of the defect size and the elastic pressure, which can be determined from experiments and has been previously referred to in the literature, are used as the only two inputs to solve the equations for each step time of bubble formation to predict the pressure change in the gas chamber. The set of first-order differential equations can be solved in Matlab ((R2014a, MathWorks Inc., Natick, MA, USA and 2016) using the 4th order Runge–Kutta method.

2.8. Back-Calculated Defect Radius

Assuming the leakage consists of a defect with the equivalent diameter d_eq, the following equation applies:

$$\frac{{dP}_g}{dt}=\mathrm{PDR}=\frac{\Delta P_g}{\Delta t}$$

(13)

The above equation can then be transferred as follows:

$$d_{eq}=\alpha \sqrt{\frac{4\ast \mathrm{PDR}\ast V_g}{0.5\ast \chi \ast Pg\ast \pi \ast \mu \ast \sqrt{\frac{2\left(P_g-P_f\right)}{{\rho }_s}}}}$$

(14)

where $P_f=P_{atm}+{\rho }_{l}gH+P_e$, α is the size-modified coefficient, which needs lots of experiments to collect and determine for each membrane module.

From this equation, for a certain membrane system, parameters such as the volume and the pressure of the membrane gas chamber, PDR, the defect-metering coefficient, the polytropic coefficient, the water depth on the membrane, water density, and the elastic pressure will be known factors, so the membrane defect size can be calculated.

Here, PDR is measured in the membrane integrity test for used or damaged membrane (Pa·s⁻¹); p_g changes in the applied test pressure (Pa) during the experiment time interval (Δt). The other parameters to be measured are V_g, the hold-up volume or pressurized volume (L), and the water depth on the membrane (H).

3. Experimental Setup and Methods

3.1. Experimental Setup

The experimental setup is shown in Figure 2. The experiments were carried out in a glass parallelepiped vessel, 60 mm in height, 30 mm in length, and 25 mm in width. PES ultrafiltration membrane (Model MSC80010, Shanghai Mosu Tech. Co. Ltd., Shanghai, China) with a MWCO of 30 kDa was tested. The ultrafiltration membrane wetted for 30 min at room temperature by permeating deionized (DI) water was fixed in the vessel by flange and rubber ring, enabling the same initial tension to be applied and thus obtaining reproducible results. The space under the membrane was used as a part of the membrane gas chamber. Three different volumes of the membrane gas chamber were realized by the connection of three ultrafiltration amicon cells (300 mL, Model MSC 300, Shanghai Mosu Tech. Co. Ltd., Shanghai, China) with the space under the membrane in the glass parallelepiped vessel. The water depth above the membrane was adjusted. Nitrogen gas was used as the pressurized gas. The pressure values in the membrane gas chamber and gas tank were converted into digital code by two pressure transducers (Range 1: 0–100 kPa; Range 2: 0–200 kPa, Model MIKP 300, Hangzhou Meacon Tech. Co. Ltd., Hangzhou, China), and the outputs of these two pressure transducers was checked against each other. The signal was received by the data acquisition card (Model USB 1210, Beijing SMACQ Tech. Co. Ltd., Beijing, China). The discrete signal frequency was adjusted to 10 Sa/s. For each run, the pressure value of the gas chamber was collected. Every experiment was repeated on three pieces of membranes with the same specification, and the average value was taken as the experimental results. During all runs, the indoor temperature was kept at 20 ± 1 °C.

3.2. Procedure

The pressure change in the membrane gas chamber for the wetted intact membrane was measured as a control experiment. To damage the membrane, microdefects were created with four kinds of acupuncture needles (0.20 mm, 0.22 mm, 0.30 mm, 0.35 mm, Model Zhongyan Taihe, Beijing Zhongyan Taihe Medical Instrument Co. Ltd., Beijing, China) puncturing on the center of an intact membrane sheet. After every series of experiments, the accurate equivalent membrane microdefect under experimental conditions was measured using a Caikon DMM-400D metallurgical microscope. The image treatment was carried out using image processing software Image-J. Data and graph processing were performed using OriginPro 8.0 (Origin Lab, Northampton, MA, USA).

To evaluate the effect of the experimental conditions on the pressure decay rate, four series of tests with a variety of damage size, applied pressure, gas chamber volume, and water depth were carried out. During the pressure decay test, once the pressure in the gas chamber arrived at the specified value, the inlet valve was closed and the pressure was measured and collected. The PDR value in the gas chamber can be calculated as follows:

$$PDR=\frac{avg\left(P_{m+1}:P_{m+10}\right)-avg\left(P_{m-9}:P_m\right)}{\Delta t}$$

(15)

where PDR is the pressure decay rate at time m (kPa/s), avg (P_m−9:P_m) is the average value of the 10 pressure values collected before time m, avg (P_m+1:P_m+10) is the average value of the 10 pressure values collected after time m, ∆t is the calculated time step (1 s in this study).

The correlation of the data curves was measured using statistics analysis software IBM SPSS statistics 22.0. For each simulation, the physical properties used were as follows: ρ_g = 2.0 kg/m³, ρ_l = 997 kg/m³, χ = 1, μ = 0.62, σ = 72.8 mN/m, and P_atm = 1.01 × 10⁵ Pa.

4. Results and Discussion

4.1. Membrane Damage Characterization

In theory, the damage is transformable due to the flexibility of the membrane, so gas chamber volume V_g and the damage equivalent diameter d_OR may change with changing applied pressures.

The membrane dynamic behavior was investigated experimentally, and it was found that the membrane obviously inflated when the pressurized gas was applied in the vessel. However, due to the limited area (750 mm²) of the membrane in the vessel, the gas chamber volume V_g of the intact membrane enlarged only about 4.5 mL when the pressurized gas (80 kPa) was pumped into the gas chamber.

In order to investigate the influence of applied pressurized gas on the damage size, the defect diameters were measured using image acquisition systems depicted previously at different applied pressure of 40, 60, 80, 100, and 120 kPa. The relationship between equivalent diameter and original damage size is shown in Figure 3. It can be seen that, with increasing applied pressure, the equivalent diameter did not obviously change. It was difficult to say with certainty whether the damage size obviously varied with the pressure applied at a limited scope. Therefore, the modified coefficient ω in Equation (4b) was assumed to be equivalent to 0. Wang et al. [20] had come up with similar results and given a reasonable explanation. Therefore, in the simulation in this study, the effect of the membrane deformation properties on defect size was ignored.

4.2. Effects of Defect Size on Gas Chamber Pressure and PDR

Before evaluating membranes with controlled defects, a series of pressure decay tests over a range of feed pressures were first conducted using a nondefective membrane. It was found that the pressure value of the gas chamber did not obviously decline. For example, with the conditions of water depth 30 mm, gas chamber volume 365.59 mL, and original applied pressure 95.48 kPa, the pressure declined from 95.48 kPa to 94.60 kPa after 100 s. This pressure decay can be mainly attributed to gas diffusion through intact pores [20], proving that the experimental system was intact, airtight, and sealed hermetically.

Figure 4 shows the time dependence of gas chamber pressure and PDR of different needle sizes (0.20 mm, 0.22 mm, 0.30 mm, and 0.35 mm). Here, the following experimental conditions were used: water depth 30 mm, gas chamber volume 365.59 mL, and original applied pressure 80 kPa. The equivalent diameters of different defects size were evaluated to be 0.185 mm, 0.189 mm, 0.276 mm, and 0.352 mm, respectively. As can be seen from the figure, the measured pressures in the gas chamber declined with time. Taking 0.185 mm defect as an example, the measured pressure decreased from 79.17 kPa to 1.86 kPa after 157.0 s. The pressure can be described as a quadratic function of time and may be presented by the following relationship:

$$P=75.5607-0.7391t+0.0018t^2,R^2=0.9999$$

(16)

In addition, it was found that the measured PDR was the highest compared with other values at the beginning. The measured PDR also decreased from 1.03 kPa/s to 0.02 kPa/s after 157.5 s. Using Equations (7) and (8), it was found that the values of the chamber pressure and PDR changed with time, although they followed different trends.

Moreover, along with the increasing defect size, the required time for the measured pressure to decrease to zero became increasingly shorter:, 157.0 s, 150.0 s, 70.0 s, and 43.3 s, respectively. Similarly, the required time for the measured PDR to decrease to zero also became increasingly shorter: 157.5 s, 150.5 s, 70.5 s, and 43.5 s, respectively. In contrast, the PDR values in the initial stages got larger: 1.03 kPa/s, 1.12 kPa/s, 2.28 kPa/s, and 4.22 kPa/s, respectively. This may be because the mass flow rate increased due to the increasing defect size, resulting in a reduction in the required time and an increase in the initial PDR value.

Furthermore, there was a good agreement between the trend of the model predictions, in which there were no adjustable parameters, and the measured data of pressure and PDR. The measured data was in close agreement with the simulated values in varying degrees. The correlation between the two curves of simulated results and experimental data of pressure and PDR are given in

Table 1. Correlation between measured data and predicted values with different defect sizes. PDR: pressure decay rate.

	D0 (mm)	0.185	0.189	0.276	0.352
r	Pressure	0.993	0.987	0.990	0.999
	PDR	0.982	0.981	0.966	0.981

. Values of Pearson’s correlation coefficient r (more than 0.950) indicated a high consistency between the two curves. The significance (less than 0.001) showed the prediction model was valid for the present study. Moreover, the differences between the measured data and simulated value changed with time. Although the initial measured pressures were approximately equal to the initial calculated pressures, the model underestimated the pressure in most cases. As for the PDR, the difference between the measured PDR and the calculated PDR changed with time, and it was relatively small in the middle of the pressure decay time. The differences corresponded to the selection parameters in the model. As noted in Section 2, the model can be adapted to predict the pressure decay in a membrane gas chamber. The system features are taken into account through several parameters: the defect size D₀, the orifice coefficient μ, the elastic pressure P_e, the modified coefficient ω, and the real surface/bubble contact diameter d_w. The following hypothesis can be put forward to explain this difference, taking into account the fact that the model resolution is very sensitive to the defect size, orifice coefficient, and elastic pressure. Firstly, the real original defect size was not absolutely equal to the diameter of the acupuncture needle, and the instantaneous defect size during the pressure decay process would have been affected by the membrane elastic pressure and applied pressure. While a constant surface/bubble contact surface diameter was considered in the model, the experimental contact surface diameter d_w varied with bubble formation time [13]. In addition, the experimental orifice coefficient μ might have been be underestimated or overestimated because the downstream of the defect outflow in this study was not gas but water. Moreover, the elastic pressure P_e changes with gas chamber pressure, but in this simulation, the elastic pressure was set to be constant. Therefore, there would be a predictable error between measured data and simulated values.

4.3. Effects of Applied Pressures on Gas Chamber Pressure and PDR

Figure 5 shows the time dependence of gas chamber pressure and PDR of different applied pressures (40 kPa, 60 kPa, 80 kPa, 100 kPa, and 120 kPa). The equivalent diameters of different defect sizes were evaluated to be 0.346 mm, 0.358 mm, 0.352 mm, 0.345 mm, and 0.350 mm, respectively. The measured pressure followed a decreasing tendency with time. Taking 120 kPa pressure as an example, the measured pressure decreased from 117.57 kPa to 1.48 kPa after 54.8 s. The measured PDR also decreased from 5.47 kPa/s to 0.02 kPa/s after 55.5 s. The pressure can be described as a quadratic function of time and may be presented by the following relationship:

$$P=113.1908-4.0960t+0.0378t^2,R^2=0.9992$$

(17)

In addition, it was found that the measured PDR had the highest value at the beginning and then decreased continuously. Moreover, along with the applied pressures increasing from 40 to 120 kPa, the required time for the measured pressure to decrease to zero became increasingly longer: 25.6 s, 34.0 s, 43.3 s, 50.7 s and 54.8 s, respectively. Similarly, the required time for the measured PDR to decrease to zero also became increasingly longer: 26.5 s, 34.5 s, 43.5 s, 51.5 s, and 55.5 s, respectively. The PDR values in the initial stages got larger: 2.74 kPa/s, 3.82 kPa/s, 4.22 kPa/s, 4.79 kPa/s, and 5.47 kPa/s, respectively. The longer required time and larger initial PDR value may have been caused by the change in gas mass or the number of moles due to the increasing applied pressure.

Similarly, for each applied pressure, the simulated curves had the same trend as that of the measured pressure and measured PDR. A fairly good agreement was observed between the experimental values and the numerical data, even though the measured data diverged a little from the simulated pressure. Unlike the results in Section 4.2, the measured pressure values were not always more than the simulated pressure values; instead, the measured pressures were higher than the simulated pressures when the applied pressure was less than 80 kPa. As for the PDR, the difference between the measured PDR and the calculated PDR changed with time, and it was relatively small in the middle of the pressure decay time. This correlation is demonstrated in

Table 2. Correlation between measured data and predicted values with different applied pressures.

	Pg (kPa)	40	60	80	100	120
r	Pressure	0.982	1.000	0.999	1.000	0.998
	PDR	0.982	0.993	0.981	0.993	0.988

. Values of Pearson’s correlation coefficient r (more than 0.980) indicated a high consistency between the two curves. The significance (less than 0.001) showed the calculation model was valid for this study.

4.4. Effects of Gas Chamber Volumes on Gas Chamber Pressure and PDR

Figure 6 shows the time dependence of gas chamber pressure and the PDR of different gas chamber volumes (365.59 mL, 690.72 mL, and 1015.85 mL). The equivalent diameters of different defect sizes were evaluated to be 0.352 mm, 0.329 mm, and 0.341 mm, respectively. Taking 365.59 mL gas chamber volume as an example, the measured pressure decreased from 79.54 kPa to 1.23 kPa after 43.3 s, and the measured PDR also decreased from 4.22 kPa/s to 0 kPa after 43.5 s. The pressure can be described as a quadratic function of time and may be presented by the following relationship:

$$P=72.6909-2.6925t+0.0240t^2,R^2=0.9827$$

(18)

Furthermore, along with the increasing gas chamber volumes, the required time for the measured pressure to decrease to zero became increasingly longer: 43.3 s, 79.5 s, and 112.3 s, respectively. The absolute values of the quadratic term ratio in the parabolic equation became increasingly smaller: 0.024, 0.0098 and 0.0057, respectively. Similarly, the required time for the measured PDR to decrease to zero also became increasingly longer: 43.5 s, 79.5 s, and 112.5 s, respectively. The absolute values of the slope in linear function also got smaller: 0.0619, 0.0189, and 0.0118, respectively. The PDR values in the initial stages got increasingly smaller: 4.22 kPa/s, 2.20 kPa/s, and 1.59 kPa/s, respectively. This may be because the mass changed higher due to the increasing gas chamber volumes, resulting in longer required time and smaller initial PDR value.

Similarly, for each gas chamber volume, the simulated curves had the same trend as that of the measured pressure and the measured PDR. A great agreement was observed between the experimental values and the numerical data. The correlation between the two curves is demonstrated in

Table 3. Correlation between measured data and predicted values with different chamber volumes.

	Vg (mL)	365.59	690.72	1015.85
r	Pressure	0.999	0.999	1.000
	PDR	0.981	0.986	0.987

. The high values of correlation coefficient (more than 0.980) indicated a good modification of the calculation model.

4.5. Effects of Water Depth on Gas Chamber Pressure and PDR

Figure 7 shows the time dependence of the gas chamber pressure and the PDR of different water depths (10 mm, 20 mm, and 30 mm). The equivalent diameters of different defect sizes were evaluated to be 0.349, 0.331, and 0.352 mm, respectively. Taking 10 mm water depth as an example, the measured pressure decreased from 81.43 kPa to 1.23 kPa after 47.7 s. The measured PDR also decreased from 3.80 kPa/s to 0.02 kPa/s after 48.5 s. The pressure can be described as a quadratic function of time and may be presented by the following relationship:

$$P=79.6956-3.0362t+0.0297t^2,R^2=0.9998$$

(19)

Furthermore, along with the water depth, the change in the required time for the measured pressure to decrease to zero was insignificant: 47.7 s, 60.0 s, and 43.3 s, respectively. Similarly, the required time for the measured PDR to decrease to zero was also roughly the same. The PDR values in the initial stages also had a similar level. This may be because the hydrostatic pressure value that limited the water depth produced, compared with applied pressure, played a limited role in bubble formation and gas flow.

Similarly, for each water depth, the simulated curves had the same trend as that of the measured pressure and the measured PDR. The correlation between the two curves is demonstrated in

Table 4. Correlation between measured data and predicted values with different water depths.

	H (mm)	10	20	30
r	Pressure	0.998	0.999	0.999
	PDR	0.985	0.987	0.981

. Values of Pearson’s correlation coefficient r of two indexes under three different water depths were beyond 0.98, which proved the effectiveness of the calculation model in this study.

4.6. Determination of Back-Calculated Defect Size

Taking the PDR simulation in Figure 5b as an example, all predicted defect diameter values versus time are plotted in Figure 8. It can be seen that most of the predicted defect diameter values are distributed around the original defect needle size (0.358 mm) before 27 s, proving that the model has certain applicative scope to fit the defect size. Here, the average back-calculated diameter was 0.376 mm, a little more than the defect diameter of 0.358, and the size modified coefficient was 0.975.

All the back-calculated defect diameter and size-modified coefficients are shown in

Table 5. The back-calculated defect diameter and size-modified coefficient.

Conditions		deq (mm)	Percentage Error (%)	Size-Modified Coefficient α
Pg = 80 kPa Vg = 365.59 mL H = 30 mm	D0 = 0.185 mm	0.165	10.81	1.15
	D0 = 0.189 mm	0.187	1.06	1.06
	D0 = 0.276 mm	0.264	4.34	1.08
	D0 = 0.352 mm	0.348	1.14	1.04
Vg = 365.59 mL H = 30 mm	Pg = 40 kPa, D0 = 0.346 mm	0.388	12.14	0.90
	Pg = 60 kPa, D0 = 0.358 mm	0.376	5.03	0.98
	Pg = 80 kPa, D0 = 0.352 mm	0.348	1.14	1.04
	Pg = 100 kPa, D0 = 0.345 mm	0.328	4.93	1.06
	Pg = 120 kPa, D0 = 0.350 mm	0.324	7.43	1.10
D0 = 0.35 mm Pg = 80 kPa H = 30 mm	Vg = 365.59 mL	0.348	1.14	1.04
	Vg = 690.72 mL	0.355	7.90	0.95
	Vg = 1015.18 mL	0.361	5.86	0.97

. It can be seen that the effect of different parameters on back-calculated accuracy was different. The product of 1-dimensional Monte Carlo analysis is the cumulative distribution function, which can express all information as variability in the theoretic d_eq. To determine the back-calculated diameter resolution (BDR), analysis was conducted using @RISK software (V7.5, Palisade Corporation, Ithaca, NY, USA and 2017). Data used in the analysis was collected from experiments. The results of the analysis regarding the correlation coefficients between parameters and BDR are shown in Figure 9.

From Figure 9, it can be seen that the most influential factors for the BDR were V_g and the PDR. The correlation coefficients of the membrane gas chamber volume V_g and PDR were 0.735 and 0.545, respectively. The correlation coefficient of the gas pressure in the membrane gas chamber P_g was −0.267. The correlation coefficients of water depth on the membrane H and elastic pressure P_e were very low. The BDR decreased with the increase in V_g and PDR as well as with the decrease in P_g.

4.7. Discussion

From the model simulation and experimental verification, it was found that the pressure decay could be simulated by the model based on the microdefect bubble dynamic behavior, although there were some differences due to the selection parameters. These results prove that the pressure decay test process, which involves gas entering the wet microdefects and balancing the resistance, bubble formation and detachment, and then gas chamber pressure decay, is in essence a bubble dynamic process. The bubble dynamic behavior of microdefects on the membrane can therefore be used to analyze pressure decay characteristics in a membrane integrity test. The results show that the PDR decreases with time in the duration of the pressure decay test and changes due to the defect size, applied test pressure, and pressurized system volume.

It is worth emphasizing that the model was developed on the basis of model assumptions and simulated under the present laboratory conditions. The model ignores the effects of thermodynamic parameters and the diffusion of membrane pores, and it has not been validated by engineering application. In the simulation experiments, the small defects (5–10 μm) created by laser drilling in the center of the membrane discs were too small to measure the actual equivalent diameter of the defect size under experimental conditions (the membrane was in the vessel and under water) using a Caikon DMM-400D metallurgical microscope, so the defects were made by different kinds of needles. In addition, the above experimental data was obtained using a flat membrane in a small vessel, so the model needs to be calibrated on lots of full-scale membrane modules. Subsequent model validation works should focus on other kinds of membrane modules and the engineering application aspect.

5. Conclusions

By means of numerical simulation using microdefect bubble dynamic behavior, the present work proposes a prediction model of pressure decay rate caused by membrane defects using the pressure decay test. The measured data for the PDR using controlled experimental parameters, such as defect size, gas chamber volume, applied initial test pressure, and water depth, was found to be in good agreement with the trend followed by the prediction model. The estimated pressure decay rate was affected by the applied pressure, gas chamber volume, and defect size and decreased with time. Comparisons proved that the pressure decay test process is in essence a bubble dynamic process. In addition, using probability bounds analysis under experimental conditions, Monte Carlo analysis identified that the BDR decreased with the increase in V_g and PDR as well as with the decrease in P_g.