A Typical Distributed Generation Scenario Reduction Method Based on an Improved Clustering Algorithm
Abstract
:1. Introduction
- (1)
- The uncertainties of wind power and photovoltaic distributed energy are modeled. The characteristics of annual scenarios, seasonal scenarios, continuous multi-day scenarios and typical day scenarios are analyzed. The uncertainties and time series characteristics of the two types of distributed energy are analyzed.
- (2)
- In order to fully reflect the timing characteristics of two types of intermittent DGs and to avoid the difficulties caused by large-scale data in multi-scenario analysis. In this paper, a typical scenario set generation method based on improved clustering algorithm is proposed to reduce the wind power and photovoltaic data in the computing cycle and form a typical scenario set that can reflect the historical data characteristics in the computing cycle.
- (3)
- The proposed scenario reduction method based on improved clustering algorithm is validated by using the wind power output scenarios obtained from uncertain modeling.
2. Characteristics of Typical Intermittent Distributed Generation
2.1. Uncertainty Model of Wind Power Generation and Photovoltaic Power Generation
2.2. Characteristic Analysis of Typical Intermittent Distributed Generation Scene
2.2.1. Characteristic Analysis of Wind power Output Scene
- (1)
- Random. As shown in Figure 1, the fitting curve of the annual wind power output curve can be clearly observed. For the hourly statistics of wind power output, the output at each moment shows obvious uncertainty.
- (2)
- Intermittence. The wind speed has obvious intermittence, and is affected by the cutting-in speed and cutting-out speed of wind turbines, so there are some points in the curve where the output of wind turbines is zero. The point where the output of these turbines is zero may be due either to the failure to reach the cut-in wind speed or to the fact that the turbine has been removed because the cut-out wind speed has been reached, thus the output of wind power is not continuous.
- (3)
- Seasonal variation characteristics. As shown in Figure 2, wind power output has a certain seasonal variation characteristic. Wind power output is relatively large in autumn and relatively small in summer, and the difference is relatively obvious. At the same time, the output curve of each season is quite different from the typical solar output curve, and the typical solar output curve cannot reflect well the characteristics of the output variation in each season.
- (4)
- Time series characteristics and similarity. It can be seen from the continuous multi-day variation curve and typical sunrise curve that the wind power output has obvious time series characteristics and similarity. The output of wind power is large at night and small at daytime, which has good peak regulation characteristics. The sunrise curve in continuous time has certain similarity, which means that it can reduce the scene effectively.
2.2.2. Characteristic Analysis of Photovoltaic Output Scene
- (1)
- Periodicity. From the solar photovoltaic output curve, it can be clearly observed that the photovoltaic output has obvious periodicity, increasing from the morning until about noon to reach the maximum photovoltaic output, and declining in the afternoon. This periodicity is evident in all curves.
- (2)
- Seasonal variation characteristics. Photovoltaic output is mainly affected by light intensity. Generally speaking, the photovoltaic output is higher in summer than in winter because of the highest illumination intensity.
- (3)
- Time series characteristics and similarity. From the continuous multi-day curve and typical daily curve, it can be seen that the photovoltaic output changes obviously with time. On sunny days, the continuous multi-day curves sampled randomly have obvious similarities. This also means that the effort scenario can be reduced.
3. Scene Reduction Method Based on Improved Clustering Algorithm
3.1. Improved Clustering Algorithm
- (1)
- Choosing a center according to the maximum and minimum distance criterion described above
- (2)
- Clustering according to k-means clustering method based on maximum and minimum distance
- (3)
- Calculate the BWP value of the clustering result and turn to step 2
- (4)
- Comparing the BWP value of clustering results, the k value of clustering results is the best clustering number when the BWP value is maximum
- (5)
- Clustering results corresponding to the maximum output BWP value
3.2. Validity Test
3.2.1. Scene Reduction Process Based on Improved Clustering Algorithm
3.2.2. Validity Test of Wind Power Output
3.2.3. Scene Reduction for Two Kinds of Intermittent DG
4. Examples and Analysis
- (1)
- Distributed generator output control
- (2)
- Switching of reactive power compensation
- (3)
- Adjustment of on load transformer
4.1. Upper Level Programming Model and Lower Level Programming Model
4.2. Bi-Level Programming Model Solving Algorithms
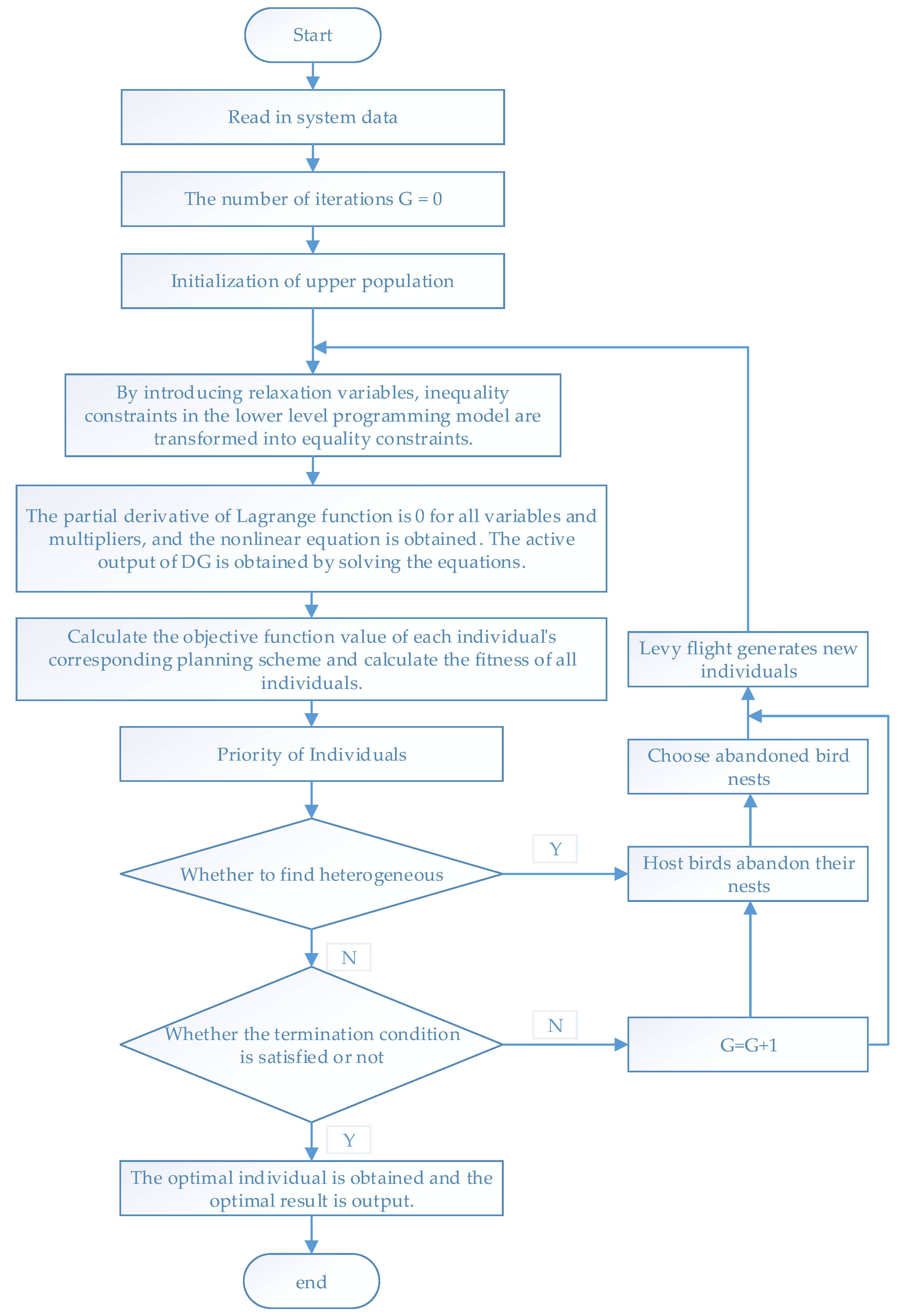
4.2.1. Cuckoo Search Algorithms
- (1)
- Cuckoos lay only one egg at a time of reproduction, and then they choose their nests arbitrarily for hatching and rearing.
- (2)
- The most suitable nest will be extended to the next generation of reproduction in a randomly selected set of options.
- (3)
- The total number of nests available N is a fixed value, and the probability that the original owner of the nest has can identify a non-self-laid bird’s egg.
4.2.2. Bi-Level Programming Model Solving Process
4.3. Introduction of Examples
5. Discussion
6. Conclusions
- (1)
- Uncertainty modeling of two kinds of distributed generators is carried out. The scene output characteristics of DG are analyzed. The analysis shows that both DGs have obvious uncertainties and time series characteristics, therefore, the typical scenes composed of the average method or the maximum sunrise of peak-valley difference cannot effectively reflect the characteristics of DG. At the same time, the output of distributed generation has some inherent similarities, which means that it can be effectively reduced.
- (2)
- To overcome the shortcomings of large-scale scene clustering algorithms, a scene reduction method based on an improved clustering algorithm is proposed, and its validity is tested. The test results show that the improved clustering algorithm can effectively retain the characteristics of the original output scenario.
- (3)
- Through a specific example, the scene reduction method is verified by using IEEE33 node system. The three scenario sets show that the proposed scenario reduction method is feasible. The scenario constructed by this method has good preservation effect on the original scenario, and can take into account both the computational efficiency and the computational accuracy in the process of distributed generation optimal configuration.
Author Contributions
Funding
Conflicts of Interest
References
- Mehigan, L.; Deane, J.P.; Gallachoir, B.P.O.; Bertsch, V. A review of the role of distributed generation (DG) in future electricity systems. Energy 2018, 163, 822–836. [Google Scholar] [CrossRef]
- Anaya, K.L.; Pollitt, M.G. Going smarter in the connection of distributed generation. Energy Policy 2017, 105, 608–617. [Google Scholar] [CrossRef] [Green Version]
- Allan, G.; Eromenko, I.; Gilmartin, M.; Kockar, M.; Mcgregor, P. The economics of distributed energy generation: A literature review. Renew. Sustain. Energy Rev. 2015, 42, 543–556. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.H.; Liang, H.; Huang, S.J.; Dinavahi, V. Multistage robust energy management for microgrids considering uncertainty. IET Gener. Transm. Dis. 2019, 13, 1906–1913. [Google Scholar] [CrossRef]
- Chen, G.; Lewis, F.L.; Feng, N.; Song, Y.D. Distributed optimal active power control of multiple generation systems. IEEE Trans. Ind. Electron. 2015, 62, 7079–7090. [Google Scholar] [CrossRef]
- Tan, Y.S.; Wang, Z.Y. Incorporating unbalanced operation constrains of three-phase distributed generation. IEEE Trans. Power Syst. 2019, 34, 2449–2452. [Google Scholar] [CrossRef]
- Ziari, I.; Ledwich, G.; Ghosh, A. Optimal allocation and sizing of DGs in distribution network. In Proceedings of the IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Othman, M.M.; El-Khattam, W.; Hegazy, Y.G.; Abdelaziz, A.Y. Optimal placement and sizing of distributed generators in unbalanced distribution systems using supervised big bang-big crunch method. IEEE Trans. Power Syst. 2015, 30, 911–919. [Google Scholar] [CrossRef]
- Kewat, S.; Singh, B. Modified amplitude adaptive control algorithm for power quality improvement in multiple distributed generation system. IET Power Eletron. 2019, 12, 2321–2329. [Google Scholar] [CrossRef]
- Giri, A.K.; Arya, S.R.; Maurya, R.; Babu, B.C. VCO-less PLL control-based voltage-source converter for power quality improvement in distributed generation system. IET Electr. Power Appl. 2019, 13, 1114–1124. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Mekhamer, S.F.; Talaat, H.E.A. Optimal power flow of power systems including distributed generation units using sunflower optimization algorithm. IEEE Access 2019, 7, 109289–109300. [Google Scholar] [CrossRef]
- Vita, V. Development of a decision-making algorithm for the optimum size and placement of distributed generation units in distribution networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Ekonomou, L.; Mastorakis, N. Economic analysis of energy storage integration with a grid connected intermittent power plant, for power quality purposes. WSEAS Trans. Power Syst. 2016, 11, 65–71. [Google Scholar]
- Vita, V.; Alimardan, T.; Ekonomous, L. The impact of distributed generation in the distribution networks’ voltage profile and energy losses. In Proceedings of the 2015 IEEE Europe Modelling Symposium (EMS), Madrid, Spain, 6–8 October 2015. [Google Scholar]
- Zhang, Y.; Sun, H.X.; Guo, Y.J. Wind power prediction based on PSO-SVR and grey combination model. IEEE Access 2019, 7, 136254–136267. [Google Scholar] [CrossRef]
- Chai, M.K.; Xia, F.; Hao, S.T.; Peng, D.G.; Cui, C.G.; Liu, W. PV power prediction based on LSTM with adaptive hyperparameter adjustment. IEEE Access 2019, 7, 115473–115486. [Google Scholar] [CrossRef]
- Yao, Q.; Liu, J.Z.; Hu, Y. Optimized active power dispatching strategy considering fatigue load of wind turbines during de-loading operation. IEEE Access 2019, 7, 17439–17449. [Google Scholar] [CrossRef]
- Cao, Y.; Li, P.; Yuan, Y.; Zhang, X.S.; Guo, S.Q.; Zhao, J.C. A novel annual wind power planning method of provincial power grid based on time sequential simulations. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014. [Google Scholar]
- Zheng, H.; Jin, N.; Xiong, Z.; Ji, C.; Fang, C.; Zhong, C. Electricity information big data based load curve clustering. In Proceedings of the 2014 China International Conference on Electricity Distribution (CICED), Shenzhen, China, 23–26 September 2014. [Google Scholar]
- Xu, L.; Ruan, X.; Mao, C. An improved optimal sizing method for wind-solar battery hybrid power system. IEEE Trans. Sustain. Energy 2013, 4, 774–785. [Google Scholar]
- Wan, C.; Lin, J.; Song, Y.H.; Xu, Z.; Yang, G.Y. Probabilistic forecasting of photovoltaic generation: An efficient statistical approach. IEEE Trans. Power Syst. 2017, 32, 2471–2472. [Google Scholar] [CrossRef]
- Du, E.S.; Zhang, N.; Kang, C.Q.; Kroposki, B.; Huang, H.; Miao, M.; Xia, Q. Managing wind power uncertainty through strategic reserve purchasing. IEEE Trans. Power Syst. 2017, 32, 2547–2559. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Z.; Botterud, A.; Zhang, K.F. Optimal wind power uncertainty intervals for electricity market operation. IEEE Trans. Sustain. Energy 2018, 9, 199–210. [Google Scholar] [CrossRef]
- Kaloudas, C.G.; Ochoa, L.F.; Marshall, B.; Majithia, S.; Fletcher, I. Assessing the feature trends of reactive power demand of distribution networks. IEEE Trans. Power Syst. 2017, 32, 4278–4288. [Google Scholar] [CrossRef]
- Chui, K.T.; Tsang, K.F.; Chuang, S.H.; Yeung, L.F. Appliance signature identification solution using K-means clustering. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Zhou, K.L.; Yang, S.L.; Ding, S.; Luo, H. On Cluster Validation. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2014&filename=XTLL201409027&v=MDY3OTBYTXBvOUhZNFI4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkxPZmJ1UnBGeURoVmI3T1BUbkhZckc0SDk= (accessed on 20 December 2012).
- Guo, J.; Hou, S. Study on the Index of Determining the Optimal Clustering Number of K-Means Algorithm. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2017&filename=RJDK201711002&v=MDM4OTVrVkw3TU55ZlBaYkc0SDliTnJvOUZab1I4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkxPZmJ1UnBGQ24= (accessed on 2 June 2017).


















| Season | Scene Reduction | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Spring | 0.57 | 0.21 | 0.07 | 0.12 | 0.03 |
| Pattern | DG | Installation Node | Installation Capacity/kW | Annual Life Cycle Investment Cost/¥ | Active Power Excision MW h | Computing Time/s |
|---|---|---|---|---|---|---|
| Annual Sequence Scene | WG | 5 | 125 | 5,123,600 | 48.26 | 1803 |
| 7 | 125 | |||||
| 11 | 375 | |||||
| 12 | 250 | |||||
| PV | 20 | 125 | ||||
| 23 | 250 | |||||
| Typical Day Scene | WG | 5 | 125 | 6,145,600 | 31.48 | 8 |
| 7 | 125 | |||||
| 11 | 250 | |||||
| 12 | 125 | |||||
| PV | 20 | 125 | ||||
| 23 | 125 | |||||
| Scene Reduction | WG | 5 | 125 | 4,547,400 | 45.77 | 60 |
| 7 | 125 | |||||
| 11 | 250 | |||||
| 12 | 250 | |||||
| PV | 20 | 125 | ||||
| 23 | 250 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, S.; Li, J.; Guo, Y.; Shi, Z. A Typical Distributed Generation Scenario Reduction Method Based on an Improved Clustering Algorithm. Appl. Sci. 2019, 9, 4262. https://doi.org/10.3390/app9204262
Lv S, Li J, Guo Y, Shi Z. A Typical Distributed Generation Scenario Reduction Method Based on an Improved Clustering Algorithm. Applied Sciences. 2019; 9(20):4262. https://doi.org/10.3390/app9204262
Chicago/Turabian StyleLv, Sitong, Jianguo Li, Yongxin Guo, and Zhong Shi. 2019. "A Typical Distributed Generation Scenario Reduction Method Based on an Improved Clustering Algorithm" Applied Sciences 9, no. 20: 4262. https://doi.org/10.3390/app9204262
APA StyleLv, S., Li, J., Guo, Y., & Shi, Z. (2019). A Typical Distributed Generation Scenario Reduction Method Based on an Improved Clustering Algorithm. Applied Sciences, 9(20), 4262. https://doi.org/10.3390/app9204262





