Integrated Optimum Layout of Conformal Cooling Channels and Optimal Injection Molding Process Parameters for Optical Lenses
Abstract
:1. Introduction
2. Methods
2.1. Materials
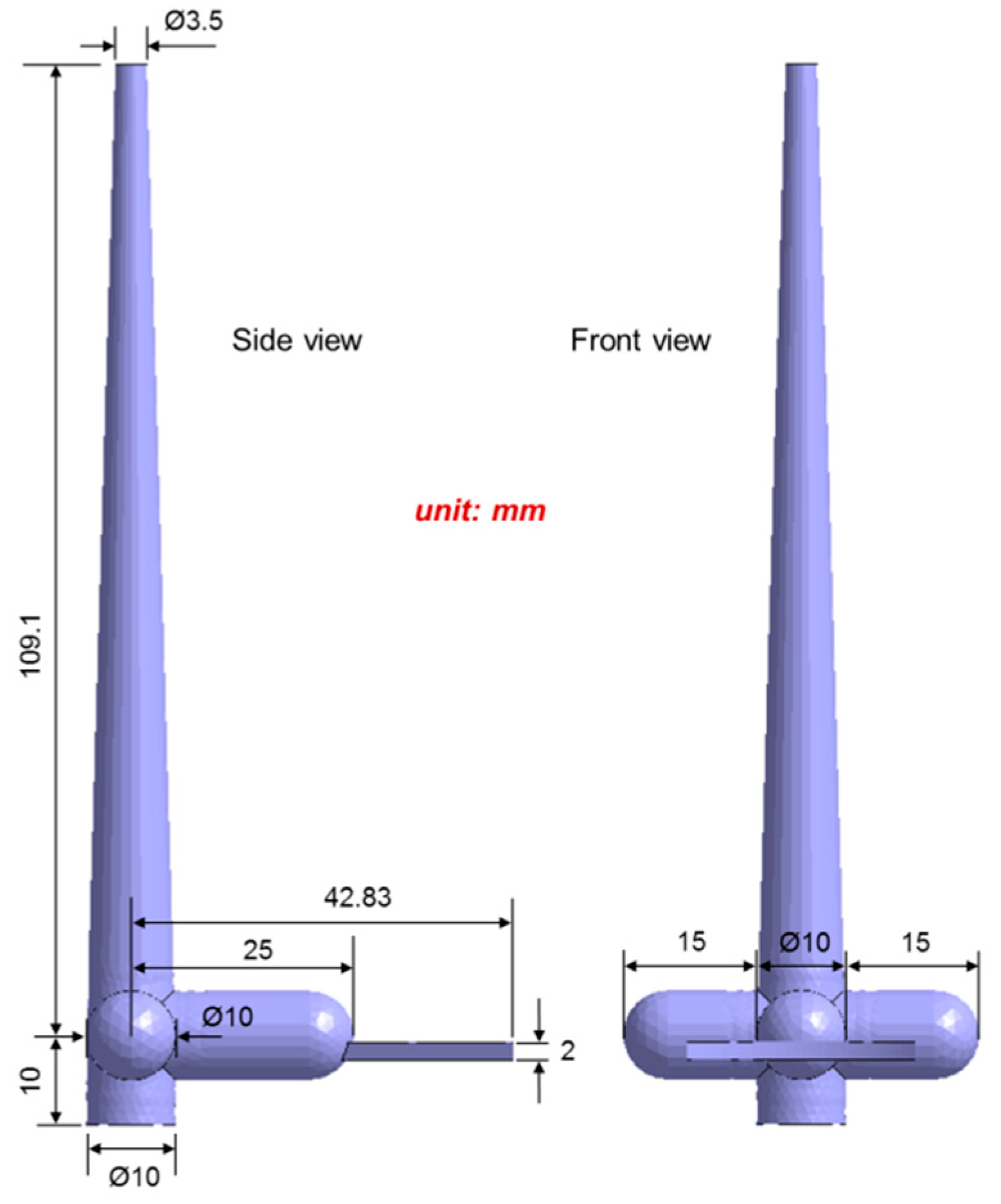
2.2. Design of the Runner and Gate System
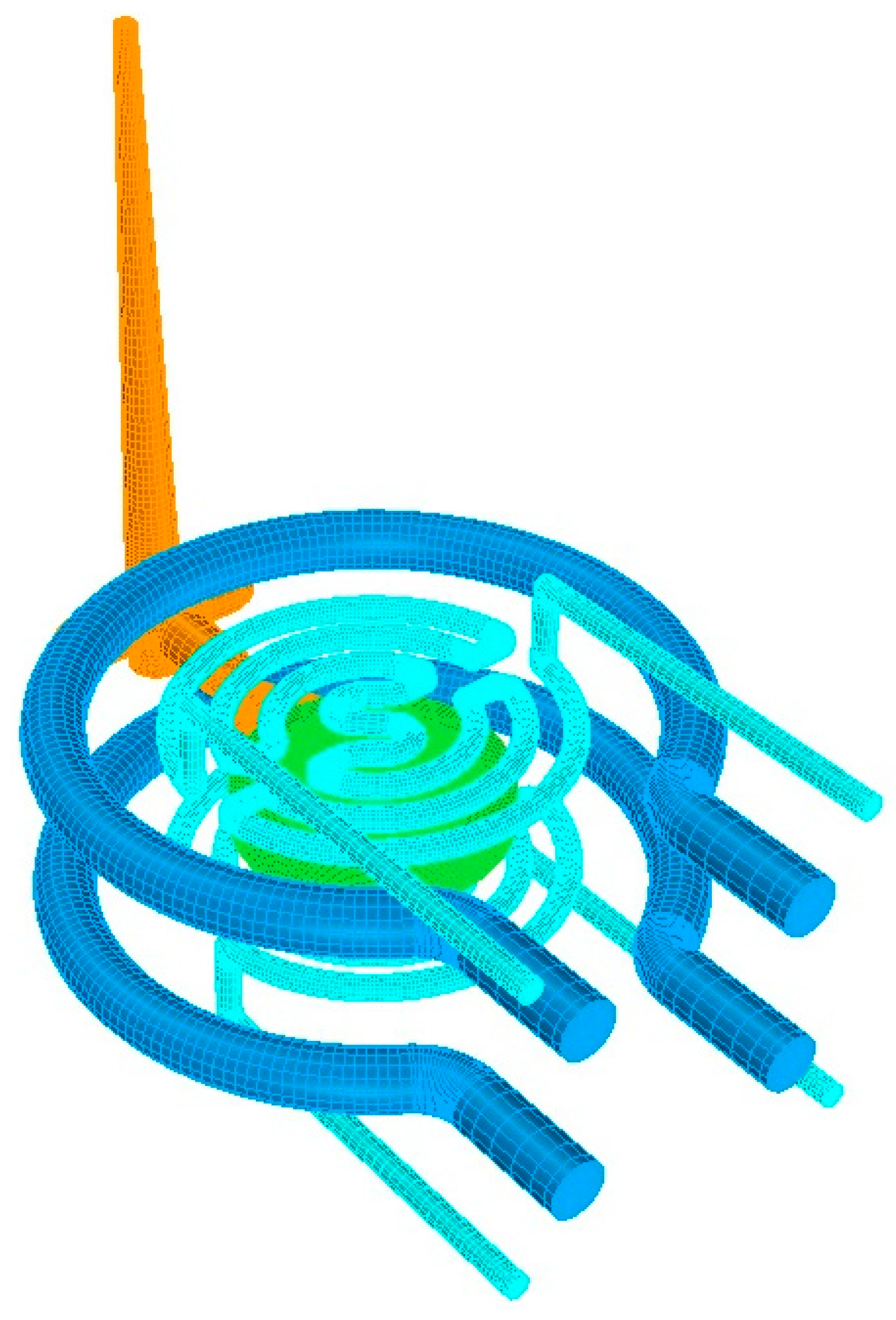
2.3. Mold Design for Conventional and Planar Conformal Cooling Channels
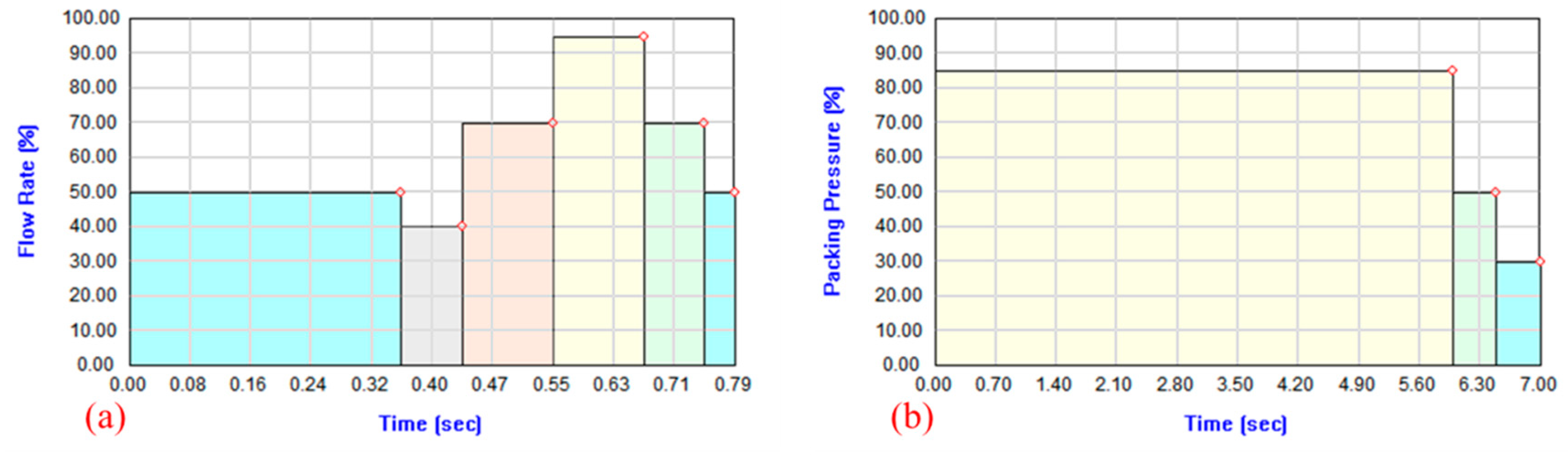
2.4. Simulation of the Filling and Packing Stages
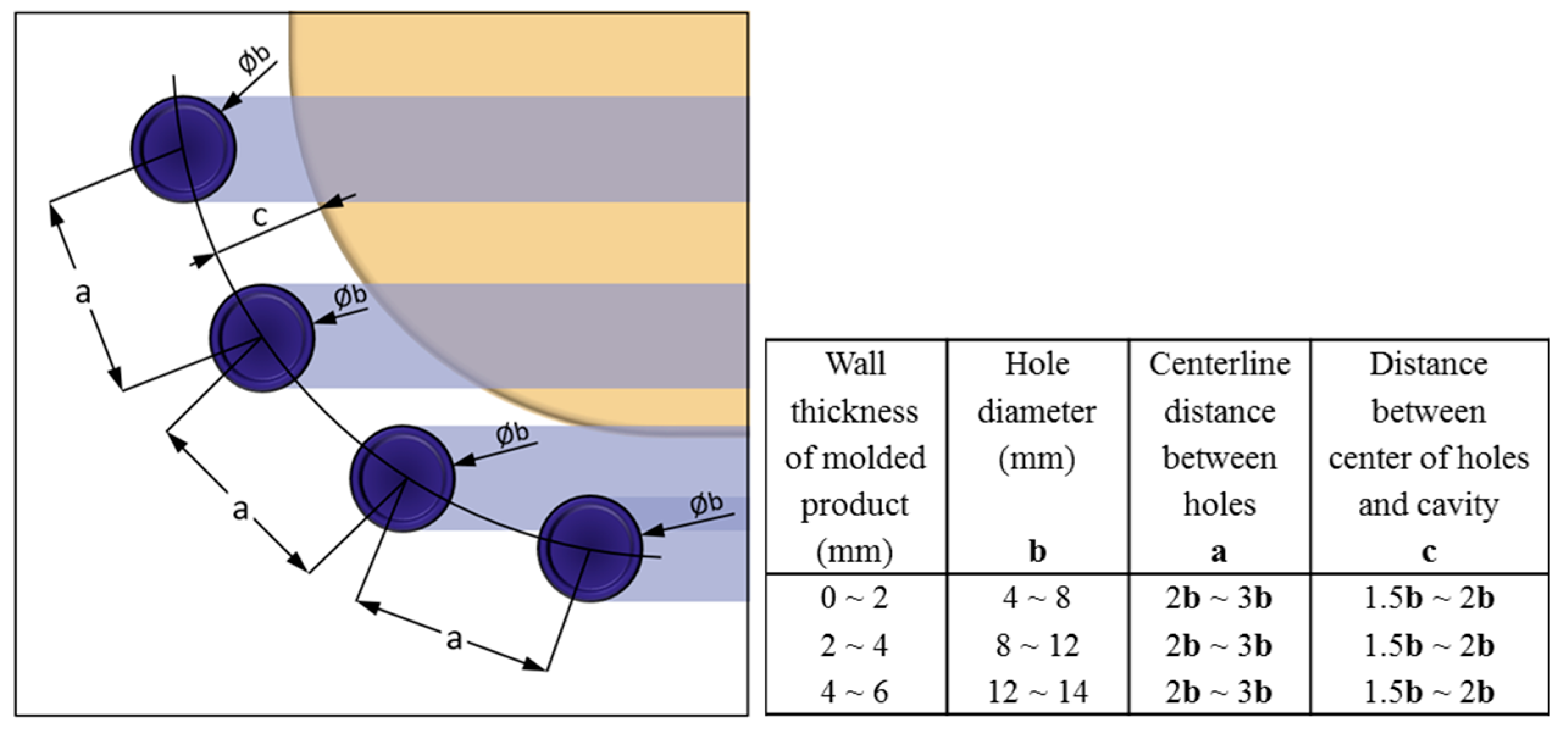
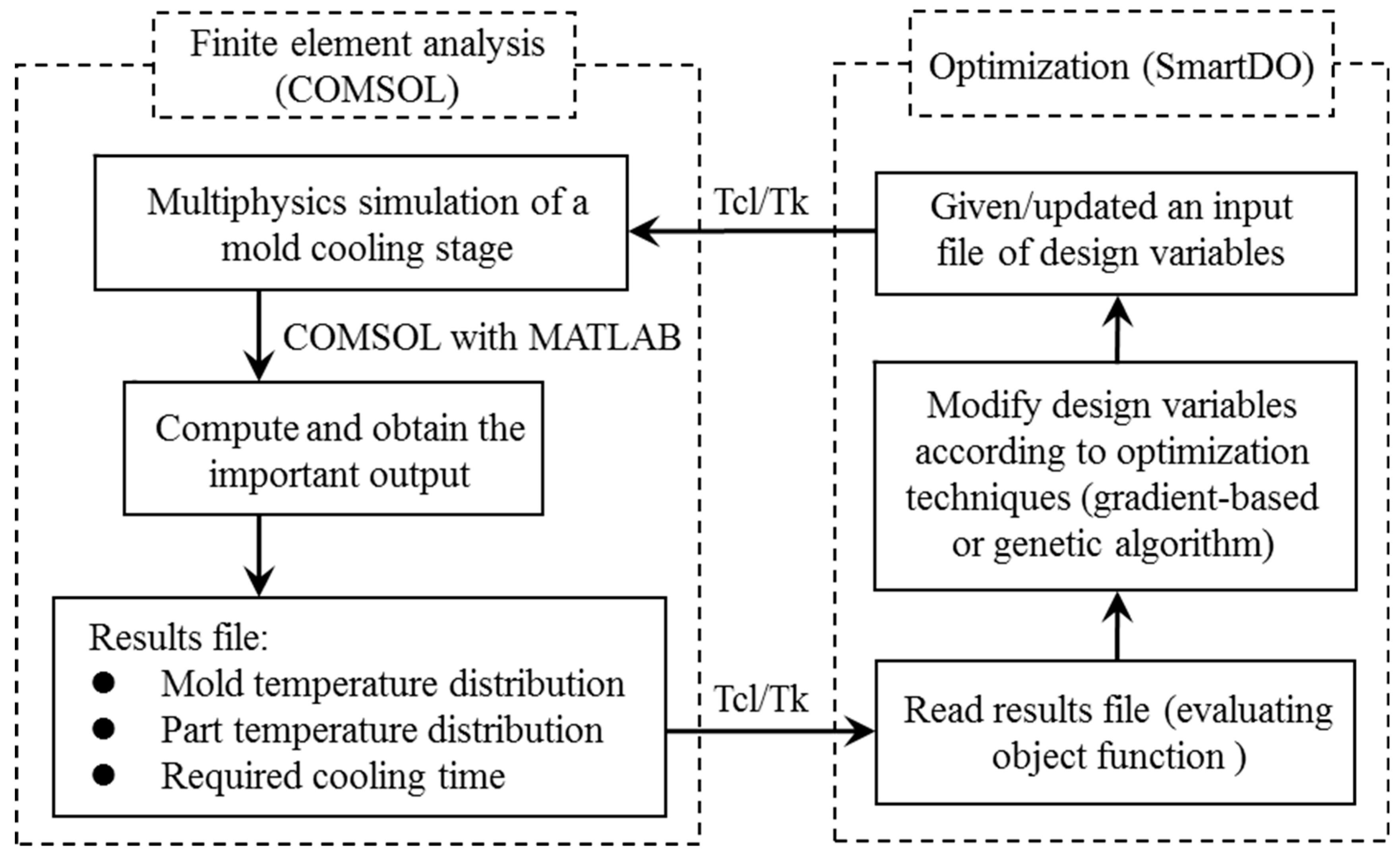
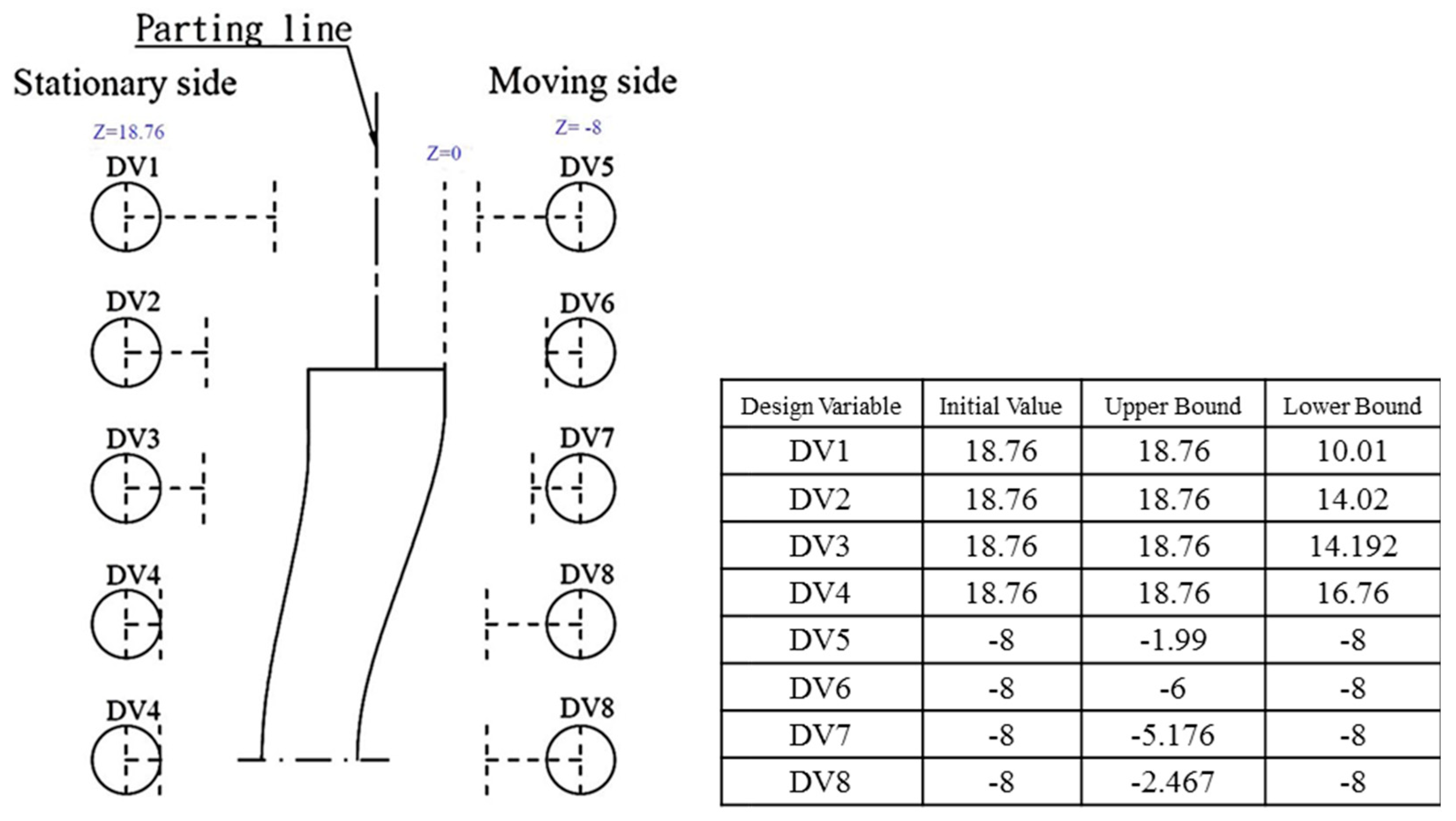
2.5. Geometric Optimization of the Conformal Cooling Channels
2.6. Molding Process Optimization for the Optimized Conformal Cooling Channels
3. Results and Discussion
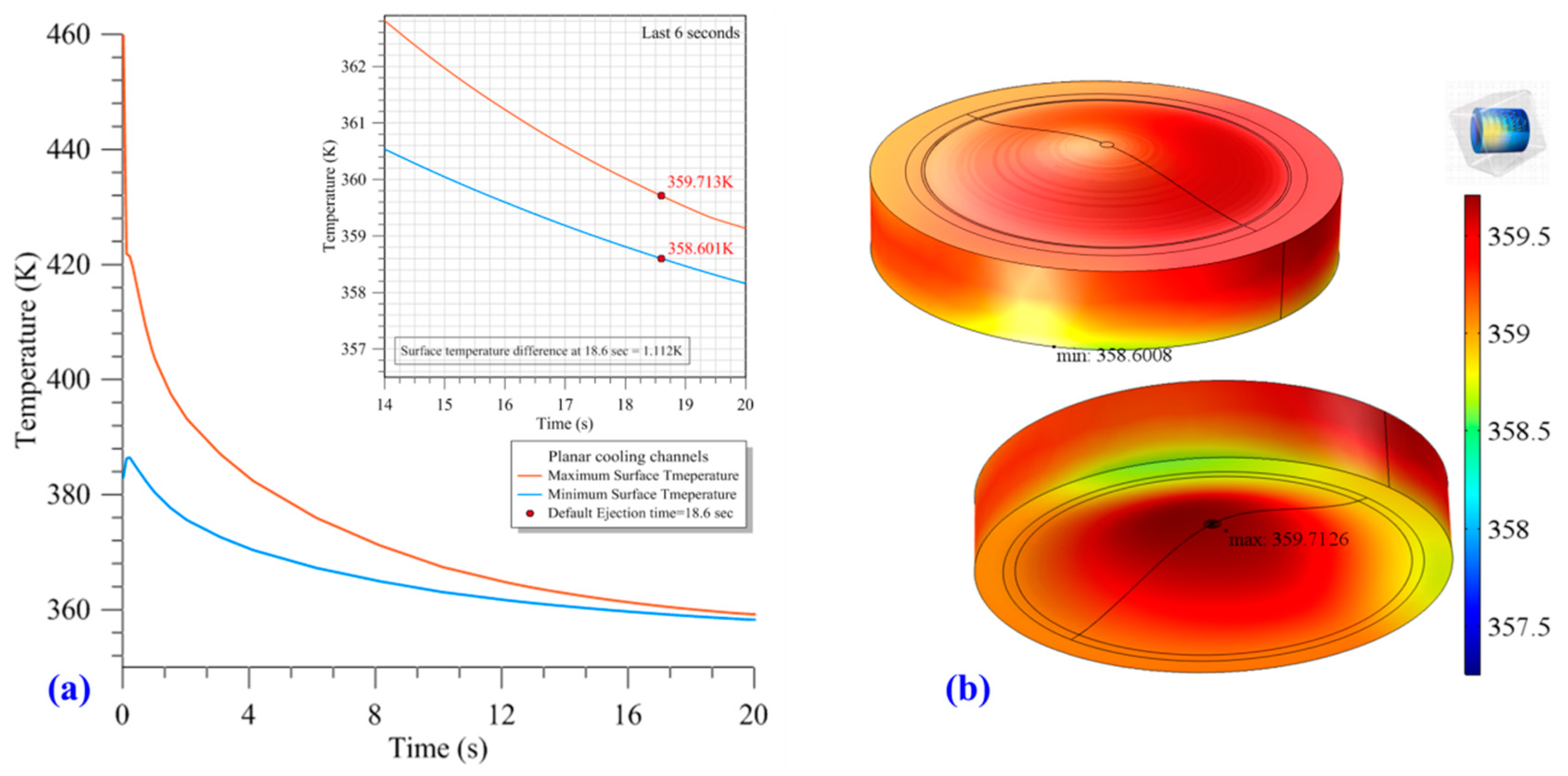
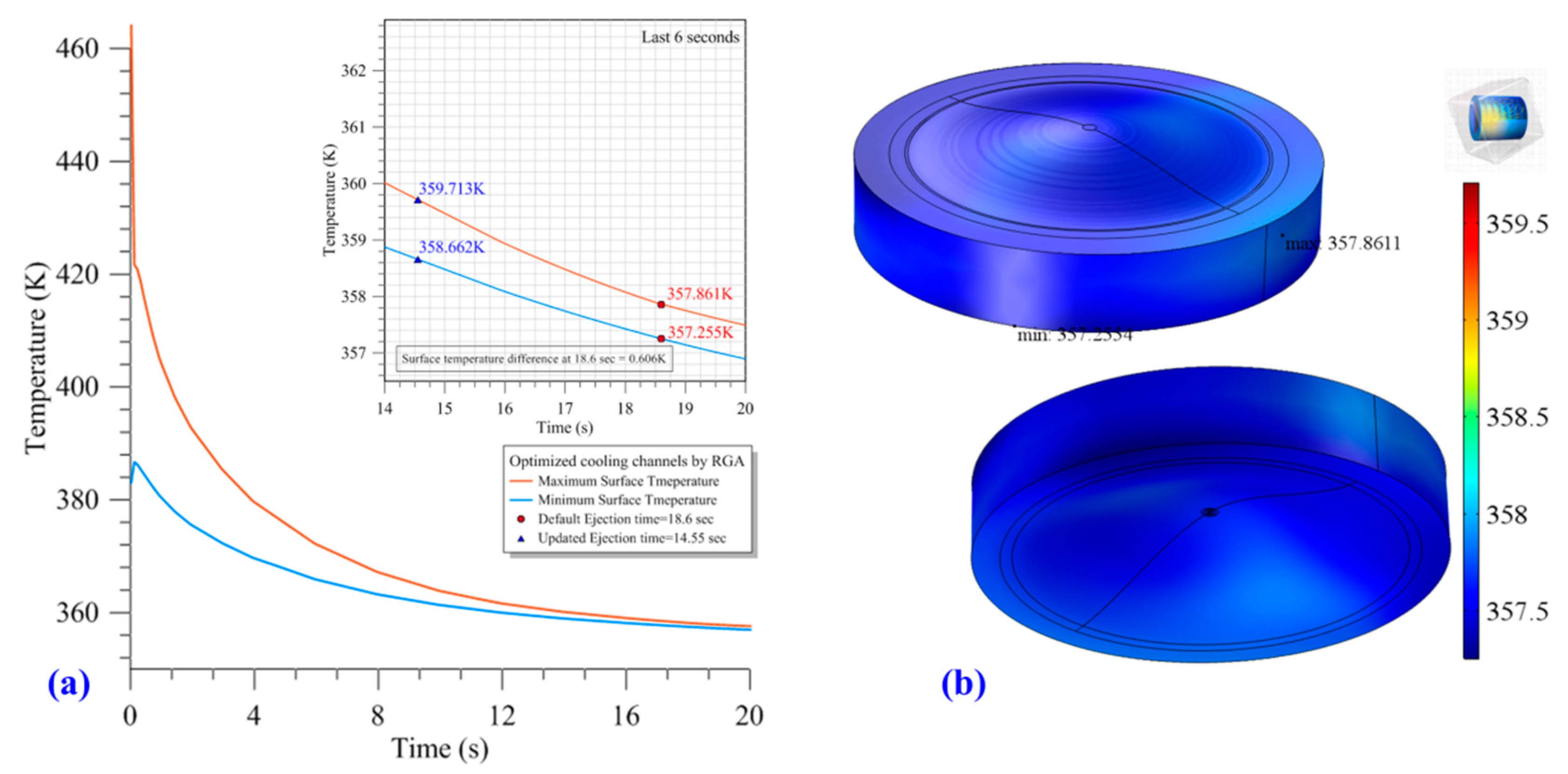
3.1. Optimum Layout of Conformal Cooling Channels for the Cooling Stage
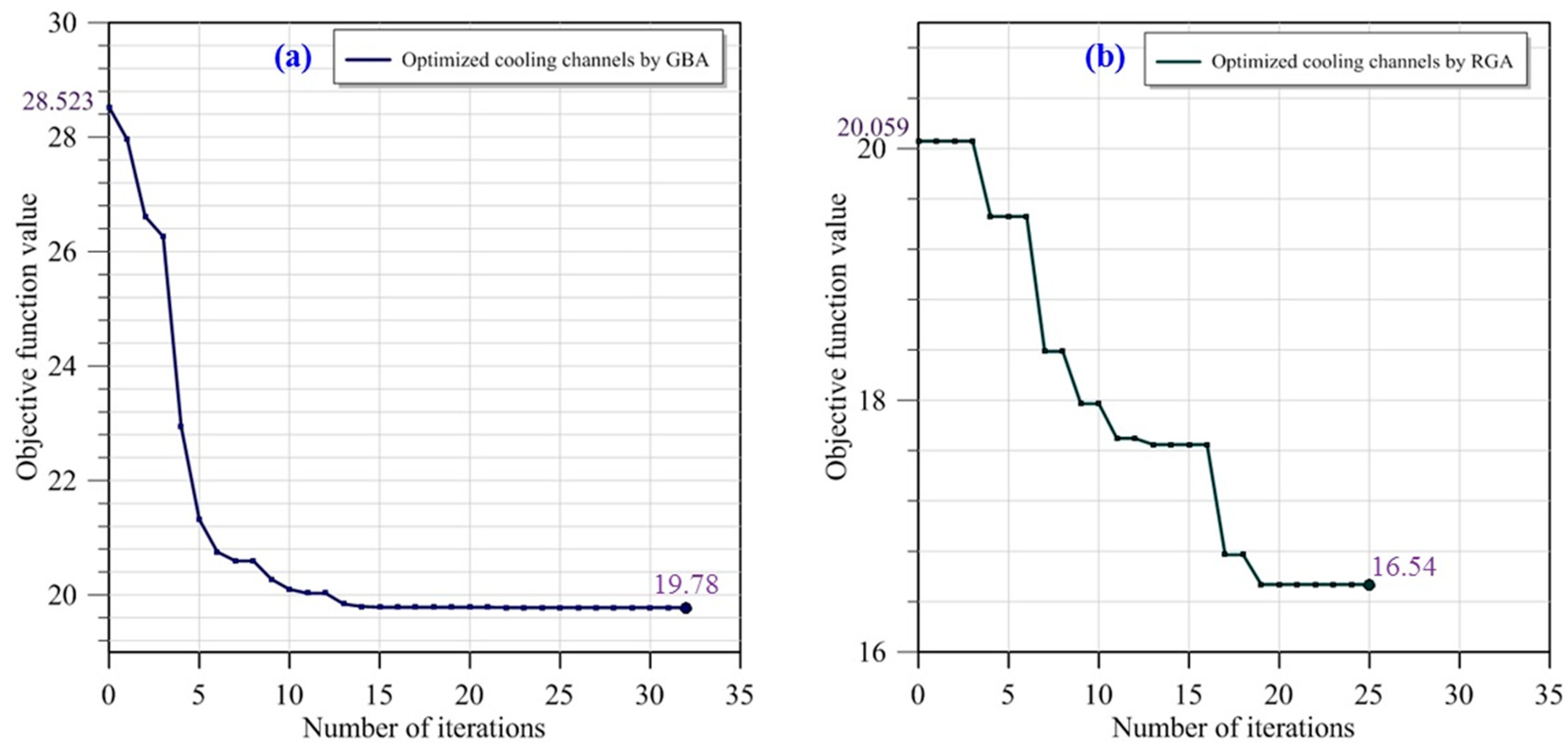
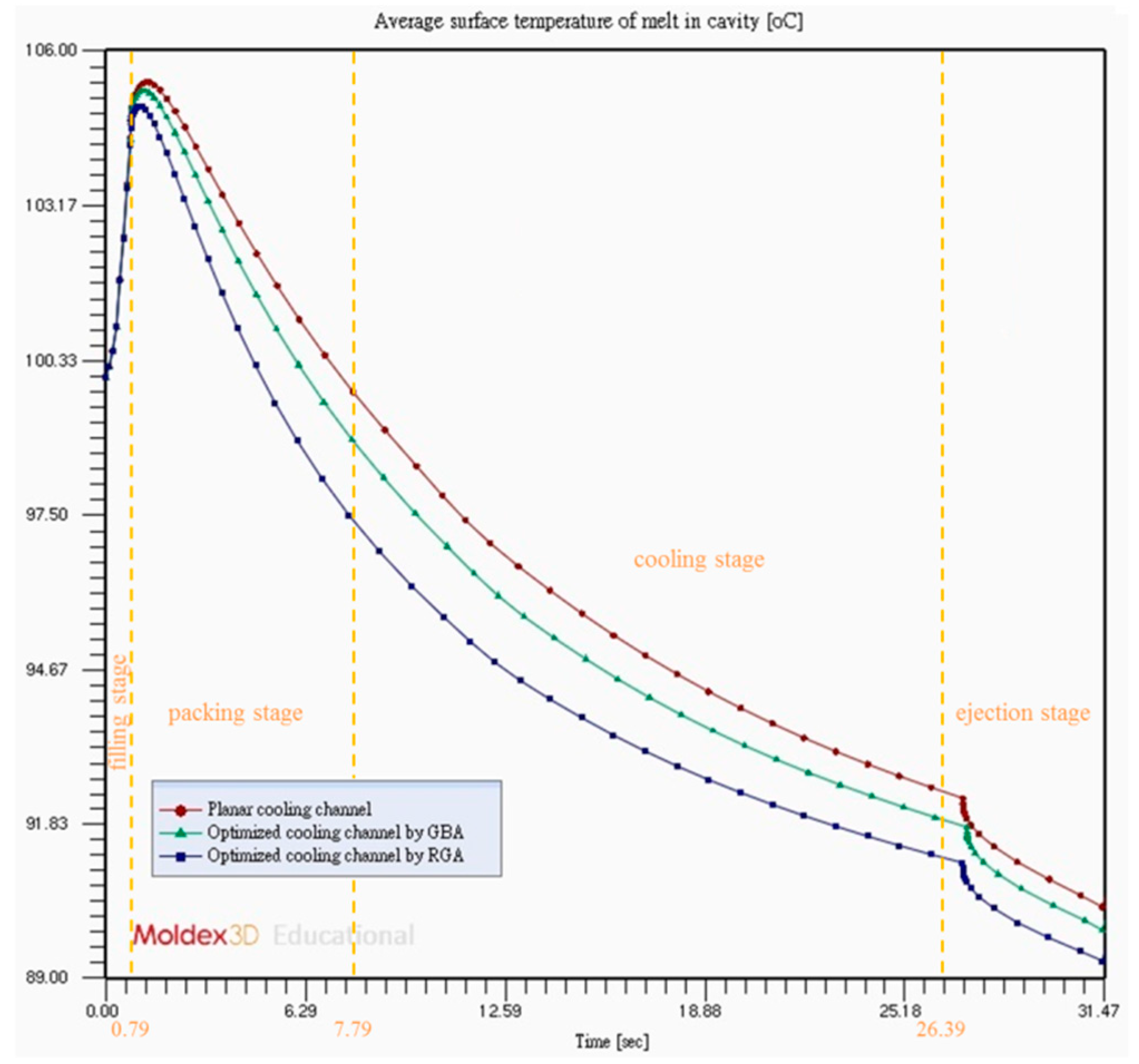
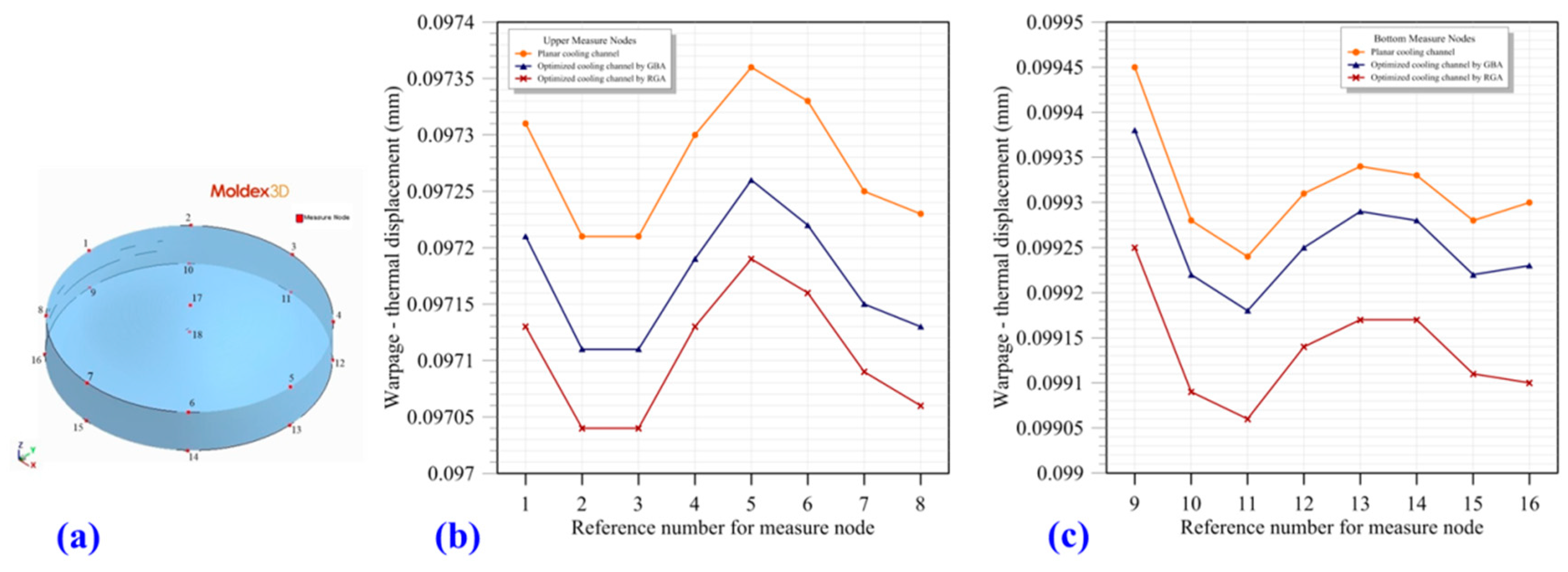
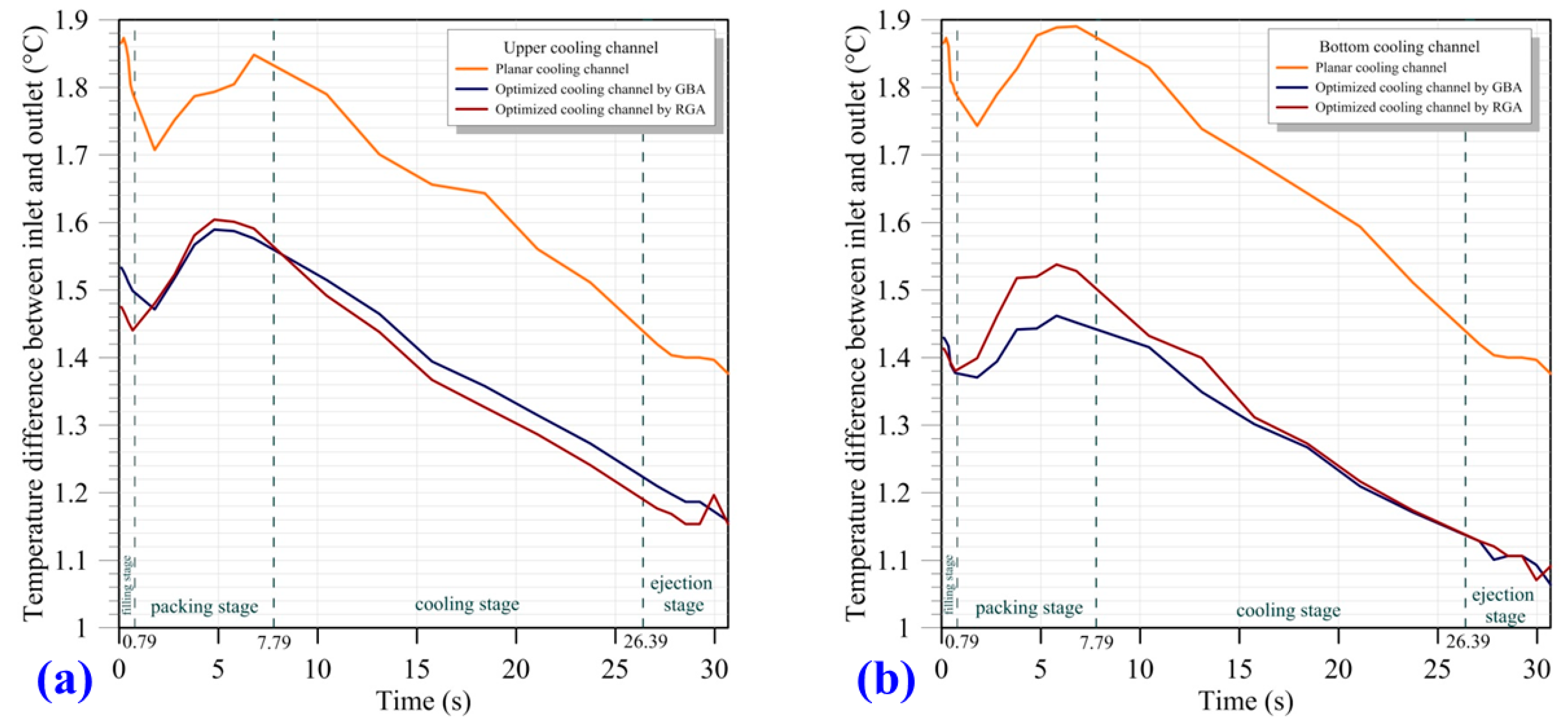
3.2. Comparison of the Conformal Cooling Channels Designed by Using Different Algorithms for the Entire Injection Molding Process
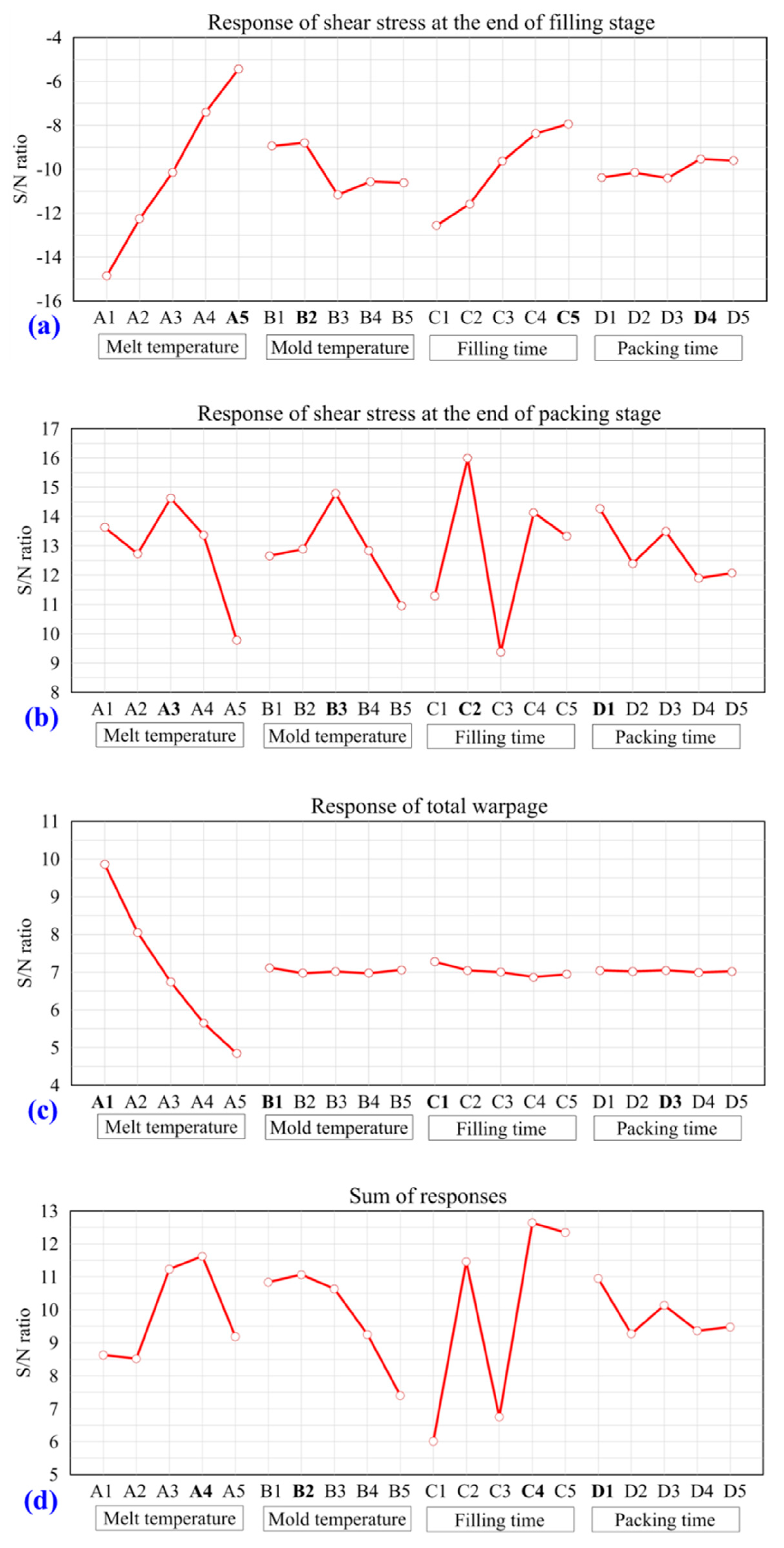
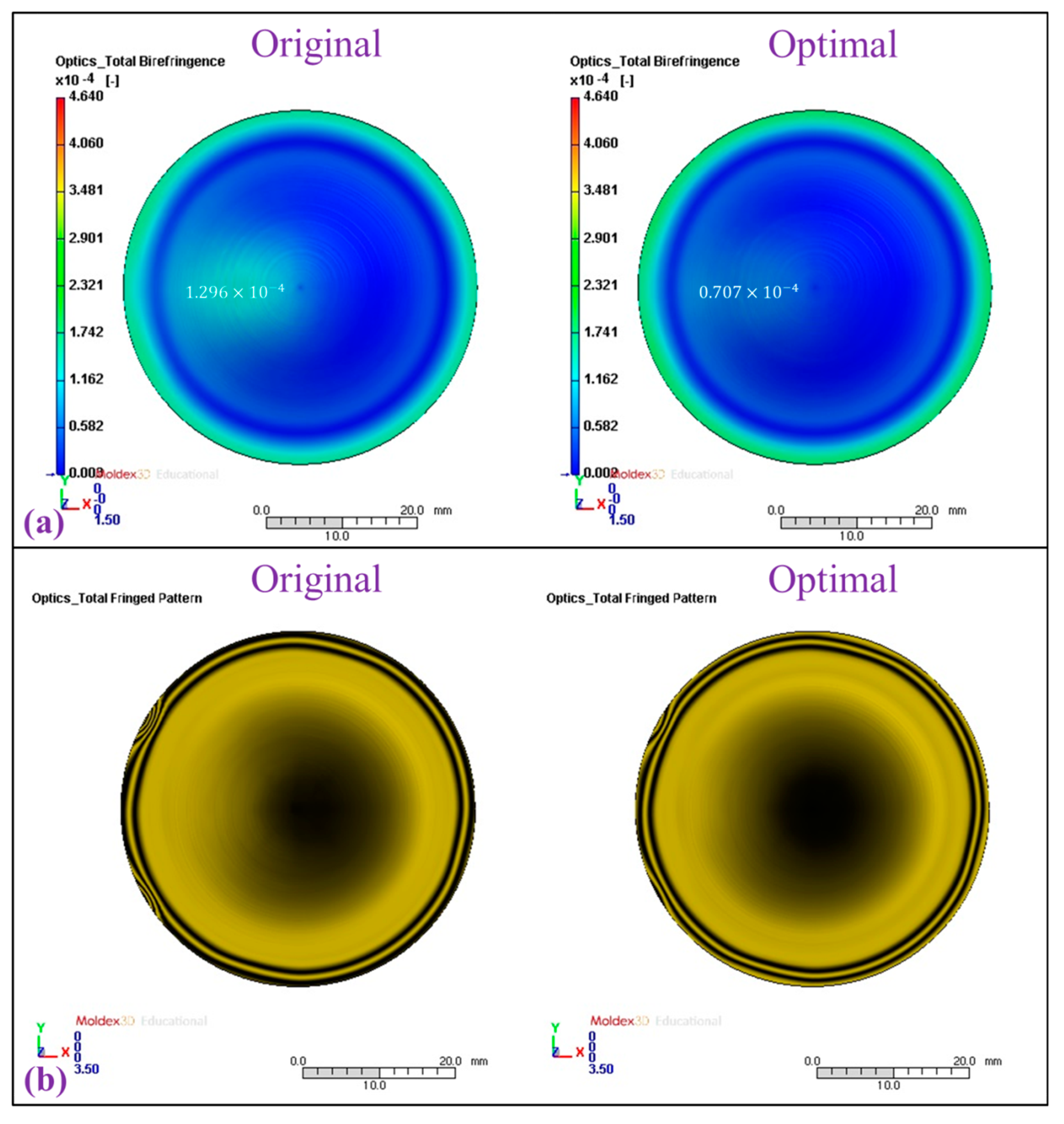
3.3. Optimal Process Parameters for Injection Molding
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garrette, B.; Karnani, A. Challenges in marketing socially useful goods to the poor. Calif. Manag. Rev. 2010, 52, 29–47. [Google Scholar] [CrossRef]
- Kohara, T. Development of new cyclic olefin polymers for optical uses. Macromol. Symp. 1996, 101, 571–579. [Google Scholar] [CrossRef]
- Lee, Y.B.; Kwon, T.H. Modeling and numerical of residual stresses and birefringence in injection molded center-gated disks. J. Mater. Process. Technol. 2001, 111, 214–218. [Google Scholar] [CrossRef]
- AC Technology Inc. C-MOLD Design Guide: A Resource for Plastics Engineers; Advanced CAE Technology: Ithaca, NY, USA, 1995. [Google Scholar]
- Sachs, E.; Wylonis, E.; Allen, S.; Cima, M.; Guo, H. Production of injection molding tooling with conformal cooling channels using the three dimensional printing process. Polym. Eng. Sci. 2000, 40, 1232–1247. [Google Scholar] [CrossRef] [Green Version]
- Dalgarno, K.W.; Stewart, T.D. Manufacture of production injection mould tooling incorporating conformal cooling channels via indirect selective laser sintering. Proc. Inst. Mech. Eng. Part B 2001, 215, 1323–1332. [Google Scholar] [CrossRef]
- Yan, C.; Hsu, A. Introduction of Composite Technology, Combining Machining with Selective Laser Melting for Metal Powder Forming. In Molding Innovation Newsletter Feb. 2012; CoreTech System Co., Ltd.: Chupei City, Taiwan, 2012; pp. 5–10. [Google Scholar]
- Hsu, F.H.; Wang, K.; Huang, C.T.; Chang, R.Y. Investigation on conformal cooling system design in injection molding. Adv. Prod. Eng. Manag. 2013, 8, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Qiao, H. A systematic computer-aided approach to cooling system optimal design in plastic injection molding. Int. J. Mech. Sci. 2006, 48, 430–439. [Google Scholar] [CrossRef]
- Park, H.-S.; Dang, X.-P. Optimization of conformal cooling channels with array of baffles for plastic injection mold. Int. J. Precis. Eng. Manuf. 2010, 11, 879–890. [Google Scholar] [CrossRef]
- Dang, X.-P.; Park, H.-S. Design of U-shape milled groove conformal cooling channels for plastic injection mold. Int. J. Precis. Eng. Manuf. 2011, 12, 73–84. [Google Scholar] [CrossRef]
- Jahan, S.A.; Wu, T.; Zhang, Y.; Zhang, J.; Tovar, A.; El-Mounayri, H. Thermo-mechanical design optimization of conformal cooling channels using design of experiments approach. Procedia Manuf. 2017, 10, 898–911. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Gu, J.; Ruan, S.; Shen, C.; Lyu, Y.; Zhao, Y. Topology optimization for the design of conformal cooling system in thin-wall injection molding based on BEM. Int. J. Adv. Manuf. Technol. 2018, 94, 1041–1059. [Google Scholar] [CrossRef]
- Jahan, S.A.; El-Mounayri, H. A thermomechanical analysis of conformal cooling channels in 3D printed plastic injection molds. Appl. Sci. 2018, 8, 2567. [Google Scholar] [CrossRef]
- Chen, C.-C.A.; Vu, L.T.; Qiu, Y.-T. Study on injection molding of shell mold for aspheric contact lens fabrication. Procedia Eng. 2017, 184, 344–349. [Google Scholar] [CrossRef]
- Lin, C.-M.; Hsieh, H.-K. Processing optimization of Fresnel lenses manufacturing in the injection molding considering birefringence effect. Microsyst. Technol. 2017, 23, 5689–5695. [Google Scholar] [CrossRef]
- Shieh, J.-Y.; Wang, L.K.; Ke, S.-Y. A feasible injection molding technique for the manufacturing of large diameter aspheric plastic lenses. Opt. Rev. 2010, 17, 399–403. [Google Scholar] [CrossRef]
- Chen, C.-C.A.; Tang, J.-C.; Teng, L.-M. Effects of mold design of aspheric projector lens for head up display. In Proceedings of the Polymer Optics Design, Fabrication, and Materials, San Diego, CA, USA, 12 August 2010; Volume 7788, p. 778806. [Google Scholar]
- Mayer, S. Optimised Mould Temperature Control Procedure Using DMLS; EOS Whitepaper 2005; EOS GmbH Ltd.: Krailling, Germany, 2005; pp. 1–10. [Google Scholar]
- G-Plast Pvt. Ltd. Synergy of True & Full 3D Simulation and Conformal Cooling. In Molding Innovation Newsletter Feb. 2012; CoreTech System Co., Ltd.: Chupei City, Taiwan, 2012; pp. 18–20. [Google Scholar]
- Wang, P.-J.; Lai, H.-E. Study of residual birefringence in injection molded lenses. In Annual Technical Conference (ANTEC); SPE- the Society of Plastics Engineers: Cincinnati, OH, USA, 2007; pp. 2494–2498. [Google Scholar]
- Lai, H.-E.; Wang, P.-J. Study of process parameters on optical qualities for injection-molded plastic lenses. Appl. Opt. 2008, 47, 2017–2027. [Google Scholar] [CrossRef] [Green Version]
- COMSOL Inc. Application ID: 12371, Cooling of an Injection Mold. Available online: http://www.comsol.com/model/12371 (accessed on 1 July 2016).
- Chung, C.-Y.; Mansour, J.M. Determination of poroelastic properties of cartilage using constrained optimization coupled with finite element analysis. J. Mech. Behav. Biomed. Mater. 2015, 42, 10–18. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Huang, B.-K.; You, Z.-T.; Chan, C.-Y.; Huang, T.-M. Optimization of lightweight structure and supporting bipod flexure for a space mirror. Appl. Opt. 2016, 55, 10382–10391. [Google Scholar] [CrossRef]
- Chen, S.-Y. An approach for impact structure optimization using the robust genetic algorithm. Finite Elem. Anal. Des. 2001, 37, 431–446. [Google Scholar] [CrossRef]
- Lin, C.-M.; Wang, C.-K. Processing optimization of optical lens in the injection molding. Adv. Mater. Res. 2013, 813, 161–164. [Google Scholar] [CrossRef]
- Himasekhar, K.; Lottey, J.; Wang, K.K. CAE of mold cooling in injection molding using a three-dimensional numerical simulation. J. Eng. Ind. 1992, 114, 213–221. [Google Scholar] [CrossRef]
- Chen, D.-C.; Huang, C.-K. Study of injection molding warpage using analytic hierarchy process and Taguchi method. Adv. Technol. Innov. 2016, 1, 46–49. [Google Scholar]
- Mazur, M.; Brincat, P.; Leary, M.; Brandt, M. Numerical and experimental evaluation of a conformally cooled H13 steel injection mould manufactured with selective laser melting. Int. J. Adv. Manuf. Technol. 2017, 93, 881–900. [Google Scholar] [CrossRef]
- Abbès, B.; Abbès, F.; Abdessalam, H.; Upganlawar, A. Finite element cooling simulations of conformal cooling hybrid injection molding tools manufactured by selective laser melting. Int. J. Adv. Manuf. Technol. 2019, 103, 2515–2522. [Google Scholar] [CrossRef]
- Kitayama, S.; Miyakawa, H.; Takano, M.; Aiba, S. Multi-objective optimization of injection molding process parameters for short cycle time and warpage reduction using conformal cooling channel. Int. J. Adv. Manuf. Technol. 2017, 88, 1735–1744. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Jiang, Z.-F. Numerical and experimental investigations of a conformally cooled maraging steel injection molding tool fabricated by direct metal printing. Int. J. Adv. Manuf. Technol. 2019. [Google Scholar] [CrossRef]



| Control factors | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | |
|---|---|---|---|---|---|---|
| A | Melt temperature (°C) | 240 | 255 | 270 | 285 | 300 |
| B | Mold temperature (°C) | 80.00 | 89.75 | 99.50 | 109.25 | 119.00 |
| C | Filling time (sec) | 0.69 | 0.79 | 0.89 | 0.99 | 1.09 |
| D | Packing time (sec) | 6 | 7 | 8 | 9 | 10 |
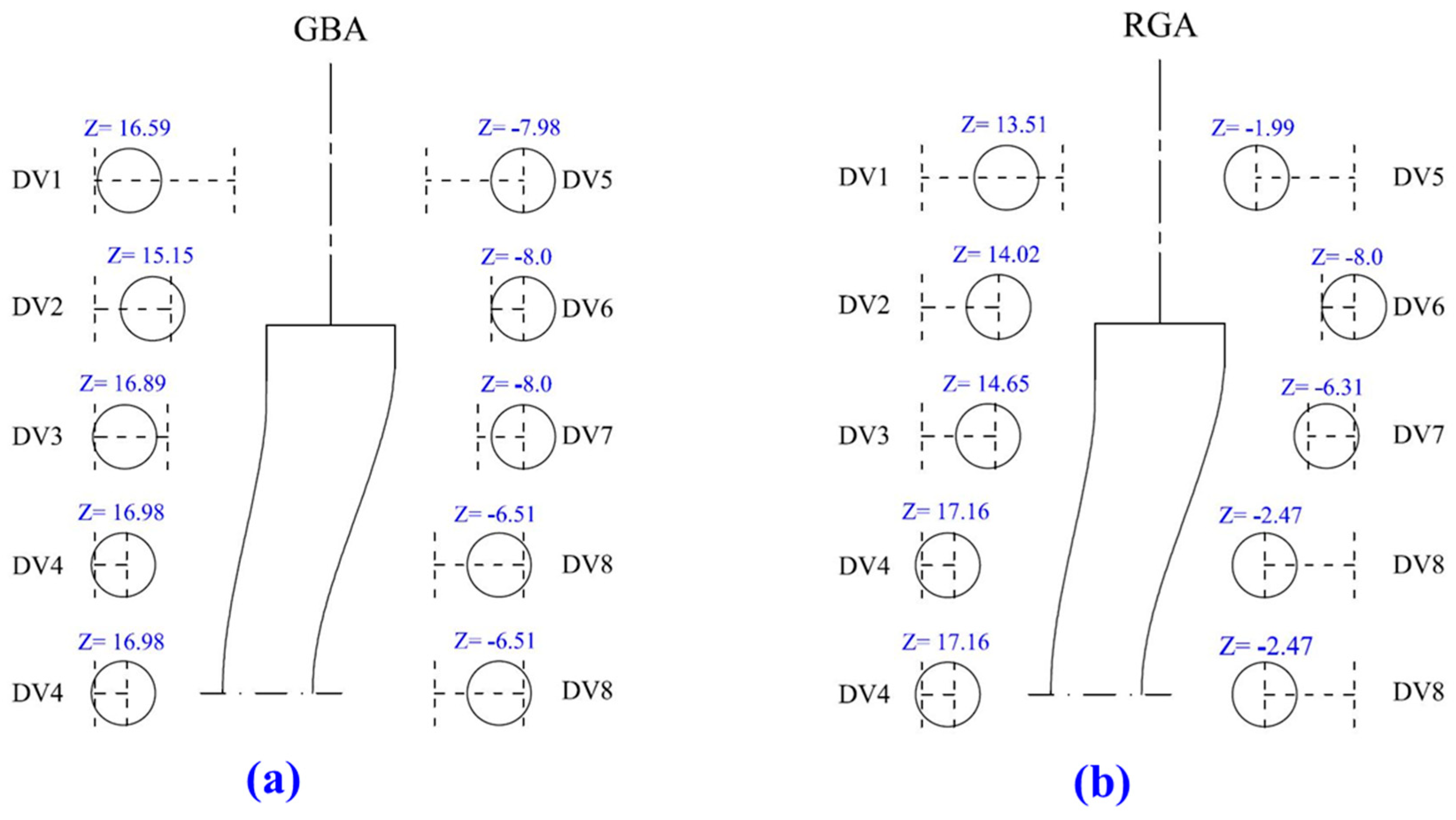
| Optimized Parameters | DV1 | DV2 | DV3 | DV4 | DV5 | DV6 | DV7 | DV8 |
|---|---|---|---|---|---|---|---|---|
| Results of GBA | 16.59 | 15.15 | 16.89 | 16.98 | −7.98 | −8.00 | −8.00 | −6.51 |
| Results of RGA | 13.51 | 14.02 | 14.65 | 17.16 | −1.99 | −8.00 | −6.31 | −2.47 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, C.-Y. Integrated Optimum Layout of Conformal Cooling Channels and Optimal Injection Molding Process Parameters for Optical Lenses. Appl. Sci. 2019, 9, 4341. https://doi.org/10.3390/app9204341
Chung C-Y. Integrated Optimum Layout of Conformal Cooling Channels and Optimal Injection Molding Process Parameters for Optical Lenses. Applied Sciences. 2019; 9(20):4341. https://doi.org/10.3390/app9204341
Chicago/Turabian StyleChung, Chen-Yuan. 2019. "Integrated Optimum Layout of Conformal Cooling Channels and Optimal Injection Molding Process Parameters for Optical Lenses" Applied Sciences 9, no. 20: 4341. https://doi.org/10.3390/app9204341
APA StyleChung, C.-Y. (2019). Integrated Optimum Layout of Conformal Cooling Channels and Optimal Injection Molding Process Parameters for Optical Lenses. Applied Sciences, 9(20), 4341. https://doi.org/10.3390/app9204341




