Estimation of Seismically-Induced Crest Settlement of Earth Core Rockfill Dams
Abstract
:1. Introduction
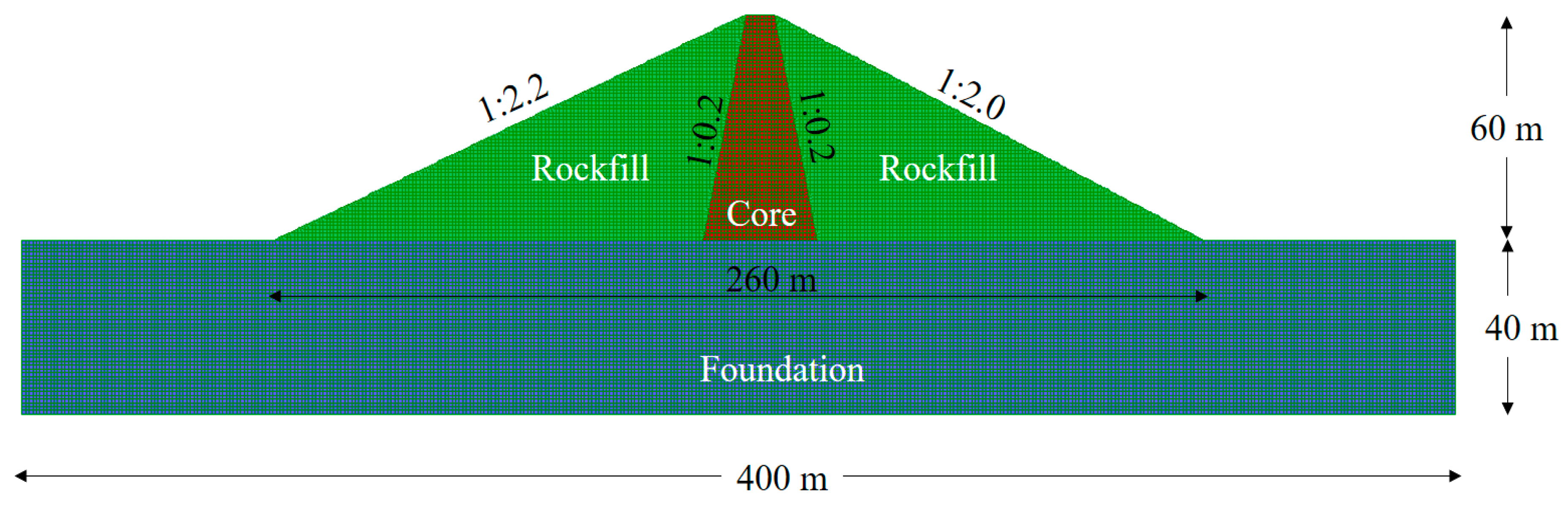
2. Numerical Model
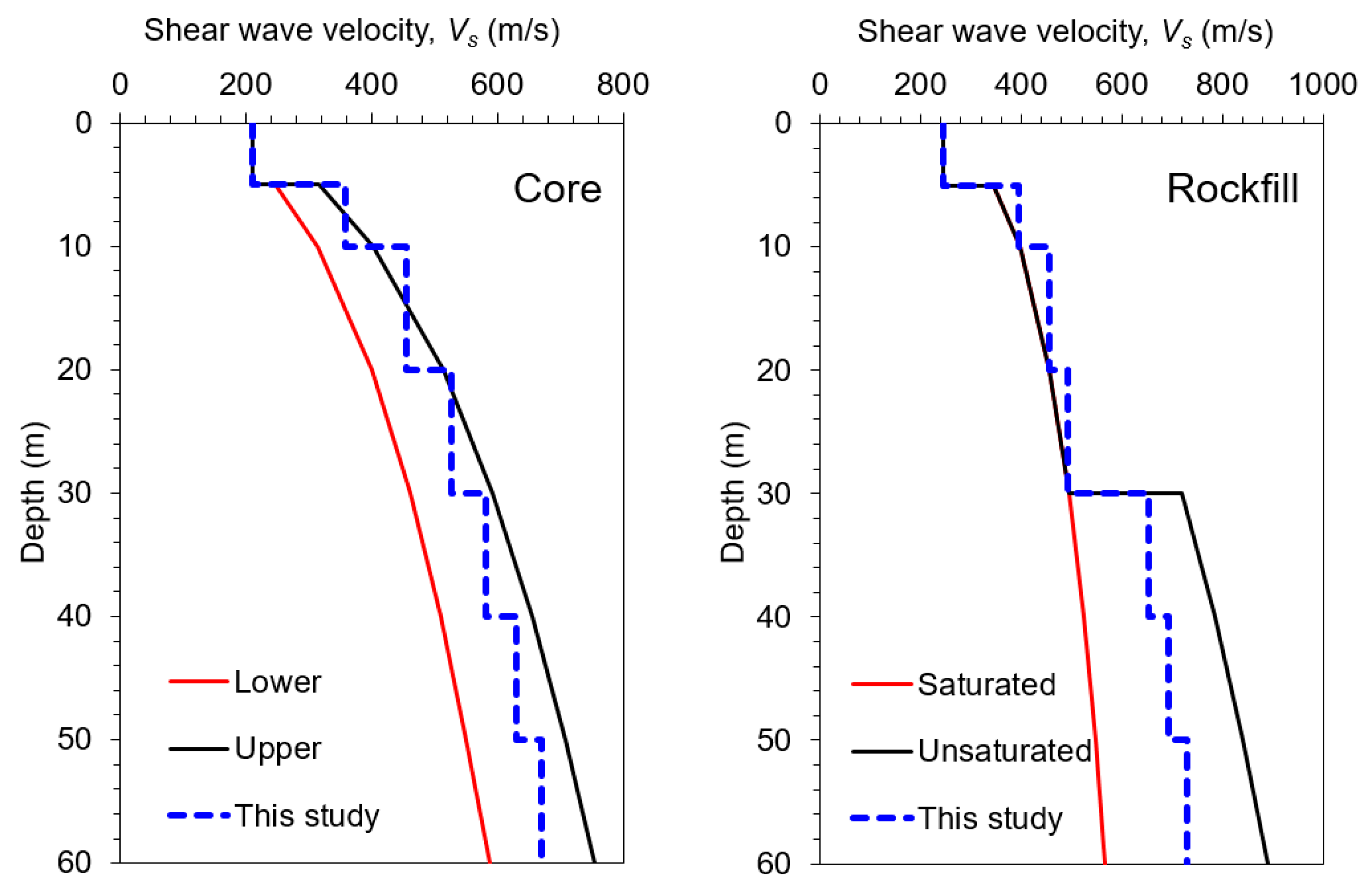
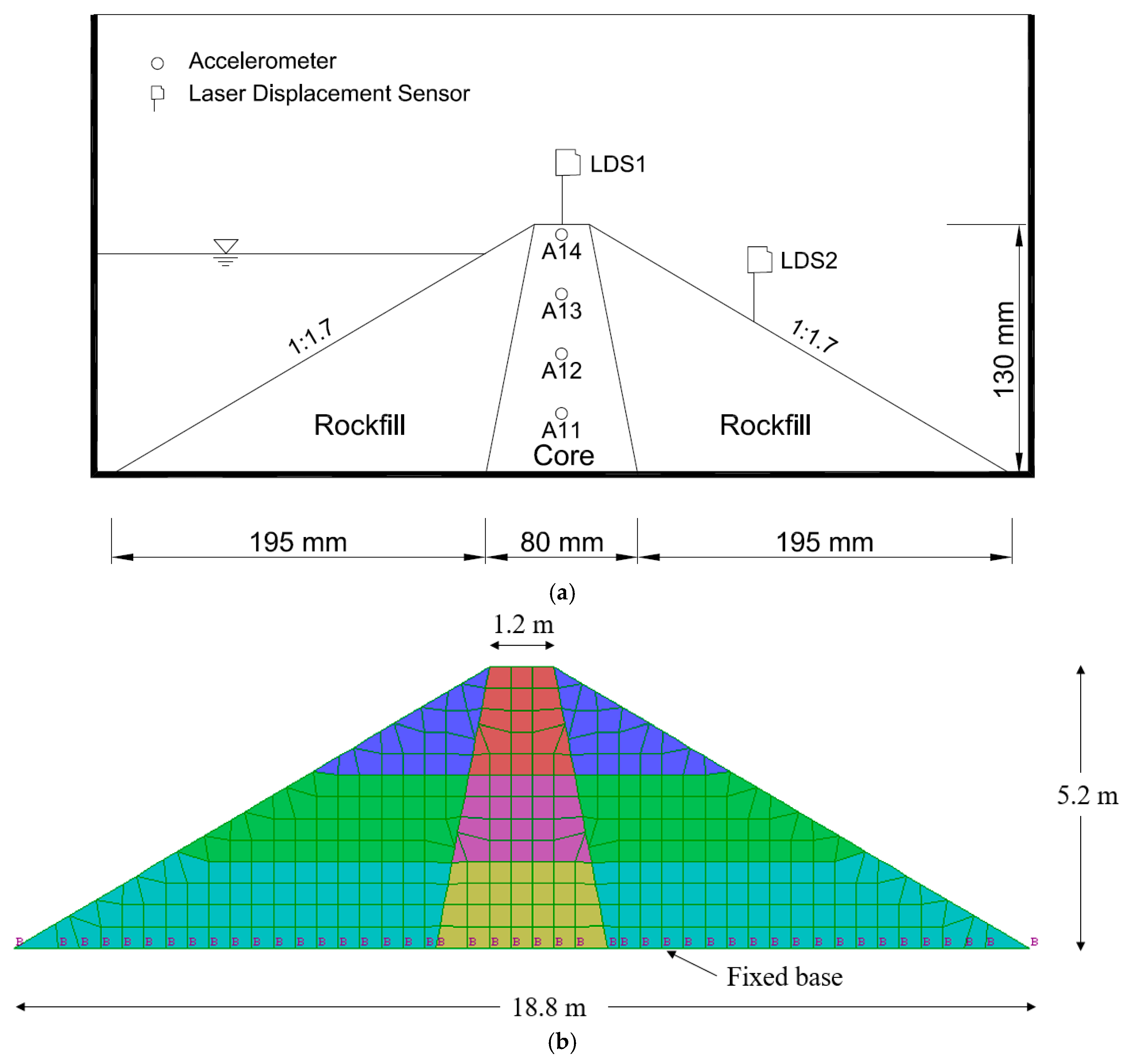
3. Validation of the Numerical Model
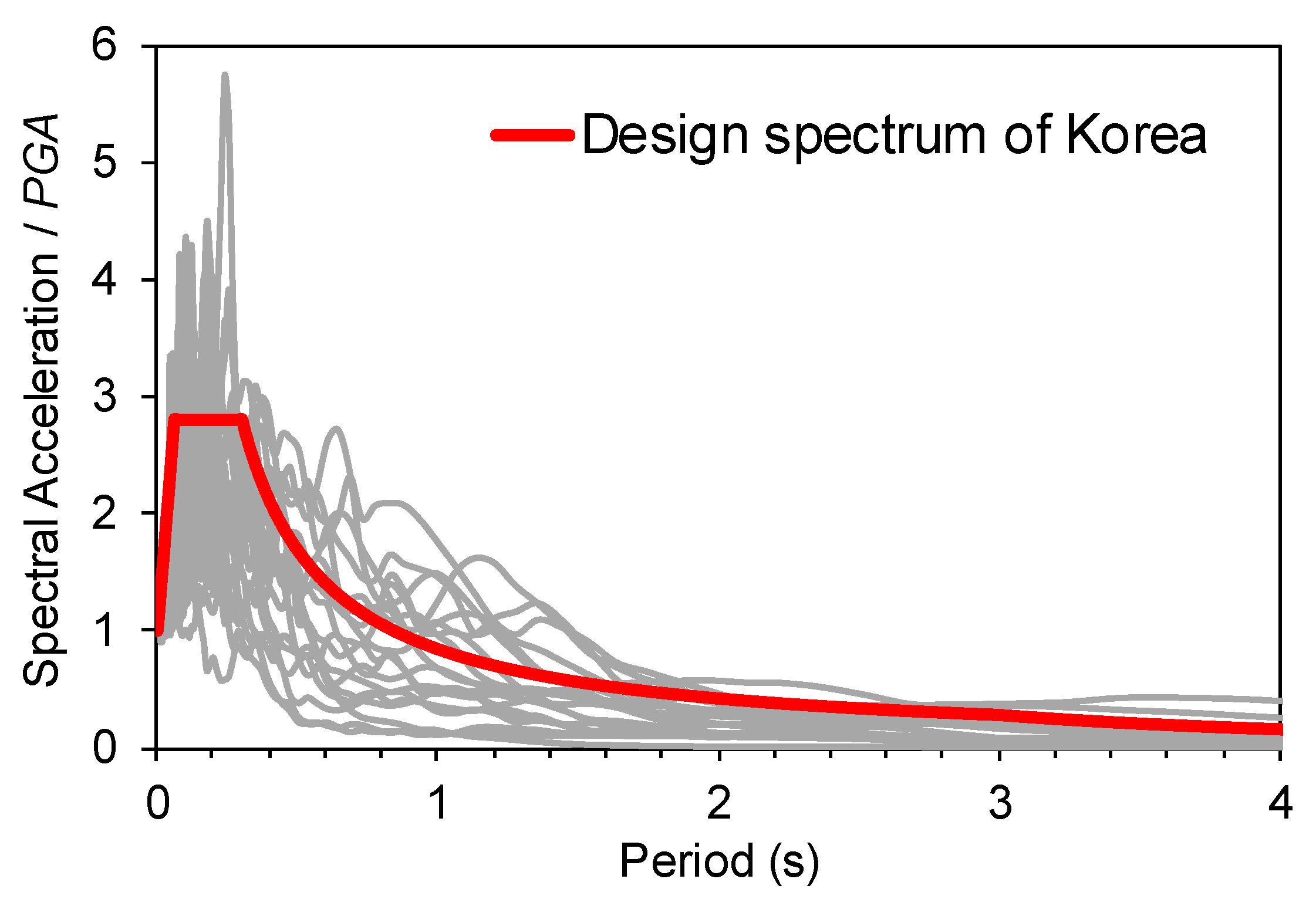
4. Crest Settlement Calculations and Correlation with Ground Motion Parameters
5. Conclusions
- The nonlinear model of the dam was demonstrated to provide reliable estimate of the seismic response of ECRDs when compared with the centrifuge test measurements. It was therefore revealed that the nonlinear model was capable of predicting the settlement and could be used for the evaluation of the seismic performance of ECRDs.
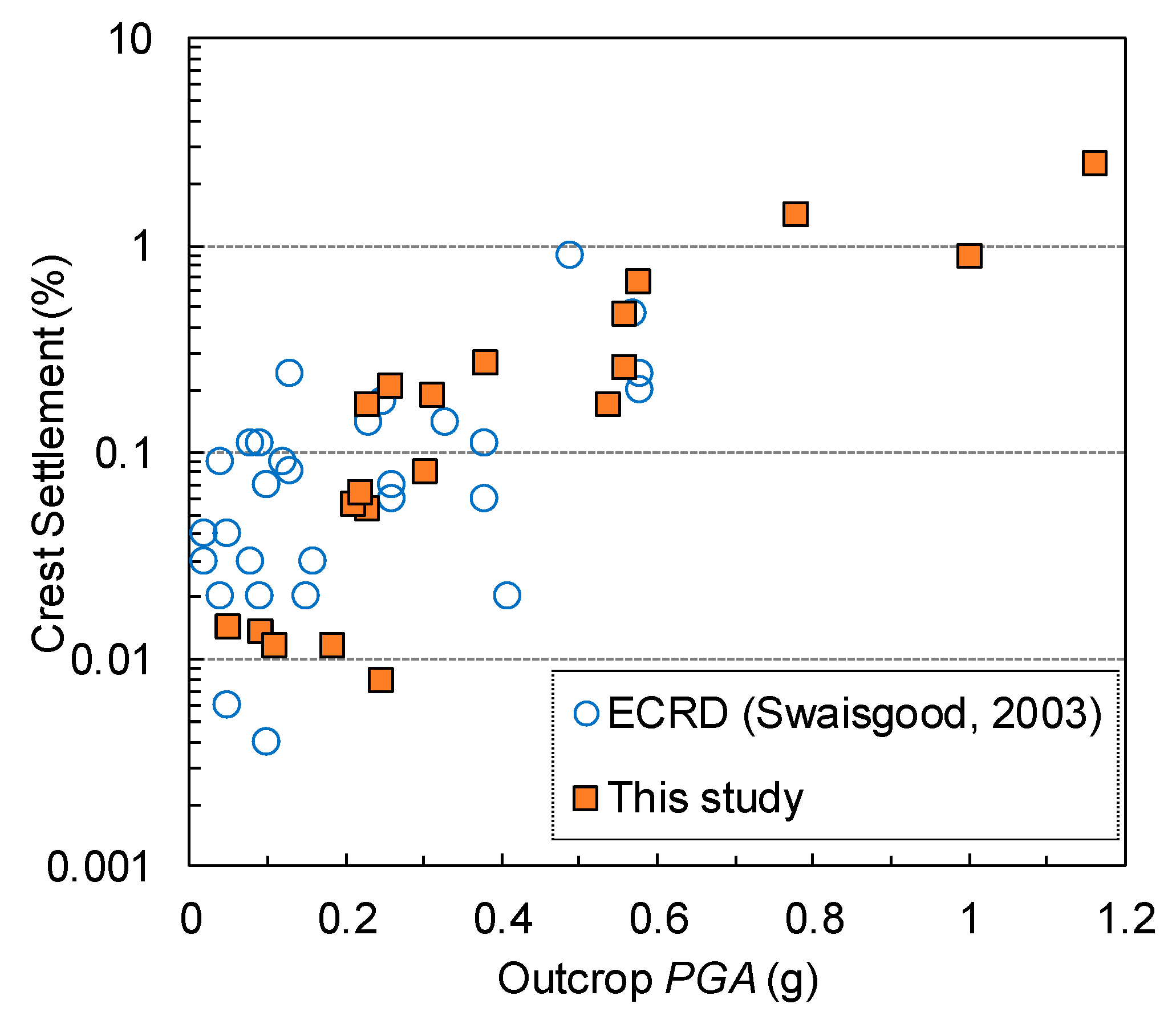
- The calculated settlements using twenty ground motions were compared with field recordings. The results compared well with the recordings for peak ground acceleration (PGA) exceeding 0.2 g. It was therefore further validated that the numerical model could be used in the seismic design.
- The settlements were also plotted against ground motion parameters, including the free-field surface PGA, peak ground velocity (PGV), Arias intensity (Ia), and moment magnitude (M). Predictive equations for the crest settlement were also presented. It was demonstrated that PGA provided a good estimate of the settlement. However, Ia provided the most favorable fit with the calculations. Therefore, using the primary parameter to predict the crest was recommended.
Author Contributions
Funding
Conflicts of Interest
References
- Swaisgood, J. Embankment dam deformations caused by earthquakes. In Proceedings of the 2003 Pacific Conference on Earthquake Engineering, Christchurch, New Zealand, 13–15 February 2003. [Google Scholar]
- Yang, X.-G.; Chi, S.-C. Seismic stability of earth-rock dams using finite element limit analysis. Soil Dyn. Earthq. Eng. 2014, 64, 1–10. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Kong, X.; Zou, D. Seismic fragility for high CFRDs based on deformation and damage index through incremental dynamic analysis. Soil Dyn. Earthq. Eng. 2018, 104, 432–436. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.; Wei, Y.; Liang, J.; Hu, J. Examining the seismic stress evolution in the face slab of concrete-faced rock-fill dams using dynamic centrifuge tests. Soil Dyn. Earthq. Eng. 2019, 123, 337–356. [Google Scholar] [CrossRef]
- Itasca Consulting Group. FLAC—Fast Lagrange Analysis of Continua; User Manual, Version7.0; Itasca Consulting Group: Minneapolis, MN, USA, 2011. [Google Scholar]
- Sawada, Y.; Takahashi, T. Study on the material properties and the earthquake behaviors of rockfill dam. In Proceedings of the 4th Japan Earthquake Engineering Symposium, Tokyo, Japan, 26–28 November 1975; pp. 695–702. [Google Scholar]
- Ha, I.S.; Kim, N.R.; Lim, J.Y. Estimation of Shear Wave Velocity of Earth Dam Materials Using Artificial Blasting Vibration Test. J. Korea Soc. Civ. Eng. 2013, 33, 619–629. [Google Scholar]
- Ha, I.-S. Estimation of shear wave velocity of earth dam materials using artificial blasting test. Soil Dyn. Earthq. Eng. 2013, 55, 120–129. [Google Scholar] [CrossRef]
- Lee, J.-H.; Ahn, J.-K.; Park, D. Prediction of seismic displacement of dry mountain slopes composed of a soft thin uniform layer. Soil Dyn. Earthq. Eng. 2015, 79, 5–16. [Google Scholar] [CrossRef]
- Callisto, L.; Ricci, C. Interpretation and back-analysis of the damage observed in a deep tunnel after the 2016 Norcia earthquake in Italy. Tunn. Undergr. Space Technol. 2019, 89, 238–248. [Google Scholar] [CrossRef]
- Lu, C.-C.; Hwang, J.-H. Implementation of the modified cross-section racking deformation method using explicit FDM program: A critical assessment. Tunn. Undergr. Space Technol. 2017, 68, 58–73. [Google Scholar] [CrossRef]
- Sanderson, S.T. Non-Linear Deformation Analysis of an Embankment Dam. Master’s Thesis, Portland State University, Portland, OR, USA, 18 June 2018. [Google Scholar]
- Aliberti, D.; Cascone, E.; Biondi, G. Seismic performance of the San Pietro dam. Procedia Eng. 2016, 158, 362–367. [Google Scholar] [CrossRef]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, August 2001. [Google Scholar]
- Chopra, A. Structural Dynamics: Theory and Applications to Earthquake Engineering, 2nd ed.; Prentice Hall: Bergen County, NJ, USA, 2001. [Google Scholar]
- Ziotopoulou, R.W.B.A.K. PM4Sand (Version 2): A Sand Plasticity Model for Earthquake Engineering Applications; Report No. UCD/CGM-12/01; University of California: Davis, CA, USA, 2012; p. 100. [Google Scholar]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar]
- Kim, M.-K.; Lee, S.-H.; Choo, Y.W.; Kim, D.-S. Seismic behaviors of earth-core and concrete-faced rock-fill dams by dynamic centrifuge tests. Soil Dyn. Earthq. Eng. 2011, 31, 1579–1593. [Google Scholar] [CrossRef]
- Ministry of Public Safety and Security (MPSS). Common Application of Seismic Design Criteria; Ministry of Public Safety and Security: Sejong, Korea, 2017. (In Korean)


| Layer | Unit Weight (kN/m3) | Friction Angle (o) | Cohesion (kPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Rockfill | 21 | 45 | 0 | 0.30 |
| Core | 20 | 27 | 32.5 | 0.35 |
| Foundation soil | 24 | 50 | - | 0.25 |
| Layer | Unit Weight (kN/m3) | Friction Angle (o) | Cohesion (kPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Rockfill | 21.09 | 40 | 2 | 0.30 |
| Core | 21 | 33 | 64 | 0.35 |
| No. | Earthquake Name | Station Name | PGA (g) | PGV (cm/s) | Magnitude, M |
|---|---|---|---|---|---|
| 1 | Nahanni, Canada | Nahanni Station #3 | 0.148 | 6.1 | 6.8 |
| 2 | Loma Gilroy, USA | Gilroy Array #2 | 0.17 | 14.2 | 6.9 |
| 3 | Whittier Narrow, USA | Rancho Palos Verdes | 0.186 | 4.6 | 6 |
| 4 | San Fernando, USA | Pacoima Dam | 0.209 | 18.9 | 6.6 |
| 5 | Northridge, USA | Beverly Hills | 0.217 | 9.8 | 6.7 |
| 6 | Kocaeli, Turkey | Arcelik | 0.218 | 17.7 | 7.4 |
| 7 | Landers, USA | Yermo Fire | 0.244 | 25.7 | 7.3 |
| 8 | Hector, USA | North Palm Spr. | 0.265 | 28.5 | 7.1 |
| 9 | Loma Gilroy, USA | Gilroy Array #3 | 0.357 | 28.6 | 6.9 |
| 10 | Parkfield, USA | Parkfield–Cholame | 0.357 | 21.5 | 6.1 |
| 11 | El Centro, USA | Imperial Valley Distr. | 0.4 | 37.8 | 6.9 |
| 12 | Mammoth Lakes, USA | Long Valley Dam | 0.43 | 23.5 | 6.3 |
| 13 | Duzce, Turkey | Bolu | 0.727 | 56.4 | 7.1 |
| 14 | Kobe, Japan | Nishi–Akashi | 0.509 | 37.3 | 6.9 |
| 15 | Tabas, Iran | Mhud–Bajestan | 0.899 | 55 | 7.8 |
| 16 | Chi-chi, Taiwan | Taiwan | 0.057 | 2.3 | 6.2 |
| 17 | Tottori, Japan | HYG007 | 0.035 | 1.2 | 6.61 |
| 18 | Northridge, USA | Vasquez Rocks Park | 0.15 | 11.1 | 6.69 |
| 19 | Morgan Hill, USA | Gilroy Array | 0.069 | 2.7 | 6.19 |
| 20 | San Fernando, USA | Pasadena, Old Seismo Lab | 0.095 | 5.8 | 6.61 |
| 1-Parameter Model | 2-Parameter Model | 3-Parameter Model | 4-Parameter Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GM1 | PGA | PGV | Ia | M | PGA | PGA | PGA | PGA | PGA | PGA | PGA |
| GM2 | PGV | Ia | M | PGV | M | PGV | PGV | ||||
| GM3 | M | Ia | Ia | Ia | |||||||
| GM4 | M | ||||||||||
| 1.803 | 2.16 | 0.127 | 0.774 | 1.735 | 1.606 | 0.845 | 2.197 | 0.748 | 1.616 | 2.15 | |
| 0.089 | 0.264 | 0.079 | −0.847 | 0.203 | −1.25 | −2.422 | |||||
| 0.339 | 0.075 | 0.094 | 0.1 | ||||||||
| 0.396 | |||||||||||
| 0.773 | 0.71 | 0.334 | 0.82 | 0.774 | 0.803 | 0.873 | 0.811 | 0.89 | 0.891 | 0.941 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.-C.; Nguyen, V.-Q.; Kim, J.-H.; Park, D.; Choi, B.-H. Estimation of Seismically-Induced Crest Settlement of Earth Core Rockfill Dams. Appl. Sci. 2019, 9, 4343. https://doi.org/10.3390/app9204343
Park K-C, Nguyen V-Q, Kim J-H, Park D, Choi B-H. Estimation of Seismically-Induced Crest Settlement of Earth Core Rockfill Dams. Applied Sciences. 2019; 9(20):4343. https://doi.org/10.3390/app9204343
Chicago/Turabian StylePark, Ki-Chun, Van-Quang Nguyen, Jung-Hyun Kim, Duhee Park, and Byoung-Han Choi. 2019. "Estimation of Seismically-Induced Crest Settlement of Earth Core Rockfill Dams" Applied Sciences 9, no. 20: 4343. https://doi.org/10.3390/app9204343
APA StylePark, K.-C., Nguyen, V.-Q., Kim, J.-H., Park, D., & Choi, B.-H. (2019). Estimation of Seismically-Induced Crest Settlement of Earth Core Rockfill Dams. Applied Sciences, 9(20), 4343. https://doi.org/10.3390/app9204343





