Impact of Different Nose Lengths on Flow-Field Structure around a High-Speed Train
Abstract
1. Introduction
2. Methodology
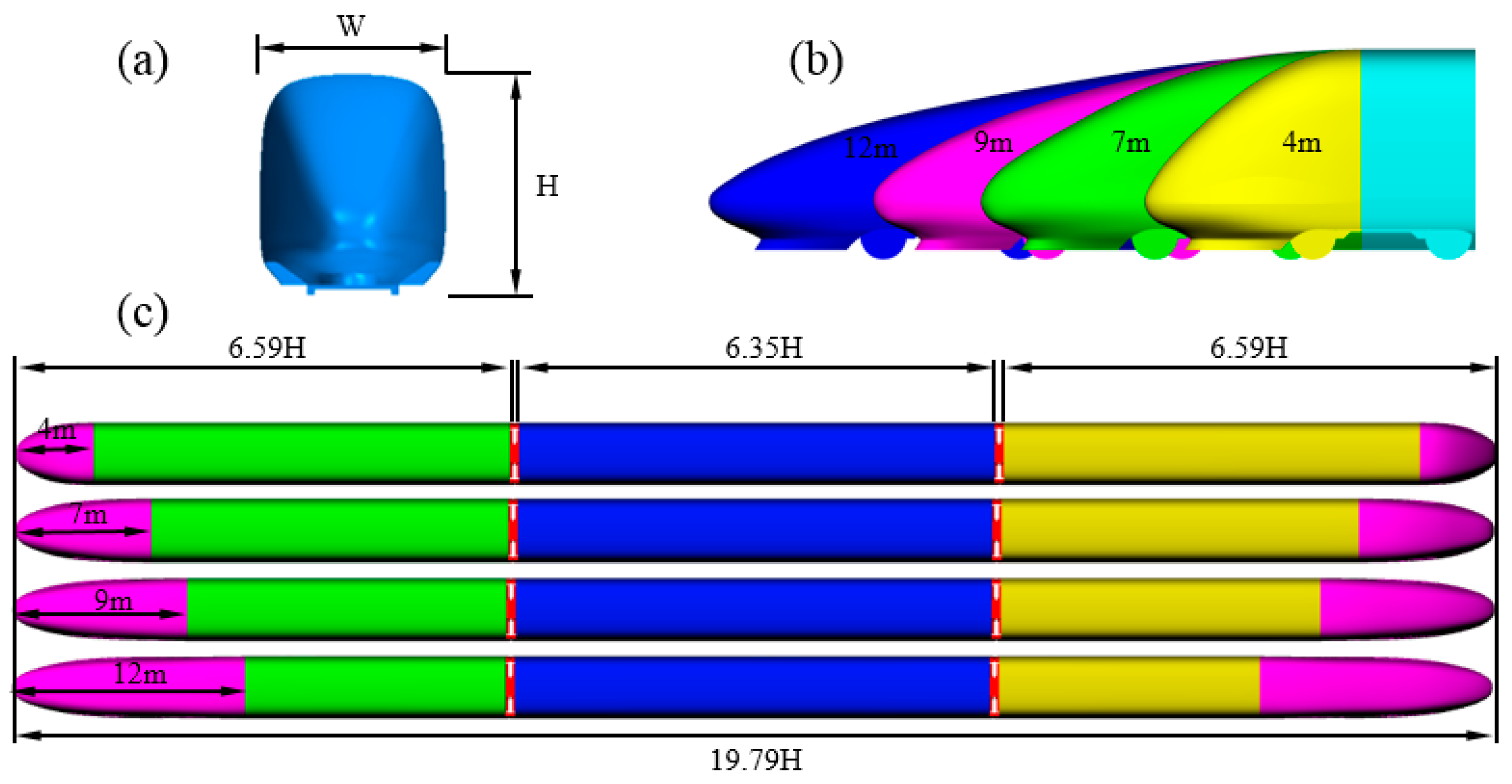
2.1. Model Geometry
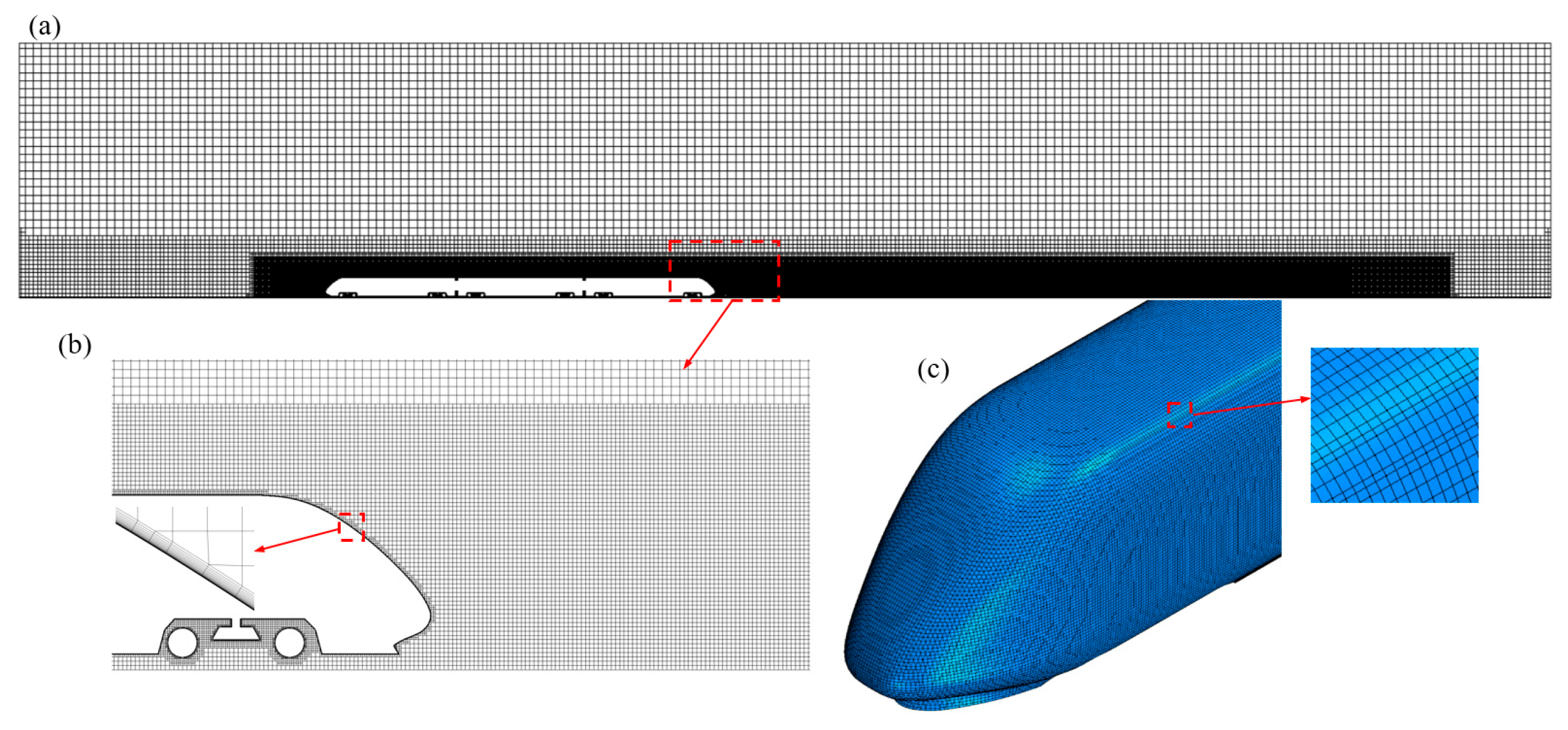
2.2. Computational Domain and Boundary Conditions
2.3. Numerical Method
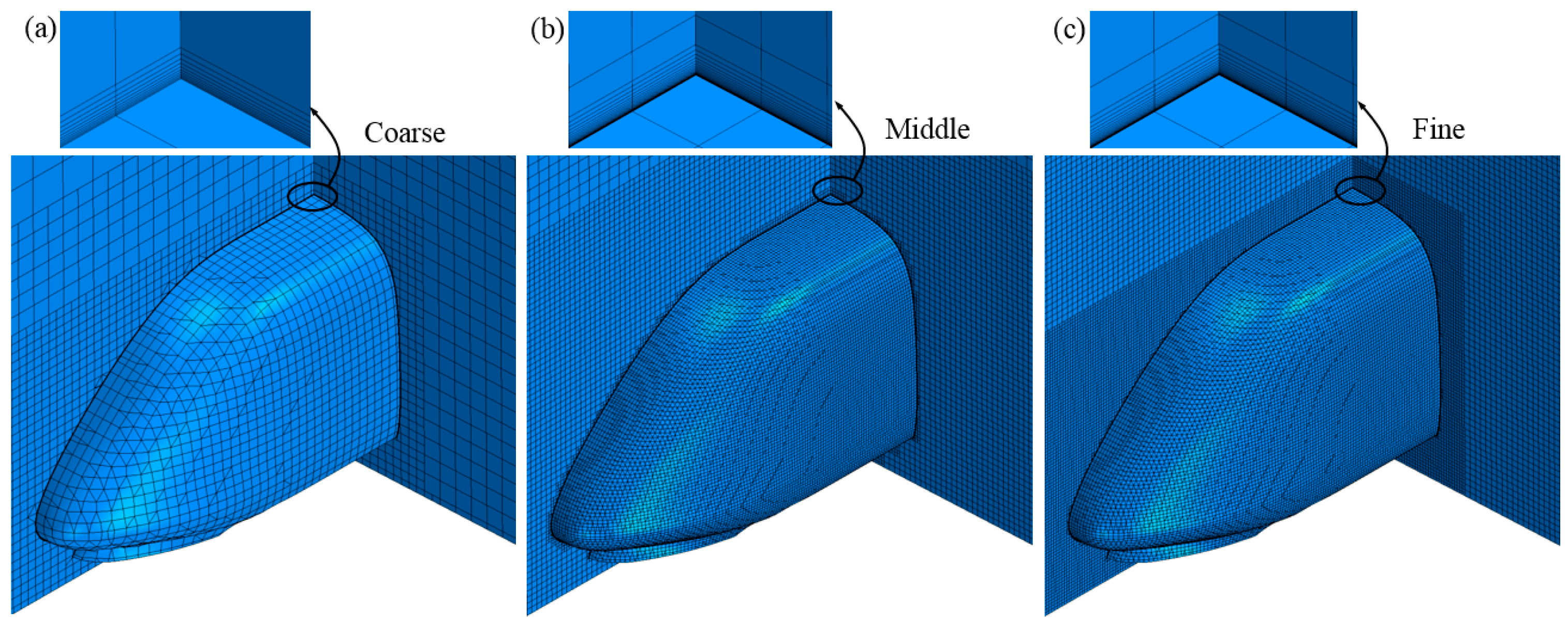
2.4. Grid Strategy
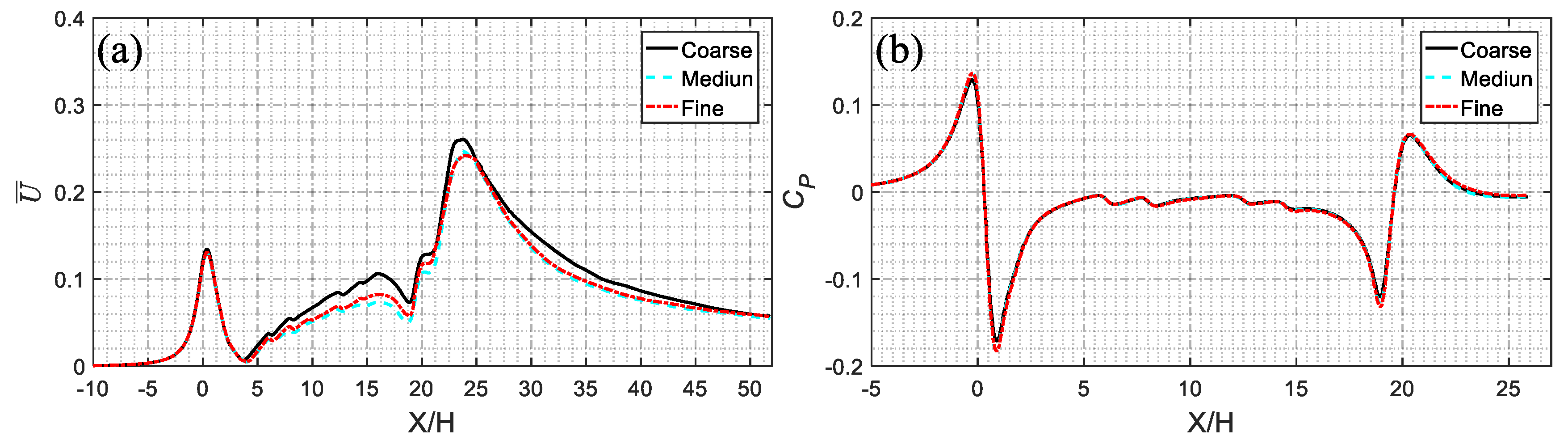
2.5. Grid Sensitivity
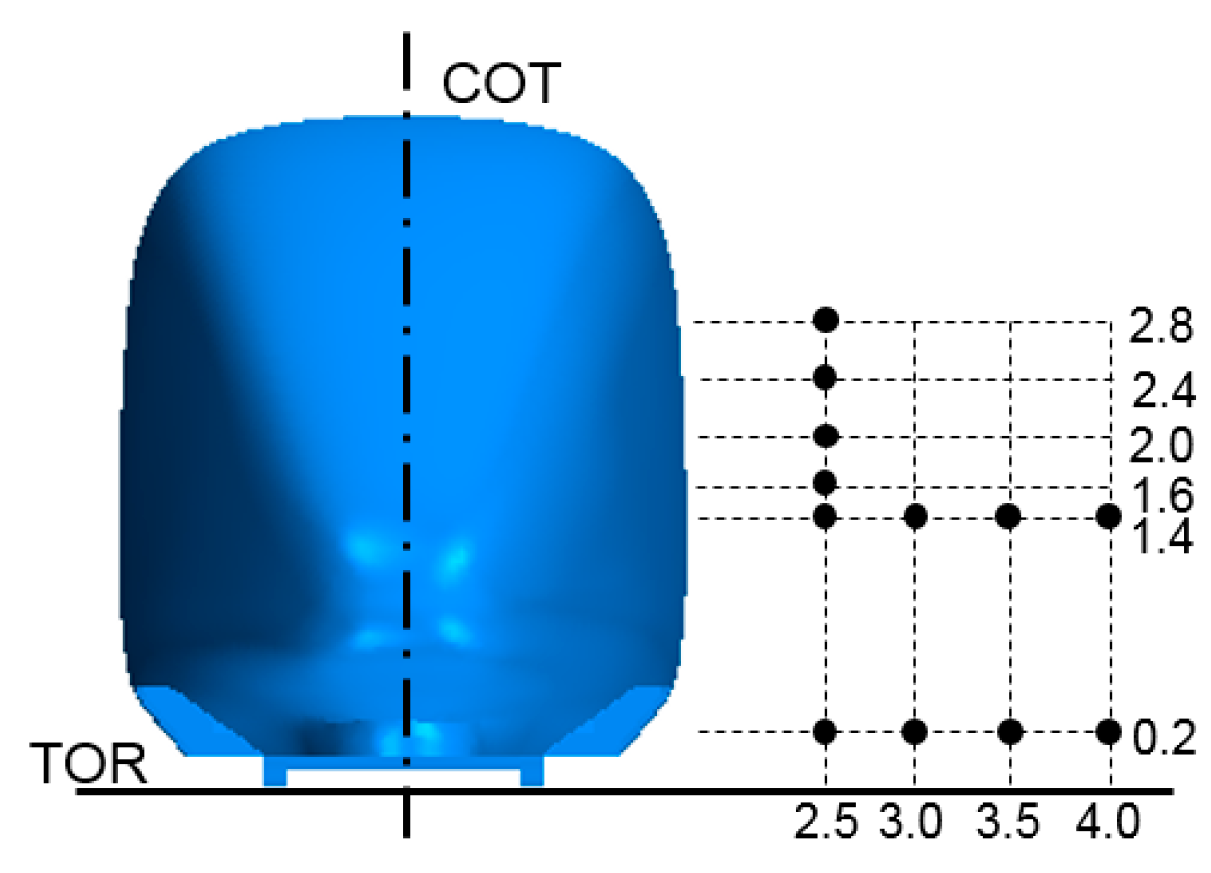
2.6. Data Processing
3. Algorithm Validation
4. Results and Analysis
4.1. Aerodynamic Force Coefficient
4.2. Time-Averaged Flow
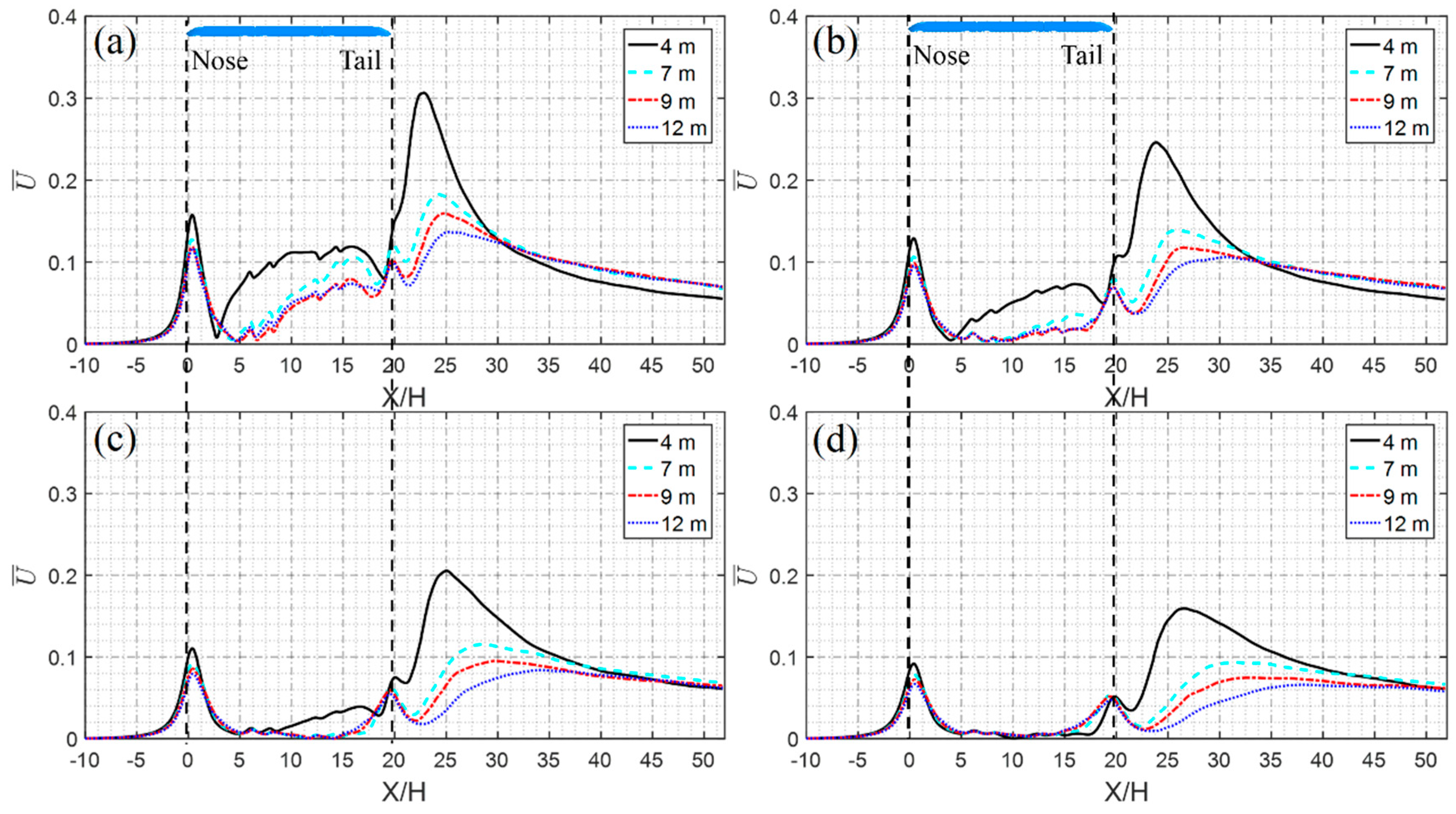
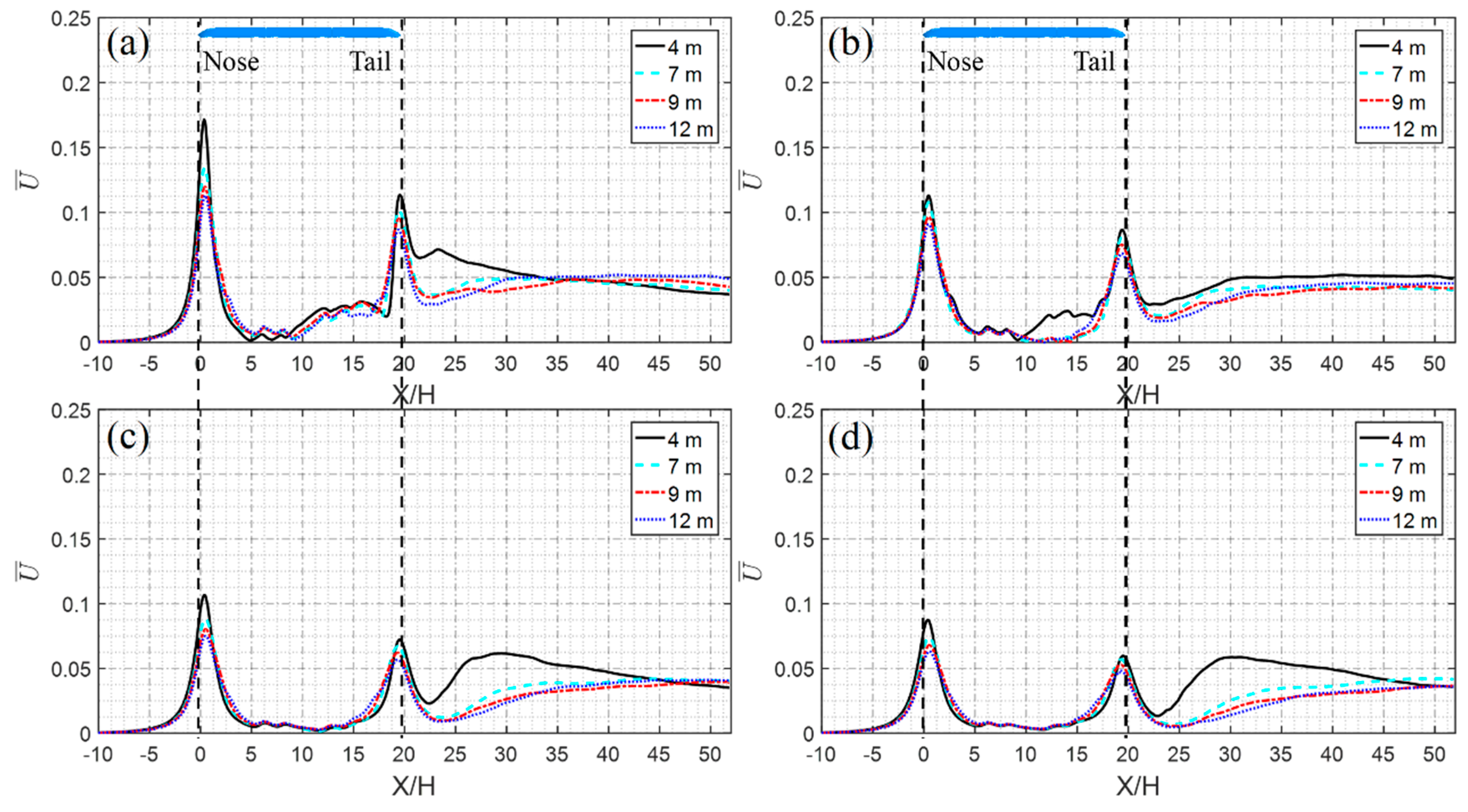
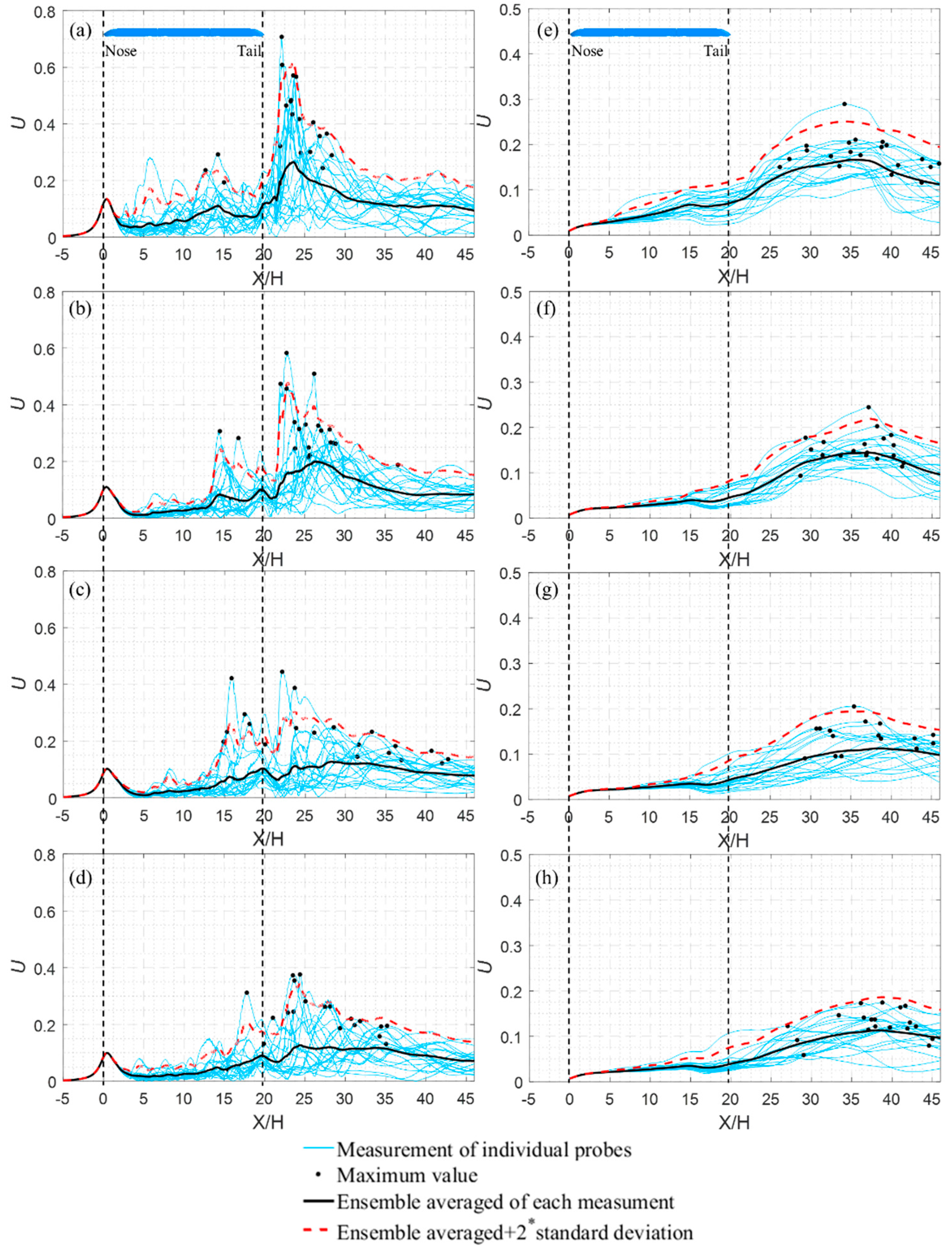
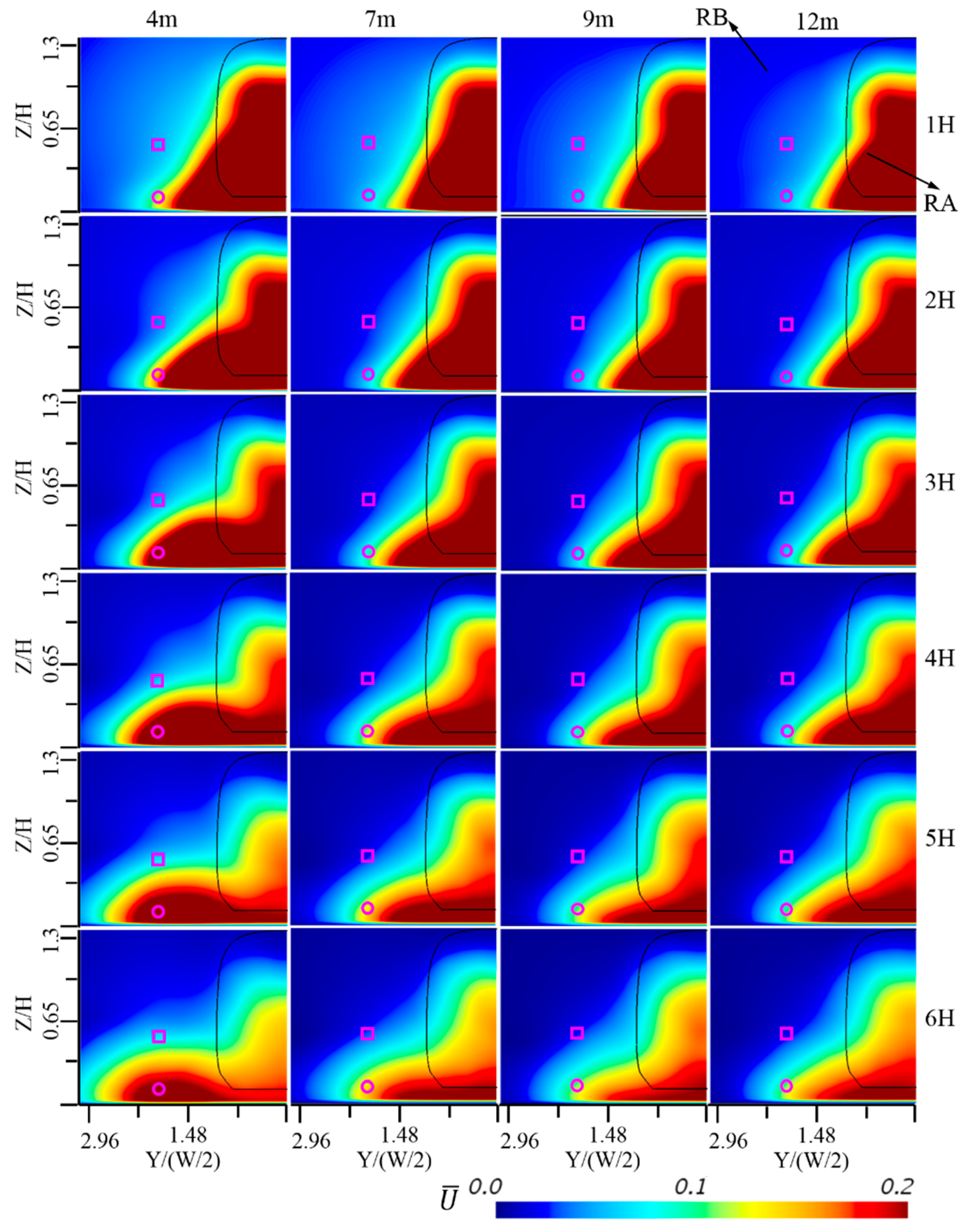
4.2.1. Time-Averaged Slipstream Velocity
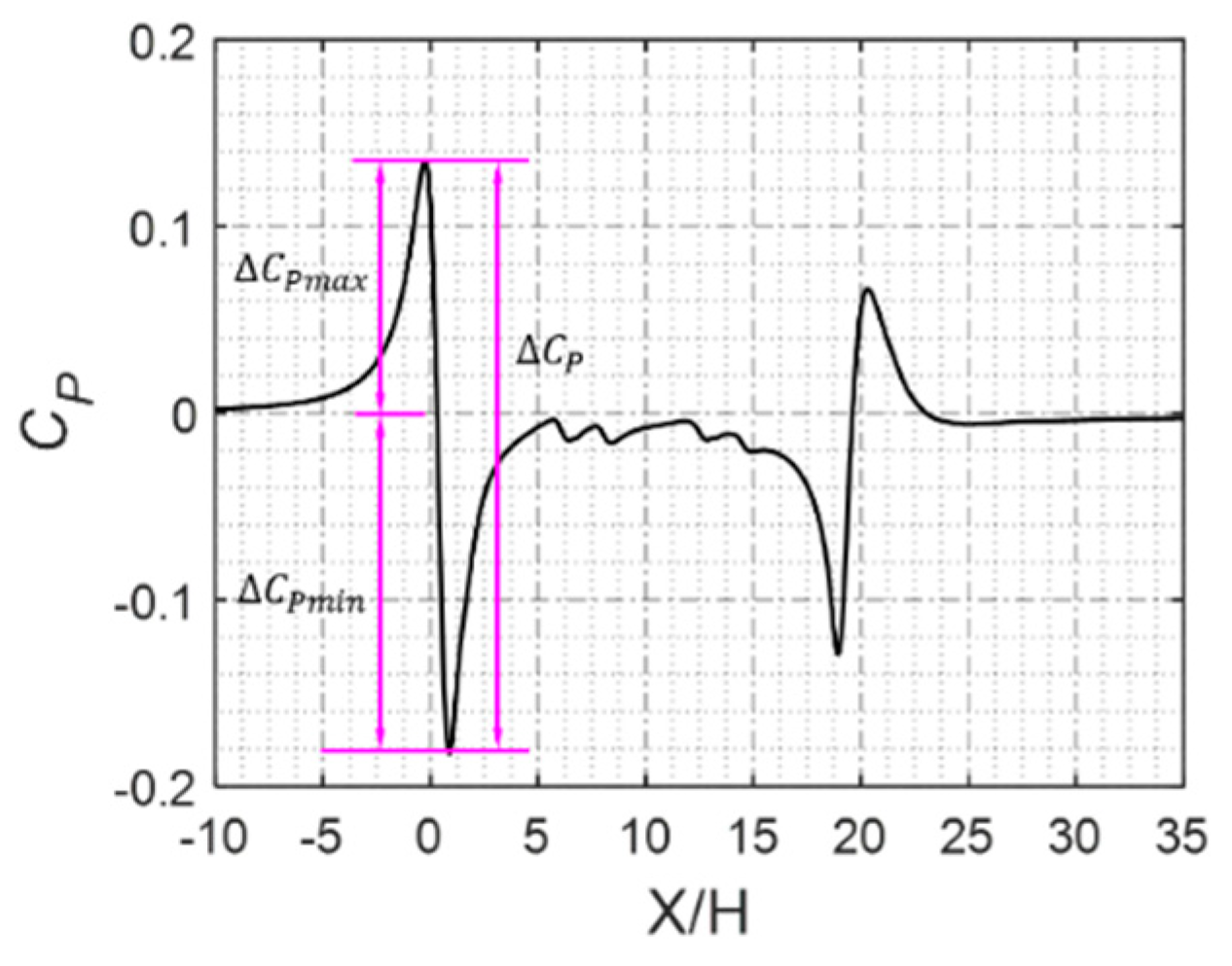
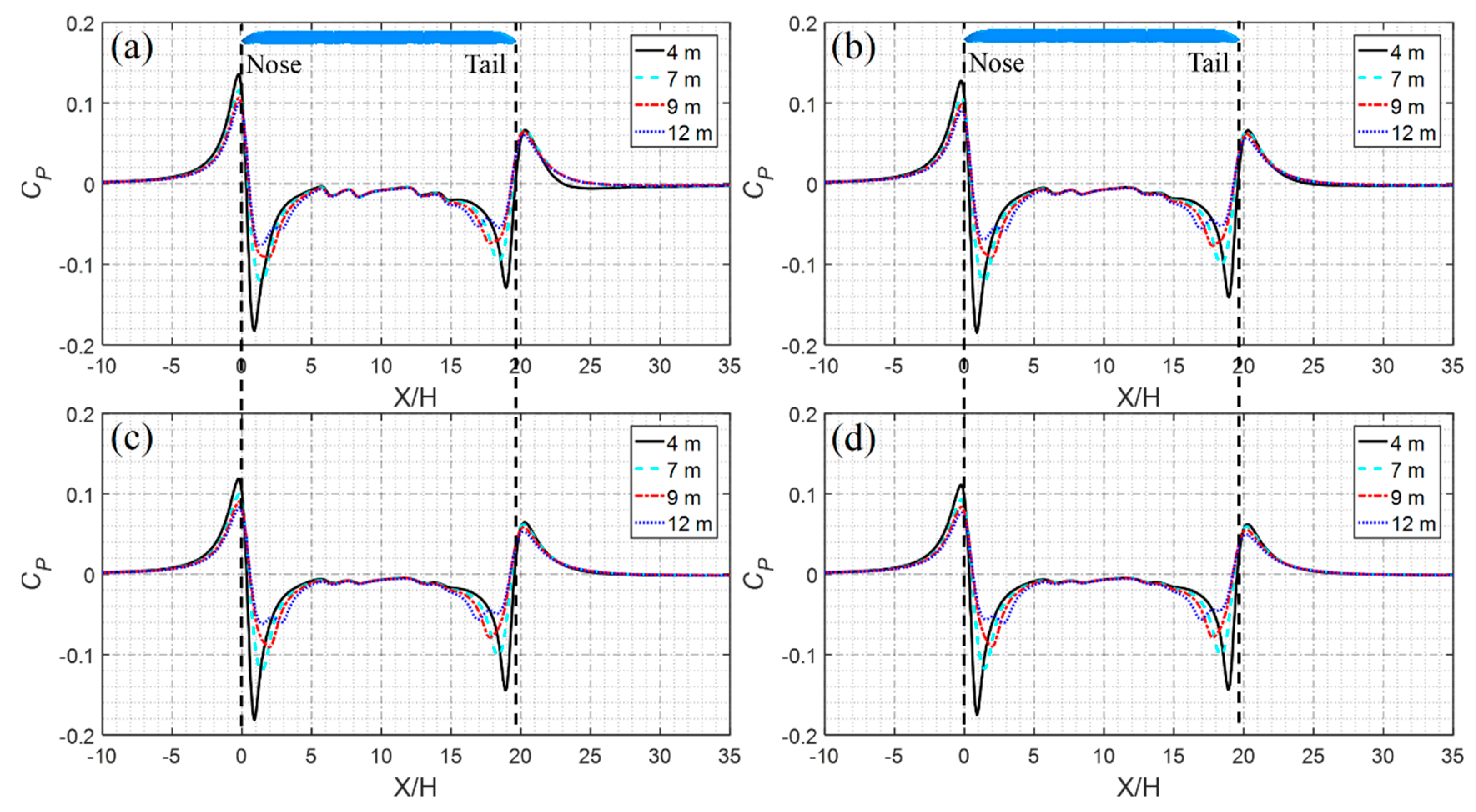
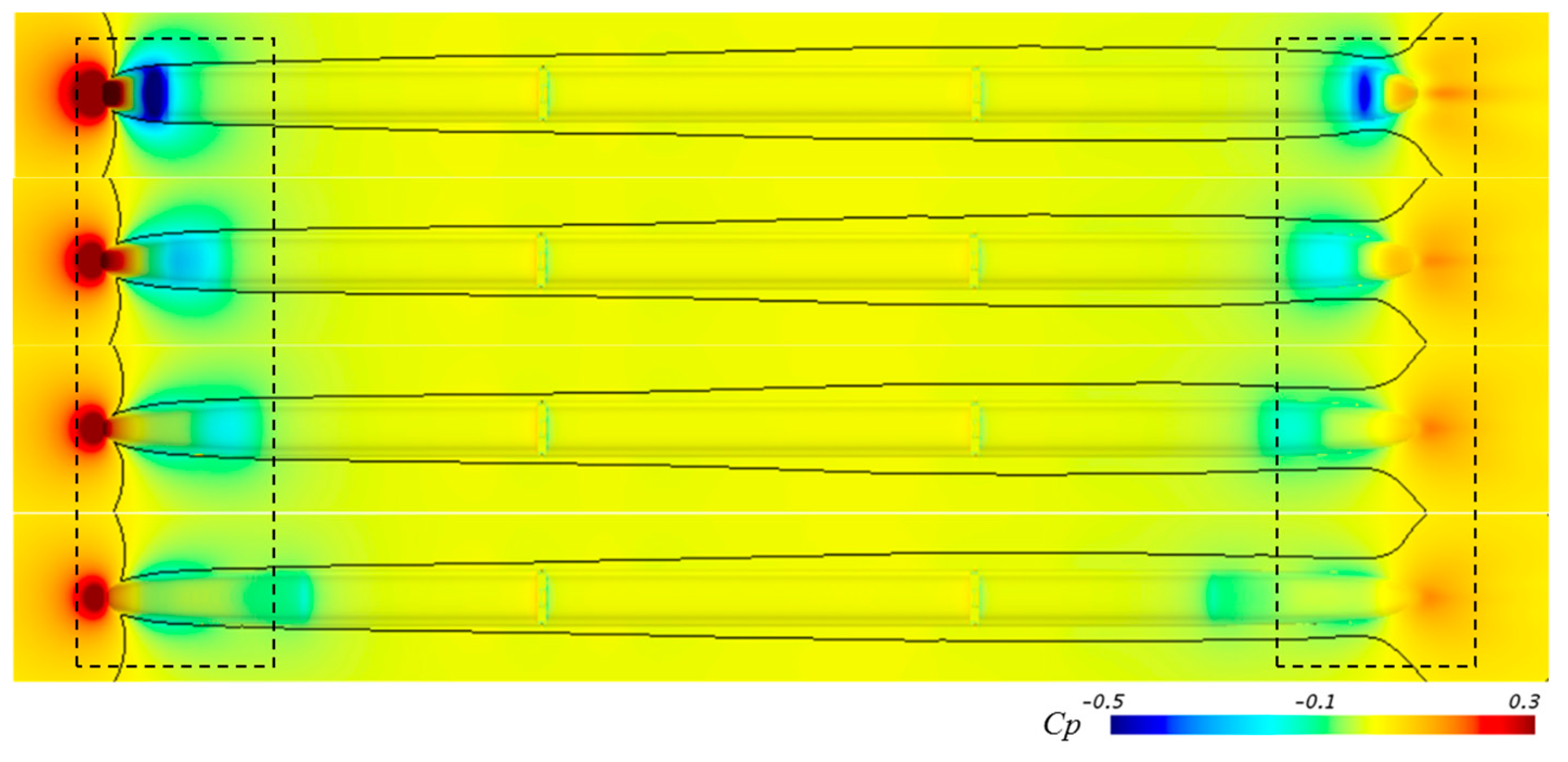
4.2.2. Time-Averaged Pressure
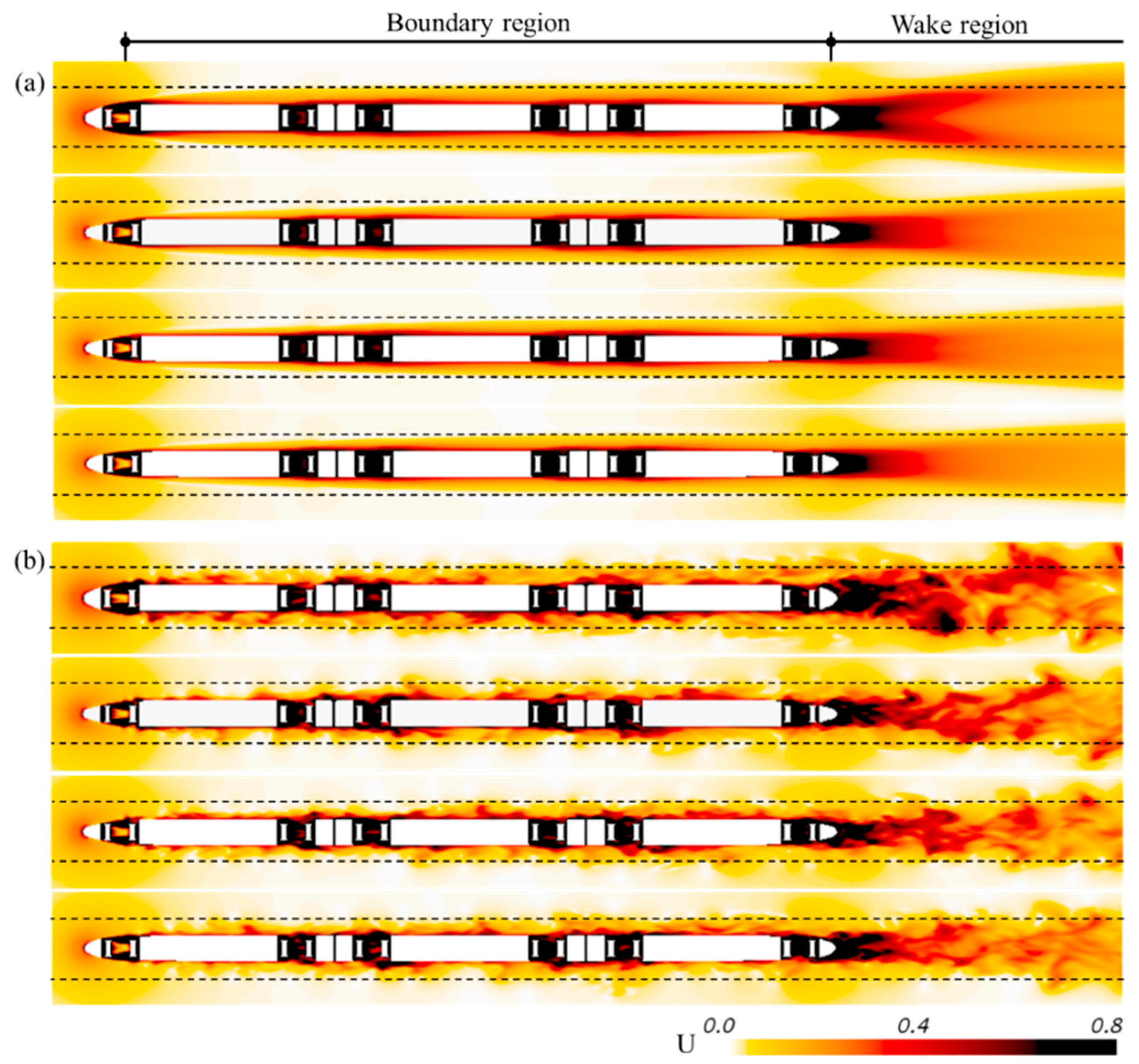
4.3. Instantaneous Flow
4.4. Flow-Field Visualization
4.4.1. Slipstream and Pressure
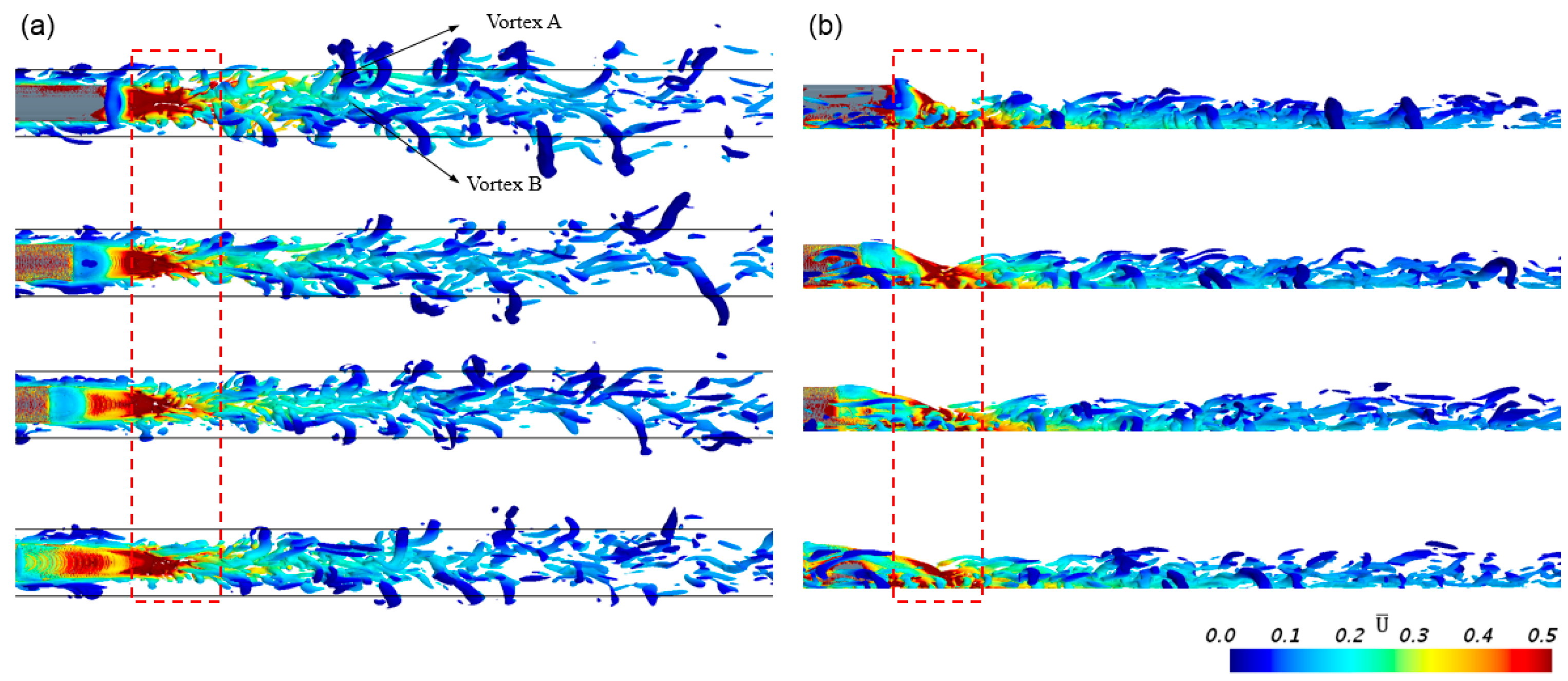
4.4.2. Wake Flows
5. Conclusions
- (1)
- When the nose length increases from 4 to 7 m, the drag and lift force coefficients change obviously, in which the head car drag coefficient decreases by 17.6%, the tail car drag coefficient decreases by 29.3%, the head car lift force coefficient decreases by 15.8%, and the tail car lift force coefficient decreases by 75.7%. When the nose length increased from 7 to 12 m, the difference between drag and lift force coefficients was not obvious.
- (2)
- With increasing nose length, the peak value of time-averaged U in the same position decreases. When the nose length increases from 4 to 12 m, the peak value of time-averaged U in the trackside position decreases by 57%, and the peak value of time-averaged U in the platform position decreases by 19.5%. With increasing distance from the COT, the peak value of time-averaged U decreases. The maximum U value of the trackside position appears in the near wake, while the maximum U value of the platform position appears in the nose region. The slipstream is usually evaluated by characteristic velocity U2σ. In this study, the characteristic velocity U2σ of the trackside position is studied. It is found that the characteristic velocity U2σ decreases with increasing nose length. When the nose length increases from 4 to 12 m, the U2σ value decreases by 28.1%.
- (3)
- For the measuring points of trains with different nose lengths in different positions, the maximum value of ΔCP appears in the nose region. With increasing nose length, the ΔCP values of the measuring points at different positions decrease continuously. For ΔCP max, |ΔCP min|, and ΔCP at a height of 1.6 m from the TOR, the nose length increases from 4 to 12 m, which decreases by 26.5%, 58.5%, and 44.8%, respectively, with increasing nose length.
- (4)
- The nose length also has a great impact on the wake flow of the train. When the nose length is 4 m, the lateral fluctuation of instantaneous U and wake vortex is more intense, and the lateral fluctuation is also wider and more intense. When the nose length is longer, the shedding distance of the wake vortex is longer in the longitudinal direction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tian, H.Q. Train Aerodynamics, 1st ed.; China Railway Publishing House: Beijing, China, 2007; pp. 214–215. [Google Scholar]
- Zhang, J.; Wang, J.B.; Wang, Q.X.; Xiong, X.H.; Gao, G.J. A study of the influence of bogie cut outs’ angles on the aerodynamic performance of a high speed train. J. Wind Eng. Ind. Aerodyn. 2018, 175, 153–168. [Google Scholar] [CrossRef]
- Niu, J.Q.; Wang, Y.M.; Zhang, L.; Yuan, Y.P. Numerical analysis of aerodynamic characteristics of high-speed train with different train nose lengths. Int. J. Heat Mass. Trans. 2018, 127, 188–199. [Google Scholar] [CrossRef]
- Krajnović, S. Shape optimization of high-speed trains for improved aerodynamic performance. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transp. 2009, 223, 439–451. [Google Scholar] [CrossRef]
- Yao, S.B.; Guo, D.L.; Sun, Z.X.; Chen, D.W.; Yang, G.W. Parametric design and optimization of high speed train nose. Optim. Eng. 2016, 17, 605–630. [Google Scholar] [CrossRef]
- Vytla, V.V. Multidisciplinary Optimization Framework for High Speed Train using Robust Hybrid GA-PSO Algo. Ph.D. Thesis, Wright State University, Dayton, OH, USA, 2011. [Google Scholar]
- Howe, M.S. The genetically optimized tunnel entrance hood. J. Fluid Struct. 2007, 23, 1231–1250. [Google Scholar] [CrossRef]
- Muñoz-Paniagua, J.; García, J.; Crespo, A. Genetically aerodynamic optimization of the nose shape of a high-speed train entering a tunnel. J. Wind Eng. Ind. Aerodyn. 2014, 130, 48–61. [Google Scholar] [CrossRef]
- Jakubek, D.; Wagner, C. Shape optimization of train head cars using adjointbased computational fluid dynamics. In Proceedings of the First International Conference on Railway Technology: Research, Development and Maintenance, Las Palmas de Gran Canaria, Spain, 18–20 April 2012; Pombo, J., Ed.; Civil-Comp Press: Stirlingshire, UK, 2012. [Google Scholar]
- Munoz-Paniagua, J.; García, J.; Crespo, A.; Laspougeas, F. Aerodynamic Optimization of the Nose Shape of a Train Using the Adjoint Method. J. Appl. Fluid Mech. 2015, 8, 601–612. [Google Scholar] [CrossRef]
- Hemida, H.; Krajnović, S. LES study of the influence of the nose shape and yaw angles on flow structures around trains. J. Wind Eng. Ind. Aerodyn. 2010, 98, 34–46. [Google Scholar] [CrossRef]
- Chen, Z.W.; Liu, T.H.; Jiang, Z.H.; Guo, Z.J.; Zhang, J. Comparative analysis of the effect of different nose lengths on train aerodynamic performance under crosswind. J. Fluid Struct. 2018, 78, 69–85. [Google Scholar] [CrossRef]
- Xie, T.Z.; Liu, T.H.; Chen, Z.W.; Li, W.H.; Chen, X.D.; Zhou, X.S. Assessment and analysis on variation of trackside pressure induced by trains with different head shapes. J. Chin. Railw. Soc. 2019, 41, 41–49. (In Chinese) [Google Scholar]
- Cheli, F.; Ripamonti, F.; Rocchi, D.; Tomasini, G. Aerodynamic behaviour investigation of the new EMUV250 train to cross wind. J. Wind Eng. Ind. Aerodyn. 2010, 98, 189–201. [Google Scholar] [CrossRef]
- Bell, J.R.; Burton, D.; Thompson, M.C.; Herbst, A.H.; Sheridan, J. The effect of tail geometry on the slipstream and unsteady wake structure of high-speed trains. Exp. Therm. Fluid Sci. 2017, 83, 215–230. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Zhou, D. Wind tunnel experiment on aerodynamic characteristic of streamline head of high speed train with different head shapes. J. Cent. South Univ. 2013, 44, 2603–2608. [Google Scholar]
- Bell, J.R.; Burton, D.; Thompson, M.; Herbst, A.; Sheridan, J. Wind tunnel analysis of the slipstream and wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2014, 134, 122–138. [Google Scholar] [CrossRef]
- Meng, S.; Zhou, D.; Wang, Z. Moving model analysis on the transient pressure and slipstream caused by a metro train passing through a tunnel. PLoS ONE 2019, 14, e0222151. [Google Scholar] [CrossRef]
- Flynn, D.; Hemida, H.; Baker, C.J. On the effect of crosswinds on the slipstream of a freight train and associated effects. J. Wind Eng. Ind. Aerodyn. 2016, 156, 14–28. [Google Scholar] [CrossRef]
- Rocchi, D.; Tomasini, G.; Schito, P.; Somaschini, C. Wind effects induced by high speed train pass-by in open air. J. Wind Eng. Ind. Aerodyn. 2018, 173, 279–288. [Google Scholar] [CrossRef]
- Wang, S.B.; Bell, J.R.; Burton, D.; Herbst, A.H.; Sheridan, J.; Thompson, M.C. The performance of different turbulence models (URANS, SAS and DES) for predicting high-speed train slipstream. J. Wind Eng. Ind. Aerodyn. 2017, 164, 46–57. [Google Scholar] [CrossRef]
- Wang, S.B.; Burton, D.; Herbst, A.H.; Sheridan, J.; Thompson, M.C. The effect of the ground condition on high-speed train slipstream. J. Wind Eng. Ind. Aerodyn. 2018, 172, 230–243. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.F.; Shan, X.H.; Yang, Z.G.; Li, Q.L. Effects of ground configurations on the slipstream and near wake of a high-speed train. J. Wind Eng. Ind. Aerodyn. 2017, 168, 177–189. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A.K. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comp. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- CEN European Standard. Part 6: Requirements and Test Procedures for Aerodynamics on Open Track. In Railway Applications-Aerodynamics; CEN EN 14067-6; BSI Standards Limited: London, UK, 2010. [Google Scholar]
- CEN European Standard. Part 4: Requirements and Test Procedures for Aerodynamics on Open Track. In Railway Applications-Aerodynamics; CEN EN 14067-4; BSI Standards Limited: London, UK, 2013; Available online: https://infostore.saiglobal.com/preview/is/en/2013/i.s.en14067-4-2013.pdf?sku=1694040 (accessed on 28 October 2019).
- Baker, C.J.; Jones, J.; Lopez-Calleja, F.; Munday, J. Measurements of the cross wind forces on trains. J. Wind Eng. Ind. Aerodyn. 2004, 92, 547–563. [Google Scholar] [CrossRef]
- Niu, J.Q.; Zhou, D.; Liu, T.H.; Liang, X.F. Numerical simulation of aerodynamic performance of a couple multiple units high-speed train. Veh. Syst. Dyn. 2017, 55, 681–703. [Google Scholar] [CrossRef]
- Niu, J.Q.; Zhou, D.; Liang, X.F. Numerical simulation of the effects of obstacle deflectors on the aerodynamic performance of stationary high-speed trains at two yaw angles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transp. 2018, 232, 913–927. [Google Scholar] [CrossRef]
- Baker, C.J. The flow around high speed trains. J. Wind Eng. Ind. Aerodyn. 2010, 98, 277–298. [Google Scholar] [CrossRef]
- CEN European Standard. Part 4: Requirements and Test Procedures for Aerodynamics on Open Track. In Railway Applications-Aerodynamics; EN 14067-4:2005+A1; BSI Standards Limited: London, UK, 2009; Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwi435acpb7lAhWDxIsBHSM4CKYQFjAAegQIBRAC&url=http%3A%2F%2Fgost-snip.su%2Fdownload%2Fbds_en_14067_4_2005_a1_2009_railway_applications_aerodynamic&usg=AOvVaw34ZkFIe61QJ8LqDEWd8fR- (accessed on 28 October 2019).
- European Union Agency for Railways. Commission Regulation (EU) No 1302/2014 concerning a technical specification for interoperability relating to the ‘rolling stock — locomotives and passenger rolling stock’ subsystem of the rail system. Off. J. Eur. Union 2014, 356, 288–290. [Google Scholar]
- Chen, G.; Li, X.B.; Liu, Z.; Zhou, D.; Wang, Z.; Liang, X.F.; Krajnovic, S. Dynamic analysis of the effect of nose length on train aerodynamic performance. J. Wind Eng. Ind. Aerodyn. 2018, 184, 198–208. [Google Scholar] [CrossRef]
- Zhang, J.; He, K.; Xiong, X.H.; Wang, J.B.; Gao, G.J. Numerical Simulation with a DES Approach for a HighSpeed Train Subjected to the Crosswind. J. Appl. Fluid Mech. 2017, 10, 1329–1342. [Google Scholar]
- Munoz-Paniagua, J.; García, J.; Lehugeur, B. Evaluation of RANS, SAS and IDDES models for the simulation of the flow around a high-speed train subjected to crosswind. J. Wind Eng. Ind. Aerodyn. 2017, 171, 50–66. [Google Scholar] [CrossRef]
- Yao, Y.F.; Sun, Z.X.; Yang, G.W.; Liu, W.; Prasert, P. Analysis of Aerodynamic Noise Characteristics of High-Speed Train Pantograph with Different Installation Bases. Appl. Sci. 2019, 9, 2332. [Google Scholar] [CrossRef]





| Case | Cx | Cz | ||
|---|---|---|---|---|
| Head Car | Tail Car | Head Car | Tail Car | |
| Numerical simulation | 0.1371 | 0.1195 | −0.0251 | 0.0587 |
| Wind tunnel test | 0.1446 | 0.1144 | −0.0184 | 0.0709 |
| Error (%) | 5.19 | 4.46 | 36.41 | −17.21 |
| Height (m) | Length (m) | ΔCP max | ΔCP min | ΔCP | Height (m) | ΔCP max | ΔCP min | ΔCP |
|---|---|---|---|---|---|---|---|---|
| 1.6 | 4 | 0.136 | −0.183 | 0.319 | 2.4 | 0.119 | −0.182 | 0.301 |
| 7 | 0.115 | −0.121 | 0.236 | 0.099 | −0.12 | 0.219 | ||
| 9 | 0.107 | −0.091 | 0.198 | 0.09 | −0.091 | 0.181 | ||
| 12 | 0.1 | −0.076 | 0.176 | 0.083 | −0.062 | 0.145 | ||
| 2.0 | 4 | 0.128 | −0.185 | 0.313 | 2.8 | 0.111 | −0.175 | 0.286 |
| 7 | 0.107 | −0.122 | 0.229 | 0.093 | −0.117 | 0.21 | ||
| 9 | 0.098 | −0.091 | 0.189 | 0.084 | −0.09 | 0.174 | ||
| 12 | 0.091 | −0.069 | 0.16 | 0.076 | −0.06 | 0.136 |
| Length (m) | Without 1s MA | With 1s MA | ||||
|---|---|---|---|---|---|---|
| σ | σ | |||||
| 4 | 0.2643 | 0.1762 | 0.6167 | 0.1665 | 0.0471 | 0.2607 |
| 7 | 0.1995 | 0.1579 | 0.5189 | 0.1447 | 0.0372 | 0.2191 |
| 9 | 0.1275 | 0.1085 | 0.3445 | 0.113 | 0.0441 | 0.2009 |
| 12 | 0.127 | 0.1015 | 0.33 | 0.1127 | 0.0372 | 0.1874 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, G.; Zhou, D.; Chen, Z. Impact of Different Nose Lengths on Flow-Field Structure around a High-Speed Train. Appl. Sci. 2019, 9, 4573. https://doi.org/10.3390/app9214573
Li X, Chen G, Zhou D, Chen Z. Impact of Different Nose Lengths on Flow-Field Structure around a High-Speed Train. Applied Sciences. 2019; 9(21):4573. https://doi.org/10.3390/app9214573
Chicago/Turabian StyleLi, Xianli, Guang Chen, Dan Zhou, and Zhengwei Chen. 2019. "Impact of Different Nose Lengths on Flow-Field Structure around a High-Speed Train" Applied Sciences 9, no. 21: 4573. https://doi.org/10.3390/app9214573
APA StyleLi, X., Chen, G., Zhou, D., & Chen, Z. (2019). Impact of Different Nose Lengths on Flow-Field Structure around a High-Speed Train. Applied Sciences, 9(21), 4573. https://doi.org/10.3390/app9214573





