Development of a Comprehensive Model for the Coulombic Efficiency and Capacity Fade of LiFePO4 Batteries under Different Aging Conditions
Abstract
1. Introduction
2. Experimental Setup and Procedures
2.1. Experimental Process
2.2. Coulombic Efficiency Analysis of a Battery under Different Temperatures and Discharge C Rates
2.3. Capacity Fade Analysis of a Battery under Different Temperatures and Discharge Rates for 400 Cycles
2.4. Parameter Analysis and Comparison
3. Comprehensive Model Development
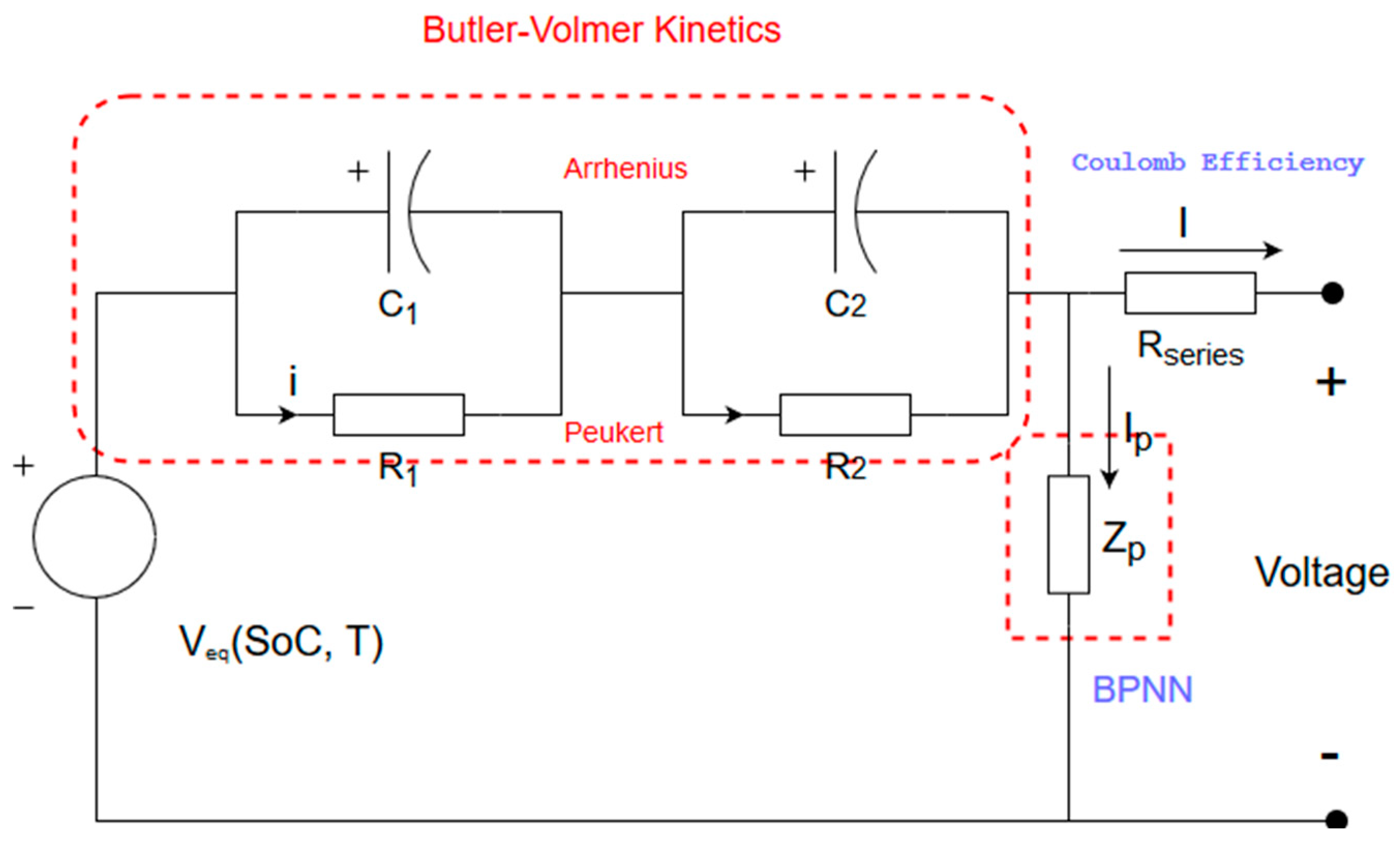
3.1. Thevenin Equivalent Circuit Model
3.2. Butler–Volmer Equation
3.3. Arrhenius and Peukert Laws
4. Results
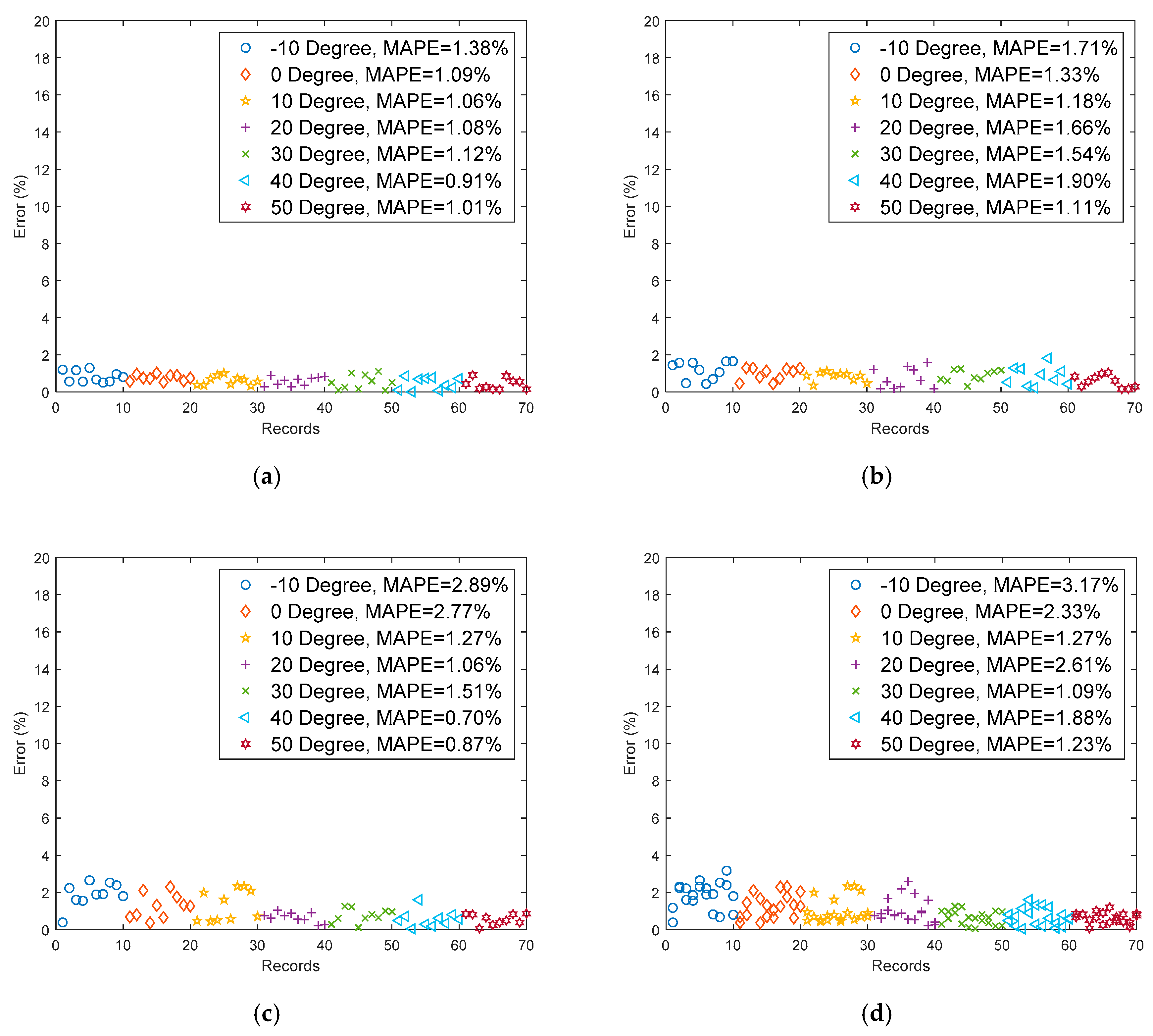
4.1. Analysis and Modeling with the Comprehensive Model
4.2. Using Artificial Neural Networks to Estimate Remaining Capacity
4.3. Establishing the Comprehensive Model
5. Discussions and Verification
6. Conclusions
Funding
Conflicts of Interest
References
- Kurzweil, P.; Brandt, K. Secondary batteries–lithium rechargeable systems| Overview. In Encyclopedia of Electrochemical Power Sources; Newnes: Oxford, UK, 2009; pp. 1–26. [Google Scholar]
- Garche, J.; Dyer, C.K.; Moseley, P.T.; Ogumi, Z.; Rand, D.A.; Scrosati, B. Encyclopedia of Electrochemical Power Sources; Newnes: Oxford, UK, 2013. [Google Scholar]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.J.J.E. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Miao, Y.; Hynan, P.; von Jouanne, A.; Yokochi, A.J.E. Current Li-Ion Battery Technologies in Electric Vehicles and Opportunities for Advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Bai, P.; Cogswell, D.A.; Bazant, M.Z. Suppression of phase separation in LiFePO(4) nanoparticles during battery discharge. Nano Lett. 2011, 11, 4890–4896. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.L. A new battery model for use with battery energy storage systems and electric vehicles power systems. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; Volume 1, pp. 470–475. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Dargaville, S.; Farrell, T.W. Predicting Active Material Utilization in LiFePO4 Electrodes Using a Multiscale Mathematical Model. J. Electrochem. Soc. 2010, 157, A830–A840. [Google Scholar] [CrossRef]
- Kuo, T.J.; Lee, K.Y.; Huang, C.K.; Chen, J.H.; Chiu, W.L.; Huang, C.F.; Wu, S.D. State of charge modeling of lithium-ion batteries using dual exponential functions. J. Power Sources 2016, 315, 331–338. [Google Scholar] [CrossRef]
- Sun, S.; Guan, T.; Shen, B.; Leng, K.; Gao, Y.; Cheng, X.; Yin, G. Changes of Degradation Mechanisms of LiFePO 4 /Graphite Batteries Cycled at Different Ambient Temperatures. Electrochim. Acta 2017, 237, 248–258. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Tang, Y.; Li, R.; Liang, G.; Sham, T.K.; Sun, X. Surface aging at olivine LiFePO4: A direct visual observation of iron dissolution and the protection role of nano-carbon coating. J. Mater. Chem. A 2013, 1, 1579–1586. [Google Scholar] [CrossRef]
- Chang, W.; Kim, S.J.; Park, I.T.; Cho, B.W.; Chung, K.Y.; Shin, H.C. Low temperature performance of LiFePO4 cathode material for Li-ion batteries. J. Alloys Compd. 2013, 563, 249–253. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. A new approach toward improved low temperature performance of Li-ion battery. Electrochem. Commun. 2002, 4, 928–932. [Google Scholar] [CrossRef]
- Abraham, D.P.; Heaton, J.R.; Kang, S.H.; Dees, D.W.; Jansen, A.N. Investigating the Low-Temperature Impedance Increase of Lithium-Ion Cells. J. Electrochem. Soc. 2008, 155, A41. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle aging studies of lithium nickel manganese cobalt oxide-based batteries using electrochemical impedance spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; González, M. Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule. J. Power Sources 2017, 356, 36–46. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries—A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Agubra, V.; Fergus, J.J.M. Lithium ion battery anode aging mechanisms. Materials 2013, 6, 1310–1325. [Google Scholar] [CrossRef]
- Hendricks, C.; Williard, N.; Mathew, S.; Pecht, M. A failure modes, mechanisms, and effects analysis (FMMEA) of lithium-ion batteries. J. Power Sources 2015, 297, 113–120. [Google Scholar] [CrossRef]
- Song, W.; Chen, M.; Bai, F.; Lin, S.; Chen, Y.; Feng, Z. Non-uniform effect on the thermal/aging performance of Lithium-ion pouch battery. Appl. Therm. Eng. 2018, 128, 1165–1174. [Google Scholar] [CrossRef]
- Yao, X.Y.; Pecht, M.G. Tab Design and Failures in Cylindrical Li-ion Batteries. IEEE Access 2019, 7, 24082–24095. [Google Scholar] [CrossRef]
- Ko, S.T.; Lee, J.; Ahn, J.H.; Lee, B.K.J.E. Innovative Modeling Approach for Li-Ion Battery Packs Considering Intrinsic Cell Unbalances and Packaging Elements. Energies 2019, 12, 356. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Zhang, X.; Yang, C.; Xu, N.; Xia, B. Study of the storage performance of a Li-ion cell at elevated temperature. Electrochim. Acta 2010, 55, 927–934. [Google Scholar] [CrossRef]
- Guan, T.; Sun, S.; Gao, Y.; Du, C.; Zuo, P.; Cui, Y.; Zhang, L.; Yin, G. The effect of elevated temperature on the accelerated aging of LiCoO 2 /mesocarbon microbeads batteries. Appl. Energy 2016, 177, 1–10. [Google Scholar] [CrossRef]
- Kassem, M.; Delacourt, C. Postmortem analysis of calendar-aged graphite/LiFePO4 cells. J. Power Sources 2013, 235, 159–171. [Google Scholar] [CrossRef]
- Smith, A.J.; Burns, J.C.; Trussler, S.; Dahn, J.R. Precision Measurements of the Coulombic Efficiency of Lithium-Ion Batteries and of Electrode Materials for Lithium-Ion Batteries. J. Electrochem. Soc. 2010, 157, A196–A202. [Google Scholar] [CrossRef]
- Bond, T.M.; Burns, J.C.; Stevens, D.A.; Dahn, H.M.; Dahn, J.R. Improving Precision and Accuracy in Coulombic Efficiency Measurements of Li-Ion Batteries. J. Electrochem. Soc. 2013, 160, A521–A527. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Online estimation of the state of charge of a lithium ion cell. J. Power Sources 2006, 161, 1346–1355. [Google Scholar] [CrossRef]
- Huang, S.C.; Tseng, K.H.; Liang, J.W.; Chang, C.L.; Pecht, M.G. An Online SOC and SOH Estimation Model for Lithium-Ion Batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Berrueta, A.; Urtasun, A.; Ursúa, A.; Sanchis, P. A comprehensive model for lithium-ion batteries: From the physical principles to an electrical model. Energy 2018, 144, 286–300. [Google Scholar] [CrossRef]
- Tippmann, S.; Walper, D.; Balboa, L.; Spier, B.; Bessler, W.G. Low-temperature charging of lithium-ion cells part I: Electrochemical modeling and experimental investigation of degradation behavior. J. Power Sources 2014, 252, 305–316. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Geers, M.G.D. Governing equations for a two-scale analysis of Li-ion battery cells. Int. J. Solids Struct 2015, 59, 90–109. [Google Scholar] [CrossRef]
- Gu, L.; Xiao, D.; Hu, Y.S.; Li, H.; Ikuhara, Y. Atomic-scale structure evolution in a quasi-equilibrated electrochemical process of electrode materials for rechargeable batteries. Adv. Mater. 2015, 27, 2134–2149. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation Phenomena in Lithium-Ion-Insertion Cells. J. Electrochem. Soc. 1994, 141, 982–990. [Google Scholar] [CrossRef]
- Singh, M.; Kaiser, J.; Hahn, H. Effect of Porosity on the Thick Electrodes for High Energy Density Lithium Ion Batteries for Stationary Applications. Batteries 2016, 2, 35. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M.A. Advancements in OCV Measurement and Analysis for Lithium-Ion Batteries. IEEE Trans. Energy Convers. 2013, 28, 675–681. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C.; Gualous, H. Aging prediction and state of charge estimation of a LiFePO 4 battery using input time-delayed neural networks. Electr. Power Syst. Res. 2017, 146, 189–197. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N.J.E. A Data-Driven Predictive Prognostic Model for Lithium-Ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Wang, Y.J.; Yang, D.; Zhang, X.; Chen, Z.H. Probability based remaining capacity estimation using data-driven and neural network model. J. Power Sources 2016, 315, 199–208. [Google Scholar] [CrossRef]
- Dong, G.Z.; Zhang, X.; Zhang, C.B.; Chen, Z.H. A method for state of energy estimation of lithium-ion batteries based on neural network model. Energy 2015, 90, 879–888. [Google Scholar] [CrossRef]
- Hu, X.S.; Li, S.B.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wang, Q.K.; He, Y.J.; Shen, J.N.; Ma, Z.F.; Zhong, G.B. A unified modeling framework for lithium-ion batteries: An artificial neural network based thermal coupled equivalent circuit model approach. Energy 2017, 138, 118–132. [Google Scholar] [CrossRef]
- Jokar, A.; Désilets, M.; Lacroix, M.; Zaghib, K. Mesoscopic modeling and parameter estimation of a lithium-ion battery based on LiFePO4/graphite. J. Power Sources 2018, 379, 84–90. [Google Scholar] [CrossRef]
- Saxena, S.; Kang, M.; Xing, Y.; Pecht, M. Anomaly Detection During Lithium-ion Battery Qualification Testing. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–6. [Google Scholar]
- Diao, W.; Saxena, S.; Han, B.; Pecht, M. Algorithm to Determine the Knee Point on Capacity Fade Curves of Lithium-Ion Cells. Energies 2019, 12. [Google Scholar] [CrossRef]
- Razavi-Far, R.; Farajzadeh-Zanjani, M.; Chakrabarti, S.; Saif, M. Data-driven prognostic techniques for estimation of the remaining useful life of lithium-ion batteries. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–8. [Google Scholar]
- Jiang, J.; Gao, Y.; Zhang, C.; Zhang, W.; Jiang, Y. Lifetime Rapid Evaluation Method for Lithium-Ion Battery with Li(NiMnCo)O2 Cathode. J. Electrochem. Soc. 2019, 166, A1070–A1081. [Google Scholar] [CrossRef]
- Kennedy, B.; Patterson, D.; Camilleri, S. Use of lithium-ion batteries in electric vehicles. J. Power Sources 2000, 90, 156–162. [Google Scholar] [CrossRef]
- Zhang, T.; Fuchs, B.; Secchiaroli, M.; Wohlfahrt-Mehrens, M.; Dsoke, S. Electrochemical behavior and stability of a commercial activated carbon in various organic electrolyte combinations containing Li-salts. Electrochim. Acta 2016, 218, 163–173. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Wang, C.Y.; Tang, X.D. Cycling degradation of an automotive LiFePO4 lithium-ion battery. J. Power Sources 2011, 196, 1513–1520. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Shim, J.; Striebel, K.A. Cycling performance of low-cost lithium ion batteries with natural graphite and LiFePO4. J. Power Sources 2003, 119, 955–958. [Google Scholar] [CrossRef]
- Tran, N.T.; Khan, A.; Nguyen, T.T.; Kim, D.W.; Choi, W.J.E. SOC Estimation of Multiple Lithium-Ion Battery Cells in a Module Using a Nonlinear State Observer and Online Parameter Estimation. Energies 2018, 11, 1620. [Google Scholar] [CrossRef]
- Huangfu, Y.; Xu, J.; Zhao, D.; Liu, Y.; Gao, F.J.E. A novel battery state of charge estimation method based on a super-twisting sliding mode observer. Energies 2018, 11, 1211. [Google Scholar] [CrossRef]
- Heubner, C.; Schneider, M.; Michaelis, A. Investigation of charge transfer kinetics of Li-Intercalation in LiFePO4. J. Power Sources 2015, 288, 115–120. [Google Scholar] [CrossRef]
- Bai, P.; Bazant, M.Z. Charge transfer kinetics at the solid-solid interface in porous electrodes. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Hess, A.; Roode-Gutzmer, Q.; Heubner, C.; Schneider, M.; Michaelis, A.; Bobeth, M.; Cuniberti, G. Determination of state of charge-dependent asymmetric Butler–Volmer kinetics for LixCoO2 electrode using GITT measurements. J. Power Sources 2015, 299, 156–161. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, J.; Shi, W.; Ma, Z.; Wang, L.Y.; Guo, H. Butler–Volmer-Equation-Based Electrical Model for High-Power Lithium Titanate Batteries Used in Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 7557–7568. [Google Scholar] [CrossRef]
- O’Malley, R.; Liu, L.; Depcik, C. Comparative study of various cathodes for lithium ion batteries using an enhanced Peukert capacity model. J. Power Sources 2018, 396, 621–631. [Google Scholar] [CrossRef]
- Kalogirou, S. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Golden, R.M.; Golden, R. Mathematical Methods for Neural Network Analysis and Design; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Fang, K.; Mu, D.; Chen, S.; Wu, B.; Wu, F. A prediction model based on artificial neural network for surface temperature simulation of nickel–metal hydride battery during charging. J. Power Sources 2012, 208, 378–382. [Google Scholar] [CrossRef]
- Miller, W.T.; Werbos, P.J.; Sutton, R.S. Neural Networks for Control; MIT press: Cambridge, MA, USA, 1995. [Google Scholar]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper sardeliver, NJ, USA, 1994. [Google Scholar]

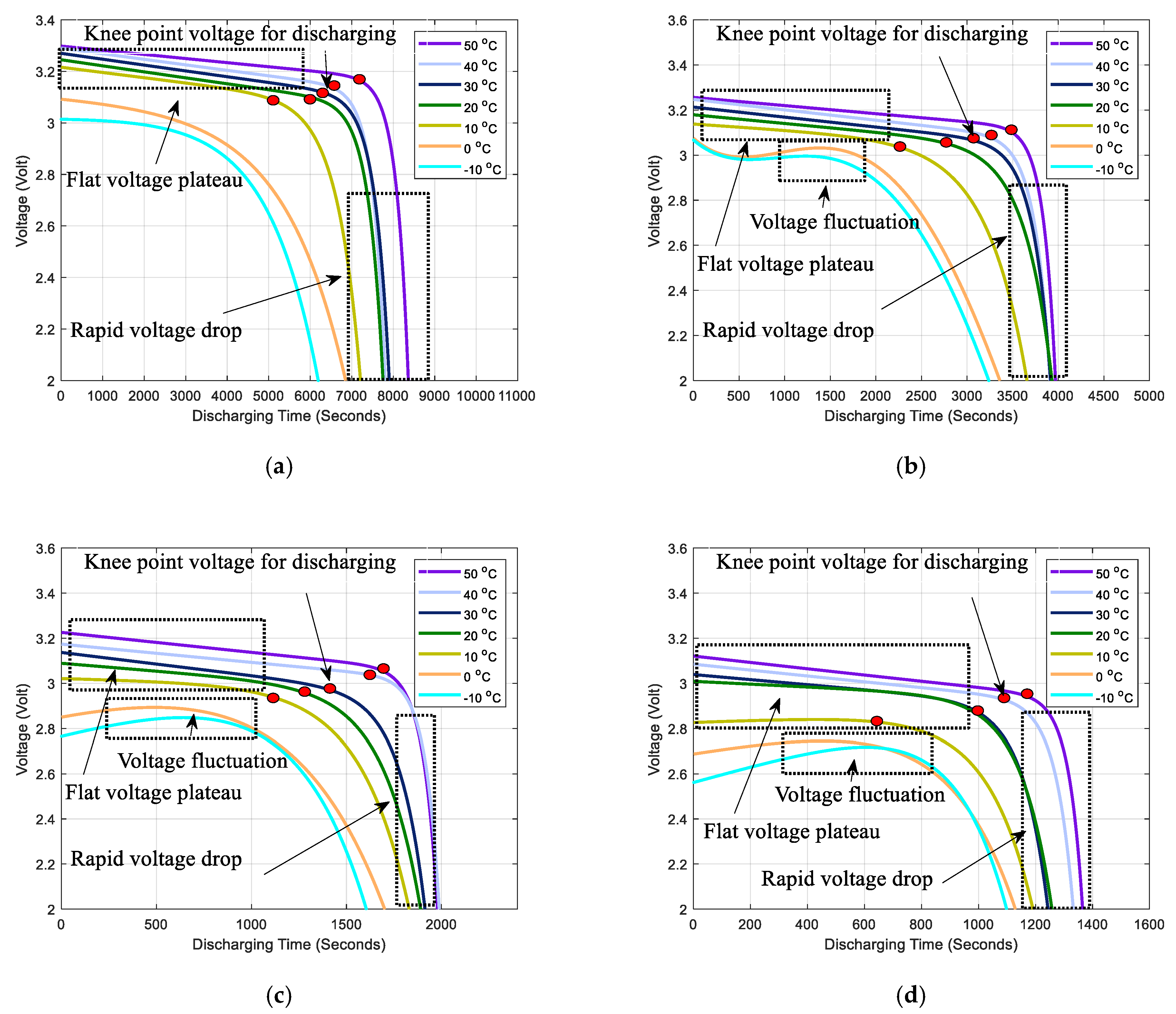
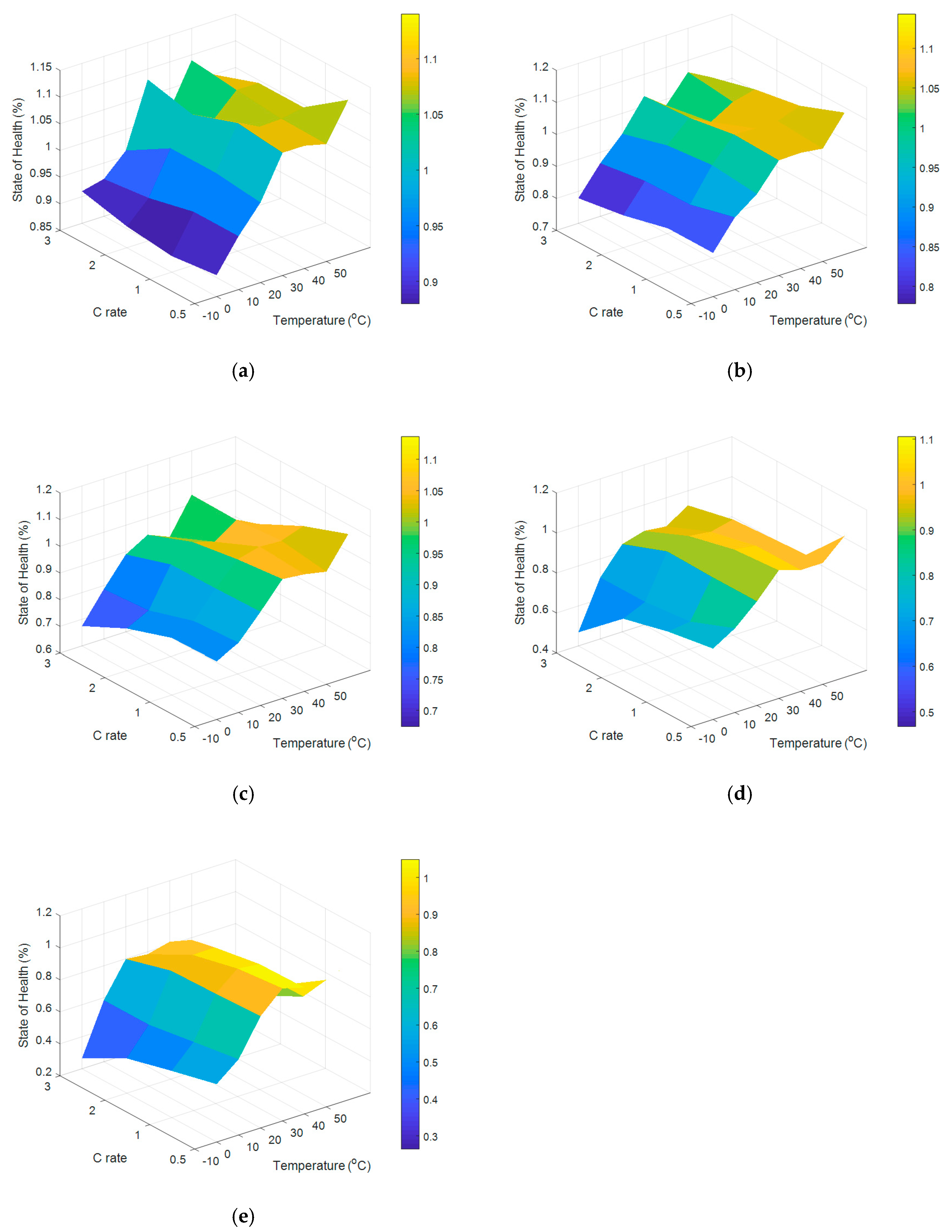

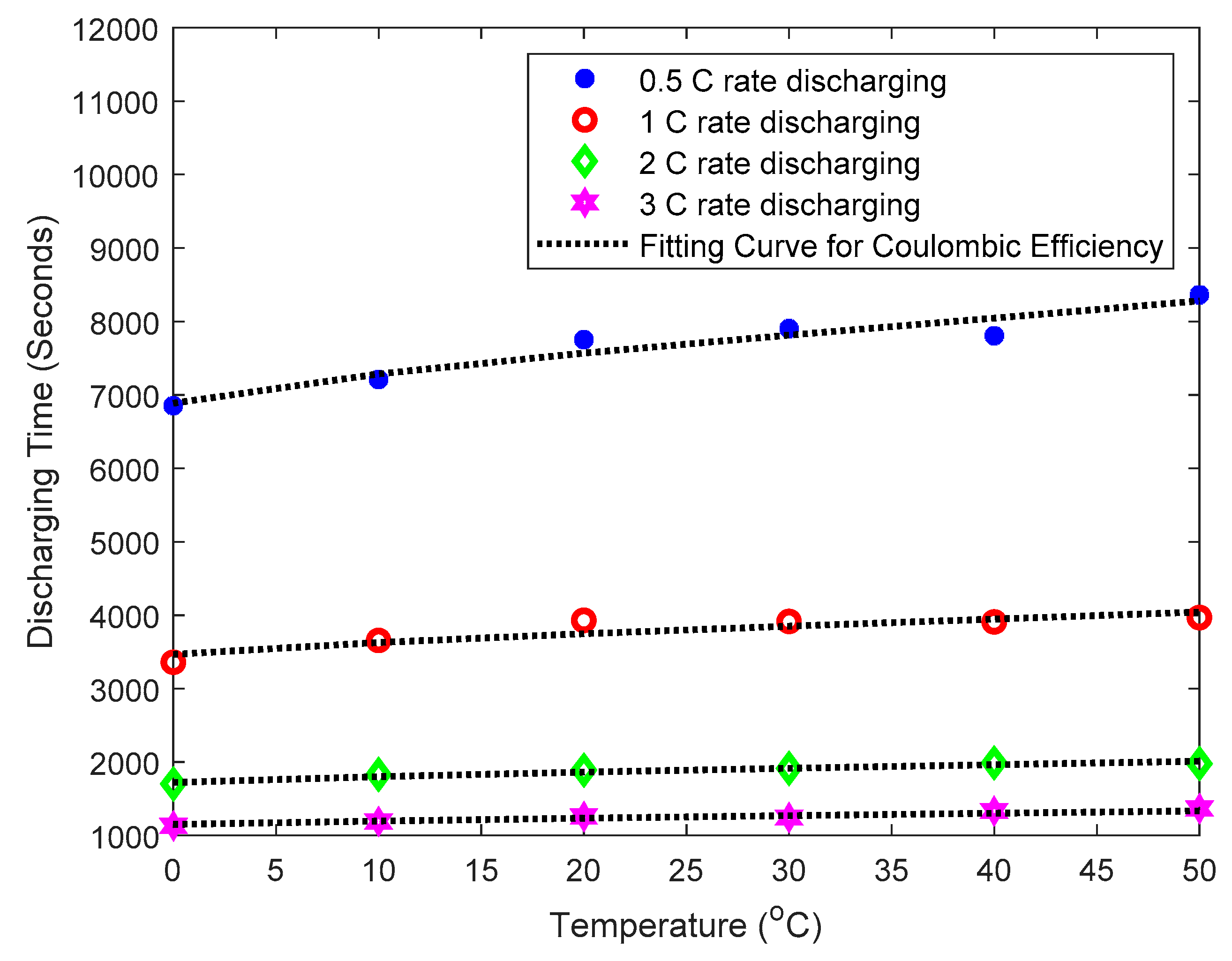

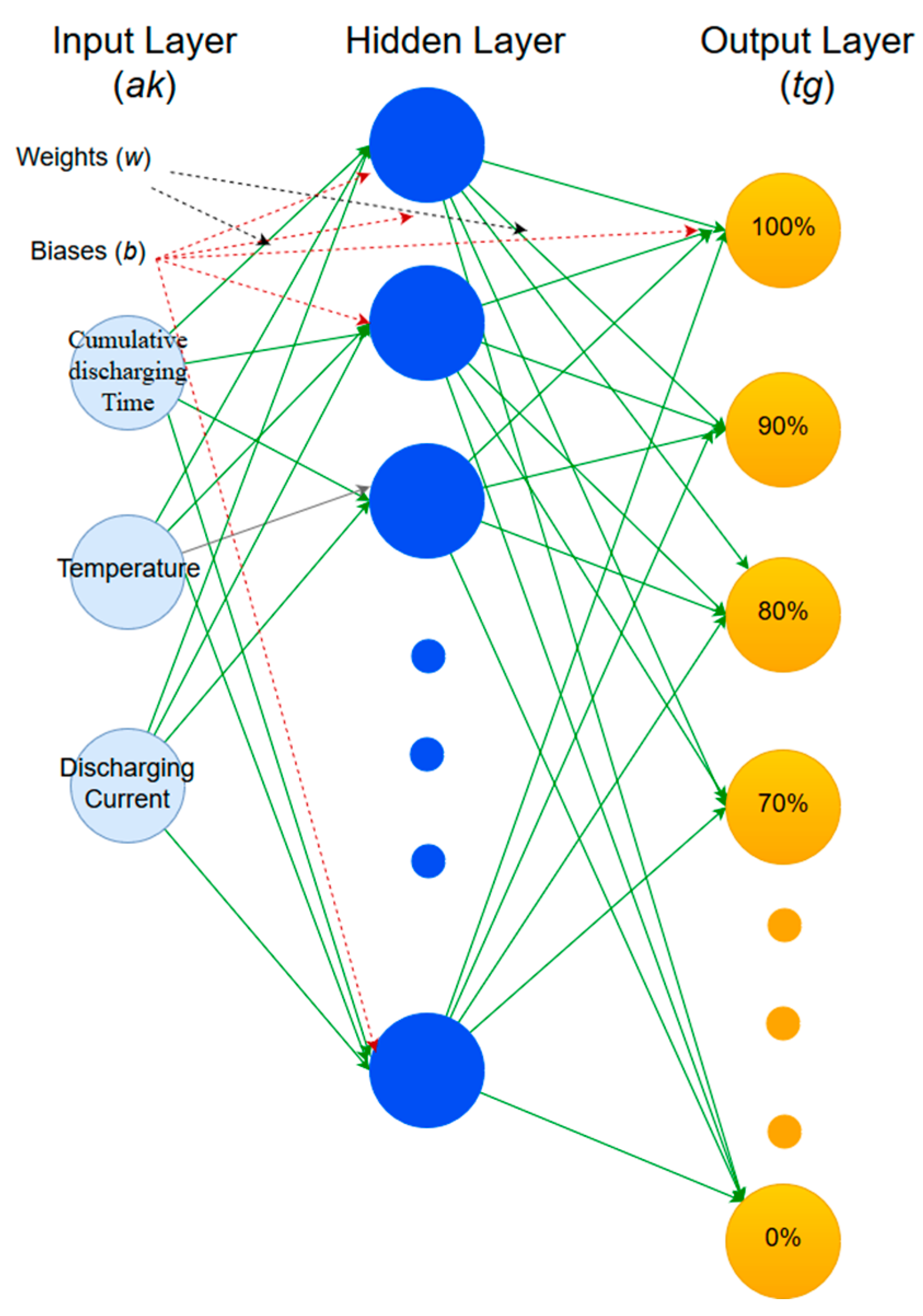
| SoHN (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| C Rate | 0.5 C | 1 C | 2 C | 3 C | ||||
| T (°C) | 20 | 30 | 20 | 30 | 20 | 30 | 20 | 30 |
| Cycle | ||||||||
| 1 | 108.11 | 108.29 | 109.00 | 107.69 | 106.94 | 104.28 | 108.33 | 101.58 |
| 100 | 105.97 | 106.15 | 106.42 | 106.14 | 104.06 | 100.56 | 103.17 | 98.08 |
| 200 | 104.61 | 103.78 | 102.83 | 105.00 | 100.17 | 97.67 | 93.75 | 90.33 |
| 300 | 103.85 | 100.51 | 102.11 | 100.47 | 96.56 | 95.22 | 86.92 | 85.67 |
| 400 | 102.86 | 98.97 | 99.92 | 98.36 | 93.22 | 93.56 | 78.42 | 81.83 |
| SoHN (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| C Rate | 0.5 C | 1 C | 2 C | 3 C | ||||
| T (°C) | 40 | 50 | 40 | 50 | 40 | 50 | 40 | 50 |
| Cycle | ||||||||
| 1 | 107.03 | 114.50 | 107.17 | 108.94 | 108.94 | 108.22 | 109.67 | 105.08 |
| 100 | 105.25 | 114.31 | 106.25 | 108.83 | 104.61 | 106.33 | 106.25 | 102.58 |
| 200 | 102.12 | 113.60 | 104.56 | 107.44 | 103.17 | 99.06 | 103.50 | 93.17 |
| 300 | 100.51 | 110.54 | 99.33 | 87.33 | 97.83 | 82.00 | 92.67 | 77.50 |
| 400 | 99.39 | 104.83 | 80.83 | 69.36 | 79.50 | 54.17 | 78.58 | 49.33 |
| SoHN (%) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C Rate | 0.5 C | 1 C | 2 C | 3 C | ||||||||
| T (°C) | −10 | 0 | 10 | −10 | 0 | 10 | −10 | 0 | 10 | −10 | 0 | 10 |
| Cycle | ||||||||||||
| 1 | 89.63 | 95.31 | 100.0 | 88.94 | 95.33 | 101.5 | 89.50 | 93.89 | 101.2 | 91.08 | 92.42 | 96.67 |
| 100 | 83.63 | 92.58 | 97.64 | 83.64 | 88.92 | 99.08 | 80.11 | 88.67 | 97.61 | 77.83 | 86.58 | 93.58 |
| 200 | 81.72 | 86.04 | 95.00 | 81.33 | 85.03 | 94.61 | 75.67 | 79.83 | 94.44 | 67.42 | 78.67 | 89.00 |
| 300 | 75.31 | 81.93 | 91.85 | 71.56 | 73.06 | 91.83 | 65.78 | 70.72 | 92.39 | 46.75 | 70.67 | 83.83 |
| 400 | 56.17 | 67.31 | 89.78 | 49.17 | 62.89 | 88.61 | 41.67 | 58.44 | 87.78 | 26.42 | 58.42 | 79.75 |
| Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| C Rate | ||||||||
| 0.5 C | ||||||||
| 1 C | ||||||||
| 2 C | ||||||||
| 3 C | ||||||||
| Parameters | ||||||||
| Value | ||||||||
| Operating T | −10 | 0 | 10 | 20 | 30 | 40 | 50 | |
|---|---|---|---|---|---|---|---|---|
| C rate | 0.5C | 0.3 | 0.49 | 1.11 | 2.21 | 0.90 | 3.40 | 0.60 |
| 1C | 2.28 | 2.59 | 0.87 | 4.42 | 1.15 | 1.73 | 2.87 | |
| 2C | 0.44 | 1.38 | 1.52 | 1.46 | 0.05 | 1.31 | 1.53 | |
| 3C | 1.33 | 1.87 | 0.66 | 1.69 | 2.04 | 2.51 | 2.75 | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, T.-J. Development of a Comprehensive Model for the Coulombic Efficiency and Capacity Fade of LiFePO4 Batteries under Different Aging Conditions. Appl. Sci. 2019, 9, 4572. https://doi.org/10.3390/app9214572
Kuo T-J. Development of a Comprehensive Model for the Coulombic Efficiency and Capacity Fade of LiFePO4 Batteries under Different Aging Conditions. Applied Sciences. 2019; 9(21):4572. https://doi.org/10.3390/app9214572
Chicago/Turabian StyleKuo, Ting-Jung. 2019. "Development of a Comprehensive Model for the Coulombic Efficiency and Capacity Fade of LiFePO4 Batteries under Different Aging Conditions" Applied Sciences 9, no. 21: 4572. https://doi.org/10.3390/app9214572
APA StyleKuo, T.-J. (2019). Development of a Comprehensive Model for the Coulombic Efficiency and Capacity Fade of LiFePO4 Batteries under Different Aging Conditions. Applied Sciences, 9(21), 4572. https://doi.org/10.3390/app9214572




