The Performance Assessment of a Precast, Panel-Segmented Arch Bridge with Outriggers
Abstract
:1. Introduction
2. Overview of the Proposed Arch Bridge System
3. Performance Assessment of the Proposed Arch Bridge System
3.1. Specifications of Target Structure
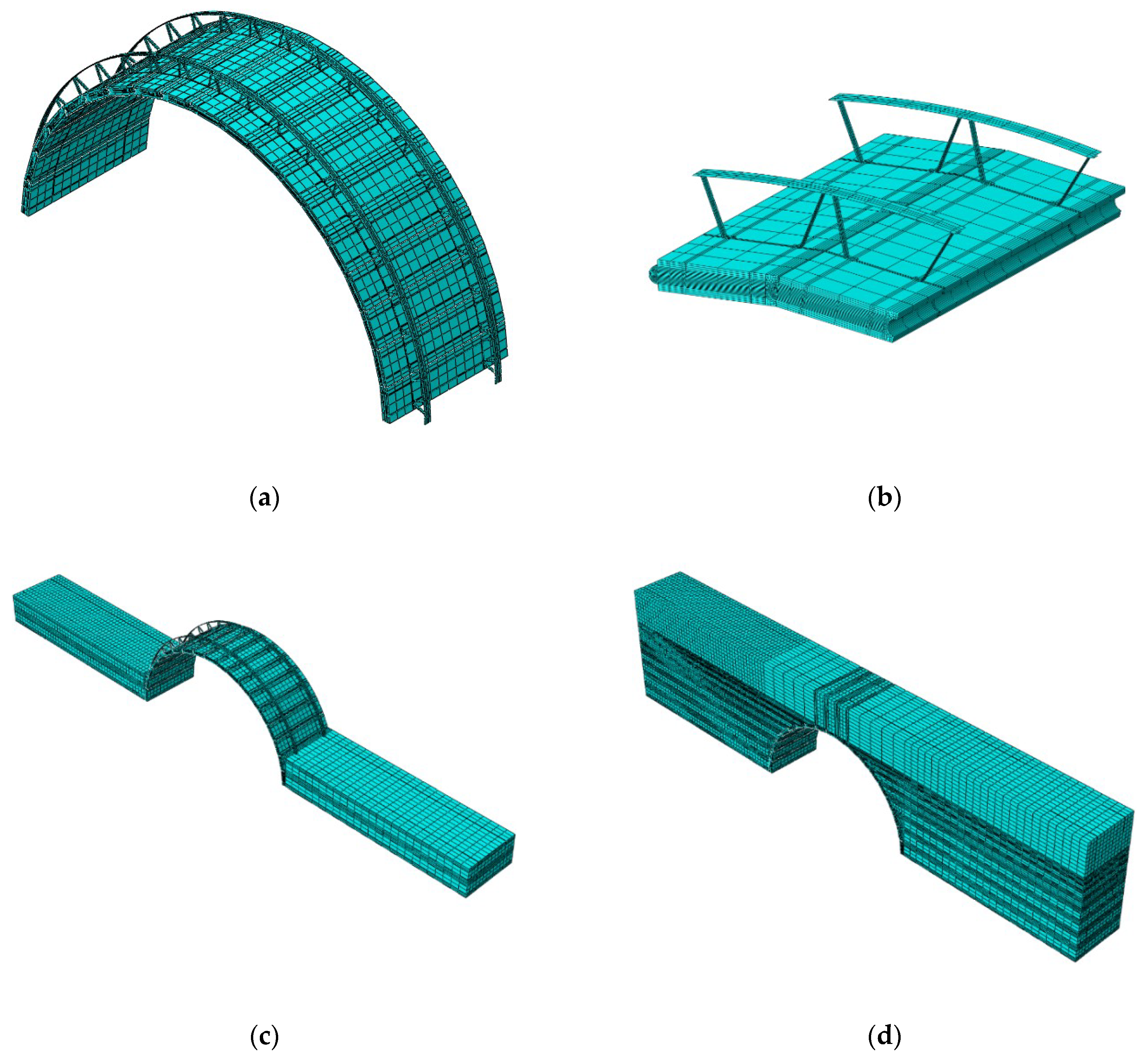
3.2. Three-Dimensional Structural Analysis Modeling
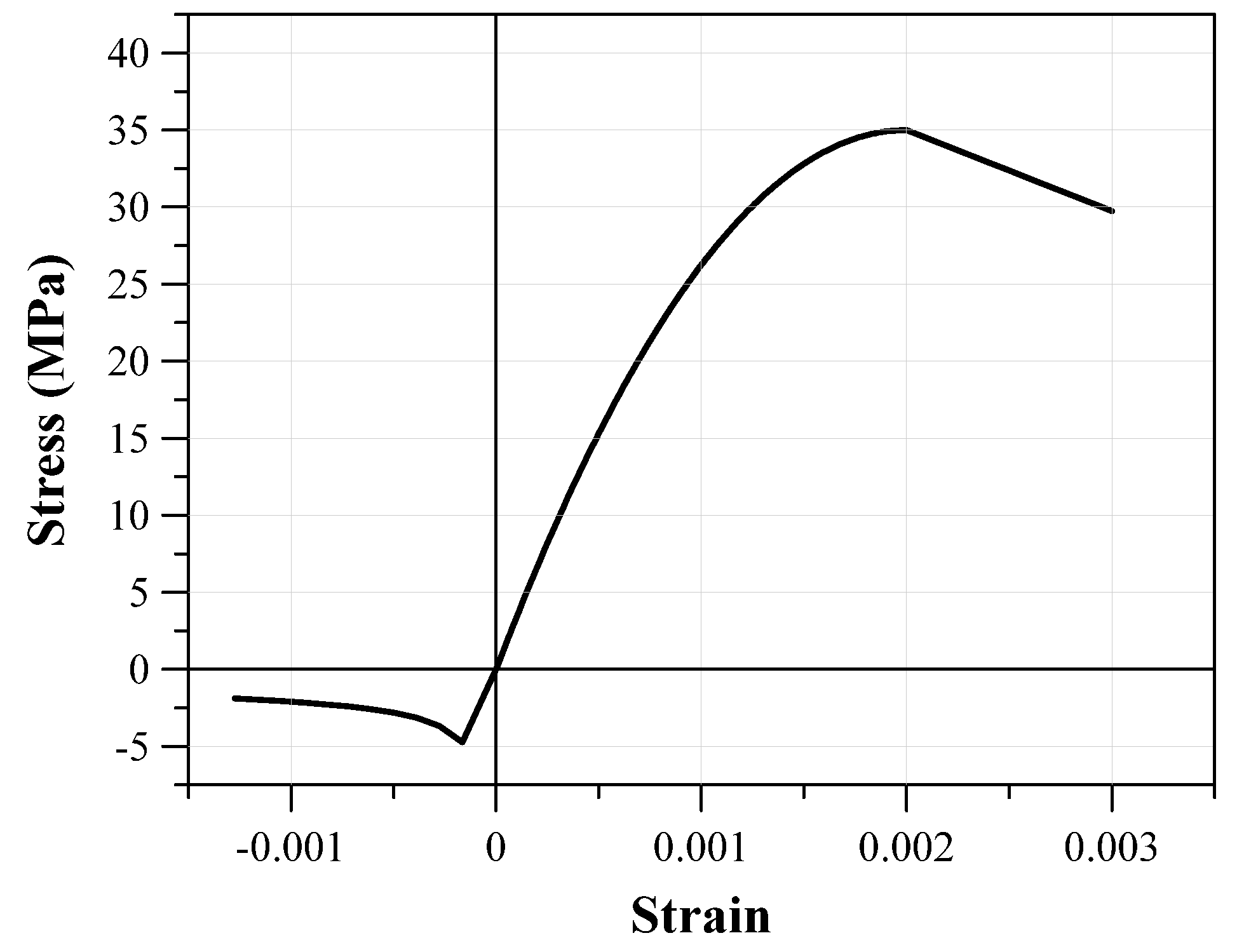
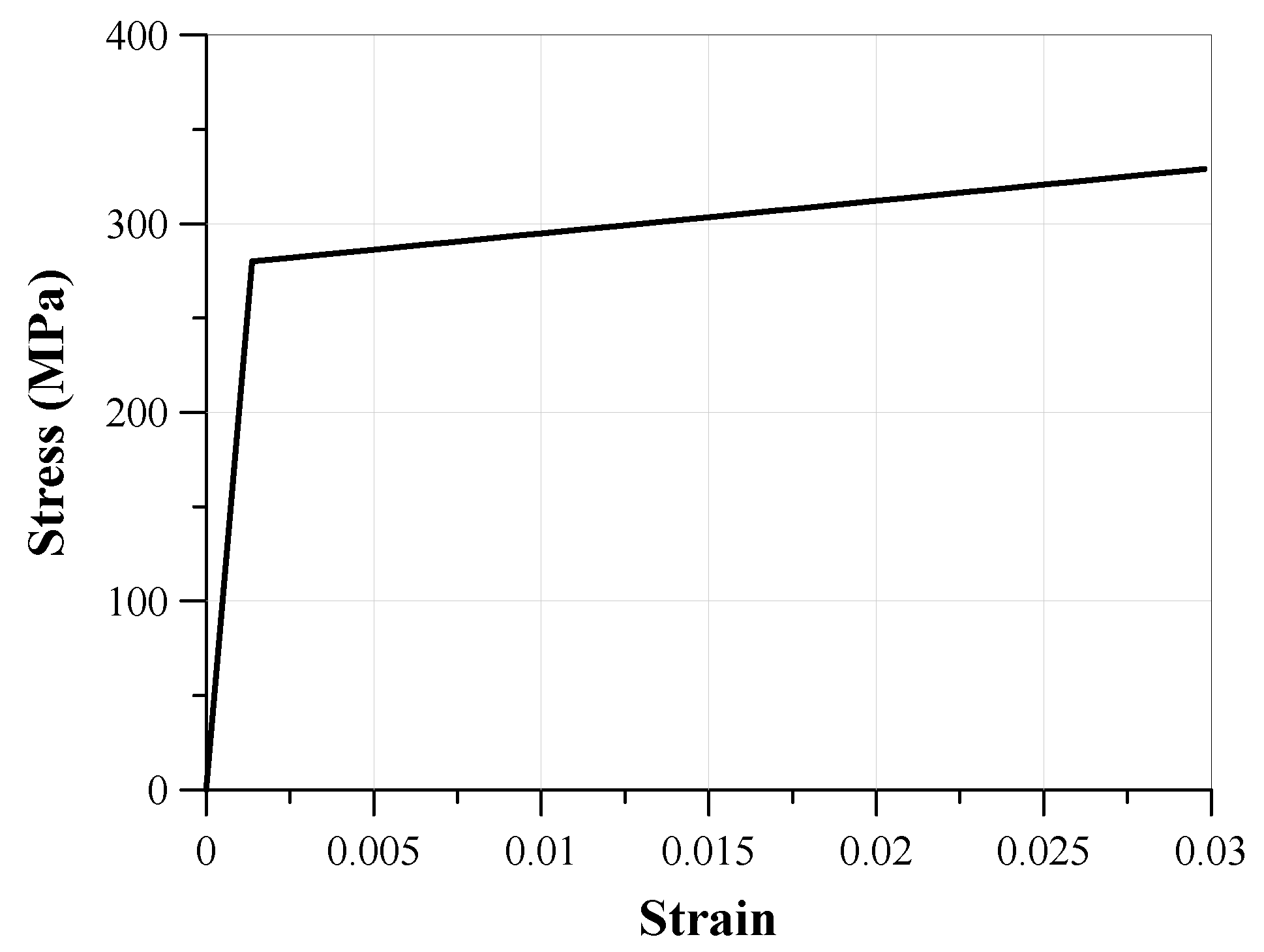
3.2.1. Material Properties of Structural Analysis Model
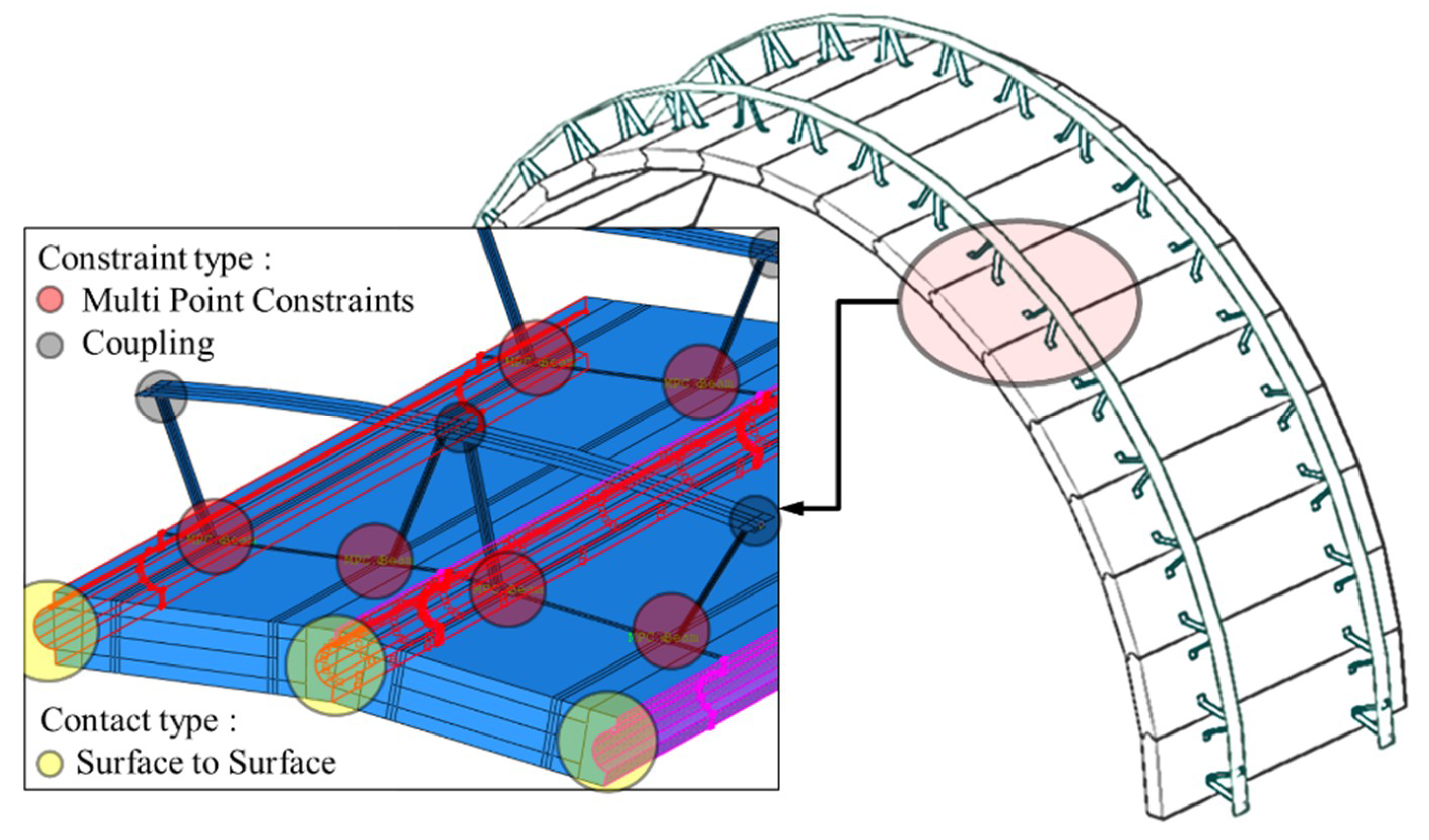
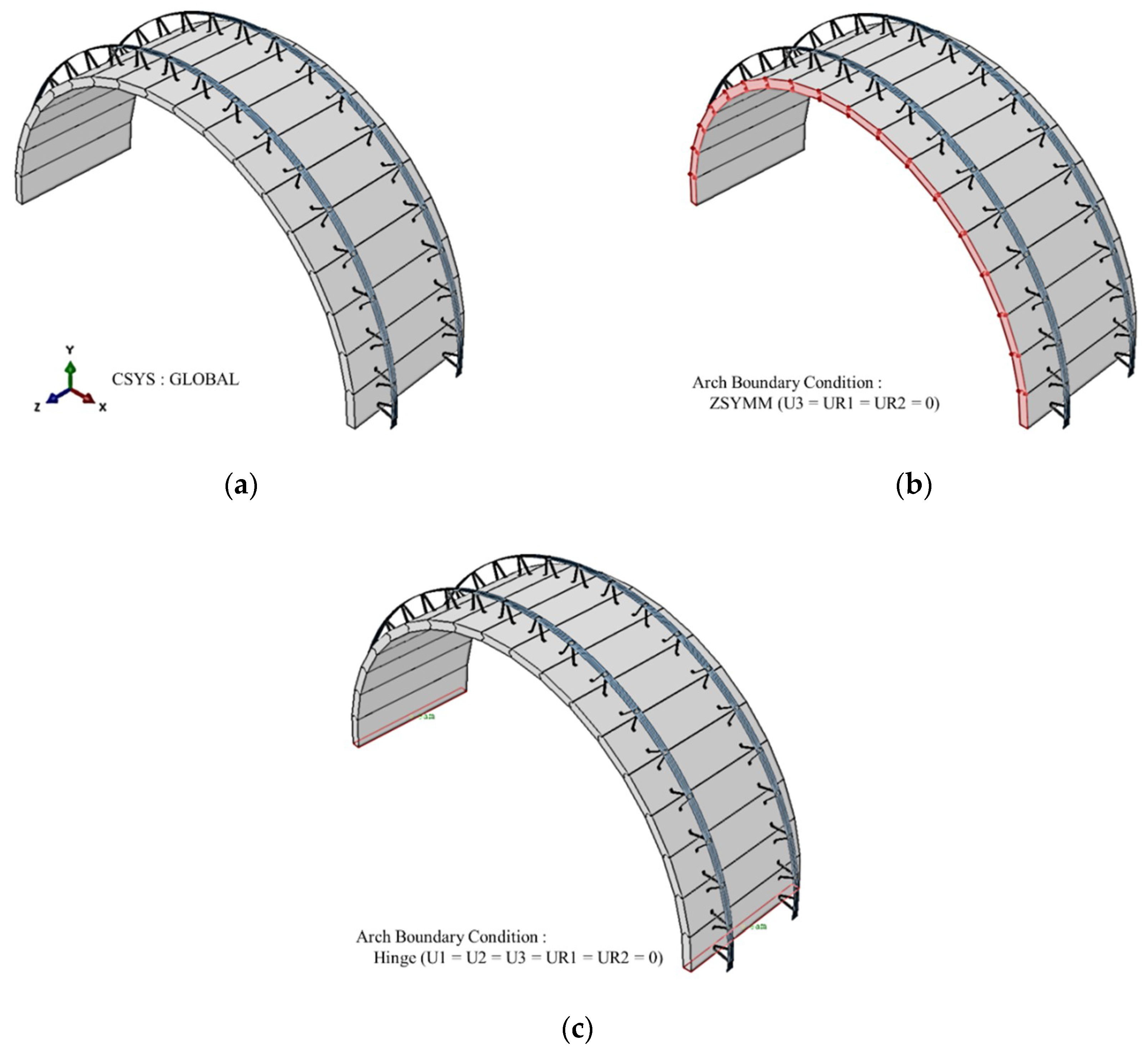
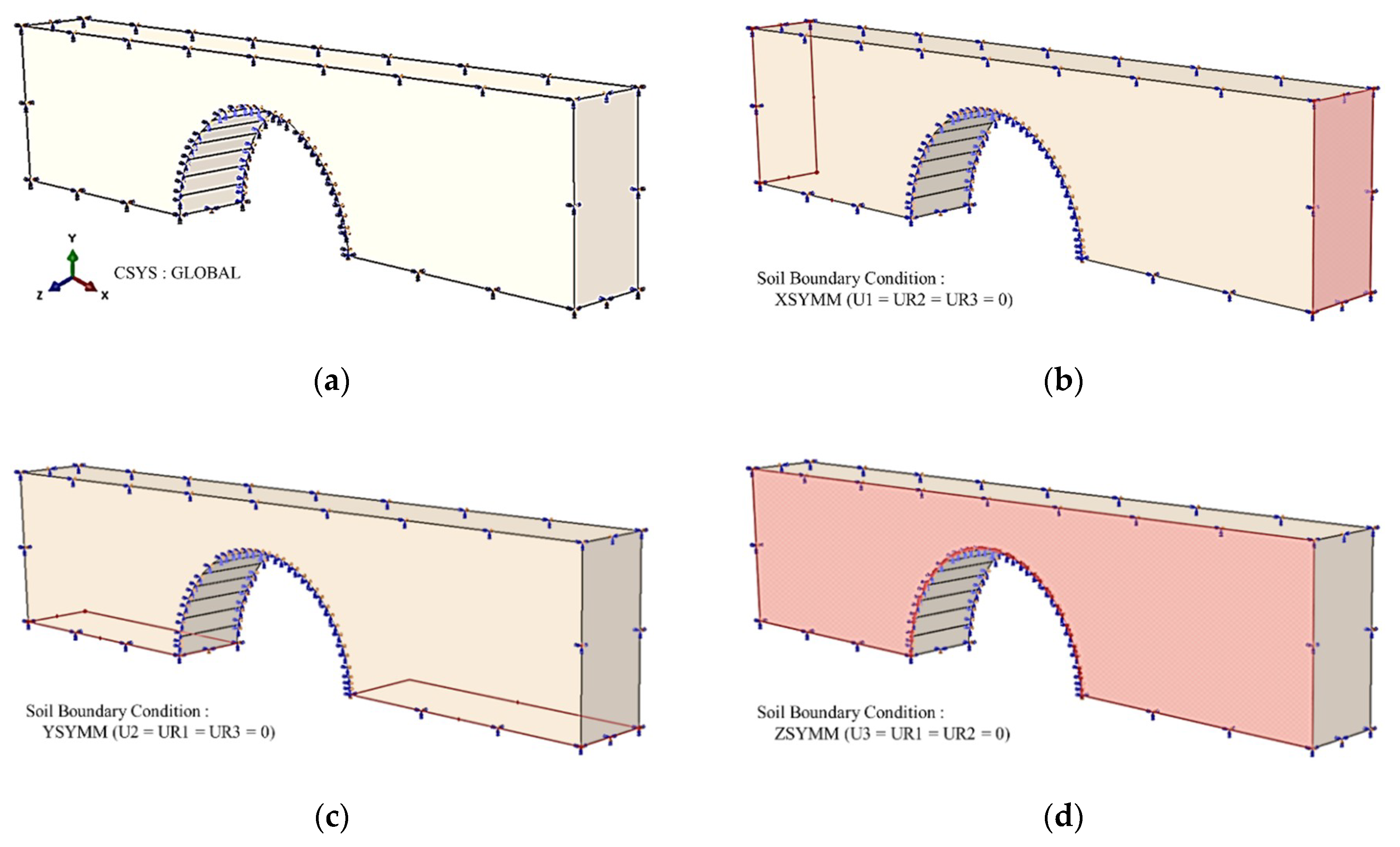
3.2.2. Structural Analysis Model’s Contact and Boundary Conditions
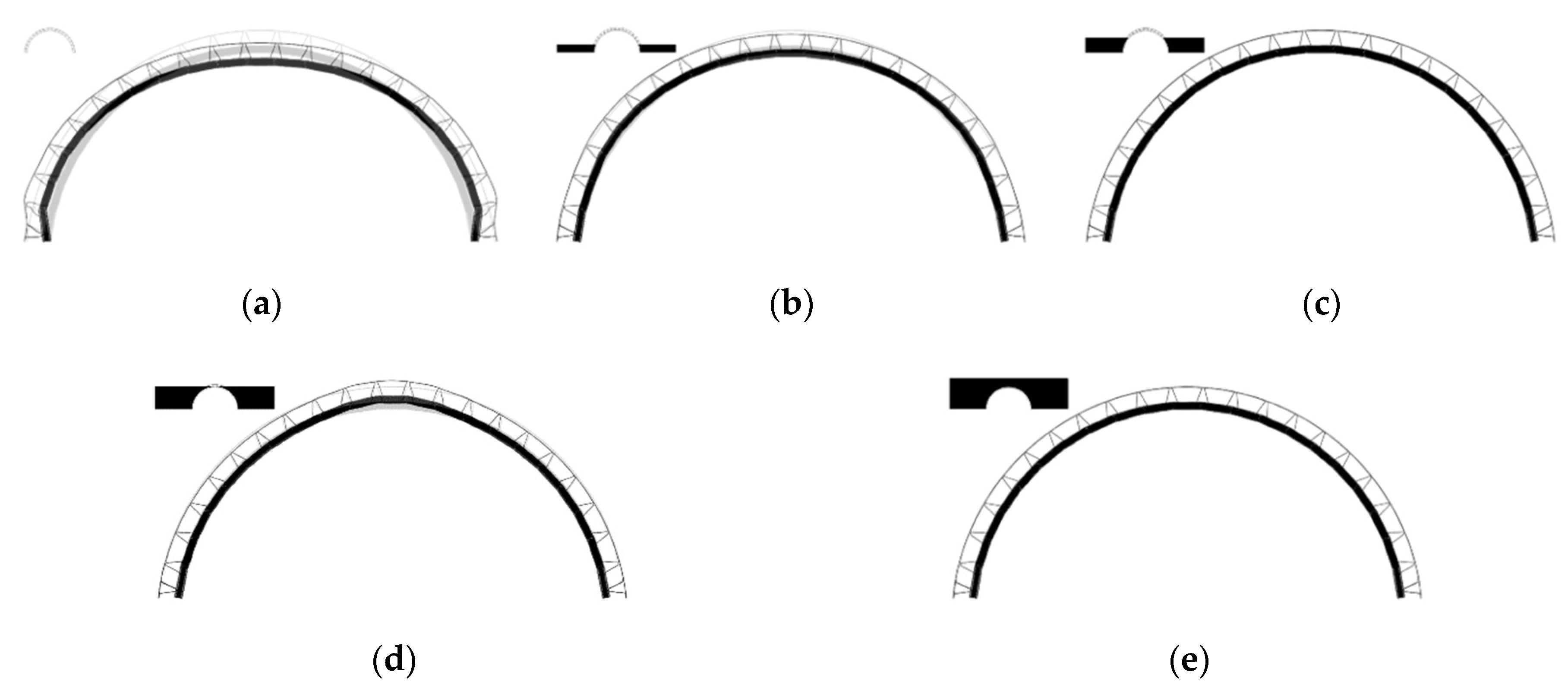
4. Analysis of Target’s Structure Behavior
4.1. The Result of the Behavior Evaluation of 3D Structural Analysis Model
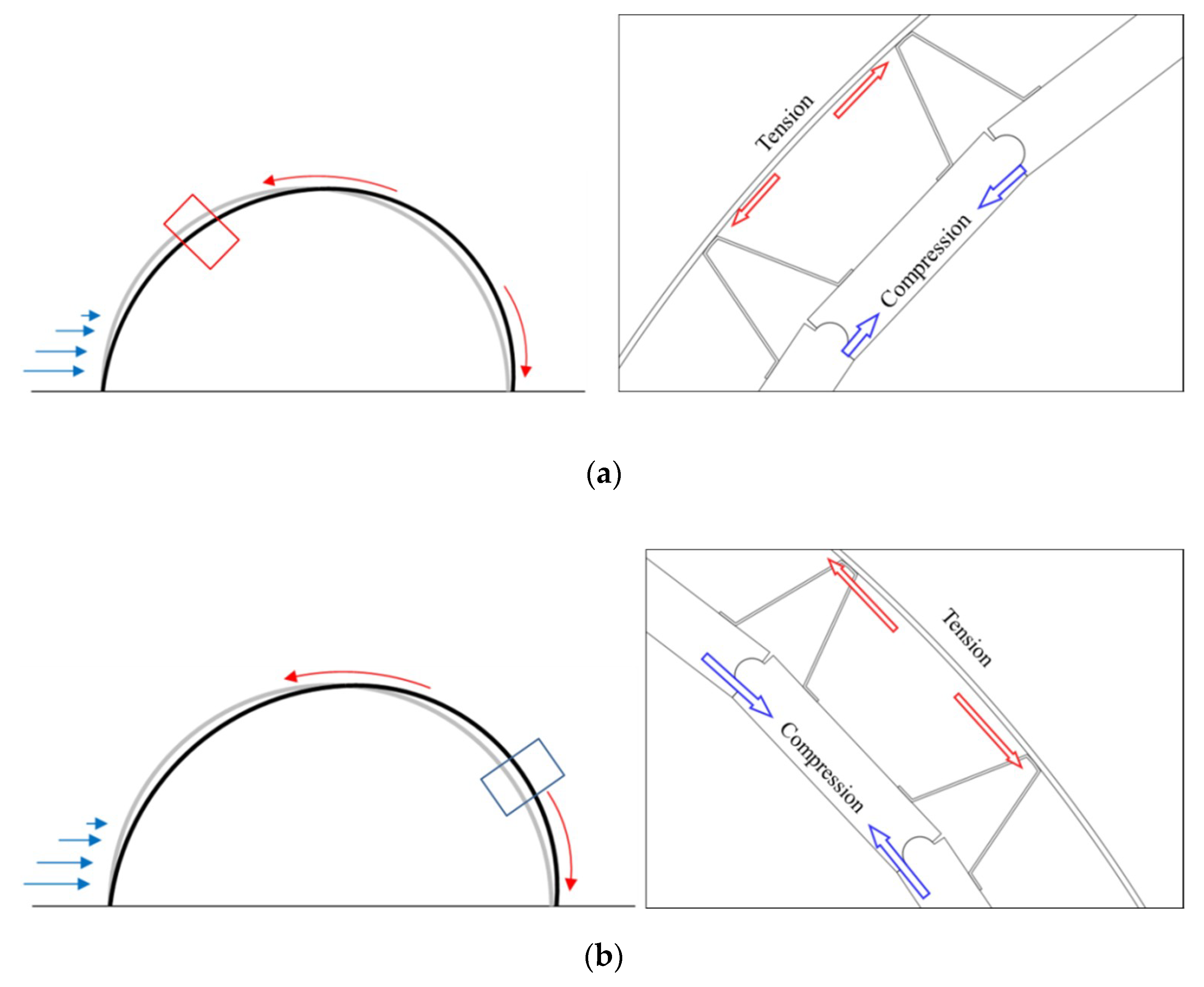
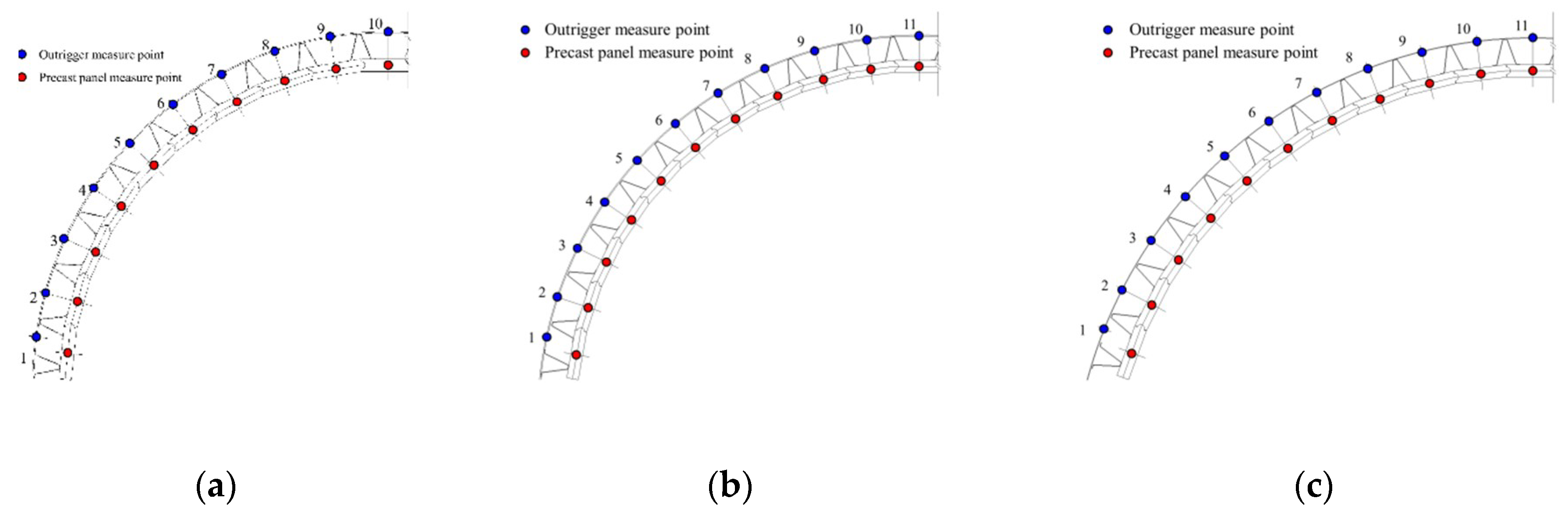
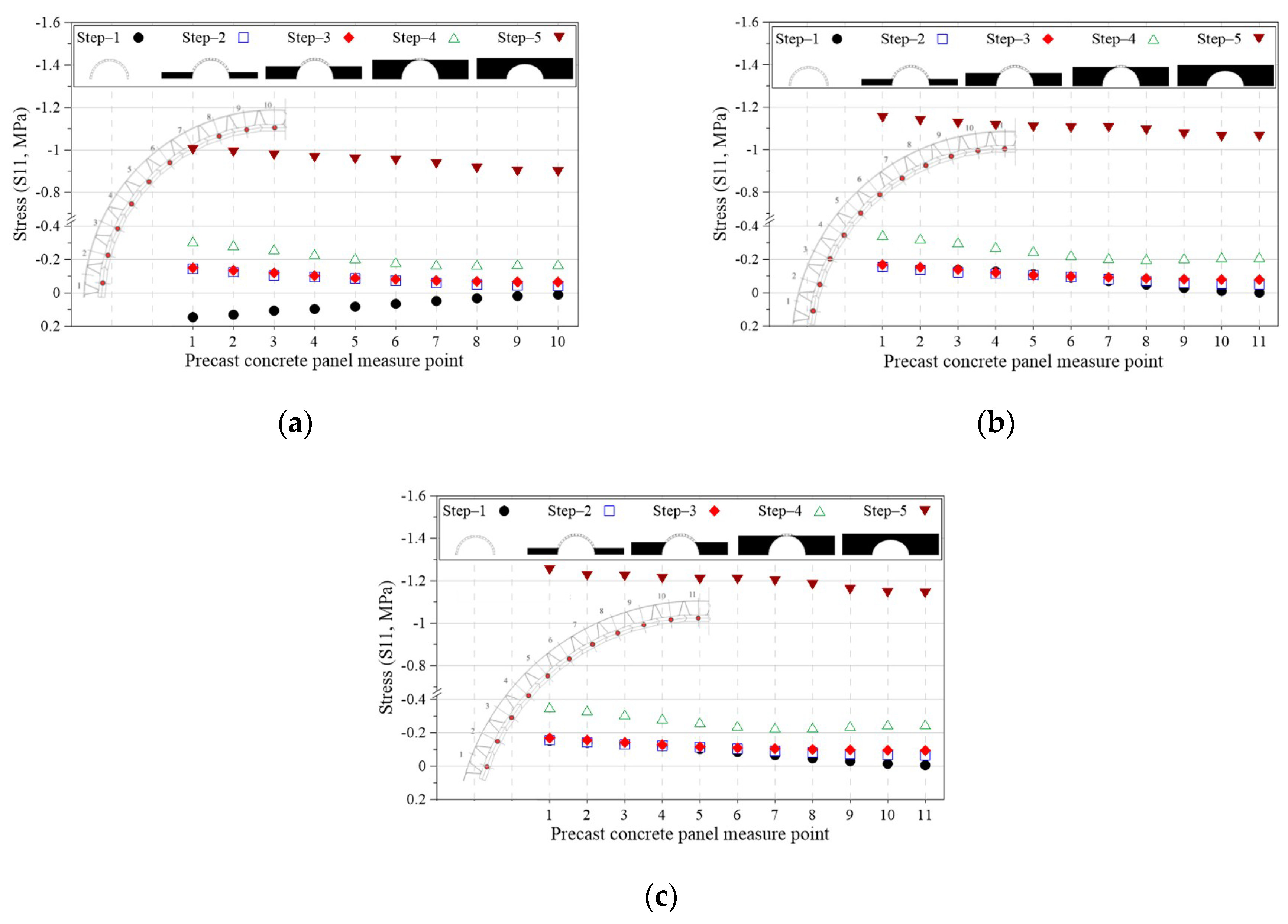
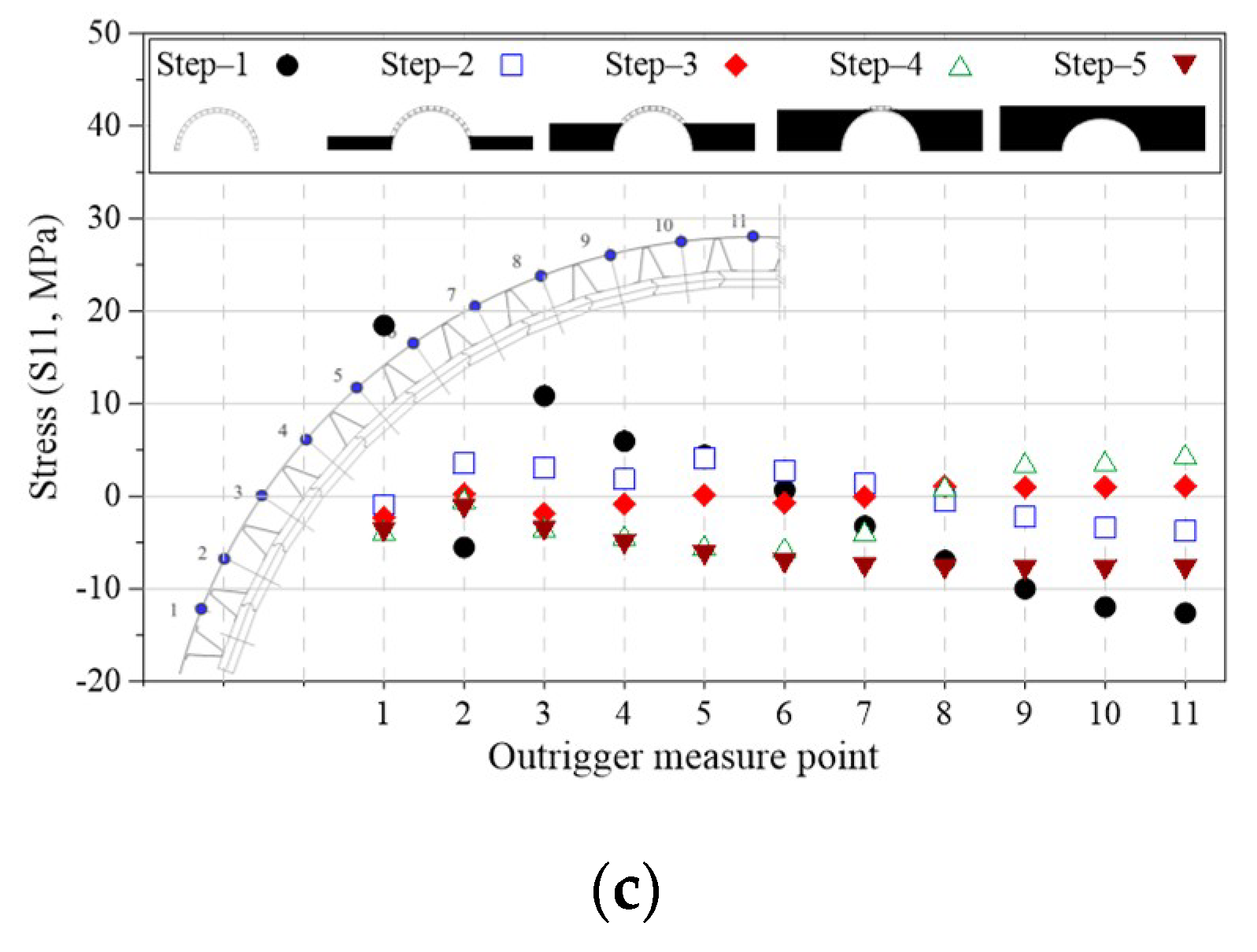
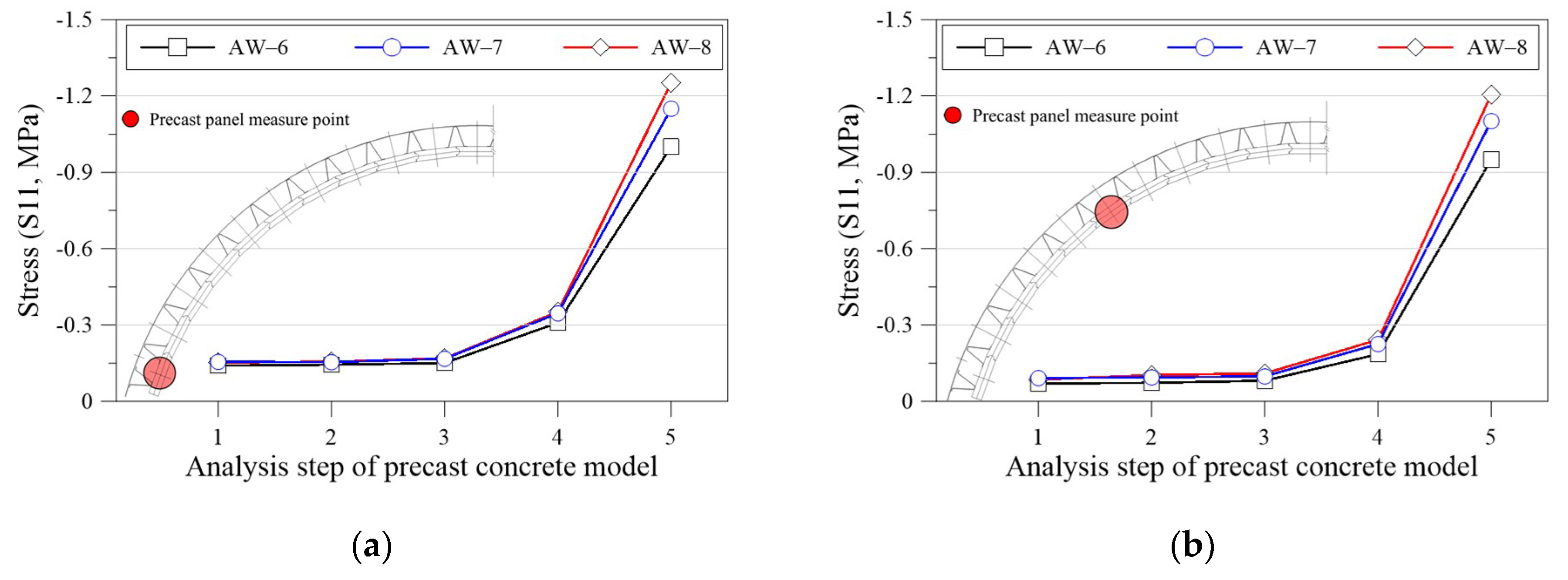
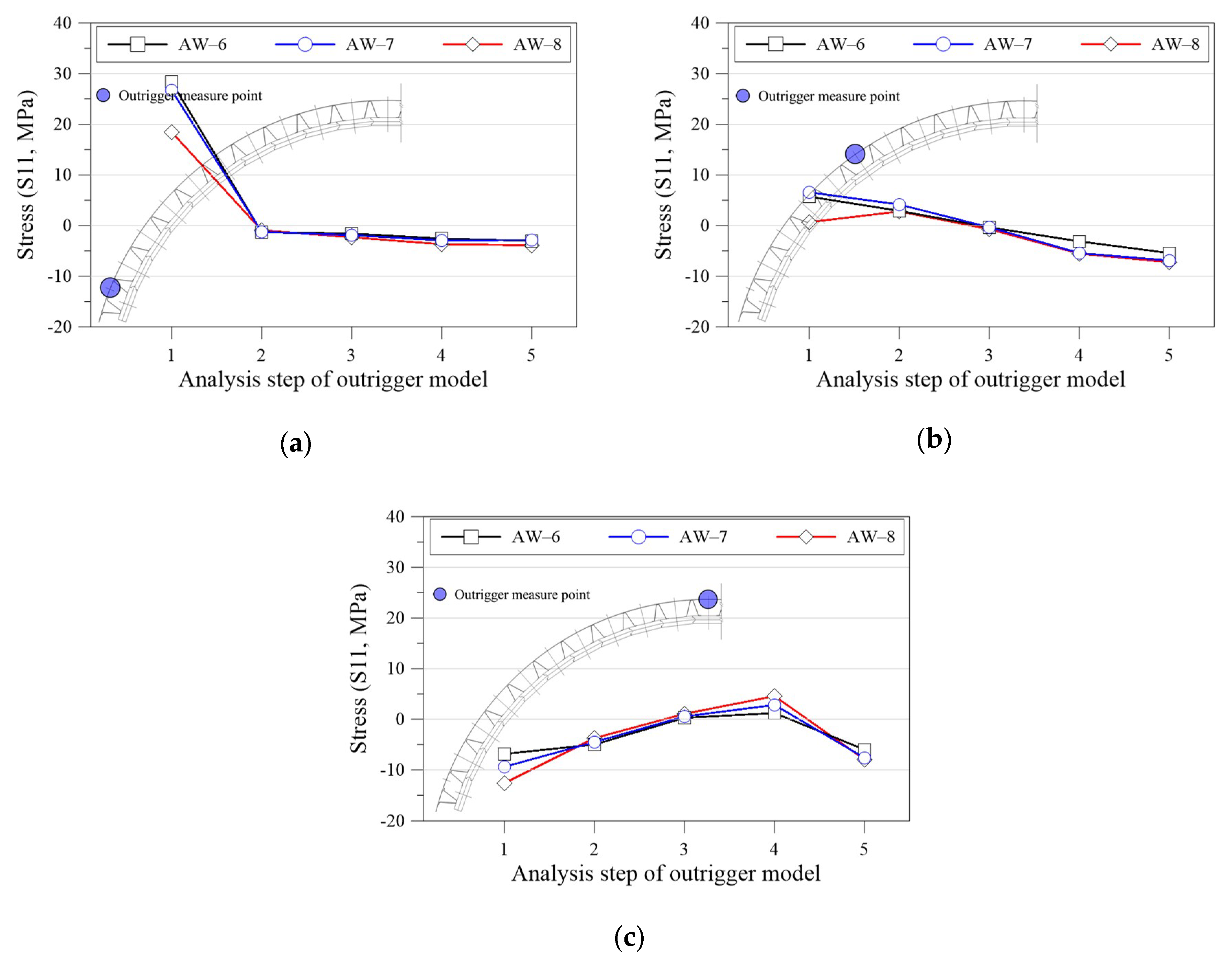
4.1.1. Precast Panel and Outrigger Stress Results
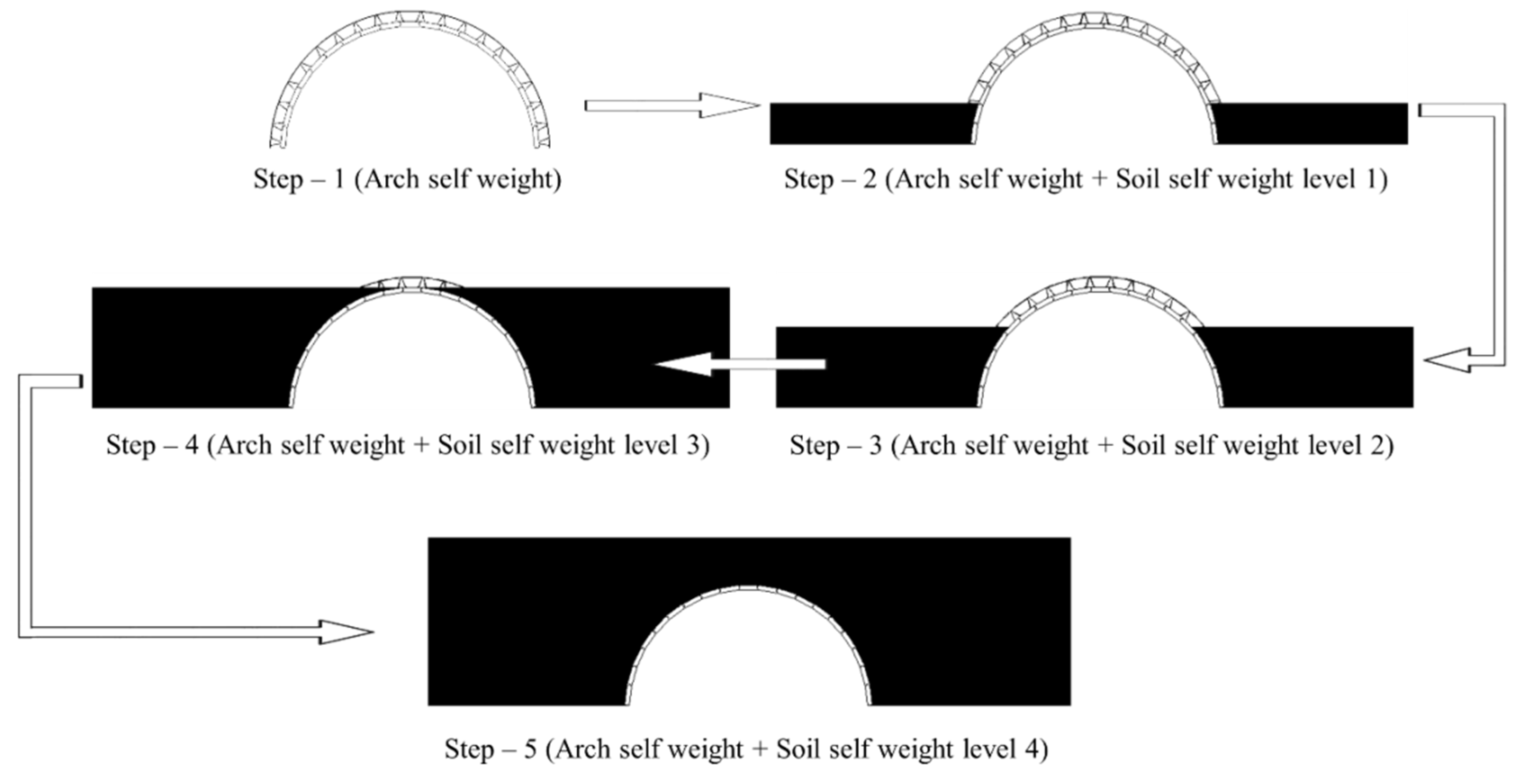
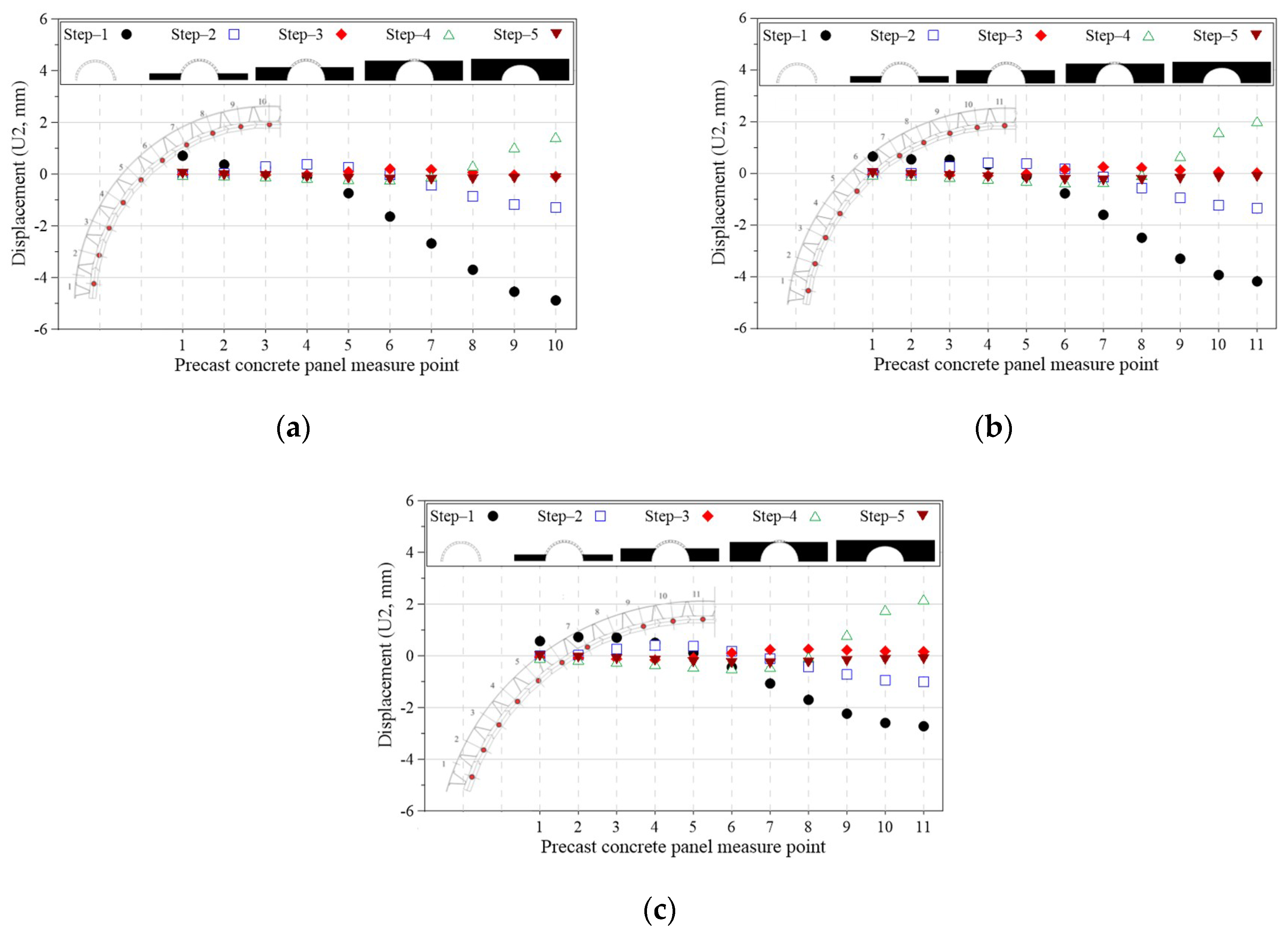
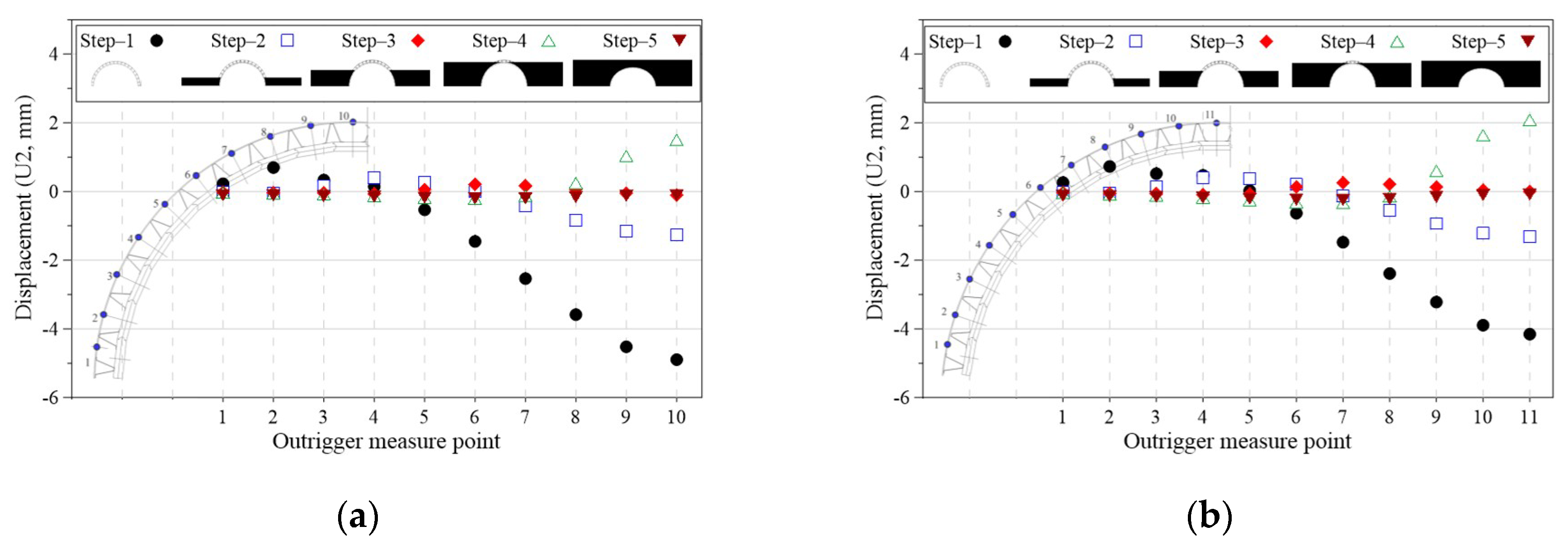
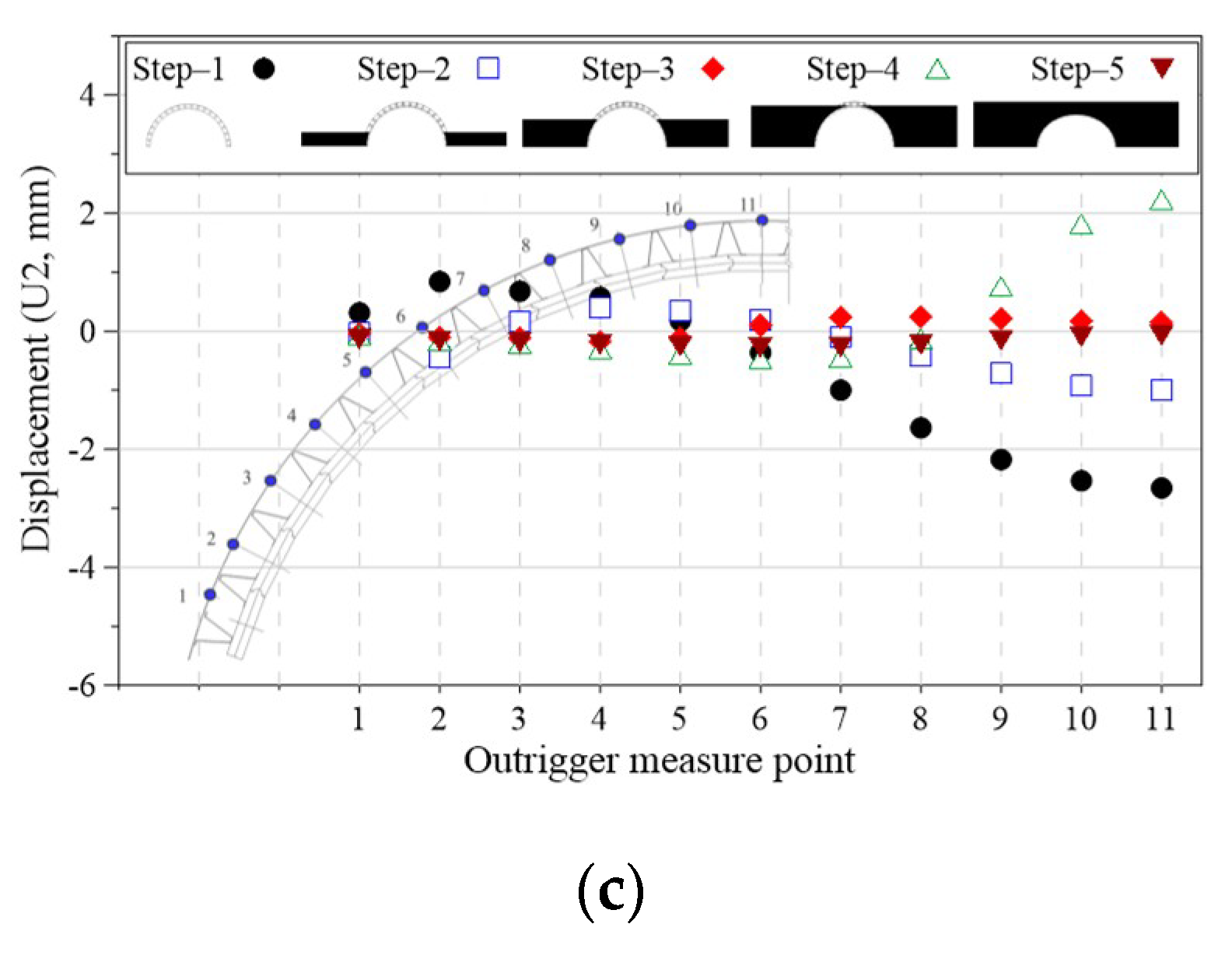
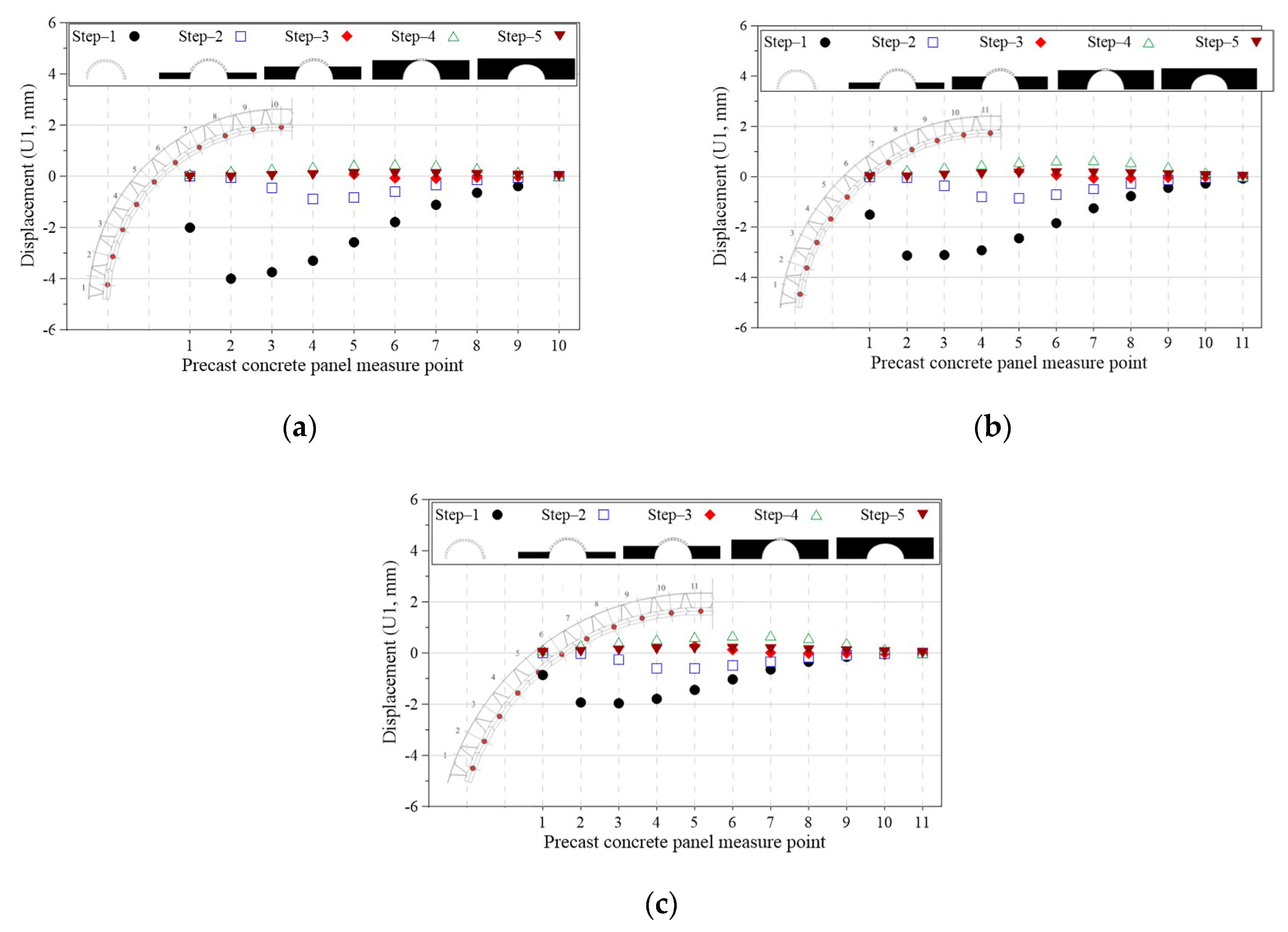
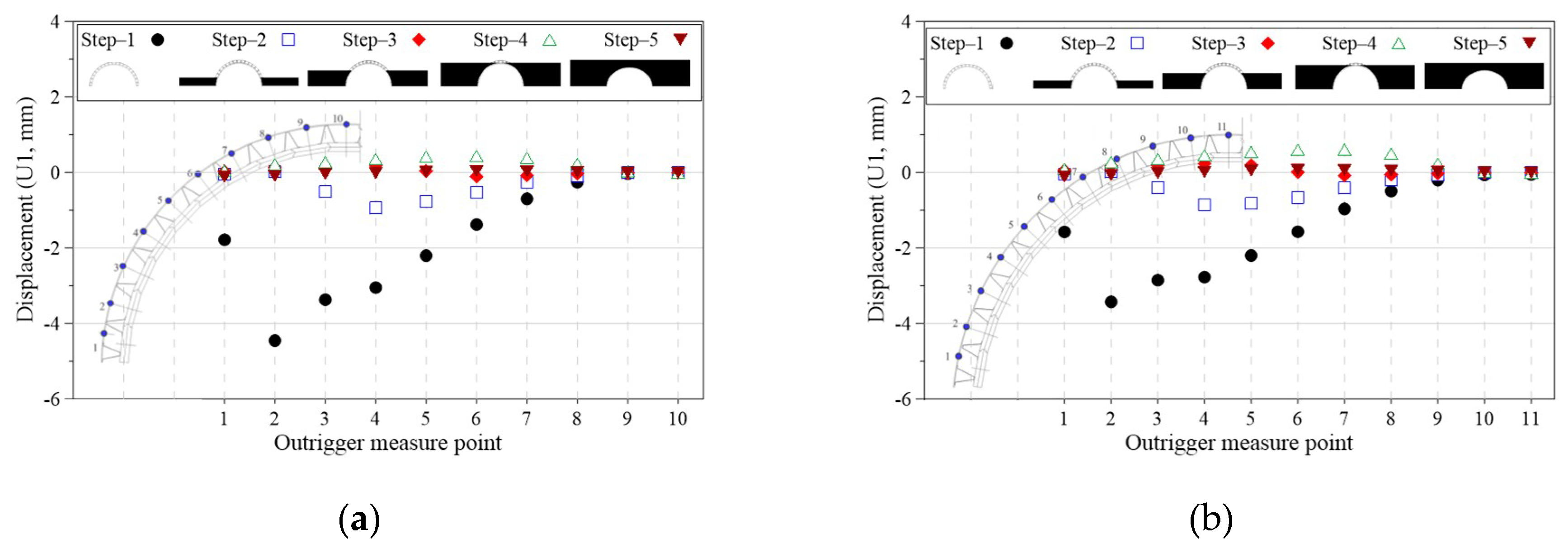
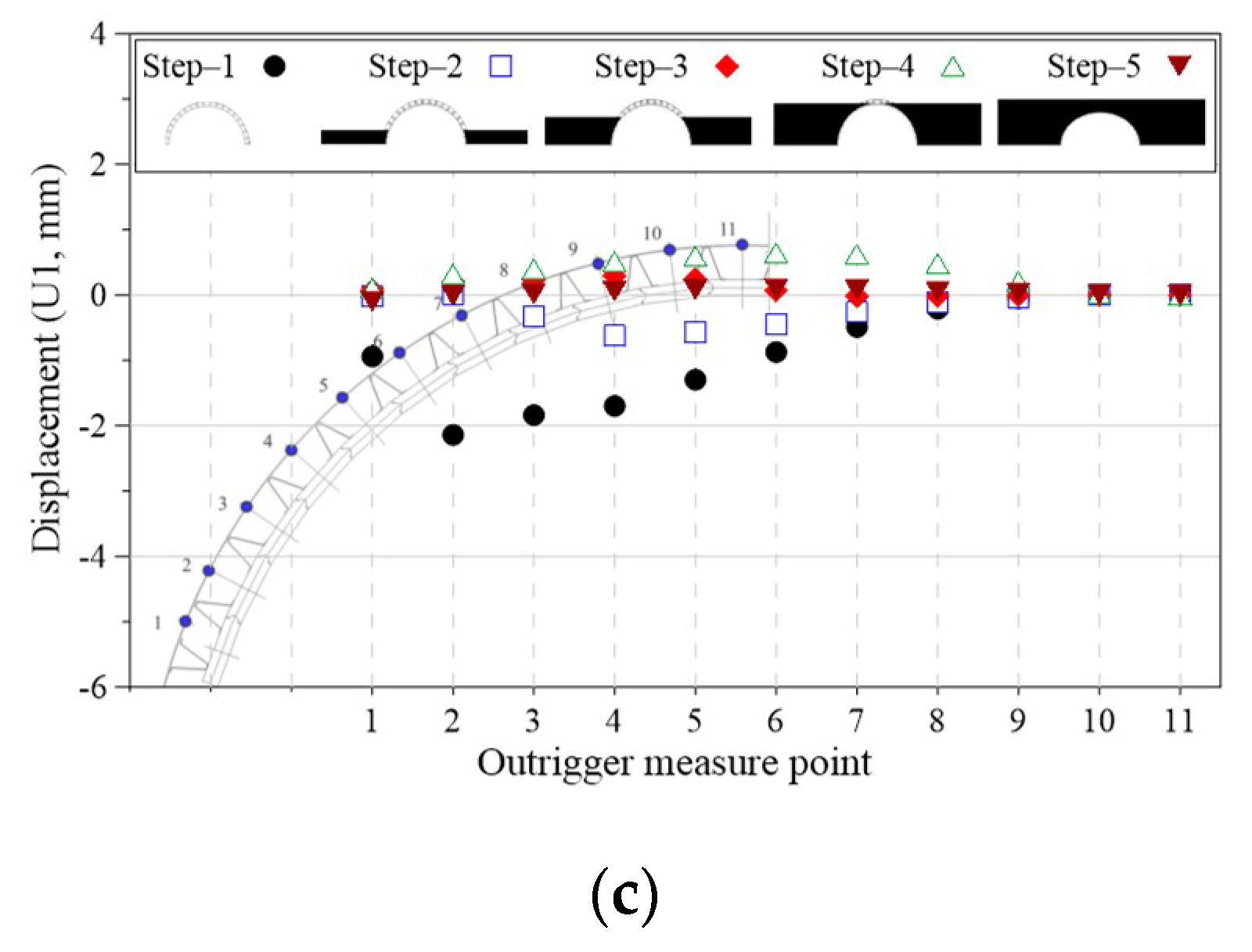
4.1.2. Deformed State and Displacement Results of Precast Panels and Outriggers at Each Construction Step
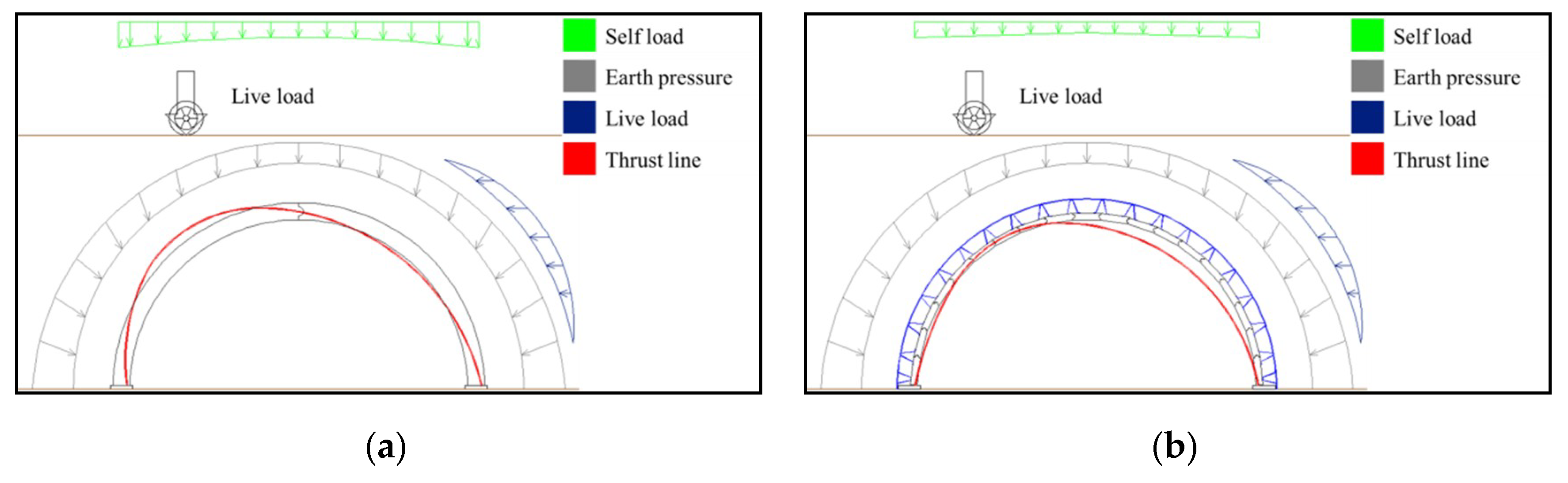
4.1.3. Precast Panel and Outrigger Thrust Line Calculations
4.2. Stress Comparison by Arch Member According to Rise Ratio of 3D Structural Analysis Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Block, P. Equilibrium Systems: Studies in Masonry Structure. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Block, P.; Ciblac, T.; Ochsendorf, J. Real-time limit analysis of vaulted masonry buildings. Comput. Struct. 2006, 84, 1841–1852. [Google Scholar] [CrossRef]
- Heyman, J. The Masonry Arch; Ellis Horwood Ltd.: Chichester, UK, 1982. [Google Scholar]
- Kim, N.H.; Koh, H.M.; Hong, S.G. Study on Structural Behavior of Traditional Stone Bridges. Comput. Struct. Eng. Inst. Korea 2008, 78–83. (In Korean) [Google Scholar]
- Collings, D. Steel-Concrete Composite Bridges; ICE: Washington, DC, USA, 2005. [Google Scholar]
- Brencich, A.; Morbiducci, R. Masonry Arches: Historical Rules and Modern Mechanics. Int. J. Archit. Herit. 2007, 1, 165–189. [Google Scholar] [CrossRef]
- Loo, Y.C.; Yang, Y. Cracking and failure analysis of masonry arch bridges. J. Struct. Eng. ASCE 1991, 117, 1641–1659. [Google Scholar] [CrossRef]
- Kim, N.H.; Koh, H.M.; Hong, S.G. Development of a structural safety evaluation system for stone voussoir arch bridges. J. Comput. Struct. Eng. Inst. Korea 2009, 22, 15–23. (in Korean). [Google Scholar]
- Lacidogna, G.; Accornero, F. Elastic, plastic, fracture analysis of masonry arches: A multi-span bridge case study. Curved Layer Struct. 2018, 5, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.S. Development of Temporary Arch Bridges by Using Snap-Fit GFRP Composite Decks. Master’s Thesis, Kookmin University, Seoul, Korea, 2008. (In Korean). [Google Scholar]
- Tan, G.E.; Ong, T.B.; Ong, C.Y.; Choong, K.K. Development and Standardisation of New Precast Concrete Open Spandrel Arch Bridge System. In Proceedings of the 37th IABSE Symposium in Madrid, Madrid, Spain, 3–5 September 2014; pp. 799–806. [Google Scholar]
- Ong, C.Y.; Choong, K.K.; Tan, G.E.; Ong, T.B. Precast Concrete Closed Spandrel Arch Bridge System As Viable Alternative to Conventional Beam Bridge System. Appl. Mech. Mater. 2015, 802, 261–266. [Google Scholar]
- Lee, S.M.; Shin, J.S.; Jeon, S.J.; Han, M.Y. Optimal Design of Arch Rise to Span Ratio in Arch Bridges. Proc. Korea Concr. Inst. 2012, 24, 541–542. (In Korean) [Google Scholar]
- Bernini, J.; BEBO of America, Inc. Overfilled precast concrete arch bridge structures. In Proceedings of the International Bridge Conference and Exhibition, Zurich, Switzerland, 15–17 June 2000. [Google Scholar]
- Canadian Standards Association. CAN/CSA-S6-14: Canadian Highway Bridge Design Code, Rexdale, Ontario; Canadian Standards Association: Toronto, ON, Canada, 2014. [Google Scholar]
- ABAQUS. Abaqus Analysis User Manual, Version 6.14; Dassault Systems Simulia Corp; ABAQUS Inc.: Johnston, UI, USA, 2014. [Google Scholar]
- Hognestad, E. A Study of Combined Bending Axial Load in Reinforced Concrete Members; Bulletin Series; Engineering Experimental Station; The University of Illinois: Urbana, IL, USA, 1951; Volume 49. [Google Scholar]
- BSI British Standards. BS 5975: Code of Practice for Temporary Works Procedures and the Permissible Stress Design of Falsework; BSI British Standards: London, UK, 2008. [Google Scholar]
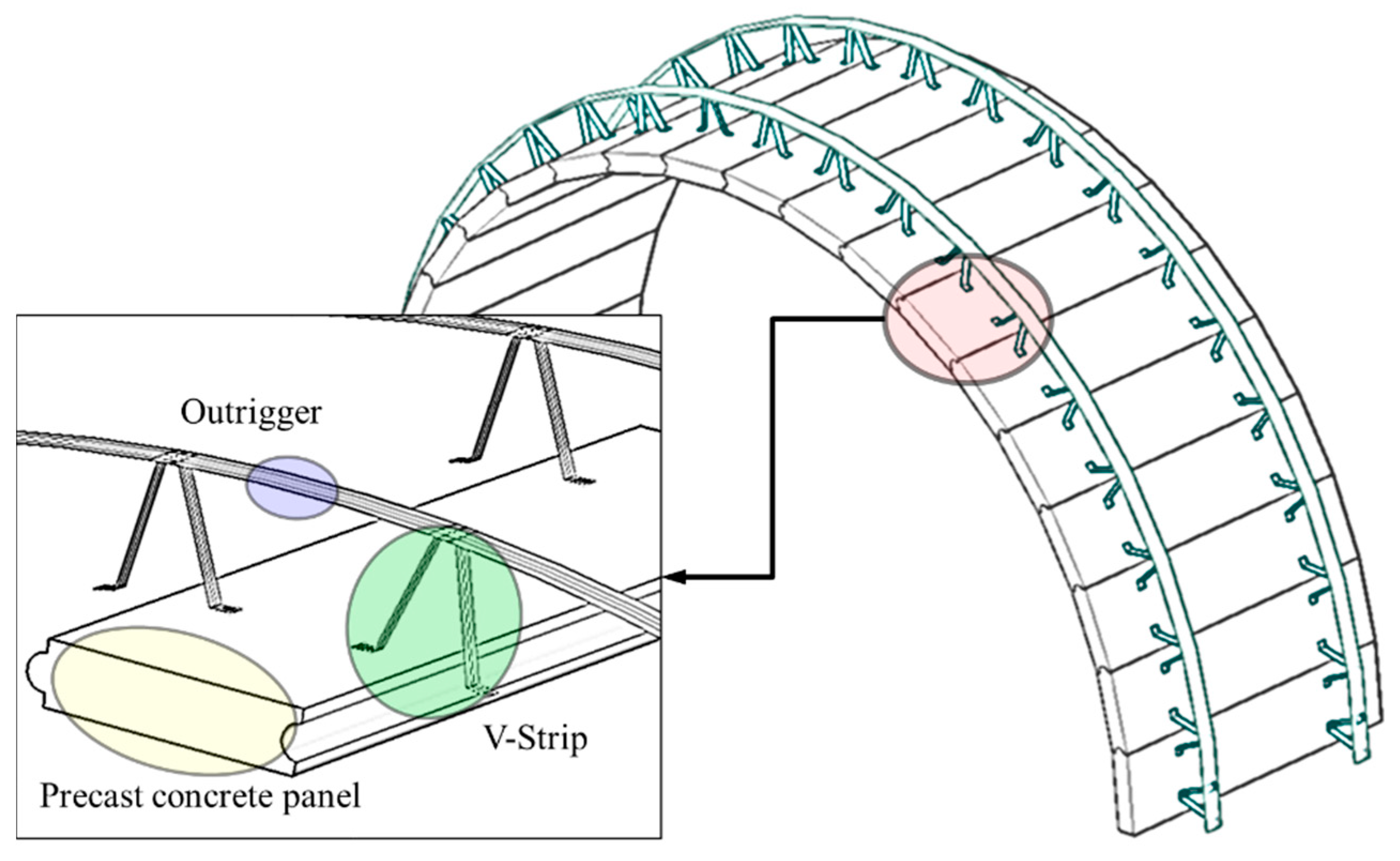
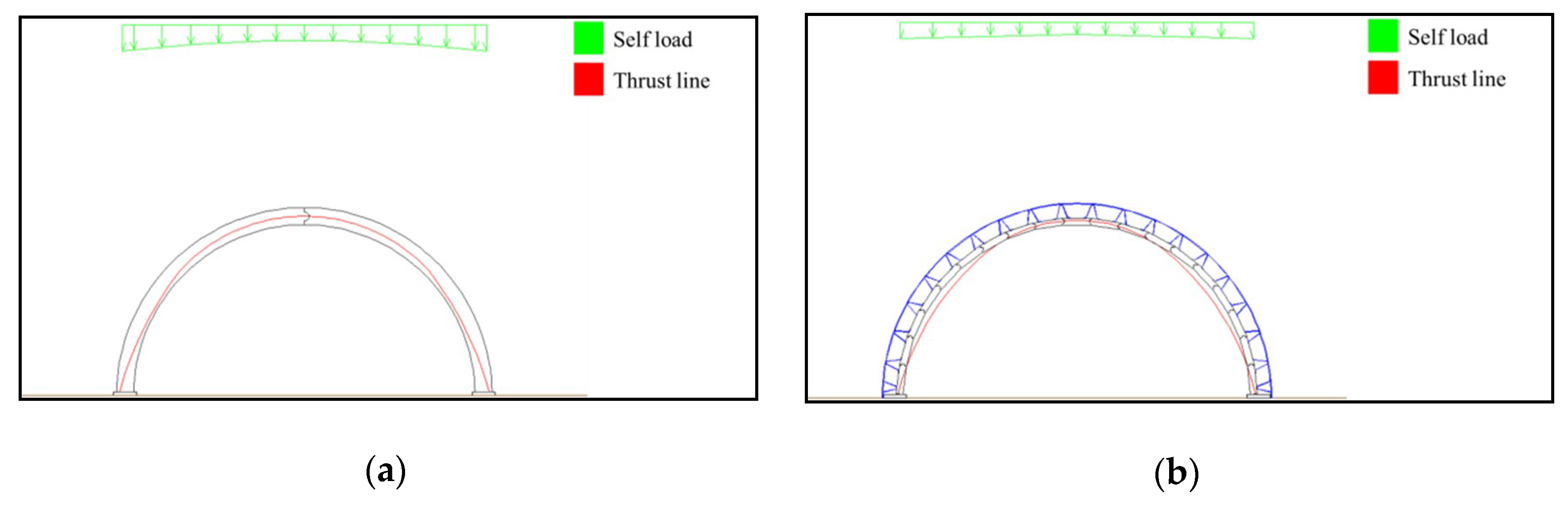
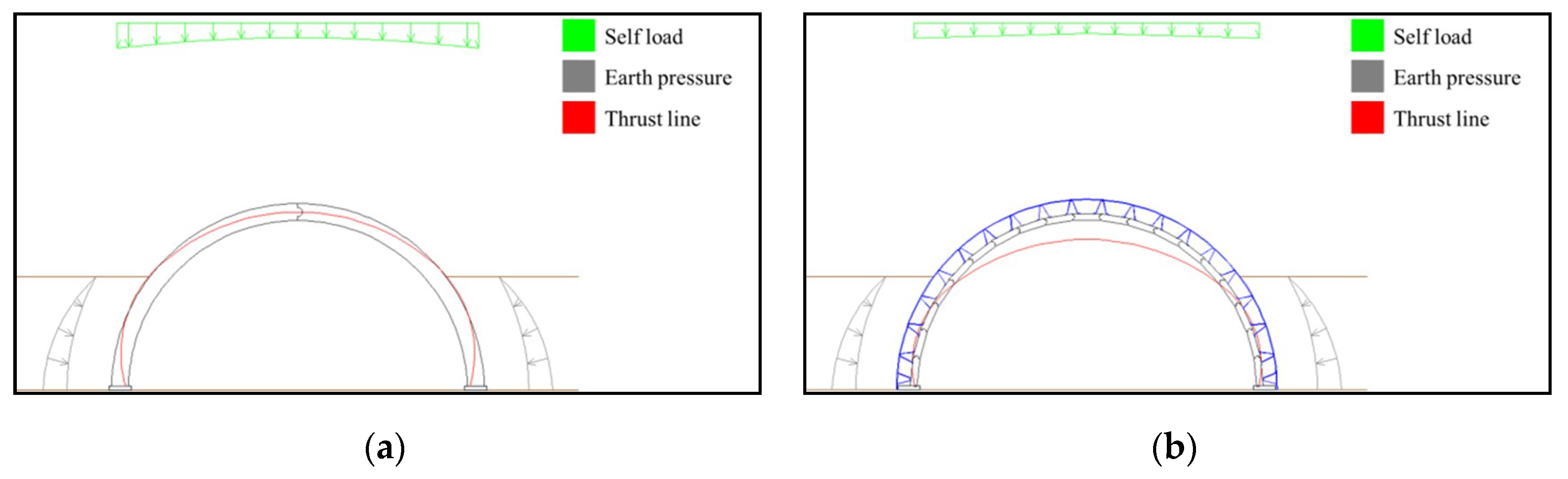
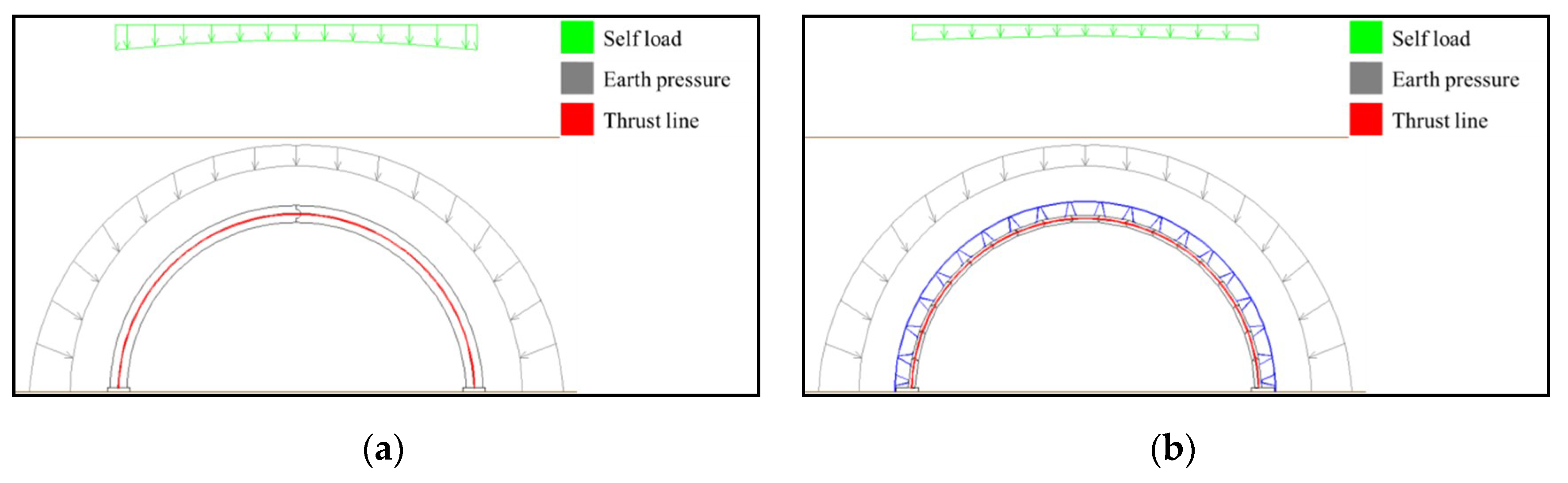
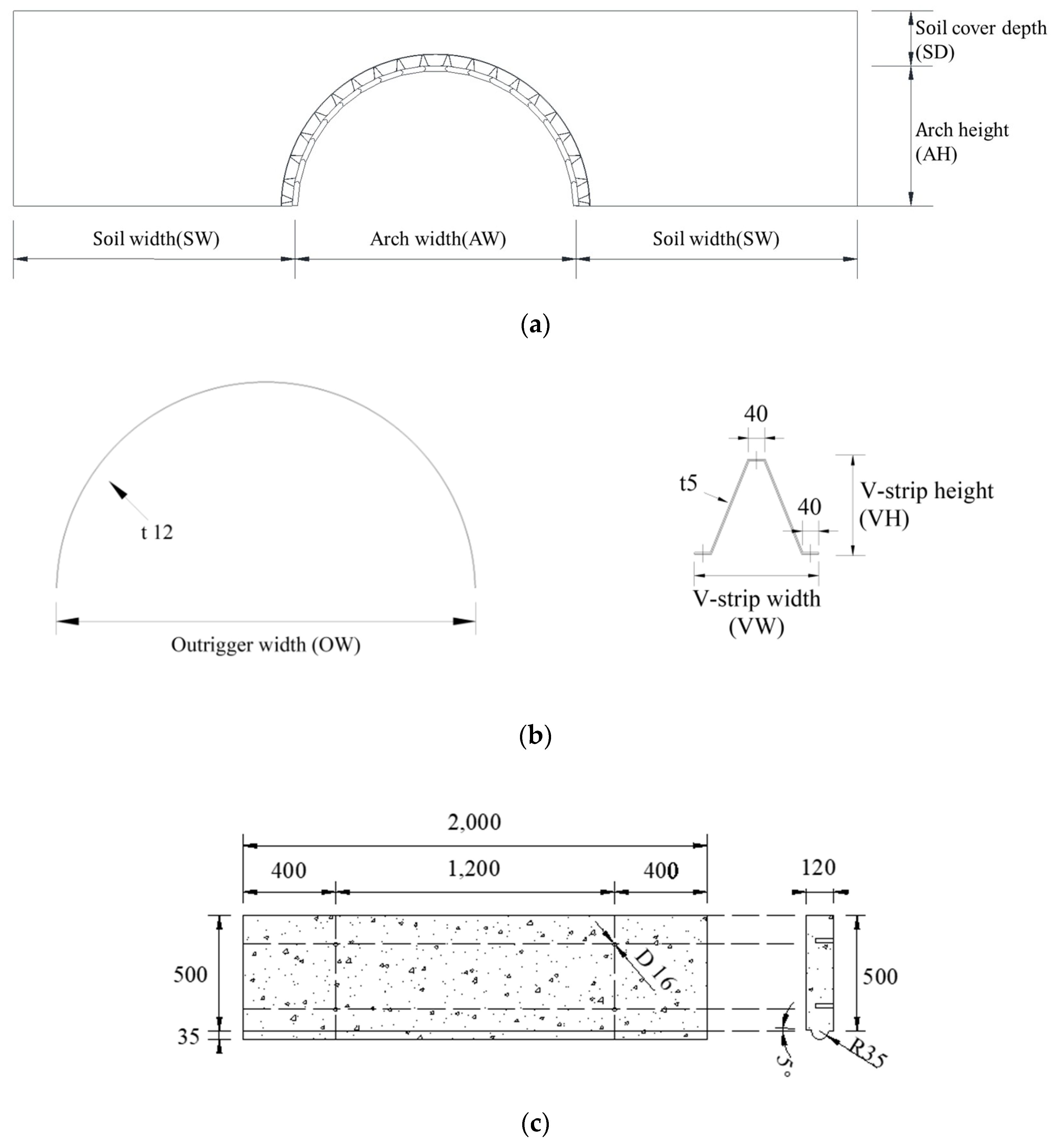








| AW (m) | AH (m) | OW, SW (m) | VW (mm) | VH (mm) | SD (m) | RR |
|---|---|---|---|---|---|---|
| 6.3 (6 m) | 3.0 | 6.7 | 304.5 | 234.2 | 1.2 | 0.48 (0.5) |
| 7.2 (7 m) | 3.2 | 7.8 | 302.5 | 244.2 | 0.44 (0.45) | |
| 8.0 (8 m) | 3.0 | 8.6 | 296.5 | 247.2 | 0.38 (0.4) |
| Category | Precast Concrete Panels | Outriggers and V-Strips | Backfill Soil and Fill |
|---|---|---|---|
| Compressive strength (MPa) | 35 | - | - |
| Yield strength (MPa) | - | 280 | - |
| Tensile Strength (MPa) | 4.74 | 450 | - |
| Elastic modulus (MPa) | 28,825.3 | 205,000 | 200 |
| Unit mass (kg/m3) | 2,400 | 7,850 | 1,940 |
| Poisson’s ratio | 0.16 | 0.3 | 0.33 |
| Internal friction angle (°) | - | - | 30 |
| Coefficient of friction (with precast concrete panels) | 0.4 | - | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, S.H.; Cho, K.-I.; Huh, J.; Ahn, J.-H. The Performance Assessment of a Precast, Panel-Segmented Arch Bridge with Outriggers. Appl. Sci. 2019, 9, 4646. https://doi.org/10.3390/app9214646
Jeon SH, Cho K-I, Huh J, Ahn J-H. The Performance Assessment of a Precast, Panel-Segmented Arch Bridge with Outriggers. Applied Sciences. 2019; 9(21):4646. https://doi.org/10.3390/app9214646
Chicago/Turabian StyleJeon, Seok Hyeon, Kwang-Il Cho, Jungwon Huh, and Jin-Hee Ahn. 2019. "The Performance Assessment of a Precast, Panel-Segmented Arch Bridge with Outriggers" Applied Sciences 9, no. 21: 4646. https://doi.org/10.3390/app9214646
APA StyleJeon, S. H., Cho, K.-I., Huh, J., & Ahn, J.-H. (2019). The Performance Assessment of a Precast, Panel-Segmented Arch Bridge with Outriggers. Applied Sciences, 9(21), 4646. https://doi.org/10.3390/app9214646






