Multichannel Active Noise Control Based on Filtered-x Affine Projection-Like and LMS Algorithms with Switching Filter Selection

Abstract

Affine projection (AP) algorithms have been demonstrated to have faster convergence speeds than the conventional least mean square (LMS) algorithms. However, LMS algorithms exhibit smaller steady-state mean square errors (MSEs) when compared with affine projection (AP) algorithms. Recently, several authors have proposed alternative methods based on convex combinations to improve the steady-state MSE of AP algorithms, even with the increased computational cost from the simultaneous use of two filters. In this paper, we present an alternative method based on an affine projection-like (APL-I) algorithm and least mean square (LMS) algorithm to solve the ANC under stationary Gaussian noise environments. In particular, we propose a switching filter selection criteria to improve the steady-state MSE without increasing the computational cost when compared with existing models. Here, we validate the proposed strategy in a single and a multichannel system, with and without automatically adjusting the scaling factor of the APL-I algorithm. The results demonstrate that the proposed scheme exploits the best features of each filter (APL-I and LMS) to guarantee rapid convergence with a low steady-state MSE. Additionally, the proposed approach demands a low computational burden compared with existing convex combination approaches, which will potentially lead to the development of real-time ANC applications.

1. Introduction

In recent years, advanced adaptive algorithms have attracted much interest in the development of effective active noise control (ANC) systems [1,2]. Specifically, the affine projection (AP) algorithm [3] has emerged as an attractive solution for effective noise reduction since this algorithm converges more rapidly than the least mean square (LMS) algorithm; however, their high computational cost restricts its use in some ANC applications. Currently, new alternatives to reduce the computational cost of the AP algorithms have been proposed. As a consequence, these new approaches potentially allow the construction of efficient ANC systems [4,5]. For example, Avalos et al. [6] proposed a new variant of filtered-x AP (FXAP) algorithm, which is based on an affine projection-like (APL-I) algorithm, to significantly minimize the computational cost and maintain the high convergence speed compared with that of the conventional FXAP algorithms. In fact, their proposed algorithm can thus be potentially used in ANC systems that require lower computational power compared to AP algorithms and to retain a high convergence speed when compared with existing approaches. Even with these advantages, system performance can be improved because the algorithms based on affine projections suffer from a large steady-state mean square error (MSE) [6,7,8], causing less noise reduction. To improve the MSE, variable-step algorithms have been presented [4]. Nevertheless, the user must know some parameters a priori, which are not always available, to ensure the proper operation of the algorithm. Recently, alternative methods based on combination schemes to ensure high convergence speed and small MSE have been reported [9,10,11]. These combination schemes are commonly composed of a fast filter and a slow filter. The use of a fast filter results in a rapid convergence rate, while a slow filter yields a steady-state MSE. With respect to this application, very few works have been proposed to process ANC systems using convex combination methods. In particular, Ferrer et al. [12] presented an alternative method based on convex combination of filtered-x least mean square (FXLMS) algorithms for single-channel and multichannel ANC systems. However, the convergence speed is slow, and the overall computational cost is very high since both adaptive filters operate simultaneously during the entire process. Nithin et al. [13] proposed a convex combination based on a functional link artificial neural network (FLANN) filter along with a Volterra filter for a single-channel ANC system. Their proposal focused on nonlinear adaptive filters. Additionally, both filters process the signals concurrently, similar to in the previous case [12]. Recently, Al Omour et al. [14] developed a convex combination of the filtered-X least mean fourth (FXLMF) and FXLMS algorithms. However, both algorithms belong to the LMS family, resulting in a slow convergence speed. Recently, Song et al. [15] proposed a combination of two filtered-x generalized mixed norm (FXGMN) algorithms for a single-channel ANC system. This algorithm exhibits lower computational cost than AP algorithms, because this approach is based on LMS algorithms. However, the user must adjust several parameters to tune the algorithm by trial and error, resulting a significant time-consuming. Analyzing previous works, these approaches employ at least twice the computational burden when compared with conventional adaptive filters. Therefore, the development of alternative methods with low computational complexity, low MSE and high convergence speed to efficiently process multichannel ANC systems is still a great challenge. In this paper, we present a scheme based on the filtered-x affine projection-like (FXAPL-I) and FXLMS algorithms for single-channel and multichannel ANC applications. In our scheme, high convergence speed with a lower MSE is achieved by alternating the selection between these filters. Therefore, it is not necessary to enable both filters during the entire process. To evaluate the effectiveness of the proposed scheme, we simulate single-channel and multichannel ANC systems. The results demonstrate that the proposed algorithm exhibits a good convergence rate, a small MSE and a reduced computational burden when compared with existing schemes based on linear active noise control. This paper is organized as follows. In Section 2, the conventional filtered-x structure is described. The proposed combination with switching selection is described in Section 3. In Section 4, the analysis of the computational complexity of the derived algorithm is presented. In Section 5, some experiments to evaluate the proposal are described. Finally, the conclusions are presented in Section 7.

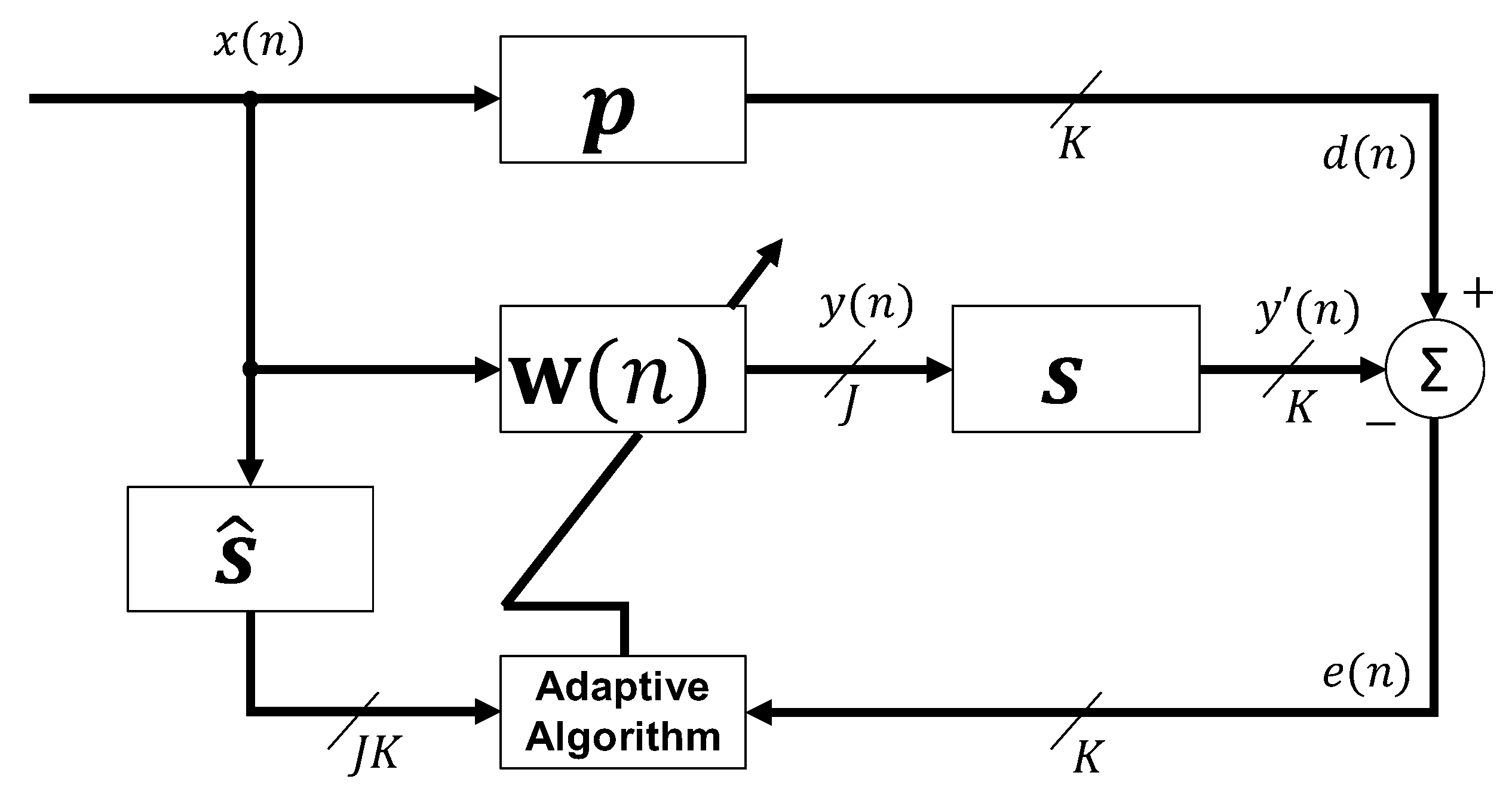
2. A Brief Introduction to the Multichannel Filtered-x Affine Projection-Like (FXAPL-I) and Filtered-x Least Mean Square (FXLMS) Algorithms

In this section, the general background on adaptive filters based on filtered-x affine projection-like (FXAPL-I) and filtered-x least mean square (FXLMS) algorithms is briefly presented because they are used in the development of the multichannel ANC systems in this work. The generic structure of a multichannel ANC system is shown in Figure 1. The blocks p and s are the primary and secondary paths, respectively; K is the number of error sensors; J is the number of actuators; $x_i\left(n\right)$ is the ith reference signal obtained from I reference sensors; and $y_j\left(n\right)$ is the adaptive filter output as follows:

$$y_j\left(n\right)={\mathbf{w}}_{ji}^t\left(n\right){\mathbf{x}}_i\left(n\right)$$

(1)

The reference signal is defined as follows:

$${\mathbf{x}}_i\left(n\right)={\left[\begin{array}{cccc}{x}_i\left(n\right)& x_i(n-1)& \cdots & x_i(n-N+1)\end{array}\right]}^t$$

(2)

and the adaptive filter coefficients are as follows:

$${\mathbf{w}}_{ji}\left(n\right)={\left[\begin{array}{cccc}{w}_{j,i,1}\left(n\right)& w_{j,i,2}\left(n\right)& \cdots & w_{j,i,N}\end{array}\right]}^t$$

(3)

where N is the length of the adaptive filter. To compensate for the effects caused by the secondary paths ${\mathbf{s}}_{kj}\left(n\right)$, the reference signal $x_i\left(n\right)$ is filtered using the following expression:

$$x_{ijk}^{\prime }\left(n\right)={\widehat{\mathbf{s}}}_{kj}^t\left(n\right){\mathbf{v}}_i\left(n\right)$$

(4)

where ${\widehat{\mathbf{s}}}_{kj}$ is a fixed FIR filter of length M that models ${\mathbf{s}}_{kj}\left(n\right)$ and $v_i\left(n\right)={\left[\begin{array}{cccc}{x}_i\left(n\right)& x_i(n-1)& \cdots & x_i(n-M+1)\end{array}\right]}^t$.

In practical ANC systems, the desired signal $\mathbf{d}\left(n\right)$, which is used for the error computation, is unavailable. However, the error signal $\mathbf{e}\left(n\right)$ can be obtained. As a consequence, the error signal vector $\mathbf{e}\left(n\right)$ is estimated by means of an approximation. The estimation can thus be performed by employing past samples of the error signals $\mathbf{e}\left(n\right)$ as follows:

$${\mathbf{e}}_k\left(n\right)\approx {\left[\begin{array}{cccc}{e}_k\left(n\right)& e_k(n-1)& \cdots & e_k(n-L+1)\end{array}\right]}^t$$

(5)

As shown in Figure 1, the generic structure of the ANC system uses a block that is known as an adaptive algorithm. This block can use either the FXAPL-I or the FXLMS algorithm.

• FXLMS
  The FXLMS algorithm updates the coefficients as follows:

  $${\mathbf{w}}_{ji}(n+1)={\mathbf{w}}_{ji}\left(n\right)+\sum _{k=1}^K{\mu }_{ijk}{x}_{ijk}^{\prime }\left(n\right)e_k\left(n\right),j=1,2,\cdots ,J,i=1,2,\cdots ,I$$

  (6)

  where ${\mu }_{ijk}$ is a fixed value between [0,1] and is usually chosen by trial and error. The FXLMS algorithm is widely used because of its simplicity, robustness and steady-state MSE. However, its convergence speed is low, which can restrict its use in some practical applications. The algorithms based on AP overcome the aforementioned problem because its convergence speed is very fast by paying a penalty in terms of computational complexity and a large MSE at the steady state.
• FXAPL-I
  To calculate the coefficient update of the FXAPL-I algorithm, the filtered-x signals are arranged in a matrix, as follows:

  $${\mathbf{X}}_{ijk}\left(n\right)=\left[\begin{array}{cccc}{\mathbf{x}}_{ijk}^{\prime }\left(n\right)& {\mathbf{x}}_{ijk}^{\prime }(n-1)& \cdots & {\mathbf{x}}_{ijk}^{\prime }(n-L+1)\end{array}\right]$$

  (7)

  where ${\mathbf{x}}_{ijk}^{\prime }\left(n\right)$ represents the filtered-x signals as follows:

  $${\mathbf{x}}_{ijk}^{\prime }\left(n\right)={\left[\begin{array}{cccc}{x}_{ijk}^{\prime }\left(n\right)& x_{ijk}^{\prime }(n-1)& {}_{\cdots }& x_{ijk}^{\prime }(n-N+1)\end{array}\right]}^t$$

  (8)
  Based on Equation (7), the filter update for the FXAPL-I algorithm is as follows:

  $${\mathbf{w}}_{ji}(n+1)={\mathbf{w}}_{ji}\left(n\right)+\sum _{k=1}^K{\mu }_{ijk}{\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k\left(n\right),j=1,2,\cdots ,J,i=1,2,\cdots ,I$$

  (9)

  where step size ${\mu }_{\mathrm{ijk}}$ is calculated using the following expression:

  $${\mu }_{ijk}=\frac{\Vert {\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k{\left(n\right)\Vert }^2}{\Vert {\mathbf{X}}_{ijk}^t\left(n\right){\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k{\left(n\right)\Vert }^2}·sf$$

  (10)

  where $sf$ is a scaling factor used to compensate the mismatch between ${\widehat{\mathbf{s}}}_{kj}\left(n\right)$ and ${\mathbf{s}}_{kj}\left(n\right)$. Commonly, the value of $sf$ can be defined in the interval $\left[0,1\right]$, and the designer can choose it by trial and error.
  A critical parameter of the existing FXAPL-I algorithm is the scaling factor because the convergence can be affected by choosing a wrong value by the designer. Until now, there has been no established method to determine the scaling factor. The following section presents a new method to dynamically adjust this parameter to optimize the design time.

Dynamic Adjustment of the Scaling Factor

To obtain an efficient and robust FXAPL-I algorithm, the scaling factor must be adjusted manually, requiring a time-consuming and costly effort by expert human designers. To reduce this burden, Vazquez et al. [16] introduced a novel strategy to automatically adjust the scaling factor and thus contribute to the rapid development of practical ANC applications. Their method to adjust automatically the scaling factor is based on the estimation of an auxiliary error vector ${\epsilon }_{ji}\left(n\right)$ [17]. For the FXAPL-I algorithm, the auxiliary vector is defined as ${\epsilon }_{ji}\left(n\right)={\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k\left(n\right)$. The algorithm for the coefficient update can thus be rewritten as follows:

$${\mathbf{w}}_{ji}(n+1)={\mathbf{w}}_{ji}\left(n\right)+\sum _{k=1}^K{\mu }_{ijk}{\epsilon }_{ji}\left(n\right)$$

(11)

The dynamic scaling factor can then be expressed as follows:

$${sf}_{ijk}=s{f}_{max}\frac{\parallel p_{ijk}{\left(n\right)\parallel }^2}{\parallel p_{ijk}{\left(n\right)\parallel }^2+C}$$

(12)

where $p_{ijk}\left(n\right)$ is an estimation of ${\epsilon }_{ji}\left(n\right)$ that is obtained as $p_{ijk}\left(n\right)=\alpha p_{ijk}(n-1)+(1-\alpha ){\epsilon }_{ji}\left(n\right)$ with a smoothing factor (0$<\alpha <$1) and C is a parameter related to the projection order and is approximated by $L_{ij}/$SNR, where SNR is the signal-to-noise ratio. To guarantee stability, the maximum scaling factor parameter $s{f}_{max}$ is set to less than 1. The proposed method to compute the step size ${\mu }_{ijk}$ is thus as follows:

$${\mu }_{ijk}=\frac{\Vert {\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k{\left(n\right)\Vert }^2}{\Vert {\mathbf{X}}_{ijk}^t\left(n\right){\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_k{\left(n\right)\Vert }^2}·s{f}_{ijk}$$

(13)

In this work, the use of the automatically adjustment method contributes little to the overall computational complexity. However, its use potentially allows the rapid development of practical applications by minimizing the time-consuming effort of the designers.

3. Proposed Scheme with Switching Filter Selection

In this section, the proposed scheme based on the alternating selection of parallel FXAPL-I and FXLMS filters to achieve high convergence speed with low MSE is described. The proposed strategy is based on alternating affine projection algorithm (A-AP) [18]. In this study, we propose a new strategy to be used in the development of ANC systems. Specifically, the selection criteria are based on the comparison between the error power of the combined filters and the steady-state MSE. We use the computational capabilities of the FXAPL-I algorithm to achieve high convergence speed, while the FXLMS is used to guarantee a low steady-state MSE. The proposed block diagram is shown in Figure 2, in which the outputs of the filters $y_{1ji}\left(n\right)$ and $y_{2ji}\left(n\right)$ are combined using the following equation:

$$y_{ji}\left(n\right)=\lambda \left(n\right){\mathbf{y}}_{1ji}\left(n\right)+[1-\lambda \left(n\right)]y_{2ji}\left(n\right)$$

(14)

where $\lambda \left(n\right)$ is a mixing parameter, which is in the range [0,1]. This parameter determines the combination of the two filters (FXAPL-I and FXLMS) during the entire filtering process at each iteration. According to Equation (14), the parameter $\lambda \left(n\right)$ determines the overall output $y_{ji}\left(n\right)$. If $\lambda \left(n\right)$ is near one, the overall output $y_{ji}\left(n\right)$ is equal to the output $y_{1ji}\left(n\right)$ (FXAPL-I’s output). However, if $\lambda \left(n\right)$ is near zero, the overall output $y_{ji}\left(n\right)$ is equal to the output $y_{2ji}\left(n\right)$ (FXLMS’s output). A sigmoid function is used to compute $\lambda \left(n\right)$ as follows:

$$\lambda \left(n\right)=\frac{\begin{array}{c}1\end{array}}{\begin{array}{c}1+{\mathrm{e}}^{-\mathbf{a}\left(n\right)}\end{array}}$$

(15)

where $\mathbf{a}\left(n\right)$ is an auxiliary parameter used to minimize the instantaneous square error of the filters and is computed as follows:

$$\mathbf{a}(n+1)=\mathbf{a}\left(n\right)+{\mu }_a{\mathbf{e}}_k\left(n\right)[{\mathbf{y}}_{1ji}\left(n\right)-y_{2ji}\left(n\right)]·\lambda \left(n\right)[1-\lambda \left(n\right)]+\rho [\mathbf{a}\left(n\right)+\mathbf{a}(n-1)]$$

(16)

where $\rho$ is a positive constant, ${\mu }_a$ is the step size for $\mathbf{a}\left(n\right)$ and ${\mathbf{e}}_k\left(n\right)$ represents the error signal of the overall filter and is presented as follows:

$${\mathbf{e}}_k\left(n\right)=\lambda \left(n\right){\mathbf{e}}_{1k}\left(n\right)+[1-\lambda \left(n\right)]e_{2k}\left(n\right)$$

(17)

To speed up the convergence of the FXLMS filter, the weights of the FXAPL-I filter are partially transferred to the FXLMS filter when abrupt change occurs. The adaptation rule to transfer these weights is defined as follows:

$${\mathbf{w}}_{2ji}\left(n\right)=\alpha {\mathbf{w}}_{2ji}\left(n\right)+(1-\alpha ){\mathbf{w}}_{2ji}(n-1)\mathrm{for}\lambda \left(n\right)>t$$

where the parameters t and $\alpha$ are chosen as 0.98 and 0.9, respectively [17].

Analysis of the prior research shows that the convex combinations significantly reduce the steady-state MSE but with a penalty in terms of computational complexity because two filters operate simultaneously. We propose implementing switching selection criteria to reduce the computational complexity of the convex combination because the filters (FXAPL-I and FXLMS) need not operate simultaneously during the entire filtering process. We propose selection criteria that indicate when the coefficients must be updated by analyzing the state of the overall error signal ${\mathbf{e}}_k\left(n\right)$, i.e., the selection criteria are determined by comparing the instantaneous error power with the steady-state MSE of the FXAPL-I algorithm, which is the faster filter. The theoretical MSE is determined as follows [19]:

$$\delta =\frac{2L}{2L-1}{\sigma }_{\mathbf{v}}^2$$

(18)

where ${\sigma }_{\mathbf{v}}^2$ is the variance of a noise signal. The updates of the coefficients for each filter are determined by the following rule:

$${\mathbf{w}}_{1ji}(n+1)=\left\{\begin{array}{cc}{\mathbf{w}}_{1ji}\left(n\right)+{\sum }_{k=1}^K{\mu }_{1ijk}{\mathbf{X}}_{ijk}\left(n\right){\mathbf{e}}_{1k}\left(n\right),\hfill & \mathrm{if}{e}_k^2\left(n\right)\ge \delta \hfill \\ {\mathbf{w}}_{1ji}\left(n\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(19)

$${\mathbf{w}}_{2ji}(n+1)=\left\{\begin{array}{cc}{\mathbf{w}}_{2ji}\left(n\right),\hfill & \mathrm{if}{e}_k^2\left(n\right)\ge \delta \hfill \\ {\mathbf{w}}_{2ji}\left(n\right)+{\sum }_{k=1}^K{\mu }_{2ijk}{\mathbf{x}}_{ijk}\left(n\right)e_{2k}\left(n\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(20)

Equations (19) and (20) indicate when the FXAPL-I and FXLMS algorithms must be updated. If the power of the overall error ${\mathbf{e}}_k\left(n\right)$ is larger than the steady-state MSE, the FXAPL-I filter must be updated, and the FXLMS filter does not update its coefficients, and vice versa. With the proposed scheme, a fast convergence speed using the FXAPL-I algorithm is attained, and the computational burden and the steady-state MSE are reduced by employing the FXLMS algorithm.

4. Analysis of Computational Complexity

We analyze the computational complexity of the proposed method in terms of the number of multiplications and additions per iteration for single-channel and multichannel simulations. The computational cost is compared with conventional FXAPL-I, filtered-x alternating affine projection (FXA-AP) and FXLMS algorithms. The notation used is as follows: M is the length of the secondary path, N is the length of the adaptive filter and L is the order of the projection.

4.1. Analysis of Computational Complexity under Single Channel ANC System Configuration

In

Table 1. Number of multiplications per iteration of the FXLMS, FXAPL-I, FXA-AP, FXAPL-I with switching selection and FXLMS with switching selection algorithms for a single-channel ANC system. Typical case: M = 128, N = 100 and L = 5.

Algorithm	Multiplications	Typical Case
FXLMS	$2N+M+K$	330
FXAPL-I	$3NL+L+3N+2M$	2061
FXA-AP	$O\left(L^3\right)+2L^{2}N+2LN+2N+5M+12$	6921
FXAPL-I with switching selection	$3NL+6N+4L+2M+8$	2384
FXLMS with switching selection	$5N+2M+3L+9$	780

and

Table 2. Number of additions per iteration of the FXLMS, FXAPL-I, FXA-AP, FXAPL-I with switching selection and FXLMS with switching selection algorithms for a single-channel ANC system. Typical case: M = 128, N = 100 and L = 5.

Algorithm	Additions	Typical Case
FXLMS	$2N+M-1$	326
FXAPL-I	$L(3N+M-1)+2N+M-2$	2461
FXA-AP	$O\left(L^3\right)+2L^{2}N+LN+M+3N+9$	6062
FXAPL-I with switching selection	$L(3N+M+6)+4N+M$	2698
FXLMS with switching selection	$4N+2M+7L+1$	692

, the computational complexity of the proposed filtering scheme in terms of number of multiplications and additions, respectively, is shown. We calculate the number of addition and multiplication operations required per iteration by taking into account a typical case ($M=128$, $N=100$ and $L=5$). As can be observed in Table 1 and Table 2, the FXA-AP algorithm presents the highest computational cost. However, it offers the fastest convergence speed. As shown in Table 1 and Table 2, the proposed filtering scheme adds a few computations per iteration when compared with conventional FXAPL-I and FXLMS algorithms because of the time required to select the appropriate switching filter. Nevertheless, the proposed filtering scheme converges rapidly with a low MSE by enabling one filter or the other at different moments of time, i.e., not both at the same time. The proposed filtering scheme improves these aspects by reducing the computational complexity of the FXAPL-I once the steady-state MSE is reached, i.e., at this moment, the filtering process is only performed by the FXLMS algorithm. However, if the dynamic adjustment of the scaling factor is enabled, the proposed filtering scheme requires $4N+2$ more multiplications and $2N+1$ more additions when compared with the operations required to execute the FXAP-L algorithm with a fixed scaling factor at each iteration. In addition,

Table 3. Memory requirements for the FXLMS, FXAPL-I, FXA-AP and the proposed algorithm for single-channel ANC systems.

Algorithm	Memory
FXLMS	$2N(N+M)+3$
FXAPL-I	$N(L+2)+L(L+1)+2M+4$
FXA-AP	$N(L+3)+L(L+2)+11+M$
Proposed algorithm with fixed scaling factor	$L(N+L+2)+3N+2M+14$
Proposed algorithm with dynamic scaling factor	$L(N+L+2)+2(N+1)+3N+2M+14$

shows the memory requirements of the FXLMS, FXAPL-I, FXA-AP and the proposed algorithm.

4.2. Analysis of Computational Complexity under Multichannel ANC System Configuration

For this evaluation, we consider a typical case ($M=128$, $N=100$, $L=5$, one reference sensor (I), two actuators (J) and two error sensors (K)). As in the former case, the proposed filtering scheme adds more addition and multiplication operations in comparison to the conventional FXAPL-I and FXLMS algorithms by simulating a multichannel ANC system. In this experiment, the proposed filtering scheme requires approximately two thousand additional operations per each iteration, as shown in

Table 4. Number of multiplications per iteration of the FXLMS, FXAPL-I, FXA-AP, FXAPL-I with switching selection and FXLMS with switching selection algorithms for a multichannel ANC system. Typical case: M = 128, N = 100, L = 5, I = 1 and J = K = 2.

Algorithm	Multiplications	Typical Case
FXLMS	$IJ\left[K\right(N+M)+N]+K$	1116
FXAPL-I	$(3NL+L+2N)KJI+NJI+J(MKI+2N+2MI)$	8444
FXA-AP	$IJ[K(O\left(L^3\right)+2L^{2}N+2LN+2N+M)+4M+9]+3K$	26,748
FXAPL-I with switching selection	$(3NL+L+2N)KJI+NJI+J(MKI+2N+2MI)+2\left[NJ\right(K+2I)+(L+1)J+K(2L+5\left)\right]$	10,128
FXLMS with switching selection	$J(MKI+2NK+2MI)+2\left[NJ\right(K+2I)+(L+1)J+K(2L+5\left)\right]+(NK+1)JI$	3510

and

Table 5. Number of additions per iteration of the FXLMS, FXAPL-I, FXA-AP, FXAPL-I with switching selection and FXLMS with switching selection algorithms for a multichannel ANC system. Typical case: M = 128, N = 100, L = 5, I = 1 and J = K = 2.

Algorithm	Additions	Typical Case
FXLMS	$IJ\left[K\right(M+N-1)+N]-J$	1106
FXAPL-I	$J\left[2\right(NK+L(M-1)I)+MIK]+\left[\right((2L+1)N+M-2)IJK+NIJ+J(I-1\left)\right]$	8956
FXA-AP	$IJ[K(O\left(L^3\right)+2L^{2}N+LN+M-1)+3N+10]+2(K-J)$	23,628
FXAPL-I with switching selection	$2\left[J\right(NK+(N+1)I)+(L+1\left)\right(J+2K+1\left)\right]+J\left[2\right(NK+L(M-1)I)+MIK]+\left[\right((2L+1)N+M-2)IJK+NIJ+J(I-1\left)\right]$	10,244
FXLMS with switching selection	$J\left[2\right(NK+(M-1)I)+MIK]+NIJ(2K+1)+2\left[J\right(NK+(N+1)I)+(L+1\left)\right(J+2K+1\left)\right]$	4108

. In general terms, AP algorithms exhibit high computational complexity. This computational cost is significantly increased for multichannel ANC systems. In this study, we demonstrate that the proposed filtering scheme reduces the complexity of FXAPL-I also in the case of multichannel ANC systems. The proposed filtering scheme guarantees a low computational cost; the computational cost of the proposed algorithm decreases rapidly once the steady-state MSE is reached and the FXLMS algorithm is computed. Therefore, we achieve a significant improvement in terms of convergence speed and MSE level by paying a tolerable penalty in terms of computational complexity. The proposed filtering scheme with dynamic adjustment of the scaling factor expends $4NIJK+2$ more multiplications and $2NIJK+1$ more additions than the FXAP-L algorithm with a fixed scaling factor at each iteration. In addition,

Table 6. Memory requirements for the FXLMS, FXAPL-I, FXA-AP and the proposed algorithm for multichannel ANC systems.

Algorithm	Memory
FXLMS	$IJ\left[N\right(K+1)+1]+K(JM+1)+IM+1$
FXAPL-I	$IJ\left[N\right(KL+K+1)+1]+L(L+1)+M(JK+I)+3$
FXA-AP	$IJ[K(2N+NL)+N+8]+K(JM+2L+1)+L^2+5$
Proposed algorithm with fixed scaling factor	$IJ\left[N\right(KL+3)+5]+M(KJ+I)+L(2K+L)+K+8$
Proposed algorithm with dynamic scaling factor	$IJ\left[\right((2KN+K)+1)+N(KL+3)+5]+M(KJ+I)+L(2K+L)+K+8$

shows the memory requirements of the FXLMS, FXAPL-I, FXA-AP and the proposed algorithm.

5. Simulation Results

To evaluate the proposed filtering scheme, we simulated two active noise-control systems (a single and a 1:2:2 multichannel) in MATLAB. Specifically, we evaluated the performance of the proposed filtering scheme by measuring the mean square error (MSE) at error microphones. Primary and secondary paths for both systems were modeled as finite impulse response (FIR) filters with lengths of 256 and 128 [20], respectively. In particular, the secondary path was estimated offline because it is unknown. The adaptive filters were modeled as FIR filters of length $N=100$. Specifically, FXAPL-I and FXA-AP algorithms employed a projection order $L=5$. The step sizes $\mu$ were chosen through trial and error. The scaling factor of the FXAPL-I algorithms is specified in the following paragraphs because each filtering system was evaluated under different conditions.

We must consider two different types of signals $x\left(n\right)$ to evaluate a single channel and a 1:2:2 multichannel as follows:

• A multitonal input with frequencies 200, 300, and 400 Hz. We added white Gaussian noise with an SNR of 30 dB to $x\left(n\right)$ to validate the robustness of the proposed filtering scheme.
• A white Gaussian noise signal with variance ${\sigma }_{\mathbf{v}}^2=0.1$.

To obtain the learning curves, we performed 50 experiments with 40,000 iterations each. We also induced an abrupt change at iteration 20,000, which was generated by multiplying the coefficients of the primary path by −1, to evaluate the tracking skills of the proposed filtering scheme.

5.1. Simulation of a Single-Channel ANC System

• First experiment: Multitonal noise input

We carried out two evaluations to validate the model operation using a fixed scaling factor, which was chosen by trail and error, and a dynamic adjustment of the scaling factor, as shown in

Table 7. Simulation parameters for computer experiments.

Parameters	Single-Channel ANC		Multi-Channel ANC
	Multi-Tonal Input	Gaussian Noise Input	Multi-Tonal Input	Gaussian Noise Input
$sf$	0.2	0.1	0.001	0.01
$s{f}_{max}$	0.1	0.1	0.5	0.5
$\mu$	0.00001	0.0006	0.00001	0.0007

. The parameters were chosen to provide the fastest convergence speed of the FXAPL-I algorithm and the lowest steady-state MSE in the FXLMS algorithm.

As shown in Figure 3, the FXA-AP algorithm exhibits the best performance in terms of convergence speed and MSE level by paying a penalty in terms of computational cost. In contrast, the proposed filtering scheme achieves a significant reduction in the steady-state MSE, i.e., of approximately 5 dB and 3 dB when compared to the existing FXAPL-I using a fixed and dynamic adjustment of the scaling factor $sf$, respectively. The proposed algorithm also reduces the computational cost when compared to the existing FXAPL-I algorithm. In the proposed filtering scheme, the FXAPL-I algorithm updates its coefficients 59,170 times (2.95%). Enabling the dynamic adjustment of the scaling factor, the FXAPL-I algorithm updates its coefficients 26,075 times (1.3%). When the steady-state MSE is reached, the FXLMS algorithm carries out the filtering process by updating its coefficients for the remaining part of the process. As shown in Figure 3, the steady-state MSE is reached more rapidly when the dynamic adjustment of the scaling factor is enabled. However, the MSE is higher when compared to the performance of the proposed filtering algorithm with the fixed scaling factor.

As can be observed in

Table 8. Total number of multiplications and additions of the FXAPL-I, FXLMS, FXA-AP and the proposed algorithms for a single-channel ANC system using a multitonal noise input.

Algorithm	Multiplications	Additions
FXLMS	660,000,000	652,000,000
FXAPL-I	4,122,000,000	4,922,000,000
FXA-AP	13,842,000,000	12,124,000,000
Proposed algorithm with fixed scaling factor	1,601,824,300	1,436,306,450
Proposed algorithm with dynamic scaling factor	1,631,122,340	1,502,695,020

, our proposal with fixed and dynamic scaling factor expend approximately 2.57, 2.52, 8.64, and 8.48 times fewer multiplications and 3.42, 3.27, 8.44, and 8.06 times fewer additions than do the FXAPL-I and FXA-AP algorithms, respectively. On the other hand, our proposal with fixed and dynamic scaling factor require approximately 2.42 and 2.47 more multiplications and 2.20 and 2.30 more additions than are required by the FXLMS algorithm. However, our proposal exhibits better convergence speed when compared with FXLMS algorithms. This factor is crucial in ANC applications since this factor determines the speed at which the noise is cancelled. From the engineering perspective, the use of FXLMS algorithms allows the development of easy and fast implementations. However, their application in ANC systems could be ineffective due to their low performance. Therefore, our proposal offers a good balance between convergence speed and computational cost.

• Second experiment: Gaussian noise input

We consider a Gaussian noise input to validate the robustness of the proposed filtering scheme. As shown in Figure 4, the FXA-AP algorithm presents the best MSE level compared with other algorithms. However, the convergence speed of the FXA-AP algorithm is as good as the convergence speed of our proposal. On the other hand, the convergence speed of the proposed filtering scheme is similar to the convergence speed of the existing FXAPL-I algorithms. However. the proposed filtering scheme requires fewer updates when compared with the existing FXAPL-I algorithm, i.e., the FXAPL-I algorithm with fixed and dynamic scaling factor updates its coefficients 98,765 times (4.93%) and 98,400 times (4.92%), respectively, whereas the existing FXAPL-I algorithm updates its coefficients during the entire filtering process.

As previous case, the performance of our proposal was verified in terms of operations.

Table 9. Total number of multiplications and additions of the FXAPL-I, FXLMS, FXA-AP and the proposed algorithms for a single-channel ANC system using a Gaussian noise input.

Algorithm	Multiplications	Additions
FXLMS	660,000,000	652,000,000
FXAPL-I	4,122,000,000	4,922,000,000
FXA-AP	13,842,000,000	12,124,000,000
Proposed algorithm with fixed scaling factor	1,678,715,530	1,581,390,400
Proposed algorithm with dynamic scaling factor	1,717,833,600	1,582,122,590

shows the number of additions and multiplications required to perform each algorithm by processing a Gaussian noise signal. In this case, our proposal with fixed and dynamic scaling factor expend approximately 2.45, 2.39, 8.24, and 8.057 times fewer multiplications and 3.11, 3.11, 7.66, and 7.66 times fewer additions than do the FXAPL-I and FXA-AP algorithms, respectively. In addition, our proposal exhibits similar convergence speed when compared with FXAPL-I algorithm, as shown in Figure 4. On the other hand, our proposal with fixed and dynamic scaling factor require approximately 2.54 and 2.60 more multiplications and 2.42 and 2.43 more additions than are required by the FXLMS algorithm. Despite using the minimal number of operations, the FXLMS algorithm shows slower convergence speed when compared with our proposal.

5.2. Simulation of a Multi-Channel ANC System

• First experiment: Multitonal noise input

Table 7 lists the parameters used in this experiment. As shown in Figure 5, the FXA-AP algorithm presents the fastest convergence speed. However, its MSE level varies significantly when abrupt changes occurs. On the contrary, the proposed filtering scheme employs fixed and dynamic scaling factor $sf$ to achieve a significant improvement in the steady-state MSE of approximately 3 dB when compared to the existing FXAPL-I and FXA-AP algorithms. The proposed filtering scheme exhibits a convergence speed similar to that of the existing FXAPL-I algorithm, by employing a dynamic scaling factor. In this case, the convergence speed is affected when the proposed filtering scheme with fixed scaling factor is used. As can be observed in Figure 5, the proposed algorithm with fixed scaling factor presents slow convergence speed at certain level of noise since the $sf$ is not optimal, i.e, we adjusted it by trial and error. In contrast, the proposed algorithm with dynamic scaling factor presents high convergence speed during the entire filtering process since the use of this strategy intends to achieve the optimal value automatically at each iteration. In this experiment, the FXAPL-I algorithm with fixed and dynamic scaling factor updates its coefficients 31,835 times (1.59%) and 32,747 times (1.63%), respectively.

As can be observed in

Table 10. Total number of multiplications and additions of the FXAPL-I, FXLMS, FXA-AP and the proposed algorithms for a multi-channel ANC system using a multitonal noise input.

Algorithm	Multiplications	Additions
FXLMS	2,232,000,000	2,212,000,000
FXAPL-I	16,888,000,000	17,912,000,000
FXA-AP	53,496,000,000	47,256,000,000
Proposed algorithm with fixed scaling factor	6,390,450,195	8,017,950,030
Proposed algorithm with dynamic scaling factor	8,023,620,846	10,456,255,000

, our proposal with fixed and dynamic scaling factor expend approximately 2.64, 2.10, 8.37, and 6.66 times fewer multiplications and 2.23, 1.71, 5.89, and 4.51 times fewer additions than do the FXAPL-I and FXA-AP algorithms, respectively. In addition, our proposal guarantees similar convergence speed and lower MSE level when compared with the FXAPL-I algorithm, as shown in Figure 5. On the other hand, our proposal with fixed and dynamic scaling factor require approximately 2.86 and 3.59 more multiplications and 3.62 and 4.72 more additions than are required by the FXLMS algorithm. However, our proposal exhibits better convergence speed and similar MSE level when compared with FXLMS algorithm.

• Second experiment: Gaussian noise input

In Figure 6, the learning curves created by simulating the proposed filtering scheme with fixed and dynamic scaling factors are shown. The corresponding data are listed in Table 7. The data show that the convergence speed of the proposed filtering scheme is similar to that of the existing FXAPL-I and FXA-AP algorithms. However, it requires fewer updates than the existing FXAPL-I algorithm requires. Specifically, it requires 315,200 (15.76%) and 440,434 (22.02%) updates for the fixed and dynamic scaling factors, respectively.

Table 11. Total number of multiplications and additions of the FXAPL-I, FXLMS, FXA-AP and the proposed algorithms for a multi-channel ANC system using a Gaussian noise input.

Algorithm	Multiplications	Additions
FXLMS	2,232,000,000	2,212,000,000
FXAPL-I	16,888,000,000	17,912,000,000
FXA-AP	53,496,000,000	47,256,000,000
Proposed algorithm with fixed scaling factor	7,925,438,400	9,779,913,600
Proposed algorithm with dynamic scaling factor	10,558,618,612	12,000,526,248

shows the number of additions and multiplications required to perform each algorithm for a multi-channel ANC system processing a Gaussian noise signal. In this case, our proposal with fixed and dynamic scaling factor expend approximately 2.13, 1.59, 6.74, and 5.06 times fewer multiplications and 1.83, 1.49, 4.83, and 3.93 times fewer additions than do the FXAPL-I and FXA-AP algorithms, respectively. On the other hand, our proposal with fixed and dynamic scaling factor require approximately 3.55 and 4.73 more multiplications and 4.42 and 5.42 more additions than are required by the FXLMS algorithm. Despite using the minimal number of operations, the FXLMS algorithm shows slower convergence speed when compared with our proposal.

6. Discussion

In recent years, convex combinations algorithms to improve performance in ANC systems have been reported [12,13,14,15]. The proposals generally improve the MSE by paying a significant penalty in terms of computational burden. However, this factor consequently limits its use for practical ANC systems. Specifically, single-channel ANC systems have been exhaustively studied [13,14,15]. The results have demonstrated that the performance of a single-channel ANC can be improved using two filters with complementary capabilities, which operate during the entire filtering process. However, these solutions at least double the computational cost when compared with the classic adaptive filters. For a multichannel ANC system, the computational cost is sufficiently high; thus, their implementation in practical applications is not infeasible. For example, Ferrer et al. [12] proposed a costly solution that can improve the steady-state MSE of ANC multichannel systems using convex solutions (C-FXLMS). The convex approaches promise to be potential solutions in the development of effective and robust algorithms in terms of convergence speed and steady-state MSE performance; however, they incur a significant penalty in terms of computational cost. In this work, we propose an alternative solution that exhibits high computational cost at the beginning of the filtering processing. However, the computational cost is reduced significantly once the steady-state MSE is reached. At this time, the FXLMS is used during the remaining filtering time. The final computational cost is comparable to the proposals based on conventional FXLMS, thus having potential for use in practical ANC systems.

7. Conclusions

In this study, we propose a new filtering scheme with switching selection for single-channel and multichannel ANC systems under stationary Gaussian noise environments. The proposed filtering scheme uses two types of adaptive filters as follows:

• We use the filtered-x affine projection-like (FXAPL-I) algorithm to achieve fast convergence.
• We employ a filtered-x least mean square (FXLMS) algorithm to guarantee a low steady-state MSE.

Using a combination of both approaches improves the steady-state MSE and reduces the computational cost. The proposed filtering scheme uses selection criteria that are based on the level of the error power of the combined filters and the steady-state MSE of the FXAPL-I algorithm to create an alternating switch for the adaptive filters, although the computational cost of the proposed filtering scheme algorithms is slightly greater than the computational cost of the conventional filtering schemes, such as the FXAPL-I and FXLMS algorithms. The proposed filtering scheme has a significantly improved steady-state MSE. Specifically, the filtered-x affine projection-like (FXAPL-I) algorithm with filtering switching selection uses more operations to more rapidly reach steady state. Once the steady state is reached, which means that the level of the error power of the combined filters is lower than the MSE of the FXAPL-I algorithm, the FXLMS algorithm is used for filtering. In this way, we reduce the overall computational burden and guarantee a low steady-state MSE. The simulation results confirm that the filtering scheme using the FXAP-L algorithm with fixed scaling factor achieves a lower MSE than the existing FXAP-L algorithm by paying a penalty in terms of the convergence rate. However, using the dynamic adjustment of the scaling factor, a convergence rate similar to that of the FXAPL-I algorithm is achieved. In addition, the algorithm maintains the improvement of the MSE. The results also confirm that the number of coefficient updates of the proposed FXAPL-I algorithm is greatly reduced. The proposed filtering scheme has the potential to help create cutting-edge applications for multichannel ANC systems in an efficient and more rapid manner by using a new method to dynamically adjust the scaling factor for the FXAPL-I algorithm to improve algorithm performance and reduce time expenses.