Revisiting the Meandering Instability During Step-Flow Epitaxy
Abstract
:1. Introduction
2. Stability Analysis
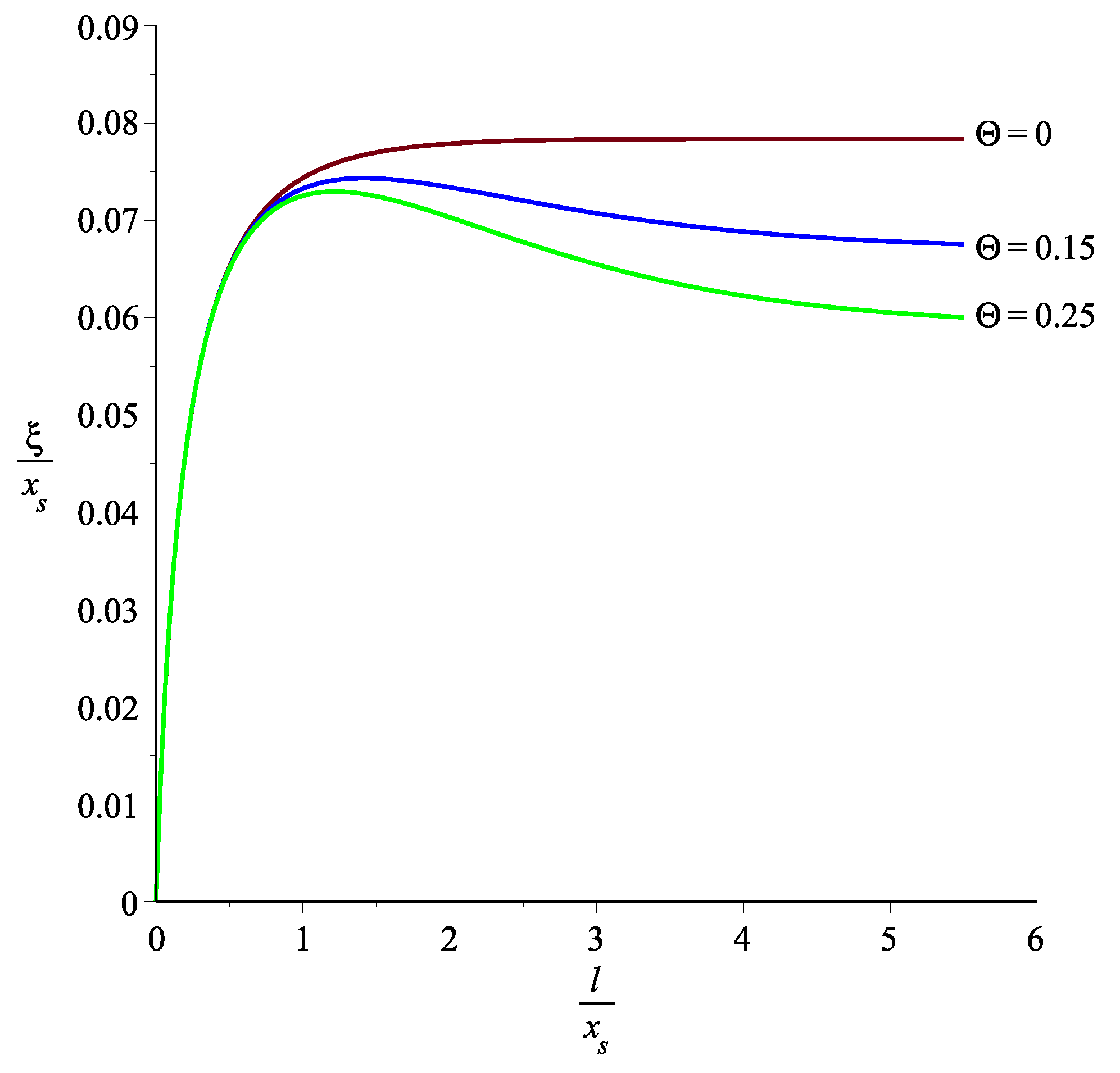
2.1. The Dependence of the Stability Function
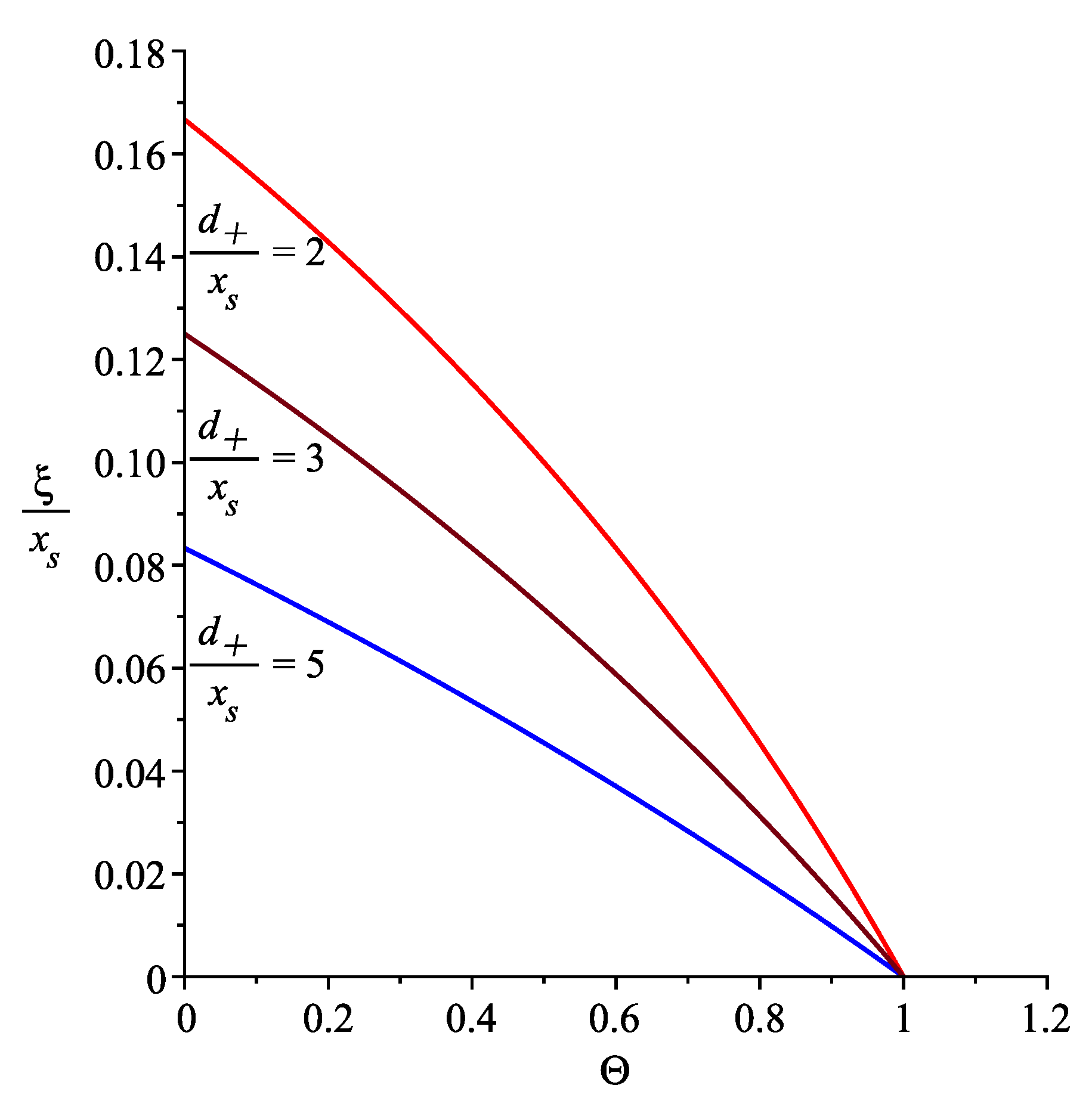
2.2. The Dependence of the Critical Capillary Length
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosenberger, F. Crystal Growth Kinetics. In Interfacial Aspects of Phase Transformations; Mutaftschiev, B., Ed.; Reidel: Dordrecht, Holland, 1982; pp. 315–364. [Google Scholar]
- Tsao, J.F. Materials Fundamentals of Molecular Beam Epitaxy; Academic Press: New York, NY, USA, 1993. [Google Scholar]
- Saito, Y. Statistical Physics of Crystal Growth; World Scientific: Singapore, 1996. [Google Scholar]
- Pimpinelli, A.; Villain, J. Physics of Crystal Growth; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Krug, J. Multiscale Modeling in Epitaxial Growth; Voigt, A., Ed.; Birkhauser: Berlin, Germany, 2005; Chapter 2; pp. 69–95. [Google Scholar]
- Jeong, H.C.; Williams, E.D. Steps on Surfaces: Experiment and Theory. Surf. Sci. Rep. 1999, 34, 171–294. [Google Scholar] [CrossRef]
- Haußer, F.; Otto, F.; Penzler, P.; Voigt, A. Numerical Methods for the Simulation of Epitaxial Growth and Their Application in the Study of a Meander Instability. In Mathematics—Key Technology for the Future; Krebs, H.J., Jäger, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Haußer, F.; Jabbour, M.E.; Voigt, A. A Step-Flow Model for the Heteroepitaxial Growth of Strained, Substitutional, Binary Alloy Films with Phase Segregation: I. Theory. Multiscale Model. Simul. 2007, 6, 158–189. [Google Scholar] [CrossRef]
- Pimpinelli, A.; Videcoq, A.; Vladimirova, M. Kinetic surface patterning in two-particle models of epitaxial growth. Appl. Surf. Sci. 2001, 175–176, 55–61. [Google Scholar] [CrossRef]
- DeVita, J.P.; Sander, L.M.; Smereka, P. Multiscale kinetic Monte Carlo algorithm for simulating epitaxial growth. Phys. Rev. B 2005, 72, 205421. [Google Scholar] [CrossRef]
- Hamouda, A.B.; Pimpinelli, A.; Phaneuf, R.J. Anomalous scaling in epitaxial growth on vicinal surfaces: Meandering and mounding instabilities in a linear growth equation with spatiotemporally correlated noise. Surf. Sci. 2008, 602, 2819–2827. [Google Scholar] [CrossRef]
- Bean, J.C. Strained-Layer Epitaxy of Germanium-Silicon Alloys. Science 1985, 230, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Wagner, S.; Klose, P.; Burlaka, V.; Nörthemann, K.; Hamm, M.; Pundt, A. Structural Phase Transitions in Niobium Hydrogen Thin Films: Mechanical Stress, Phase Equilibria and Critical Temperatures. ChemPhysChem 2019, 20, 1890–1904. [Google Scholar] [CrossRef] [PubMed]
- Eliseev, E.A.; Morozovska, A.N.; Nelson, C.T.; Kalinin, S.V. Intrinsic structural instabilities of domain walls driven by gradient coupling: Meandering antiferrodistortive-ferroelectric domain walls in BiFeO3. Phys. Rev. B 2019, 99, 014112. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Phil. Trans. R. Soc. Lond. A 1951, 243, 299–358. [Google Scholar] [CrossRef]
- Bales, G.S.; Zangwill, A. Morphological instability of a terrace edge during step-flow growth. Phys. Rev. B 1990, 41, 5500–5508. [Google Scholar] [CrossRef] [PubMed]
- Cermelli, P.; Jabbour, M.E. Possible mechanism for the onset of step-bunching instabilities during the epitaxy of single-species crystalline films. Phys. Rev. B 2007, 75, 165409. [Google Scholar] [CrossRef]
- Cermelli, P.; Jabbour, M.E. Multispecies epitaxial growth on vicinal surfaces with chemical reactions and diffusion. Proc. Roy. Soc. A 2005, 461, 3483–3504. [Google Scholar] [CrossRef]
- Tersoff, J.; Johnson, M.D.; Orr, B.G. Adatom Densities on GaAs: Evidence for Near-Equilibrium Growth. Phys. Rev. Lett. 1997, 78, 282. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y. Revisiting the Meandering Instability During Step-Flow Epitaxy. Appl. Sci. 2019, 9, 4840. https://doi.org/10.3390/app9224840
Chen Y. Revisiting the Meandering Instability During Step-Flow Epitaxy. Applied Sciences. 2019; 9(22):4840. https://doi.org/10.3390/app9224840
Chicago/Turabian StyleChen, Yue. 2019. "Revisiting the Meandering Instability During Step-Flow Epitaxy" Applied Sciences 9, no. 22: 4840. https://doi.org/10.3390/app9224840



