Wind-Induced Response Control of High-Rise Buildings Using Inerter-Based Vibration Absorbers
Abstract
:1. Introduction
2. Equations of Motion and Preliminary Concepts
3. Description of the 340 m Tall Building and Wind Tunnel Testing
4. Wind-Induced Response Mitigation Using Inerter-Based Vibration Absorbers
4.1. Optimization of the Parameters of the TMDI/TID Scheme Applied to the Benchmark Building
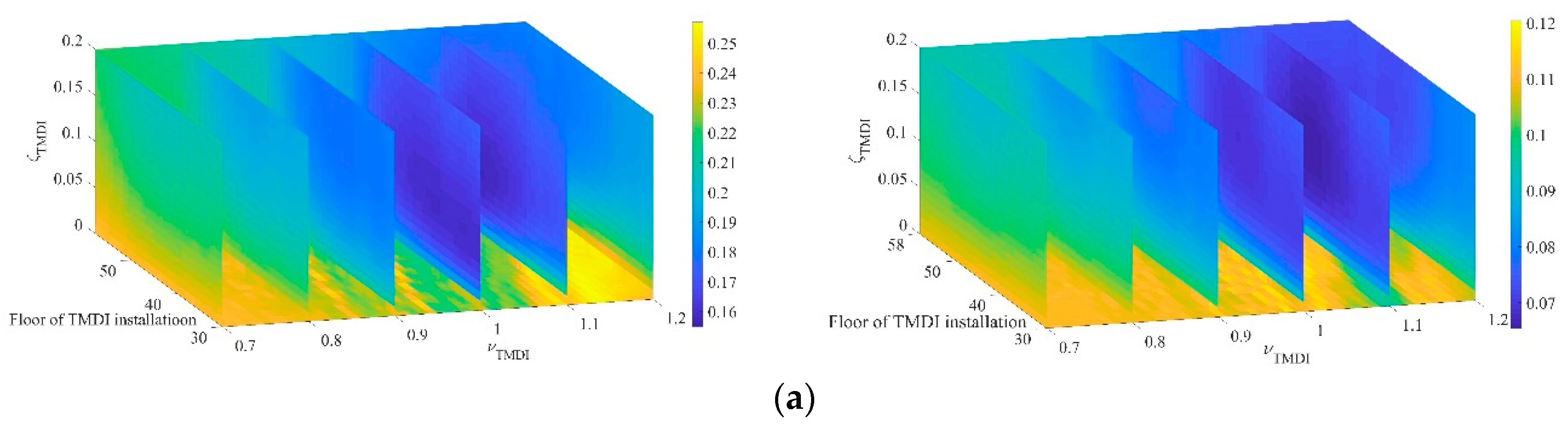
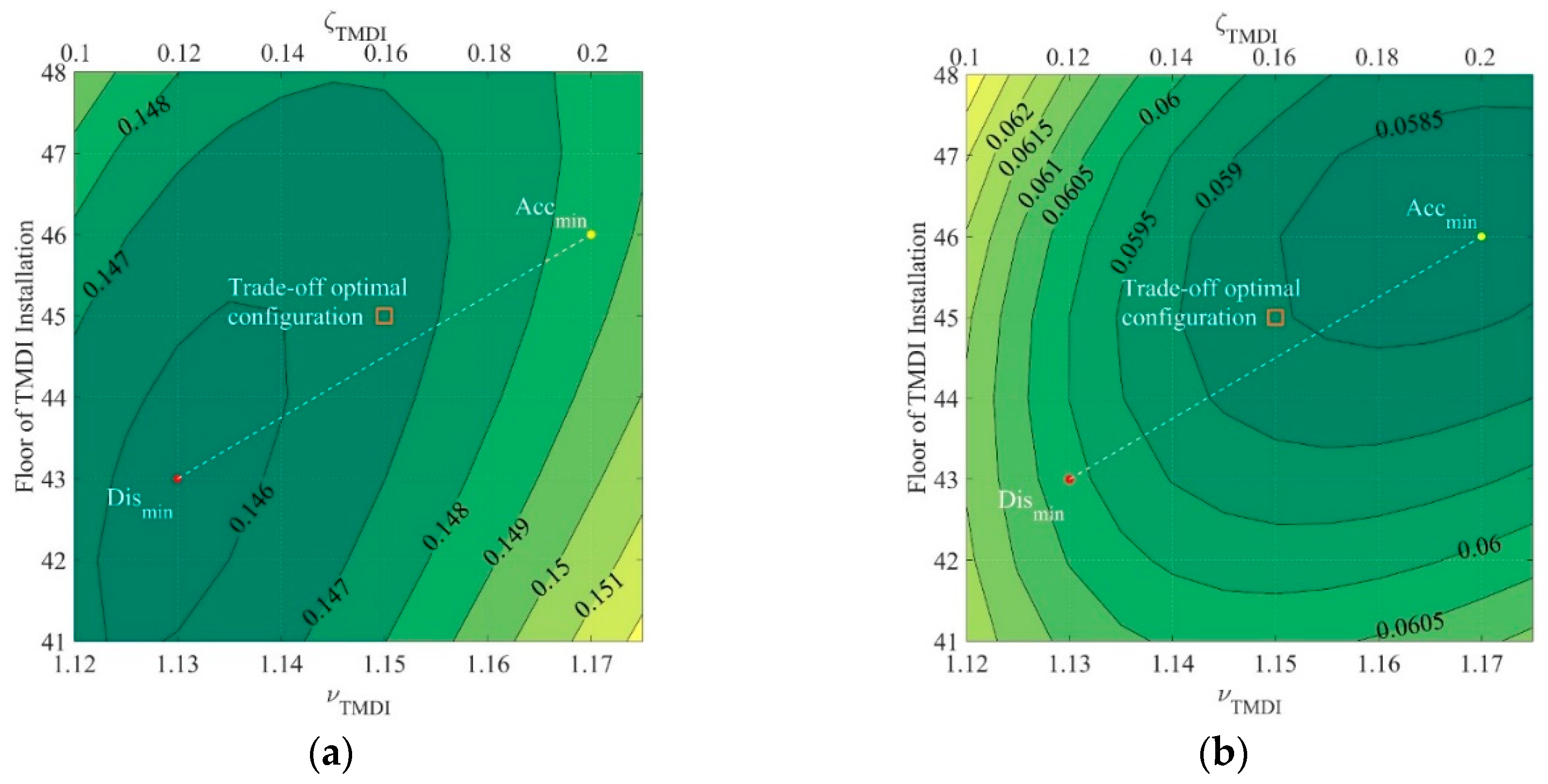
4.1.1. Optimization of Parameters of TMDI
- For TMDIs which efficiently mitigate the wind-induced displacement responses, the optimal frequency ratio lies around 1.1, which indicates that the frequency of optimal TMDI is close to the first order frequency of the primary structure;
- The minimal peak displacement and acceleration are achieved when the damping ratios are 7% and 10%, respectively;
- As for the optimal floor of installation of TMDI, it can be seen that the best vibration mitigation effect is achieved when the TMDI is installed at the middle-upper portion of the benchmark building (around 44th floor), and not in the conventional configuration of TMD, i.e., at the topmost floor;
- For acceleration mitigation purpose, the optimal frequency ratio and installation floor of TMDI is slightly larger than that of displacement-oriented optimization. Such differences may be justified in view of the fact that the transfer function of acceleration is times that of displacement, which means that a better mitigation effect of acceleration can be realized by decreasing the value of transfer function at higher frequency around the first peak under the same fluctuating wind excitations.
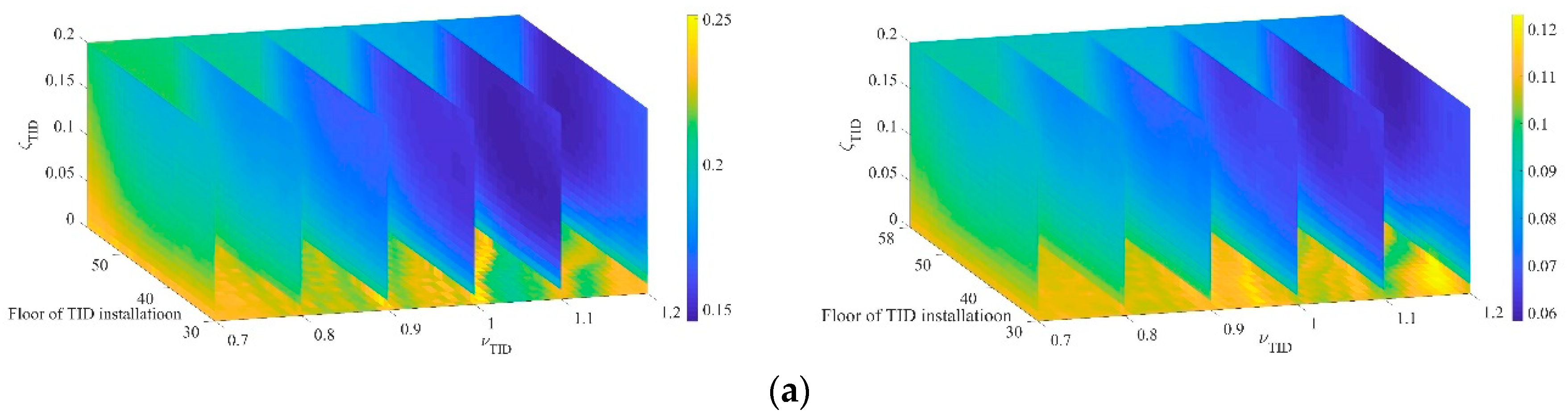
4.1.2. Optimization of Parameters of TID
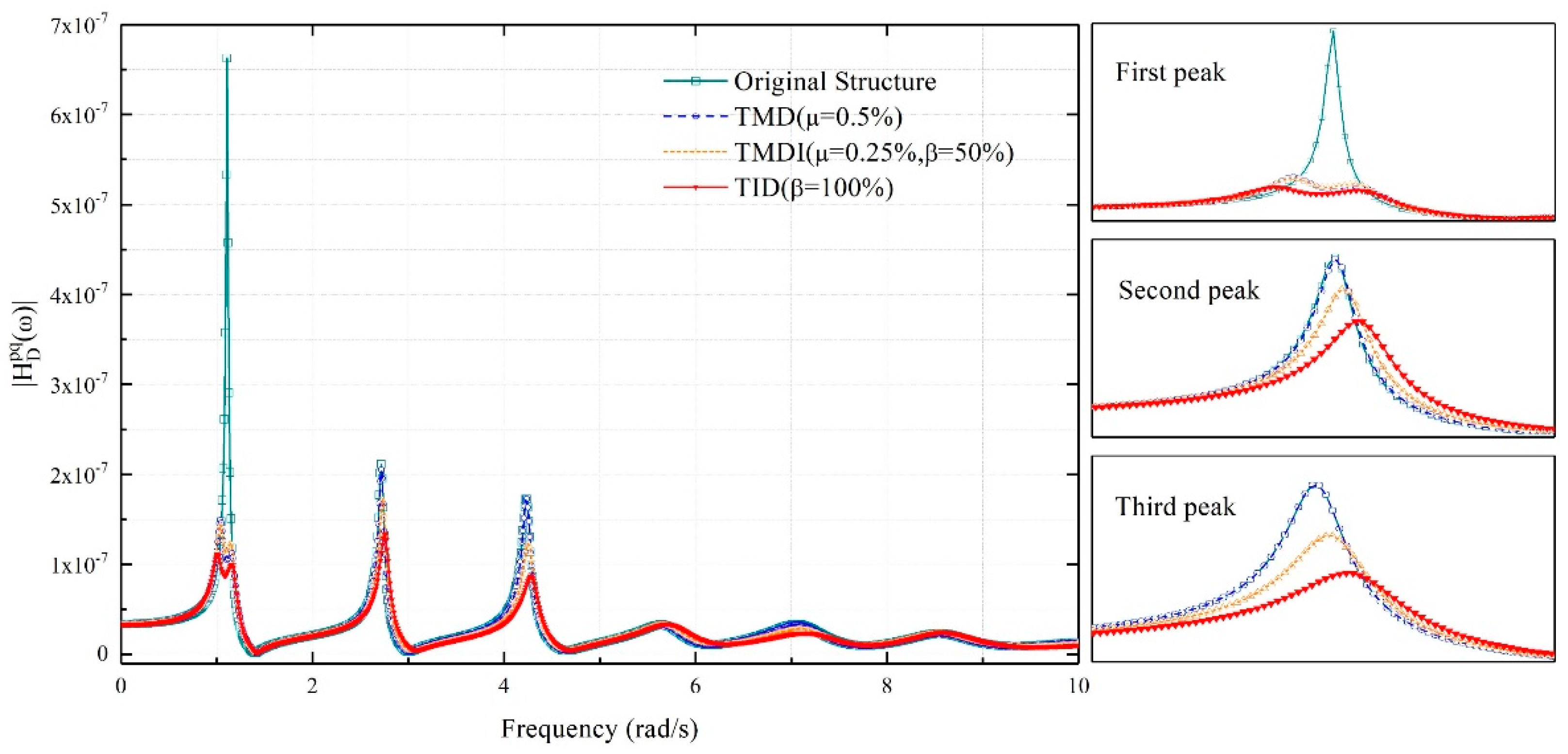
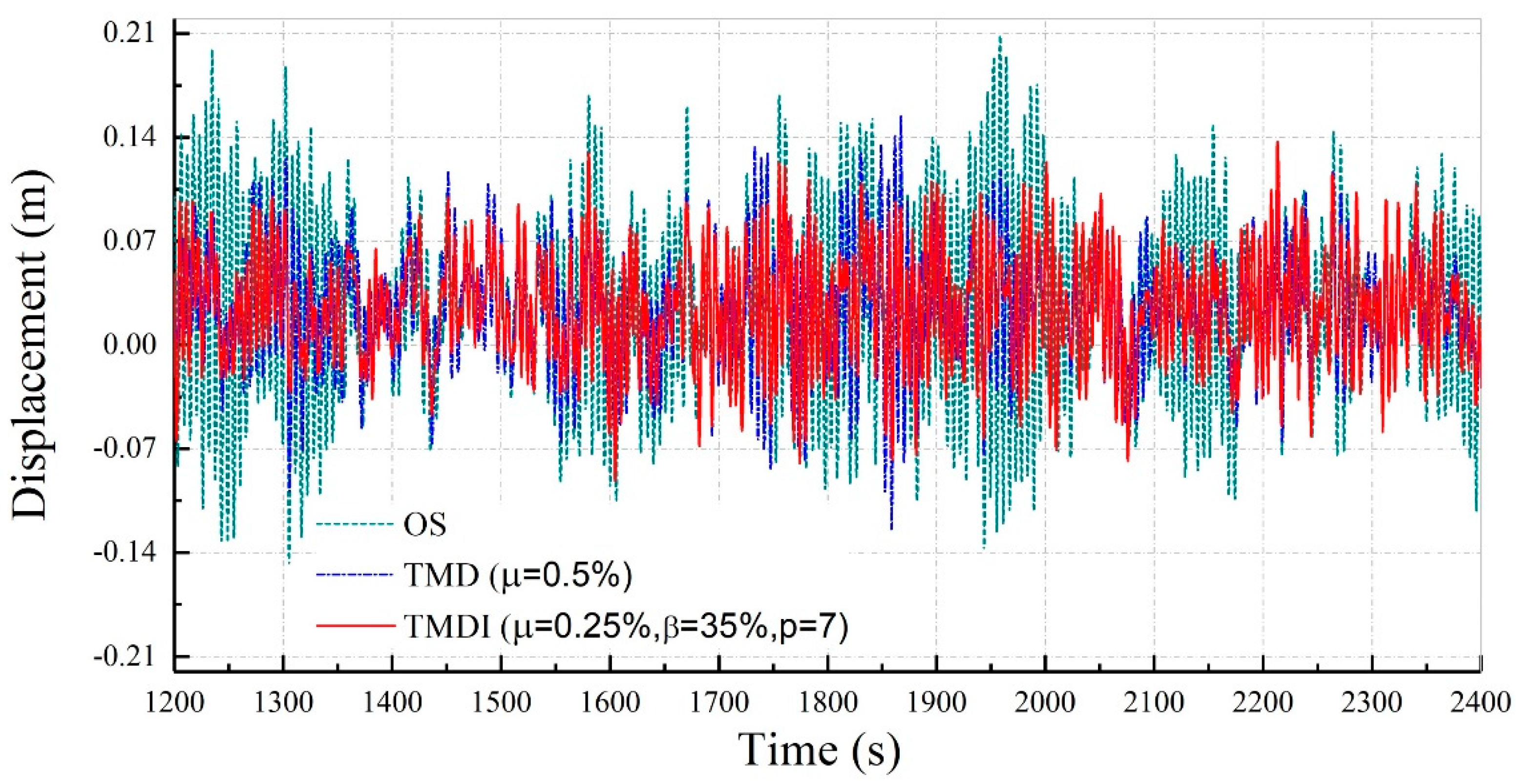
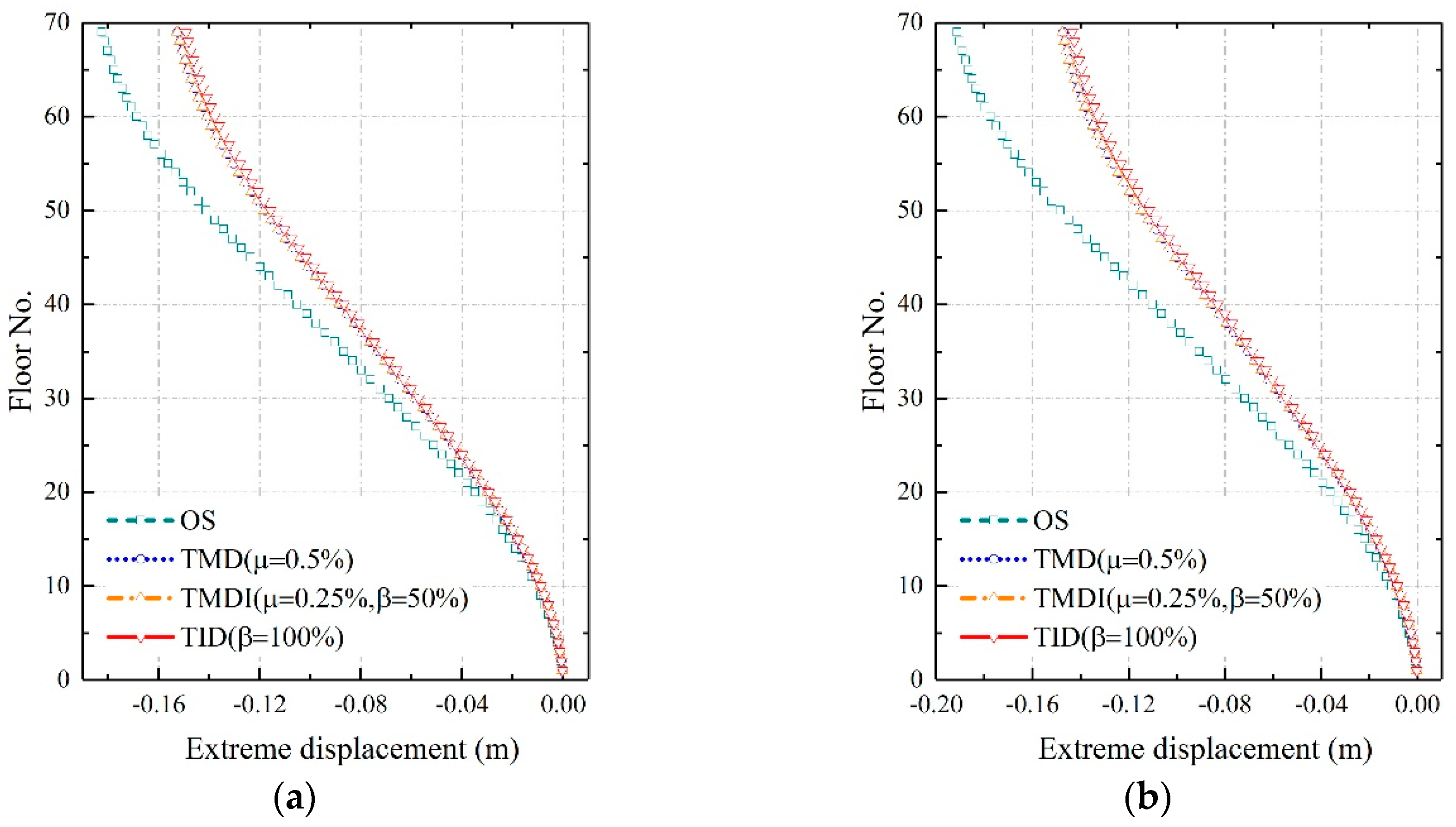
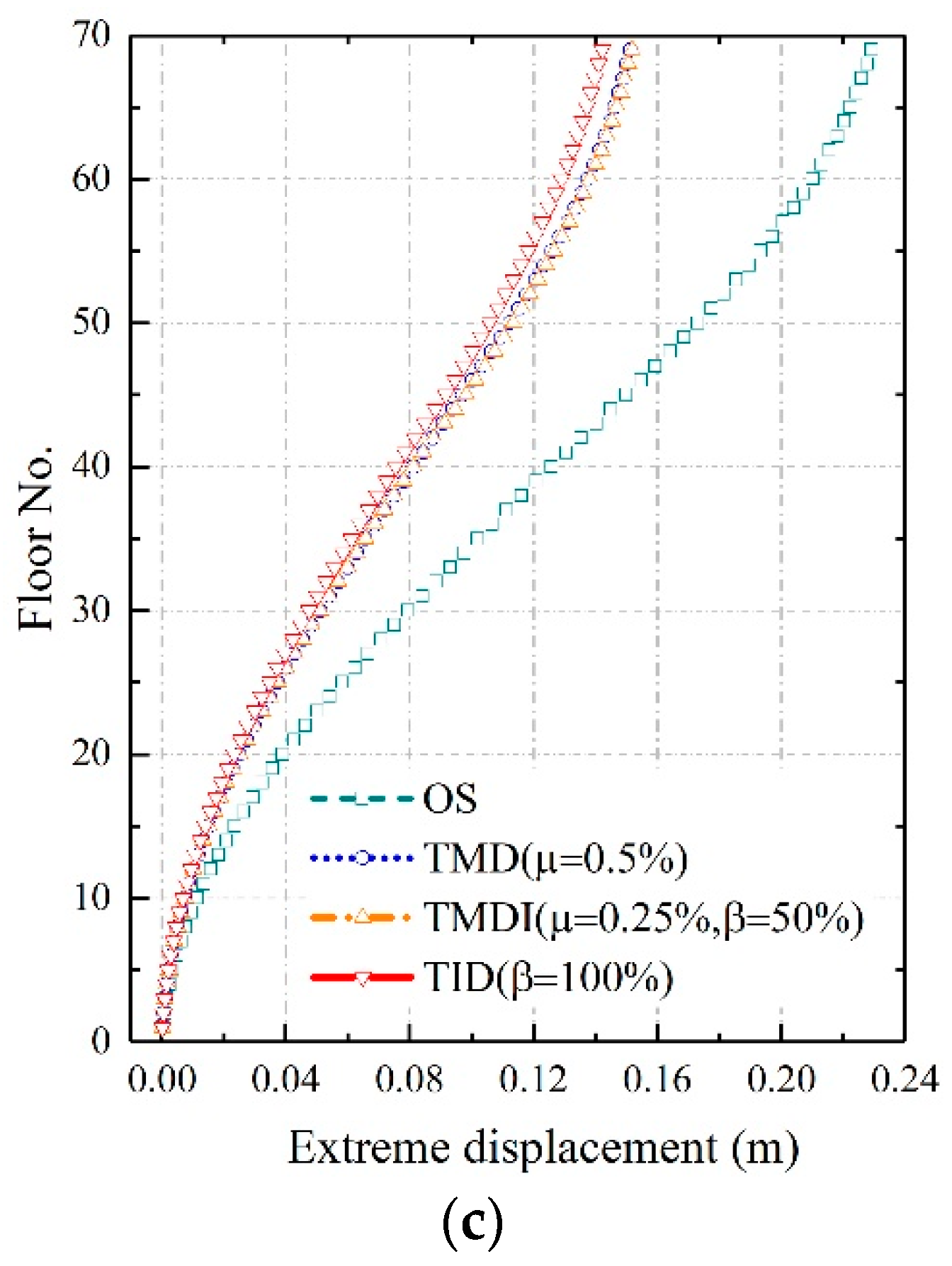
4.2. Effects of the Inerter-Based Vibration Absorbers on Wind-Induced Displacements
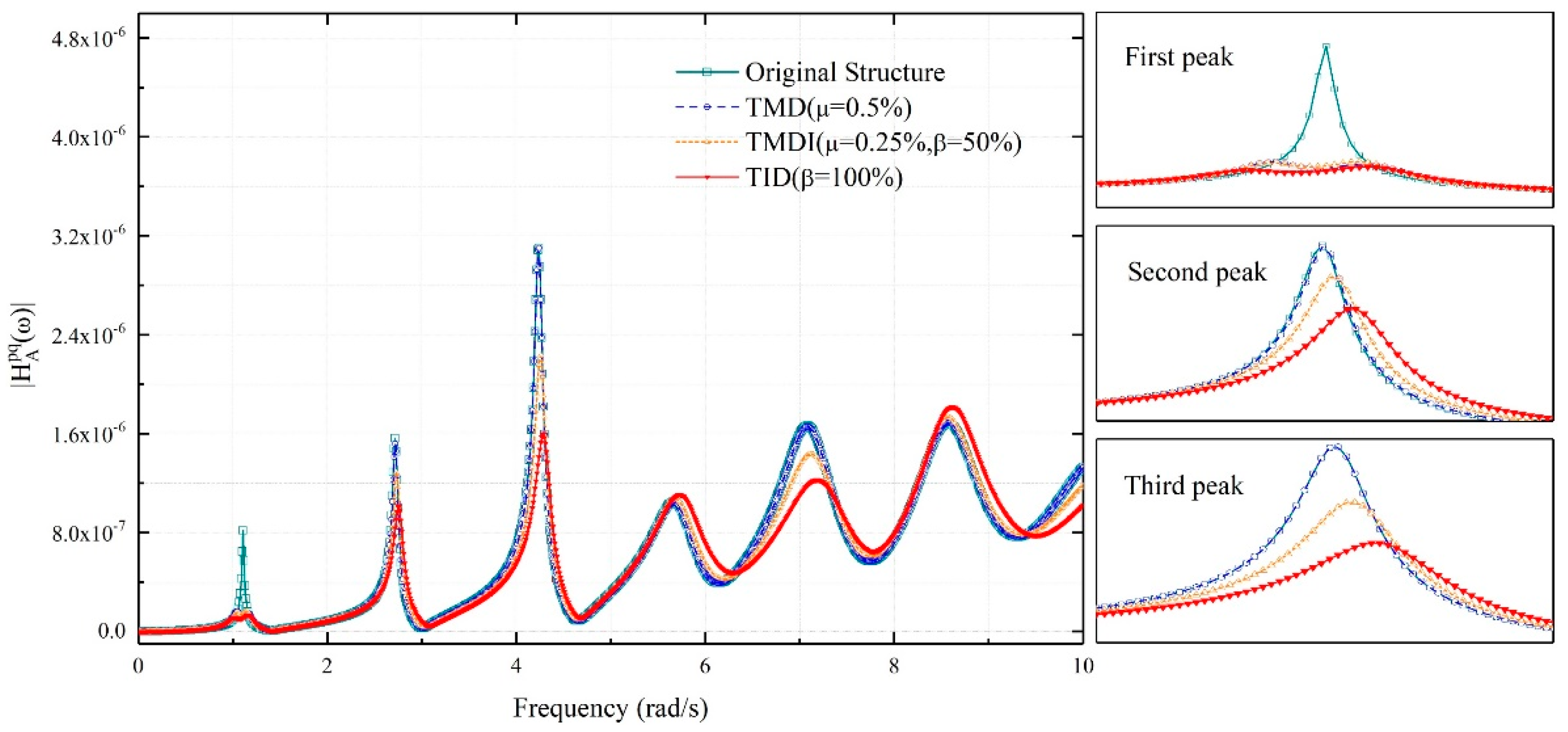
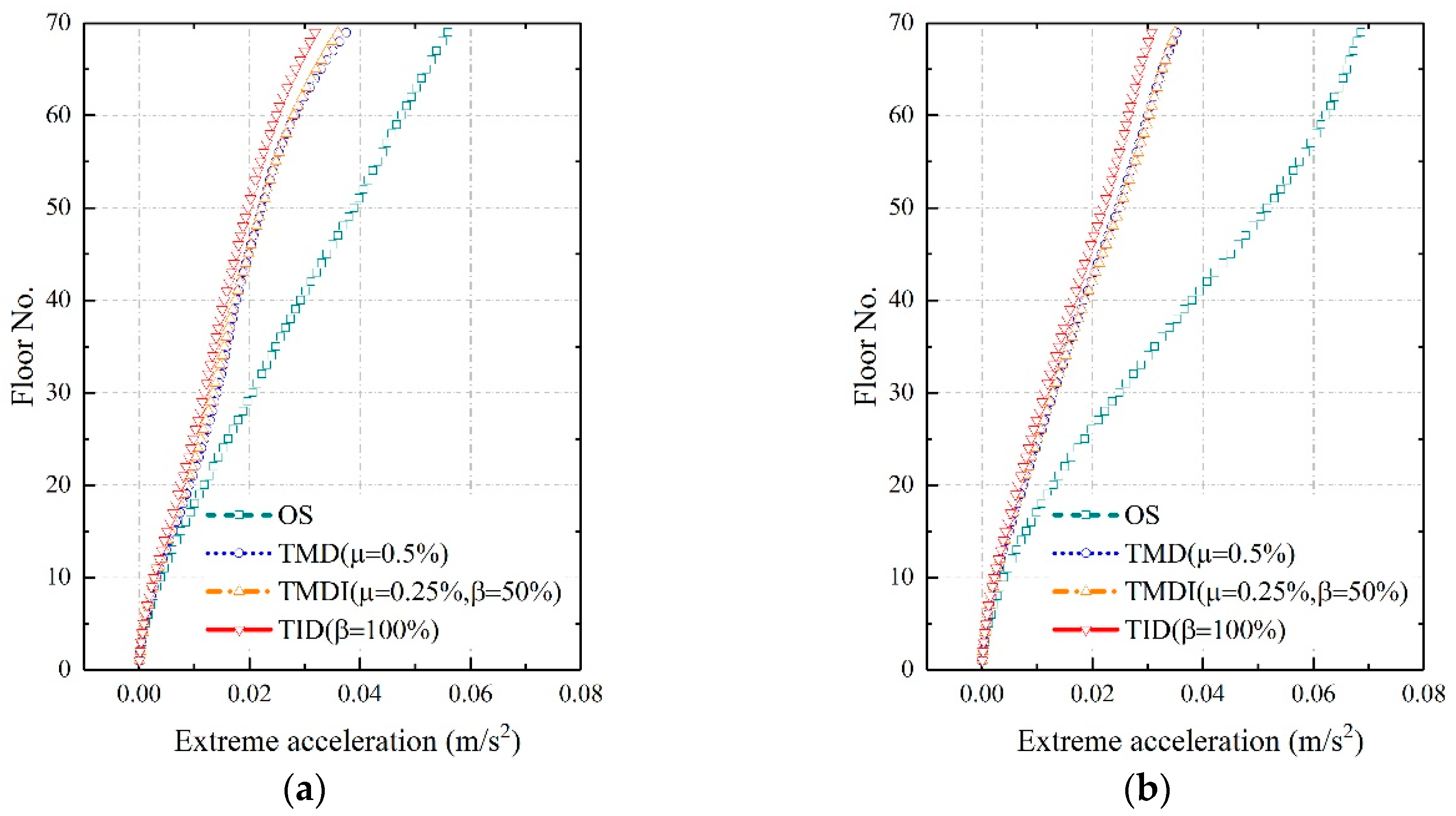
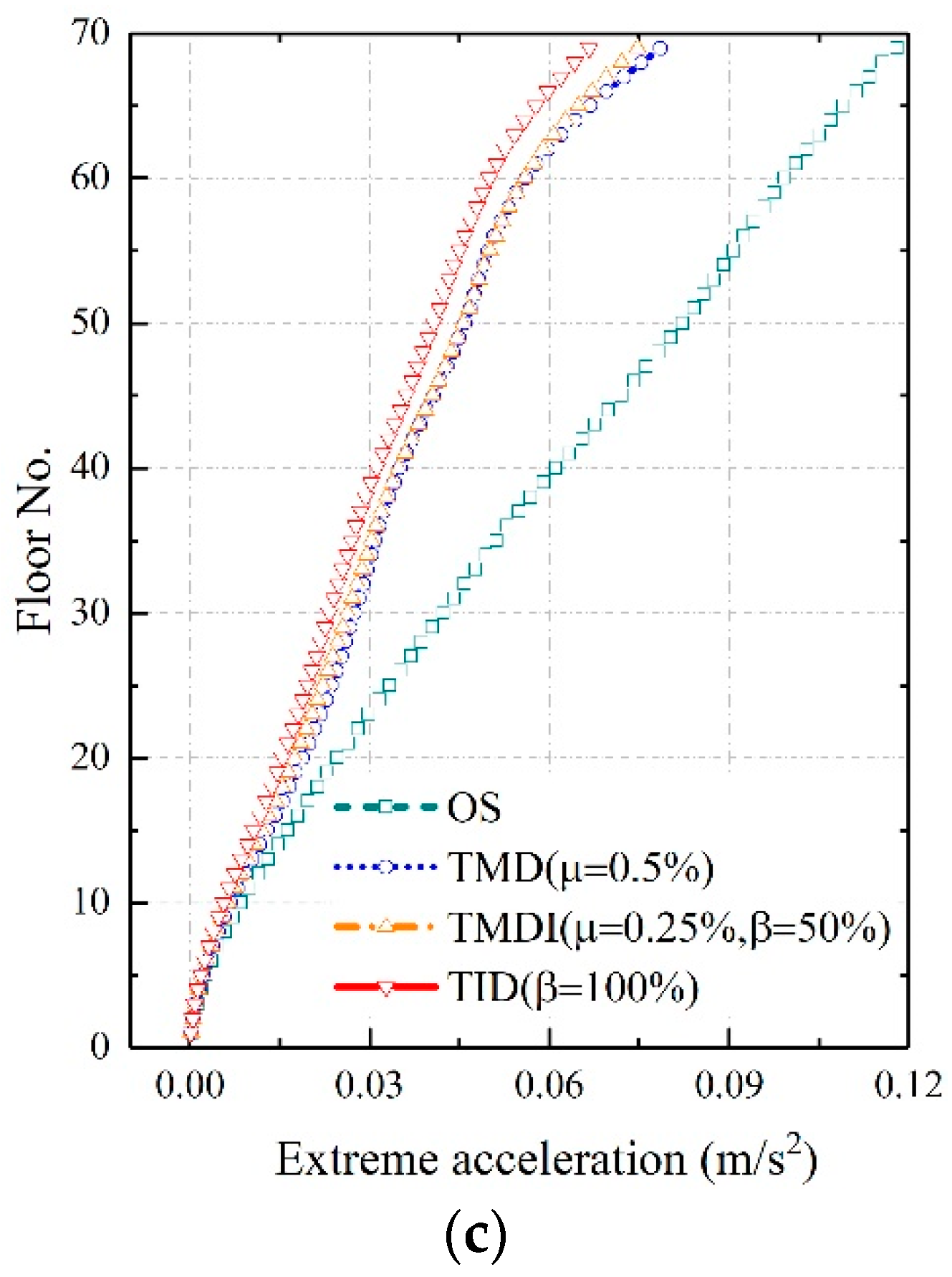
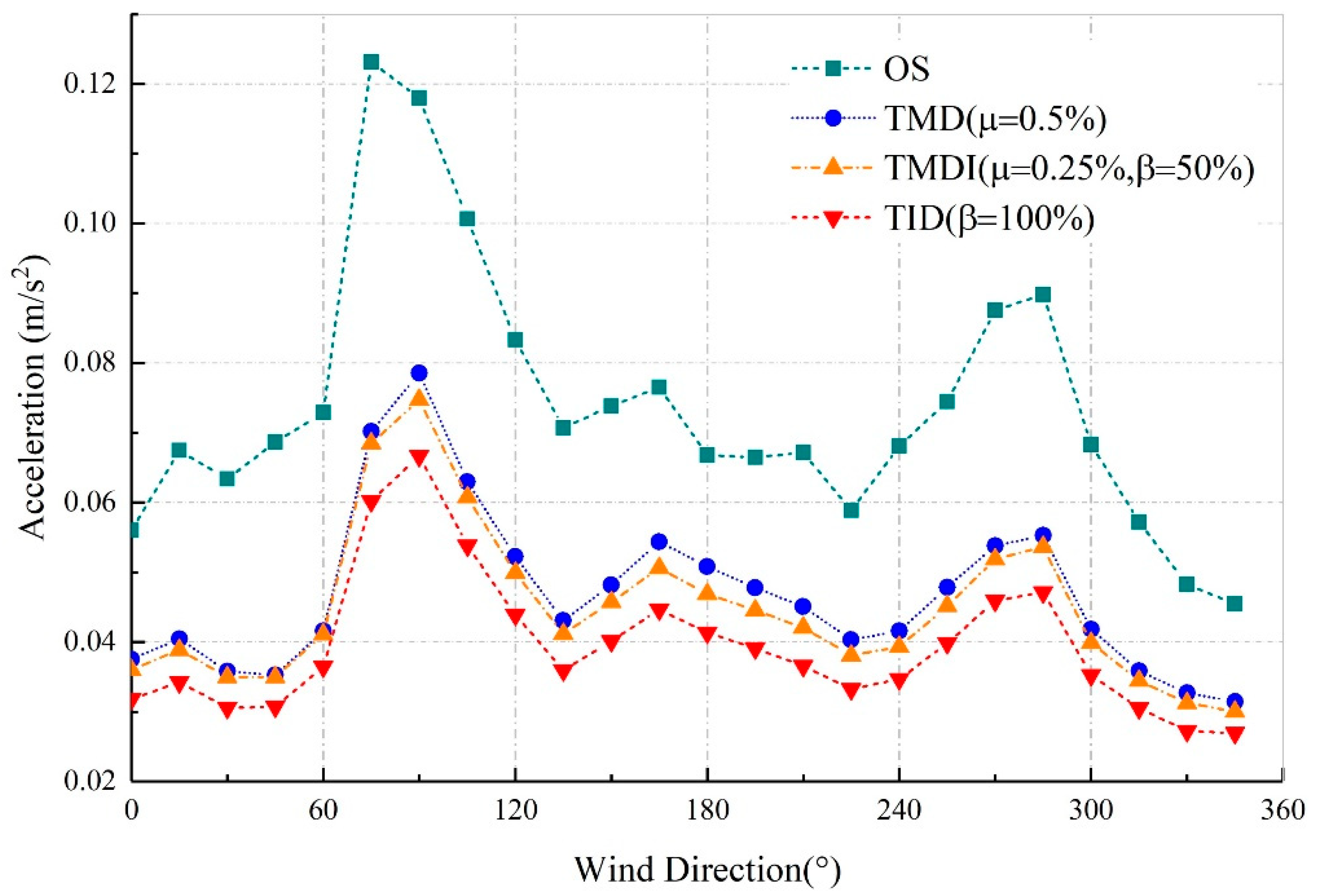
4.3. Effects of the Inerter-Based Vibration Absorbers on Wind-Induced Accelerations
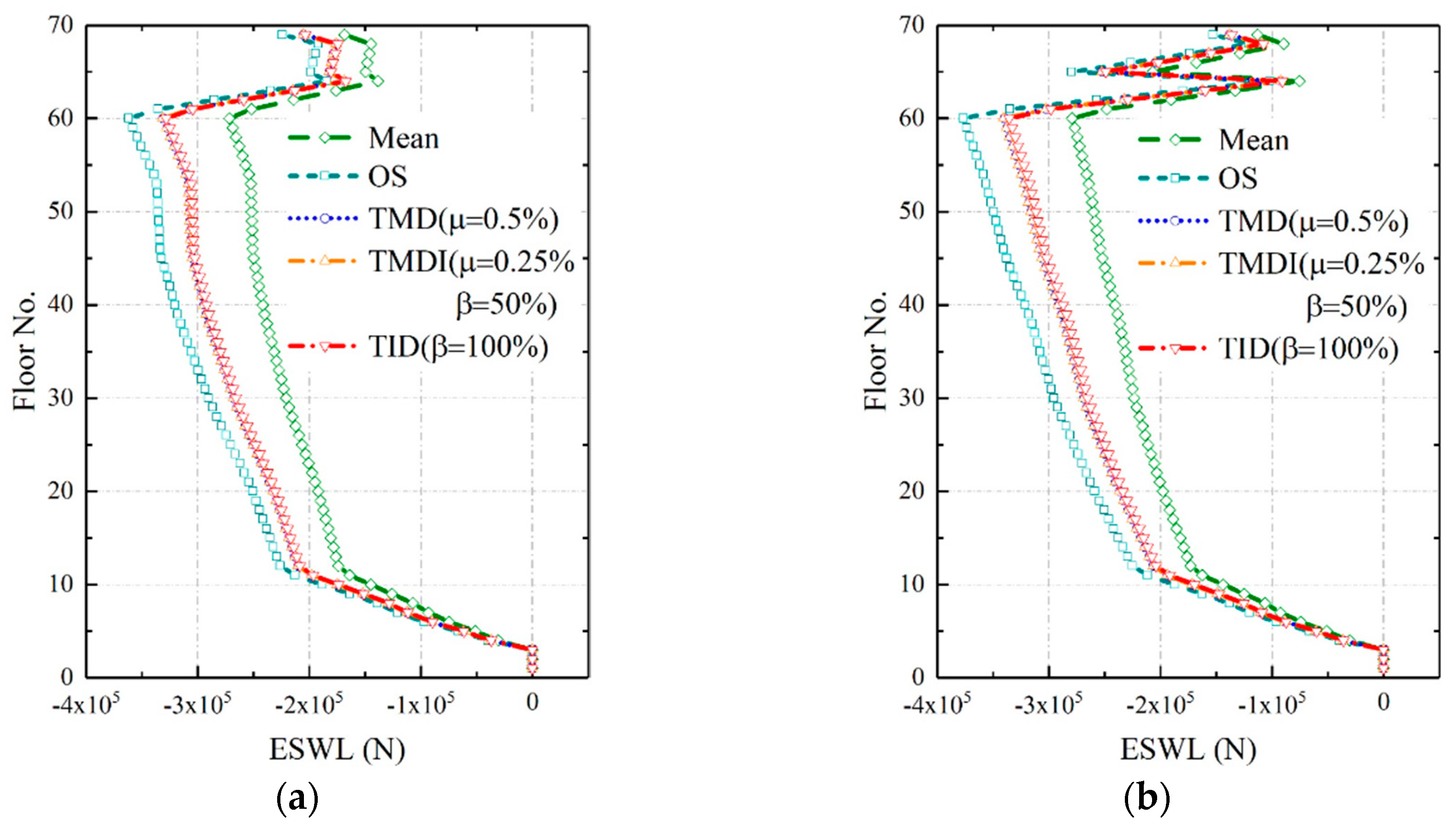
4.4. Effects of the Inerter-Based Vibration Absorbers on ESWLs
5. Conclusions
- Displacement- and acceleration-based optimizations have been performed to obtain the best parameters of the TMD, TMDI and TID in a 3D design space, including the installation floor, the frequency ratio and the damping ratio as explicit design variables. The proposed procedure attempts to find a good trade-off between displacement mitigation and acceleration mitigation, considering results from a constrained optimization problem in which the installation floor represents a design variable being incorporated in the optimization procedure;
- Both wind-induced extreme top-floor displacement and acceleration responses of the benchmark building can be effectively mitigated by the TMDI and TID. Among the three vibration absorbers, the TID outperforms the TMDI and the TMD, and the acceleration mitigation effect of the TMDI is better than that of the TMD. The extreme displacement and acceleration response of the original structure are 0.2293 m and 0.1232 m/s2, respectively. The installation of the TMDI has reduced these response values to 0.1519 m and 0.0685 m/s2, respectively, with a resulting factor of vibration absorbing equal to 33.74% and 44.40%, respectively. The best vibration mitigation effect is achieved by the TID, which reduces the extreme displacement and acceleration to 0.1421 m and 0.0602 m/s2, respectively, corresponding to of 38.02% and 51.12%, respectively;
- Comparison among the three different vibration absorbers has shown that the TID with same physical mass ratio as the TMD and TMDI can achieve better vibration mitigation effects in terms of displacement and acceleration responses. In particular, the factors of vibration absorbing of TMD, TMDI and TID for extreme displacement have been 34.01%, 33.74% and 38.02%, respectively, and the analogous factors for extreme acceleration have been 43.04%, 44.40% and 51.12%, respectively. The performance of TID slightly outperforms the other two vibration absorbers in terms of mitigating ESWLs, which is consistent with the results of displacement mitigation effect;
- Optimizations of parameters have demonstrated that the TMDI and TID achieve the best vibration mitigation effects when the first terminal is not installed at the top floor, but at the mid-upper place of the primary structure with TMDI/TID topologies such that the inerter spans four stories. In this configuration, the TID can achieve better wind-induced vibration mitigation than the TMD employing the same physical mass ratio as that of the corresponding TMD (thus implying a significant reduction in terms of physical mass actually allocated due to the mass-amplification effect of the inerter when the TID scheme is designed to achieve the same vibration mitigation effect as that of TMD);
- The TID having the same physical mass as the TMD (meaning that the inertia is entirely provided by the inerter, with ideally null attached mass) can achieve much better vibration mitigation effects than the TMD in terms of acceleration response when the frequency ratio and damping ratio of the TID are tuned to be around 1.15 and 16%, respectively, and the TID is installed at the 45th floor. A slightly better displacement mitigation effect can be achieved by adopting a relative smaller frequency ratio, damping ratio and lower installation floor, e.g., 1.13, 12% and 43rd floor, respectively.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- CTBUH. The Global Tall Buildings Database of the CTBUH. 2019. Available online: http://www.skyscrapercenter.com/ (accessed on 22 June 2019).
- Kareem, A.; Kijewski, T.; Tamura, Y. Mitigation of motions of tall buildings with specific examples of recent applications. Wind Struct. Int. J. 1999, 2, 201–251. [Google Scholar] [CrossRef]
- Kim, Y.; Kanda, J. Characteristics of aerodynamic forces and pressures on square plan buildings with height variations. J. Wind Eng. Ind. Aerodyn. 2010, 98, 449–465. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kanda, J. Wind pressures on tapered and set-back tall buildings. J. Fluids Struct. 2013, 39, 306–321. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1998, 74, 531–542. [Google Scholar] [CrossRef]
- Zheng, C.; Xie, Y.; Khan, M.; Wu, Y.; Liu, J. Wind-induced responses of tall buildings under combined aerodynamic control. Eng. Struct. 2018, 175, 86–100. [Google Scholar] [CrossRef]
- Sharma, A.; Mittal, H.; Gairola, A. Mitigation of wind load on tall buildings through aerodynamic modifications: Review. J. Build. Eng. 2018, 18, 180–194. [Google Scholar] [CrossRef]
- Zeng, X.; Peng, Y.; Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct. Des. Tall Special Build. 2017, 26, e1371. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, X.; Peng, Y. Probabilistic analysis of wind-induced vibration mitigation of structures by fluid viscous dampers. J. Sound Vib. 2017, 409, 287–305. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 2019, 179, 523–539. [Google Scholar] [CrossRef]
- Aydin, E. Optimal damper placement based on base moment in steel building frames. J. Constr. Steel Res. 2012, 79, 216–225. [Google Scholar] [CrossRef]
- Aydin, E. A simple damper optimization algorithm for both target added damping ratio and interstorey drift ratio. Earth Struct. 2013, 88, 83–109. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Warburton, G.B. Optimum Absorber Parameters for Various Combinations of Response and Excitation Parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Takewaki, I. Soil—Structure random response reduction via TMD-VD simultaneous use. Comput. Methods Appl. Mech. Eng. 2000, 190, 677–690. [Google Scholar] [CrossRef]
- Stanikzai, M.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Seismic response control of base-isolated buildings using multiple tuned mass dampers. Struct. Des. Tall Special Build. 2019, 28, e1576. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Distributed Multiple Tuned Mass Dampers for Wind Vibration Response Control of High-Rise Building. J. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Along-wind response control of chimneys with distributed multiple tuned mass dampers. Struct. Control Health Monit. 2019, 26, e2275. [Google Scholar] [CrossRef]
- Min, K.W.; Kim, H.S.; Lee, S.H.; Kim, H.; Kyung Ahn, S. Performance evaluation of tuned liquid column dampers for response control of a 76-story benchmark building. Eng. Struct. 2005, 27, 1101–1112. [Google Scholar] [CrossRef]
- Di Matteo, A.; Pirrotta, A.; Tumminelli, S. Combining TMD and TLCD: Analytical and experimental studies. J. Wind Eng. Ind. Aerodyn. 2017, 167, 101–113. [Google Scholar] [CrossRef]
- Di Matteo, A.; Furtmüller, T.; Adam, C.; Pirrotta, A. Optimal design of tuned liquid column dampers for seismic response control of base-isolated structures. Acta Mech. 2018, 229, 437–454. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. Numerical assessment of vibration control systems for multi-hazard design and mitigation of glass curtain walls. J. Build. Eng. 2018, 15, 1–13. [Google Scholar] [CrossRef]
- Pipitone, G.; Barone, G.; Palmeri, A. Optimal design of double-skin façades as vibration absorbers. Struct. Control Health Monit. 2018, 25, e2086. [Google Scholar] [CrossRef]
- Tanaka, H.; Mak, C.Y. Effect of tuned mass dampers on wind induced response of tall buildings. J. Wind Eng. Ind. Aerodyn. 1983, 14, 357–368. [Google Scholar] [CrossRef]
- Xu, Y.L.; Kwok, K.C.S.; Samali, B. The effect of tuned mass dampers and liquid dampers on cross-wind response of tall/slender structures. J. Wind Eng. Ind. Aerodyn. 1992, 40, 33–54. [Google Scholar] [CrossRef]
- Xu, Y.L.; Kwok, K.C.S.; Samali, B. Torsion response and vibration suppression of wind-excited buildings. J. Wind Eng. Ind. Aerodyn. 1992, 43, 1997–2008. [Google Scholar] [CrossRef]
- Kwok, K.C.S.; Samali, B. Performance of tuned mass dampers under wind loads. Eng. Struct. 1995, 17, 655–667. [Google Scholar] [CrossRef]
- Kim, Y.M.; You, K.P.; Kim, H.Y. Wind-induced excitation control of a tall building with tuned mass dampers. Struct. Des. Tall Special Build. 2008, 17, 669–682. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Windresponse control of tall buildings with a tuned mass damper. J. Build. Eng. 2018, 15, 51–60. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Garg, A.; Hazra, B.; Xie, Z. Effects of TMD on correlation of wind-induced responses and combination coefficients of ESWLs of high-rise buildings. Struct. Des. Tall Special Build. 2019, 28, e1597. [Google Scholar] [CrossRef]
- Wang, Q.; Fu, W.; Yu, S.; Allan, L.; Garg, A.; Gu, M. Mathematical model and case study of wind-induced responses for a vertical forest. J. Wind Eng. Ind. Aerodyn. 2018, 179, 260–272. [Google Scholar] [CrossRef]
- Love, J.S.; Haskett, T.C.; Morava, B. Effectiveness of dynamic vibration absorbers implemented in tall buildings. Eng. Struct. 2018, 176, 776–784. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar]
- De Domenico, D.; Ricciardi, G. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-Induced Vibration Mitigation in Tall Buildings Using the Tuned Mass-Damper-Inerter. J. Struct. Eng. 2017, 143, 11. [Google Scholar] [CrossRef]
- Li, Q.; He, Y.; Zhou, K.; Han, X.; He, Y.; Shu, Z. Structural health monitoring for a 600 m high skyscraper. Struct. Des. Tall Special Build. 2018, 27, e1490. [Google Scholar] [CrossRef]
- Li, Q.S.; Zhi, L.H.; Tuan, A.Y.; Kao, C.S.; Su, S.C.; Wu, C.F. Dynamic behavior of Taipei 101 tower: Field measurement and numerical analysis. J. Struct. Eng. 2011, 137, 143–155. [Google Scholar] [CrossRef] [Green Version]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef] [Green Version]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Vibrationsuppression of cables using tuned inerter dampers. Eng. Struct. 2016, 122, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probab. Eng. Mech. 2015, 38, 156–164. [Google Scholar] [CrossRef]
- Mirza Hessabi, R.; Mercan, O. Investigations of the application of gyro-mass dampers with various types of supplemental dampers for vibration control of building structures. Eng. Struct. 2016, 126, 174–186. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1367–1388. [Google Scholar] [CrossRef]
- De Domenico, D.; Impollonia, N.; Ricciardi, G. Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthq. Eng. 2018, 105, 37–53. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study. Struct. Control Health Monit. 2018, 25, e2234. [Google Scholar] [CrossRef]
- De Domenico, D.; Deastra, P.; Ricciardi, G.; Sims, N.D.; Wagg, D.J. Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Frankl. Inst. 2019, 356, 7626–7649. [Google Scholar] [CrossRef] [Green Version]
- Giaralis, A.; Taflanidis, A.A. Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria. Struct. Control Health Monit. 2018, 25, e2082. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, R.; Jiang, Y.; Pan, C. Seismic response mitigation of structures with a friction pendulum inerter system. Eng. Struct. 2019, 193, 110–120. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R. Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 2018, 25, e2169. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.; Luo, H.; Li, C.; Shen, H. Demand-based optimal design of oscillator with parallel-layout viscous inerter damper. Struct. Control Health Monit. 2018, 25, e2051. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, Z.; Dai, K. Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system. Eng. Struct. 2019, 180, 29–39. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, Z.; Pan, C. Influence of mechanical layout of inerter systems on seismic mitigation of storage tanks. Soil Dyn. Earthq. Eng. 2018, 114, 639–649. [Google Scholar] [CrossRef]
- Xu, K.; Bi, K.; Han, Q.; Li, X.; Du, X. Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: Analytical study. Eng. Struct. 2019, 182, 101–111. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, R.F.; Friswell, M.I.; Cao, Y. Suppression of the wind-induced vibration of high-rise buildings with inerter systems. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 17–19 September 2018. [Google Scholar]
- Luo, Y.; Sun, H.; Wang, X.; Zuo, L.; Chen, N. Wind Induced Vibration Control and Energy Harvesting of Electromagnetic Resonant Shunt Tuned Mass-Damper-Inerter for Building Structures. Shock Vib. 2017, 2017, 4180134. [Google Scholar]
- Liang, S.; Liu, S.; Li, Q.S.; Zhang, L.; Gu, M. Mathematical model of acrosswind dynamic loads on rectangular tall buildings. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1757–1770. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T.T. Parametric study and simplified design of TMDs. Eng. Struct. 1998, 20, 193–204. [Google Scholar] [CrossRef]
- Ruiz, R.; Taflanidis, A.; Giaralis, A.; Lopez-Garcia, D. Risk-informed optimization of the tuned mass-damper-inerter (TMDI) for the seismic protection of multi-storey building structures. Eng. Struct. 2018, 177, 836–850. [Google Scholar] [CrossRef]
- Davenport, A.G. Gust loading factors. J. Struct. Division 1967, 93, 11–34. [Google Scholar]
- Davenport, A.G. Note on the Random Distribution of the Largest Value of a Random Function with Application to Gust Loading. Proc. Inst. Civ. Eng. 1964, 24, 187–196. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Satake, N.; Suda, K.I.; Arakawa, T.; Sasaki, A.; Tamura, Y. Damping evaluation using full-scale data of buildings in Japan. J. Struct. Eng. 2003, 129, 470–477. [Google Scholar] [CrossRef]
- China, M.o.H.a.U.R.D.o.t.P.s.R.o. Chinese Code GB50009-2012, Load Code for the Design of Building Structures; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Papageorgiou, C.; Smith, M.C. Laboratory experimental testing of inerters. In Proceedings of the 44th IEEE Conference on Decision and Control, Cdc-Ecc ′05, Seville, Spain, 12–15 December 2005. [Google Scholar]
- Kareem, A.; Zhou, Y. Gust loading factor—Past, present and future. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1301–1328. [Google Scholar] [CrossRef]
- Zhou, Y.; Kareem, A. Gust Loading Factor: New Model. J. Struct. Eng. 2001, 127, 168–175. [Google Scholar] [CrossRef]
- Kasperski, M. Extreme wind load distributions for linear and nonlinear design. Eng. Struct. 1992, 14, 27–34. [Google Scholar] [CrossRef]
- Chen, X.; Kareem, A. Equivalent Static Wind Loads for Buffeting Response of Bridges. J. Struct. Eng. 2001, 127, 1467–1475. [Google Scholar] [CrossRef]




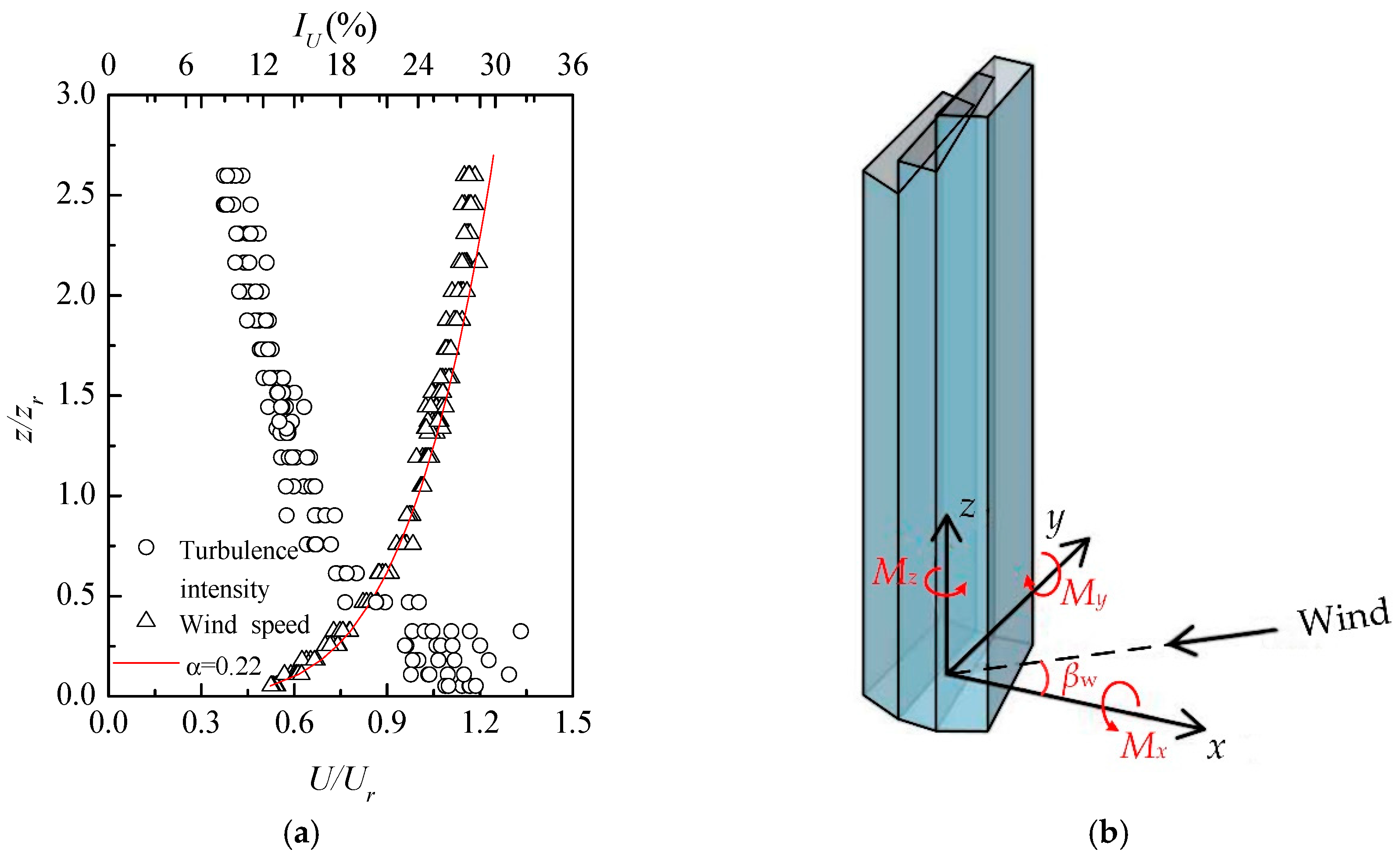
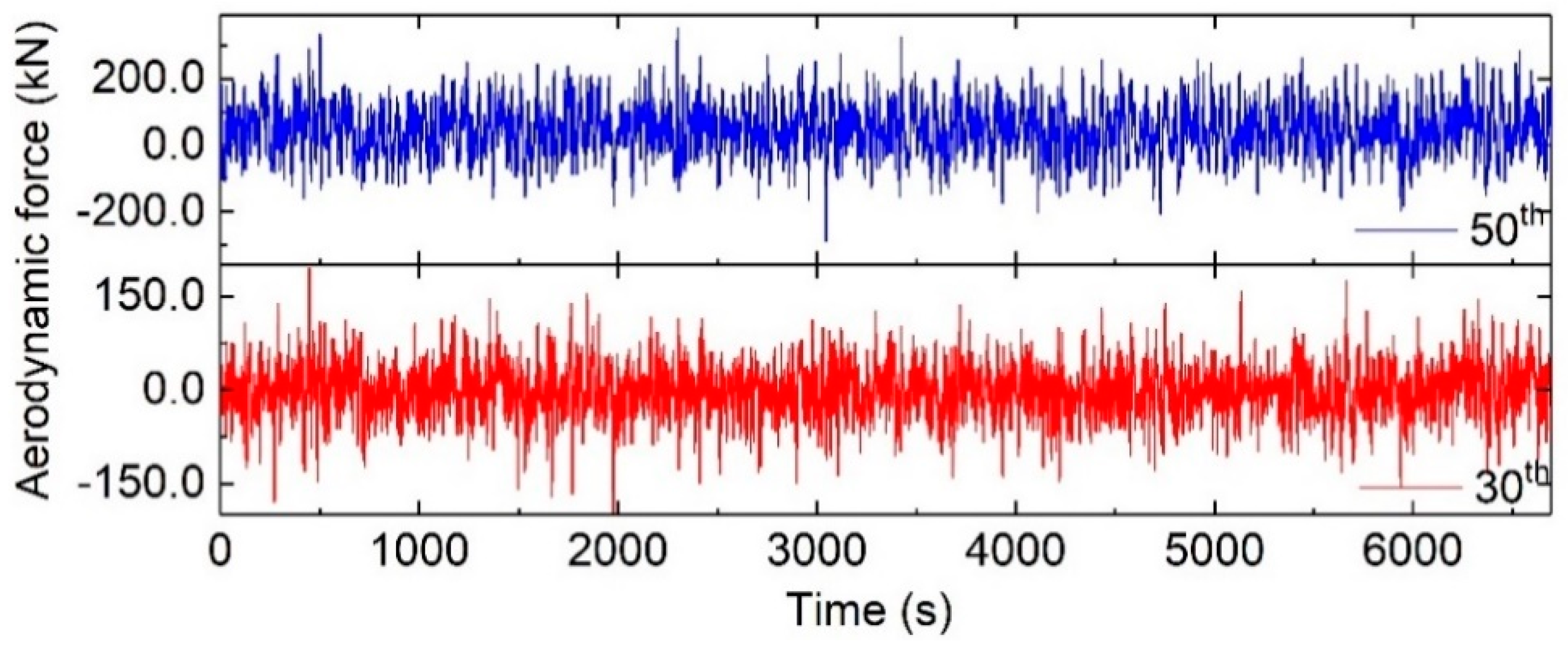





| Total Mass | First-Order Natural Frequency along x-axis | First-Order Generalized Mass | First-Order Damping Ratio (Assumed) |
|---|---|---|---|
| 231,659 t | 0.176 Hz | 61,287 t | 1% |
| Geometric Scale | Wind Speed | Sampling Frequency | Sampling Length | Incremental Step | Measuring Taps |
|---|---|---|---|---|---|
| 1:350 | 12 m/s | 312.5 Hz | 20,480 | 15° | 471 |
| Parameters | TMD | TMDI | TID |
|---|---|---|---|
| TMD installation floor | 58th floor | 45th floor | 45th floor |
| Effective mass ratio | 0.5% | 50.5% | 100% |
| Physical mass ratio | 0.5% | 0.5% | 0.5% |
| Mass ratio | 0.5% | 0.25% | \ |
| Inertance ratio | \ | 50% | 100% |
| Frequency ratio | 0.99 | 1.07 | 1.15 |
| Damping ratio | 7% | 9% | 16% |
| TMDI topology −p | \ | −4 | −4 |
| Selected Condition | Wind Direction (°) | |||||||
|---|---|---|---|---|---|---|---|---|
| Minimum (TMDI) | 330 | −0.1608 | −0.1438 | −0.1438 | −0.1416 | 10.56 | 10.52 | 11.94 |
| Maximum (TMDI) | 90 | 0.2293 | 0.1513 | 0.1519 | 0.1421 | 34.01 | 33.74 | 38.02 |
| Minimum (TID) | 330 | −0.1608 | −0.1438 | −0.1438 | −0.1416 | 10.56 | 10.52 | 11.94 |
| Maximum (TID) | 90 | 0.2293 | 0.1513 | 0.1519 | 0.1421 | 34.01 | 33.74 | 38.02 |
| Max positive displacement OS | 90 | 0.2293 | 0.1560 | 0.1519 | 0.1421 | 34.01 | 33.74 | 38.02 |
| Max negative displacement OS | 75 | −0.2130 | −0.1476 | −0.1482 | −0.1404 | 30.71 | 30.44 | 34.07 |
| Selected Condition | Wind Direction (°) | |||||||
|---|---|---|---|---|---|---|---|---|
| Minimum (TMDI) | 180 | 0.0667 | 0.0508 | 0.0469 | 0.0413 | 23.88 | 29.78 | 38.09 |
| Maximum (TMDI) | 45 | 0.0687 | 0.0353 | 0.0350 | 0.0307 | 48.63 | 49.06 | 55.26 |
| Minimum (TID) | 180 | 0.0667 | 0.0508 | 0.0469 | 0.0413 | 23.88 | 29.78 | 38.09 |
| Maximum (TID) | 45 | 0.0687 | 0.0353 | 0.0350 | 0.0307 | 48.63 | 49.06 | 55.26 |
| Maximum acceleration OS | 75 | 0.1232 | 0.0701 | 0.0685 | 0.0602 | 43.04 | 44.40 | 51.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Qiao, H.; De Domenico, D.; Zhu, Z.; Xie, Z. Wind-Induced Response Control of High-Rise Buildings Using Inerter-Based Vibration Absorbers. Appl. Sci. 2019, 9, 5045. https://doi.org/10.3390/app9235045
Wang Q, Qiao H, De Domenico D, Zhu Z, Xie Z. Wind-Induced Response Control of High-Rise Buildings Using Inerter-Based Vibration Absorbers. Applied Sciences. 2019; 9(23):5045. https://doi.org/10.3390/app9235045
Chicago/Turabian StyleWang, Qinhua, Haoshuai Qiao, Dario De Domenico, Zhiwen Zhu, and Zhuangning Xie. 2019. "Wind-Induced Response Control of High-Rise Buildings Using Inerter-Based Vibration Absorbers" Applied Sciences 9, no. 23: 5045. https://doi.org/10.3390/app9235045
APA StyleWang, Q., Qiao, H., De Domenico, D., Zhu, Z., & Xie, Z. (2019). Wind-Induced Response Control of High-Rise Buildings Using Inerter-Based Vibration Absorbers. Applied Sciences, 9(23), 5045. https://doi.org/10.3390/app9235045






