Flexible-Link Multibody System Eigenvalue Analysis Parameterized with Respect to Rigid-Body Motion
Abstract
1. Introduction
2. Modeling of Flexible-Link Multibody Systems
2.1. Motion Equations
2.2. Linearization of the Equations of Motion
2.3. Modal Analysis for Systems with Nonsymmetric Matrices
3. Polynomial Representation of the Eigenpairs of Flexible-Link Multibody Systems
3.1. Taylor Series for Multivariate Function
- (1)
- norm:
- (2)
- factorial:
- (3)
- power:
- (4)
- partial derivative:
- (5)
- number of ordered combinations of p positive integers whose sum is equal to :
- (6)
- identity: two multi-indices ans are identical, i.e., , if and only if , , ⋯, .
3.2. Eigensolution Expansion
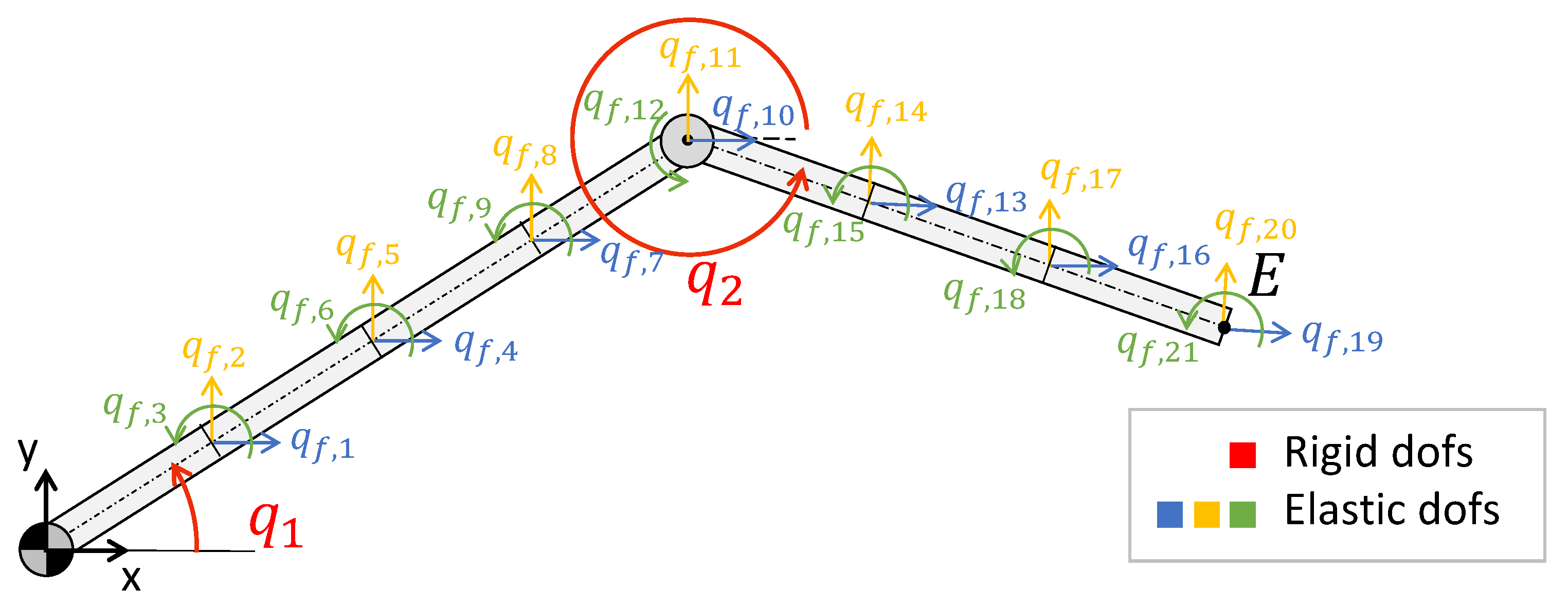
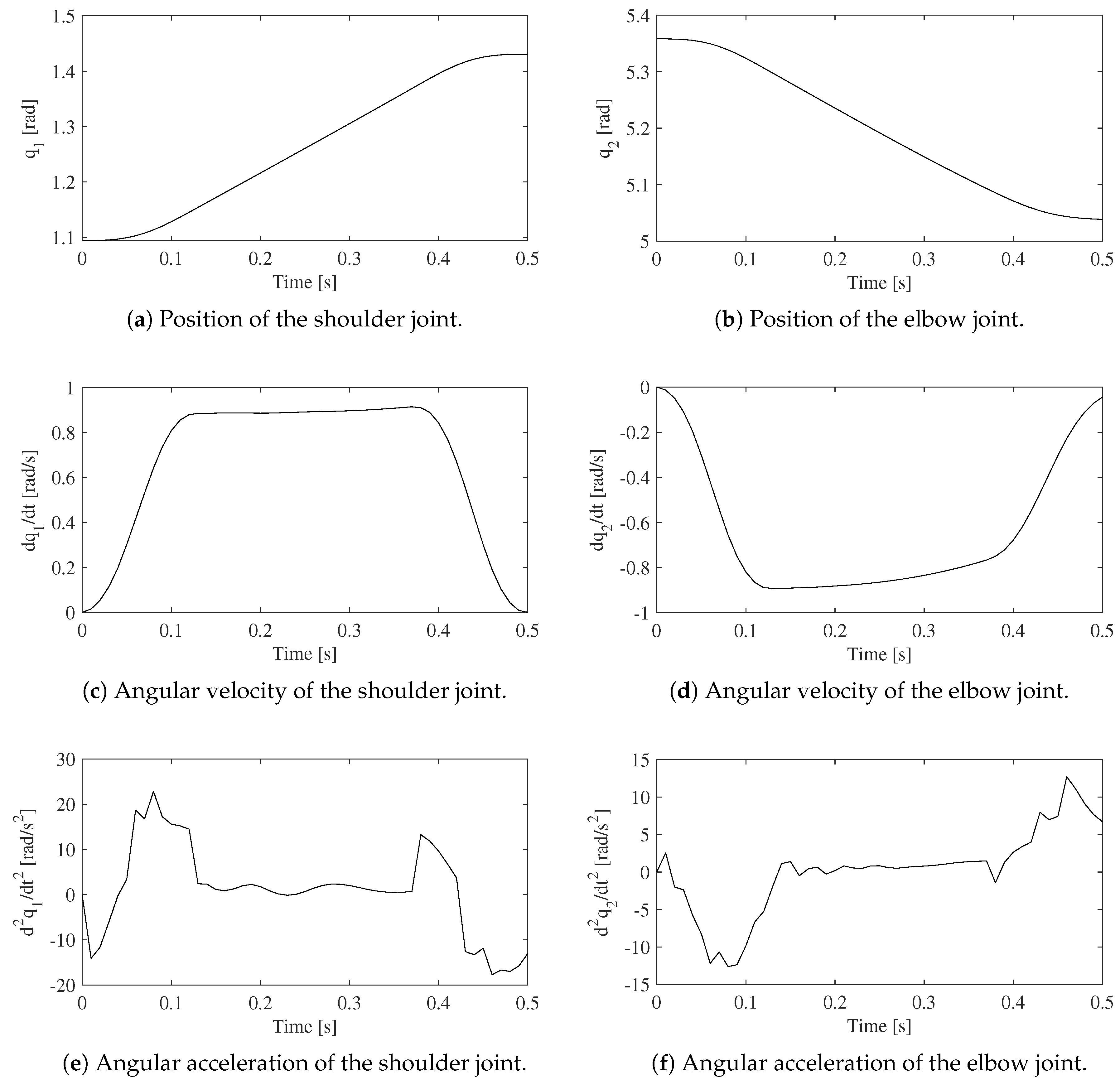
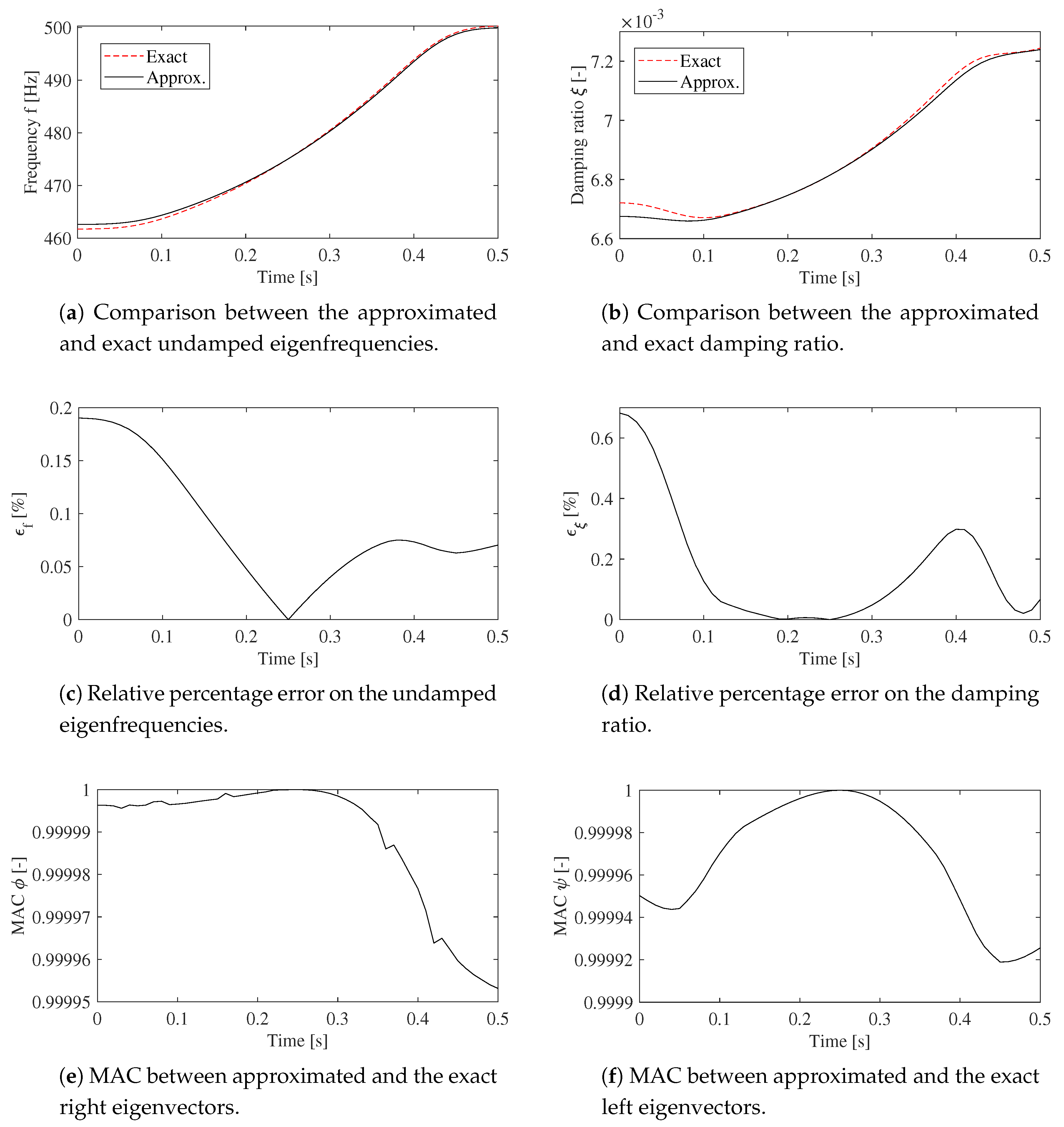
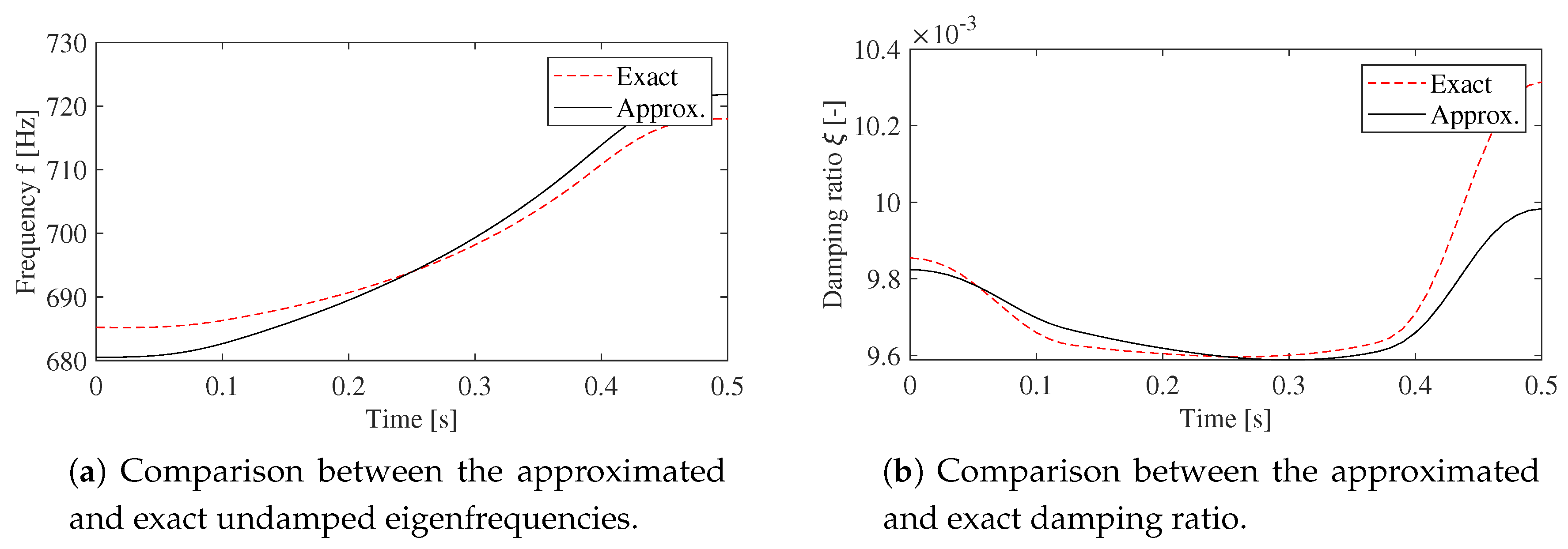
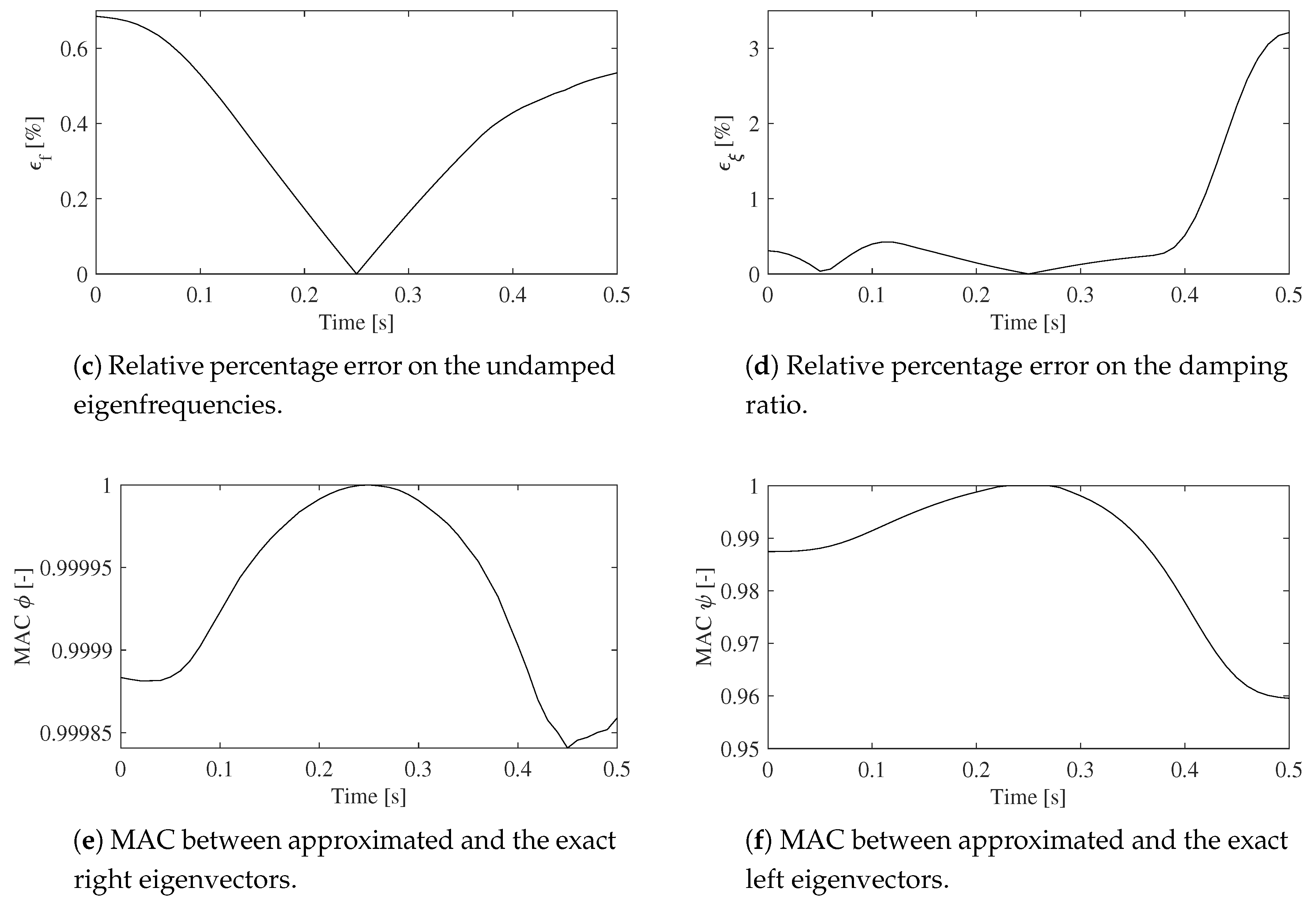
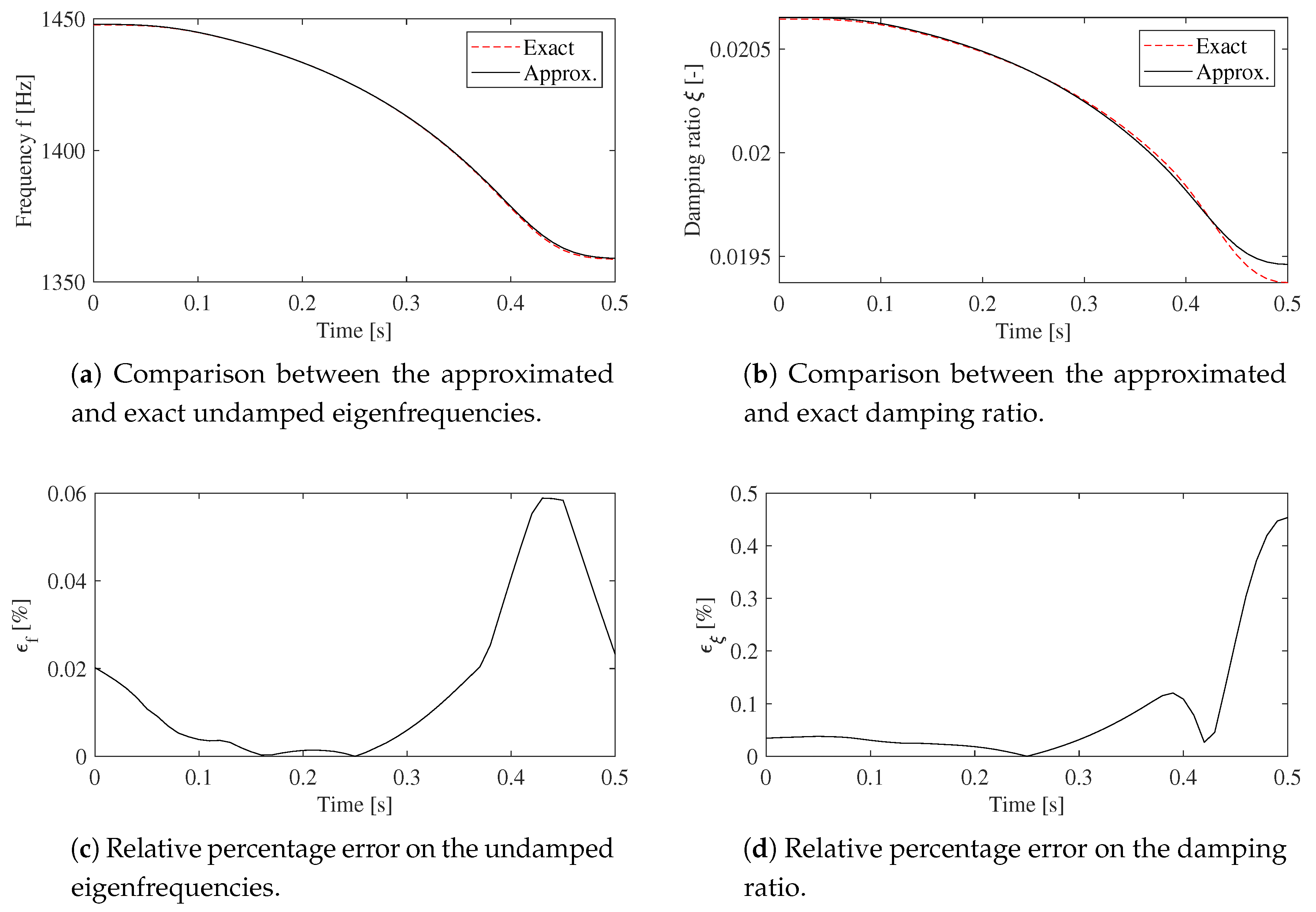
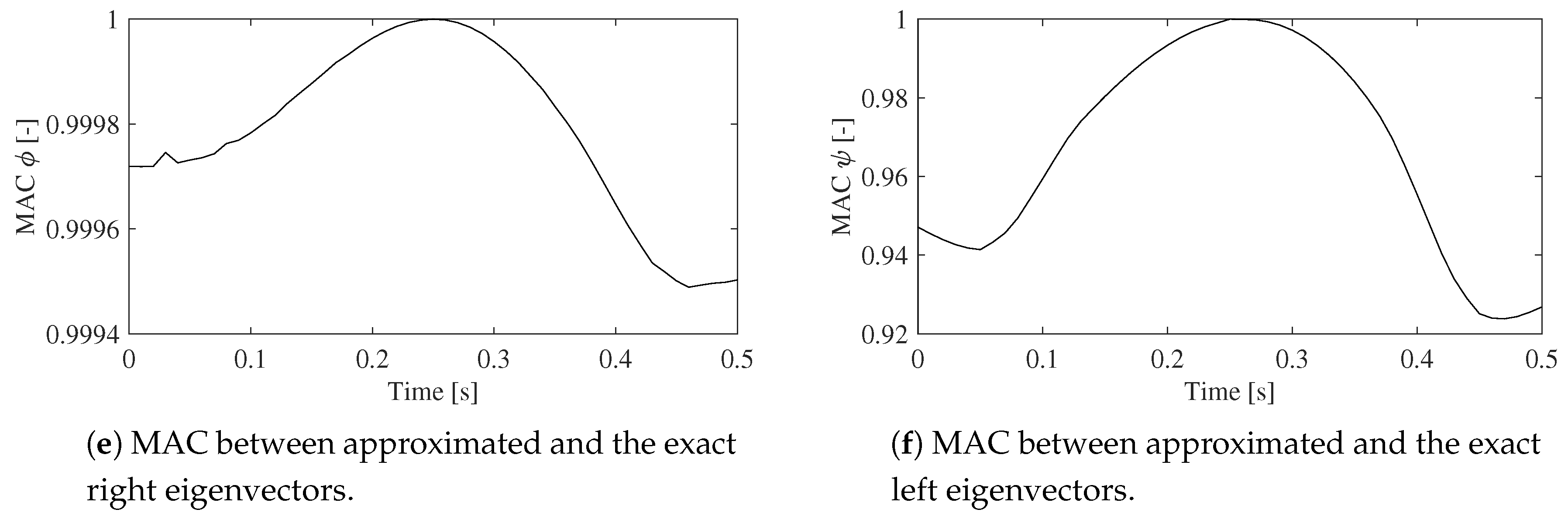
4. Results
- relative percentage error on the undamped natural frequency, :Let be a system eigenvalue, it holds:
- relative percentage error on the damping factor, :
- modal assurance criterion (MAC):
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Test Case Implementation Details
Appendix A.1. Nonlinear Dynamic Model
Appendix A.2. Dynamic Equilibrium Configuration
References
- Boscariol, P.; Richiedei, D. Robust point-to-point trajectory planning for nonlinear underactuated systems: Theory and experimental assessment. Robot. Comput.-Integr. Manuf. 2018, 50, 256–265. [Google Scholar] [CrossRef]
- Damaren, C.J. On the Dynamics and Control of Flexible Multibody Systems with Closed Loops. Int. J. Robot. Res. 2000, 19, 238–253. [Google Scholar] [CrossRef]
- Ouyang, H.; Richiedei, D.; Trevisani, A. Pole assignment for control of flexible link mechanisms. J. Sound Vib. 2013, 332, 2884–2899. [Google Scholar] [CrossRef]
- Cossalter, V.; Doria, A.; Basso, R.; Fabris, D. Experimental analysis of out-of-plane structural vibrations of two-wheeled vehicles. Shock Vib. 2004, 11, 433–443. [Google Scholar] [CrossRef][Green Version]
- Shabana, A.; Zaher, M.; Recuero, A.; Rathod, C. Study of nonlinear system stability using eigenvalue analysis: Gyroscopic motion. J. Sound Vib. 2011, 330, 6006–6022. [Google Scholar] [CrossRef]
- Brüls, O.; Duysinx, P.; Golinval, J.C. The global modal parameterization for non-linear model-order reduction in flexible multibody dynamics. Int. J. Numer. Methods Eng. 2007, 69, 948–977. [Google Scholar] [CrossRef]
- Ripepi, M.; Masarati, P. Reduced order models using generalized eigenanalysis. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2011, 225, 52–65. [Google Scholar] [CrossRef]
- Palomba, I.; Richiedei, D.; Trevisani, A. Energy-Based Optimal Ranking of the Interior Modes for Reduced-Order Models under Periodic Excitation. Shock Vib. 2015, 2015, 348106. [Google Scholar] [CrossRef]
- Palomba, I.; Richiedei, D.; Trevisani, A. A reduction strategy at system level for flexible link multibody systems. Int. J. Mech. Control 2017, 18, 59–68. [Google Scholar]
- Vidoni, R.; Scalera, L.; Gasparetto, A.; Giovagnoni, M. Comparison of model order reduction techniques for flexible multibody dynamics using an equivalent rigid-link system approach. In Proceedings of the 8th ECCOMAS Thematic Conference on Multibody Dynamics, Prague, Czech Republic, 19–22 June 2017; pp. 269–280. [Google Scholar]
- Schulze, A.; Luthe, J.; Zierath, J.; Woernle, C. Investigation of a Model Update Technique for Flexible Multibody Simulation. Comput. Methods Appl. Sci. 2020, 53, 247–254. [Google Scholar] [CrossRef]
- Belotti, R.; Caracciolo, R.; Palomba, I.; Richiedei, D.; Trevisani, A. An Updating Method for Finite Element Models of Flexible-Link Mechanisms Based on an Equivalent Rigid-Link System. Shock Vib. 2018, 2018, 1797506. [Google Scholar] [CrossRef]
- Richiedei, D.; Trevisani, A. Updating of Finite Element Models for Controlled Multibody Flexible Systems Through Modal Analysis. Comput. Methods Appl. Sci. 2020, 53, 264–271. [Google Scholar] [CrossRef]
- Belotti, R.; Richiedei, D.; Trevisani, A. Optimal Design of Vibrating Systems Through Partial Eigenstructure Assignment. J. Mech. Des. Trans. ASME 2016, 138, 071402. [Google Scholar] [CrossRef]
- Wehrle, E.; Concli, F.; Cortese, L.; Vidoni, R. Design optimization of planetary gear trains under dynamic constraints and parameter uncertainty. In Proceedings of the 8th ECCOMAS Thematic Conference on Multibody Dynamics 2017, MBD 2017, Prague, Czech Republic, 19–22 June 2017; pp. 527–538. [Google Scholar]
- Wehrle, E.; Palomba, I.; Vidoni, R. In-operation structural modification of planetary gear sets using design optimization methods. Mech. Mach. Sci. 2019, 66, 395–405. [Google Scholar] [CrossRef]
- Erdman, A.; Sandor, G. Kineto-elastodynamics—A review of the state of the art and trends. Mech. Mach. Theory 1972, 7, 19–33. [Google Scholar] [CrossRef]
- Shabana, A. Flexible Multibody Dynamics: Review of Past and Recent Developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Dwivedy, S.; Eberhard, P. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2006, 41, 749–777. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems, 4th ed.; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar] [CrossRef]
- Xie, M. Flexible Multibody System Dynamics: Theory and Applications; CRC Press: New York, NY, USA, 2017; pp. 1–214. [Google Scholar] [CrossRef]
- Palomba, I.; Richiedei, D.; Trevisani, A. Reduced-order observers for nonlinear state estimation in flexible multibody systems. Shock Vib. 2018, 2018, 6538737. [Google Scholar] [CrossRef]
- Choi, D.; Park, J.; Yoo, H. Modal analysis of constrained multibody systems undergoing rotational motion. J. Sound Vib. 2005, 280, 63–76. [Google Scholar] [CrossRef]
- Cossalter, V.; Lot, R.; Maggio, F. The Modal Analysis of a Motorcycle in Straight Running and on a Curve. Meccanica 2004, 39, 1–16. [Google Scholar] [CrossRef]
- Masarati, P. Direct eigenanalysis of constrained system dynamics. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2010, 223, 335–342. [Google Scholar] [CrossRef]
- Yang, C.; Cao, D.; Zhao, Z.; Zhang, Z.; Ren, G. A direct eigenanalysis of multibody system in equilibrium. J. Appl. Math. 2012, 2012, 638546. [Google Scholar] [CrossRef]
- González, F.; Masarati, P.; Cuadrado, J.; Naya, M. Assessment of Linearization Approaches for Multibody Dynamics Formulations. J. Comput. Nonlinear Dyn. 2017, 12, 041009. [Google Scholar] [CrossRef]
- Wittmuess, P.; Henke, B.; Tarin, C.; Sawodny, O. Parametric modal analysis of mechanical systems with an application to a ball screw model. In Proceedings of the 2015 IEEE Conference on Control and Applications, CCA2015, Sydney, Australia, 21–23 September 2015; pp. 441–446. [Google Scholar] [CrossRef]
- Wittmuess, P.; Tarin, C.; Sawodny, O. Parametric modal analysis and model order reduction of systems with second order structure and non-vanishing first order term. In Proceedings of the 54th IEEE Conference on Decision and Control, CDC 2015, Osaka, Japan, 15–18 December 2015; pp. 5352–5357. [Google Scholar] [CrossRef]
- Palomba, I.; Vidoni, R.; Wehrle, E. Application of a parametric modal analysis approach to flexible-multibody systems. Mech. Mach. Sci. 2019, 66, 386–394. [Google Scholar] [CrossRef]
- Palomba, I.; Wehrle, E.; Vidoni, R.; Gasparetto, A. Parametric eigenvalue analysis for flexible multibody systems. Mech. Mach. Sci. 2019, 73, 4117–4126. [Google Scholar] [CrossRef]
- Verlinden, O.; Huynh, H.; Kouroussis, G.; Rivière-Lorphèvre, E. Modelling of flexible bodies with minimal coordinates by means of the corotational formulation. Multibody Syst. Dyn. 2018, 42, 495–514. [Google Scholar] [CrossRef]
- Vidoni, R.; Scalera, L.; Gasparetto, A. 3-D erls based dynamic formulation for flexible-link robots: Theoretical and numerical comparison between the finite element method and the component mode synthesis approaches. Int. J. Mech. Control 2018, 19, 39–50. [Google Scholar]
- Vidoni, R.; Gasparetto, A.; Giovagnoni, M. A method for modeling three-dimensional flexible mechanisms based on an equivalent rigid-link system. JVC/J. Vib. Control 2014, 20, 483–500. [Google Scholar] [CrossRef]
- Tisseur, F.; Meerbergen, K. The quadratic eigenvalue problem. SIAM Rev. 2001, 43, 235–286. [Google Scholar] [CrossRef]
- Folland, G. Higher-Order Derivatives and Taylor’s Formula in Several Variables. Available online: https://sites.math.washington.edu/~folland/Math425/taylor2.pdf (accessed on 3 November 2019).
| Static Equilibrium | Dynamic Equilibrium | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 3 | 6 | 10 | 15 | 21 |
| 2 | 3 | 6 | 10 | 15 | 21 | 5 | 15 | 35 | 70 | 126 |
| 3 | 4 | 10 | 20 | 35 | 56 | 7 | 28 | 84 | 210 | 462 |
| 4 | 5 | 15 | 35 | 70 | 126 | 9 | 45 | 165 | 495 | 1287 |
| 5 | 6 | 21 | 56 | 126 | 252 | 11 | 66 | 286 | 1001 | 3003 |
| 6 | 7 | 28 | 84 | 210 | 462 | 13 | 91 | 455 | 1820 | 6188 |
| Property | Symbol | Value |
|---|---|---|
| Length first link | m | |
| Length second link | m | |
| Bending moment of inertia | J | |
| Circular cross-sectional area | A | |
| Mass density | 2700 | |
| Linear mass density | 1.906 | |
| Young’s modulus | E | |
| Mass proportional damping coefficients | m/s | |
| Stiffness proportional damping coefficients | m·s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palomba, I.; Vidoni, R. Flexible-Link Multibody System Eigenvalue Analysis Parameterized with Respect to Rigid-Body Motion. Appl. Sci. 2019, 9, 5156. https://doi.org/10.3390/app9235156
Palomba I, Vidoni R. Flexible-Link Multibody System Eigenvalue Analysis Parameterized with Respect to Rigid-Body Motion. Applied Sciences. 2019; 9(23):5156. https://doi.org/10.3390/app9235156
Chicago/Turabian StylePalomba, Ilaria, and Renato Vidoni. 2019. "Flexible-Link Multibody System Eigenvalue Analysis Parameterized with Respect to Rigid-Body Motion" Applied Sciences 9, no. 23: 5156. https://doi.org/10.3390/app9235156
APA StylePalomba, I., & Vidoni, R. (2019). Flexible-Link Multibody System Eigenvalue Analysis Parameterized with Respect to Rigid-Body Motion. Applied Sciences, 9(23), 5156. https://doi.org/10.3390/app9235156






