Enhanced Evolutionary Sizing Algorithms for Optimal Sizing of a Stand-Alone PV-WT-Battery Hybrid System

Abstract

An increase in the world’s population results in high energy demand, which is mostly fulfilled by consuming fossil fuels (FFs). By nature, FFs are scarce, depleted, and non-eco-friendly. Renewable energy sources (RESs) photovoltaics (PVs) and wind turbines (WTs) are emerging alternatives to the FFs. The integration of an energy storage system with these sources provides promising and economical results to satisfy the user’s load in a stand-alone environment. Due to the intermittent nature of RESs, their optimal sizing is a vital challenge when considering cost and reliability parameters. In this paper, three meta-heuristic algorithms: teaching-learning based optimization (TLBO), enhanced differential evolution (EDE), and the salp swarm algorithm (SSA), along with two hybrid schemes (TLBO + EDE and TLBO + SSA) called enhanced evolutionary sizing algorithms (EESAs) are proposed for solving the unit sizing problem of hybrid RESs in a stand-alone environment. The objective of this work is to minimize the user’s total annual cost (TAC). The reliability is considered via the maximum allowable loss of power supply probability ($LPS{P}^{max}$) concept. The simulation results reveal that EESAs provide better results in terms of TAC minimization as compared to other algorithms at four $LPS{P}^{max}$ values of 0%, 0.5%, 1%, and 3%, respectively, for a PV-WT-battery hybrid system. Further, the PV-WT-battery hybrid system is found as the most economical scenario when it is compared to PV-battery and WT-battery systems.

1. Introduction

The growth in the world’s population results in high electricity demand. Most of this demand is fulfilled by the consumption of fossil fuel (FF) resources. According to [1], 75% of the energy used by consumers is being produced by different means of FFs, including oil, coal, and other sources. The disadvantages related to the FFs are their scarcity and environmental problems that are the main cause of global warming, acid rains, and air pollutions via emission of carbon dioxide. Renewable energy sources (RESs) provide better alternatives to FFs. The advantages related to RESs include environmental friendliness and their worldwide availability. Further, RESs are not depleted by consumption. Considering the aforementioned advantages, many countries are getting encouragement to opt for RESs instead of FFs. For instance, a bill in 2018 was signed by California Governor Brown, stating that electricity retailers are to serve 60% of their load with RESs by 2030 and 100% by 2045 [2]. Currently, RESs only meet nearly 15% to 20% of the world’s energy demand [3].

RESs are considered as an effective and efficient option to solve energy problems in a stand-alone (SA) environment, where grid supply is costly or impractical due to geographical terrain. Photovoltaics (PV) and wind turbines (WT) are widely studied RESs in recent years. However, these resources are intermittent by nature due to their dependency on varying climate and weather conditions like solar irradiation, wind speed, temperature, and other factors [4]. To overcome this issue, hybrid RESs (HRESs) in conjunction with energy storage systems (ESSs) are proposed to complement one another to some extent. At the time of surplus HRESs’ energy, backup ESSs are charged to their maximum allowable limit. This energy is supplied back during the time slots when HRESs (wind speed, solar irradiation) are unavailable in an energy deficit situation [5].

HRESs are widely used sources to generate electricity in different regions of the world, depending on the availability of natural sources. To get an economical, sustainable, and reliable system, unit sizing of HRESs and their components is vital. Oversizing and undersizing are two available options if unit sizing of RESs is not considered. The oversizing of HRESs concurs with the unreliability issue; however, it also results in an increased total annual cost (TAC) of the electricity user. On the other side, undersizing of HRESs results in reduced TAC; however, it causes a situation, where the generation sources are unable to fulfill the user’s energy demand. Thus, the undersizing option causes inconvenience and discomfort for the users. Among the other available sources, PVs and WTs are considered as the most popular RESs due to the presence of solar irradiation and wind in almost every location of the world. However, due to their intermittent nature, ESSs in the form of batteries, fuel cells, flywheels, etc., are also integrated into the system to make it more reliable during varying weather conditions [6]. Further, HRESs in addition to ESSs provide a cleaner, economical, cost-effective, and reliable power solution in an SA environment as compared to a single source [7].

Reliability in the SA environment is regarded and considered via the loss of power supply probability (LPSP) concept in studies [8,9,10,11,12]. The LPSP depicts a value between zero and one. The zero value assigned to the LPSP represents that the HRESs’ system is very reliable and the user’s load will always be fulfilled. On the other side, one value assigned to the LPSP results in an unreliable system, where the user’s load is never fulfilled. In [8], Zhang et al. applied the LPSP concept to obtain the optimal sizing of the PV-WT-hydrogen system in a home, located in Khorasan, Iran. The results revealed that at low LPSP values (0% to 5%), the PV-hydrogen system with weather forecasting led to an optimal solution. When the LPSP value was set to 10%, the hybrid system resulted in being cost efficient. In [9], the authors calculated the optimum system configuration and achieved the desired LPSP with a minimum TAC. Yang et al. [10] proposed an iterative method that followed the LPSP concept to minimize the TAC values for a PV-WT-battery hybrid system. In [11], the authors used an iterative method as a benchmark along with other meta-heuristic approaches to find the optimal size of PV modules, charge controllers, inverters, and batteries via applying the LPSP concept. Abbas et al. [12] used a genetic algorithm (GA) that controlled the RESs uncertainties using a chance constrained model, which was applied to a case, located in the western part of China. Further, for this study, terms like algorithms, methods, and schemes were synonymously used.

In the literature, several research studies have reported the feasibility analysis of HRESs in rural and peri-urban areas [13,14,15]. Baghdadi et al. [13] evaluated the performance of a PV-WT-diesel-battery system on an hourly basis for a varying climate, located in Adrar, Algeria. The results revealed that 69% of FFs can be saved when HRESs are used instead of diesel generators. In [14], Bhandari et al. reported the feasibility of using a PV-WT-hydro system for an off-grid application in two locations of Nepal. The results showed that HRESs were environmentally friendly and sustainable. Hurtado et al. [15] investigated the feasibility of a PV-biomass-battery system for a laboratory complex, located in the Republic of Congo. The results indicated 98% electric stability when HRESs and ESS were adequately dimensioned.

Meta-heuristic algorithms with hybridized schemes and other optimization methodologies are widely adopted for energy management [16,17,18,19] and the unit sizing problem [20,21,22,23,24,25,26,27,28,29]. The Jaya optimization scheme was used for the optimal sizing of HRESs to minimize TAC [20,21]. In [22], Ghorbani et al. used a hybrid approach by combining the features of the GA with particle swarm optimization (PSO) for the optimal sizing of the PV-WT-battery system of a house in an SA environment, located in Tehran, Iran. The objective was to reduce the TAC and to increase the system’s reliability. The results obtained by the hybrid approach were also compared to the results obtained by a software based tool known as a hybrid optimization model for electric renewables (HOMER). The PV-WT-battery system achieved the best results in terms of TAC as compared to PV-battery and WT-battery systems. The authors in [23] used an evolutionary multi-objective, non-dominated sorting GA (NSGA-II) to find an optimum sizing of the PV-WT-battery system for a remote area, located in Tunisia. Similarly, NSGA-II with re-ranking based GA operators was proposed for a PV-WT-diesel-battery system [24]. In [25], the authors used a GA to optimize the TAC value for an SA WT-PV-tidal-battery hybrid system, located in Brittany, France. Goel et al. [26] used the HOMER software tool for the optimal sizing of a biomass-biogas system to supply electricity to a commercial agricultural farm, located in Odisha, India. Similarly, He et al. [27] used the HOMER tool for techno-economic analysis of HRESs for a large community, located in Beijing, China, using both SA and grid-connected environments. In [28], the authors used the HOMER tool for unit sizing of PV-WT and hybrid storage systems, including the fuel cell and supercapacitor for Cape Town weather conditions. Maleki et al. [29] proposed various evolutionary algorithms with the LPSP constraint for TAC minimization of a PV-WT-battery system. The results produced by artificial bee swarm optimization were more promising than other schemes.

Considering the aforementioned studies, the common objectives considered by researchers are the minimization of TAC values based on the LPSP concept. However, a few studies considered hybrid meta-heuristic approaches, which are used to explore and exploit the solution search space better. Further, the iterative method used in [11] for unit sizing problem was highly computational, which spanned several hours to find an optimal solution. Further, the HOMER software tool used by researchers [26,27,28] for techno-economical analysis of HRESs also suffers from some limitations. For instance, the HOMER tool does not take into account multi-objective problems along with its formulation, ranking of HRESs based on levelized cost, and the depth of discharge (DoD) of the battery bank. Therefore, this paper proposes meta-heuristic algorithms with their hybridization to achieve objectives, including good convergence speed, efficiency, and flexibility for the unit sizing problem. The previous work [30] is enhanced, and the contributions are given below.

• A model based on HRESs is proposed, where a PV-WT-battery system and its components are formulated and elaborated.
• Meta-heuristic algorithms: teaching-learning based optimization (TLBO), enhanced differential evolution (EDE), and salp swarm algorithm (SSA) are firstly used to find the optimal number of HRESs with an objective function to minimize the user’s TAC in an SA environment.
• Two novel hybrid approaches based on combining (TLBO + EDE and TLBO + SSA) are also proposed for the better exploitation of the search space. These hybrid approaches are called enhanced evolutionary sizing algorithms (EESAs).
• The results obtained by EESAs are compared to their ancestor schemes in three different scenarios: PV-WT-battery, PV-battery, and WT-battery systems for a yearly user’s load profile. Further, the real solar irradiation and wind speed data are used, which are obtained from Rafsanjan, Iran.
• The reliability of HRESs is considered using four maximum allowable LPSP ($LPS{P}^{max}$) values: 0%, 0.5%, 1%, and 3%, which are provided by the user. The TACs at different $LPS{P}^{max}$ values are presented and analyzed.

The remaining paper is organized as follows. Section 2 describes the system model, and Section 3 states the formulation of HRESs. The proposed algorithms are elaborated in Section 4. Section 5 discusses the simulation results, and finally, the paper is concluded in Section 6.

2. System Model

The proposed model for the PV-WT-battery hybrid system is shown in Figure 1. The model consists of an AC-bus and a DC-bus that increase the system’s performance because the power produced by the WTs is directly used to feed the AC load of the home. In the proposed model, the energy produced by dual sources, PV panels and WTs, is used to fulfill the user’s energy demand. Due to the intermittent nature of HRESs, a battery bank is also integrated into the model. In the case of surplus energy produced by HRESs, the batteries are charged up to their maximum charging limits. It is necessary to monitor continuously and to assess the charge of the battery bank. In an event when HRESs are insufficient to fulfill the user’s electricity demand, then the energy stored in the battery bank is used to supply back the deficit part. In this case, the state of charge (SoC) of the battery bank must be greater than the minimum SoC. The respective converters are installed with the HRESs’ respective components. The capacity of the converter is presented according to the capacity of the power generation system based on solar, wind, and batteries.

3. Formulation of HRESs

In this section, mathematical modeling of PVs, WTs, the battery bank, and relevant constraints is given.

3.1. Formulation of the PV System

The hourly output produced by the PV’s module is given by Equation (1) [29]:

$$P^{pv}\left(t\right)=P_{rat}^{pv}\times (I^{rad}/I_{ref}^{rad})\times \left[1+T^{cof}(T^{cel}-T^{ref})\right],$$

(1)

where $P^{pv}$ represents the total hourly PV’s power output in watts (W), which is generated at time slot $\left(t\right)$. $P_{rat}^{pv}$ shows the rated PV’s power, and $I^{rad}$ represents the solar radiation data in watts per square meter (W/m${}^2$). $I_{ref}^{rad}$ denotes the solar radiation at reference conditions, which has a value of 1000 (W/m${}^2$). $T^{cof}$ is the temperature coefficient of PV panels and is set as $-3.7$ × ${10}^{-3}$ (1/°C) for mono- and poly-crystalline silicon [29]. The temperature of PV’s cell at reference conditions is given by $T^{ref}$ having a value of 25 °C. In addition, $T^{cel}$ shows the cell temperature that can be obtained by Equation (2).

$$T^{cel}=T^{amb}+\left((T_{noct}^{cel}-20)/800\right)\times I^{rad},$$

(2)

where $T^{amb}$ represents the ambient air temperature in °C. $T_{noct}^{cel}$ shows the normal operating cell temperature in °C. The value of $T_{noct}^{cel}$ is specified by the manufacturer, which depends on the specification of the PV’s module. If $N^{pv}$ number of PVs exist, then the total generated power ${\xi }_{tot}^{pv}$ at time slot t is $N^{pv}\times P^{pv}\left(t\right)$.

3.2. Formulation of the WT System

The mathematical model for the WT’s power is calculated using the following equation [31]:

$$\left\{\begin{array}{c}{P}^{wt}\left(t\right)=0v\left(t\right)<v^{ci},\hfill \\ P^{wt}\left(t\right)=0v\left(t\right)>v^{co},\hfill \\ P^{wt}\left(t\right)=(a.v{\left(t\right)}^3-b.P_r^{wt})v^{ci}<v\left(t\right)<v^r,\hfill \\ P^{wt}\left(t\right)=P_{nom}^{wt}{v}^r<v\left(t\right)<v^{co},\hfill \end{array}\right.$$

(3)

where $P^{wt}$ is the output power generated by the WT at time slot t. The symbol v depicts the wind speed, and $P_{nom}^{wt}$ shows the nominal rated power generated by the WT in time slot t. Rated, cut-out, and cut-in wind speeds are represented by symbols $v^r$, $v^{co}$, and $v^{ci}$, respectively. a and b represent parameters calculated by Equation (4):

$$\left\{\begin{array}{c}a=P_{nom}^{wt}/({\left(v^r\right)}^3-{\left(v^{ci}\right)}^3),\hfill \\ b={\left(v^{ci}\right)}^3/({\left(v^r\right)}^3-{\left(v^{ci}\right)}^3).\hfill \end{array}\right.$$

(4)

If $N^{wt}$ number of WTs exists, then the overall produced power ${\xi }^{wt}$ at time slot t is obtained by $N^{wt}\times P^{wt}\left(t\right)$.

3.3. Formulation of User’s Load

The user’s load ${\xi }^{ld}$ at time slot t depends on the number of appliances with ON status as given by Equation (5):

$${\xi }^{ld}\left(t\right)=\sum _{i=1}^n{p}_i^{rat}\left(t\right)\times \chi \left(t\right),$$

(5)

where i represents an appliance and $p_i^{rat}$ depicts its power rating. $\chi$ is a Boolean integer, which shows the appliance status. When $\chi \left(\tau \right)=1$, the appliance status is ON in time slot t, otherwise, it is considered as OFF.

3.4. Excess and Deficit Cases of HRESs and Sizing of the Batteries

When the total energy produced by the PV and WT is greater than ${\xi }^{ld}$, then the battery bank is in the SoC at time slot t, which is obtained by Equation (6) [29].

$$\begin{array}{c}\hfill {\xi }^{str}\left(t\right)={\xi }^{str}(t-1)\times (1-{\iota }^{sdr})+\left[\left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)-\frac{{\xi }^{ld}\left(t\right)}{{\eta }_i}\right]\times {\eta }^{bat},\\ \hfill \forall \left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)>{\xi }^{ld}\left(t\right),\end{array}$$

(6)

where ${\xi }^{str}\left(t\right)$ and ${\xi }^{str}(t-1)$ depict the amount of stored energy in the battery bank at time slots t and $t-1$, respectively. ${\iota }^{sdr}$ represents the self-discharging state. The term $\left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)$ shows accumulative energy generation by PVs and WTs. ${\eta }_i$ denotes the efficiency of the inverter, and ${\eta }^{bat}$ connotes battery bank charging efficiency.

In another case, when accumulative energy generation by PVs and WTs is less than ${\xi }^{ld}\left(t\right)$ at a given time slot t, then the energy stored in the battery bank is utilized to fulfill the user’s load. In this situation, the state of the battery bank is changed to discharging. In this paper, the battery bank discharging efficiency is assumed to be one, and the temperature effects are also not considered. The discharging of the battery bank at time slot t is given as:

$$\begin{array}{c}\hfill {\xi }^{str}\left(t\right)={\xi }^{str}(t-1)\times (1-{\iota }^{sdr})-[\left(\frac{{\xi }^{ld}\left(t\right)}{{\eta }_i}-\left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)\right]/{\eta }_i,\\ \hfill \forall \left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)<{\xi }^{ld}\left(t\right).\end{array}$$

(7)

The total number of batteries ($N^b$) in the battery bank depends on the user’s load and the HRESs’ generation capacity. The size of batteries is dependent on the difference between the maximum and minimum points of a curve; where positive values indicate the generation availability by HRESs and negative values show generation deficiency. Thus, the $N^b$ required for a given system can be derived using the formula [32]:

$$N^b=\lceil \frac{max\left(point\right)-min\left(point\right)}{1.35}\rceil ,$$

(8)

where $max\left(point\right)$ and $min\left(point\right)$ represent the maximum and minimum energy generation points on the curve, respectively. The value 1.35 shows the nominal capacity of a battery. The ceil is a MATLAB function used to take the upper bound value of a variable.

3.5. Formulation of the System’s Reliability

Since, in an SA environment, the system’s reliability is an essential factor, therefore the concept of LPSP is regarded and implemented in this study. The LPSP for one year is calculated by Equation (9) [29]:

$$\begin{array}{c}\hfill LPSP=\frac{{\sum }_{t=1}^T\left[{\xi }^{ld}\left(t\right)-\left({\xi }^{pv}\left(t\right)\times {\eta }_i+{\xi }^{wt}\left(t\right)\times {\eta }_i^2\right)\right]}{{\sum }_{t=1}^T{\xi }^{ld}\left(t\right)},\forall T=8760.\end{array}$$

(9)

The loss of power supply occurs when the total energy produced by HRESs is less than the total user’s ${\xi }^{ld}$ at a given time slot.

3.6. Total Annual Cost Modeling and Constraints

In this section, an objective function based on cost modeling is given along with constraints.

3.6.1. Objective Function Formulation

The objective function evaluates the optimal number of the HRES’s components to satisfy the user’s load at minimum TAC. The total TAC is achieved by summing the capital cost and maintenance cost as given by the following formula:

$$Minimize{\zeta }^{tot}={\zeta }^{cap}+{\zeta }^{mtn},$$

(10)

where ${\zeta }^{tot}$, ${\zeta }^{cap}$, and ${\zeta }^{mtn}$ show the total, capital, and maintenance costs, respectively.

To convert the initial capital cost into the annual capital cost, the capital recovery factor (CRF) approach is used, which is obtained using the formula given below [29].

$$CRF=\frac{i^{rat}{(1+i^{rat})}^n}{{(1+i^{rat})}^n-1},$$

(11)

where $i^{rat}$ and n show the interest rate and the system’s life span in years. The values of these parameters and other HRESs’ components are summarized in

Table 1. PV-WT-battery hybrid system components and parameters [29].

Hybrid System Components	Parameters	Value
PV panel	$P_{rat}^{pv}$	120 W
	${\zeta }^{pv}$	$614
	${\zeta }_{mtn}^{pv}$	$0
	$A^{pv}$	1.07 m${}^2$
	${\eta }^{pv}$	12%
	$T_{noct}^{cel}$	33 °C
WT	$P_{nom}^{wt}$	1 kW
	$v^{ci}$	2.5 m/s
	$v^r$	11 m/s
	$v^{co}$	13 m/s
	${\zeta }^{wt}$	$3200
	${\zeta }_{mtn}^{wt}$	$100
Battery	$Voltage$	12 V
	Battery nominal capacity	1.3 kWh
	Life span	5 years
	${\eta }^{bat}$	85%
	${\rho }^{bat}$	$130
	$DoD$	0.8
	${\iota }^{sdr}$	0.0002
Power inv/conv	$P_{rat}^{ic}$	3 kW
	Life span	10 years
	${\eta }^i$	95%
	${\rho }^{ic}$	$2000
Other parameters	$i^{rat}$	5%
	n	20 years

. Furthermore, the life cycle n is twenty years for this study.

Several components used in HRESs need to be replaced during the project life span, i.e., the batteries’ estimated life is five years. Similar to the approach used in [29], the present worth factor via the single payment of a battery is derived using the formula:

$$\begin{array}{c}\hfill {\zeta }^{bat}={\rho }^{bat}\times \left(1+\frac{1}{{(1+i^{rat})}^5}+\frac{1}{{(1+i^{rat})}^{10}}+\frac{1}{{(1+i^{rat})}^{15}}\right),\end{array}$$

(12)

where ${\zeta }^{bat}$ and ${\rho }^{bat}$ represent the battery’s present worth and price, respectively.

The life time of the inverter/converter used for the HRES system is estimated as ten years, which can be obtained by the formula:

$${\zeta }^{ic}={\rho }^{ic}\times \left(1+\frac{1}{{(1+i^{rat})}^{10}}\right),$$

(13)

where ${\zeta }^{ic}$ and ${\rho }^{ic}$ depict the present worth of the inverter/converter and their price, respectively.

By breaking apart the HRESs’ system into the annual costs of PVs, WTs, batteries, and the inverter/converter, Equation (14) is achieved.

$$\begin{array}{c}\hfill {\zeta }^{cap}=CRF\times \left[N^{wt}\times {\zeta }^{wt}+N^{pv}\times {\zeta }^{pv}+N^b\times {\zeta }^{bat}+N^{ic}\times {\zeta }^{ic}\right],\end{array}$$

(14)

where ${\zeta }^{wt}$, ${\zeta }^{pv}$, ${\zeta }^{bat}$, and ${\zeta }^{ic}$ represent the unit cost of the WT, PV, battery unit, and inverter/converter, respectively. N depicts the number of each component in Equation (14). For this study, the number of inverters/converters $N^{ic}$ used is assumed as one.

The annual maintenance cost of the system is calculated using the formula:

$${\zeta }^{mtn}=N^{pv}\times {\zeta }_{mtn}^{pv}+N^{wt}\times {\zeta }_{mtn}^{wt},$$

(15)

where ${\zeta }_{mtn}^{pv}$ and ${\zeta }_{mtn}^{wt}$ represent the annual maintenance costs of PVs and WTs, respectively. In this study, the maintenance costs of the battery and inverter/converter are also not considered.

3.6.2. Constraints

The charge quantity in a battery at time slot t is subject to the minimum and maximum storage capacity constraint as given by Equation (16):

$${\xi }_{min}^{str}\le {\xi }^{str}\left(t\right)\le {\xi }_{max}^{str},$$

(16)

where ${\xi }_{max}^{str}$ depicts the maximum charge quantity showing the nominal capacity value of the battery as given in Table 1. The minimum charge quantity ${\xi }_{min}^{str}$ of the battery is calculated using the following formula:

$${\xi }_{min}^{str}=(1-DoD)\times {\xi }^{str},$$

(17)

where DoD represents the maximum DoD of a battery.

For a reliable system, the LPSP constraint is considered, which is obtained using the following formula:

$$LPSP\le LPS{P}^{max},$$

(18)

where $LPS{P}^{max}$ reveals the maximum allowable LPSP value, which is provided by the user.

Furthermore, the following constraints for the total number of PV panels, WTs, and batteries are also required.

$$0\le N^{pv}\le N_{max}^{pv},$$

(19)

$$0\le N^{wt}\le N_{max}^{wt},$$

(20)

$$0\le N^b\le N_{max}^b.$$

(21)

where $N_{max}^{pv}$, $N_{max}^b$, and $N_{max}^{wt}$ denote the maximum number of PVs, batteries, and WTs, respectively. The minimum and maximum bounds for PV panels, WTs, and batteries are set as (0–300), (0–200), and (0–20,000), respectively.

4. Proposed Algorithms for the Unit Sizing Problem

In this paper, three algorithms, TLBO, EDE, and SSA along with their hybridization schemes (TLBO + EDE and TLBO + SSA), called EESAs, are proposed. The objective function of the algorithms aims to obtain a system’s configuration that achieves the optimal number of PV-WT-battery components with a reduced TAC value and also fulfills the stated constraints. The system’s configuration S depicts a row vector of positive integers depicting three elements ($s_1$ to $s_3$). For each element in the configuration, the row vector represents the number of renewable energy subsystems. The row vector S is given as:

$$S=\left[s_1{s}_2{s}_3\right]$$

(22)

where $s_1$, $s_2$, and $s_3$ show the quantity of PV modules ($N^{pv}$), WTs ($N^{wt}$), and batteries ($N^b$), respectively. The proposed algorithms are discussed in the next subsections.

4.1. TLBO

The TLBO is a population based meta-heuristic algorithm inspired by the teaching and learning processes [33]. The advantage of TLBO lies in the fact that it does not require any algorithmic specific parameter for its functioning. Like other meta-heuristic algorithms, it also starts by generating a random population in a given search space. The rows depict learners, while columns of the population show the subjects. In TLBO, subject corresponds to the decision variable. The row vector is comprised of subjects of a learner, which presents a solution to the optimization problem.

The TLBO is based on two phases. The teacher’s phase of TLBO is inspired by the teaching by a teacher. The learner’s phase depicts learning via the interactions among different learners. In the former phase, the mean ($M^l$) of the learners is calculated subject wise, and the fitness function is used to evaluate each learner of the population. The best learner based on the fitness value is chosen as a teacher ($S_{teacher}^l$). The TLBO process now tries to shift the learners’ mean towards the teacher. Thus, a new vector is formed by the current and best mean vectors, which is obtained using the following formula [33]:

$$S_{new\left(t\right)}^l=S_{old\left(t\right)}^l+r^{rnd}\times \left(S_{teacher}^l-(T_{fcr}\times M^l)\right),$$

(23)

where $r^{rnd}$ shows a random number in the range of zero and one. $T_{fcr}$ depicts the teaching factor, whose value is selected as either one or two. $T_{fcr}$ is not taken as the input; rather, it is randomly decided with an equal probability by the TLBO optimization process. $T_{fcr}$ is obtained using Equation (24) [33]:

$$T_{fcr}=round[1+r^{rnd}\times (2-1)].$$

(24)

In the learner phase of TLBO, the learners randomly interact with each other to share and increase their knowledge. The process initiates by randomly selecting two learners, including $S_{x1}^l$ and $S_{x2}^l$, from the population, such that $(x1\ne x2)$. Upon the fitness criterion, the population is updated via the following formula:

$$S_{new\left(t\right)}^l=\left\{\begin{array}{c}{S}_{old\left(t\right)}^l+r·(S_{x1\left(t\right)}^l-S_{x2\left(t\right)}^l),if{S}_{x1\left(t\right)}^l\le S_{x2\left(t\right)}^l\hfill \\ S_{old\left(t\right)}^l+r·(S_{x2\left(t\right)}^l-S_{x1\left(t\right)}^l),otherwise.\hfill \end{array}\right.$$

(25)

In Equations (23) and (25), $S_{new}^l$ is only accepted if it provides a better TAC value based on the fitness function. Finally, the optimization process of TLBO continues until some termination criterion is met.

4.2. EDE

Arafa et al. [34] proposed an enhanced differential evolution (EDE) algorithm, which is an enhanced version of differential evolution (DE). The DE suffers from some limitations: low accuracy and a slow convergence rate. These limitations are improved in the EDE algorithm by reducing the control parameters from three to two as compared to DE. The population size and mutation factor are control parameters considered in the EDE algorithm. The population size is related to the ability of the algorithm to search the solution space, and a mutation factor is used to control the convergence speed.

The modifications in EDE are done during a stage of generating trial vectors using the crossover rate. In each iteration of the EDE process, five trial vectors are generated. The initial three trial vectors are obtained by three distinct crossover values: 0.3, 0.6, and 0.9. The fourth and fifth trial vectors aim to speed up the convergence process and increase the population diversity, respectively. These trial vectors $T_i^{vec}$ are obtained using the following formulas [18]:

$$T_i^{vec}=\left\{\begin{array}{c}\hfill M_i^{vec}if{r}^{rnd}\le 0.3\\ \hfill R_i^{vec}if{r}^{rnd}>0.3,\end{array}\right.$$

(26)

$$T_i^{vec}=\left\{\begin{array}{c}\hfill M_i^{vec}if{r}^{rnd}\le 0.6\\ \hfill R_i^{vec}if{r}^{rnd}>0.6,\end{array}\right.$$

(27)

$$T_i^{vec}=\left\{\begin{array}{c}\hfill M_i^{vec}if{r}^{rnd}\le 0.9\\ \hfill R_i^{vec}if{r}^{rnd}>0.9,\end{array}\right.$$

(28)

$$T_i^{vec}=r^{rnd}\times R_i^{vec},$$

(29)

$$T_i^{vec}=r^{rnd}\times M_i^{vec}+(1-r^{rnd})\times R_i^{vec}.$$

(30)

Here, $M_i^{vec}$ and $R_i^{vec}$ represent mutant and target vectors, respectively. The vector with the lowest TAC value is considered based on the fitness value of the trial vectors.

4.3. SSA

The SSA is a newly proposed bio-inspired meta-heuristic algorithm used for single and multi-objective engineering design problems [35]. The SSA is inspired by salp swarming behavior for foraging in deep oceans. When searching for food, salps often form a swarming behavior called a salp chain to achieve better foraging and locomotion values. The SSA starts by initializing a population of multiple salps in s-dimensional search space. Here, (s)is the number of decision variables of a given problem. Thus, salps are placed at random positions in the s-dimensional search space. Like other meta-heuristic algorithms, a fitness function is applied to evaluate each salp. The salp with the best food source is assigned a value ($F^d$), which is then chased by the salp chain. Thus, the salp chain has a leader in front of the chain with the best $F^d$ value. The rest of the salps in the salp chain act as followers. The leader position is updated using the following formula [35]:

$$s_k^1=\left\{\begin{array}{c}\hfill F_k^d+c_1\left((u_k^b-l_k^b)r_2^{rnd}+l_k^b\right)if{r}_3^{rnd}\ge 0\\ \hfill F_k^d+c_1\left((u_k^b-l_k^b)r_2^{rnd}+l_k^b\right)if{r}_3^{rnd}>0;\end{array}\right.$$

(31)

where $s_k^1$ represents the position of the leader acting as the first salp in the $k^{\mathrm{th}}$ dimension and $F_k^d$ shows the food position in the $k^{\mathrm{th}}$ dimension. The $u_k^b$ and $l_k^b$ symbols indicate the upper and lower bounds in the $k^{\mathrm{th}}$ dimension. Further, $r_2^{rnd}$ and $r_3^{rnd}$ are two random numbers whose values are generated in the range of zero and one. The balance between exploration and exploitation of the SSA algorithm is dependent on coefficient $c_1$, which is calculated using the following formula:

$$c_1=2e^{{\left(\frac{4\times i}{I}\right)}^2},$$

(32)

where i and I show the current and the maximum number of iterations, respectively.

The followers’ position is updated using the formula:

$$s_k^j=\frac{1}{2}(s_k^j+s_k^{j-1});$$

(33)

where $j\ge 2$ and $s_k^j$ depict the position of the $j^{\mathrm{th}}$ follower salp in the $k^{\mathrm{th}}$ dimension. It is pertinent to mention that salps are brought back on the boundaries if they exceed the search space. These steps are iteratively executed until some termination criterion is met.

4.4. EESAs

The research on hybrid algorithms has dramatically grown during recent years [36]. Javaid et al. [37] proposed a hybrid technique (HT) by combining the EDE and TLBO schemes for energy management. HT outperforms other schemes in terms of achieving better cost values along with other decision variables. In [38], the authors proposed a hybrid approach by merging tabu search (TS) and simulated annealing for unit sizing of a PV-WT-FC-battery system along with diesel and bio-generators. The optimal results with convergence speed were achieved by the hybrid algorithm. Mukhtaruddin et al. [39] proposed a hybrid iterative-Pareto-fuzzy approach to obtain the optimal number of components of the PV-WT-battery system for a region, located in Malaysia. The objective was to minimize the user’s TAC and also achieve maximum reliability. In another study, multi-objective GA along with multi-criteria decision making was proposed for the optimal combination of the PV-WT system in a grid connected environment [40]. Motivated by these studies, this paper presents two EESAs (TLBO + EDE and TLBO + SSA) composed of hybrid algorithms.

The flowchart of EESA (TLBO + EDE) is depicted in Figure 2. Here, the TLBO process starts by initializing the parameters, like population, termination criteria, etc. At first, the process initiates by executing the teacher phase, which is then followed by the student phase. The updated population of TLBO is further explored using trial vectors of EDE. In another case of hybrid EESA (TLBO + SSA), the steps of TLBO remain the same until the new population ($X_{new}$) is generated. The SSA steps used to update the population are shown in Figure 3. Here, the best fitness value obtained by the solution is assigned to the variable $F^d$, and then, the coefficient $C_1$ is updated using Equation (32). An iteration of a size equal to the population size is set to update the position of the leader and follower salps. The leader’s position is updated using Equation (31), while the follower’s position is updated via Equation (33). The newer solution should also satisfy the constraints. The salps’ new population ($G_{new}$) is compared with the old population $X_{new}$, and the best solutions are accepted based on the fitness criteria.

The mapping steps of EESA to the unit sizing problem for the PV-WT-battery hybrid system are given below.

(i)

The first step includes initialization of parameters: hourly input solar irradiation, ambient temperature, the speed of the wind, and user’s load profile data.

(ii)

Here, the power generated by single PV and WT is calculated using Equations (1) and (3), respectively.

(iii)

In the third step, a solution space of two decision variables is randomly generated within the upper and lower bounds as given below.

$$Ge{n}^i=\left[\begin{array}{cc}{s}_1^1& s_2^1\\ s_1^2& s_2^2\\ ⋮& ⋮\\ s_1^j& s_2^j\end{array}\right]$$

(34)

In Equation (34), the first and second columns are associated with the number of PVs and WTs, respectively.

(iv)

In this step, based on the RESs’ generation and user’s load, the total number of batteries required for each j solution is calculated using Equation (8). Thus, the cluster of configurations showing the solution space is depicted as:

$$Ge{n}^i=\left[\begin{array}{ccc}{s}_1^1& s_2^1& s_3^1\\ s_1^2& s_2^2& s_3^2\\ ⋮& ⋮& ⋮\\ s_1^j& s_2^j& s_3^j\end{array}\right]=\left[\begin{array}{c}{S}^1\\ S^2\\ ⋮\\ S^j\end{array}\right].$$

(35)

Here, the third column shows the total number of batteries $N^b$ in the battery bank. In Equation (35), for the $i^{\mathrm{th}}$ population generation, $S^i$ represents j possible configurations. Each configuration represents a possible solution competing to fulfill the EESA objective.

(v)

In the fifth step, the LPSP of all j possible configurations is calculated via applying Equation (9). The population is updated, and only those solutions are considered that satisfy the $LPS{P}^{max}$ constraint as given in Equation (18).

(vi)

Here, each configuration is evaluated using fitness criteria as depicted in Equation (10).

$$F\left(Ge{n}^i\right)=F\left[\begin{array}{c}{S}^1\\ S^2\\ ⋮\\ S^j\end{array}\right]=\left[\begin{array}{c}F\left(S^1\right)\\ F\left(S^2\right)\\ ⋮\\ F\left(S^j\right)\end{array}\right].$$

(36)

The fitness value of each configuration $F\left(S^j\right)$ shows the respective TAC, which is obtained by the summation of capital and maintenance costs.

(vii)

Here, TLBO steps are applied to update the population. First, the mean M of the learners is calculated subject wise. The best learner based on $F\left(S^j\right)$ is chosen as a teacher. The mean of learners is shifted toward the teacher via Equation (23). In the learner phase, the population is updated using Equation (25). The new solution is accepted only if it gives a better TAC value. The new population is called $X_{new}$.

(viii)

In the seventh step, the EDE process is applied, and five trial vectors $T_i^{vec}$ are generated using Equations (26)–(30). The fitness of $T_i^{vec}$ is evaluated, and the best solution is used to replace the old one. The process continues until a local termination criterion is met.

(ix)

Steps (iv)–(viii) are repeated by the EESA process until the global termination criterion of 100 generations is satisfied.

(x)

Lastly, the global best solution among 100 generations based on the TAC value is returned. The global best solution contains the respective number of $N^{pv}$, $N^{wt}$, $N^b$, TAC, and LPSP values.

5. Results and Discussion

This study performed simulations for a typical household, located in Rafsanjan, Iran. The hourly insolation and ambient temperature data profiles obtained for a year (8760 h) are shown in Figure 4. The speed of wind and user’s load data profiles during a year are represented in Figure 5 [41]. Since the RESs were locally placed near electrical consumption, therefore no electrical losses were caused due to the electricity distribution. MATLAB R2016a software was used with a processor of 2.9 GHz Intel Core i7 with 8 GB of installed memory to implement the proposed algorithms to obtain the simulation results.

Depending on the system’s reliability, which was considered via various $LPS{P}^{max}$ values, components like PV modules, WTs, and battery units were sized to supply the user’s load. This paper considers three different scenarios with different configurations of RESs by incorporating reliability at various $LPS{P}^{max}$ values of the user’s choice. These scenarios are given below:

(i)

PV-WT-battery: ($S=\left[s_1{s}_2{s}_3\right]$),

(ii)

PV-battery: ($S=\left[s_{1}0s_3\right]$), and

(iii)

WT-battery: ($S=\left[0s_2{s}_3\right]$).

The three scenarios were optimally sized in terms of their configurations based on the TAC, reliability, and other constraints.

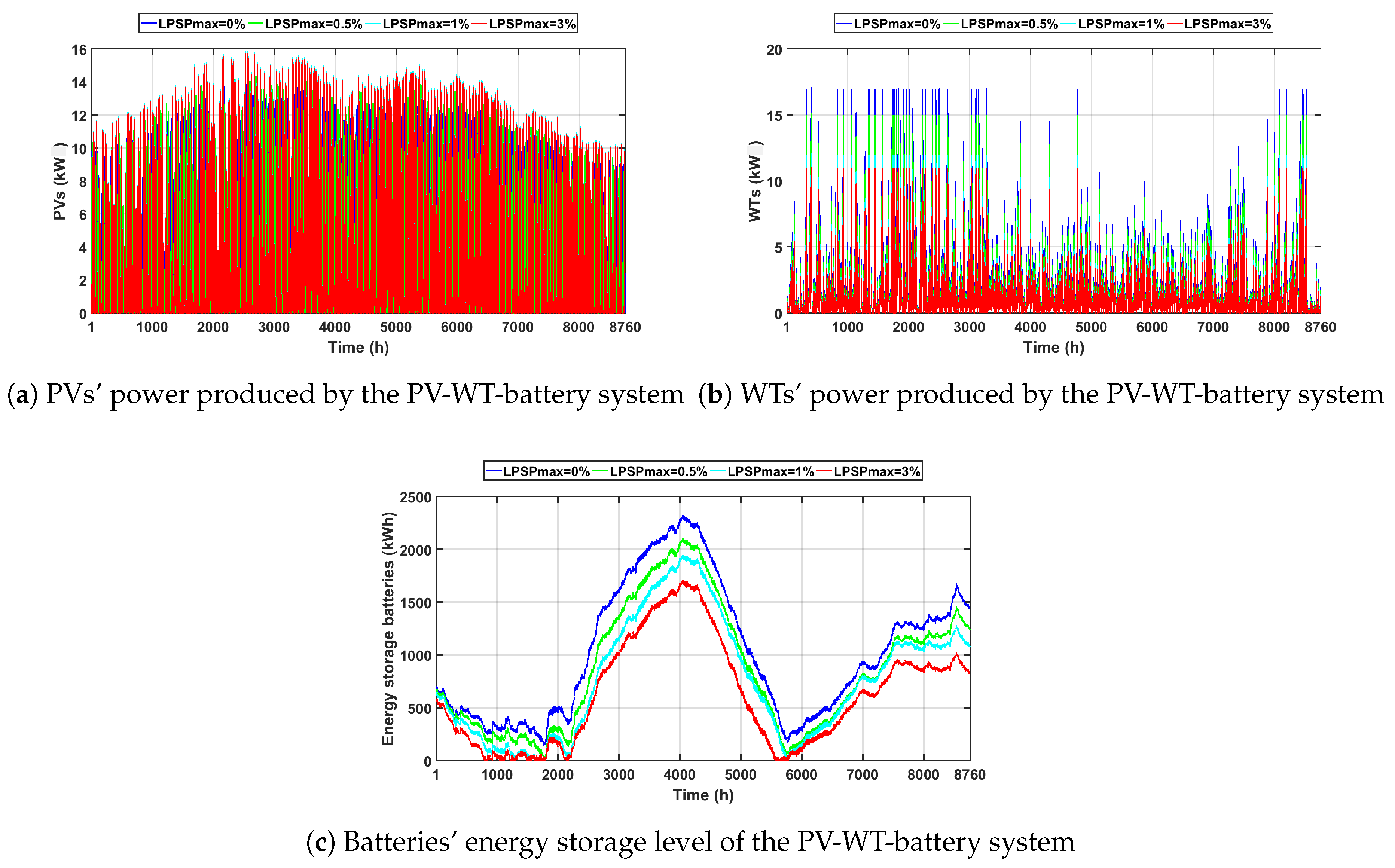
5.1. Scenario 1: PV-WT-Battery Hybrid System ($S=\left[s_1{s}_2{s}_3\right]$)

Here, energy generated from PVs, WTs, and battery units was used to fulfill the user’s load using four different $LPS{P}^{max}$ values. The TLBO, EDE, SSA, and EESA results are summarized in

Table 2. Summary of TLBO, EDE, SSA, and EESA results for the PV-WT-battery hybrid system at various $LPS{P}^{max}$ values.

System	TLBO						EDE					SSA					EESA
	$\mathit{LPSP}$${}^{\mathit{max}}$ (%)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)
PV-WT-Battery	0	0	111	17	1753	64,430	0	126	14	1837	66,621	0	112	17	1794	65,710	0	111	17	1753	64,430
	0.5	0.2762	113	16	1688	62,220	0.3641	122	14	1711	62,640	0.4778	136	11	1771	64,061	0.3779	117	15	1685	61,970
	1	0.6543	116	15	1654	60,990	0.8524	133	11	1673	60,971	0.9725	132	11	1640	59,931	0.9645	127	12	1612	59,200
	3	2.7274	122	12	1461	54,420	2.9859	142	7	1539	55,964	1.6359	125	12	1552	57,300	2.8168	126	11	1458	54,171
	Average rank					60,515					61,549					61,750					59,943
	Final rank					2					3					4					1

. As both algorithms (TLBO + EDE and TLBO + SSA) used in EESAs achieved the same optimal results, therefore their results are solely discussed. The average values of TAC at four $LPS{P}^{max}$ values were calculated, and the final ranking of algorithms was given accordingly. EESA achieved the optimal results as compared to the TLBO, EDE, and SSA algorithms because of their high exploration and exploitation abilities in more promising areas of the solution space. The system’s configurations achieved by EESA at four different $LPS{P}^{max}$ values are given as:

• $S=\left[111171753\right]$ at $LPS{P}^{max}=0\%$,
• $S=\left[117151685\right]$ at $LPS{P}^{max}=0.5\%$,
• $S=\left[127121612\right]$ at $LPS{P}^{max}=1\%$, and
• $S=\left[126111458\right]$ at $LPS{P}^{max}=3\%$.

For $LPS{P}^{max}$ values of 0%, 0.5%, 1%, and 3%, EESA achieved TACs of $64,430, $61,970, $59,200, and $54,171, respectively. It is noted from Table 2 that the TAC values decreased as $LPS{P}^{max}$ values were increased. This phenomenon was due to the trade-off between TAC and LPSP. The system was very reliable and would always satisfy the user’s load demand at $LPS{P}^{max}=0\%$. As the $LPS{P}^{max}$ values were increased, the system became less reliable with reduced TAC values.

Table 2’s results reveal that the EESA, TLBO, EDE, and SSA algorithms were ranked as first, second, third, and fourth, respectively based on their final ranking obtained from the average of all TACs at four $LPS{P}^{max}$ values. The average TAC values for the EESA, TLBO, EDE, and SSA algorithms were $59,943, $60,515, $61,549, and $61,750, respectively. The performance of EESA was found to be better due to the hybridization of the algorithms, which resulted in better exploitation of the search space to obtain the optimal results.

The hourly PVs’ power produced, WTs’ power produced, and energy storage level of the PV-WT-battery system obtained by EESA during a year at various $LPS{P}^{max}$ values are depicted in Figure 6. In Figure 6a, the highest PVs’ power is generated by $s_1$ = 127 and $s_1$ = 126 PVs; at $LPS{P}^{max}$ values of 1% and 3%, respectively. Figure 6b shows the WTs’ power of the PV-WT-battery system produced. The highest WTs’ power was produced when $s_2$ = 17 at $LPS{P}^{max}$ = 0%, as compared to other $LPS{P}^{max}$ values. The hourly expected batteries’ energy storage level of the PV-WT-battery system is depicted in Figure 6c. As the system was very reliable at $LPS{P}^{max}$ = 0%, therefore it contained the highest number of batteries, i.e., $s_3$ = 1753. With an increase in the $LPS{P}^{max}$ value, the required number of battery units also decreased, resulting in lower TACs. Besides, loss of load (LOL) was caused at the time slots when the amount of stored energy in battery units reached the minimum allowable limit.

The breakdown of the TAC values of PV-WT-battery system at various $LPS{P}^{max}$ values is presented in

Table 3. Breakdown of TAC by EESA for the PV-WT-battery hybrid system at various $LPS{P}^{max}$ values.

System	EESA
	${\mathit{LPSP}}^{\mathit{max}}$ (%)	Configuration	${\mathit{\zeta }}^{\mathit{pv}}$ ($)	${\mathit{\zeta }}^{\mathit{wt}}$ ($)	${\mathit{\zeta }}^{\mathit{bat}}$ ($)	${\mathit{\zeta }}^{\mathit{ic}}$ ($)	${\mathit{\zeta }}^{\mathit{mtn}}$ ($)	TAC ($)
PV-WT-battery	0	$S=\left[111171753\right]$	5469	4365	52,637	259	1700	64,430
	0.5	$S=\left[117151685\right]$	5764	3852	50,595	259	1500	61,970
	1	$S=\left[127121612\right]$	6257	3081	48,403	259	1200	59,200
	3	$S=\left[126111458\right]$	6208	2825	43,779	259	1100	54,171

and also illustrated in Figure 7. The costs contributed by PVs, WTs, and the number of battery units ($N^b$) for PV-WT-battery system are given in Table 3. Figure 7c,d shows similar pie charts because the average values are rounded to their nearest integers. The major portion of the total cost was spent on $N^b$. The maintenance cost was only caused by WTs. The PVs’ maintenance cost is not considered in this work. In the next section, the PV-battery scenario is discussed at various $LPS{P}^{max}$ values.

5.2. Scenario 2: PV-Battery System ($S=\left[s_{1}0s_3\right]$)

In this scenario, the energy of the PVs and battery units was used to satisfy the user’s load at various $LPS{P}^{max}$ values. The PV-battery results are summarized in

Table 4. Summary of TLBO, EDE, SSA, and EESA results for the PV-battery hybrid system at various $LPS{P}^{max}$ values.

System	TLBO						EDE					SSA					EESA
	$\mathit{LPSP}$${}^{\mathit{max}}$ (%)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)
PV-Battery	0	0	199	0	3150	104,640	0	199	0	3150	104,640	0	200	0	3200	106,200	0	199	0	3150	104,640
	0.5	0.4932	194	0	2898	96,840	0.4932	194	0	2898	96,840	0.4932	194	0	2898	96,840	0.4932	194	0	2898	96,840
	1	0.8820	191	0	2746	92,120	0.7526	192	0	2797	93,700	0.6160	193	0	2847	95,250	0.8820	191	0	2746	92,120
	3	2.8942	178	0	2090	71,790	2.8942	178	0	2090	71,790	2.7459	179	0	2141	73,370	2.8942	178	0	2090	71,790
	Average rank					91,348					91,743					92,915					91,348
	Final rank					1					2					3					1

. Based on the final rankings, the EESA and TLBO schemes performed equally in terms of TAC minimization for all $LPS{P}^{max}$ values. The EDE and SSA schemes were placed into the second and third categories based on their achieved TACs. The achieved PV-battery system’s configurations of EESA at four $LPS{P}^{max}$ values were given as:

• $S=\left[19903150\right]$ at $LPS{P}^{max}=0\%$,
• $S=\left[19402898\right]$ at $LPS{P}^{max}=0.5\%$,
• $S=\left[19102746\right]$ at $LPS{P}^{max}=1\%$, and
• $S=\left[17802090\right]$ at $LPS{P}^{max}=3\%$.

In Table 4, the lowest TAC was achieved by TLBO and EESA. Here, the TAC achieved was $104,640 at $LPS{P}^{max}$ = 0% with configuration $S=\left[19903150\right]$. As $LPS{P}^{max}$ values were increased from 0%, EESA resulted in minimized TACs along with reduced system’s components. For instance, at $LPS{P}^{max}$ = 3%, the system’s configuration was $S=\left[17802090\right]$ with a reduced TAC of $71,790.

The hourly PVs’ power produced and energy storage level of the PV-battery system obtained by EESA during a year at various $LPS{P}^{max}$ values are plotted in Figure 8. In Figure 8a, the highest energy generation was achieved by $s_1$ = 199 and $s_1$ = 194 PVs at $LPS{P}^{max}$ values of 0% and 0.5%, respectively. The lowest energy was produced by the PW-battery system with configuration $S=\left[17802090\right]$ at $LPS{P}^{max}$ = 3%. Here, the TAC value achieved was also lowest, i.e., $71,790. The expected amount of energy stored in battery units at four $LPS{P}^{max}$ values is plotted in Figure 8b. The system was very reliable at $LPS{P}^{max}$ = 0% because it contained the highest storage capacity with $N^b$ = 3150. As the $LPS{P}^{max}$ values were increased from 0%, a decline in the number of battery units was observed along with TACs. From Figure 8b, it is also evident that LOL occurred at time slots where battery units reached their minimum capacity limit at higher $LPS{P}^{max}$ values.

The breakdown of TACs for four $LPS{P}^{max}$ values is given in

Table 5. Breakdown of TAC by EESA for the PV-battery hybrid system at various $LPS{P}^{max}$ values.

System	EESA
	${\mathit{LPSP}}^{\mathit{max}}$ (%)	Configuration	${\mathit{\zeta }}^{\mathit{pv}}$ ($)	${\mathit{\zeta }}^{\mathit{wt}}$ ($)	${\mathit{\zeta }}^{\mathit{bat}}$ ($)	${\mathit{\zeta }}^{\mathit{ic}}$ ($)	${\mathit{\zeta }}^{\mathit{mtn}}$ ($)	TAC ($)
PV-battery	0	$S=\left[19903150\right]$	9800	0	94,580	260	0	10,4640
	0.5	$S=\left[19402898\right]$	9560	0	87,020	260	0	96,840
	1	$S=\left[19102746\right]$	9410	0	82,450	260	0	92,120
	3	$S=\left[17802090\right]$	8770	0	62,760	260	0	71,790

and also plotted in Figure 9. In this work, the maintenance cost of PVs is ignored. Table 5 shows that a major portion of TAC was caused by the number of battery units $N^b$. At $LPS{P}^{max}$ = 3%, the TAC was $71,790 with configuration $S=\left[17802090\right]$. Here, the sub-costs: ${\zeta }^{pv}$ = $8770, ${\zeta }^{bat}$ = $62,760, and ${\zeta }^{ic}$ = $260 resulted in a TAC of $71,790. Figure 9b,c shows similar pie charts because the average values were rounded to the nearest integer. The detailed breakdown of costs is given in Table 5.

The next section discusses the last scenario of the WT-battery system at various $LPS{P}^{max}$ values. TACs achieved by the evolutionary algorithms are reported.

5.3. Scenario 3: WT-Battery System ($S=\left[0s_2{s}_3\right]$)

The summary of TLBO, EDE, SSA, and EESA results for the WT-battery hybrid system at various $LPS{P}^{max}$ values is given in

Table 6. Summary of TLBO, EDE, SSA, and EESA results for the WT-battery hybrid system at various $LPS{P}^{max}$ values.

System	TLBO						EDE					SSA					EESA
	$\mathit{LPSP}$${}^{\mathit{max}}$ (%)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)	$\mathit{LPSP}$ (%)	${\mathit{N}}^{\mathit{pv}}$	${\mathit{N}}^{\mathit{wt}}$	${\mathit{N}}^{\mathit{b}}$	TAC ($)
PV-Battery	0 and 0.5	0	0	50	3552	124,750	0	0	50	3552	124,750	0	0	50	3552	124,750	0	0	50	3552	124,750
	1 and 3	0.5503	0	49	3362	118,690	0.5503	0	49	3362	118,690	0.5503	0	49	3362	118,690	0.5503	0	49	3362	118,690
	Average rank					121,720					121,720					121,720					121,720
	Final rank					1					1					1					1

. In Table 6, all algorithms achieved the same results in terms of average rank values. Thus, all algorithms were ranked equally with one final rank value. The configurations achieved for four $LPS{P}^{max}$ values are given as:

• $S=\left[0503552\right]$ at $LPS{P}^{max}=0\%$,
• $S=\left[0503552\right]$ at $LPS{P}^{max}=0.5\%$,
• $S=\left[0493362\right]$ at $LPS{P}^{max}=1\%$, and
• $S=\left[0493362\right]$ at $LPS{P}^{max}=3\%$.

The configurations achieved at $LPS{P}^{max}$ values of 0% and 0.5% were the same; thus, this resulted in an equal amount of TAC of $124,750. Similarly, at $LPS{P}^{max}$ values of 1% and 3%, EESA achieved the same TAC of $118,690 with configuration $S=\left[0493362\right]$. The hourly WTs’ power produced along with the energy storage level achieved by EESA during a year at four $LPS{P}^{max}$ values is depicted in Figure 10 for the WT-battery system. As the WTs were the highest for $LPS{P}^{max}$ values of 0% and 0.5%, i.e., $N^{wt}$ = 50, therefore they also produced a larger amount of energy, as shown in Figure 10a. At $LPS{P}^{max}$ values of 1% and 3%, WTs were low ($N^{wt}$ = 49). Figure 10b shows the hourly expected amount of stored energy for the WT-battery system. The LOL occurred when $LPS{P}^{max}$ values were set to 1% and 3%.

The breakdown of the TAC values of the WT-battery at various $LPS{P}^{max}$ is given in

Table 7. Breakdown of TAC by EESA for the WT-battery hybrid system at various $LPS{P}^{max}$ values.

System	EESA
	${\mathit{LPSP}}^{\mathit{max}}$ (%)	Configuration	${\mathit{\zeta }}^{\mathit{pv}}$ ($)	${\mathit{\zeta }}^{\mathit{wt}}$ ($)	${\mathit{\zeta }}^{\mathit{bat}}$ ($)	${\mathit{\zeta }}^{\mathit{ic}}$ ($)	${\mathit{\zeta }}^{\mathit{mtn}}$ ($)	TAC ($)
WT-Bat.	0 and 0.5	$S=\left[0503552\right]$	0	12,840	106,650	260	5000	124,750
	1 and 3	$S=\left[0493362\right]$	0	12,580	100,950	260	4900	118,690

. The illustration is provided in Figure 11. Unlike the case of the PV-battery system, where the maintenance cost of PVs was ignored, here the WTs’ maintenance cost was considered according to the value as given in Table 1. Similar to the previous two scenarios, the breakdown of TAC for the WT-battery system showed that the major portion of the cost was caused by the battery units.

5.4. Convergence Process of the EESA Algorithm for Three Scenarios

The convergence process of the EESA algorithm to achieve the optimal results at different $LPS{P}^{max}$ values is illustrated in Figure 12. All three scenarios were tested on 100 iterations. It is shown in Figure 12 that the EESA reduced TAC during the initial iterations, which showed the efficiency of the proposed hybrid algorithm towards achieving the objective function.

From Figure 12a, it is noticed that due to the high number of decision variables ($N^{pv}$, $N^{wt}$, and $N^b$) involved in the PW-WT-battery hybrid system, the convergence process was achieved at later iterations. However, for the PV-battery and WT-battery systems with fewer decision variables, the EESA achieved the convergence process earlier, as displayed in Figure 12b and Figure 12c, respectively.

6. Conclusions and Future Work

In this paper, the HRESs were composed of PVs, WTs, and battery units. The reliability of the HRESs was obtained using the $LPS{P}^{max}$ concept. The fitness function of the algorithms was based on the TAC minimization subject to the $LPS{P}^{max}$ and other constraints. In contrast to the EDE and SSA optimization schemes, the TLBO used for unit sizing did not require any algorithm specific parameters for execution. Due to this advantage, TLBO was used in both hybrid EESAs. From this paper, the following key points are concluded.

(i)

Hybrid EESAs were developed for better exploration and exploitation of the search space. EESAs accepted inputs, including solar irradiation, ambient temperature, wind speed, and user’s load data.

(ii)

The PV-WT-battery hybrid system was found with the best optimal configuration of RESs with reduced TACs as compared to the PV-battery and WT-battery systems. The TACs achieved by EESA were $64,430, $61,970, $59,200, and $54,171 at $LPS{P}^{max}$ values of 0%, 0.5%, 1%, and 3%, respectively. In the PV-WT-battery hybrid system, the algorithms EESA, TLBO, EDE, and SSA were ranked as 1^st, 2^nd, 3^rd, and 4^th, respectively, based on their average TAC values. EESA performed better than other algorithms due to the better search on more promising areas of the solution space. On the other hand, TLBO’s performance was found better compared to the EDE and SSA schemes because it neither required any algorithm specific parameter, nor its calibration to obtain the optimal results.

(iii)

The PV-battery system provided the second most economical results. The TACs achieved were $104,640, $96,840, $92,120, and $71,790 at $LPS{P}^{max}$ values of 0%, 0.5%, 1%, and 3%, respectively. In this scenario, EESA and TLBO performed equally and were placed in the first category. EDE and SSA achieved second and third rankings based on their average TACs, respectively.

(iv)

The third scenario: The WT-battery system was the most expensive case, due to the high price of WTs. The TACs $124,750 and $118,690 were achieved by EESA at $LPS{P}^{max}$ values of (0%, 0.5%) and (1%, 3%), respectively. Here, all algorithms achieved the same optimal results due to a fewer number of decision variables compared to the PV-WT-battery hybrid system, thus being ranked equally.

(v)

The trade-off analysis between TAC and $LPS{P}^{max}$ was also evaluated. It was found that when the $LPS{P}^{max}$ values were increased from 0%, TACs were minimized and vice versa.

In the future, the hybrid algorithms proposed will be compared to a non-algorithm specific parameter based algorithm, i.e., Jaya, and also other schemes that require algorithm specific parameters, including particle swarm optimization and wind driven optimization.