Evaluation of Skin Friction Drag Reduction in the Turbulent Boundary Layer Using Riblets †
Abstract
:1. Introduction
2. Wind Tunnel Apparatus, Equipment, and Test Conditions
2.1. Wind Tunnel Facility
2.2. Flat-Plate Model
2.3. Riblets
2.4. Test Conditions
3. Measurement Technique and Data Reduction Methodologies
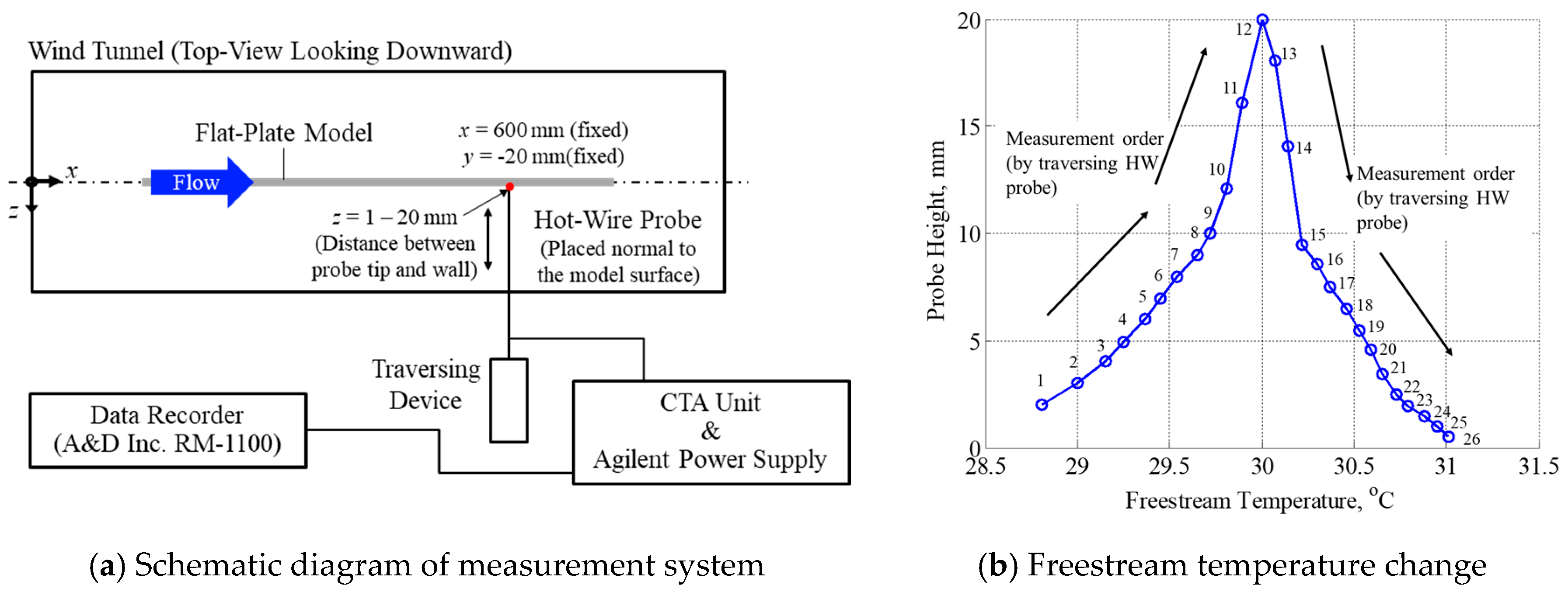
3.1. Hot-Wire Anemometry
3.2. Pitot-Rake Measurement
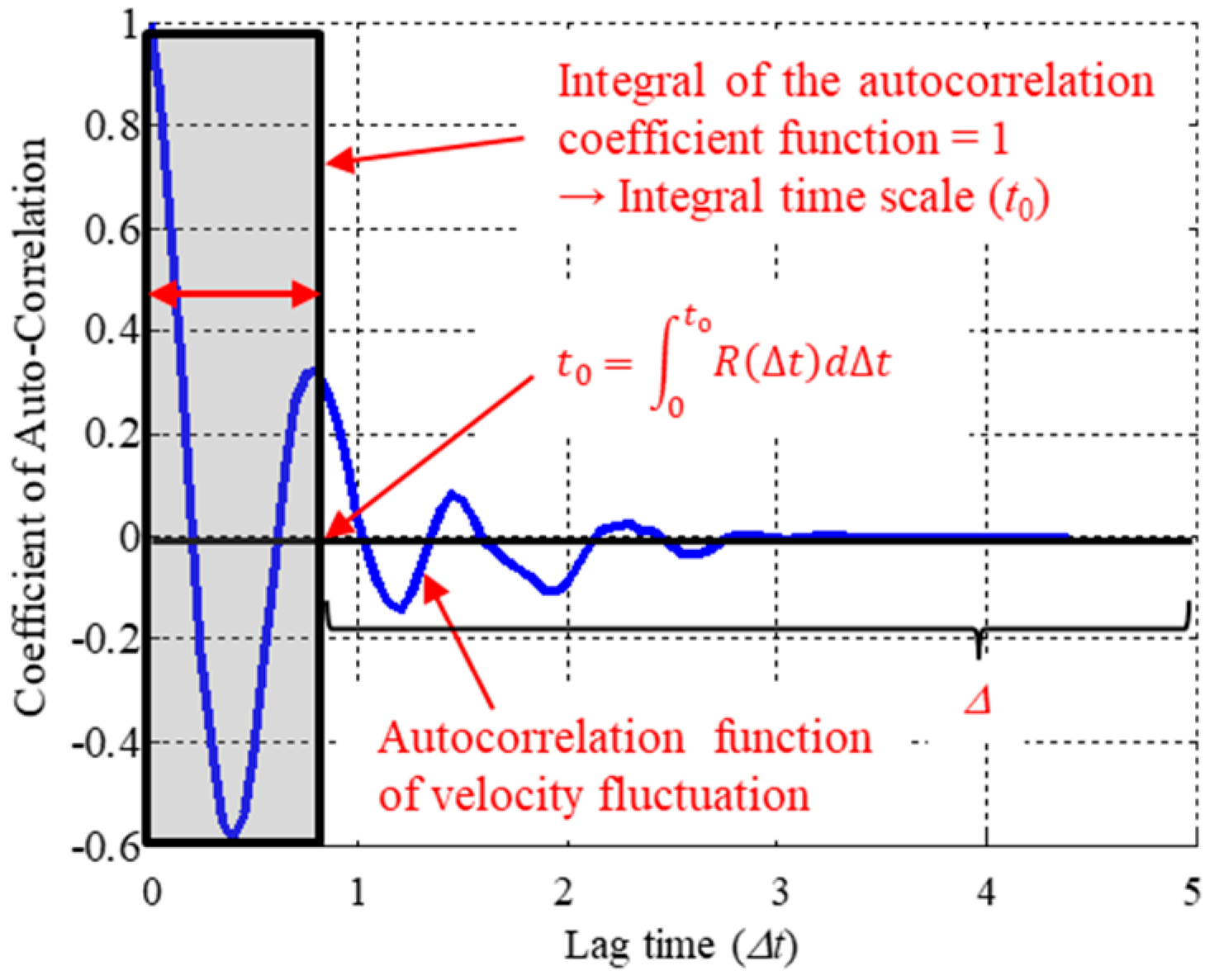
3.3. Integral Time and Length Scales
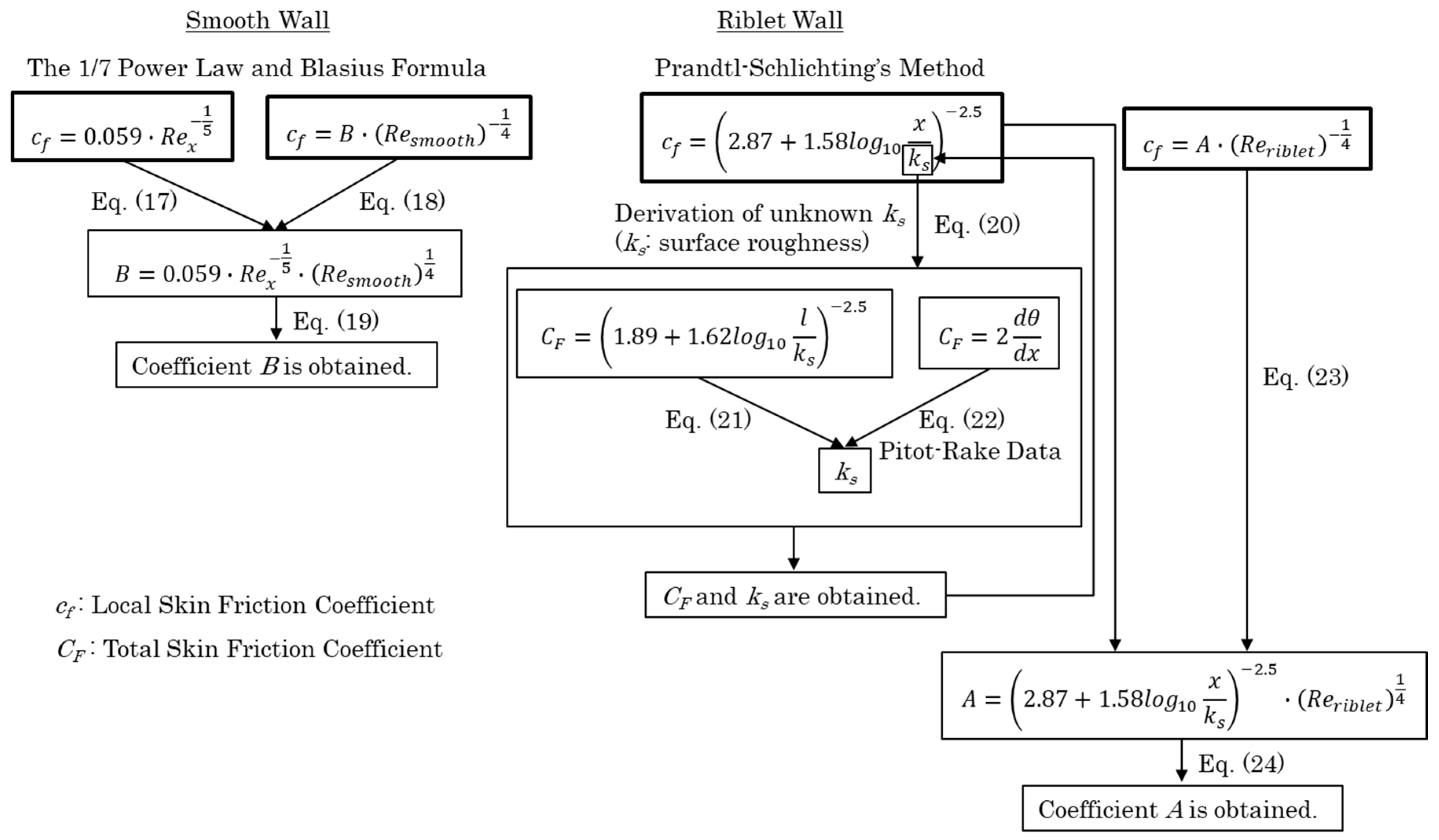
3.4. Evaluation of Skin Friction Drag Reduction
3.5. Quantitative Interpretation for Output Signals from Hot-Wire Anemometry
4. Results and Discussion
4.1. Uncertainty Analysis
4.2. General Characteristics of Velocity Profiles
4.3. Integral Time and Length Scales
4.4. Smaller Scale Turbulence
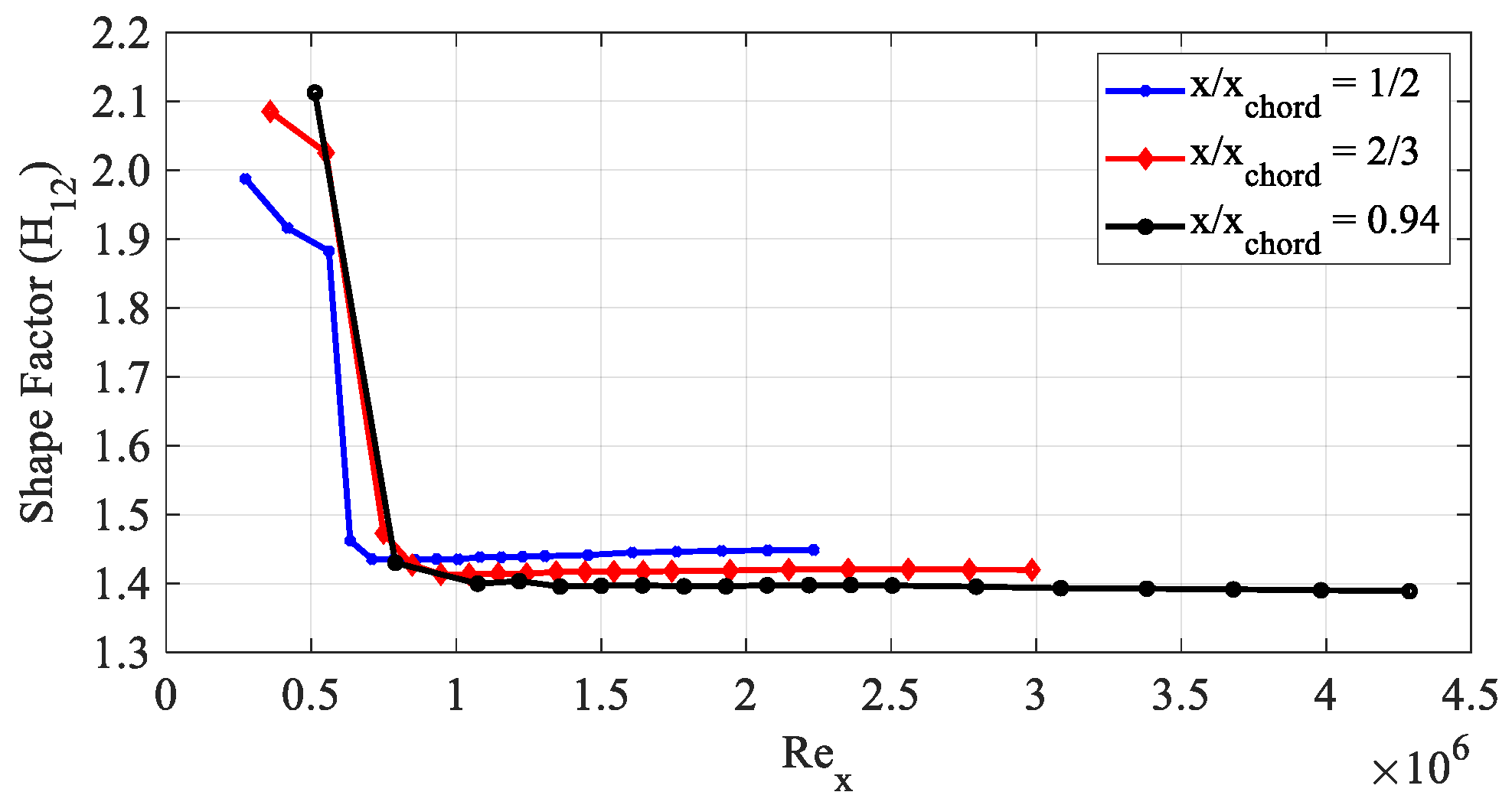
4.5. Quantitative Evaluation of Reduction of Skin Friction Drag
5. Conclusions
- (1)
- The riblet surface made from aircraft paint successfully demonstrated a reduction of skin friction drag.
- (2)
- The riblet surface increased both the integral time scale and the length scale by 30% from those for the smooth wall at a freestream velocity of 41.7 m/s (Mach 0.12) and a chord length of 67% (x/xchord = 2/3) from the model’s leading edge.
- (3)
- The proposed method evaluated the skin friction drag for the riblets at a freestream velocity of 41.7 m/s (Mach 0.12) and a chord length of 67% (x/xchord = 2/3) from the leading edge of the flat-plate model by 2.8%. This is consistent with that obtained by the momentum integration method based on the pitot-rake measurement of 2.9%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A, B, C | constant (coefficient) |
| CF | total skin friction coefficient |
| CH, CK | directional sensitivity factor |
| cf | local skin friction coefficient |
| d | diameter, mm |
| E | voltage, V |
| f | sampling frequency, Hz |
| H | probe height, mm |
| H12 | shape factor |
| h | height of riblet, μm |
| k | thermal conductivity, W/(m⋅K) |
| ks | surface roughness, mm |
| L0 | integral length scale, mm |
| m | data length |
| N | data length |
| q | uncertainty, % |
| R | correlation coefficient |
| Re | Reynolds number |
| s | width of riblet, μm |
| s+ | nondimensional width of riblet |
| T | temperature, K or °C |
| Tu | turbulent kinetic energy |
| t0 | integral time scale, s |
| U | streamwise velocity component (U-velocity), m/s |
| u’ | streamwise component of velocity fluctuation, m/s |
| u+ | nondimensional U velocity |
| uτ | friction velocity, m/s |
| v’ | spanwise component of velocity fluctuation, m/s |
| w’ | vertical component of velocity fluctuation, m/s |
| x | coordinate in streamwise direction |
| y | coordinate in spanwise direction |
| z | coordinate in vertical direction |
| z+ | nondimensional height |
| δ | boundary layer thickness, mm |
| δ** | displacement thickness, mm |
| ε | energy dissipation rage, m2/s3 |
| ν | kinematic viscosity, m2/s |
| θ | momentum thickness, mm |
| ρ | density, kg/m3 |
| σ | standard deviation |
| τ0 | Reynolds stress, Pa |
| Δt | lag time, s |
Subscripts
| 1, 2, 3… | component number |
| A | freestream (air) |
| chord | chord |
| eff | effective |
| i | index number |
| laminar | laminar flow state |
| riblet | riblet surface |
| smooth | smooth surface |
| total | total |
| turb | turbulent |
| u | u velocity |
| w | wire |
References
- Szodruch, J. Viscous Drag Reduction on Transport Aircraft. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. AIAA Paper 91-0685. [Google Scholar]
- Saravi, S.S.; Cheng, K. A Review of Drag Reduction by Riblets and Micro-Textures in the Turbulent Boundary Layers. Eur. Sci. J. 2013, 9, 62–81. [Google Scholar]
- Walsh, M.J. Viscous Drag Reduction in Boundary Layers; edited by Bushness and Hefner. Prog. Astronaut. Aeronaut. 1989, 123, 203–261. [Google Scholar]
- Walsh, M.J. Riblets as a Viscous Drag Reduction Technique. AIAA J. 1983, 21, 485–486. [Google Scholar] [CrossRef]
- Bushnell, D.M.; Hefner, J.N.; Ash, R.L. Effect of Compliant Wall Motion on Turbulent Boundary Layers. Phys. Fluids 1977, 20. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kasagi, N. Turbulent Drag Reduction Mechanism Above a Riblet Surface. AIAA J. 1994, 32, 1781–1790. [Google Scholar] [CrossRef]
- Dean, B.; Bhushan, B. Shark-Skin Surfaces for Fluid-Drag Reduction in Turbulent Flow: A Review. Philos. Trans. R. Soc. A 2010, 368, 4775–4806. [Google Scholar] [CrossRef]
- Viswanath, P.R. Aircraft Viscous Drag Reduction Using Riblets. Prog. Aerosp. Sci. 2002, 38, 571–600. [Google Scholar] [CrossRef]
- Okabayashi, K. Direct Numerical Simulation for Modification of Sinusoidal Riblets. J. Fluid Sci. Technol. 2016, 11. [Google Scholar] [CrossRef]
- Sawyer, W.; Winter, K. An Investigation of the Effect on Turbulent Skin Friction of Surface with Streamwise Grooves. In Turbulent Drag Reduction by Passive Means, Proceedings of the International Conference, London, England, 15–17 September 1987; Royal Aeronautical Society: London, UK, 1987; pp. 330–362. [Google Scholar]
- Walsh, M.J. Turbulent Boundary Layer Drag Reduction Using Riblets. In Proceedings of the 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982. AIAA Paper 82-0169. [Google Scholar]
- Bechert, D.W.; Bruse, M.; Hage, W.; Van Der Hoeven, J.G.T.; Hoppe, G. Experiments on Drag-Reducing Surfaces and their Optimization with an Adjustable Geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- MBB Transport Aircraft Group. Microscopic Rib Profiles Will Increase Aircraft Economy in Flight. Aircr. Eng. 1988, 60, 11. [Google Scholar] [CrossRef]
- Grüneberger, R.; Kramer, F.; Wassen, E.; Hage, W.; Meyer, R.; Thiele, F. Influence of Wave-Like Riblets on Turbulent Friction Drag. Nat. Inspired Fluid Mech. 2012, 119, 311–329. [Google Scholar]
- Peet, Y.; Sagaut, P.; Charron, Y. Turbulent Drag Reduction using Sinusoidal Riblets with Triangular Cross-Section. In Proceedings of the 38th Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008. AIAA Paper 2008-3745. [Google Scholar]
- Peet, Y.; Sagaut, P.; Charron, Y. Pressure Loss Reduction in Hydrogen Pipelines by Surface Restructuring. Int. J. Hydrogen Energy 2009, 34, 8964–8973. [Google Scholar] [CrossRef]
- Peet, Y.; Sagaut, P. Theoretical Prediction of Turbulent Skin Friction on Geometrically Complex Surfaces. Phys. Fluids 2009, 21, 10. [Google Scholar] [CrossRef]
- Kurita, M.; Nishizawa, A.; Okabayashi, K.; Koga, S.; Kwak, T.; Nakakita, K.; Naka, Y. FINE: Flight Investigation of Skin-Friction Reducing Eco-Coating. In Proceedings of the 54th Aircraft Symposium, Toyama, Japan, 24–26 October 2016. JSASS-2016-5180 (In Japanese). [Google Scholar]
- Koga, S.; Kurita, M.; Iijima, H.; Okabayashi, K.; Nishizawa, A.; Takahashi, H.; Endo, S. Wind Tunnel Tests for Measurement System Design of Flight Investigation of Skin-Friction Reducing Eco-Coating (FINE). In Proceedings of the 54th Aircraft Symposium, Toyama, Japan, 24–26 October 2016. JSASS-2016-5105 (In Japanese). [Google Scholar]
- Liu, T. Extraction of Skin-Friction Fields from Surface Flow Visualizations as an Inverse Problem. Meas. Sci. Technol. 2013, 24, 124004. [Google Scholar] [CrossRef]
- Bottini, H.; Kurita, M.; Iijima, H.; Fukagata, K. Effects of Wall Temperature on Skin-Friction Measurements by Oil-Film Interferometry. Meas. Sci. Technol. 2015, 26, 105301. [Google Scholar] [CrossRef]
- Takahashi, H.; Tomioka, S.; Sakuranaka, N.; Tomita, T.; Kuwamori, K.; Masuya, G. Effects of Plume Impingements of Clustered Nozzles on the Surface Skin Friction. J. Propuls. Power 2015, 31, 485–495. [Google Scholar] [CrossRef]
- Marshakov, A.V.; Scheta, J.A.; Kiss, T. Direct Measurement of Skin Friction in a Turbine Cascade. J. Propuls. Power 1996, 12, 245–249. [Google Scholar] [CrossRef]
- Takahashi, H.; Kurita, M.; Koga, S.; Endo, S. Turbulent Boundary Layer Characteristics of Riblet Surface Responsible for Skin Friction Drag. In Proceedings of the 54th Aircraft Symposium, Toyama, Japan, 24–26 October 2016. JSASS-2016-5102 (In Japanese). [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary Layer Theory: 8th Revised and Enlarged Edition; Springer: Berlin, Germany, 1999; p. 436. [Google Scholar]
- Stenzel, V.; Wilke, Y.; Hage, W. Drag-Reducing Paints for the Reduction of Fuel Consumption in Aviation and Shipping. Prog. Org. Coat. 2011, 70, 224–229. [Google Scholar] [CrossRef]
- Potter, M.C.; Wiggert, D.C.; Ramadan, B.; Shin, T.I.-P. Mechanics of Fluids; Cengage Learning: Boston, MA, USA, 2015; p. 393. [Google Scholar]
- Takahashi, H.; Kanamori, M.; Naka, Y.; Makino, Y. Statistical Characterization of Atmospheric Turbulence Behavior Responsible for Sonic Boom Waveform Deformation. AIAA J. 2018, 56, 673–686. [Google Scholar] [CrossRef]
- Chanson, H. Applied Hydrodynamics: An. Introduction; CRC Press: Boca Raton, FL, USA, 2014; p. 293. [Google Scholar]
- Houghton, E.L.; Carpenter, P.W.; Colicott, S.H.; Valentine, D.T. Aerodynamics for Engineering Students 6th Edition; Elsevier: Amsterdam, The Netherlands, 2013; p. 557. [Google Scholar]
- King, L.B. On the Convection of Heat From Small Cylinders in a Stream of Fluid: Determination of the Convection Constants of Small Platinum Wires, with Applications to Hot-Wire Anemometry. Proc. R. Soc. A 1914, 90. [Google Scholar] [CrossRef]
- Hultmark, M.; Smits, A.J. Temperature Corrections for Constant Temperature and Constant Current Hot-Wire Anemometers. Meas. Sci. Technol. 2010, 21, 105404. [Google Scholar] [CrossRef]
- Kannuluik, W.G.; Carman, E.H. The Temperature Dependence of the Thermal Conductivity of Air. Aust. J. Sci. Res. Ser. A Phys. Sci. 1951, 4, 305–314. [Google Scholar] [CrossRef]
- Lomas, C.G. Fundamentals of Hot Wire Anemometry; Cambridge University Press: Cambridge, UK, 1986; Chapter 2. [Google Scholar]
- Frehlich, R.; Meillier, Y.; Jensen, M.L.; Balsley, B. Measurements of Boundary Layer Profiles in an Urban Environment. J. Appl. Meteorol. Climatol. 2006, 45, 821–837. [Google Scholar] [CrossRef]










| Wall Type | Mean Freestream Velocity | Tw, °C |
|---|---|---|
| Smooth | 41.7 m/s (Mach 0.12) | 111 |
| Riblet | 41.7 m/s (Mach 0.12) | 77 |
| Uncertainty Source | Symbol | Value, % | Note |
|---|---|---|---|
| Temperature correction | q1 | 0.26 | Obtained from the difference between the temperature corrected hot-wire data and the pitot probe data for z = 1.0–4.0 mm |
| Hot-wire anemometry | q2 | 0.035 + 0.05 | Variance from five measurement points in the freestream region (z = 12–20 mm) |
| Systematic error | q3 | 0.56 | Equations. (28) through (30) accounting for the directional sensitivity of the velocity measurement |
| Derivation of integral time scale | q4 | 1.72 | q4 = 0.1Δt/(t0: freestream in smooth wall) = 0.005 ms/0.291 ms |
| Statistical Properties | Smooth Wall | Riblet | ||
|---|---|---|---|---|
| z = 2 mm (z/δsmooth = 0.196: Inside the Boundary Layer) | z = 20 mm (z/δsmooth = 19.6: Freestream Region) | z = 2 mm (z/δsmooth = 0.198: Inside the Boundary Layer) | z = 20 mm (z/δsmooth = 19.8: Freestream Region) | |
| Mean (), m/s | 30.10 | 41.85 | 30.41 | 41.83 |
| Standard deviation (σu), m/s | 2.88 | 0.89 | 2.68 | 0.85 |
| Kurtosis, m/s | 2.76 | 8.36 | 2.76 | 9.13 |
| Skewness, m/s | 0.13 | 0.28 | 0.15 | 0.26 |
| Turbulence intensity () | 0.096 | 0.021 | 0.088 | 0.020 |
| Wall Type | δ | δ* | θ | Reδ | Reθ |
|---|---|---|---|---|---|
| Smooth Wall | 10.2 | 1.63 | 1.24 | 2.66 × 104 | 3.22 × 104 |
| Riblet | 10.2 | 1.56 | 1.20 | 2.66 × 104 | 3.12 × 104 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, H.; Iijima, H.; Kurita, M.; Koga, S. Evaluation of Skin Friction Drag Reduction in the Turbulent Boundary Layer Using Riblets. Appl. Sci. 2019, 9, 5199. https://doi.org/10.3390/app9235199
Takahashi H, Iijima H, Kurita M, Koga S. Evaluation of Skin Friction Drag Reduction in the Turbulent Boundary Layer Using Riblets. Applied Sciences. 2019; 9(23):5199. https://doi.org/10.3390/app9235199
Chicago/Turabian StyleTakahashi, Hidemi, Hidetoshi Iijima, Mitsuru Kurita, and Seigo Koga. 2019. "Evaluation of Skin Friction Drag Reduction in the Turbulent Boundary Layer Using Riblets" Applied Sciences 9, no. 23: 5199. https://doi.org/10.3390/app9235199
APA StyleTakahashi, H., Iijima, H., Kurita, M., & Koga, S. (2019). Evaluation of Skin Friction Drag Reduction in the Turbulent Boundary Layer Using Riblets. Applied Sciences, 9(23), 5199. https://doi.org/10.3390/app9235199





