Determination of Clamping Force Using Bolt Vibration Responses during the Tightening Process
Abstract
:Featured Application
Abstract
1. Introduction
2. Nondestructive Method to Estimate Clamping Force
3. Estimation of Clamping Force from Vibration Measured in the Clamped Parts
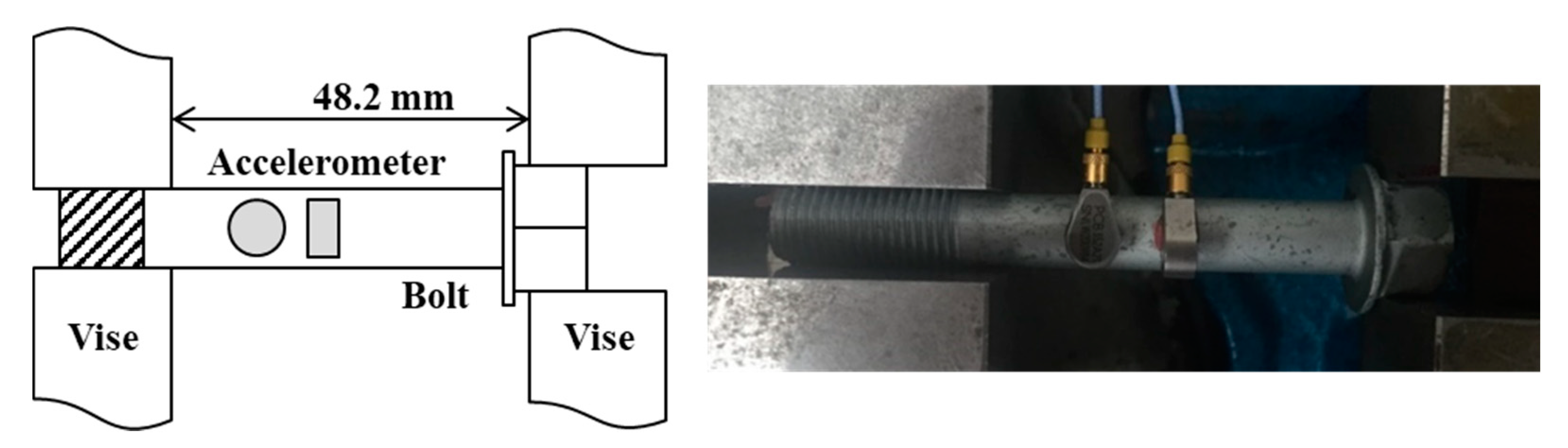
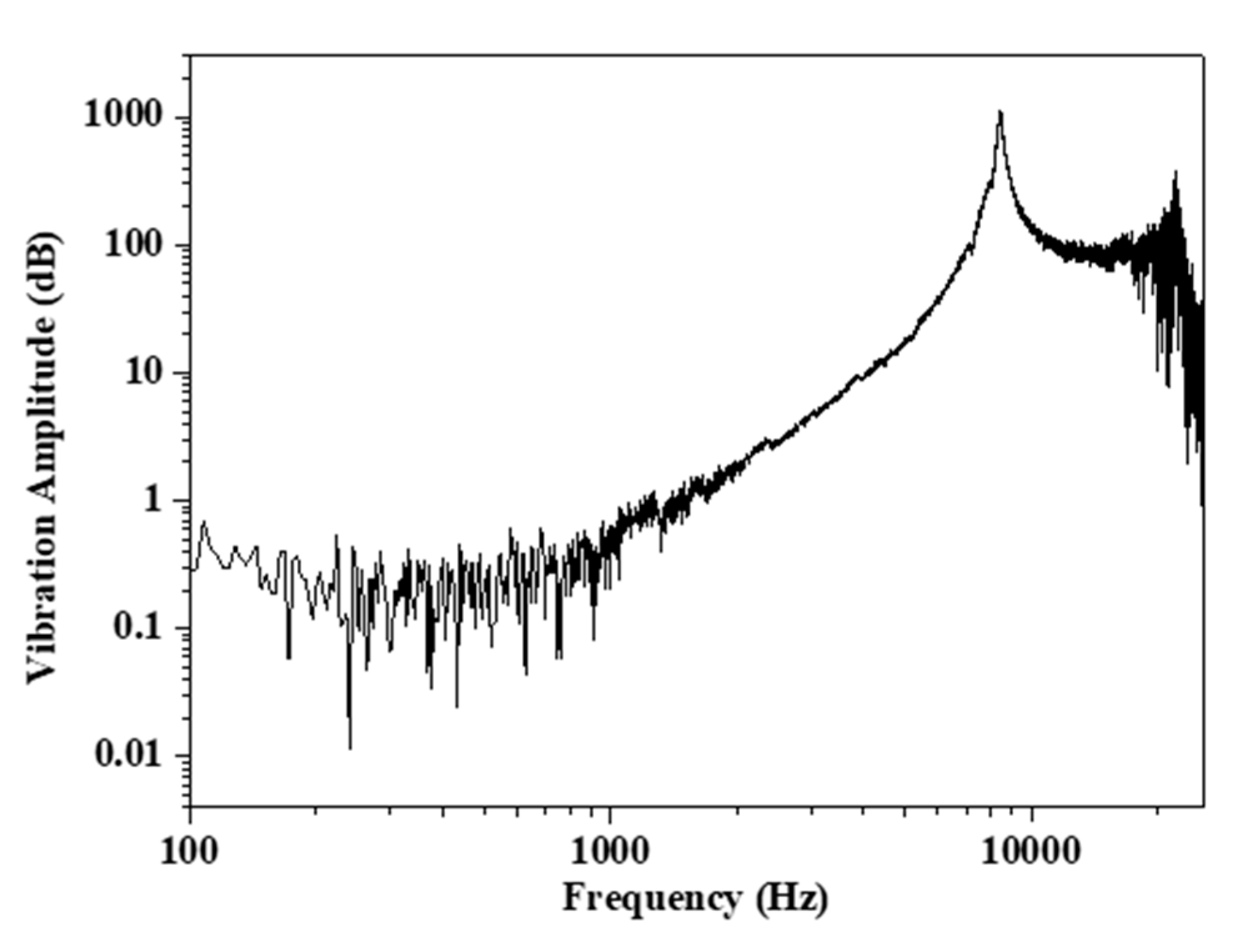
3.1. Natural Frequency of a Bolt Specimen
3.2. Dynamic Characteristics of a Fastening Bolt
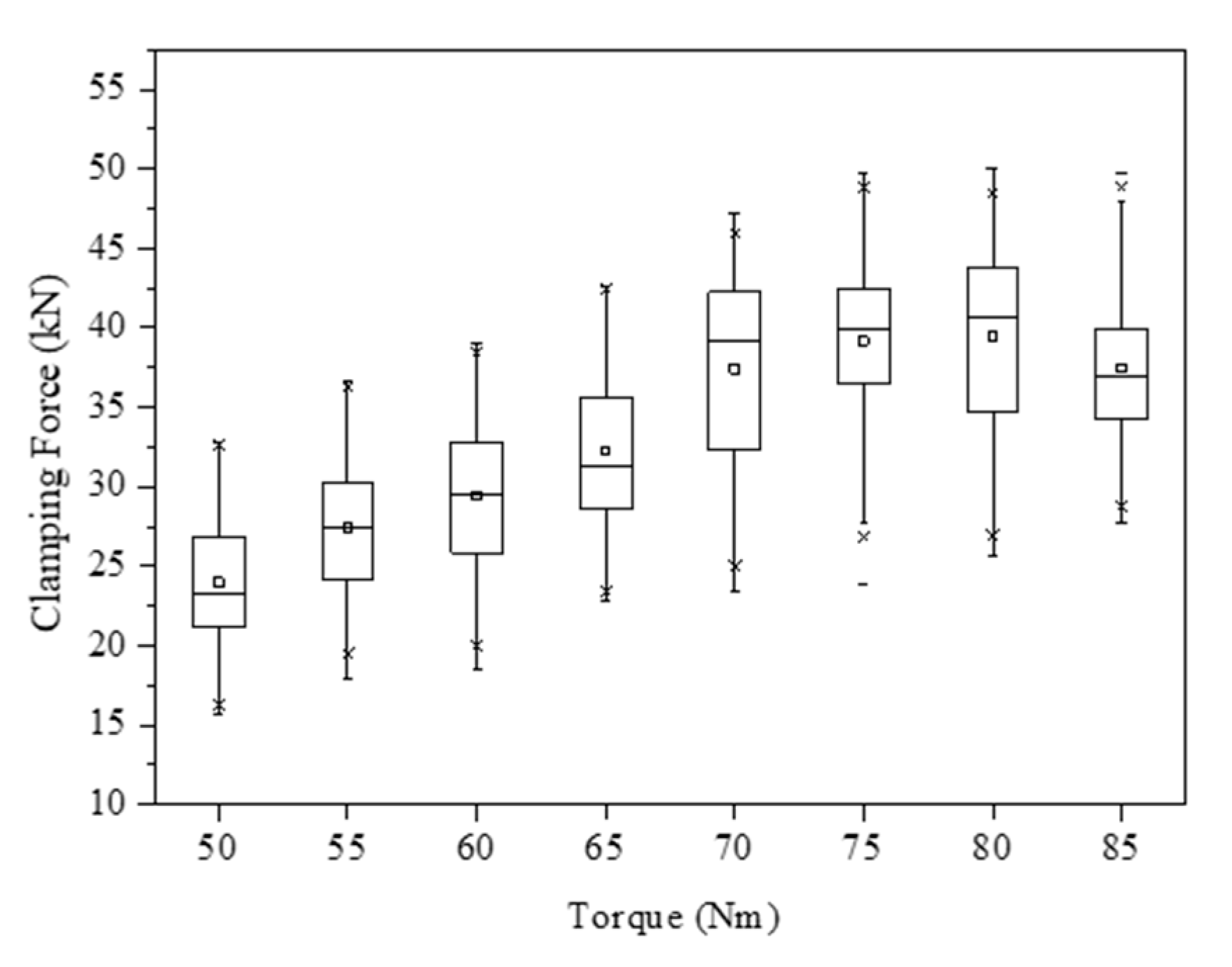
3.3. Clamping on a Load Cell
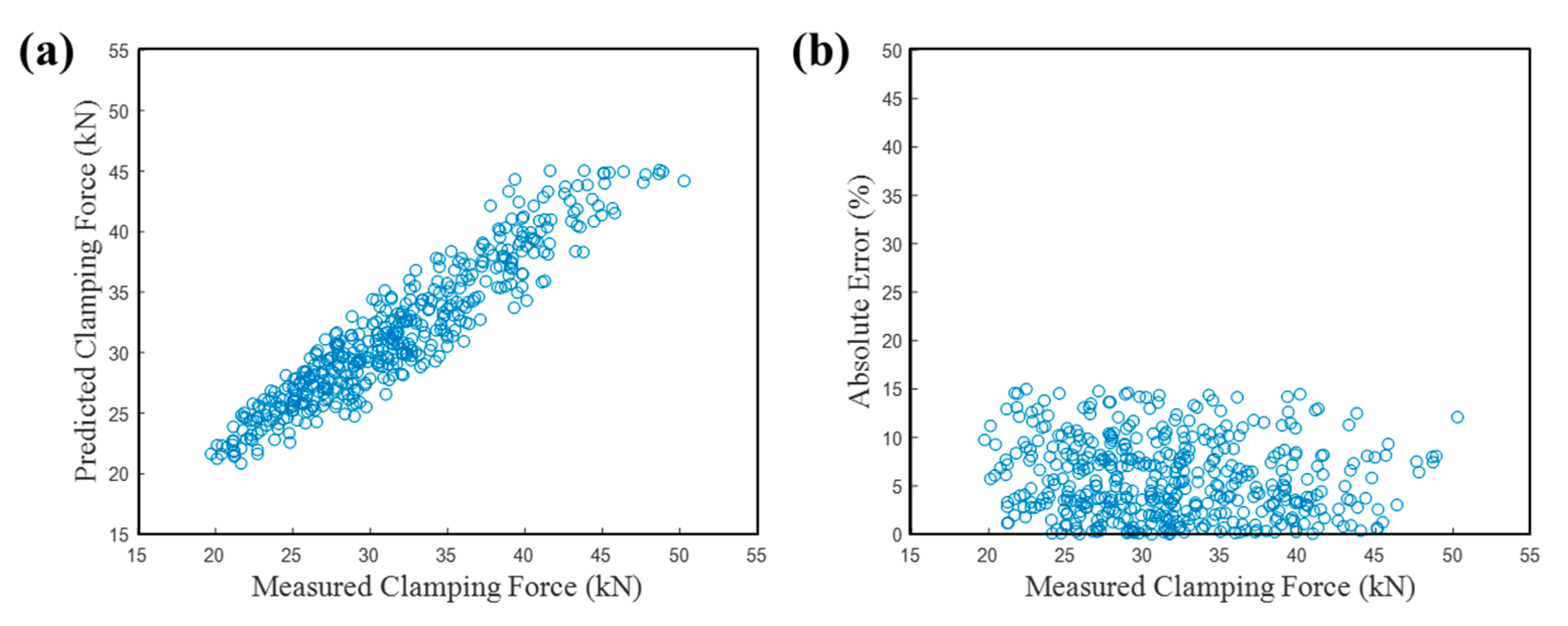
3.4. Test Results with Accelerometer Attached to the Nutrunner
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ibrahim, R.; Pettit, C. Uncertainties and dynamic problems of bolted joints and other fasteners. J. Sound Vib. 2005, 279, 857–936. [Google Scholar] [CrossRef]
- Thoppul, S.D.; Finegan, J.; Gibson, R.F. Mechanics of mechanically fastened joints in polymer-matrix composite structures—A review. Compos. Sci. Technol. 2009, 69, 301–329. [Google Scholar] [CrossRef]
- Adel, F.; Shokrollahi, S.; Jamal-Omidi, M.; Ahmadian, H. A model updating method for hybrid composite/aluminum bolted joints using modal test data. J. Sound Vib. 2017, 396, 172–185. [Google Scholar] [CrossRef]
- Cole, G.; Sherman, A. Light weight materials for automotive applications. Mater. Charact. 1995, 35, 3–9. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Troclet, B.; Bareille, O.; Ichchou, M. Modeling the response of composite panels by a dynamic stiffness approach. Compos. Struct. 2013, 96, 111–120. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, H.; Wang, T.; Qing, X. On-Site Health Monitoring of Composite Bolted Joint Using Built-In Distributed Eddy Current Sensor Network. Materials 2019, 12, 2785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zenkert, D. An Introduction to Sandwich Construction; Engineering Materials Advisory Services: Cradley Heath, Warley, UK, 1995. [Google Scholar]
- Sui, N.; Yan, X.; Huang, T.-Y.; Xu, J.; Yuan, F.-G.; Jing, Y. A lightweight yet sound-proof honeycomb acoustic metamaterial. Appl. Phys. Lett. 2015, 106, 171905. [Google Scholar] [CrossRef]
- Yin, H.; Wang, T.; Yang, D.; Liu, S.; Shao, J.; Li, Y. A smart washer for bolt looseness monitoring based on piezoelectric active sensing method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Wu, J.; Cui, X.; Xu, Y. A novel RFID-based sensing method for low-cost bolt loosening monitoring. Sensors 2016, 16, 168. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wang, C.; Li, H.; Zhang, C.; Hao, J.; Fan, S. Health monitoring of bolted spherical joint connection based on active sensing technique using piezoceramic transducers. Sensors 2018, 18, 1727. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Dong, J.; Li, H.; Zhang, C.; Ho, S.C. Looseness Monitoring of Bolted Spherical Joint Connection Using Electro-Mechanical Impedance Technique and BP Neural Networks. Sensors 2019, 19, 1906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huynh, T.-C.; Dang, N.-L.; Kim, J.-T. Preload monitoring in bolted connection using piezoelectric-based smart interface. Sensors 2018, 18, 2766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oregui, M.; Li, S.; Núñez, A.; Li, Z.; Carroll, R.; Dollevoet, R. Monitoring bolt tightness of rail joints using axle box acceleration measurements. Struct. Control Health Monit. 2017, 24, e1848. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, M.; Liao, Y.; Su, Z.; Xiao, Y. Contact acoustic nonlinearity (CAN)-based continuous monitoring of bolt loosening: Hybrid use of high-order harmonics and spectral sidebands. Mech. Syst. Signal Process. 2018, 103, 280–294. [Google Scholar] [CrossRef]
- Yeager, M.; Whitaker, A.; Todd, M. A method for monitoring bolt torque in a composite connection using an embedded fiber Bragg grating sensor. J. Intell. Mater. Syst. Struct. 2018, 29, 335–344. [Google Scholar] [CrossRef]
- Yeaple, F. Bolt torque equations predict stresses. Prod. Eng. 1978, 49, 28–33. [Google Scholar]
- Bickford, J. Handbook of Bolts and Bolted Joints; CRC press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Joshi, S.; Pathare, R. Ultrasonic instrument for measuring bolt stress. Ultrasonics 1984, 22, 261–269. [Google Scholar] [CrossRef]
- Nassar, S.A.; Veeram, A.B. Ultrasonic control of fastener tightening using varying wave speed. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Waikoloa, HI, USA, 16–20 July 2017; pp. 189–198. [Google Scholar]
- Fukuoka, T.; Takaki, T. Evaluations of the tightening process of bolted joint with elastic angle control method. In Proceedings of the ASME/JSME 2004 Pressure Vessels and Piping Conference, San Diego, CA, USA, 25–29 July 2004; pp. 11–18. [Google Scholar]
- Fujinaka, T.; Nakano, H.; Omatu, S. Bolt tightening control using neural networks. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics. e-Systems and e-Man for Cybernetics in Cyberspace (Cat. No. 01CH37236), Tucson, AZ, USA, 7–10 October 2001; pp. 1390–1395. [Google Scholar]
- Vand, E.H.; Oskouei, R.; Chakherlou, T. An experimental method for measuring clamping force in bolted connections and effect of bolt threads lubrication on its value. World Acad. Sci. Eng. Technol. 2008, 22, 457–460. [Google Scholar]
- Jhang, K.-Y.; Quan, H.-H.; Ha, J.; Kim, N.-Y. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement. Ultrasonics 2006, 44, e1339–e1342. [Google Scholar] [CrossRef]
- Wang, C.; Wang, N.; Ho, S.-C.; Chen, X.; Pan, M.; Song, G. Design of a novel wearable sensor device for real-time bolted joints health monitoring. IEEE Internet Things J. 2018, 5, 5307–5316. [Google Scholar] [CrossRef]
- Chaki, S.; Corneloup, G.; Lillamand, I.; Walaszek, H. Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts. J. Press. Vessel Technol. 2007, 129, 383–390. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, C.; Lu, Y.; Yang, X.; Liang, Y.; Zhang, L. Application of FRP bolts in monitoring the internal force of the rocks surrounding a mine-shield tunnel. Sensors 2018, 18, 2763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tiwari, V. MFCC and its applications in speaker recognition. Int. J. Emerg. Technol. 2010, 1, 19–22. [Google Scholar]
- Randall, R.B.; Tech, B. Frequency Analysis; Brüel & Kjær: Nærum, Denmark, 1987. [Google Scholar]
- Bogert, B.; Healy, M.; Tukey, J. The quefrency analysis of time series for echos. In Proceedings of the Symposium on Time Series Analysis; John Willey & Sons: New York, NY, USA, 1962; pp. 209–243. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. From frequency to quefrency: A history of the cepstrum. IEEE Signal Process. Mag. 2004, 21, 95–106. [Google Scholar] [CrossRef]
- Schafer, R.W. Echo Removal by Discrete Generalized Linear Filtering. Ph.D. Thesis, M.I.T., Cambridge, MA, USA, 1969. [Google Scholar]
- Randall, R.B. A history of cepstrum analysis and its application to mechanical problems. Mech. Syst. Signal Process. 2017, 97, 3–19. [Google Scholar] [CrossRef]
- Hasan, M.R.; Jamil, M.; Rahman, M. Speaker identification using mel frequency cepstral coefficients. Variations 2004, 1, 565–568. [Google Scholar]
- Dib, L.; Carbone, A. CLAG: An unsupervised non hierarchical clustering algorithm handling biological data. BMC Bioinform. 2012, 13, 194. [Google Scholar] [CrossRef]
- Drineas, P.; Frieze, A.; Kannan, R.; Vempala, S.; Vinay, V. Clustering large graphs via the singular value decomposition. Mach. Learn. 2004, 56, 9–33. [Google Scholar] [CrossRef] [Green Version]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: Norwell, MA, USA, 2013. [Google Scholar]
- Pelleg, D.; Moore, A.W. X-means: Extending k-means with efficient estimation of the number of clusters. In Proceedings of the Seventeenth International Conference on Machine Learning (ICML), Stanford, CA, USA, 26 June–2 July 2000; pp. 727–734. [Google Scholar]
- Pelleg, D.; Moore, A. Accelerating Exact k-Means Algorithms with Geometric Reasoning; Carnegie-Mellon University Pittsburgh PA School of Computer Science: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Yiakopoulos, C.; Gryllias, K.C.; Antoniadis, I.A. Rolling element bearing fault detection in industrial environments based on a K-means clustering approach. Expert Syst. Appl. 2011, 38, 2888–2911. [Google Scholar] [CrossRef]
- Timoshenko, S. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Courier Corporation: North Chelmsford, MA, USA, 1983. [Google Scholar]
- Bokaian, A. Natural frequencies of beams under compressive axial loads. J. Sound Vib. 1988, 126, 49–65. [Google Scholar] [CrossRef]
- Bokaian, A. Natural frequencies of beams under tensile axial loads. J. Sound Vib. 1990, 142, 481–498. [Google Scholar] [CrossRef]
- Park, J. Transfer function methods to measure dynamic mechanical properties of complex structures. J. Sound Vib. 2005, 288, 57–79. [Google Scholar] [CrossRef]
- Won, S.-H.P.; Golnaraghi, F.; Melek, W.W. A fastening tool tracking system using an IMU and a position sensor with Kalman filters and a fuzzy expert system. IEEE Trans. Ind. Electron. 2008, 56, 1782–1792. [Google Scholar] [CrossRef]



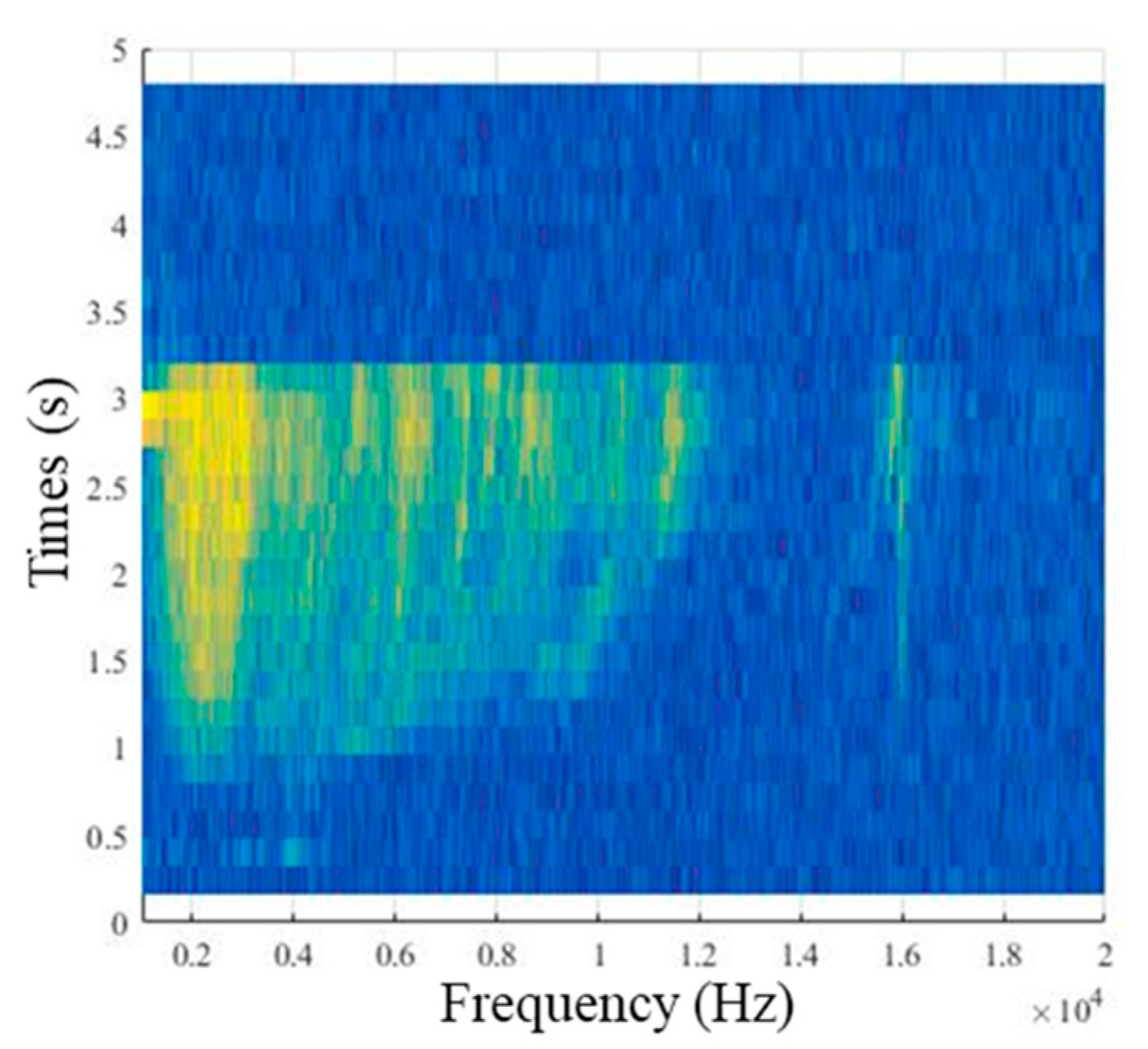
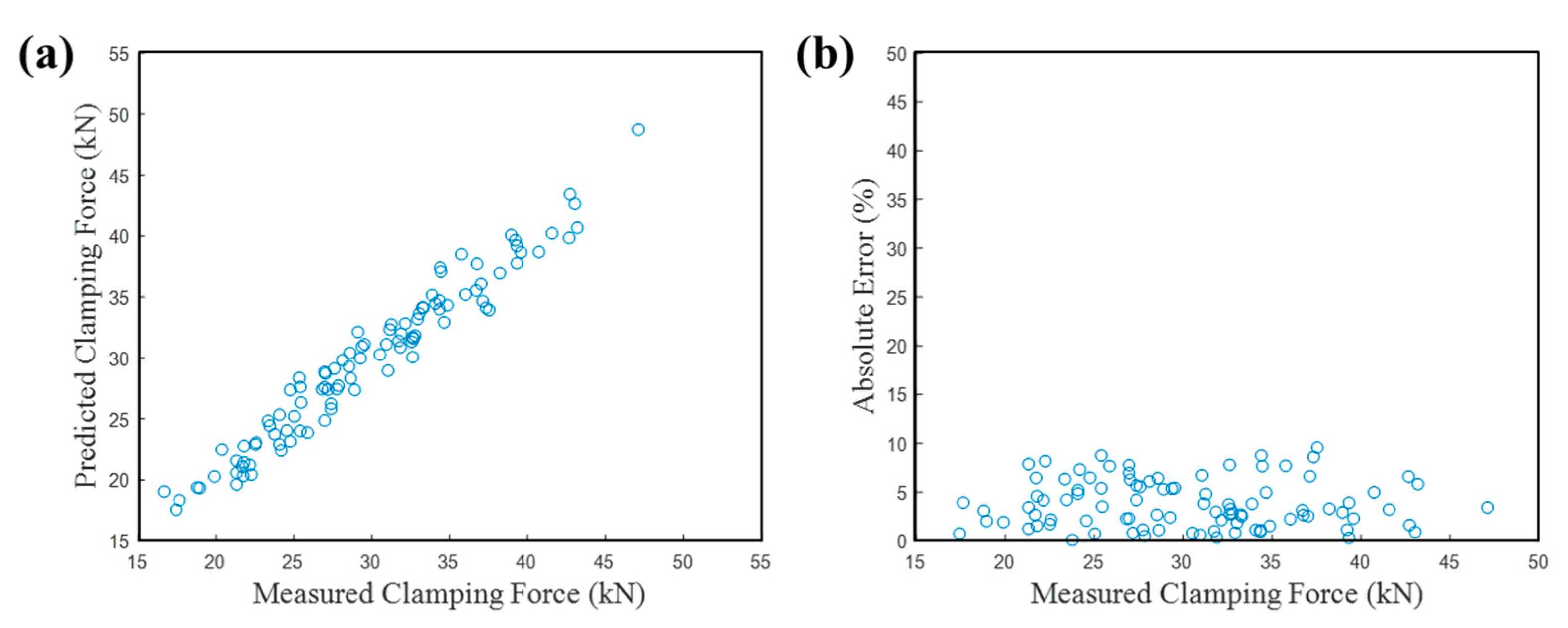
| Torque Measurement | Load Cell Vibration Measurement | Nut Runner Vibration Measurement |
|---|---|---|
| 35.83% | 14.99% | 9.57% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toh, G.; Gwon, J.; Park, J. Determination of Clamping Force Using Bolt Vibration Responses during the Tightening Process. Appl. Sci. 2019, 9, 5379. https://doi.org/10.3390/app9245379
Toh G, Gwon J, Park J. Determination of Clamping Force Using Bolt Vibration Responses during the Tightening Process. Applied Sciences. 2019; 9(24):5379. https://doi.org/10.3390/app9245379
Chicago/Turabian StyleToh, Gyungmin, Jaesoo Gwon, and Junhong Park. 2019. "Determination of Clamping Force Using Bolt Vibration Responses during the Tightening Process" Applied Sciences 9, no. 24: 5379. https://doi.org/10.3390/app9245379
APA StyleToh, G., Gwon, J., & Park, J. (2019). Determination of Clamping Force Using Bolt Vibration Responses during the Tightening Process. Applied Sciences, 9(24), 5379. https://doi.org/10.3390/app9245379






