An IVTIFN–TOPSIS Based Computational Approach for Pipe Materials Selection
Abstract
:1. Introduction
2. Materials and Methods
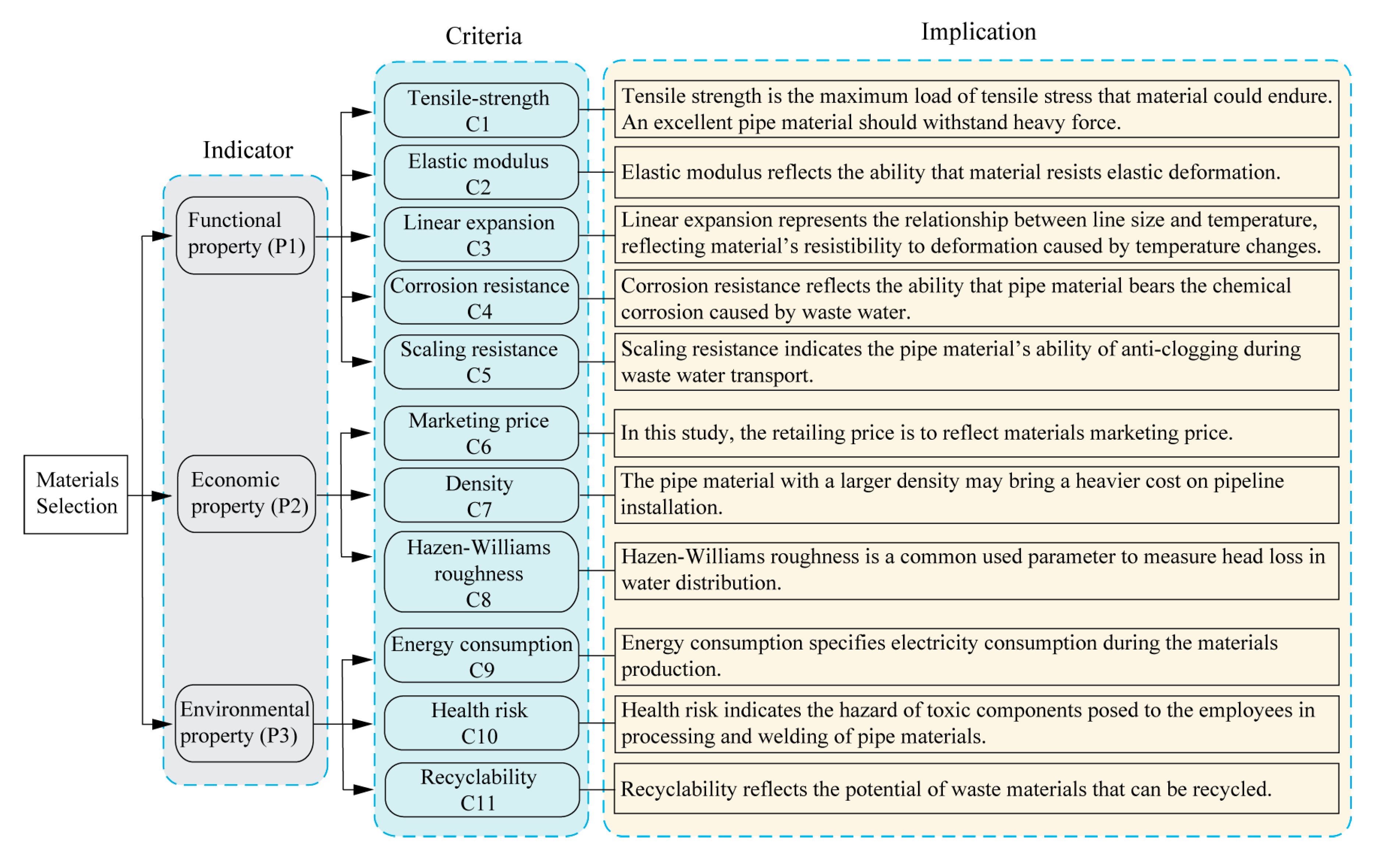
2.1. An Indicator System for Pipe Materials Selection
2.2. Intervalued Trapezoidal Intuitionistic Fuzzy Number
2.3. TOPSIS
3. An Illustrative Case Example
4. Results and Discussion
4.1. Evaluation Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xia, Y.; Zhang, H.; Phoungthong, K.; Shi, D.X.; Shen, W.H.; Shao, L.M.; He, P.J. Leaching characteristics of calcium-based compounds in MSWI Residues: From the viewpoint of clogging risk. Waste Manag. 2015, 42, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Maniya, K.; Bhatt, M.G. A selection of material using a novel type decision-making method: Preference selection index method. Mater. Des. 2010, 31, 1785–1789. [Google Scholar] [CrossRef]
- Zhou, C.C.; Yin, G.F.; Hu, X.B. Multi-objective optimization of material selection for sustainable products: Artificial neural networks and genetic algorithm approach. Materi. Des. 2009, 30, 1209–1215. [Google Scholar] [CrossRef]
- Albiñana, J.C.; Vila, C. A framework for concurrent material and process selection during conceptual product design stages. Mater. Des. 2012, 41, 433–446. [Google Scholar] [CrossRef]
- Mercer, K. Choosing the Right Pipe. J. Am. Water Works Ass. 2013, 105, 10–12. [Google Scholar] [CrossRef]
- Anojkumar, L.; Ilangkumaran, M.; Sasirekha, V. Comparative analysis of MCDM methods for pipe material selection in sugar industry. Expert Syst. Appl. 2014, 41, 2964–2980. [Google Scholar] [CrossRef]
- Zhang, W.W.; Wang, C.L.; Chen, R.H.; Tian, W.X.; Su, G.H. Preliminary design and thermal analysis of a liquid metal heat pipe radiator for TOPAZ-II power system. Ann. Nucl. Energy 2016, 97, 208–220. [Google Scholar] [CrossRef]
- Jahan, A.; Ismail, M.Y.; Mustapha, F.; Sapuan, S.M. Material selection based on ordinal data. Mater. Des. 2010, 31, 3180–3187. [Google Scholar] [CrossRef]
- İpek, M.; Selvi, İ.H.; Findik, F.; Torkul, O.; Cedimoğlu, I.H. An expert system based material selection approach to manufacturing. Mater. Des. 2013, 47, 331–340. [Google Scholar] [CrossRef]
- Kayfeci, M. Determination of energy saving and optimum insulation thicknesses of the heating piping systems for different insulation materials. Energy Build. 2014, 69, 278–284. [Google Scholar] [CrossRef]
- Mendrinos, D.; Katsantonis, S.; Karytsas, C. Pipe materials for borehole heat exchangers. In Proceedings of the European Geothermal Congress, Strasbourg, France, 19–24 September 2016. [Google Scholar]
- Zhao, R.; Su, H.; Chen, X. Commercially available materials selection in sustainable design: An integrated multi-attribute decision making approach. Sustainability 2016, 8, 79. [Google Scholar] [CrossRef] [Green Version]
- Hosseinijou, S.A.; Mansour, S.; Shirazi, M.A. Social life cycle assessment for material selection: A case study of building materials. Int. J. Life Cycle Ass. 2014, 19, 620–645. [Google Scholar] [CrossRef]
- Du, F.; Woods, G.J.; Kang, D. Life cycle analysis for water and wastewater pipe materials. J. Environ. Eng. 2012, 139, 703–711. [Google Scholar] [CrossRef]
- Akhtar, S.; Reza, B.; Hewage, K.; Shahriar, A.; Zargar, A.; Sadiq, R. Life cycle sustainability assessment (LCSA) for selection of sewer pipe materials. Clean Technol. Envir. 2015, 17, 973–992. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef] [Green Version]
- Tian, G.; Zhang, H.; Feng, Y.; Wang, D.; Peng, Y.; Jia, H. Green decoration materials selection under interior environment characteristics: A grey-correlation based hybrid MCDM method. Renew. Sust. Energ. Rev. 2018, 81, 682–692. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Ghorbanzadeh, O.; Moslem, S.; Blaschke, T.; Duleba, S. Sustainable Urban Transport Planning Considering Different Stakeholder Groups by an Interval-AHP Decision Support Model. Sustainability 2018, 11, 9. [Google Scholar] [CrossRef] [Green Version]
- Duleba, S.; Moslem, S. Examining Pareto optimality in analytic hierarchy process on real Data: An application in public transport service development. Expert Syst. Appl. 2019, 116, 21–30. [Google Scholar] [CrossRef]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R.; Hashemi, H. A new design of the elimination and choice translating reality method for multi-criteria group decision-making in an intuitionistic fuzzy environment. Appl. Math. Model. 2013, 37, 1781–1799. [Google Scholar] [CrossRef]
- Chatterjee, P.; Athawale, V.M.; Chakraborty, S. Selection of materials using compromise ranking and outranking methods. Mater. Des. 2009, 30, 4043–4053. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Mulliner, E.; Malys, N.; Maliene, V. Comparative analysis of MCDM methods for the assessment of sustainable housing affordability. Omega 2016, 59, 146–156. [Google Scholar] [CrossRef]
- Rashidi, M.; Ghodrat, M.; Samali, B.; Kendall, B.; Zhang, C.W. Remedial Modelling of Steel Bridges through Application of Analytical Hierarchy Process (AHP). Appl. Sci. 2017, 7, 168. [Google Scholar] [CrossRef] [Green Version]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A new multi-criteria decision making approach for sustainable material selection problem: A critical study on rank reversal problem. J. Clean. Prod. 2018, 182, 466–484. [Google Scholar] [CrossRef]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater. Des. 2017, 121, 237–253. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. VIKOR method for material selection problems with interval numbers and target-based criteria. Mater. Des. 2013, 47, 759–765. [Google Scholar] [CrossRef]
- Zhang, N.; Wei, G. Extension of VIKOR method for decision making problem based on hesitant fuzzy set. Appl. Math. Model. 2013, 37, 4938–4947. [Google Scholar] [CrossRef]
- Bairagi, B.; Dey, B.; Sarkar, B.; Sanyal, S. Selection of robot for automated foundry operations using fuzzy multi-criteria decision making approaches. Int. J. Manag. Sci. Eng. Manag. 2014, 9, 221–232. [Google Scholar] [CrossRef]
- Yazdani, M.; Payam, A.F. A comparative study on material selection of microelectromechanical systems electrostatic actuators using Ashby, VIKOR and TOPSIS. Mater. Des. 2015, 65, 328–334. [Google Scholar] [CrossRef]
- Feng, Y.X.; Zhang, Z.F.; Tian, G.D.; Fathollahi-Fard, A.M.; Hao, N.N.; Li, Z.W.; Wang, W.J.; Tan, J.R. A Novel Hybrid Fuzzy Grey TOPSIS Method: Supplier Evaluation of a Collaborative Manufacturing Enterprise. Appl. Sci. 2019, 9, 3770. [Google Scholar] [CrossRef] [Green Version]
- Govindan, K.; Khodaverdi, R.; Jafarian, A. A fuzzy multi criteria approach for measuring sustainability performance of a supplier based on triple bottom line approach. J. Clean. Prod. 2013, 47, 345–354. [Google Scholar] [CrossRef]
- He, Y.H.; Wang, L.B.; He, Z.Z.; Xie, M. A fuzzy TOPSIS and Rough Set based approach for mechanism analysis of product infant failure. Eng. Appl. Artif. Intel. 2016, 47, 25–37. [Google Scholar] [CrossRef]
- Falqi, I.I.; Ahmed, M.; Mallick, J. Siliceous Concrete Materials Management for Sustainability Using Fuzzy-TOPSIS Approach. Appl. Sci. 2019, 9, 3457. [Google Scholar] [CrossRef] [Green Version]
- Maity, S.R.; Chakraborty, S. Grinding wheel abrasive material selection using fuzzy TOPSIS method. Mater. Manuf. Process. 2013, 28, 408–417. [Google Scholar] [CrossRef]
- Şengül, Ü.; Eren, M.; Shiraz, S.E.; Gezder, V.; Şengül, A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energ. 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Liao, T.W. Two interval type 2 fuzzy TOPSIS material selection methods. Mater. Des. 2015, 88, 1088–1099. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, V.T.; Duong, D.H.; Thai, H.T.N. A Hybrid Fuzzy Analysis Network Process (FANP) and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) Approaches for Solid Waste to Energy Plant Location Selection in Vietnam. Appl. Sci. 2018, 8, 1100. [Google Scholar] [CrossRef] [Green Version]
- Dubois, D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Set. Syst. 2011, 184, 3–28. [Google Scholar] [CrossRef] [Green Version]
- Moslem, S.; Ghorbanzadeh, O.; Blaschke, T.; Duleba, S. Analysing Stakeholder Consensus for a Sustainable Transport Development Decision by the Fuzzy AHP and Interval AHP. Sustainability 2019, 11, 3271. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Q.; Wu, J.T.; Wang, J.; Zhang, H.Y.; Chen, X.H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inform. Sci. 2014, 288, 55–72. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G. Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio linepipe. Int. J. Pres. Ves. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Toutanji, H.; Dempsey, S. Stress modeling of pipelines strengthened with advanced composites materials. Thin. Wall. Struct. 2001, 39, 153–165. [Google Scholar] [CrossRef]
- Reddy, G.P.; Gupta, N. Material selection for microelectronic heat sinks: An application of the Ashby approach. Mater. Des. 2010, 31, 113–117. [Google Scholar] [CrossRef]
- Jiang, G.M.; Sun, J.; Sharma, K.R.; Yuan, Z.G. Corrosion and odor management in sewer systems. Curr. Opin. Biotech. 2015, 33, 192–197. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wang, G.X.; Massarotto, P.; Rudolph, V. Optimization of pipeline transport for CO2 sequestration. Energ. Convers. Manag. 2006, 47, 702–715. [Google Scholar] [CrossRef]
- Davis, P.; Sullivan, E.; Marlow, D.; Marney, D. A selection framework for infrastructure condition monitoring technologies in water and wastewater networks. Expert Syst. Appl. 2013, 40, 1947–1958. [Google Scholar] [CrossRef]
- Zhao, R.; Neighbour, G.; Deutz, P.; McGuire, M. Materials selection for cleaner production: An environmental evaluation approach. Mater. Des. 2012, 37, 429–434. [Google Scholar] [CrossRef]
- Zhao, R.; Xi, B.; Liu, Y.; Su, J.; Liu, S. Economic potential of leachate evaporation by using landfill gas: A system dynamics approach. Resour. Conserv. Recycl. 2017, 124, 74–84. [Google Scholar] [CrossRef]
- Bharati, S.K.; Singh, S.R. Transportation problem under interval-valued intuitionistic fuzzy environment. Int. J. Fuzzy Syst. 2018, 20, 1511–1522. [Google Scholar] [CrossRef]
- Bobyr, M.V.; Milostnaya, N.A.; Kulabuhov, S.A. A method of defuzzification based on the approach of areas’ ratio. Appl. Soft Comput. 2017, 59, 19–32. [Google Scholar] [CrossRef]
- Chang, C.H.; Lin, J.J.; Lin, J.H.; Chiang, M.C. Domestic open-end equity mutual fund performance evaluation using extended TOPSIS method with different distance approaches. Expert Syst. Appl. 2010, 37, 4642–4649. [Google Scholar] [CrossRef]
- Petit-Boix, A.; Sanjuan-Delmás, D.; Gasol, C.M.; Villalba, G.; Suárez-Ojeda, M.E.; Gabarrell, X.; Josa, A.; Rieradevall, J. Environmental Assessment of Sewer Construction in Small to Medium Sized Cities Using Life Cycle Assessment. Water Resour. Manag. 2014, 28, 979–997. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.R. Study on Scaling and Corrosion of HDPE Pipeline Material in Leachate Transportation. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Ashby, M.F.; Shercliff, H.; Cebon, D. Materials: Engineering, Science, Processing and Design; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- de la Fuente, A.; Pons, O.; Josa, A.; Aguado, A. Multi-Criteria Decision Making in the sustainability assessment of sewerage pipe systems. J. Clean. Prod. 2016, 112, 4762–4770. [Google Scholar] [CrossRef] [Green Version]


| Linguistic Remark | Fuzzy Number | |
|---|---|---|
| Performances of Alternatives | Relative Importance of Criteria | |
| Very Poor (VP) | Extremely Low (EL) | ((0.1, 0.1, 0.2), (0.05,0.1, 0.25)) |
| Poor (P) | Low (L) | ((0.2, 0.3, 0.4), (0.15, 0.3, 0.45)) |
| Fair (F) | Medium (M) | ((0.4, 0.5,0.6), (0.35, 0.5,0.65)) |
| Good (G) | High (H) | ((0.6, 0.7,0.8), (0.55, 0.7, 0.85)) |
| Excellent (E) | Extremely High (EH) | ((0.8, 0.9, 0.9), (0.75, 0.9, 0.95)) |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Engineer 1 | M1 | E | E | VP | VP | VP | G | G | F | G | G | G |
| M2 | E | E | VP | P | P | E | G | F | E | E | E | |
| M3 | F | F | F | G | G | P | P | E | P | P | P | |
| M4 | P | P | E | E | E | F | VP | G | P | VP | VP | |
| Engineer 2 | M1 | E | E | F | P | P | E | E | F | E | E | G |
| M2 | E | E | F | P | P | E | E | F | E | E | G | |
| M3 | F | F | G | G | G | P | P | E | P | P | F | |
| M4 | VP | VP | E | E | E | F | VP | G | P | P | P | |
| Engineer 3 | M1 | E | E | P | P | VP | F | G | F | G | G | G |
| M2 | P | VP | G | G | G | P | P | G | P | F | P | |
| M3 | F | F | E | E | E | F | P | G | VP | P | VP | |
| M4 | E | E | VP | VP | VP | G | G | F | G | G | G | |
| Engineer 4 | M1 | E | E | VP | P | P | E | G | F | E | E | E |
| M2 | F | F | F | G | G | P | P | E | P | P | P | |
| M3 | P | P | E | E | E | F | VP | G | P | VP | VP | |
| M4 | E | E | F | P | P | E | E | F | E | E | G | |
| Engineer 5 | M1 | E | E | F | P | P | E | E | F | E | E | G |
| M2 | F | F | G | G | G | P | P | E | P | P | F | |
| M3 | VP | VP | E | E | E | F | VP | G | P | P | P | |
| M4 | E | E | P | P | VP | F | G | F | G | G | G |
| Criteria | Engineer 1 | Engineer 2 | Engineer 3 | Engineer 4 | Engineer 5 | |
|---|---|---|---|---|---|---|
| Functional attribute | C1 | EL | L | L | L | EL |
| C2 | EL | L | EL | L | EL | |
| C3 | EL | EL | EL | EL | EL | |
| C4 | EH | H | H | H | EH | |
| C5 | EH | EH | H | H | H | |
| Economic attribute | C6 | EH | EH | EH | EH | EH |
| C7 | L | M | L | L | L | |
| C8 | L | M | M | L | L | |
| Environmental attribute | C9 | EL | EL | EL | EL | EL |
| C10 | EL | EL | L | L | L | |
| C11 | EL | EL | L | L | L | |
| Model | M1 | M2 | M3 | M4 | |
|---|---|---|---|---|---|
| IVTIFN–TOPSIS (E) | 0.3272 | 0.2185 | 0.7170 | 0.6426 | |
| Ranking order | 3 | 4 | 1 | 2 | |
| Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 1 | 0.9949 | 0.9951 | −0.996 | −0.996 | −0.576 | −0.952 | −0.854 | −0.974 | −0.907 | 0.4032 |
| C2 | 0.9949 | 1 | 0.9996 | −0.987 | −0.996 | −0.655 | −0.924 | −0.902 | −0.985 | −0.87 | 0.4158 |
| C3 | 0.9951 | 0.9996 | 1 | −0.99 | −0.998 | −0.652 | −0.92 | −0.9 | −0.98 | −0.864 | 0.4396 |
| C4 | −0.996 | −0.987 | −0.99 | 1 | 0.9966 | 0.5508 | 0.9364 | 0.8357 | 0.9499 | 0.8906 | −0.476 |
| C5 | −0.996 | −0.996 | −0.998 | 0.9966 | 1 | 0.6165 | 0.9224 | 0.8779 | 0.9665 | 0.869 | −0.473 |
| C6 | −0.576 | −0.655 | −0.652 | 0.5508 | 0.6165 | 1 | 0.3526 | 0.9172 | 0.6853 | 0.2399 | −0.407 |
| C7 | −0.952 | −0.924 | −0.92 | 0.9364 | 0.9224 | 0.3526 | 1 | 0.6882 | 0.9967 | 0.9922 | −0.16 |
| C8 | −0.854 | −0.902 | −0.9 | 0.8357 | 0.8779 | 0.9172 | 0.6882 | 1 | 0.9108 | 0.5947 | −0.455 |
| C9 | −0.974 | −0.985 | −0.98 | 0.9499 | 0.9665 | 0.6853 | 0.9967 | 0.9108 | 1 | 0.8713 | −0.274 |
| C10 | −0.907 | −0.87 | −0.864 | 0.8906 | 0.869 | 0.2399 | 0.9922 | 0.5947 | 0.8713 | 1 | −0.077 |
| C11 | 0.4032 | 0.4158 | 0.4396 | −0.476 | −0.473 | −0.407 | −0.16 | −0.455 | −0.274 | −0.077 | 1 |
| Model | M1 | M2 | M3 | M4 | |
|---|---|---|---|---|---|
| IVTIFN−TOPSIS (M) | 0.1461 | 0.3269 | 0.6430 | 0.7094 | |
| Ranking order | 4 | 3 | 2 | 1 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Huang, Y.; Yu, Y.; Guo, S. An IVTIFN–TOPSIS Based Computational Approach for Pipe Materials Selection. Appl. Sci. 2019, 9, 5457. https://doi.org/10.3390/app9245457
Zhao R, Huang Y, Yu Y, Guo S. An IVTIFN–TOPSIS Based Computational Approach for Pipe Materials Selection. Applied Sciences. 2019; 9(24):5457. https://doi.org/10.3390/app9245457
Chicago/Turabian StyleZhao, Rui, Ya Huang, Yang Yu, and Sidai Guo. 2019. "An IVTIFN–TOPSIS Based Computational Approach for Pipe Materials Selection" Applied Sciences 9, no. 24: 5457. https://doi.org/10.3390/app9245457
APA StyleZhao, R., Huang, Y., Yu, Y., & Guo, S. (2019). An IVTIFN–TOPSIS Based Computational Approach for Pipe Materials Selection. Applied Sciences, 9(24), 5457. https://doi.org/10.3390/app9245457





