1. Introduction
The amplitude variation with offset (AVO) or amplitude variation with incidence angle (AVA) inverts from the measured amplitudes of seismic reflectivities to the rock properties [
1,
2,
3]. Due to the complexity of Zoeppritz equations, most AVO/AVA inversions are based on linear approximations [
4,
5,
6]. The most widely used classical approximations are proposed by Aki–Richards and Shuey [
7,
8]. These classical approximations, however, are only valid for weak elastic contrasts and relatively small incidence angles [
9,
10,
11]. Actually, there are many target zones that have strong elastic contrast interfaces or long-offset seismic data used. Thus, the accurate partial derivatives of the reflection coefficients with respect to the unknown parameters should be derived for more accurate AVO/AVA inversion [
12,
13,
14].
Rock physics plays a significant role in oil and gas explorations, such as hydrocarbon detection, lithology determination and fluid identification [
15,
16,
17]. Biot–Gassmann equations are widely used in rock physics, which establish the relationship between elastic moduli (bulk and shear moduli) and seismic P-and S-wave velocities [
18,
19,
20,
21]. Fluid substitution is a technique used to predict P-, S-wave velocities and density based on the analyses of their porosity and dry rock moduli [
22,
23,
24,
25]. The elastic moduli of dry rock could be obtained from the rock physics experiments, well logging or numerical modeling [
26,
27]. Benson and Wu predicted dry rock bulk modulus, rigidity modulus and reflection coefficients with the application of laboratory rock samples and well logs [
28]. Li and Zhang derived the analytical approximations of bulk and shear moduli of dry rock based on the differential effective medium theory [
29]. However, the direct inversion of dry rock moduli from seismic data is always a challenging problem.
During recent decades, some researchers proposed to invert the fluid or elastic moduli from seismic data. Goodway et al. provided an AVO approximate equation through incorporating the dry and saturated properties of rock into the P-wave velocity expression, which is named as the lambda-mu-rho (LMR) method [
30]. Russell et al. combined this concept with the Biot–Gassmann theory to derive an approximation equation for AVO inversion [
31]. Based on Russell’s fluid factor, Yin et al. carried out the Bayesian-based elastic impedance inversion, which is more suitable for seismic data with large incidence angles [
32]. Zong et al. further proposed FMR–AVA inversion (Fluid Factor, Mu (Shear modulus), Rho (Density)–Amplitude Variation with Angle) using the approximations [
33]. We propose to combine the exact Zoeppritz equations with the Biot–Gassmann equations.
The best way to get an accurate elastic moduli of dry rock from seismic data is to use AVO/AVA inversion with exact Zeoppritz equations. The most difficult part of AVO/AVA inversion based on the exact Zoeppritz equations, however, is to obtain the accurate Jacobian matrix (partial derivatives of the reflection coefficients with respect to dry rock moduli) [
34,
35]. An accurate algorithm was proposed to compute the gradients of the seismic reflection coefficients with respect to P-, S-wave velocities and density by solving the partial derivative equations of the exact Zoeppritz equations [
36,
37]. Lu et al. carried out joint PP and PS AVA seismic inversion using exact Zoeppritz equations [
38]. Nevertheless, the direct inversion of bulk and shear moduli of dry rock was not taken into consideration in the previous studies. We propose to combine the exact Zoeppritz equations with the Biot–Gassmann equations and derive the accurate Jacobian matrix for inverting dry rock moduli directly without any simplifications. This derived matrix can be used further to invert bulk and shear moduli of dry rock. Due to the usage of exact Zoeppritz equations, it overcomes the weaknesses that the approximate Zoeppritz equations have.
We derive the accurate partial derivatives of reflection coefficients with respect to dry rock parameters (bulk and shear moduli) through combining the exact Zoeppritz equations and the Biot–Gassmann equations. During the numerical tests, the characteristics of these partial derivatives are observed. Additionally, we compare the partial derivatives and their errors using this proposed method with those from the classical Aki–Richards and Shuey approximations.
2. Zoeppritz and Biot–Gassmann Equations
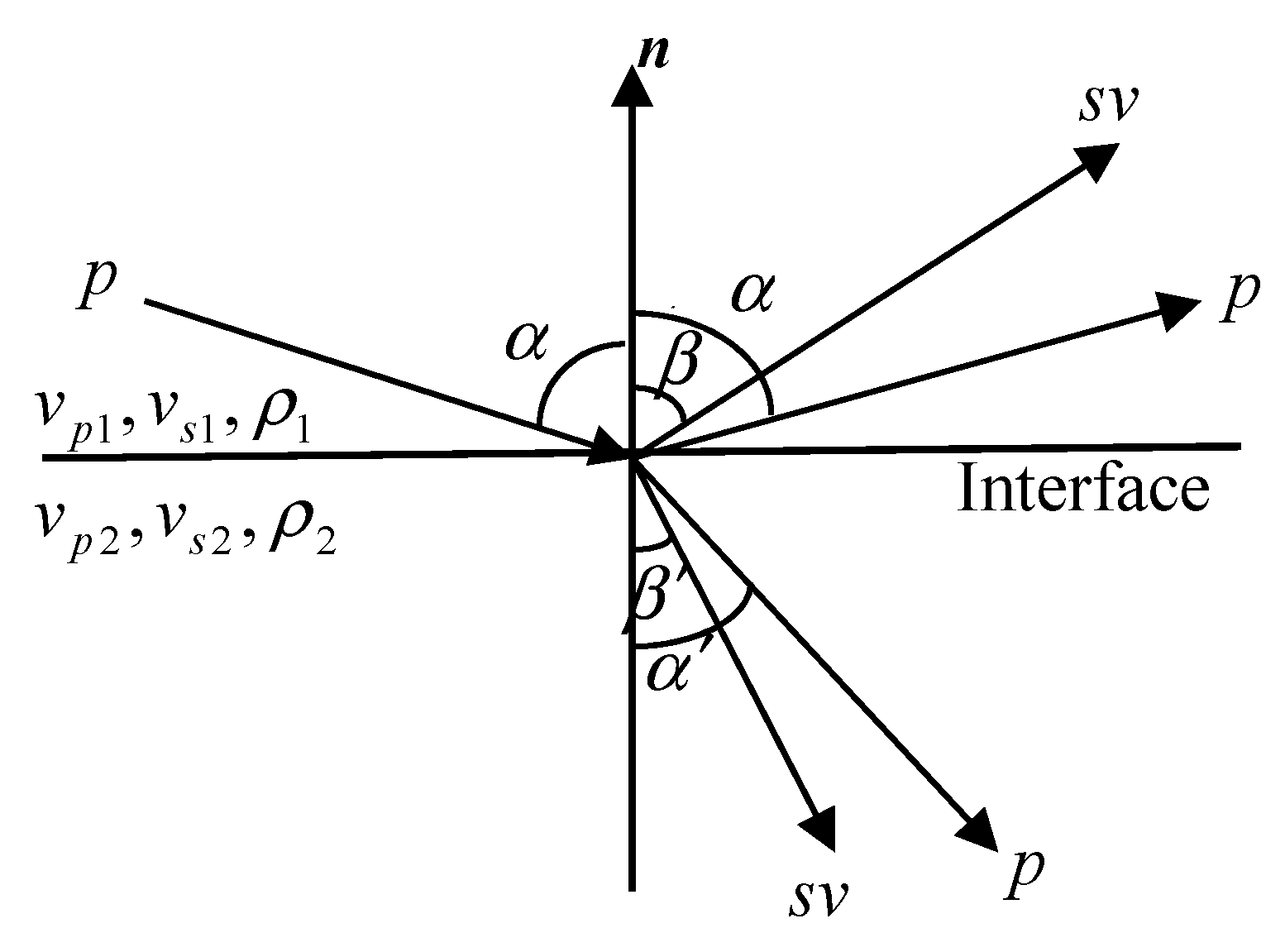
Zoeppritz equations describe the relationship between the seismic reflection coefficients and the elastic rock properties [
39,
40]. The Zoeppritz equations for only P-wave incidence are written as:
where
where
,
,
and
are the reflection and transmission coefficients of P-and SV-wave (P–SV conversion), respectively. The elements a and b in the matrix A and B are
Here,
denotes the incidence and reflection angle of P-wave;
is the reflection angle of SV-wave;
and
denote the transmission angles of the P-and SV-waves, respectively;
,
,
and
,
,
are the P-, S-wave velocities and density in layer 1 and 2, respectively (shown in
Figure 1).
The Biot–Gassmann equations describe the relationship between velocity, density and elastic moduli in porous media. It can be expressed as Hilterman, [
41]:
where
is porosity;
,
and
denote the bulk moduli of effective fluid, solid mineral and dry rock, respectively;
,
and
are the densities of saturated medium, solid mineral and pore fluid, respectively;
and
denote the shear moduli of saturated medium and dry frame, respectively.
The approximation of bulk modulus of the effective fluid is as demonstrated by Hilterman, [
41]:
where
,
and
are the bulk moduli of oil, gas and water, respectively.
,
and
are saturations when pores are filled with oil, gas and water, respectively.
The effective density can be approximated as
where
,
and
are the densities of oil, gas and water, respectively.
3. The Partial Derivatives of P- and S-Wave Velocities with Respect to Dry Rock Moduli
To accurately invert the dry rock parameters, the most important step is to derive the Jacobian matrix (partial derivatives of PP and PS reflection coefficients with respect to dry rock moduli). Letting
represent the unknown parameters
,
,
and
, the partial derivatives of the Zoeppritz equations with respect to
can be expressed as Liu et al., [
11]
Equation (8) shows matrix A depends on the incidence angle. The reflectivity R can be calculated using Zoeppritz Equations (1) and (2). The two remaining parameters needed to be calculated are and . The following sections will derive these two partial derivatives.
To derive
and
, intermediate partial derivatives of P- and S-wave velocities need to be derived first. Using chain rules and Equation (3), the partial derivatives of P-wave velocity with respect to elastic moduli
and
of dry rock are:
where
and
.
Using Equations (3) and (4), we have:
Additionally, the partial derivatives of S-wave velocity with respect to elastic modulus
and
of dry rock are:
5. Numerical Examples
To observe the characteristics of these partial derivatives with exact Zoeppritz equations, a two-layer model filled with water and oil is built. Regarding the first oil–water interface case, the upper and lower sandstone layers are filled with oil and water, respectively. Concerning the second water–oil interface case, the upper and lower layers are filled with water and oil, respectively. The model parameters are:
,
,
,
,
;
,
,
,
,
;
and
Liu et al., [
37].
5.1. Oil–Water Interface
Seismic waves penetrate from the oil-saturated sandstone to the water-saturated sandstone. The water, oil and gas saturations in two sandstone layers are , , , , respectively. The partial derivative curves of reflectivities and with respect to the elastic moduli , , and of dry rock are complex numbers.
Figure 2 shows the real and imaginary values of partial derivatives of reflectivity
with respect to the bulk moduli
and
. One can observe that there is a peak (singular point) at the critical angle (
). It is because the partial derivative matrix
contains
. When the incidence angle is larger than the critical angle, the results of the partial derivatives become complex numbers rather than real numbers. Due to the existence of this discontinuous point, big errors will be observed around the critical angle when carrying out seismic inversion of bulk moduli.
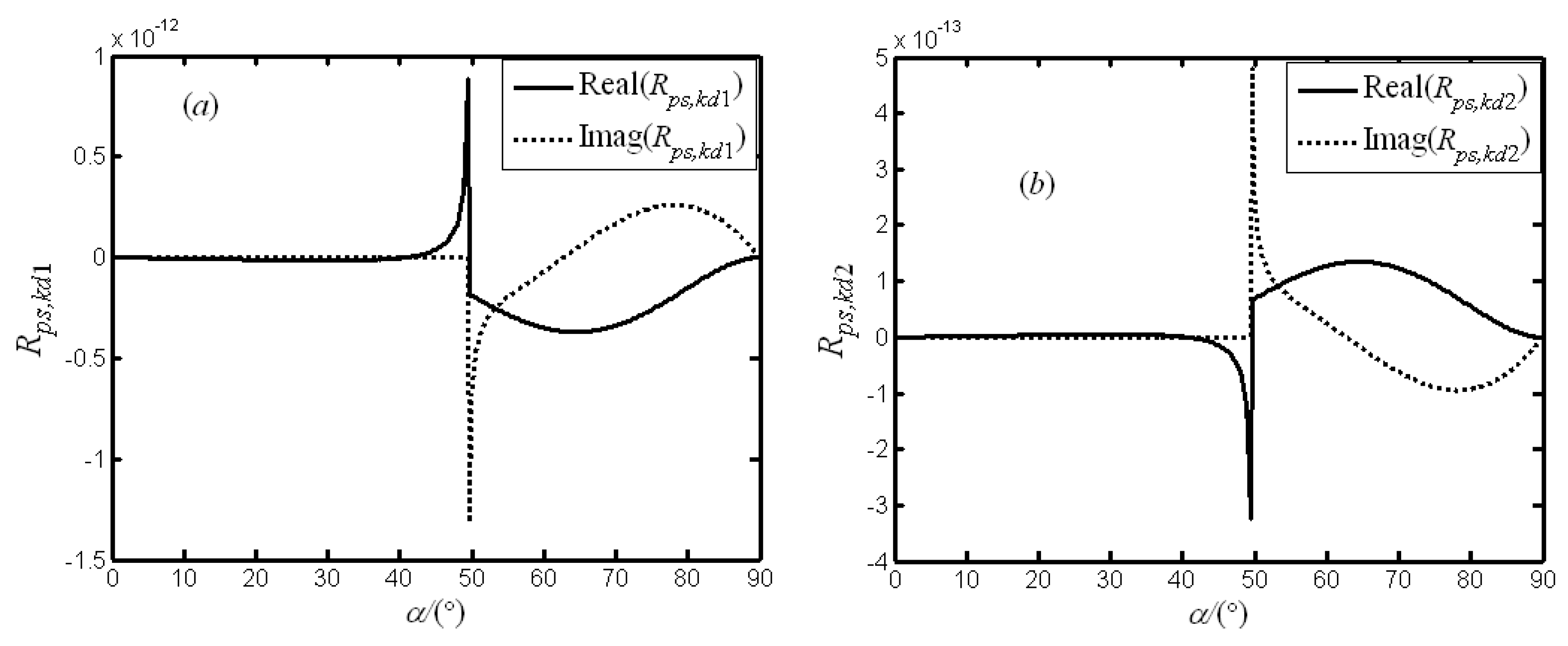
Figure 3 shows the real and imaginary curves of partial derivatives of reflectivity
with respect to the shear moduli
and
, respectively. Different from
Figure 2, there is a zero point rather than a singular point at the critical angle. The polarities of
with respect to
and
are opposite.
Figure 4 shows the partial derivatives of reflectivity
with respect to the bulk moduli
and
, respectively.
Figure 4a,b show similar characteristics to
Figure 2a,b, but their polarities are different. Additionally, a singular point also is found at the critical angle. The absolute value of the partial derivatives of the PP-wave is almost two times larger than that of the PS-wave. One can observe that the slopes of all curves are nearly zero when the incidence angle is smaller than
, which means the reflectivity
is not sensitive to the bulk moduli and not suitable to be used to invert the bulk moduli.
Figure 5 shows the partial derivatives of reflectivity
with respect to the shear moduli
and
of the dry rock, respectively. Different from
Figure 3, only one zero point is found here. The variation of the “real” part in
Figure 5 is smaller than that in
Figure 3, when the incidence angle is larger than the critical angle. This phenomenon could be caused by fluid substitution.
5.2. Water–Oil Interface
A water–oil model is built to further check the efficiency of this algorithm. When seismic waves penetrate from the water-saturated layer to the oil-saturated layer, the partial derivatives of reflectivities and with respect to the elastic moduli , , and of dry rock become real numbers rather than complex numbers.
Figure 6 shows the partial derivatives of reflectivity
with respect to the elastic moduli
,
,
and
, respectively. Different from
Figure 2 and
Figure 3, there is no singular or zero point at the critical angle. Due to the substitution of pore fluids, the curves of partial derivatives of
with respect to the elastic moduli are asymmetric. Comparing with other curves, the variation of partial derivative of
with respect to
is much smaller (
Figure 6a). The enlarged details can be observed in
Figure 6b by zooming in the curve.
Figure 7 shows the partial derivatives of the reflectivity
with respect to the elastic moduli
,
,
and
, respectively. Similar to
Figure 6, these curves are asymmetric. The partial derivative of
with respect
is much larger than others. The enlarged partial derivatives of
, with respect to
,
and
, are shown in
Figure 7b.
5.3. Gradient Comparison between the Exact and the Classical Approximations of Zoeppritz Equations
To test the accuracy of this proposed method, we compare the partial derivatives calculated using the exact Zoeppritz equations with those using two classical approximations: Aki–Richards and Shuey [
6,
7]. Here, the same oil–water model is used. These two Zoeppritz approximations are used to calculate the partial derivatives of the seismic reflectivities with respect to the dry rock properties directly.
Figure 8 compares the partial derivatives of reflectivity
with respect to
and
using different algorithms.
and
are the results of the exact Zoeppritz equations;
and
are the results of the Aki–Richards approximation;
and
are the results of the Shuey approximation. Seen in the AVO/AVA inversion, the incidence angles of seismic data are normally smaller than the critical angle. The largest incidence angle is
in
Figure 8b,d. When the incidence angle is smaller than
, the values calculated using these three algorithms are very similar. One can observe that differences between the exact solution and two approximations are becoming larger and larger with the increase in the incidence angle. The results prove that the approximations are only suitable for the AVO inversion with small incidence angles.
Figure 9 shows the comparison of the absolute and relative errors of partial derivatives of reflectivity
with respect to
and
using Aki–Richards and Shuey approximations.
,
,
and
are the relative and absolute errors of the Aki–Richards approximation, respectively.
,
,
and
are the relative and absolute errors of the Shuey approximation, respectively. Two zero points can be observed when the incidence angles are
and
. Therefore, there are two discontinuity points on the relative errors which make other curves close to zero. Considering this circumstance, the absolute error curves are more helpful to observe the accuracy of each algorithm.
Figure 9b,d show the relative and absolute errors of two classic approximations when the incidence angle is smaller than the critical angle and the errors are still very large.
Figure 10 compares the partial derivatives of
with respect to
and
using different algorithms.
and
are the results of the exact Zoeppritz equations;
and
are the results of the Aki–Richards approximation;
and
are the results of the Shuey approximation. The enlarged details of partial derivatives of the exact Zeoppritz are shown in
Figure 10b. The values of the approximations are still different with the exact Zoeppritz, even when the incidence angle is pretty small.
Figure 11 compares the absolute and relative errors of partial derivatives of reflectivity
with respect to
and
using the Aki–Richards and Shuey approximations.
,
,
and
are the relative and absolute errors of the Aki–Richards approximation, respectively.
,
,
and
are the relative and absolute errors of the Shuey approximation, respectively.
Figure 11a shows there are three singular points when the incidence angles are
,
and
, respectively.
Figure 11b,c show the results without these three singular points. The errors of the Shuey and Aki–Richards approximations are still very large when the incidence angle is between
and
.
6. Discussion
Recently, AVA (AVO) or elastic impedance inversion has been carried out using approximations of the exact Zoeppritz equations. These approximations are only applicable for the formations with weak reflection interfaces and seismic data with small incidence angles (or small offsets). To overcome the weaknesses of these approximations, it is necessary to derive the accurate Jacobian matrix, which consists of the partial derivatives of reflection coefficients with respect to unknown parameters.
Regarding reservoir geophysics, an important step is to establish a theoretical model between the seismic attributes and the physical properties of rocks. Gassmann proposed equations to represent the influences of rock pore and fluid properties on seismic responses and attributes [
21]. Although there are many assumptions, the Biot–Gassmann equations are still the most practical and commonly used methods.
Previous research demonstrated these dry rock moduli are mainly obtained indirectly from rock physics experiments, well logging or numerical modeling. Researchers had not built a direct inversion relationship between the theoretical rock physics model and the Zoeppritz equations. Here, we combined the Biot–Gassmann and the Zoeppritz equations to establish the relationship between the seismic wave responses of lithology and dry rock properties. The derived accurate Jacobian matrix, which consists of the partial derivatives of reflection coefficients with respect to bulk and shear moduli of dry rock, can be used in the further AVO/AVA inversion. The characteristics of the partial derivatives were analyzed and indicate that the reflectivity should not be used to invert the bulk moduli. Our future research will incorporate these partial derivatives to the AVA inversion and get the dry rock moduli directly from seismic data.
7. Conclusions
Here, the Biot–Gassmann equations and the exact Zoeppritz equations were combined to calculate the partial derivatives of seismic wave reflection coefficients with respect to the dry rock moduli (bulk and shear moduli). It was an accurate way to get the Jacobian matrix rather than using the Zoeppritz approximations. This accurate matrix was further used in the AVO/AVA inversions to invert bulk and shear moduli of dry rock directly. The numerical tests above indicated that, when a seismic wave refracts from the low impedance medium (rock filled with oil) to the high impedance medium (rock filled with water), the partial derivatives of reflection coefficients, with respect to the elastic moduli of dry rock, had a singular or zero point at the critical angle. When a seismic wave refracted from the high impedance medium (rock filled with water) to the low impedance medium (rock filled with oil), the partial derivatives of reflection coefficients, with respect to the elastic moduli of dry rock, were no longer complex numbers. There was no singular or zero point at the critical angle in this case. Additionally, the reflectivity of the PS-wave was not sensitive to the bulk moduli and not suitable to be used in the inversion of them. The errors of classical Shuey and Aki–Richards approximations were still very large, even when the incidence angles were relatively small. Our proposed algorithm provides an important theoretical basis for direct and accurate inversion of dry rock parameters from seismic data in future AVO/AVA inversions.