Phase Transitions in Wireless MESH Networks and Their Application in Early Detection of Network Coherence Loss
Abstract
:Featured Application
Abstract
1. Introduction
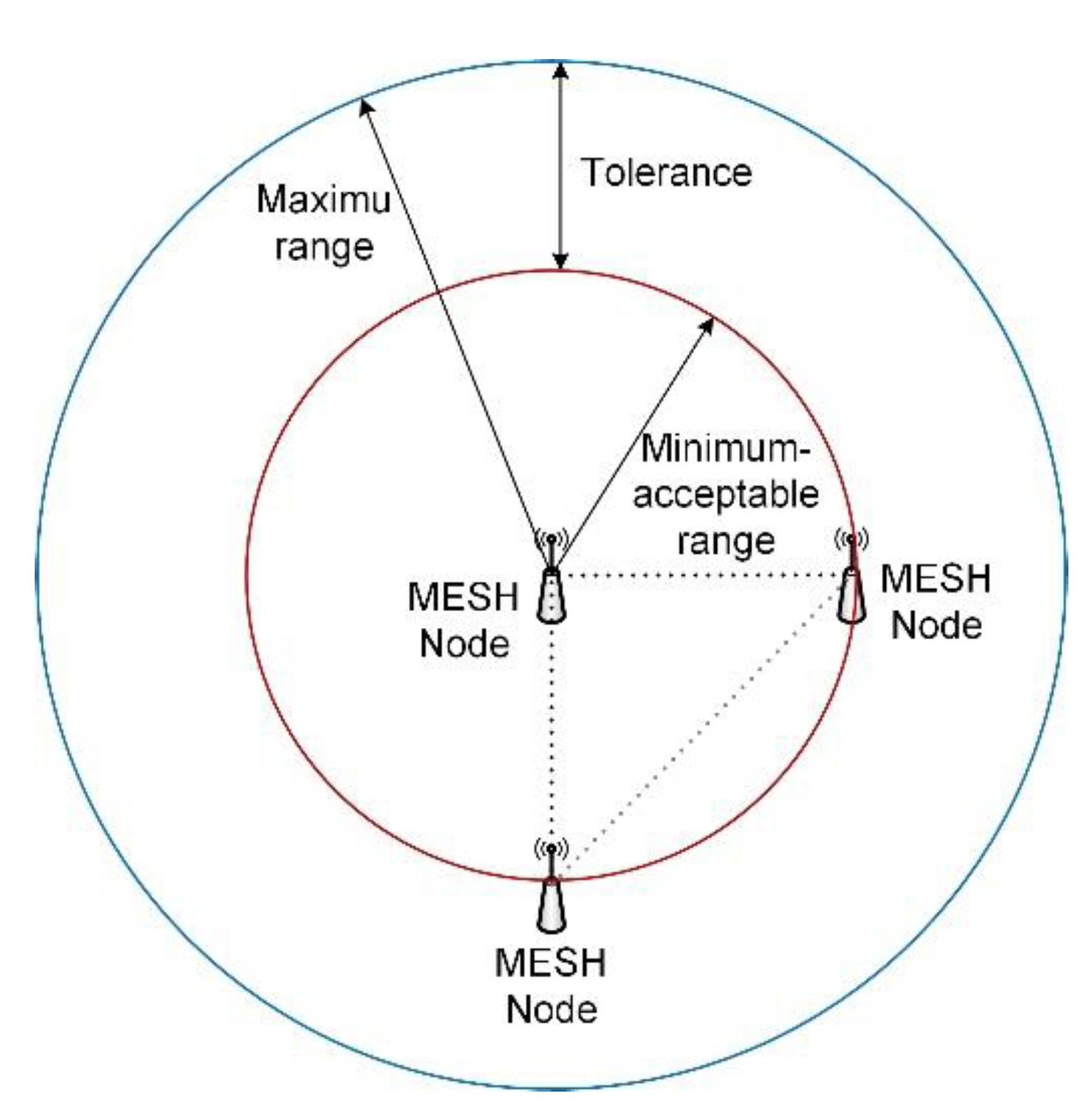
2. Wireless MESH Networks
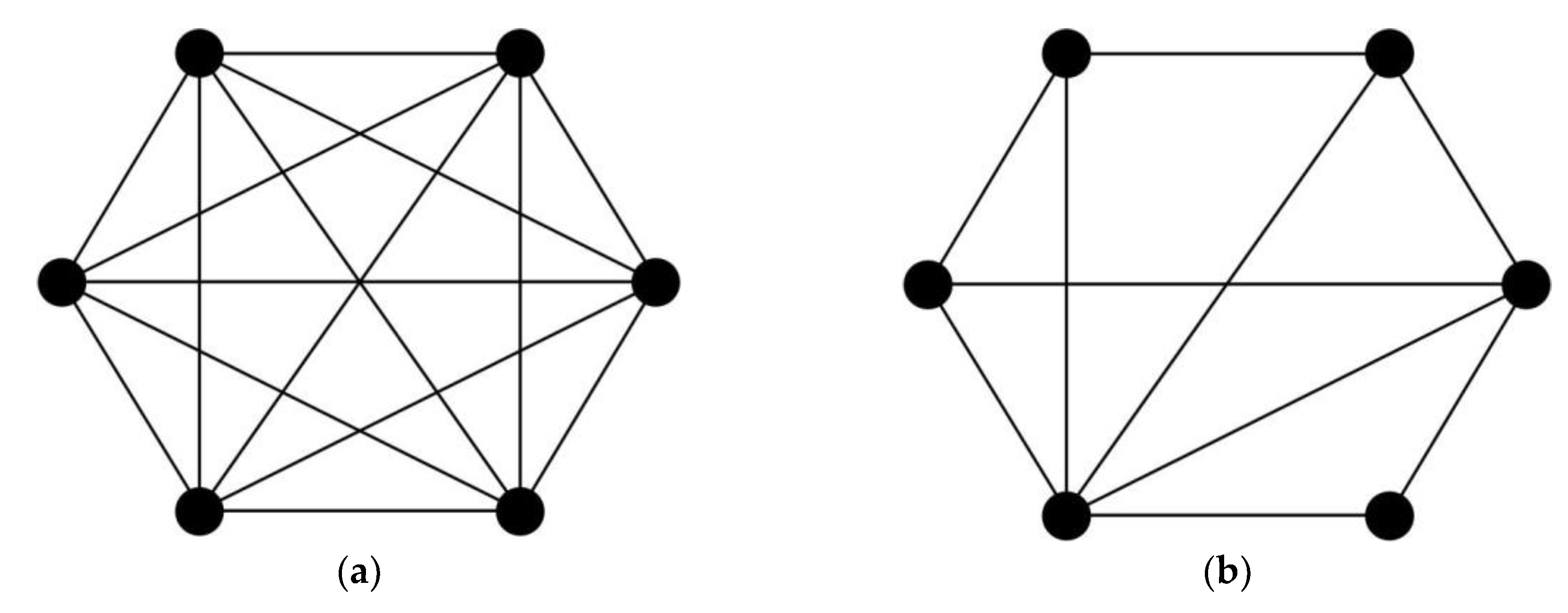
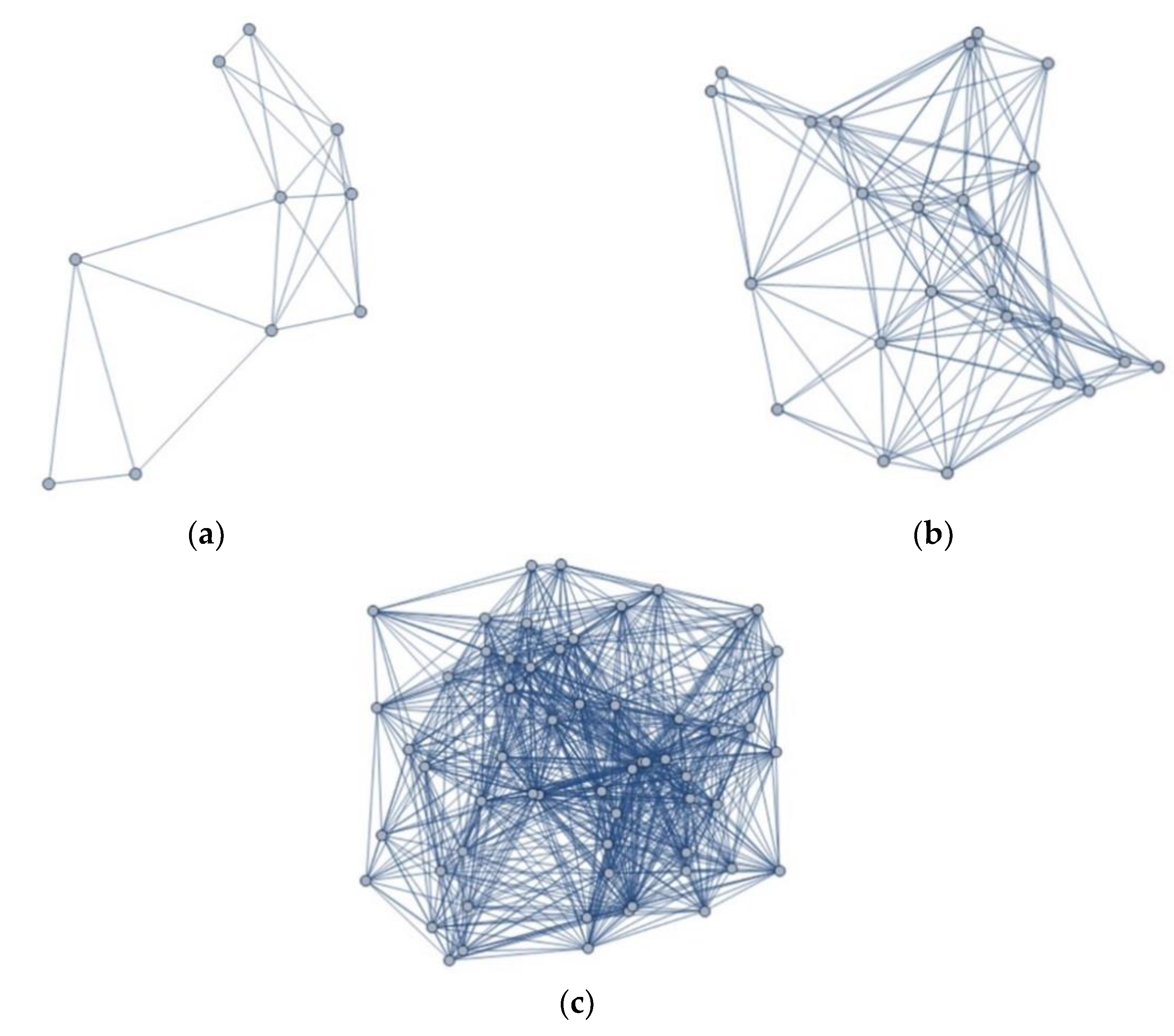
3. Phase Transitions in the Structure of a Wireless Network
4. Analysis of Phase Transitions in the MESH Network
5. Application
- Actual node radius—in this message the nodes in the network transmit the current value of the transmitter power which is then transformed to the form of .
- Keep alive—is information periodically sent to the arbiter by each network node, informing it about its proper functioning, similar to the mechanisms used in classic routing protocols. The node may initiate sending information periodically or create a response to a message sent by the arbiter. It depends on the specificity of the network and the protocols used. In case this message is not received, the arbiter acknowledges that the node is unreachable and a response from technical staff is required. It is possible to define a threshold value for the number of unreceived messages, which allows us to conclude that a given node is permanently unavailable.
- Position—this message provides information about the current position of the node (its location). The message is important for networks with mobile elements and should be treated as options. For static networks, the location of static nodes can be implemented at the network construction stage and remembered by the arbiter.
- Huge and constantly growing costs of maintaining own IT department responsible for maintaining the company’s IT systems, including the considered network system [46]. In order to reduce operation costs, companies use outsourcing of ICT services. Generally, the costs of such a service include: cost of maintaining engineers’ readiness (fixed monthly fee), cost of response time (fixed monthly fee), cost of work performed on site (variable man-hour charge), maintenance of spare parts warehouse (fixed fee monthly). If the company operates a critical communication system, it strives to ensure that the response time is as short as possible (maximum 4 h), and that the outsourcing company maintains all types of spare parts. In this case, the value pt should be close to 1 (e.g., 0.9). Early failure prediction, based on the proposed algorithm, will extend the response time and eliminate the need to maintain full hot stock of spare parts. This will significantly reduce the fixed operating costs of the system.
- Some companies base operations on a risk management model. In this case, the model analysis enables precise determination of the value pt, which in turn allows achieving the level of risk acceptable for the entire system (direct connection of the value pt with the residual risks).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Buchanan, M. Biological transitions. Nat. Phys. 2019, 15. [Google Scholar] [CrossRef]
- Torres, J.J.; Marro, J. Brain Performance versus Phase Transitions. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [Green Version]
- Perc, M. Phase transitions in models of human cooperation. Phys. Lett. A 2016, 380, 2803–2808. [Google Scholar] [CrossRef]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Papon, P.; Leblond, J.; Meijer, P.H.E. The Physics of Phase Transition: Concepts and Applications; Springer: Berlin, Germany, 2002. [Google Scholar]
- Oprisan, A.; Garrabos, Y.; Lecoutre, C.; Beysens, D. Pattern Evolution during Double Liquid-Vapor Phase Transitions under Weightlessness. Molecules 2017, 22, 947. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Han, Y.; Chen, L.; Aihara, K. Multiple Phase Transitions in the Culture Dissemination. Complex Sci. 2009, 4, 286–290. [Google Scholar]
- Novotny, J.; Lavička, H. Non-equilibrium Phase Transitions of Economic Systems under Exogenous Structural Shocks. Phys. Rev. B 2014. [Google Scholar] [CrossRef]
- Wiltshire, T.J.; Butner, J.E.; Fiore, S.M. Problem-Solving Phase Transitions during Team Collaboration. Cogn. Sci. A Multidiscip. J. 2018, 42, 129–167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huberman, B.A. Social Computing and the Attention Economy. J. Stat. Phys. 2013, 151, 329–339. [Google Scholar] [CrossRef]
- Fronczak, P.; Fronczak, A.; Hołyst, J.A. Phase transitions in social networks. Eur. Phys. J. B 2007, 59, 133–139. [Google Scholar] [CrossRef]
- Okamoto, H.; Schlesinger, M.E.; Mueller, E.M. ASM International Volume 3. Alloy Phase. Available online: https://www.asminternational.org/documents/10192/1849770/05442G_TOC.pdf/ecbf0e0e-cbe5-4d00-a82e-edc48bc156a4. (accessed on 14 October 2019).
- Bondareva, A.; Levchenko, T.; Zmievskaya, G.I. Computer Simulation Model for First-Order Phase Transition Fluctuation Stage. Defect Diffus. Forum 2010, 297, 502–507. [Google Scholar] [CrossRef]
- Seoane, L.F.; Solé, R. Phase transitions in Pareto optimal complex networks. Phys. Rev. E 2015, 92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moore, C. The Computer Science and Physics of Community Detection: Landscapes, Phase Transitions, and Hardness. Available online: https://arxiv.org/pdf/1702.00467.pdf (accessed on 14 October 2019).
- Misra, S.; Misra, S.C.; Zhang, I. Guide to Wireless Mesh Networks; Springer: London, UK, 2009. [Google Scholar]
- Darroudi, S.M.; Gomez, C. Bluetooth Low Energy Mesh Networks: A Survey. Sensors 2017, 17, 1467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cilfone, A.; Davoli, L.; Belli, L.; Ferrari, G. Wireless Mesh Networking: An IoT-Oriented Perspective Survey on Relevant Technologies. Future Internet 2019, 11, 99. [Google Scholar] [CrossRef] [Green Version]
- Hortelano, D.; Olivares, T.; Ruiz, M.C.; Garrido-Hidalgo, C.; López, L. From Sensor Networks to Internet of Things. Bluetooth Low Energy, a Standard for This Evolution. Sensors 2017, 17, 372. [Google Scholar] [CrossRef] [Green Version]
- Pau, G.; Chaudet, C.; Zhao, D.; Collotta, M. Next Generation Wireless Technologies for Internet of Things. Sensors 2018, 18, 221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Pascale, E.; Macaluso, I.; Nag, A.; Kelly, M.; Doyle, L. The Network as a Computer: A Framework for Distributed Computing Over IoT Mesh Networks. IEEE Internet Things J. 2018, 5, 2107–2119. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, S.; Singh, B. Routing in Wireless Mesh Networks: Three New Nature Inspired Approaches. Wirel. Pers. Commun. 2015, 83, 3157–3179. [Google Scholar] [CrossRef]
- Tsado, Y.; Gamage, K.A.A.; Adebisi, B.; Lund, D.; Rabie, K.M.; Ikpehai, A. Improving the Reliability of Optimised Link State Routing in a Smart Grid Neighbour Area Network based Wireless Mesh Network Using Multiple Metrics. Energies 2017, 10, 287. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Zeng, X.-J. Regional condition-aware hybrid routing protocol for hybrid wireless mesh network. Comput. Netw. 2019, 148, 120–128. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Shi, W.; Shi, T.; Yang, X. An efficient cooperative hybrid routing protocol for hybrid wireless mesh networks. Wirel. Netw. 2017, 23, 1387–1399. [Google Scholar] [CrossRef]
- Chen, J.-L.; Ma, Y.-W.; Lai, C.-P.; Hu, C.-C.; Huang, Y.-M. Multi-Hop Routing Mechanism for Reliable Sensor Computing. Sensors 2009, 9, 10117–10135. [Google Scholar] [CrossRef] [PubMed]
- Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Reliability and Availability Evaluation of Wireless Sensor Networks for Industrial Applications. Sensors 2012, 12, 806–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.H. All-Terminal Reliability Analysis of Wireless Networks of Redundant Radio Modules. IEEE Internet Things J. 2016, 3, 219–230. [Google Scholar] [CrossRef]
- Rosyidi, L.; Pradityo, H.P.; Gunawan, D.; Harwahyu, R.; Sari, R.F. Dual hop multicast ping method for node failure detection in ZigBee loop network. Int. Conf. Inf. Technol. Syst. Innov. (ICITSI) 2014. [Google Scholar] [CrossRef]
- Yaqini, A.; Popalyar, F. An artificial neural network based fault detection and diagnosis for wireless mesh networks. Wirel. Days Conf. 2018. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Wang, D.; Song, C.; Liu, M.; Li, J.; Lou, L.; Liu, Z. Failure prediction using machine learning and time series in optical network. Opt. Express 2017, 25, 18553–18565. [Google Scholar] [CrossRef]
- Hayajna, T.; Kadoch, M. Hello-Based Link Detection Failure Analysis in Wireless Mesh Networks. In Proceedings of the IEEE 4th International Conference on Future Internet of Things and Cloud (FiCloud), Vienna, Austria, 22–24 August 2016. [Google Scholar]
- Lindhorst, T.; Lukas, G.; Nett, E.; Mock, M. Data-Mining-Based Link Failure Detection for Wireless Mesh Networks. IEEE Symp. Reliab. Distrib. Syst. 2010. [Google Scholar] [CrossRef]
- Sota, N.; Higaki, H. Cooperative Watchdog for Malicious Failure Notification in Wireless Ad-Hoc Networks. In Proceedings of the 8th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Larnaca, Cyprus, 21–23 November 2016. [Google Scholar]
- Tanha, M.; Sajjadi, D.; Pan, J. Demystifying Failure Recovery for Software-Defined Wireless Mesh Networks. In Proceedings of the 4th IEEE Conference on Network Softwarization and Workshops (NetSoft), Montreal, QC, Canada, 25–29 June 2018. [Google Scholar]
- Singh, M. Routing Protocol for WMNs; Springer: Berlin, Germany, 2018. [Google Scholar]
- Peng, Y.; Song, Q.; Yu, Y.; Wang, F. Fault-tolerant routing mechanism based on network coding in wireless mesh networks. J. Netw. Comput. Appl. 2014, 37, 259–272. [Google Scholar] [CrossRef]
- Wang, G.; Wang, G.; Shan, Z. Fault tolerance analysis of mesh networks with uniform versus nonuniform node failure probability. Inf. Process. Lett. 2012, 112, 396–401. [Google Scholar] [CrossRef]
- Khichar, J.; Choudhary, S. Fault aware adaptive routing algorithm for mesh based NoCs. In Proceedings of the International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017. [Google Scholar]
- Guerin, J.; Portmann, M.; Pirzada, A. Routing metrics for multi-radio wireless mesh networks. Telecommun. Netw. Appl. Conf. 2007, 343–348. [Google Scholar] [CrossRef] [Green Version]
- Hiertz, G.R.; Denteneer, D.; Max, S.; Taori, R.; Cardona, J.; Berlemann, L.; Walke, B. IEEE 802.11s: The WLAN Mesh Standard. IEEE Wirel. Commun. 2010, 17, 104–111. [Google Scholar] [CrossRef]
- Sgora, A.; Vergados, D.D.; Chatzimisios, P. IEEE 802.11s Wireless Mesh Networks: Challenges and Perspectives. Soc. Inform. Telecommun. Eng. 2009, 13, 263–271. [Google Scholar]
- Sznajd-Weron, K. Teoria Przejść Fazowych I Zjawiska Krytyczne; Uniwersytet Wrocławski Instytut Fizyki Teoretycznej: Wrocław, Poland, 2012. [Google Scholar]
- Gonczarek, R. Teoria przejść fazowych, wybrane zagadnienia; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2004. [Google Scholar]
- Du, Y.-C.; Lin, D.T.; Jen, C.-P.; Ng, C.W.; Chang, C.-Y.; Wen, Y.-X. Development of a Wireless Mesh Sensing System with High-Sensitivity LiNbO3 Vibration Sensors for Robotic Arm Monitoring. Sensors 2019, 19, 507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Opening Report published by the Council IT Sector Competencies 2018. Available online: https://www.radasektorowa.pl. (accessed on 14 October 2019).
- Mazur, D.; Paszkiewicz, A.; Bolanowski, M.; Budzik, G.; Oleksy, M. Analysis of possible SDN use in the rapid prototyping process part of the Industry 4.0. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 21–30. [Google Scholar]
- Ji, W.; Duan, S.; Chen, R.; Wang, S.; Ling, Q. A CNN-based network failure prediction method with logs. In Proceedings of the Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018. [Google Scholar]
- Di, X.; Zhang, Z.; Li, H.; Ao, C.; Tian, J.; Ozaki, K.; Wen, Y.; Fujita, H. Low-overhead and high-accuracy failure detection method for wireless multi-hop ad hoc networks. In Proceedings of the International Wireless Communications and Mobile Computing Conference (IWCMC), Nicosia, Cyprus, 4–8 August 2014. [Google Scholar]
- Draz, U.; Ali, T.; Yasin, S.; Waqas, U.; Rafiq, U. Towards Formalism of Link Failure Detection Algorithm for Wireless Sensor and Actor Networks. In Proceedings of the International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 21–22 February 2019. [Google Scholar]












| Method | Network Failure Detection | Prediction of Network Failure | Network Size | Models of the Method Implementation in the Real Network | Network Type |
|---|---|---|---|---|---|
| Proposed method based on Phase transitions analysis | Yes | Yes | No limit, tested for network with 2000 nodes | Network with arbiter, SDN networks | Wireless, MESH, cable, fiber, LAN, MAN, WAN |
| Classical Network management systems | Yes, but only for previously defined elements (nodes, links, devices elements) | Limited based on:—network baseline,—human decision in Network Operating Center | No limit, often dedicated for homogeneous network (devices from one vendor). Tested for network with 150 devices | Classical network with one or more NMS station | Wireless, cable, fiber, LAN, MAN, WAN |
| Log Data mining [48] | No | Yes | No limit, a large amount of data transmitted from network nodes to central management node | Network with arbiter, SDN networks | cable, fiber, MAN, WAN |
| Model of Link Failure Detection Algorithm (LFDA) [50] | Yes (limited) | Yes | N/A | Network with arbiter | MESH, cable, fiber, MAN, WAN |
| Root Node Reduction method [49] | Yes | No | No limit, tested for several nodes | Distributed architectures, application layer, communication overhead, calculations in node | Wireless, cable, fiber, LAN |
| DES-SVM prediction method (machine learning) [31] | Yes | Yes | No limit, large amount of data transmitted from network nodes to central management node | SDMAN, SDN | Mesh optical topology, LAN, MAN |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paszkiewicz, A.; Bolanowski, M.; Zapała, P. Phase Transitions in Wireless MESH Networks and Their Application in Early Detection of Network Coherence Loss. Appl. Sci. 2019, 9, 5508. https://doi.org/10.3390/app9245508
Paszkiewicz A, Bolanowski M, Zapała P. Phase Transitions in Wireless MESH Networks and Their Application in Early Detection of Network Coherence Loss. Applied Sciences. 2019; 9(24):5508. https://doi.org/10.3390/app9245508
Chicago/Turabian StylePaszkiewicz, Andrzej, Marek Bolanowski, and Przemysław Zapała. 2019. "Phase Transitions in Wireless MESH Networks and Their Application in Early Detection of Network Coherence Loss" Applied Sciences 9, no. 24: 5508. https://doi.org/10.3390/app9245508
APA StylePaszkiewicz, A., Bolanowski, M., & Zapała, P. (2019). Phase Transitions in Wireless MESH Networks and Their Application in Early Detection of Network Coherence Loss. Applied Sciences, 9(24), 5508. https://doi.org/10.3390/app9245508






