Angiography Simulation and Planning Using a Multi-Fluid Approach
Abstract
:1. Introduction
2. Overview of Simulation Framework
- (1)
- The software system components, see Figure 1b, include three simulation modules: the human-computer interaction (HCI) module, the physics simulation module, and the visualization module.
- In the HCI module, a virtual guidewire/catheter is steered by a “Geomagic touch” haptic device [11], and the syringe tool is to deliver the contrast fluid media. Realistic haptic feedback is modelled by the haptic device, simulating the force feedback via the software simulation module.
- The physics simulation module contains a discrete elastic rod model for physically based guidewire simulation [10,14]. The discrete elastic rod model is capable of real-time realistic simulation of complex dynamic interactions of guidewires within blood vessel geometry [15], which allows efficient computation the haptics effect. Contrast media injection model and its simulation are further integrated into the system.
- The visualization module renders the simulation results generated by the physics and HCI modules in real time using GPU graphics rendering techniques.
- (2)
- Figure 2 demonstrates the syringe device tool and the corresponding circuit, which mainly includes a power module, a stepper motor module, a potentiometer, an air pressure sensor, a force sensing resistor, an Advanced RISC Machine (ARM) processor, an air cylinder, a lead screw and a coronary control syringe normally used in the real medical operations.
- The analog-to-digital converter (ADC) interface of ARM processor samples the voltage of slide potentiometer and the piston of syringe is fixed with the slide potentiometer for injection together with the same distance. When moving the piston, the voltage of the slide potentiometer changes, thereby using the sampled voltage data to calculate the injection dosage and injection speed of contrast media in real time.
- The force feedback from the syringe is mainly influenced by the cardiac blood pressure. Therefore, the air cylinder is adopted to imitate the condition inside the blood vessel. We employ a stepper motor to control the piston rod of the air cylinder to change its inner air pressure. In this device, the lead screw is adopted to convert the rotary motion of the stepper motor to a linear motion of screw. Then, the stepper motor can push and release the piston of the air cylinder to produce corresponding blood pressures in inner air cylinder to allow the user to feel the pressure force when he/she pushes the piston of the syringe.
3. Diffusion Simulation of Contrast Media
3.1. Multi-Fluids Mixture Model
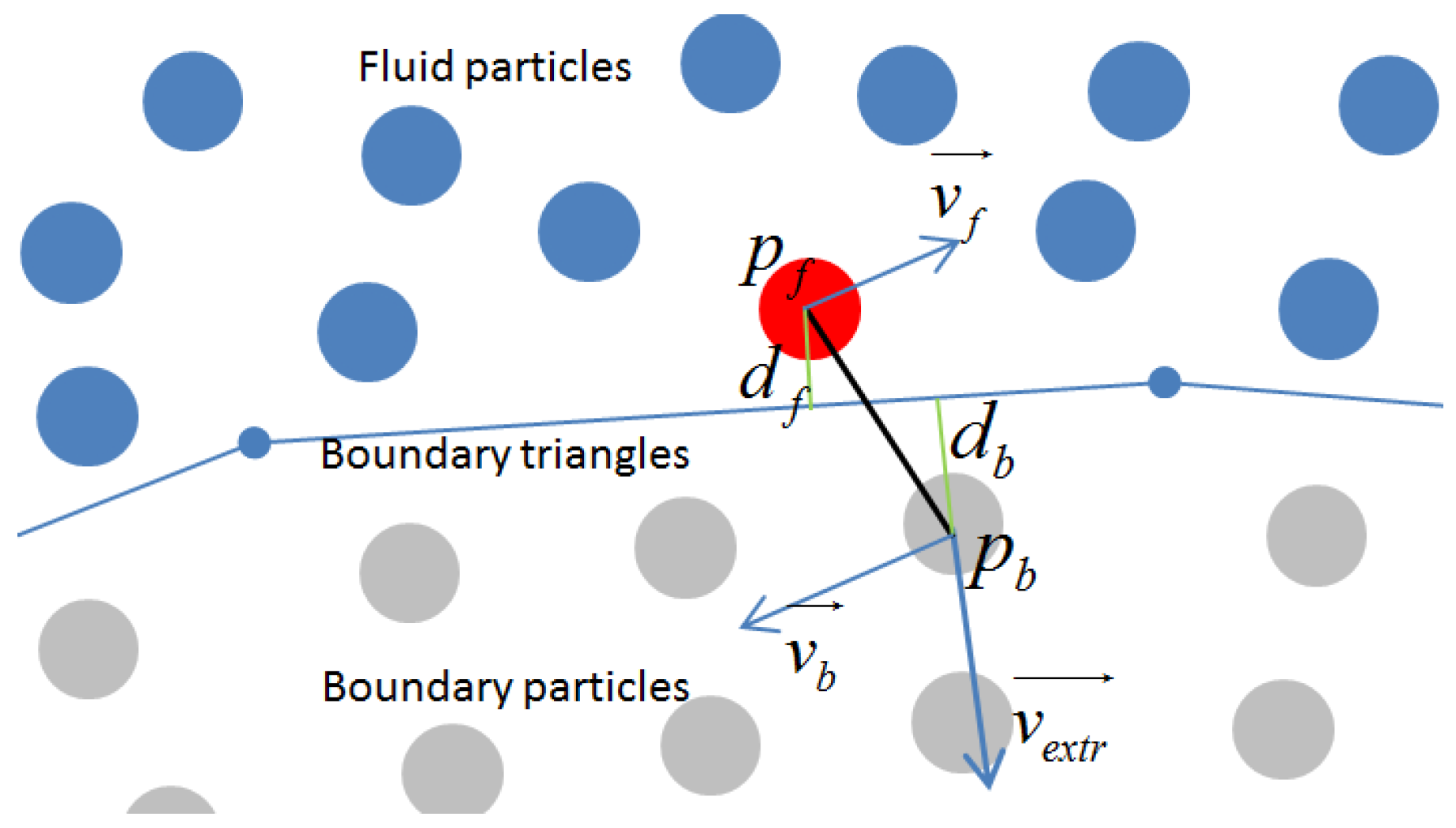
3.2. Boundary Conditions
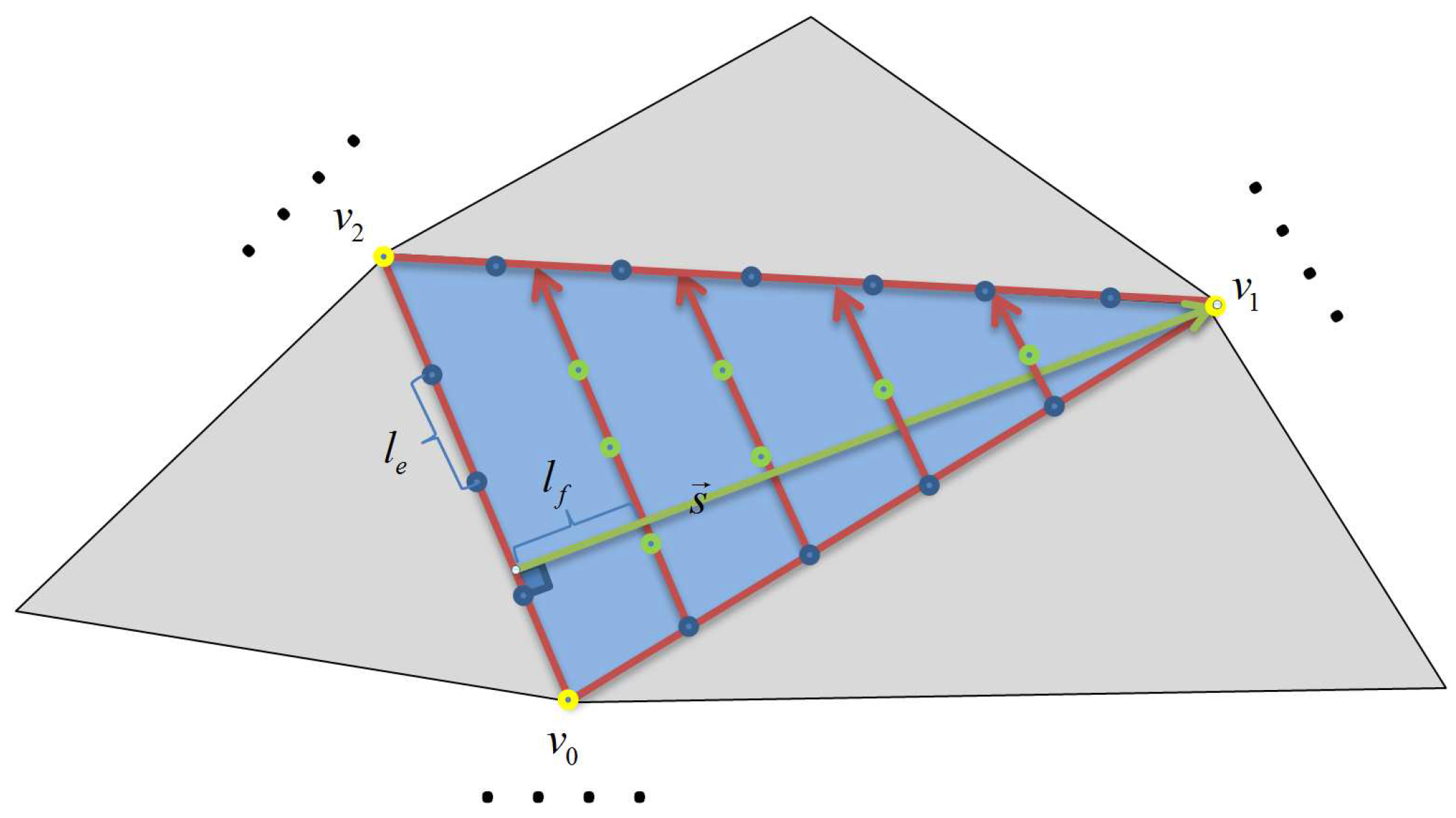
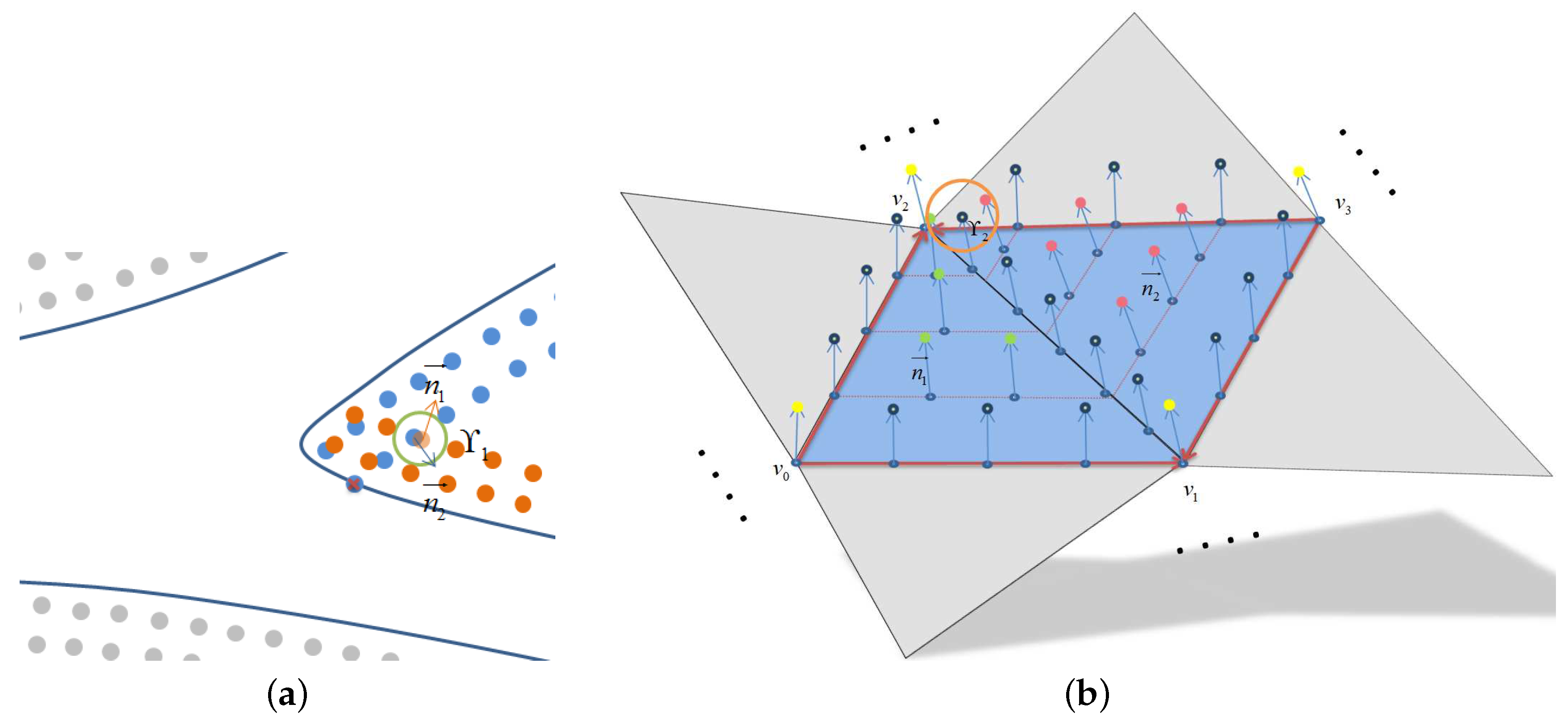
3.2.1. Boundary Constructions
3.2.2. The Application of Boundary Condition
4. Results and Discussions
4.1. Experiment 1
4.1.1. Stenosis Vessels
4.1.2. Y-Type Vessels
4.2. Experiment 2
4.2.1. Influence of Injection Dosage
4.2.2. Influence of Injection Velocity
4.2.3. Virtual and Real Angiography Results Comparison
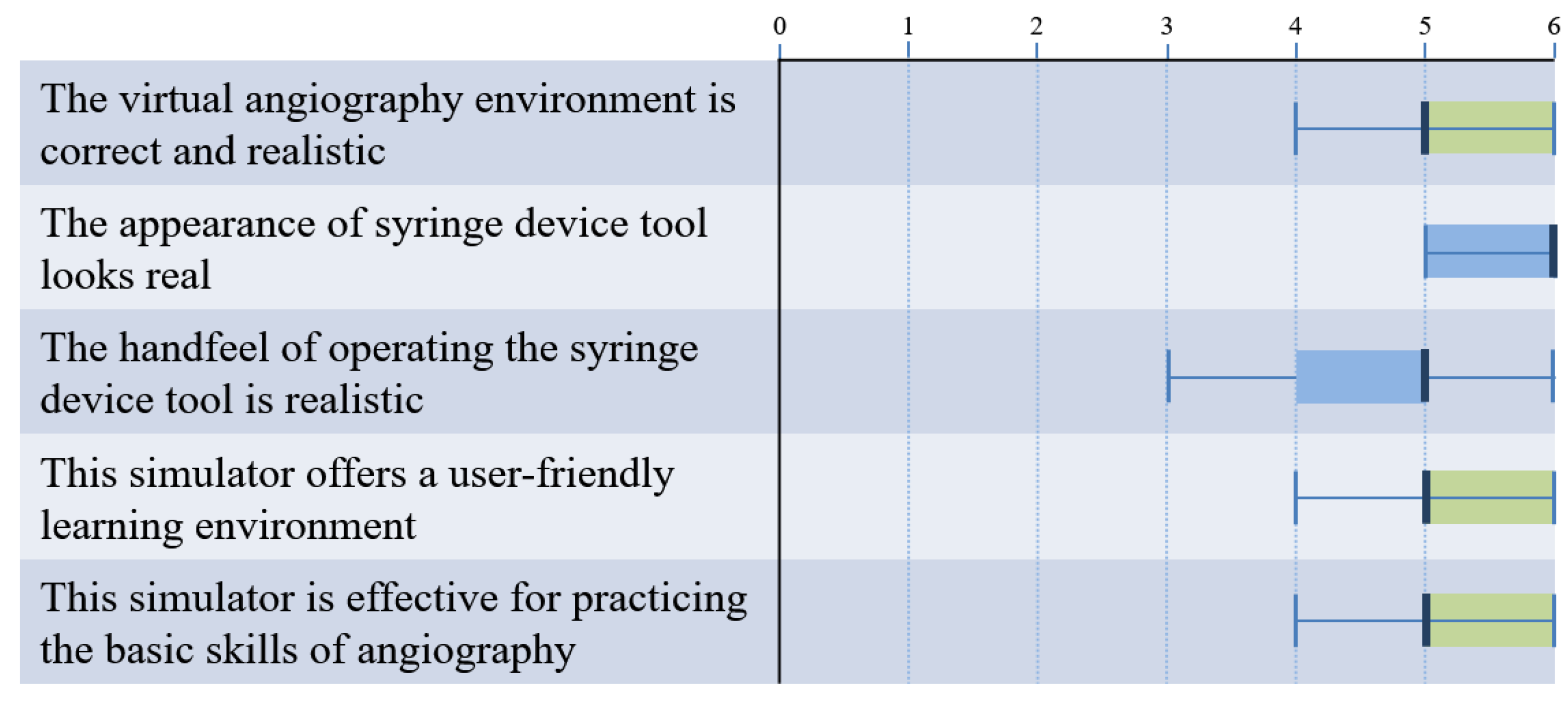
4.3. Subjective Assessment by Experts
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lunderquist, A.; Ivancev, K.; Wallace, S.; Enge, I.; Laerum, F.; Kolbenstvedt, A.N. The acquisition of skills in interventional radiology by supervised training on animal models: a three-year multicenter experience. Cardiovasc. Interv. Radiol. 1995, 18, 209–211. [Google Scholar] [CrossRef]
- Bunce, N.; Mohiaddin, R. An Atlas of Contrast-Enhanced Angiography: Three-Dimensional Magnetic Resonance Angiography; Taylor & Francis: Oxford, UK, 2003. [Google Scholar]
- Luboz, V.; Zhang, Y.; Johnson, S.; Song, Y.; Kilkenny, C.; Hunt, C.; Woolnough, H.; Guediri, S.; Zhai, J.; Odetoyinbo, T. ImaGiNe Seldinger: First simulator for Seldinger technique and angiography training. Comput. Methods Programs Biomed. 2013, 111, 419–434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duriez, C.; Cotin, S.; Lenoir, J.; Neumann, P. New approaches to catheter navigation for interventional radiology simulation. Comput. Aided Surg. 2006, 11, 300–308. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Duratti, L.; Samur, E.; Spaelter, U.; Bleuler, H. A computer-based real-time simulation of interventional radiology. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1742–1745. [Google Scholar]
- Wang, Y. Simulation of Blood Flow and Contrast Medium Propagation for a Vascular Interventional Radiology Simulator. Master’s Thesis, Department of Computing, Imperial College, London, UK, 2009. [Google Scholar]
- Nicholson, W.J.; Cates, C.U.; Patel, A.D.; Niazi, K.; Palmer, S.; Helmy, T.; Gallagher, A.G. Face and content validation of virtual reality simulation for carotid angiography: Results from the first 100 physicians attending the Emory NeuroAnatomy Carotid Training (ENACT) program. Simul. Healthc. 2006, 1, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Jensen, U.J.; Jensen, J.; Olivecrona, G.K.; Ahlberg, G.; Tornvall, P. Technical skills assessment in a coronary angiography simulator for construct validation. Simul. Healthc. 2013, 8, 324–328. [Google Scholar] [CrossRef] [PubMed]
- Grund-Pedersen, J.; Ohlsson, F. Interventional Simulator Control System. U.S. Patent US 8,491,307 B2, 2013. [Google Scholar]
- Tang, W.; Lagadec, P.; Gould, D.; Wan, T.R.; Zhai, J.; How, T. A realistic elastic rod model for real-time simulation of minimally invasive vascular interventions. Vis. Comput. 2010, 26, 1157–1165. [Google Scholar] [CrossRef]
- Huang, D.; Tang, W.; Wan, T.R.; John, N.W.; Gould, D.; Ding, Y.; Chen, Y. A new approach to haptic rendering of guidewires for use in minimally invasive surgical simulation. Comput. Animat. Virtual Worlds 2011, 22, 261–268. [Google Scholar] [CrossRef]
- Höfer, U.; Langen, T.; Nziki, J.; Zeitler, F.; Hesser, J.; Müller, U.; Voelker, W.; Männer, R. Cathi-catheter instruction system. In CARS 2002 Computer Assisted Radiology and Surgery; Springer: Berlin, Germany, 2002; pp. 101–106. [Google Scholar]
- Schuetz, M.; Moenk, S.; Vollmer, J.; Kurz, S.; Mollnau, H.; Post, F.; Heinrichs, W. High degree of realism in teaching percutaneous coronary interventions by combining a virtual reality trainer with a full scale patient simulator. Simul. Healthc. 2008, 3, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Wan, T.R.; Gould, D.; How, T.; John, N.W. A stable and real-time nonlinear elastic approach to simulating guidewire and catheter insertions based on cosserat rod. IEEE Trans. Biomed. Eng. 2012, 59, 2211–2218. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Wang, Y.; Tang, P.; Xie, Z.; Tang, W.; Ding, Y. Modeling and Simulation of Multi-frictional Interaction Between Guidewire and Vasculature. In Image and Graphics; Springer: Berlin, Germany, 2015; pp. 524–537. [Google Scholar]
- Park, J.; Kim, Y.; Wi, D.; Kang, N.; Shin, S.Y.; Noh, J. A unified handling of immiscible and miscible fluids. Comput. Animat. Virtual Worlds 2008, 19, 455–467. [Google Scholar] [CrossRef] [Green Version]
- Bao, K.; Wu, X.; Zhang, H.; Wu, E. Volume fraction based miscible and immiscible fluid animation. Comput. Animat. Virtual Worlds 2010, 21, 401–410. [Google Scholar] [CrossRef]
- Kang, N.; Park, J.; Noh, J.; Shin, S.Y. A hybrid approach to multiple fluid simulation using volume fractions. Comput. Graph. Forum 2010, 29, 685–694. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Q.; Peng, Q. Realistic simulation of mixing fluids. Visual Comput. 2011, 27, 241–248. [Google Scholar] [CrossRef]
- Ren, B.; Li, C.; Yan, X.; Lin, M.C.; Bonet, J.; Hu, S.M. Multiple-fluid SPH simulation using a mixture model. ACM Trans. Graph. (TOG) 2014, 33, 171. [Google Scholar] [CrossRef]
- Müller, M.; Solenthaler, B.; Keiser, R.; Gross, M. Particle-based fluid-fluid interaction. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer Animation, Los Angeles, CA, USA, 29–31 July 2005; pp. 237–244. [Google Scholar]
- Wu, X.; Allard, J.; Cotin, S. Real-time modeling of vascular flow for angiography simulation. In Medical Image Computing and Computer-Assisted Intervention–Miccai 2007; Springer: Berlin, Germany, 2007; pp. 557–565. [Google Scholar]
- Yeoh, G.H.; Tu, J. Computational Techniques for Multiphase Flows; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Müller, M.; Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Eurographics Association, San Diego, CA, USA, 26–27 July 2003; pp. 154–159. [Google Scholar]
- Clavet, S.; Beaudoin, P.; Poulin, P. Particle-based viscoelastic fluid simulation. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium On Computer Animation, Los Angeles, CA, USA, 29–31 July 2005; pp. 219–228. [Google Scholar]
- Akinci, N.; Ihmsen, M.; Akinci, G.; Solenthaler, B.; Teschner, M. Versatile rigid-fluid coupling for incompressible SPH. ACM Trans. Graph. (TOG) 2012, 31, 62. [Google Scholar] [CrossRef]
- Fujisawa, M.; Miuralunderquist1995acquisition, K.T. An Efficient Boundary Handling with a Modified Density Calculation for SPH. Comput. Graph. Forum 2015, 34, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Wan, T.R. Constraint-based soft tissue simulation for virtual surgical training. IEEE Trans. Biomed. Eng. 2014, 61, 2698–2706. [Google Scholar] [CrossRef] [PubMed]
- Day, M.A. The no-slip condition of fluid dynamics. Erkenntnis 1990, 33, 285–296. [Google Scholar] [CrossRef]
- Akinci, N.; Cornelis, J.; Akinci, G.; Teschner, M. Coupling elastic solids with smoothed particle hydrodynamics fluids. Comput. Animat. Virtual Worlds 2013, 24, 195–203. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]






| Angiography Results | (a) | (b) | (c) |
|---|---|---|---|
| Particle number | 200 | 400 | 600 |
| Injection dosage | 0.65 mL | 1.30 mL | 1.95 mL |
| Injection velocity | 6.50 mL/s | 6.50 mL/s | 6.50 mL/s |
| Total injection time | 0.10 s | 0.20 s | 0.30 s |
| Angiography Results | (a) | (b) | (c) |
|---|---|---|---|
| Particle number | 600 | 600 | 600 |
| Injection dosage | 1.95 mL | 1.95 mL | 1.95 mL |
| Injection velocity | 3.25 mL/s | 6.50 mL/s | 13.00 mL/s |
| Time of finishing injection | 0.60 s | 0.30 s | 0.15 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Tang, P.; Tang, W.; Wan, T.R. Angiography Simulation and Planning Using a Multi-Fluid Approach. Appl. Sci. 2019, 9, 379. https://doi.org/10.3390/app9030379
Huang D, Tang P, Tang W, Wan TR. Angiography Simulation and Planning Using a Multi-Fluid Approach. Applied Sciences. 2019; 9(3):379. https://doi.org/10.3390/app9030379
Chicago/Turabian StyleHuang, Dongjin, Pengbin Tang, Wen Tang, and Tao Ruan Wan. 2019. "Angiography Simulation and Planning Using a Multi-Fluid Approach" Applied Sciences 9, no. 3: 379. https://doi.org/10.3390/app9030379
APA StyleHuang, D., Tang, P., Tang, W., & Wan, T. R. (2019). Angiography Simulation and Planning Using a Multi-Fluid Approach. Applied Sciences, 9(3), 379. https://doi.org/10.3390/app9030379





