Author Contributions
Conceptualization, G.W., L.Z. and K.Y.; Methodology, G.W.; Investigation, G.W. and L.Z.; Data Curation, G.W.; Writing-Original Draft Preparation, G.W.; Writing-Review and Editing, G.W.; Project Administration, K.Y.; Funding Acquisition, G.W. and K.Y.
Figure 1.
Google map of the wind farm.
Figure 1.
Google map of the wind farm.
Figure 2.
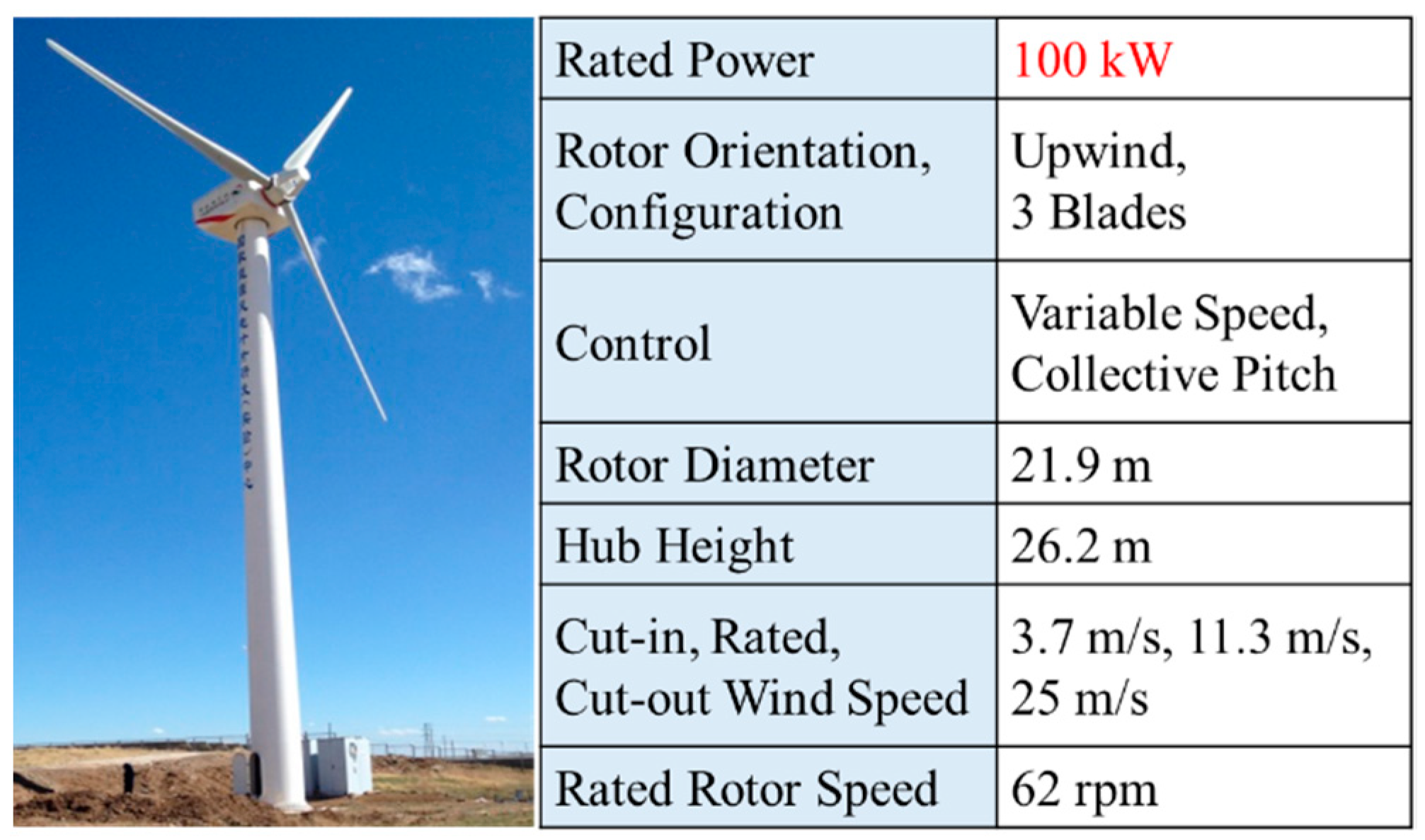
Photo and parameters of the 100 kW wind turbine.
Figure 2.
Photo and parameters of the 100 kW wind turbine.
Figure 3.
Overall layout of field measurement platform.
Figure 3.
Overall layout of field measurement platform.
Figure 4.
(a) Geometry of seven-hole probe, and (b) photo of the probe at the leading edge.
Figure 4.
(a) Geometry of seven-hole probe, and (b) photo of the probe at the leading edge.
Figure 5.
(a) Sketch diagram, and (b) photo of surface pressure measurement system on blades.
Figure 5.
(a) Sketch diagram, and (b) photo of surface pressure measurement system on blades.
Figure 6.
Photo of the tested blade.
Figure 6.
Photo of the tested blade.
Figure 7.
The measuring and controlling system.
Figure 7.
The measuring and controlling system.
Figure 8.
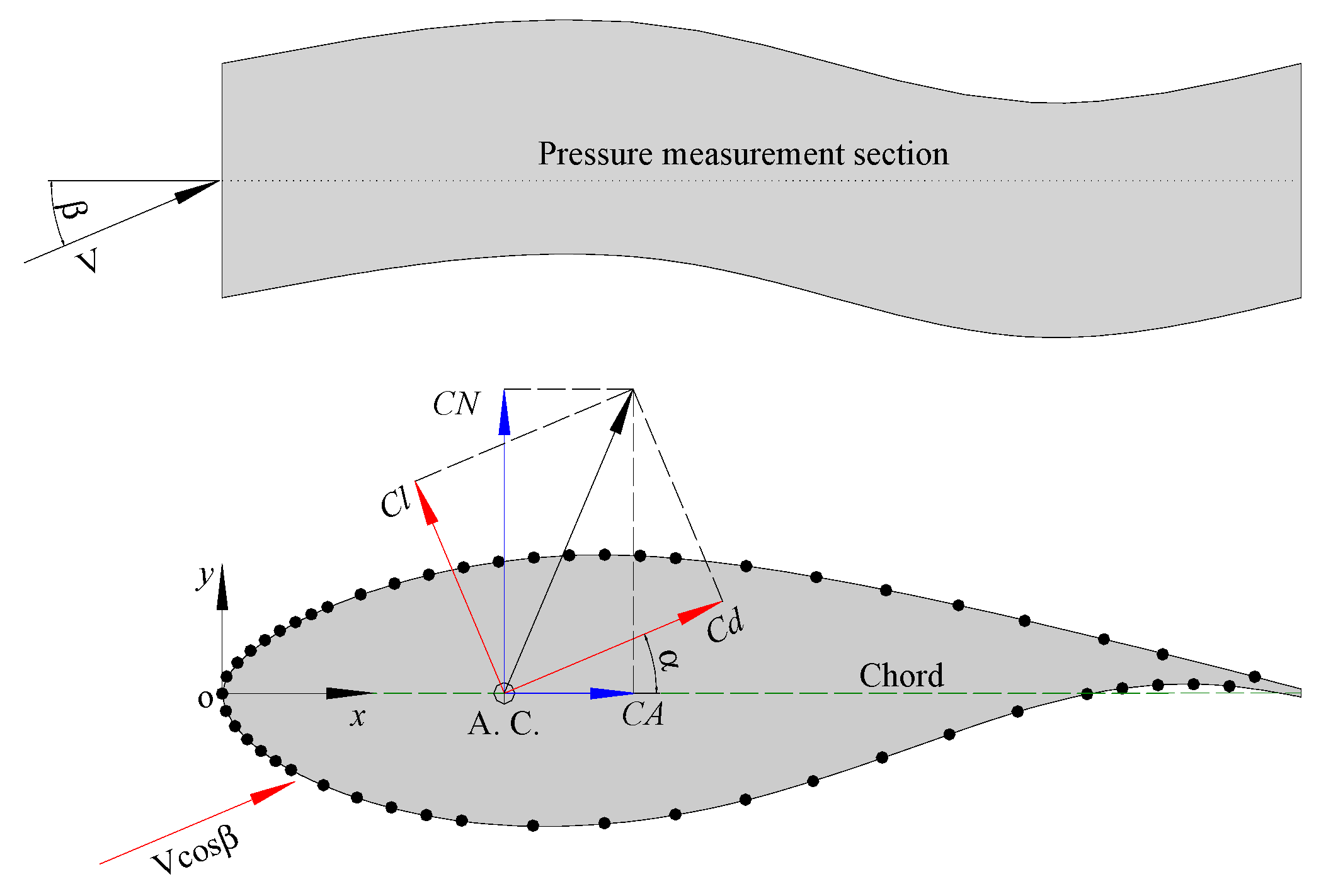
Sketch diagram of the body-axis and air-axis force.
Figure 8.
Sketch diagram of the body-axis and air-axis force.
Figure 9.
Effective angle of attack measured by leading-edge probe.
Figure 9.
Effective angle of attack measured by leading-edge probe.
Figure 10.
The flowchart to calculate the effective angle of attack.
Figure 10.
The flowchart to calculate the effective angle of attack.
Figure 11.
Biot–Savart integral law.
Figure 11.
Biot–Savart integral law.
Figure 12.
Definitions of azimuth angle of rotor and yaw angle of wind turbine.
Figure 12.
Definitions of azimuth angle of rotor and yaw angle of wind turbine.
Figure 13.
Inflow speed (a) and yaw angle (b) at the nacelle in the testing cases.
Figure 13.
Inflow speed (a) and yaw angle (b) at the nacelle in the testing cases.
Figure 14.
Time history of azimuth angle (a) and rotor speed (b) in the testing cases.
Figure 14.
Time history of azimuth angle (a) and rotor speed (b) in the testing cases.
Figure 15.
Instantaneous lift coefficients at r/R = 0.64 with different pitching angles.
Figure 15.
Instantaneous lift coefficients at r/R = 0.64 with different pitching angles.
Figure 16.
Angle-averaged lift coefficients from each pitching angle case (a) and all the cases (b).
Figure 16.
Angle-averaged lift coefficients from each pitching angle case (a) and all the cases (b).
Figure 17.
Reynolds number range at different pitching angle cases.
Figure 17.
Reynolds number range at different pitching angle cases.
Figure 18.
Comparison of lift coefficients of DU93-W-210 between the field test and 2D wind tunnel test.
Figure 18.
Comparison of lift coefficients of DU93-W-210 between the field test and 2D wind tunnel test.
Figure 19.
Comparison of pressure coefficients: (a) α = 6°, (b) α = 12°.
Figure 19.
Comparison of pressure coefficients: (a) α = 6°, (b) α = 12°.
Figure 20.
Standard deviations of the lift coefficient.
Figure 20.
Standard deviations of the lift coefficient.
Figure 21.
Time history of azimuth angle, angle of attack, and lift coefficient in Case 1.
Figure 21.
Time history of azimuth angle, angle of attack, and lift coefficient in Case 1.
Figure 22.
(a) The variation of angle of attack and lift coefficient in one rotation period, and (b) dynamic response of lift coefficient varying with the angle of attack.
Figure 22.
(a) The variation of angle of attack and lift coefficient in one rotation period, and (b) dynamic response of lift coefficient varying with the angle of attack.
Figure 23.
Comparison of yaw angle and variation amplitude of angle of attack measured by probe in Case 1.
Figure 23.
Comparison of yaw angle and variation amplitude of angle of attack measured by probe in Case 1.
Table 1.
The existing work on aerodynamic measurement in the field.
Table 1.
The existing work on aerodynamic measurement in the field.
| Test Projects or Research Teams | Turbines | Project Period | Determination Method of Angle of Attack |
|---|
| Combined Experiment Phase I and II by NREL | 3-bladed, 10 m diameter | 1987–1993 | Wind tunnel method |
| Unsteady Aerodynamics Experiment Phases III–IV by NREL | 3-bladed, 10 m diameter | 1993–1998 | Wind tunnel method |
| Delft University of Technology (DUT) | 2-bladed, 10 m diameter | – | Inverse BEM method and Vortex wake method |
| RISØ National Laboratory in Denmark | 3-bladed, 19 m diameter | 1987–1993 | Power method |
| Netherlands Energy Research Foundation (ECN) | 2-bladed, 27.4 m diameter | 1993–1997 | Stagnation method |
| Imperial College (IC) and Rutherford Appleton Laboratory (RAL) | 3-bladed, 16.9 m diameter | – | Probe method |
| Mie University in Japan | 3-bladed, 10 m diameter | since 1997 | Wind tunnel method |
| DAN-AERO MW by RISØ | 3-bladed, 80 m diameter | 2007–2010 | Wind tunnel method |
| Lanzhou University of Technology in China | 2-bladed, 14.8 m diameter | since 2007 | – |
Table 2.
Distributions of anemometers and wind vanes on the anemometer mast.
Table 2.
Distributions of anemometers and wind vanes on the anemometer mast.
| Upstream anemometer mast | Downstream anemometer mast |
|---|
| Sensor | Height | Sensor | Height |
|---|
| Atmospheric pressure meter | 10 m | Anemometer | 10 m |
| Temperature and humidity meter | 10 m | Anemometer | 15 m |
| Anemometer | 10 m | Anemometer | 20 m |
| Anemometer | 15 m | Anemometer | 26.2 m |
| Anemometer | 26.2 m | Anemometer | 30 m |
| Anemometer | 35 m | Anemometer | 40 m |
| Anemometer | 40 m | Anemometer | 50 m |
| Wind vane | 10 m | Wind vane | 10 m |
| Wind vane | 15 m | Wind vane | 15 m |
| Wind vane | 26.2 m | Wind vane | 26.2 m |
| Wind vane | 40 m | Wind vane | 50 m |
Table 3.
Chord and twist angle distributions of blades.
Table 3.
Chord and twist angle distributions of blades.
| Span/m | Chord/m | Twist Angle/° | Airfoil |
|---|
| 0 | 0.42 | 14.99 | Circle |
| 0.54 | 0.42 | 14.99 | Circle |
| 0.79 | 0.53 | 14.99 | CAS W2-450 |
| 2.79 | 0.67 | 8.40 | DU00-W-350 |
| 3.79 | 0.55 | 5.69 | DU97-W-350 |
| 4.79 | 0.47 | 3.84 | DU91-W2-250 |
| 6.54 | 0.37 | 1.50 | DU93-W-210 |
| 9.04 | 0.28 | −1.55 | NACA 63418 |
Table 4.
Calibration errors of leading-edge probes.
Table 4.
Calibration errors of leading-edge probes.
| Flow Attribute | Angle of Attack (°) | Sideslip Angle (°) | Dynamic Pressure (%) |
|---|
| Error | 0.96 | 0.77 | 1.64 |
Table 5.
Locations of probe tip.
Table 5.
Locations of probe tip.
| Probe Name | P1 | P2 | P3 | P4 | P5 |
|---|
| Span Location (m) | 1.798 | 3.085 | 4.008 | 5.122 | 6.905 |
| Length beyond the leading edge (m) | 0.55 | 0.4 | 0.345 | 0.293 | 0.22 |
Table 6.
Parameters of five pressure measurement sections.
Table 6.
Parameters of five pressure measurement sections.
| Section Name | S1 | S2 | S3 | S4 | S5 |
|---|
| Airfoil | CAS-W2-450 | DU00-W-350 | DU97-W-300 | DU91-W2-250 | DU93-W-210 |
| Span Location (m) | 1.498 | 2.785 | 3.708 | 4.822 | 6.605 |
| Pressure Tap Number | 53 | 57 | 49 | 51 | 46 |
| Chord (m) | 0.758 | 0.658 | 0.558 | 0.467 | 0.369 |
Table 7.
The testing cases to compare with the 2D wind tunnel.
Table 7.
The testing cases to compare with the 2D wind tunnel.
| Case | Status of Turbine | Pitching Angle (°) | Sampling Frequency (Hz) | Sampling Time (sec) |
|---|
| 1 | Stop | 60 | 50 | 60 |
| 2 | Stop | 65 | 50 | 60 |
| 3 | Stop | 70 | 50 | 60 |
| 4 | Stop | 75 | 50 | 60 |
| 5 | Stop | 80 | 50 | 60 |
| 6 | Stop | 85 | 50 | 60 |
| 7 | Stop | 90 | 50 | 60 |
Table 8.
Computation methods of angle of attack.
Table 8.
Computation methods of angle of attack.
| | Method I | Method II | Method III |
|---|
| Sideslip angle correction | ● | ○ | ● |
| Induced velocity correction | ○ | ● | ● |