Defining the Minimum Security Baseline in a Multiple Security Standards Environment by Graph Theory Techniques

Abstract

One of the best ways to protect an organization’s assets is to implement security requirements defined by different standards or best practices. However, such an approach is complicated and requires specific skills and knowledge. In case an organization applies multiple security standards, several problems can arise related to overlapping or conflicting security requirements, increased expenses on security requirement implementation, and convenience of security requirement monitoring. To solve these issues, we propose using graph theory techniques. Graphs allow the presentation of security requirements of a standard as graph vertexes and edges between vertexes, and would show the relations between different requirements. A vertex cover algorithm is proposed for minimum security requirement identification, while graph isomorphism is proposed for comparing existing organization controls against a set of minimum requirements identified in the previous step.

1. Introduction

In response to the increasing amount of cyberattacks, government regulatory authorities’ pressure is increasing since they are concerned in the current situation with information and personal data protection. As an example of increasing regulatory pressure, the European Union General Data Protection Regulation (GDPR) [1] can be mentioned, which came into power on May 2018 and is applicable for all organizations.

Trying to protect their most valuable assets, organizations deploys controls that reduce existing risks. One of the best approaches for the organization would be the implementation of all applicable security standard controls. The main issue in such a case is related to the fact that applied controls have different effectiveness and cost, and from an organization’s point of view it is critical to ensure that enforced security controls are cost-effective and guarantee the needed level of protection. This task can be solved by implementing only mandatory requirements, which would be part of the minimum security baseline of a security standard or set of standards.

Another problem, which is becoming more and more important nowadays, is related to the fact that in order to achieve a competitive advantage, an organization has to be aligned with more than one security standard. For example, financial organizations could be required to be compliant with the Payment Card Industry Data Security Standard (PCI DSS) [2] requirements (in case they process cardholder data) and the Sarbanes–Oxley (SOX) Act [3], which is applicable for all organization that provide financial services in the USA. The fact that SOX controls can be covered by implementing different frameworks, such as Control Objectives for Information and Related Technologies COBIT [4] or Committee of Sponsoring Organizations of the Treadway Commission COSO [5], complicates the situation even more. In such a case it is necessary to ensure that redundant controls are not implemented and there are no overlapping or conflicting controls. However, when an organization is fulfilling requirements from a set of standards, it is difficult to ensure effective cost management of security control implementation. The main issues are related to the fact that different standards define requirements with a different level of detail. This can lead to a situation where different technical solutions might cover the same requirement coming from different standards in the same organization. The most common solutions currently used are different harmonization techniques that visualize possible results. There exist a few different methods on how different standards can be linked. These techniques can be grouped into four main areas: semantic compatibility, mapping, adaptive mapping, and integration. Furthermore, 2.5D [6], 3D [7], or chord diagrams [8] can be used for harmonization results visualization. These techniques for harmonization and visualization allow us to understand links of different standards. However, identification of mandatory requirements still requires manual review of mapped information.

In order to solve this problem, we propose linking different standards with the help of graphs, where security requirements are presented as a graph’s vertexes. It allows us to use graph theory methods and especially graph optimization algorithms, such as vertex cover and graph isomorphism properties, for identifying overlapping and redundant controls. In our case, we propose the usage of a vertex cover algorithm for identification of the minimum set of security requirements in instances where an organization has to be aligned with multiple security standards. When a set of minimum security requirements is identified, graph isomorphism algorithms are applied for automatic verification of similarities between controls already implemented by the organization and the minimum security set determined by the vertex cover algorithm.

In the review part of this article, a brief summary of information on existing methods of various security standard harmonization, minimum security baseline definition, vertex cover, and graph isomorphism verification algorithms will be provided. Then, the proposed methods on security standards representation in the form of a graph, graph-based mapping of multiple security standards, and extraction of minimum security baseline by means of a vertex cover algorithm are described and tested. The method for collating the received minimum security baseline with currently implemented controls is proposed and verified. Finally, the conclusions are provided, and topics for further research are discussed.

2. Prior and Related Work

From the security point of view, an organization has to implement controls that would let an organization protect its most valuable assets, which can be achieved using different methods and techniques. One of the ways would be to apply a multi-criteria model for management decision making oriented to cost-effective management [9]. Another approach is the implementation of requirements defined by information security standards or best practices. In such a case, an organization would be able to prove that it ensures “due diligence” and “due care” principles. Organizations that are planning to implement information security standards or best practices have to verify the organization’s components to be protected and the applicable requirements for protection. While some regulations and standards are mandatory (e.g., GDPR [1], PCI DSS [2], and Health Insurance Portability and Accountability Act (HIPAA) [10]), others are not, however, making it important to ensure that an organization’s environment and information are protected adequately.

Problems arise from the fact that organizations are required to be aligned with more than one security standard or other regulating documents. A most famous example would be requirements for financial organizations to be aligned with Payment Card Industry Data Security Standard [2] (PCI DSS) requirements and the Sarbanes–Oxley Act [3], or requirement to be alignment with ISO 27001/ISO27002 [11] and PCI DSS. To solve this issue, scientists and researchers are using harmonization techniques [12,13]. The most popular technique is mapping when two different documents or framework requirements are linked to one another [14]. We have proposed the use of adaptive mapping through security ontology [15], which would allow the linking of different standards and identification of the level of coverage between different standards. Another method of analysis of information security standard requirements and their interlinks would be the usage of data mining and knowledge discovery techniques [16].

In many cases, organizations decide to implement only mandatory security standard requirements that are named as a minimum security baseline (MSB). MSB is a set of primary security objectives that must be met by any given service or system [17]. In other words, the MSB would be a subset of an information security standard and could be represented as a subpart of it. The standard approach for minimum security baseline identification is the use of expert knowledge [18]. Information security specialists review the standard or framework and identify which requirements are mandatory and are a part of the MSB. Some researchers propose the use of Delphi method research for IT governance MSB identification [19]. The main disadvantages of these methods are related to the fact that they are based on expert knowledge, could be influenced by subjective opinion, are not affordable for small and medium-sized enterprises (SMEs), and cannot be easily adapted for dynamic changes in the information security area.

The previously proposed adaptive mapping method [15] was useful for an understanding of the overall security requirements and visualization of their connections but could not be used for MSB identification. It was proved in articles [20,21], that where security requirement implementation cost evaluation through control-based method were proposed, security controls and security standard requirement presentation as nodes and their connections as a link between nodes, was effective.

For MSB identification, we propose to present information security standards as undirected graphs, where the graph is defined as a pair of sets (V, E), where V is the set of vertices and E is the set of edges formed by pairs of vertices [22]. In our case, security requirements are graph nodes, and edges between graph nodes show the links between these requirements. When two or more information security standards have to be mapped, a new graph is created by establishing relationships between the corresponding requirements of these standards. Previously created graphs of information security standards will be the subgraphs of a newly created graph. For simplicity purposes, we state that if requirements of different standards are linked, i.e., have edges between vertexes, then they define the same requirement and duplicate each other, although in reality requirements cannot be entirely identical and could define security requirement with different levels of detail. For MSB identification duplication, requirements will be removed from the new graph by applying vertex cover algorithms.

Vertex cover is one of the graph related problems, where the primary objective is to extract a set of vertices of a specific graph, which cover all graph edges. A vertex cover in an undirected graph G = (V, E) is the subset of vertices S ⊆ V where every edge (u, v) in the graph G is connected to at least one vertex of S; in other words, if edge (u, v) is an edge of G, then either u is in V or v is in S or both. The size of a vertex cover is the number of vertices it contains [23]. A minimum vertex cover is a vertex cover having the smallest possible number of vertices for a given graph [24]. Vertex cover and Minimum vertex cover examples presented on Figure 1. There also exist minimum weighted vertex cover algorithms with a weight function R associated with each vertex [25].

Vertex cover problems are widely used in the information technology area, for example in solving network base routing delays [26] or network traffic measurements [27]. They are also used in biology for analysis of population-based evolutionary research [28] and many other areas. Vertex cover is an NP-complete problem. This statement was proved by Karp [29] in 1972. Chataval [30] has proposed the use of the approximation algorithm “maximum degree greedy”, Clarkson has modified this approach and offered to perform a selection based on the degree [31], and Balaji, Swaminathan, and Kannan [32] have proposed a method based on new criteria, which was named support of vertex. There exist other vertex cover algorithms, such as nearly optimal vertex cover NOVAC-1 [33], advanced vertex support algorithm AVSA [34] and modified vertex support algorithm MVSA [35], and heuristic algorithms ListLeft and ListRight [36]. Some studies performed comparisons [37] of existing minimum vertex cover algorithms. Pseudo code for minimum vertex cover algorithms can be found in the article [38].

After identification of MSB, we can compare how controls implemented by an organization are aligned with it. Controls implemented by an organization can also be presented as a graph. This graph can be compared with a received MSB graph to verify their alignment. We propose the use of a subgraph isomorphism algorithm for this purpose. Graphs G and G′ are said to be isomorphic [39] if there exists a pair of functions f: V → V′ and g: E → E′ such that f associates each element in V with precisely one element in V′ and vice versa; g associates each element in E with just one element in E′ and vice versa; and for each v ∈ V and each e ∈ E, if v is an endpoint of the edge e, then f(v) is an endpoint of the edge g(e). Subgraph isomorphism from H to G is a function f: V_H → V such that if (u, v) ∈ E_H, then (f(u), f(v)) ∈ E. Furthermore, f is an induced subgraph isomorphism if in addition (u, v) ∉ E_H, then (f(u), f(v)) ∉ E. In other words graph isomorphism helps in verifying exact structural matching between 2 different graphs, even if they are represented in different ways. Graph matching is the process of comparing two graphs to find an appropriate correspondence between their vertexes and edges. It refers to finding mapping solution S from the nodes of one graph G to the nodes of other graph G’ that satisfies predefined criteria and ensure that the structure of one graph is similar to substructures of another graph. Subgraph isomorphism example presented on Figure 2. Subgraph isomorphism helps to verify structural matching between the graph and part of another graph.

This property is widely used to analyze information and search similar patterns in different structures, which are presented as graphs, e.g., image processing [40,41], where graph isomorphism is used to match two different images or social networks [42,43], where it is used for patterns analysis. However, the main area of isomorphism applicability is biology and chemistry, where subgraph isomorphism is used for chemical bond structure [44] and protein structure analysis [45]. It is necessary to mention that this problem could be solved in polynomial time. However, it was not proved that this problem is NP-complete and different researchers have proposed two main ways to do subgraph isomorphism problem solving: try to identify exact subgraph matching identification or use approximate subgraph matching.

A generic subgraph isomorphism identification algorithm is presented in the article [46]. Other examples of exact matching algorithms are GraphGrep [47] and FG-Index [48]. These algorithms use indexes, which allow one to reduce the number of candidates for a potential solution and later perform verification of chosen candidates. Other algorithms, like Ullmann [49], VF2 [50], QuickSI [51], and SPath [52] find all embedding for the given query and original graph. Approximate algorithms, such as SIGMA [53] and Ness [54], are finding approximate embedding and verify isomorphism through similarity measures.

3. The Proposed Method for MSB Identification and Verification Against Deployed Controls

Identification of a minimum set of security requirements, i.e., of only mandatory security standard requirements, is a challenging task. The scope of the MSB depends on the needs of the organization [55]. The objectives are chosen to be pragmatic and complete and do not impose technical means. Since MSB is a set of compulsory requirements for all systems [17] and presents a subset of information security standard requirements, formation of such a set of sets in cases of multiple security standards becomes even more complicated. Currently, organizations are solving this issue by applying risk analysis and risk management techniques, which allow them to evaluate business demands and existing environments, and to summarize the list of security requirements applicable to the organization. Unfortunately, such an approach is based on subjective factors, such as security expert knowledge, skills, and experience. Well known vendors, such as Microsoft [56] and Cisco [57], are publishing recommendations related to the configuration of their products. International associations, such as the Center of Internet Security [58], are publishing recommendations with a list of the most effective risk mitigation controls. However, such approaches are ad hoc-based and are not directly linked with existing security standards. MSB verification could be implemented in different ways, starting from the expert review [18], including information security consultant analysis. Authors of [18] conducted an explorative expert study to derive a set of COBIT 5 processes that could serve as a basis for an enterprise governance of IT implementation and discussed how this approach could contribute to complexity reduction. This research was based on an earlier [19] study, which was focused on identifying which practices (structures, processes, and relational mechanisms) an organization could leverage to ensure that IT governance becomes a reality in the organization. However, it is also necessary to state that both [18] and [19] concentrated on general IT management processes, rather than security MSB. Some other approaches utilize penetration testing or use of specific tools, such as vulnerability scanners, for potential security gap identification [59]. However, the use of tools will not link the identified gaps with applicable security standards.

In this article, we are presenting a holistic method for solving two different problems: MSB identification and its verification against controls implemented by the organization. The method is based on graph theory and graph optimization algorithms (vertex cover and subgraph isomorphism).

For MSB identification the use of a vertex cover algorithm is proposed. It is used for amending the created mapping graph, by removing from it specific vertexes. However, we have to ensure that only duplicated requirements will be removed. To achieve that we have two options:

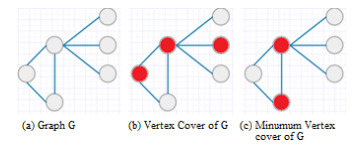
• to apply minimum weighted vertex cover algorithms in order to ensure those critical requirements having a lower value will be presented in a newly generated graph;
• to apply the selected minimum vertex cover algorithm with additional rules to ensure that higher level security requirements will not be overwritten by lower level requirements, and requirements without direct connections with another standard will not be removed.

The second option was selected for implementation for simplicity reasons. The following rules were specified to ensure prioritization of specific requirements:

• Restriction to remove requirements, with a connection to parent vertex but no links to other standards. To achieve that, additional null vertex to such vertex will be added.
• Additional evaluation of removed vertexes in order to ensure that vertexes without a direct connection to other standards are not removed from the graph. If such vertex were removed, we would restore them manually.

The method is formed of 4 main steps (schematic method representation is provided on Figure 3):

• represent information security standards’ requirements to be mapped as separate graphs;
• generate a new graph by linking requirements of N subgraphs (representing different information security standards);
• add a vertex to the vertexes with a single edge;
• apply minimum vertex cover algorithm.

After the vertex cover algorithm is applied, we have to ensure that vertexes without a direct connection to other standards that were removed from the graph are restored. The outcome of this process will be the MSB graph.

The formal MSB identification method described with the help of a Business Process Model and Notation (BPMN) diagram is presented in Figure 4.

In

Table 1. Minimum security baseline (MSB) identification method action description.

Action No.	Description
I	Standards’ requirements are presented hierarchically. If vertexes have edges between them that means that requirements are identical. Differentiation by coverage level is out of scope for this method feasibility verification. In case our task link directions are not important.
II	Generated graph is reviewed, and temporary vertexes are added. Additional vertexes are added to the graph in order to ensure that the minimum vertex cover algorithm will not remove existing vertexes that do not have direct connections with other standards.
III	The mapping graph is represented as an adjacency matrix for technical processing by a vertex cover algorithm.
IV	Vertex cover algorithm is applied. The result is presented in the form of rows. Since we assume that duplicated vertexes are identical, and the removal of any vertex would provide a suitable result, this leads to the situation when several similar solutions (several rows) can be generated. To present it as a graph, we extract identified vertexes and edges from the initial mapping graph.
V	Vertexes without a direct connection to other standards that were removed from the mapping graph are restored (the process is currently manual). Due to different levels of detail in various standards, the future approach could make use of additional criteria, which would allow removing vertexes, with a specified level of detail.

a detailed description of actions defined in Figure 4 is provided.

When the MSB graph is identified in the next step, we perform its verification against controls already deployed by the organization. As stated earlier, subgraph isomorphism algorithms are used for that task. In our case, it is not significantly important which subgraph isomorphism algorithm will be used, since our primary goal is to perform a feasibility study of such an approach and its practical applicability.

In this step, controls implemented by the organization are presented as a deployed control graph (DCG), which is compared to the received MSB graph to verify their alignment.

It is important to mention that the DCG graph may have stand-alone vertexes, i.e., not connected with any other vertexes, which is usually caused by inconsistency while developing the information security management system (ISMS). As such, it is necessary to ensure that all controls (even stand-alone) are verified, which is achieved by introducing two additional conditions.

For simplicity reasons, while implementing the subgraph isomorphism algorithm, any other vertex verification properties (e.g., name matching or properties matching) will not be used. Usage of additional verification properties potentially could make the approach more effective. However, it is not so important at this stage when just method feasibility is evaluated.

Because of the fact that the DCG graph could have stand-alone vertexes or small subgraphs as separate parts of the DCG graph, we have to ensure that all of them are compared against the MSB graph.

The formal MSB verification against deployed controls method description with the help of the BPMN diagram is presented in Figure 5.

In

Table 2. The formal MSB verification against deployed controls method actions description.

Action No.	Description
I	This action includes two main activities: Information gathering about controls deployed; Presentation of information gathered in the form of a graph. Information gathering could be done manually or by automation tools that can process Business Process Model and Notation (BPMN) or Event-Driven Process Chain (EPC) diagrams. The generated graph may have stand-alone vertexes, i.e., not connected with any other vertexes. The process of identification of links between controls in the organization is a complicated task and could be accelerated if it is known if the organization is compliant with one or another security standard.
II	MSB and deployed control graphs (DCGs) (or their representation form, like adjacency matrix, table) are imported to the graph processing tool, and the subgraph isomorphism algorithm is executed. If DCG graph has stand-alone vertexes or small subgraphs, then the subgraph isomorphism algorithm is executed for each of them separately.
III	Since a stand-alone vertex is isomorphic to any vertex of MSB, additional verification based on a specified criterion (e.g., semantic similarity) should be used. Error verification can be done automatically, by applying addition verification criteria and re-executing the subgraph isomorphism algorithm against subgraph or manually by a security specialist.
IV	Controls required by MSB but are not present in DCG are identified.

a detailed description of actions defined in Figure 5 is provided.

The method concept was tested experimentally in order to prove its feasibility for real-life applications. The test results are presented and discussed in the “Experimental Method Verification Results and Discussion” section.

4. Experimental Method Verification Results and Discussion

Three regulating documents were selected for mapping: ISO27002, PCI DSS, and a newly introduced GDPR. Mapping (see Figure 6) was based on the HITRUST CSF 9.1 framework [60], which provides a table-based mapping of the majority of modern information security standards and other regulating documents.

Each of the standards (ISO27002, PCI DSS, GDPR) was presented as a graph (sample presented in Figure 7). Cytoscape 3.6.1 application [61] was used for graph visualization.

Later, mapping of separately generated graphs from HITRUST CSF 9.1 framework was performed, although other mapping methods, like the expert-based approach, can be applied. The resulting graph (Figure 8) had 1267 vertexes (150 related to ISO27002 standard, 264 vertexes associated with PCI DSS standard, and 853 to GDPR) and 2512 edges.

Null vertexes were added in order to ensure that vertexes that do not have direct connections with other standards were not removed. Addition of null vertexes increased the size of the mapping graph by 463 vertexes.

The mapping graph was converted to the adjacency matrix by Cytoscape plug-in “Adj Exporter”. The resulting matrix (Figure 9) was saved in *.adj file.

In Figure 9, part A presents a small part of the generated adjacency matrix and part B provides a presentation of the whole matrix. Black dots on the screen provide information on graph components and connections between them. Part B view was created by an open source TreeView 3.0 Java application [62].

After the adjacency matrix was created, the vertex cover algorithm was applied. For our experiment, a C++ application developed by Dharwadker [63] implementing his proposed polynomial time, vertex cover algorithm was used. The application requires one to specify the desired size k of the resulting vertex cover. In our case, k was defined as equal to 2 in order to find all possible vertex covers. The result of vertex cover search was provided in a *.txt file and includes information on the minimum amount of vertexes and provides the list of all vertexes involved in a found vertex cover (Figure 10).

Since all obtained vertex covers with a minimum number of vertexes were equivalent, any of them could be selected for further processing. Based on the chosen vertex cover, unnecessary vertexes were removed from the mapping graph with the help of the Cytoscape application. As it can be seen, the number of vertexes was reduced significantly (from 1267 vertexes in the initial graph to 322 vertexes). The resulting MSB graph is presented in Figure 11.

For MSB verification against controls already deployed by the organization a hypothetical organization, ACME Corporation was used. It was assumed that it has already implemented logging and monitoring and backup requirements. The DCG graph for ACME Corporation was created in Cytoscape tool (Figure 12).

For identifying subgraph isomorphism between the received MSB graph and the created DCG graph for ACME Corporation, the Cytoscape plug-in “CyIsomorphism” was used [64]. The DCG graph was evaluated against the MSB graph to identify pattern similarity. In our experiment, only information about vertexes and their connections was used. Because of that more than one potential alignment was recognized by the Cytoscape tool. In order to solve this issue, additional criteria should be used in future. Manual review of alignments was performed during our experiment. The final result of DCG verification against MSB is provided on Figure 13.

The controls already deployed by ACME Corporation are shown on MSB in a yellow colour. As can be seen, the presentation of MSB in the form of the graph provides a valuable tool for a security officer for evaluating the current state of ISMS.

The performed experiment has proved the concept that vector cover and subgraph isomorphism can be used for optimizing the process of standards mapping, removing duplicated requirements, and evaluating the current state of security controls against the desired MSB level.

5. Conclusions and Future Work

The analysis performed has shown that companies are facing the steadily increasing regulating pressure in the sphere of information security. It can lead to a situation where the same requirements coming from different standards in the same organization might be covered by different technical solutions, thus increasing the company’s expenses. The problem can be solved by the consequent mapping of compulsory standards and further determination of MSB. Unfortunately, currently available methods for MSB identification are mainly expert-based, which are not affordable for SMEs and can be subjective.

A method for solving two different problems—MSB identification and its verification against controls already implemented by the organization—was proposed. The method is based on graph theory and graph optimization algorithms: minimum vertex cover and subgraph isomorphism, respectively. The method was formally described and later experimentally verified.

For proof of method feasibility, three regulating documents (ISO27002, PCI DSS, and GDPR) were presented as graphs and later mapped, forming an initial graph with 1276 vertexes. The initial graph was amended according to the method restrictions, and a new polynomial time, vertex cover algorithm was applied. The resulting MSB graph of 322 vertexes was compared against the graph, representing controls deployed by a fictional ACME Corporation, and coinciding controls were identified. The experimental test has shown the following:

• Application of graph theory and graph optimization algorithms, such as minimum vertex cover algorithms, to the standards mapping graph can be effectively used for removing duplicating requirements and ensuring spending minimization on information security;
• The method is capable of processing original graphs with relatively high numbers of vertexes, and the optimization rate of removed duplicated vertexes has reached 74.5% in the case of our experiment and can be even higher if a more significant number of regulating documents have to be applied;
• Application of isomorphism features provides a user-friendly way of evaluating the current state of controls deployed by the organization against the desired MSB state.

Further research on the topic should be concentrated on minimum vertex cover algorithm and subgraph isomorphism algorithm selection and optimization for better performance, automation of actions that currently are made manually, and integration of the proposed method with our previously proposed approaches based on security ontology fostering symbiosis of these two approaches.