Characteristics of Coherent Optical Phonons in a Hexagonal YMnO3 Thin Film
Abstract
:1. Introduction
2. Generation Mechanisms of Coherent Phonons
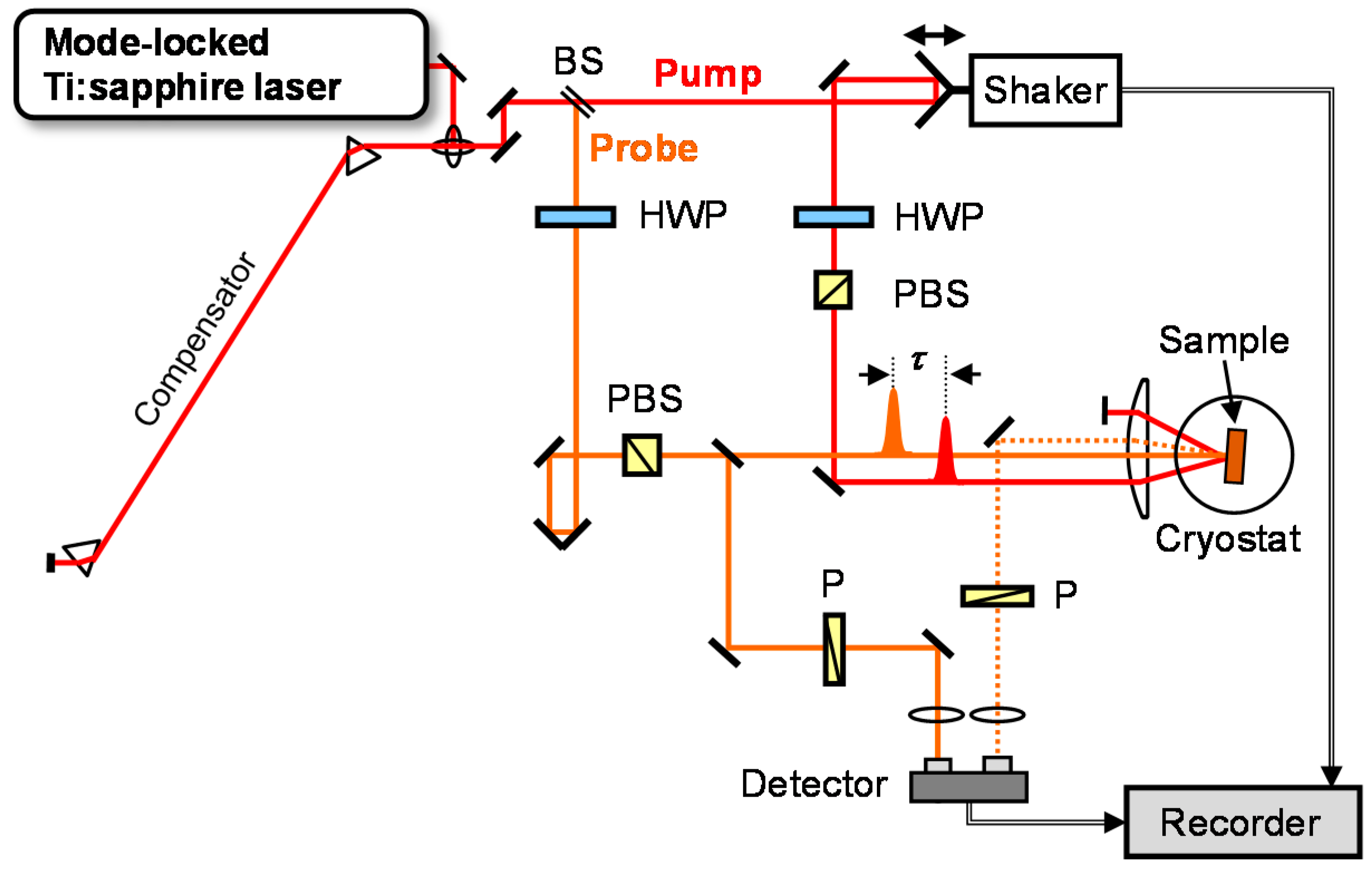
3. Experimental Procedure of Time-Resolved Pump-Probe Spectroscopy
4. Results and Discussions
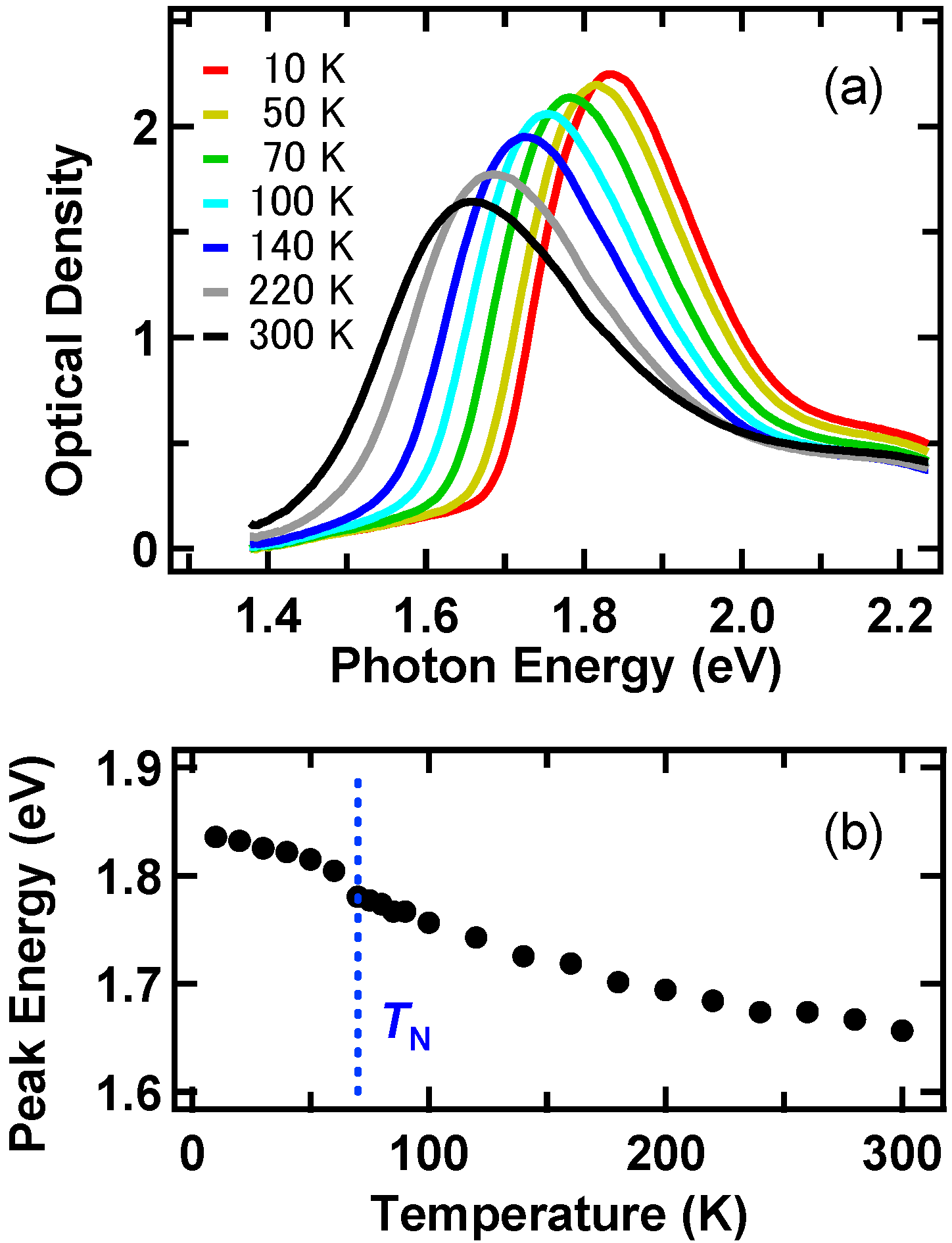
4.1. Optical Transition Property
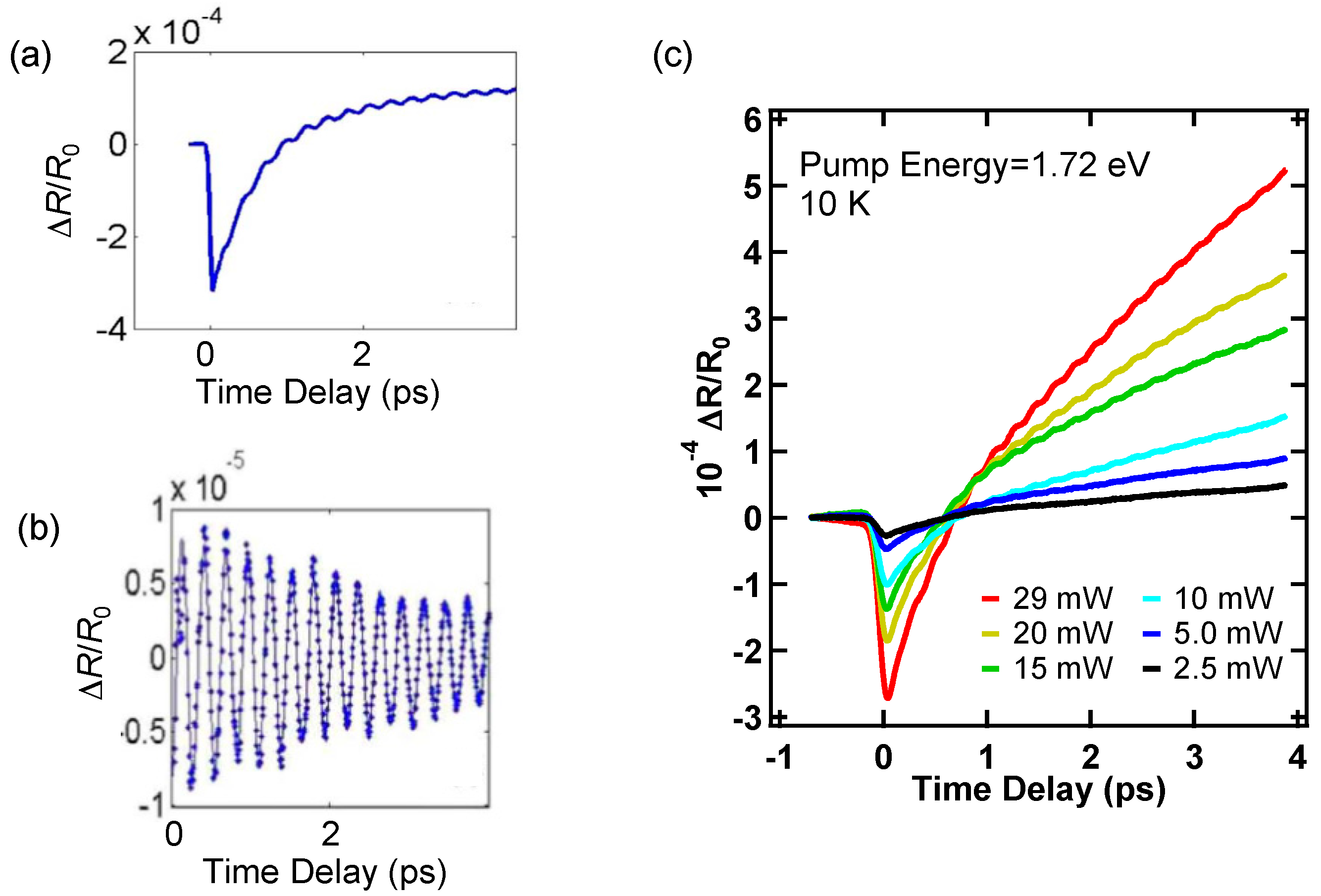
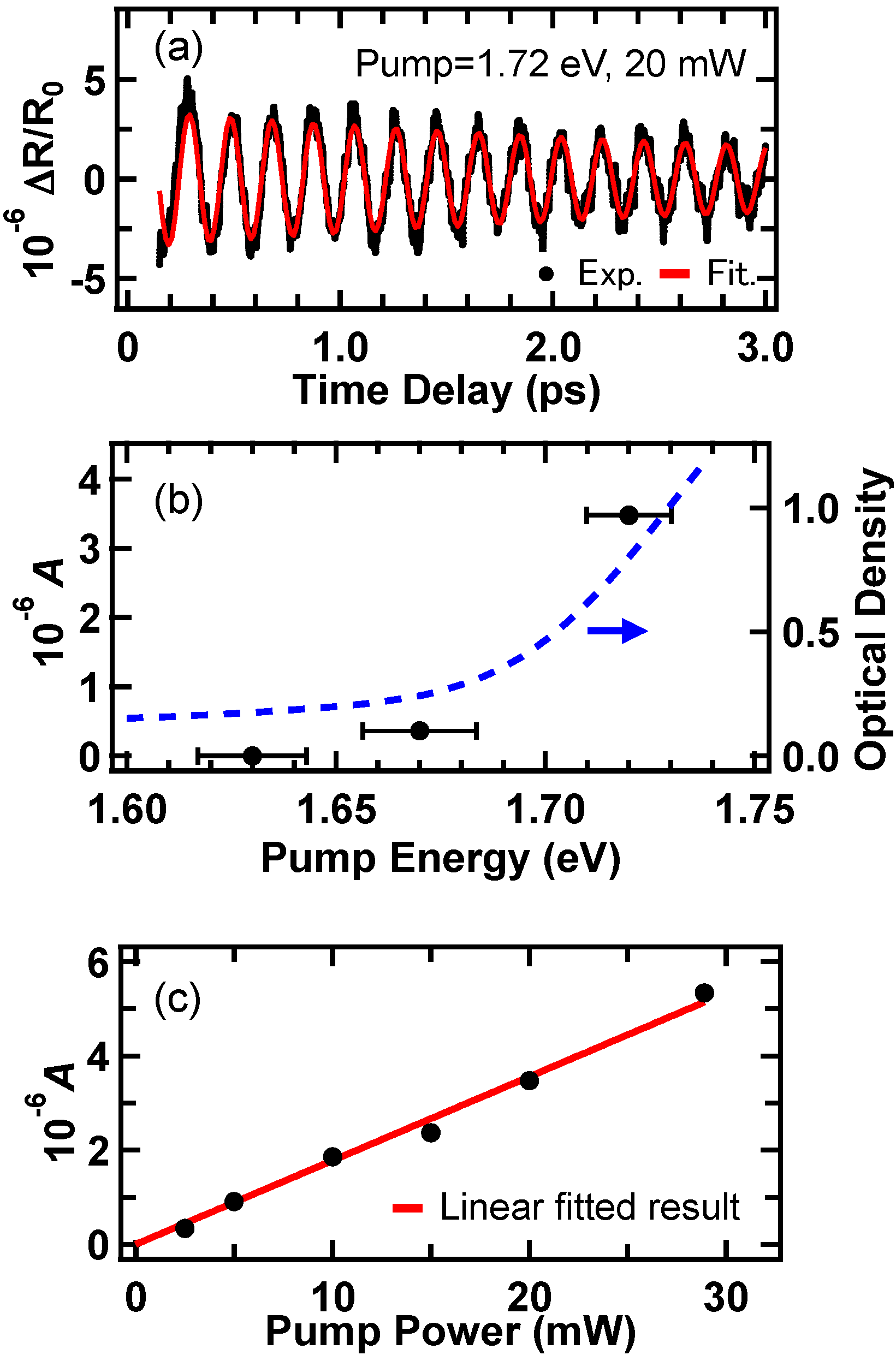
4.2. Observation of Coherent Optical Phonons
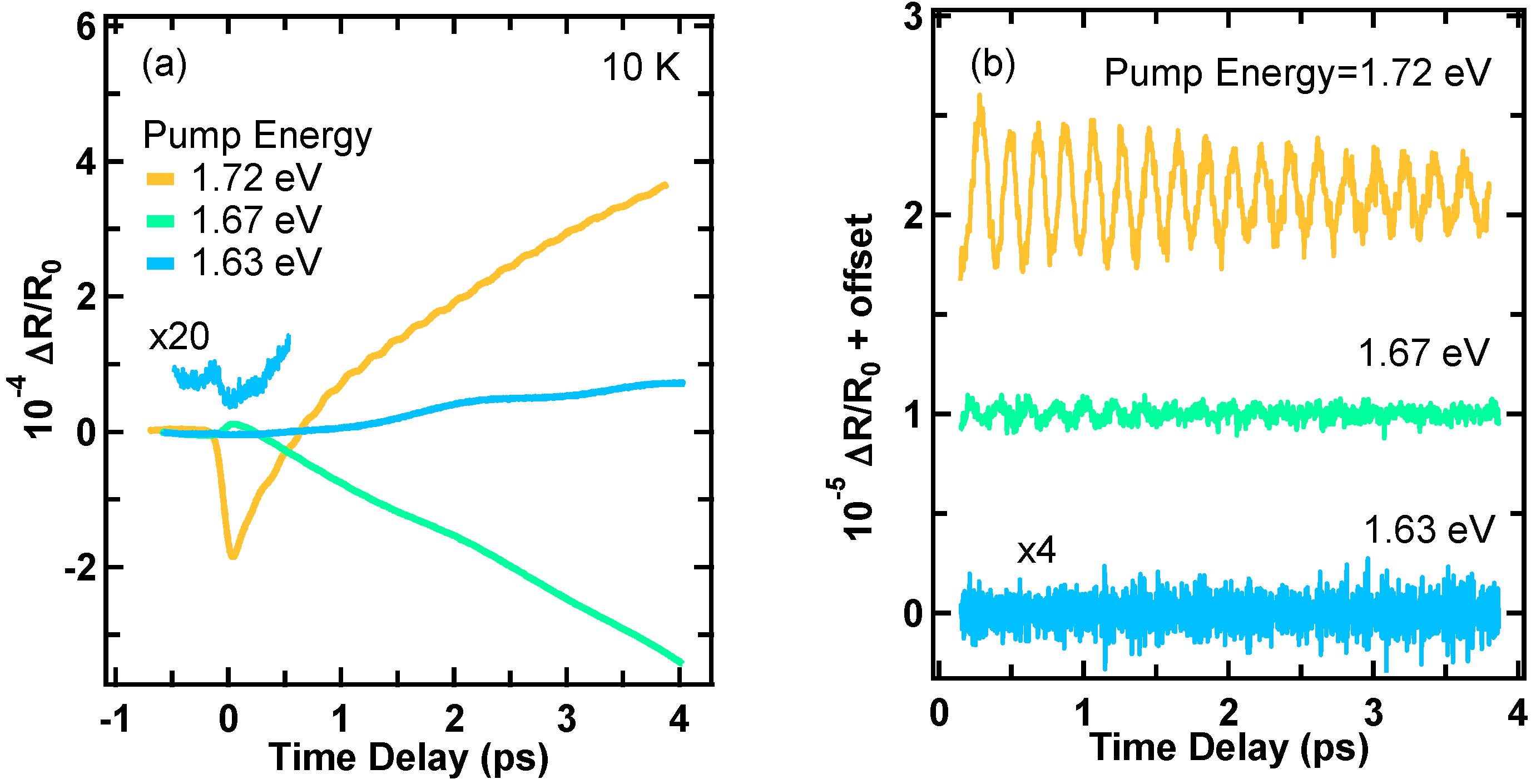
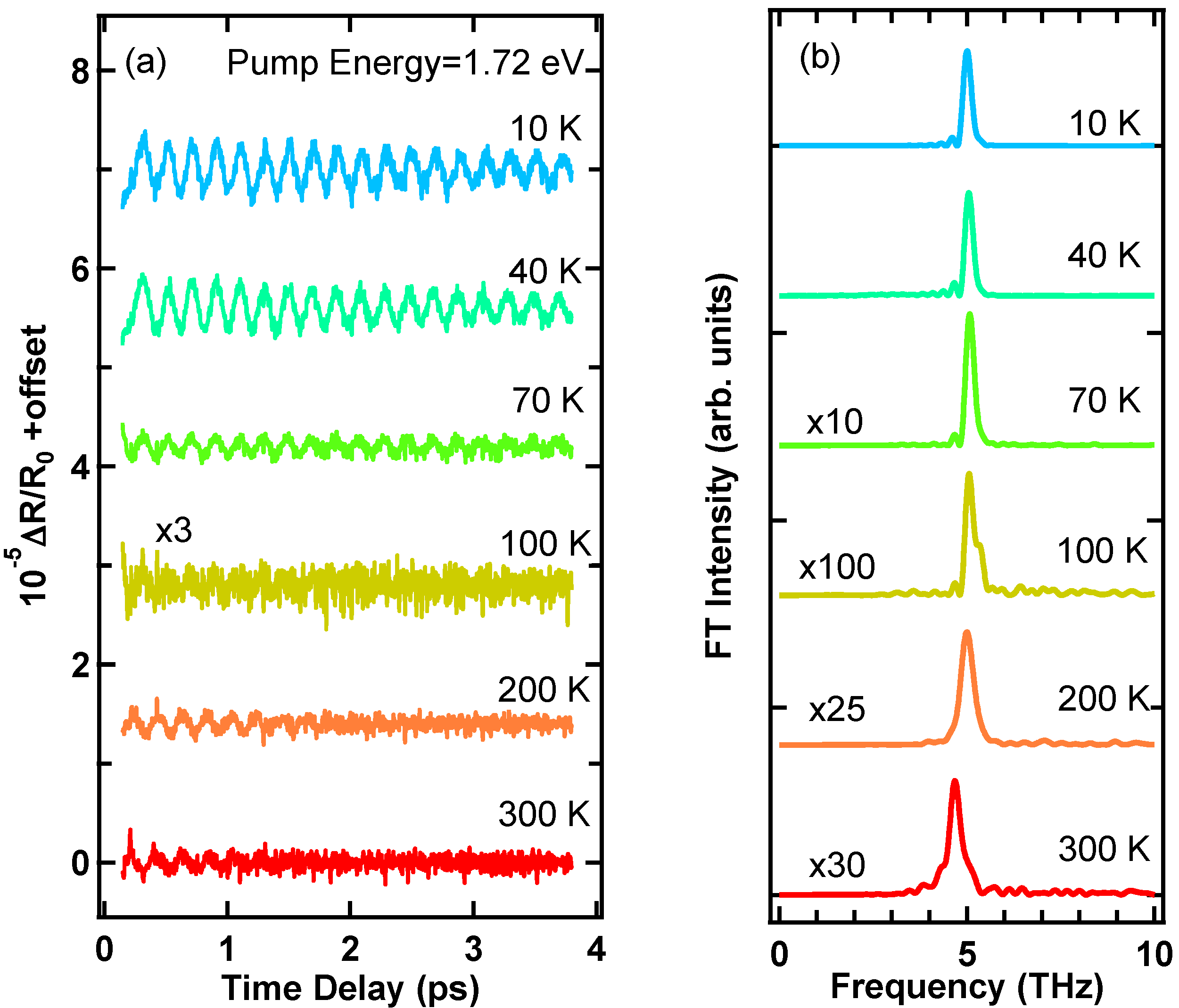
4.3. Temperature Dependence of Coherent Optical Phonons
4.4. Ultrafast Incoherent Responses of Excited Electron States
5. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Shah, J. Ultrafast Spectroscopy of Semiconductors and Semiconductor Nanostructures, 2nd ed.; Springer: Berlin, Germany, 1999. [Google Scholar]
- Ulbricht, R.; Hendry, E.; Shan, J.; Heinz, T.F.; Born, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 2011, 83, 543–586. [Google Scholar] [CrossRef] [Green Version]
- Eerenstein, W.; Mathur, N.D.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.F.; Liu, J.-M.; Ren, Z.F. Multiferroicity: The coupling between magnetic and polarization orders. Adv. Phys. 2009, 58, 321–448. [Google Scholar] [CrossRef]
- Fiebig, M.; Lottermoser, T.; Meier, D.; Trassin, M. The evolution of multiferroics. Nat. Rev. Mat. 2016, 1, 1–14. [Google Scholar] [CrossRef]
- Kubacka, T.; Johnson, J.A.; Hoffmann, M.C.; Vicario, C.; de Jong, S.; Beaud, P.; Grübel, S.; Huang, S.-W.; Huber, L.; Patthey, L.; et al. Large-Amplitude Spin Dynamics Driven by a THz Pulse in Resonance with an Electromagnon. Science 2014, 343, 1333–1336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yakel, H.L.; Koehler, W.C.; Bertaut, E.F.; Forrat, E.F. On the Crystal Structure of the Manganese (III) Trioxides of the Heavy Lanthanides and Yttrium. Acta Cryst. 1963, 16, 957–962. [Google Scholar] [CrossRef]
- Huang, Z.J.; Cao, Y.; Sun, Y.Y.; Xue, Y.Y.; Chu, C.W. Coupling between the ferroelectric and antiferromagnetic orders in YMnO3. Phys. Rev. B 1997, 56, 2623–2626. [Google Scholar] [CrossRef]
- Katsufuji, T.; Mori, S.; Masaki, M.; Moritomo, Y.; Yamamoto, N.; Takagi, H. Dielectric and magnetic anomalies and spin frustration in hexagonal RMnO3 (R = Y, Yb, and Lu). Phys. Rev. B 2001, 64, 104419. [Google Scholar] [CrossRef]
- Fiebig, M.; Lottermoser, T.; Fröhlich, D.; Goltsev, A.V.; Pisarev, R.V. Observation of coupled magnetic and electric domains. Nature 2002, 419, 818–820. [Google Scholar] [CrossRef]
- Lottermoser, T.; Lonkai, T.; Amann, U.; Hohwein, D.; Ihringer, J.; Fiebig, M. Magnetic phase control by an electric field. Nature 2004, 430, 541–544. [Google Scholar] [CrossRef]
- Choi, W.S.; Moon, S.J.; Seo, S.S.A.; Lee, D.; Lee, J.H.; Murugavel, P.; Noh, T.W.; Lee, Y.S. Optical spectroscopic investigation on the coupling of electronic and magnetic structure in multiferroic hexagonal RMnO3 (R = Gd, Tb, Dy, and Ho) thin films. Phys. Rev. B 2008, 78, 054440. [Google Scholar] [CrossRef]
- Lee, S.; Pirogov, A.; Han, J.H.; Park, J.-G.; Hoshikawa, A.; Kamiyama, T. Direct observation of a coupling between spin, lattice and electric dipole moment in multiferroic YMnO3. Phys. Rev. B 2005, 71, 180413. [Google Scholar] [CrossRef]
- Lee, S.; Pirogov, A.; Kang, M.; Jang, K.-H.; Yonemura, M.; Kamiyama, T.; Cheong, S.-W.; Gozzo, F.; Shin, N.; Kimura, H.; et al. Giant magneto-elastic coupling in multiferroic hexagonal manganites. Nature 2008, 451, 805–809. [Google Scholar] [CrossRef] [PubMed]
- Fabrèges, X.; Petit, S.; Mirebeau, I.; Pailhès, S.; Pinsard, L.; Forget, A.; Fernandez-Diaz, M.T.; Porcher, F. Spin-Lattice Coupling, Frustration, and Magnetic Order in Multiferroic RMnO3. Phys. Rev. Lett. 2009, 103, 067204. [Google Scholar] [CrossRef]
- Singh, A.K.; Patnaik, S.; Kaushik, S.D.; Siruguri, V. Dominance of magnetoelastic coupling in multiferroic hexagonal YMnO3. Phys. Rev. B 2010, 81, 184406. [Google Scholar] [CrossRef]
- Fukumura, H.; Matsui, S.; Harima, H.; Kisoda, K.; Takahashi, T.; Yoshimura, T.; Fujimura, N. Raman scattering studies on multiferroic YMnO3. J. Phys. Condens. Matter 2007, 19, 365239. [Google Scholar] [CrossRef] [PubMed]
- Zaghrioui, M.; Phuoc, V.T.; Souza, R.A.; Gervais, M. Polarized reflectivity and lattice dynamics calculation of multiferroic YMnO3. Phys. Rev. B 2008, 78, 184305. [Google Scholar] [CrossRef]
- Vermette, J.; Jandl, S.; Mukhin, A.A.; Ivanov, V.Y.; Balbashov, A.; Gospodinov, M.M.; Pinsard-Gaudart, L. Raman study of the antiferromagnetic phase transitions in hexagonal YMnO3 and LuMnO3. J. Phys. Condens. Matter 2010, 22, 356002. [Google Scholar] [CrossRef]
- Toulouse, C.; Liu, J.; Gallais, Y.; Measson, M.-A.; Sacuto, A.; Cazayous, M.; Chaix, L.; Simonet, V.; de Brion, S.; Pinsard-Godart, L.; et al. Lattice and spin excitations in multiferroic h-YMnO3. Phys. Rev. B 2014, 89, 094415. [Google Scholar] [CrossRef]
- Lim, D.; Averitt, R.D.; Demsar, J.; Taylor, A.J.; Hur, N.; Cheong, S.W. Coherent acoustic phonons in hexagonal manganite LuMnO3. Appl. Phys. Lett. 2003, 83, 4800–4802. [Google Scholar] [CrossRef]
- Lou, S.-T.; Zimmermann, F.M.; Bartynski, R.A.; Hur, N.; Cheong, S.-W. Femtosecond laser excitation of coherent optical phonons in ferroelectric LuMnO3. Phys. Rev. B 2009, 79, 214301. [Google Scholar] [CrossRef]
- Jang, K.-J.; Lee, H.-G.; Lee, S.; Ahn, J.; Ahn, J.S.; Hur, N.; Cheong, S.-W. Strong spin-lattice coupling in multiferroic hexagonal manganite YMnO3 probed by ultrafast optical spectroscopy. Appl. Phys. Lett. 2010, 97, 031914. [Google Scholar] [CrossRef]
- Jang, K.-J.; Lim, J.; Ahn, J.; Kim, J.-H.; Yee, K.-J.; Ahn, J.S.; Cheong, S.-W. Ultrafast IR spectroscopic study of coherent phonons and dynamic spin–lattice coupling in multiferroic LuMnO3. New J. Phys. 2010, 12, 023017. [Google Scholar] [CrossRef]
- Shih, H.C.; Chen, L.Y.; Luo, C.W.; Wu, K.H.; Lin, J.-Y.; Juang, J.Y.; Uen, T.M.; Lee, J.M.; Chen, J.M.; Kobayashi, T. Ultrafast thermoelastic dynamics of HoMnO3 single crystals derived from femtosecond optical pump-probe spectroscopy. New J. Phys. 2011, 13, 053003. [Google Scholar] [CrossRef]
- Wang, Y.T.; Luo, C.W.; Kobayashi, T. Understanding Multiferroic Hexagonal Manganites by Static and Ultrafast Optical Spectroscopy. Adv. Condens. Mater. Phys. 2013, 2013, 104806. [Google Scholar] [CrossRef]
- Hasegawa, T.; Fujimura, N.; Nakayama, M. Ultrafast dynamics of coherent optical phonon correlated with the antiferromagnetic transition in a hexagonal YMnO3 epitaxial film. Appl. Phys. Lett. 2017, 111, 192901. [Google Scholar] [CrossRef]
- Iliev, M.N.; Lee, H.-G.; Popov, V.N.; Abrashev, M.V.; Hamed, A.; Meng, R.L.; Chu, C.W. Raman- and infrared-active phonons in hexagonal YMnO3: Experiment and lattice-dynamical calculations. Phys. Rev. B 1997, 56, 2488–2494. [Google Scholar]
- Zeiger, H.J.; Vidal, J.; Cheng, T.K.; Ippen, E.P.; Dresselhaus, G.; Dresselhaus, M.S. Theory for displacive excitation of coherent phonons. Phys. Rev. B 1992, 45, 768–778. [Google Scholar] [CrossRef]
- Yan, Y.-X.; Nelson, K.A. Impulsive stimulated light scattering. I. General theory. J. Chem. Phys. 1987, 87, 6240–6256. [Google Scholar] [CrossRef]
- Yan, Y.-X.; Nelson, K.A. Impulsive stimulated light scattering. II. Comparison to frequency-domain light-scattering spectroscopy. J. Chem. Phys. 1987, 87, 6257–6265. [Google Scholar] [CrossRef]
- Garrett, G.A.; Albrecht, T.F.; Whitaker, J.F.; Merlin, R. Coherent THz Phonons Driven by Light Pulses and the Sb Problem: What is the Mechanism? Phys. Rev. Lett. 1996, 77, 3661–3664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gulde, S.; Jochim, S.; Moll, N.; Mahrt, R.F. A pump-and-probe method for the characterization of nonlinear material parameters within Fabry-Pérot microcavities. J. Appl. Phys. 2006, 100, 043112. [Google Scholar] [CrossRef]
- Hasegawa, T.; Takagi, Y.; Nakayama, M. Electric field effects on excitonic quantum beats in a single quantum well embedded in a GaAs/AlAs superlattice. Phys. Rev. B 2011, 83, 205309. [Google Scholar] [CrossRef]
- Nakayama, M.; Furukawa, Y.; Maeda, K.; Yoshimura, T.; Uga, H.; Fujimura, N. Correlation between the intra-atomic Mn3+ photoluminescence and antiferromagnetic transition in an YMnO3 epitaxial film. Appl. Phys. Express 2014, 7, 023002. [Google Scholar] [CrossRef]
- Shigemitsu, N.; Sakata, H.; Ito, D.; Yoshimura, T.; Ashida, A.; Fujimura, N. Pulsed-Laser-Deposited YMnO3 Epitaxial Films with Square Polarization-Electric Field Hysteresis Loop and Low-Temperature Growth. Jpn. J. Appl. Phys. 2004, 43, 6613–6616. [Google Scholar] [CrossRef]
- Jin, Z.; Ma, H.; Li, G.; Xu, Y.; Ma, G.; Cheng, Z. Ultrafast dynamics of the Mn3+ d-d transition and spin-lattice interaction in YMnO3 film. Appl. Phys. Lett. 2012, 100, 021106. [Google Scholar] [CrossRef]
- Kalashnikova, A.M.; Pisarev, R.V. Electronic Structure of Hexagonal Rare-Earth Manganites RMnO3. JETP Lett. 2003, 78, 143–147. [Google Scholar] [CrossRef]
- Choi, W.S.; Kim, D.G.; Seo, S.S.A.; Moon, S.J.; Lee, D.; Lee, J.H.; Lee, H.S.; Cho, D.-Y.; Lee, Y.S.; Murugavel, P.; et al. Electronic structures of hexagonal RMnO3 (R = Gd, Tb, Dy, and Ho) thin films: Optical spectroscopy and first-principles calculations. Phys. Rev. B. 2008, 77, 045137. [Google Scholar] [CrossRef]
- Wu, K.H.; Chen, H.-J.; Chen, Y.T.; Hsieh, C.C.; Luo, C.W.; Uen, T.M.; Juang, J.Y.; Lin, J.-Y.; Kobayashi, T.; Gospodinov, M. Marked enhancement of Néel temperature in strained YMnO3 thin films probed by femtosecond spectroscopy. EPL 2011, 94, 27006. [Google Scholar] [CrossRef]
- Rai, R.C.; Cao, J.; Musfeldt, J.L.; Kim, S.B.; Cheong, S.-W.; Wei, X. Spin-charge coupling and the high-energy magnetodielectric effect in hexagonal HoMnO3. Phys. Rev. B 2007, 75, 184414. [Google Scholar] [CrossRef]
- Hase, M.; Mizoguchi, K.; Nakashima, S. Generation of coherent THz phonons in GeTe ferroelectrics. J. Lumin. 2000, 87–89, 836–839. [Google Scholar] [CrossRef]
- Thomsen, C.; Strait, J.; Vardeny, Z.; Maris, H.J.; Tauc, J.; Hauser, J.J. Coherent Phonon Generation and Detection by Picosecond Light Pulses. Phys. Rev. Lett. 1984, 53, 989. [Google Scholar] [CrossRef]





© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasegawa, T. Characteristics of Coherent Optical Phonons in a Hexagonal YMnO3 Thin Film. Appl. Sci. 2019, 9, 704. https://doi.org/10.3390/app9040704
Hasegawa T. Characteristics of Coherent Optical Phonons in a Hexagonal YMnO3 Thin Film. Applied Sciences. 2019; 9(4):704. https://doi.org/10.3390/app9040704
Chicago/Turabian StyleHasegawa, Takayuki. 2019. "Characteristics of Coherent Optical Phonons in a Hexagonal YMnO3 Thin Film" Applied Sciences 9, no. 4: 704. https://doi.org/10.3390/app9040704
APA StyleHasegawa, T. (2019). Characteristics of Coherent Optical Phonons in a Hexagonal YMnO3 Thin Film. Applied Sciences, 9(4), 704. https://doi.org/10.3390/app9040704



