A Time–Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform
Abstract
1. Introduction
2. Principles
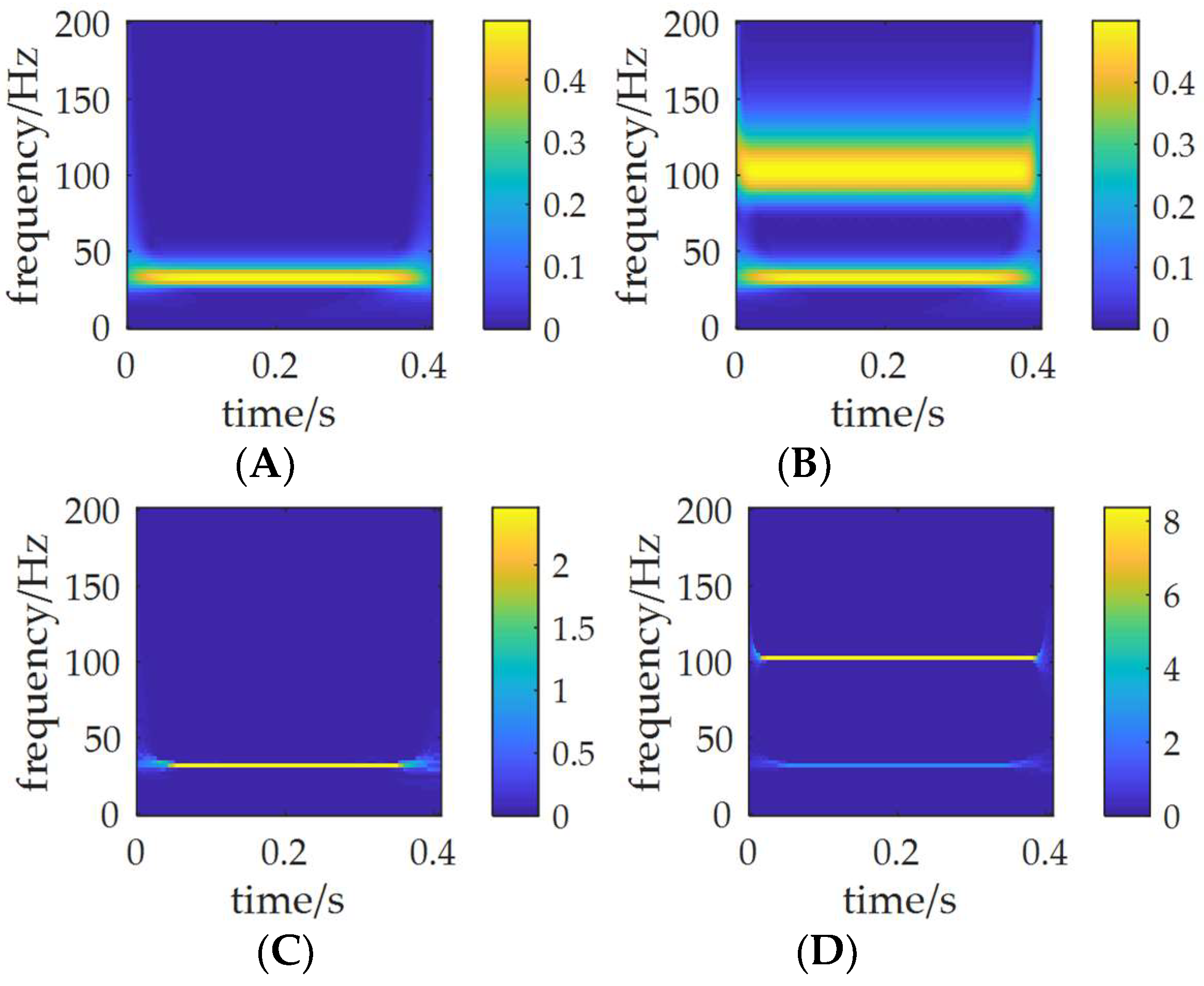
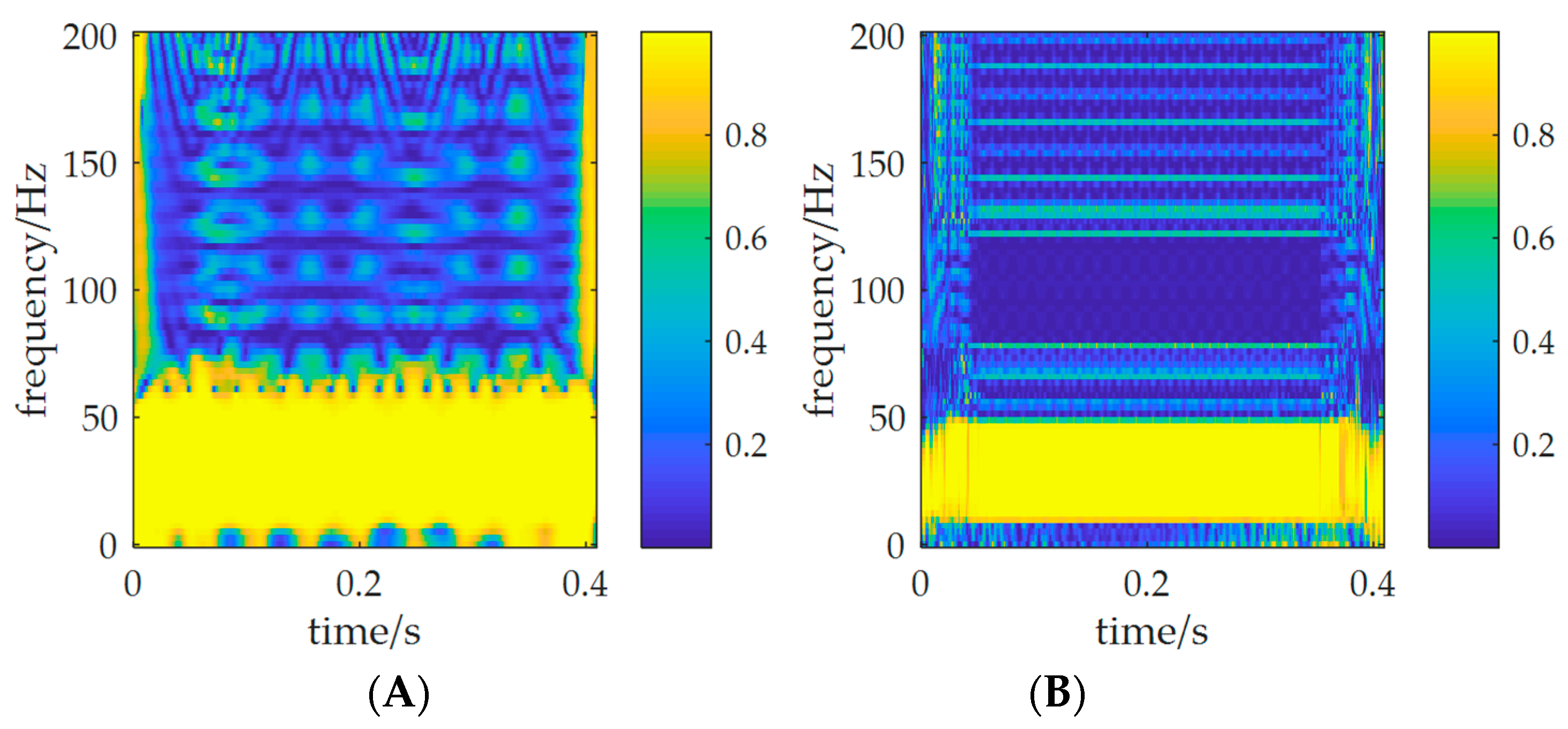
2.1. S Transform (ST)
2.2. Synchrosqueezed S Transform (SSST)
2.3. Time Series Decomposition Algorithm (TD)
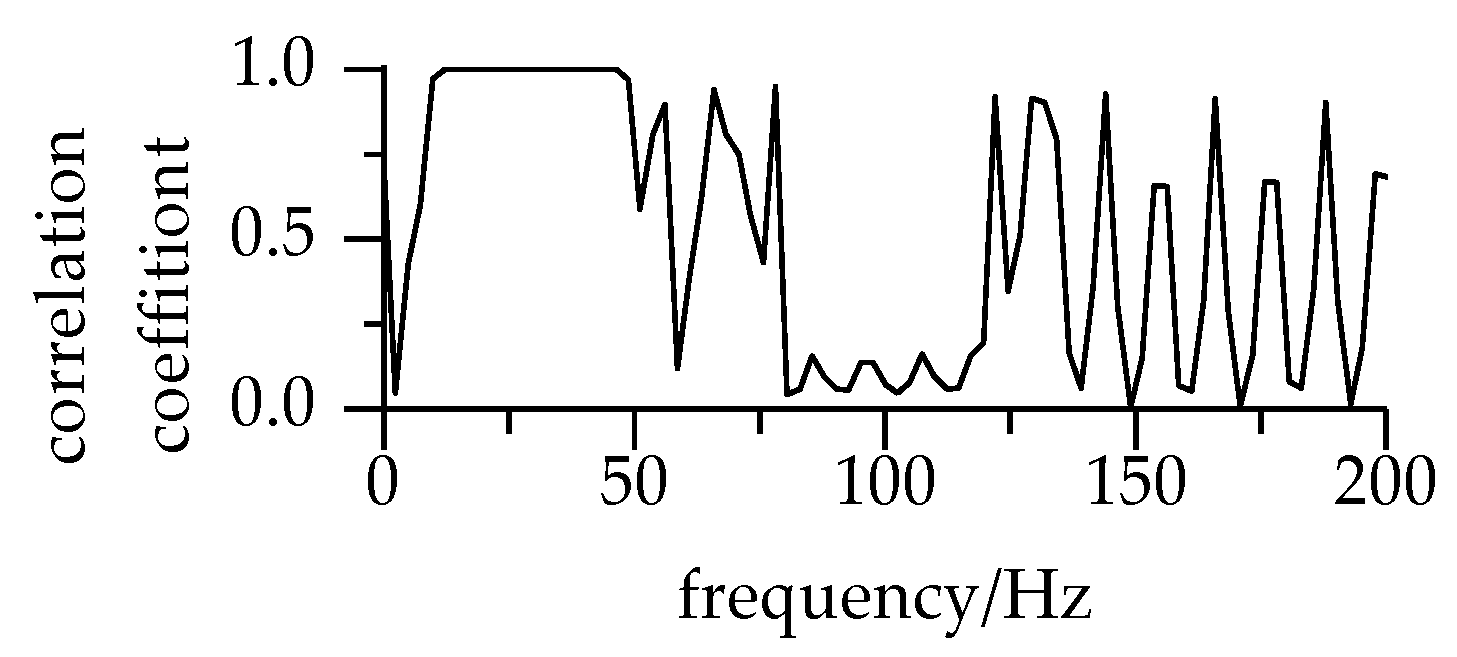
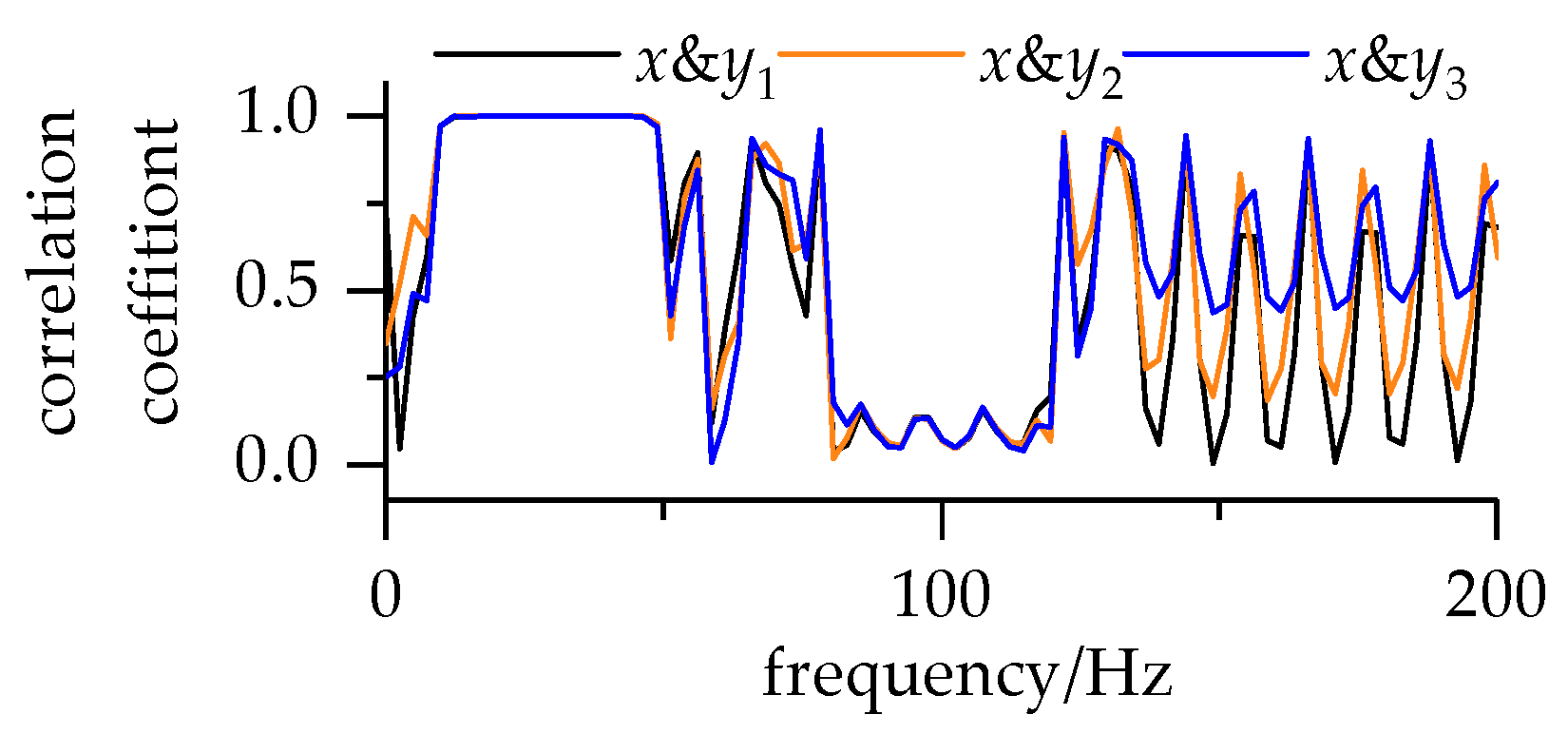
2.4. Correlation Analysis
2.5. Steps of the SSST-TD TF Correlation Analysis
- (1)
- For the time domain signal and , obtain the time–frequency spectrum by the SSST.
- (2)
- Perform time series decomposition on the time–frequency spectrum. That is, the inverse Fourier transform is applied to the frequency-axis of the SSST to obtain the two-dimensional complex valued time series matrix.
- (3)
- Carry out correlation analysis on each local time b between the two-dimensional time series matrix of and , thus getting the local correlation between the signals.
- (4)
- Observe the time–frequency distributions of the signals in the ST/SSST time–frequency spectrum and then analyze and judge the local correlation between the signals.
3. Synthetic Examples
3.1. Simulation of Cosine Signals
3.2. Simulation of Different Phase Signals
3.3. Simulation of Signals With Noise
3.4. Simulation of Non-Stationary Signals
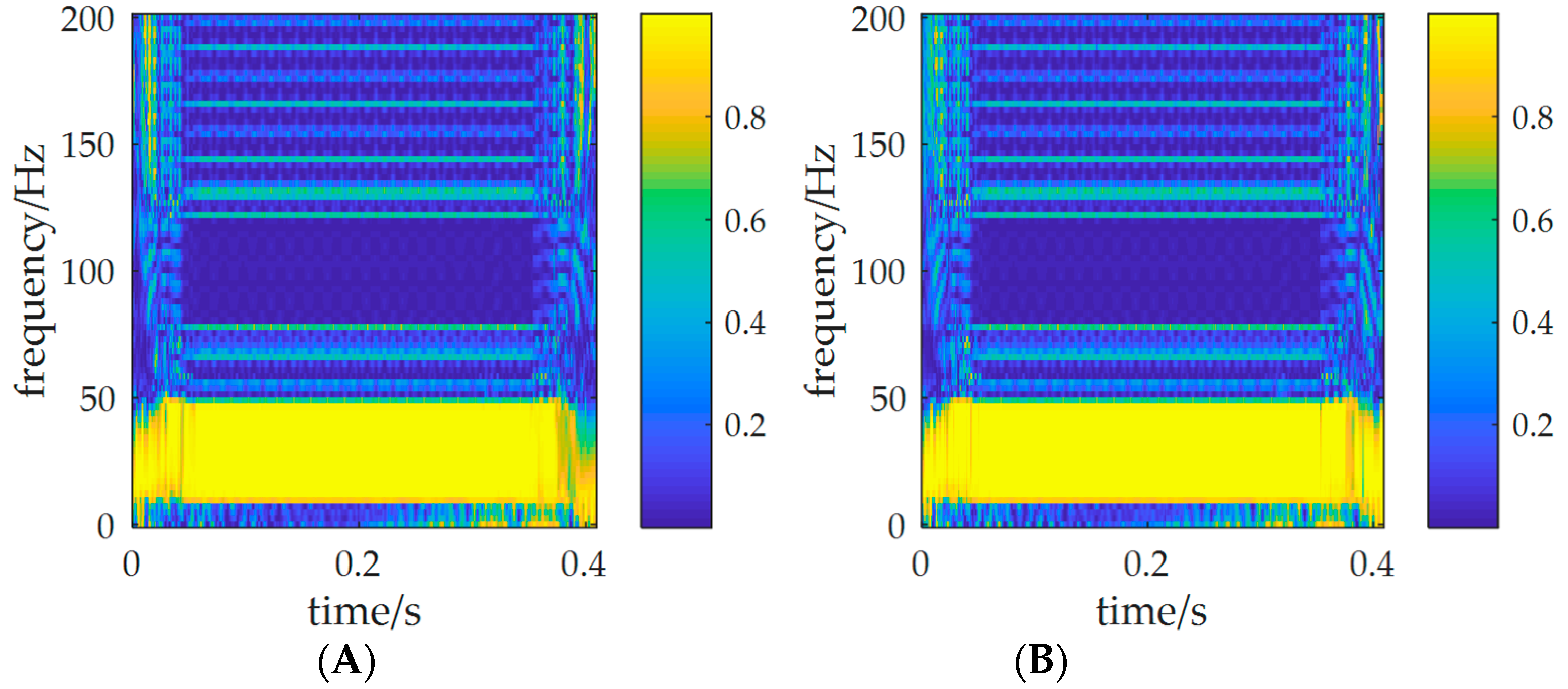
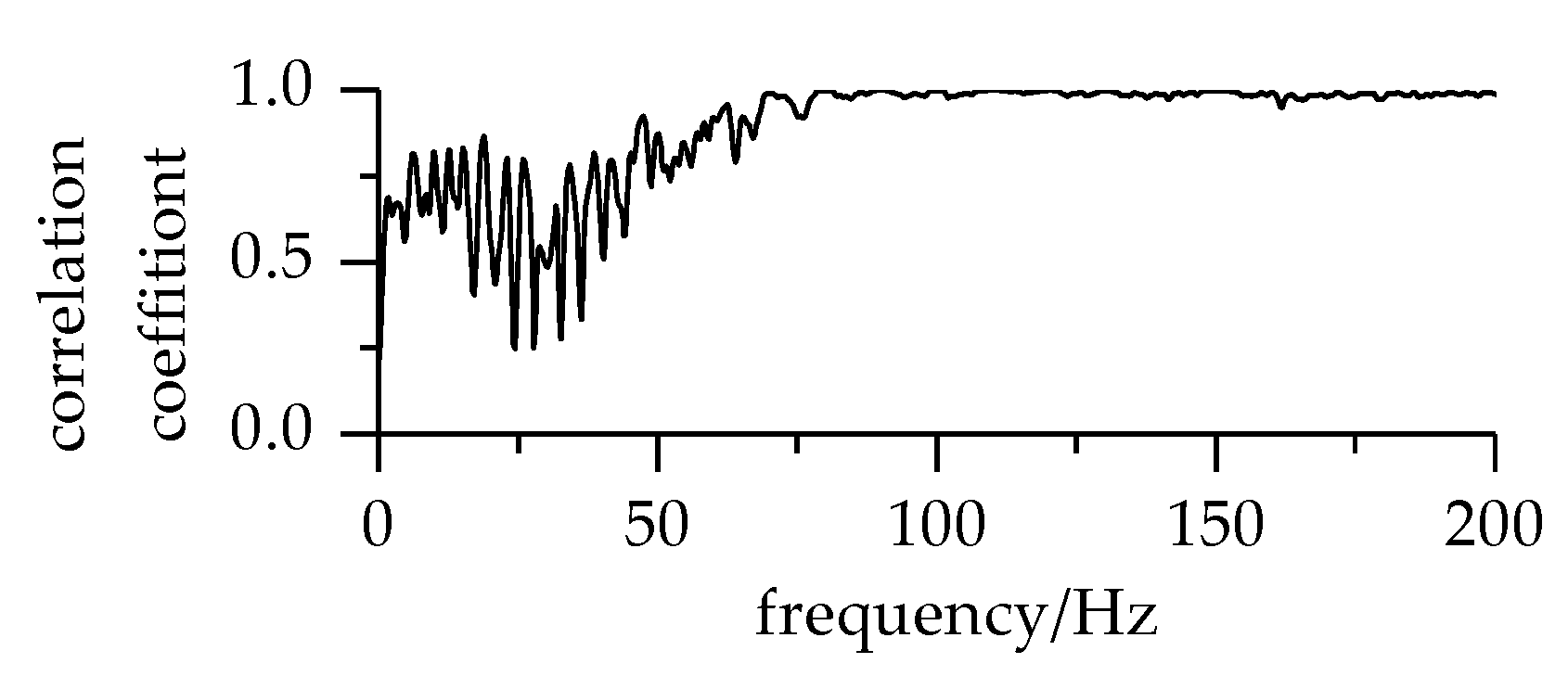
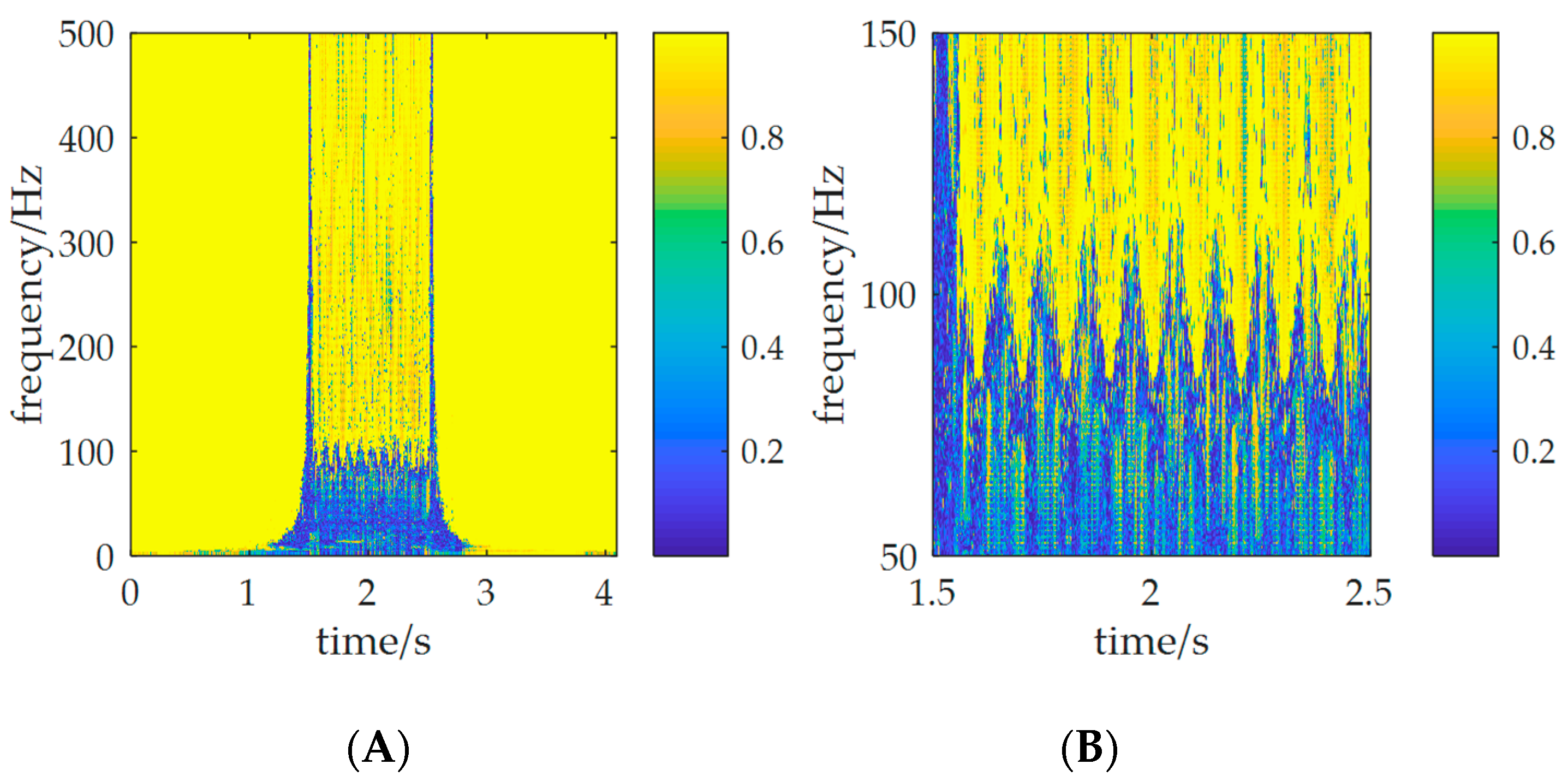
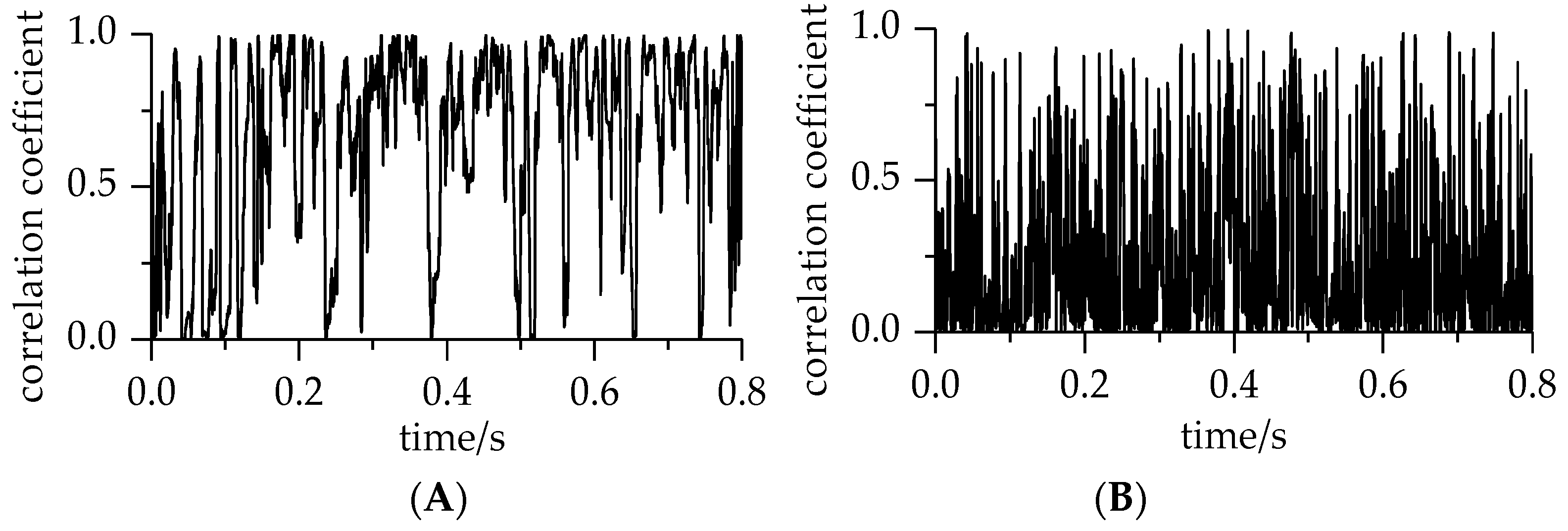
4. Gearbox Noise Signal Analysis
4.1. Experimental Equipment
4.2. Experimental Signal Analysis
5. Conclusions
- 1
- For stationary signals, both the traditional correlation and the SSST-TD TF correlation methods can identify the correlations between signals, and the SSST-TD TF correlation method can also obtain the correlation as it changes with time and frequency.
- 2
- Noise and the phase will affect the correlation coefficient. The traditional correlation method cannot recognize the influence of the phase, but the SSST-TD TF correlation method can get the effect of the phase of the cosine signals.
- 3
- For time-varying signals, the correlation between the signals cannot be recognized by the traditional correlation method. The SSST-TD TF correlation method can obtain the correlation of non-stationary signals and can also reflect the time-varying and frequency-varying characteristics between the signals.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Derivation of the Formula of Inverse SSST
References
- Darsena, D.; Gelli, G.; Paura, L.; Verde, F. Blind Channel Shortening for Space-Time-Frequency Block Coded MIMO-OFDM Systems. IEEE Trans. Wireless Commun. 2012, 11, 1022–1033. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, Z.; Li, R.; Gao, X.; Jin, J. Survey on statistical dependent source separation model and algorithms. Control Decision 2015, 30, 1537–1545. [Google Scholar] [CrossRef]
- Liang, M.; Xi-Hai, L.; Wan-Gang, Z.; Dai-Zhi, L. The generalized cross-correlation Method for time delay estimation of infrasound signal. In Proceedings of the Fifth International Conference on Instrumentation & Measurement, Computer, Communication, and Control (IMCCC), Qinhuangdao, China, 18–20 September 2015; pp. 1320–1323. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, The Sparse Way, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Zhang, X.; Zhao, J. Application of the DC Offset Cancellation Method and S Transform to Gearbox Fault Diagnosis. Appl. Sci. 2017, 7, 207. [Google Scholar] [CrossRef]
- Suzuki, T.; Matsui, H.; Choi, S.; Sasaki, O. Low-coherence interferometry based on continuous wavelet transform. Opt Commun 2013, 311, 172–176. [Google Scholar] [CrossRef]
- Zhang, Z.; Leng, Y.; Yang, Y.; Xiao, X.; Ge, S. Comparative study on wavelet coherence and HHT coherence. In Proceedings of the IEEE International Congress on Image & Signal Processing, Dalian, China, 14–16 October 2014; pp. 867–872. [Google Scholar] [CrossRef]
- Pinnegar, C.R.; Mansinha, L. The S-transform with windows of arbitrary and varying shape. Geophys. 2003, 68, 381–385. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Sun, S.; Hu, Y.; Feng, J. A High-Precision Time-Frequency Entropy Based on Synchrosqueezing Generalized S-Transform Applied in Reservoir Detection. Entropy 2018, 20, 428. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, W.; Li, P.; Yang, S.; Tian, Y. An Ultrahigh Frequency Partial Discharge Signal De-Noising Method Based on a Generalized S-Transform and Module Time-Frequency Matrix. Sensors 2016, 16, 941. [Google Scholar] [CrossRef]
- Daubechies, I.; Wang, Y.; Wu, H.T. ConceFT: Concentration of Frequency and Time via a multitapered synchrosqueezed transform. Philos. Trans. Math. Phys. Eng. Sci. 2015, 374, 2065. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Gao, J.; Wang, Z. Time-Frequency Analysis of Seismic Data Using Synchrosqueezing Transform. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2042–2044. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Liu, N.; Jiang, X. High-Resolution Seismic Time-Frequency Analysis Using the Synchrosqueezing Generalized S Transform. IEEE Geosci. Remote Sens. Lett. 2018, 15, 374–378. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, J.; Zhao, T. Synchrosqueezing based-transform and Its Application in Seismic Spectral Decomposition. IEEE Trans. Geosci. Remote Sens. 2015, 54, 817–825. [Google Scholar] [CrossRef]
- Pinnegar, C. Time-frequency and time-time filtering with the S-transform and TT-transform. Digital Signal Process. 2005, 15, 604–620. [Google Scholar] [CrossRef]
- Jashfar, S.; Esmaeili, S.; Zareian-Jahromi, M.; Rahmanian, M. Classification of power quality disturbances using S-transform and TT-transform based on the artificial neural network. Turk. J. Electr. Eng. Computer Sci. 2013, 21, 1528–1538. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal. Process. 2002, 44, 998–1001. [Google Scholar] [CrossRef]
- Thakur, G.; Brevdo, E.; Fučkar, N.S.; Wu, H.T. The Synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications. Signal. Process. 2013, 93, 1079–1094. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, W.; Liu, J. A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction. J. Sound Vib. 2013, 332, 6016–6028. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P.; Lin, Y.T.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.T. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, J. Synchrosqueezing S-Transform and Its Application in Seismic Spectral Decomposition. IEEE Trans. Geosci. Remote Sens. 2016, 54, 817–825. [Google Scholar] [CrossRef]
- Iatsenko, D.; McClintock, P.V. Linear and synchrosqueezed time–frequency representations revisited: Overview, standards of use, resolution, reconstruction, concentration, and algorithms. Digital Signal Process. 2015, 42, 1–26. [Google Scholar] [CrossRef]
- Nadarajah, S. Comments on “Approximation of statistical distribution of magnitude squared coherence estimated with segment overlapping”. Signal Process. 2007, 87, 2834–2836. [Google Scholar] [CrossRef]

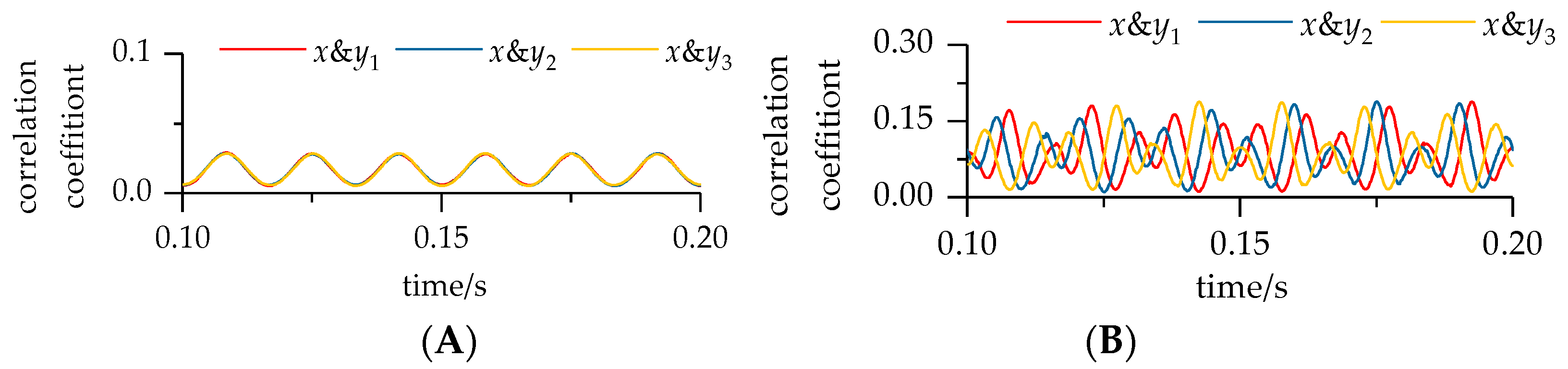


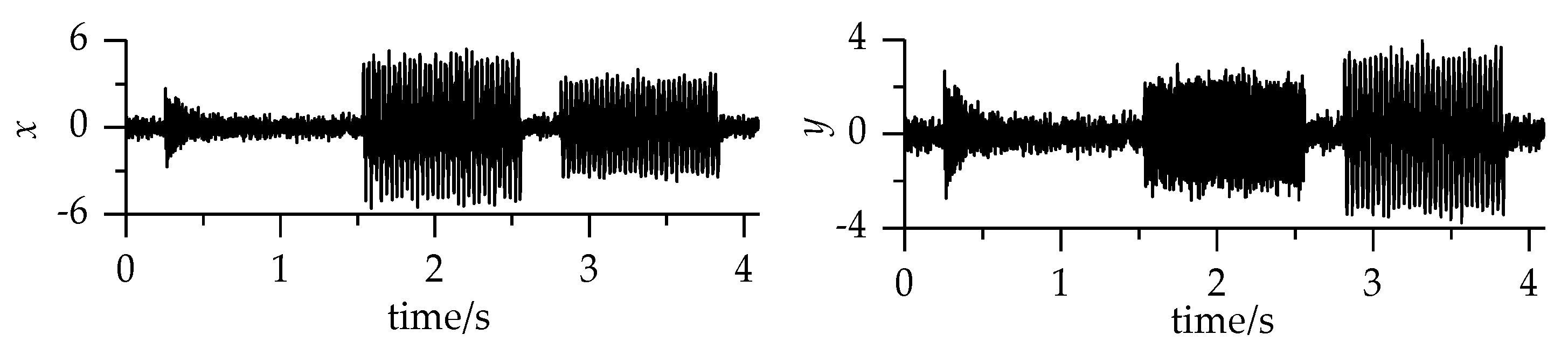







| Gear Name | Number | Teeth Number | Gear Pressure Angle (°) | Gear Modulus (mm) |
|---|---|---|---|---|
| ring | 1 | 72 | 20 | 2 |
| pinion | 3 | 18 | 20 | 2 |
| sun | 1 | 36 | 20 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, G.; Li, S.; Zhu, Y. A Time–Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform. Appl. Sci. 2019, 9, 777. https://doi.org/10.3390/app9040777
Pan G, Li S, Zhu Y. A Time–Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform. Applied Sciences. 2019; 9(4):777. https://doi.org/10.3390/app9040777
Chicago/Turabian StylePan, Gaoyuan, Shunming Li, and Yanqi Zhu. 2019. "A Time–Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform" Applied Sciences 9, no. 4: 777. https://doi.org/10.3390/app9040777
APA StylePan, G., Li, S., & Zhu, Y. (2019). A Time–Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform. Applied Sciences, 9(4), 777. https://doi.org/10.3390/app9040777






