A Novel Method to Assess Safety of Buried Pressure Pipelines under Non-Random Process Seismic Excitation based on Cloud Model
Abstract
:1. Introduction
2. Non-random Process
2.1. Basic Theory of Non-random Process
2.2. Non-stationary Non-random Process Model for Seismic Loads
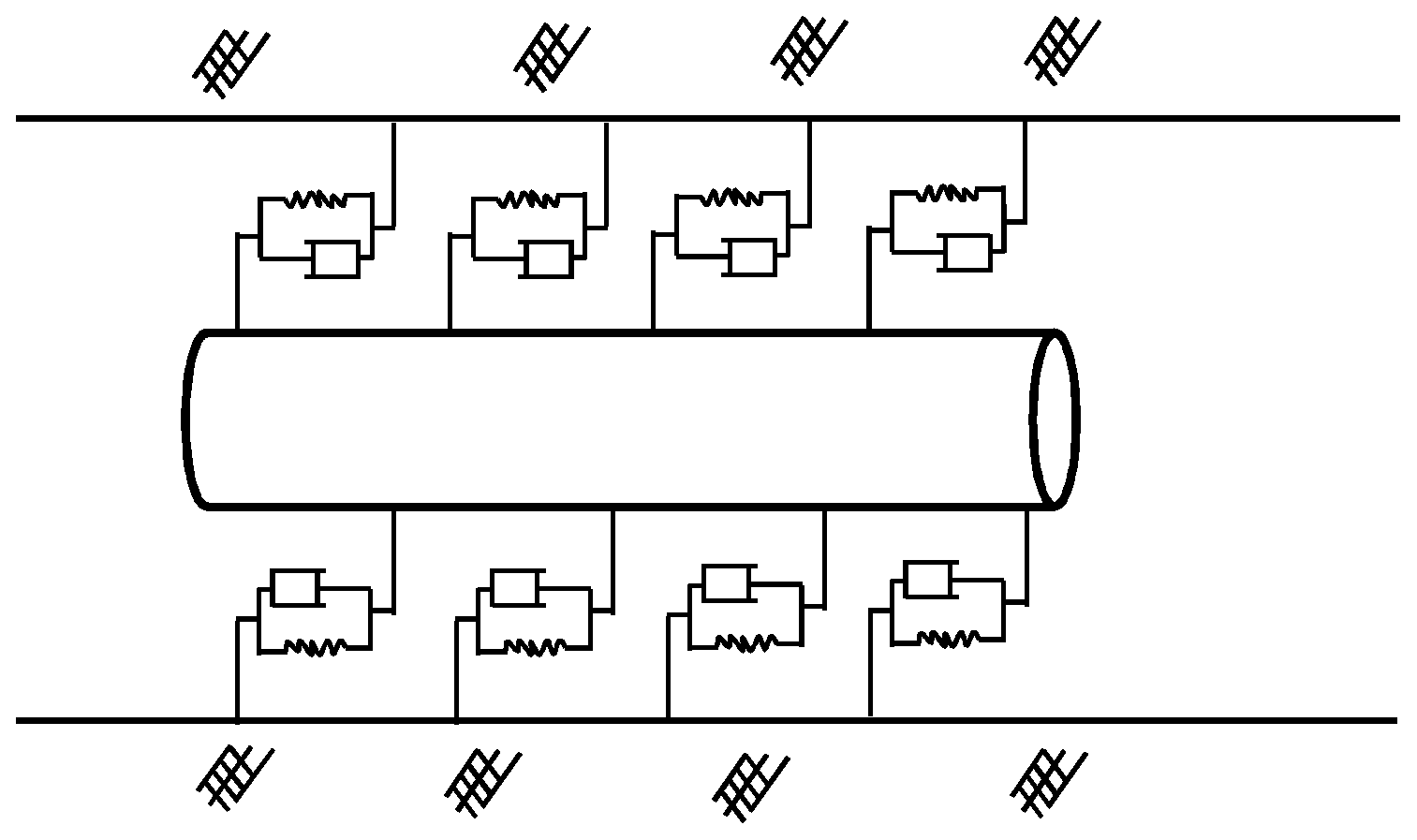
3. Dynamic Analysis of Buried Pressure Pipelines
3.1. Seismic Response of Buried Pipelines
3.2. Response of Buried Pressure Pipelines based on Fourth Strength Theory
4. Seismic Damage Assessment based on Cloud Model
4.1. Theory of Cloud Model
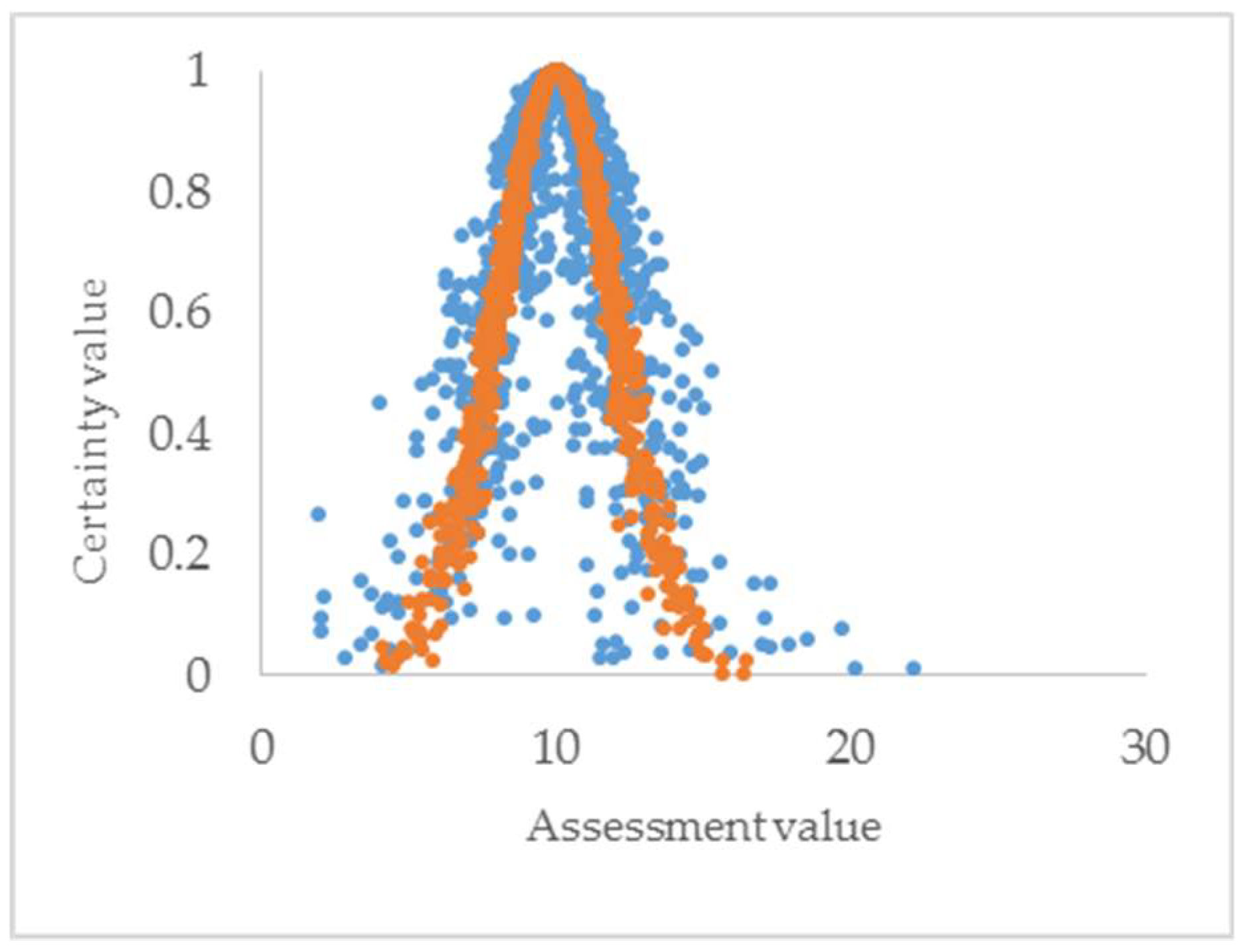
4.2. Damage Samples based on Normal Forward Cloud Generator
4.3. Damage Samples based on Normal Backward Cloud Generator
4.4. Assessment Process
5. Example
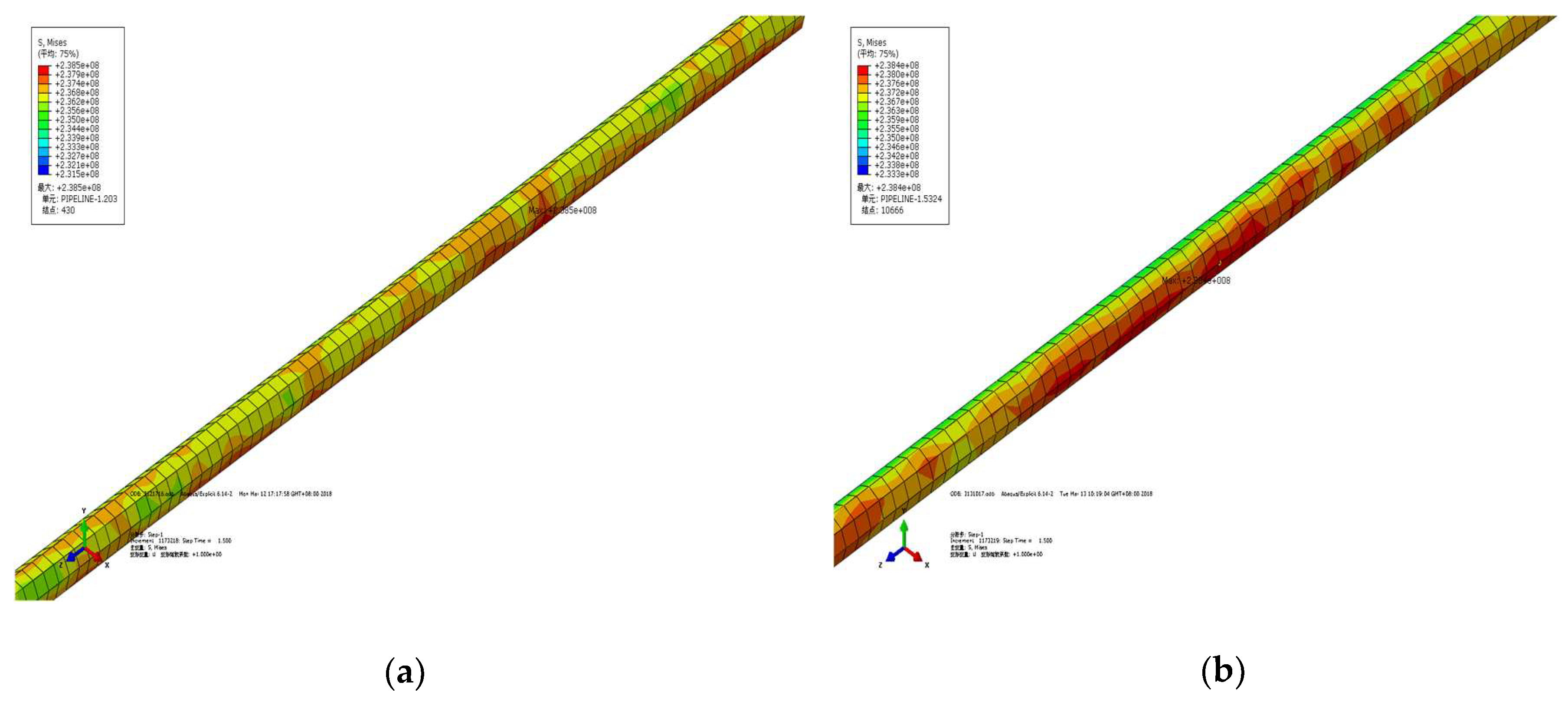
5.1. Calculation Based on Finite Element
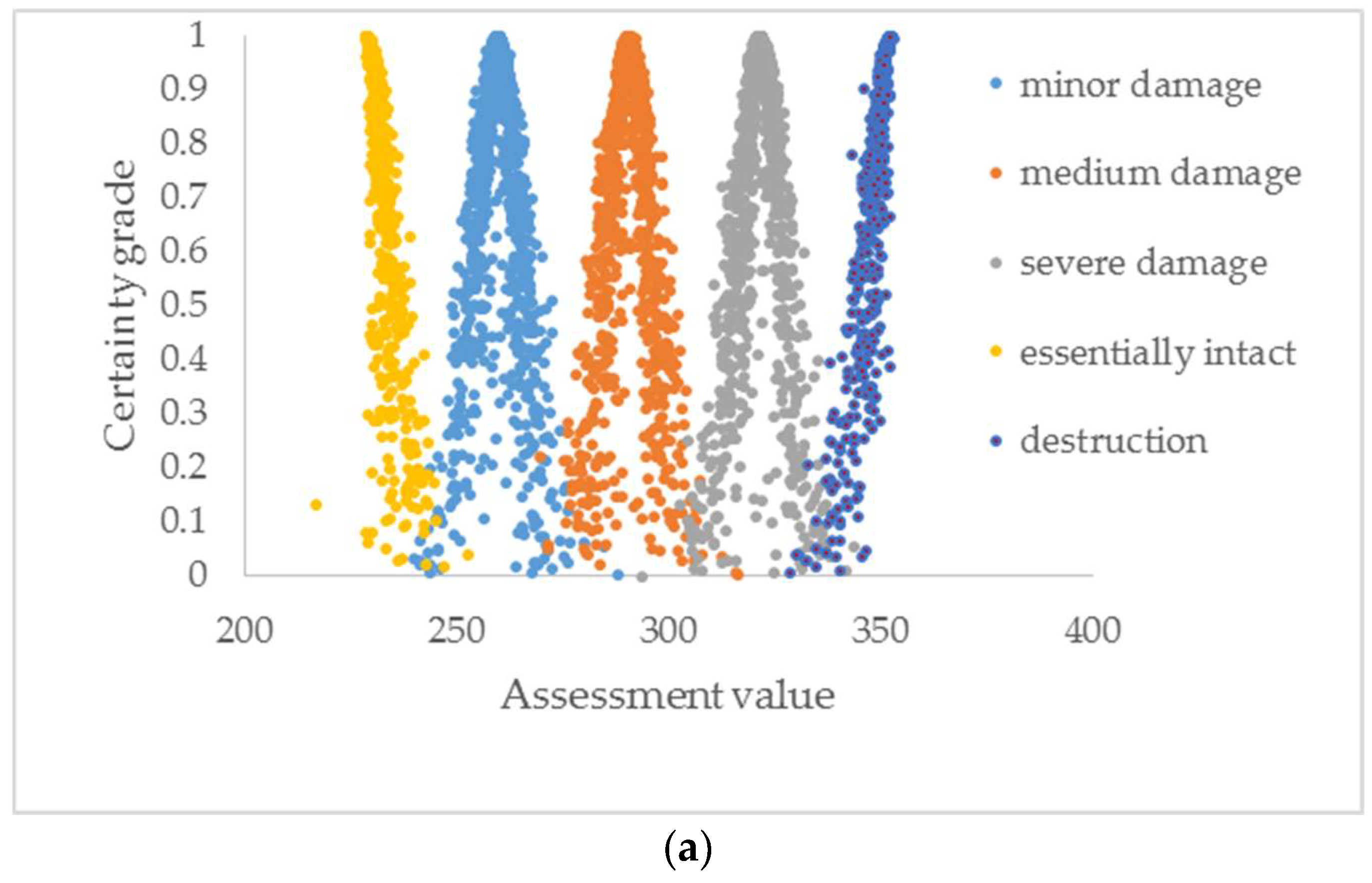
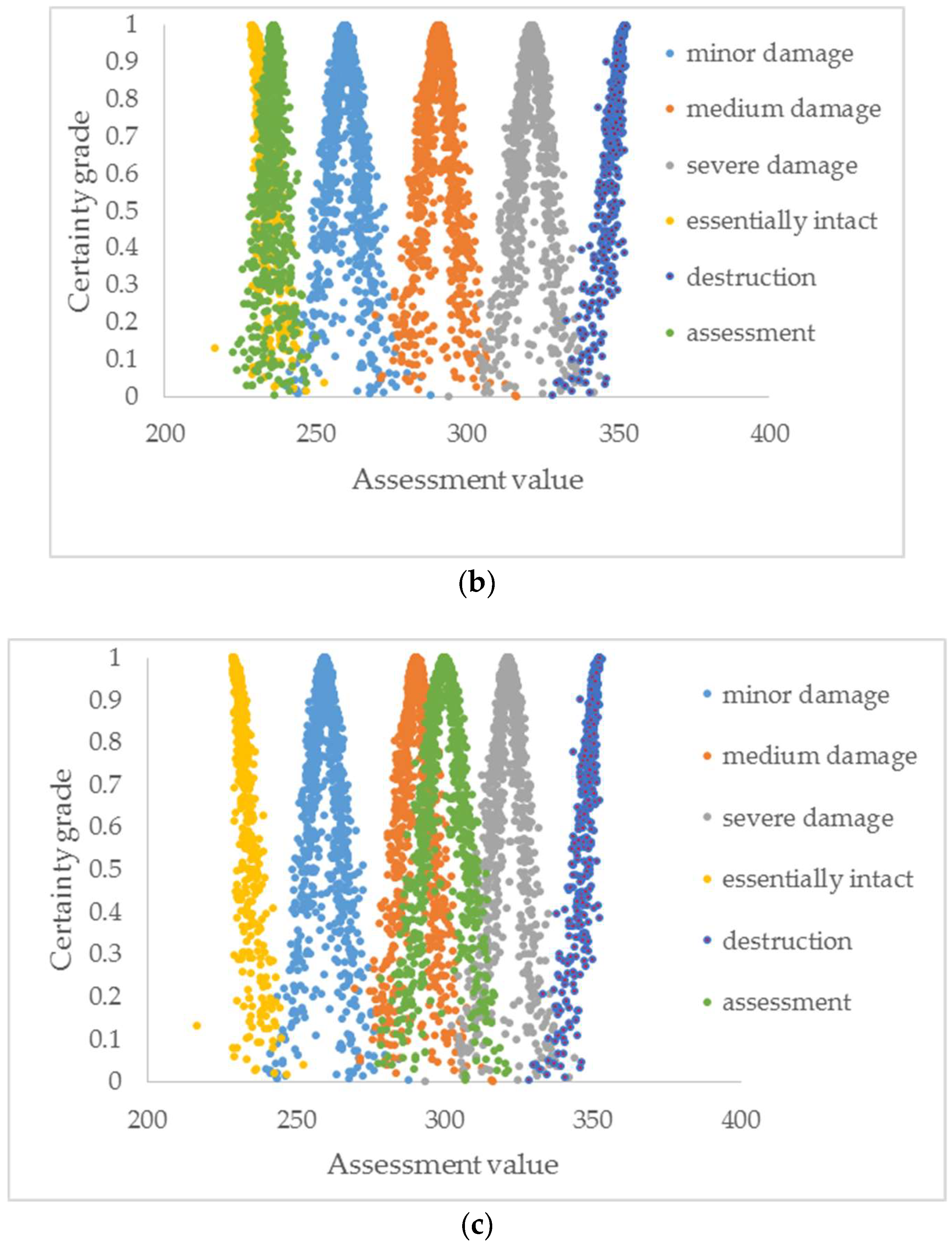
5.2. Damage Assessment of a Pipeline
6. Conclusion
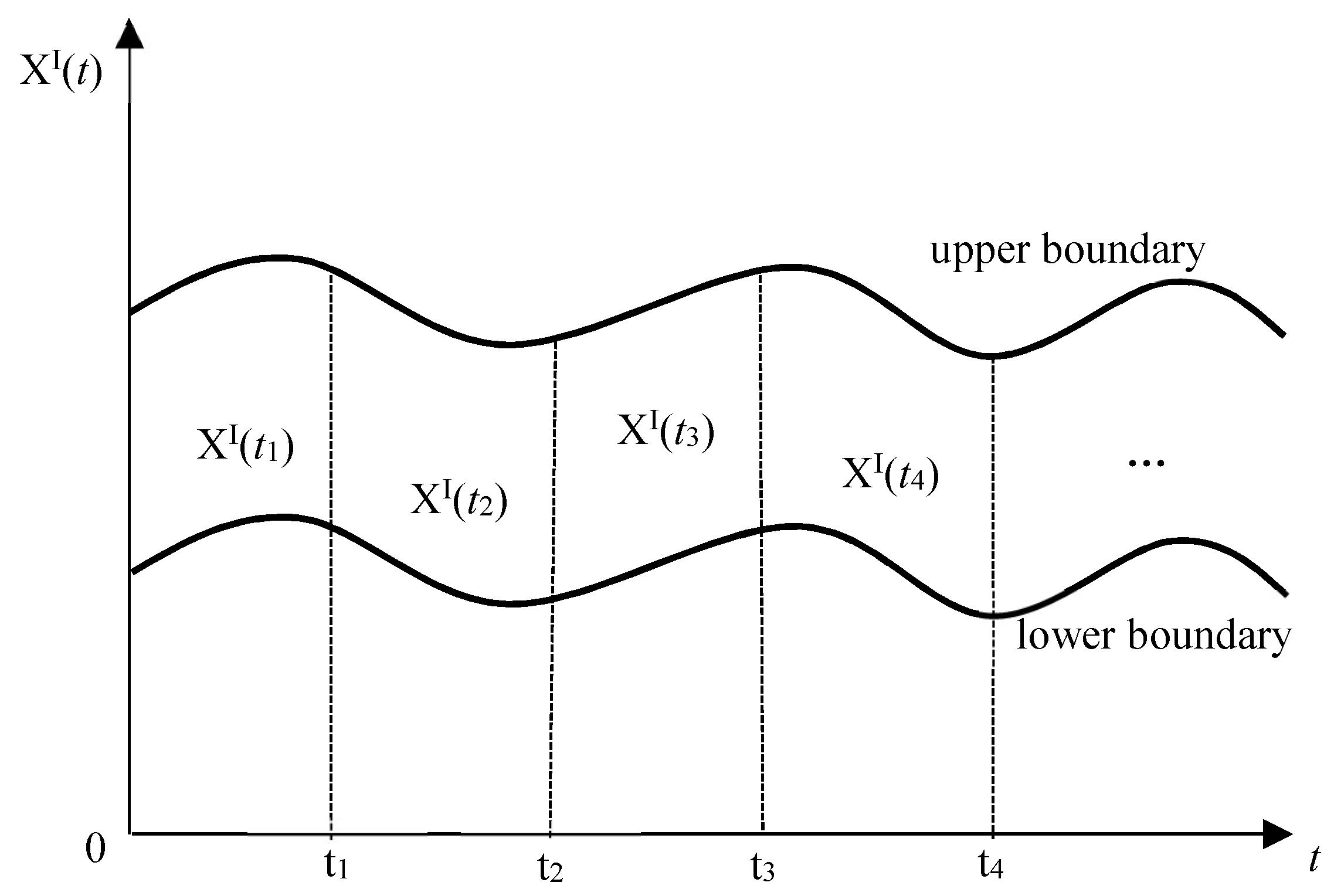
- The seismic excitation with small data is investigated by using non-random process, and the response of pipeline exposed to earthquake can be obtained.
- For the design of buried pressure pipeline, the result of dynamic response boundary is easier for engineers to understand. Therefore, it can be used as a supplement of random process excitation.
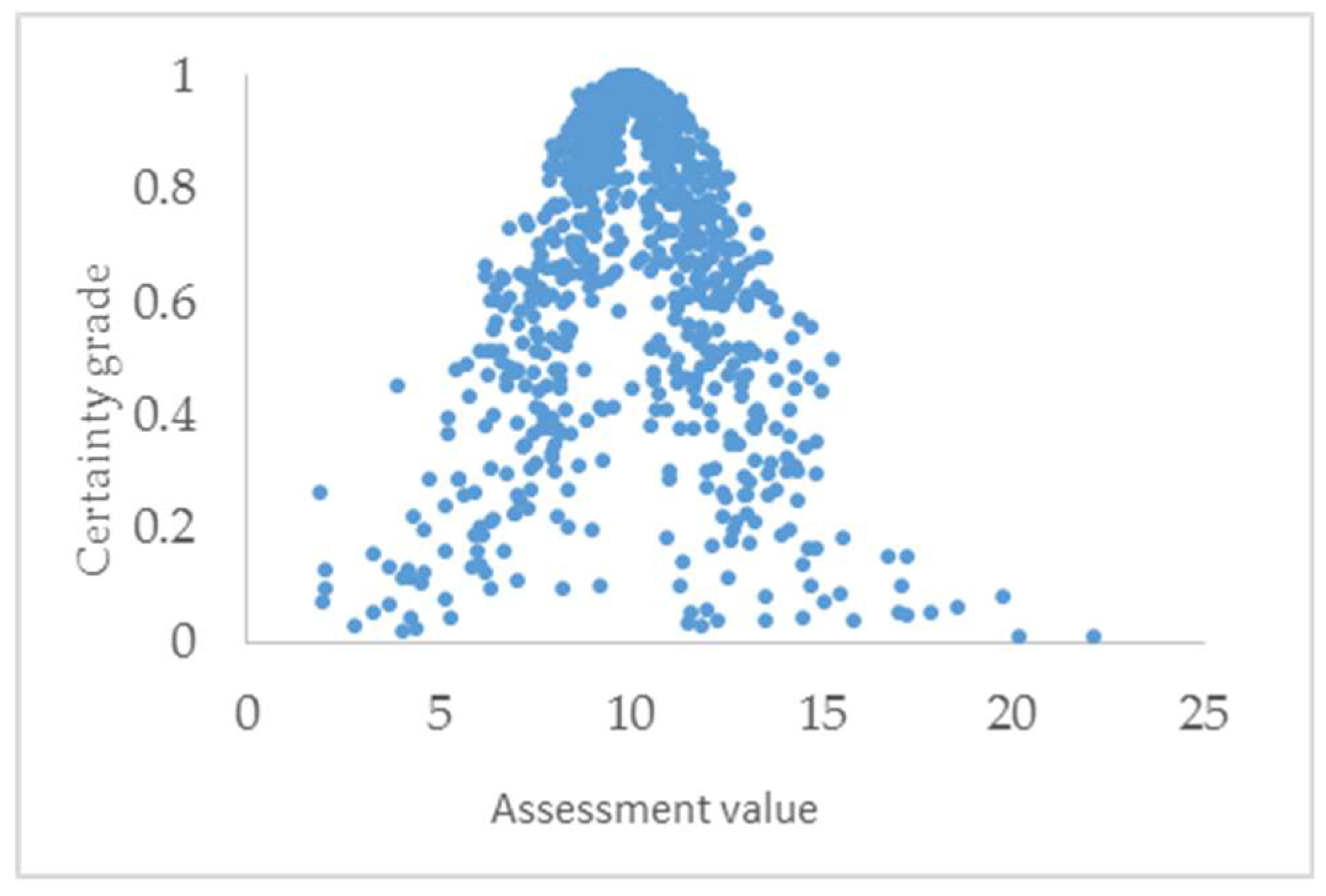
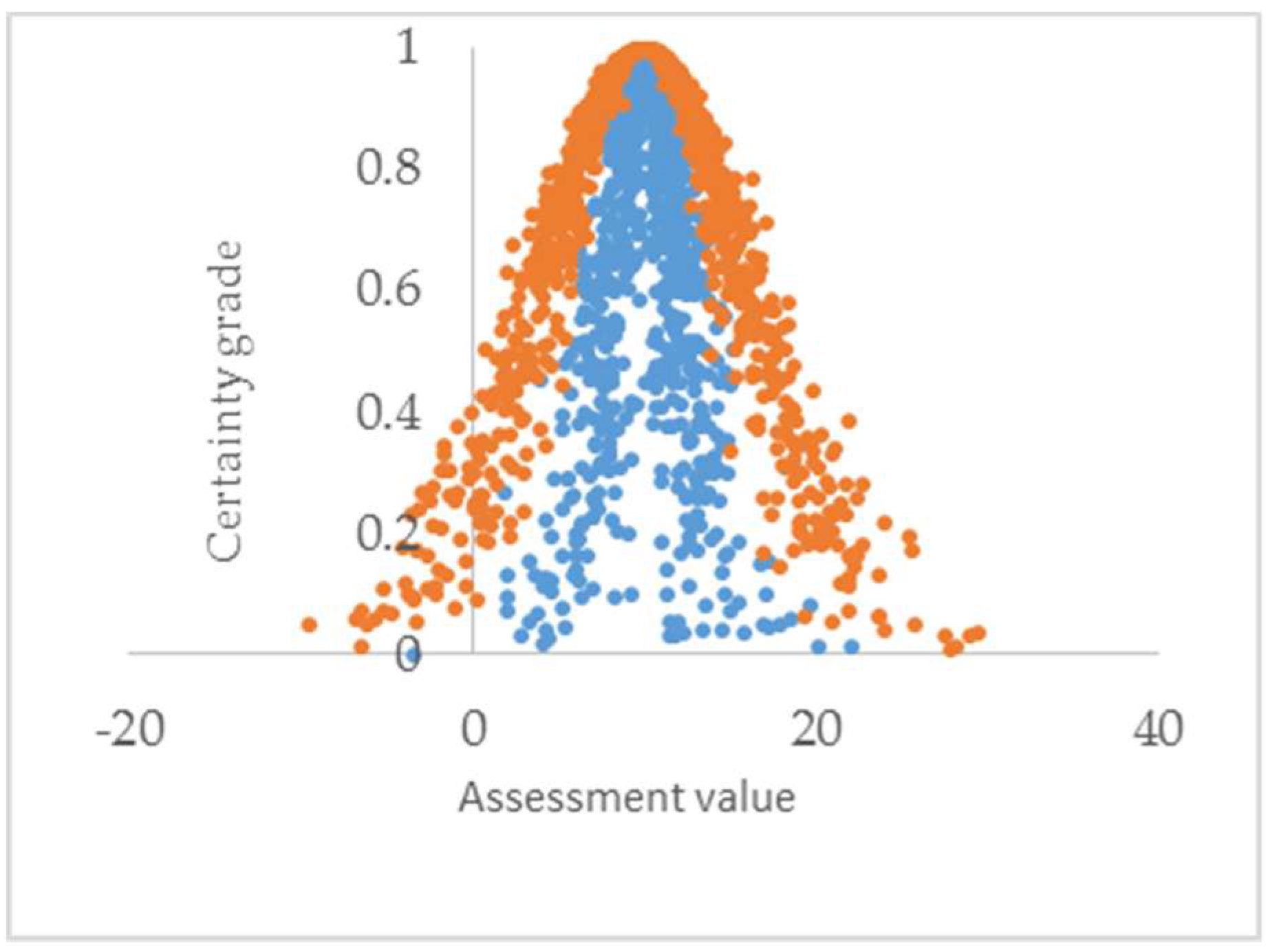
- Combined with the response of non-random process, the method to realize fuzziness and randomness of interval sample is proposed, and it achieves the conversion between quantitative and qualitative. Thus, this method can effectively reduce the impact of human factors in the assessment process and can accurately describe the intermediate state of pipeline damage and the uncertainty of pipeline stress.
- The damage model of the pipeline based on cloud model established here can more reasonably describe the damage of the structure with a certain level, and the assessment result is shown visually using a cloud chart. This approach has laid the foundation for the safety evaluation of seismic engineering with small sample in the future.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hu, G.; Zhang, P.; Wang, G.; Zhang, M.; Li, M. The Influence of Rubber Material on Sealing Performance of Packing Element in Compression Packer. J. Nat. Gas. Sci. Eng. 2017, 38, 120–138. [Google Scholar] [CrossRef]
- Zhang, P.; Qin, G.; Wang, Y. Optimal Maintenance Decision Method for Urban Gas Pipelines Based on as Low as Reasonably Practicable Principle. Sustainability 2019, 11, 153. [Google Scholar] [CrossRef]
- Li, D.S.; Lu, D.; Hou, Y.L. Pipeline Damage Identification Based on Additional Virtual Masses. Appl. Sci. 2017, 7, 1040. [Google Scholar] [CrossRef]
- Martini, A.; Rivola, A.; Troncossi, M. Autocorrelation Analysis of Vibro-Acoustic Signals Measured in a Test Field for Water Leak Detection. Appl. Sci. 2018, 8, 2450. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Leak Detection in Water-Filled Small-Diameter Polyethylene Pipes by Means of Acoustic Emission Measurements. Appl. Sci. 2017, 7, 2. [Google Scholar] [CrossRef]
- EPA—United States Environmental Protection Agency. Control and Mitigation of Drinking Water Losses in Distribution Systems; EPA 816-R-10-019 Report; United States Environmental Protection Agency: Washington, DC, USA, 2010.
- Xu, C.; Gong, P.; Xie, J.; Shi, H.; Chen, G.; Song, G. An acoustic emission based multi-level approach to buried gas pipeline leakage localization. J. Loss Prev. Process Ind. 2016, 44, 397–404. [Google Scholar] [CrossRef]
- Nedjati, A.; Vizvari, B.; Izbirak, G. Correction to: Post-earthquake response by small UAV helicopters. nat. Hazard. 2018, 90, 511. [Google Scholar] [CrossRef]
- Feng, Q.S.; Chen, J.F.; Ai, M.Y.; Cui, T.; Han, X.M. Application of Pipeline Integrity Technology in Earthquake Disaster. Acta Petrolei Sinica 2010, 31, 139–143. [Google Scholar] [CrossRef]
- Scawthorn, C.; Yanev, P.I. 17 January 1995, Hyogo–ken Nambu, Japanese Earthquake. Eng. Struct. 1995, 17, 146–157. [Google Scholar] [CrossRef]
- Hwang, H.; Chiu, Y.H.; Chen, W.Y.; Shih, B.J. Analysis of Damage to Steel Gas Pipelines Caused by Ground Shaking Effects during the Chi-Chi, Taiwan Earthquake. Earthquake Spectra 2004, 20, 1095–1110. [Google Scholar] [CrossRef]
- Hindy, A.; Novak, M. Earthquake Response of Underground Pipelines. Earthquake Eng. Struct. Dyn. 2010, 7, 451–476. [Google Scholar] [CrossRef]
- Wang, L.R.L.; Cheng, K.M. Seismic Response Behavior of Buried Pipelines. J. Press. Vessel Technol. 1979, 101, 21–30. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.H. Random Seismic Analysis of Multi-Supported Pipelines Subjected to Spatially Varying Ground Motions. Appl. Math. Mech. 2015, 36, 582–592. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, B.H.; Lee, H.; Kong, J.S. Seismic Behavior of a Buried Gas Pipeline under Earthquake Excitations. Eng. Struct. 2009, 31, 1011–1023. [Google Scholar] [CrossRef]
- Ben-Haim, Y.; Elishakoff, I. Convex Models of Uncertainties in Applied Mechanics; Elsevier Science: Amsterdam, Netherlands, 1990. [Google Scholar]
- Qiu, Z.; Wang, X. Parameter Perturbation Method for Dynamic Responses of Structures with Uncertain-but-bounded Parameters based on Interval Analysis. Int. J. Solids Struct. 2005, 42, 4958–4970. [Google Scholar] [CrossRef]
- Sainz, Á.M.; Armengol, J.; Vehí, J. Fault Detection and Isolation of the Three-tank System Using the Modal Interval Analysis. J. Process. Control. 2002, 12, 325–338. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, N.Y.; Ni, B.Y.; Han, X. Giving Dynamic Response Bounds under Uncertain Excitations—A Non-Random Vibration Analysis Method. Chin. J. Theor. and Appl. Mech. 2016, 48, 447–463. [Google Scholar] [CrossRef]
- Sooraj, T.R.; Mohanty, R.K.; Tripathy, B.K. Fuzzy Soft Set Theory and Its Application in Group Decision Making. Adv. Comput. Commun. Technol. 2016, 452, 171–178. [Google Scholar]
- Li, D.Y.; Du, F. Artificial Intelligence with Uncertainty, 2nd ed.; National Defense Industry Press: Beijing, China, 2014. [Google Scholar]
- Wang, G.; Xu, C.; Li, D. Generic Normal Cloud Model. Inf. Sci. 2014, 280, 1–15. [Google Scholar] [CrossRef]
- Dai, C.H.; Zhu, Y.F.; Chen, W.R. Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms Based on Cloud Model. Proc. IEEE Inf. Theor. Workshop 2006, 24, 710–713. [Google Scholar] [CrossRef]
- Carassale, L. Random Process. as Earthquake Motions; Springer: Berlin, Heidelberg, 2015. [Google Scholar]
- Liu, N.Y. Non-random Process Model and Non-random Vibration Analysis. Master’s Thesis, Hunan University, Changsha, China, 2016. [Google Scholar]
- Jiang, C.; Ni, B.Y.; Han, X.; Tao, Y.R. Non-probabilistic convex model process: A New Method of Time-variant Uncertainty Analysis and Its Application to Structural Dynamic Reliability Problems. Comput. Meth. Appl. Mech. Eng. 2014, 268, 656–676. [Google Scholar] [CrossRef]
- Davenport, A.G. Note on the Distribution of the Largest Value of a Random Function with Application to Gust Loading. Proc. Inst. Civ. Eng. 1964, 28, 187–196. [Google Scholar] [CrossRef]
- Pineda-Porras, O.; Ordaz, M. A New Seismic Intensity Parameter to Estimate Damage in Buried Pipelines due to Seismic Wave Propagation. J. Earthquake Eng. 2007, 11, 14. [Google Scholar] [CrossRef]
- Xue, J.H.; Ou, J.P.; Sun, J.Q. Dynamic Analysis of Fluid-conveying Pipelines. World Inf. Earthquake Eng. 2001, 17, 29–32. [Google Scholar] [CrossRef]
- Ariman, T.; Muleski, G.E. A Review of the Response of Buried Pipelines under Seismic Excitations. Earthquake Eng. Struct. Dyn. 2010, 9, 133–152. [Google Scholar] [CrossRef]
- Qu, T.J.; Wang, Q.X. Response of Underground Pipeline to Multi-support Longitudinal Excitations. Earthquake Eng. Eng. Vibr. 1993, 4, 39–46. [Google Scholar]
- Qu, T.J.; Wang, J.J.; Wang, Q.X. A Practical Model for the Power Spectrum of Spatially Variant Ground Motion. Acta Seismol. Sin. 1996, 9, 69–79. [Google Scholar] [CrossRef]
- Bubenik, T.A.; Olson, R.J.; Stephens, D.R.; Francini, R.B. Analyzing the Pressure Strength of Corroded Pipeline, In Proceedings of 11th. International Conference On Offshore Mechchanics and Arctic Engineering, Calgary, Canada, 7–12 June 1992; pp. 225–231. [Google Scholar]
- Li, Z.Z. Material Mechanics; Wuhan University of Technology Press: Wuhan, China, 2016. [Google Scholar]
- Li, L.L.; Liu, L.X.; Yang, C.W.; Li, Z. The Comprehensive Evaluation of Smart Distribution Grid Based on Cloud Model. Energy Procedia 2012, 17, 96–102. [Google Scholar] [CrossRef] [Green Version]
- Li, D.Y.; Liu, C.W.; Du, Y.; Han, X. Uncertain Artificial Intelligence. J. Software 2004, 15, 1583–1594. [Google Scholar]
- Li, D.; Liu, C.; Gan, W. A New Cognitive Model: Cloud Model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Ma, T.X.; Yang, Y.H.; Xu, Z.; Li, A.J.; Tang, Y. The Constitutive Relation and Failure Criterion of X60 Pipeline Steel. J. Chongqing Univ. 2014, 37, 67–75. [Google Scholar] [CrossRef]
- Neumann, F. The analysis of the El Centro record of the Imperial Valley earthquake of May 18, 1940. Eos Trans. Am. Geophys. Union 1941, 22, 400. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Liu, X.H.; Gong, S.L. The Artificial Earthquake Ground Motions Compatible with Standard Response Spectra. Chin. Acad. Build. Res. 1981, 2, 34–43. [Google Scholar] [CrossRef]






| Grades of Damage | Description | Indices |
|---|---|---|
| essential integrity | good condition | |
| minor damage | non-destructive or appears micro-cracks locally. | |
| medium damage | joint fracture, local deformation or cracking of weld seam, slight leakage | |
| severe damage | severe deformation or fracture, cracked weld, heavy leakage, difficult to repair | |
| destruction | breakage, severe damage to the interface weld, severe leakage, no repair value |
| Type of Material | Density/(kg·m−3) | Elastic Modulus/Pa | Poisson Ratio | Expansion Angle/° | Friction Angle/° | Flow Stress Ratio |
|---|---|---|---|---|---|---|
| Soil | 1867.3 | 2 108 | 0.4 | 28.7 | 18.4 | 0 |
| Pipeline | 7850.0 | 2.07 1011 | 0.3 | — | — | — |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wang, Y.; Qin, G. A Novel Method to Assess Safety of Buried Pressure Pipelines under Non-Random Process Seismic Excitation based on Cloud Model. Appl. Sci. 2019, 9, 812. https://doi.org/10.3390/app9040812
Zhang P, Wang Y, Qin G. A Novel Method to Assess Safety of Buried Pressure Pipelines under Non-Random Process Seismic Excitation based on Cloud Model. Applied Sciences. 2019; 9(4):812. https://doi.org/10.3390/app9040812
Chicago/Turabian StyleZhang, Peng, Yihuan Wang, and Guojin Qin. 2019. "A Novel Method to Assess Safety of Buried Pressure Pipelines under Non-Random Process Seismic Excitation based on Cloud Model" Applied Sciences 9, no. 4: 812. https://doi.org/10.3390/app9040812
APA StyleZhang, P., Wang, Y., & Qin, G. (2019). A Novel Method to Assess Safety of Buried Pressure Pipelines under Non-Random Process Seismic Excitation based on Cloud Model. Applied Sciences, 9(4), 812. https://doi.org/10.3390/app9040812





