Packing Characteristics of Aggregate with Consideration of Particle size and Morphology
Abstract
:1. Introduction
2. Aggregates and Test Design
2.1. Aggregates
2.2. Test Design
- (1)
- The characteristics of single-size packing and the size effect;
- (2)
- The characteristics of two-size packing and the effects of size and size ratio;
- (3)
- The effect of particle morphology on the packing characteristics of single-size and two-size packing.
3. Packing Characteristics of Packed Single-Size Particles
4. Packing Characteristics of Packed Blends with Two-Size Particles
5. Effects of Particle Morphology
6. Effect of Particle Size Ratio
7. Size Effect
8. Conclusions
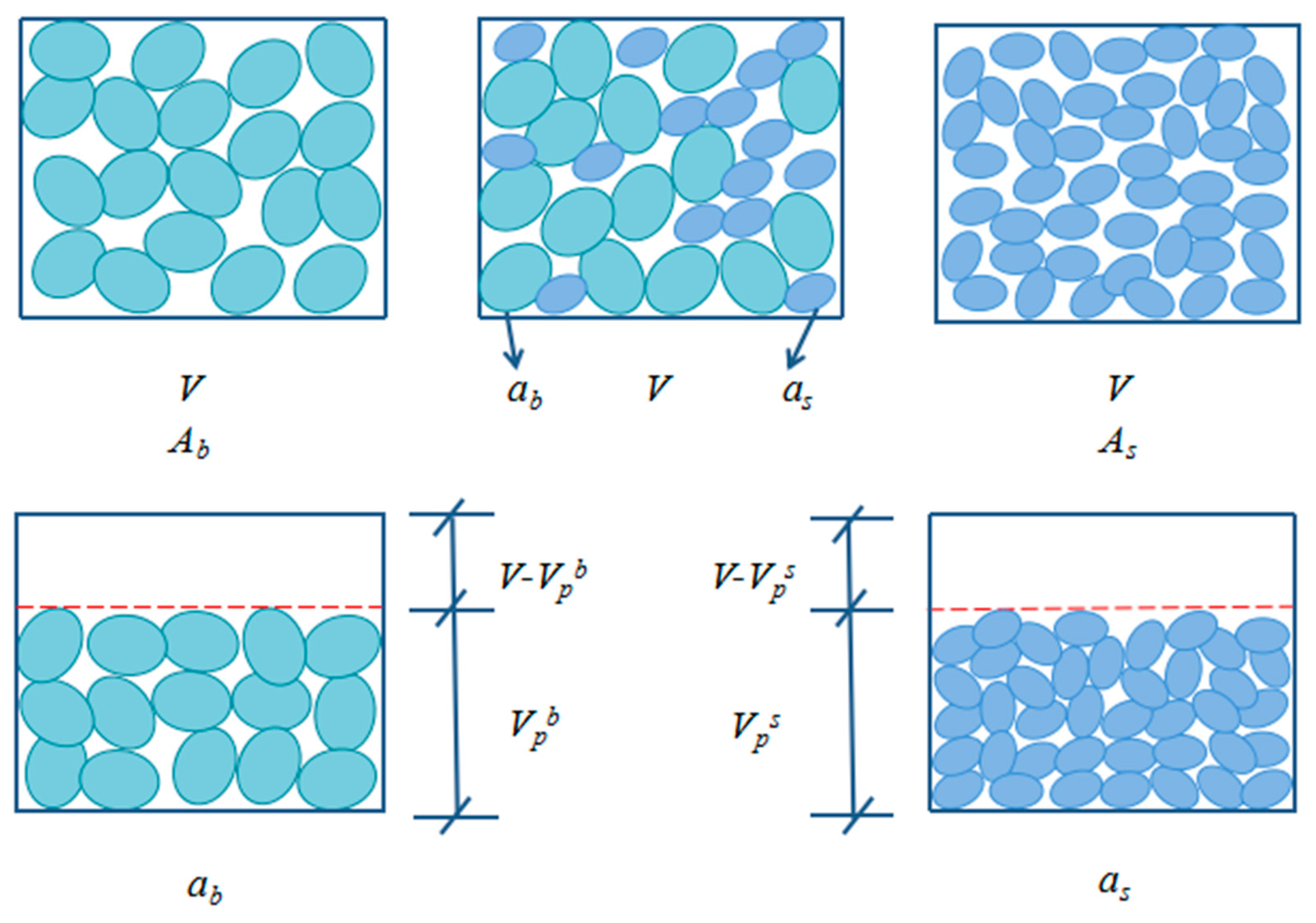
- The comparison between the SSP test and sphere packing models shows that the results of packing analysis using ideal spheres cannot be simply used to describe the packing characteristics of real aggregate mixtures. The morphology of aggregate particles is different from each other. Even the particles in the aggregate with single size do not have exactly equal size. The packing behavior of aggregate particles is more complex than that of ideal spheres.
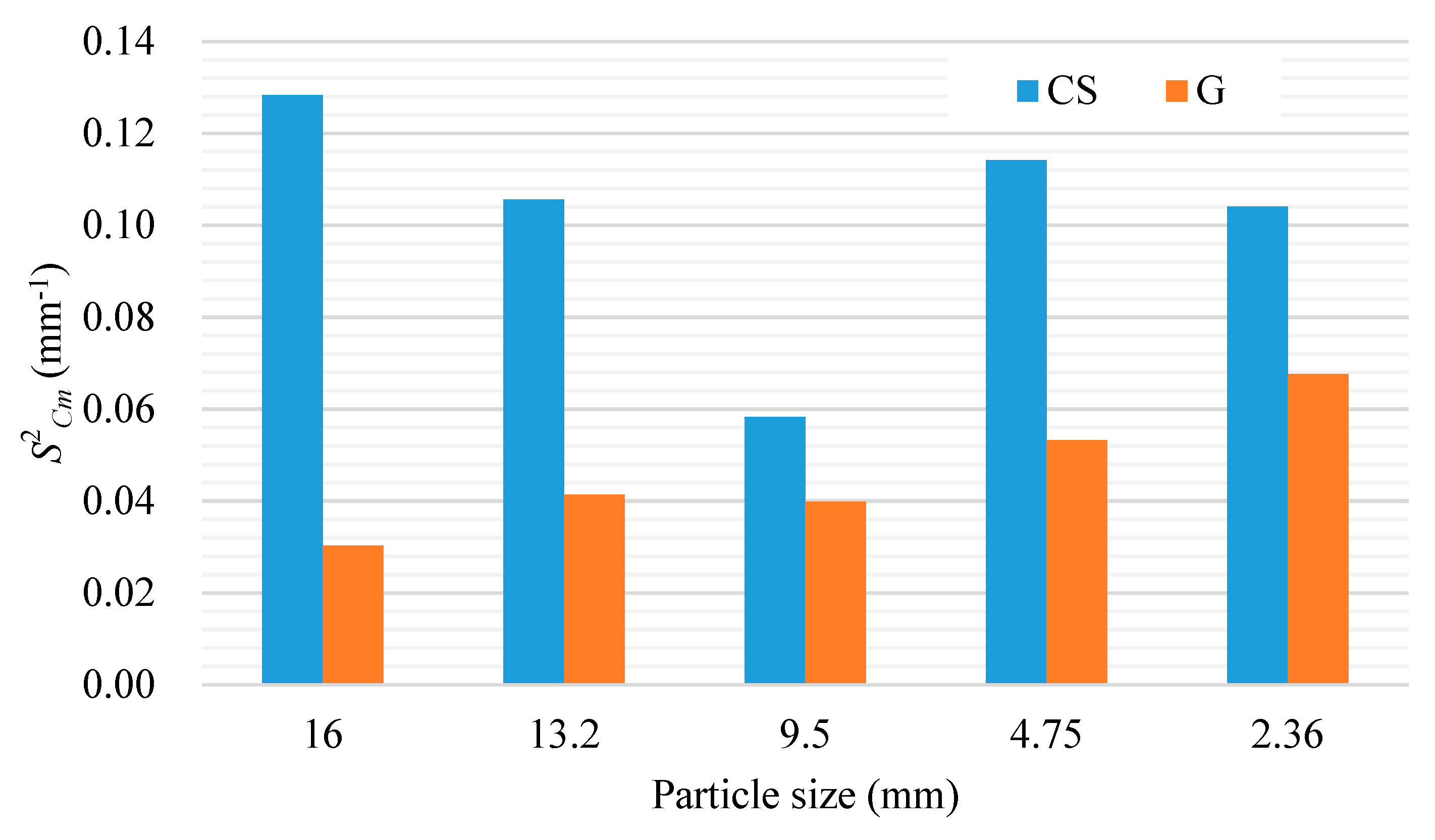
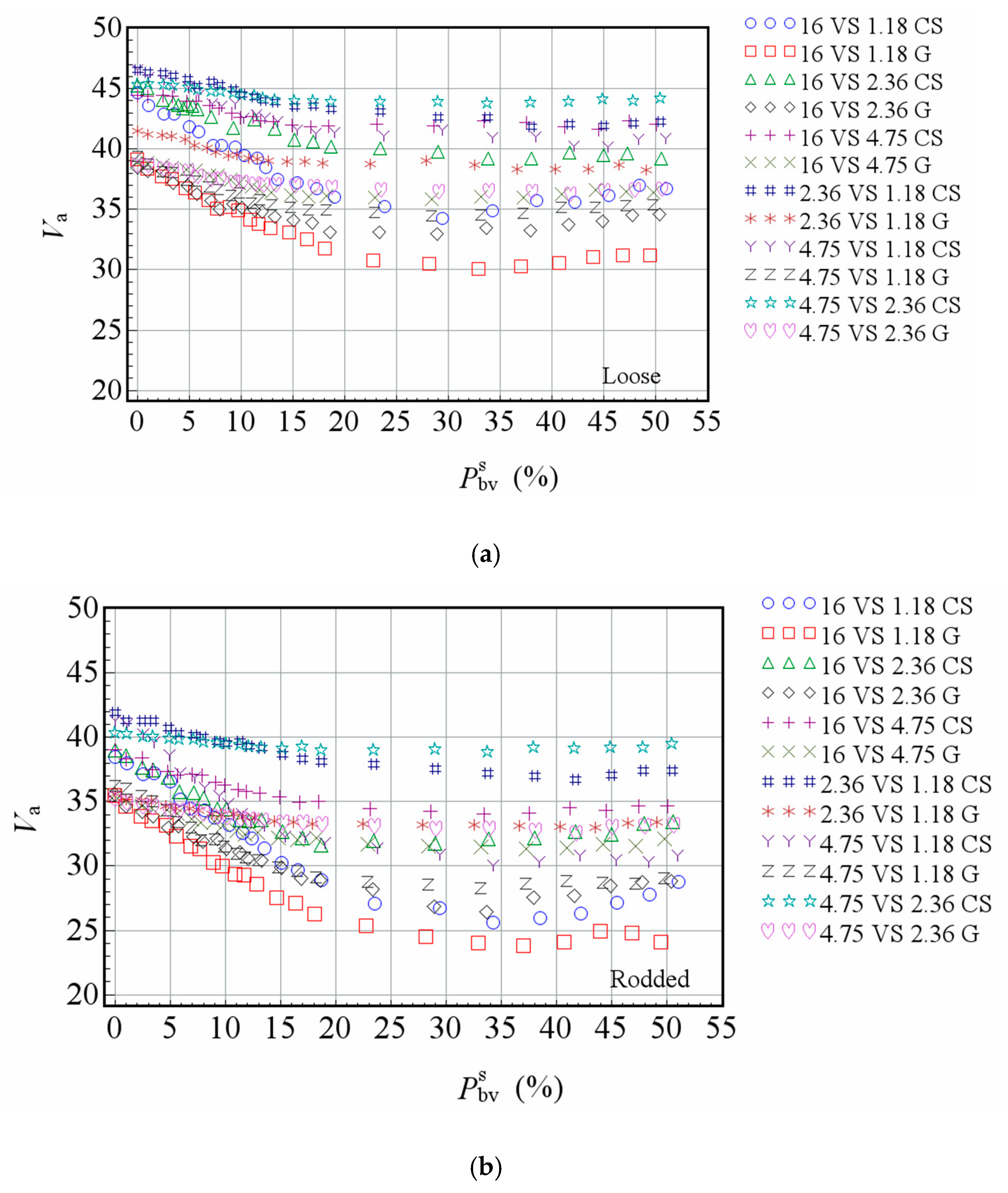
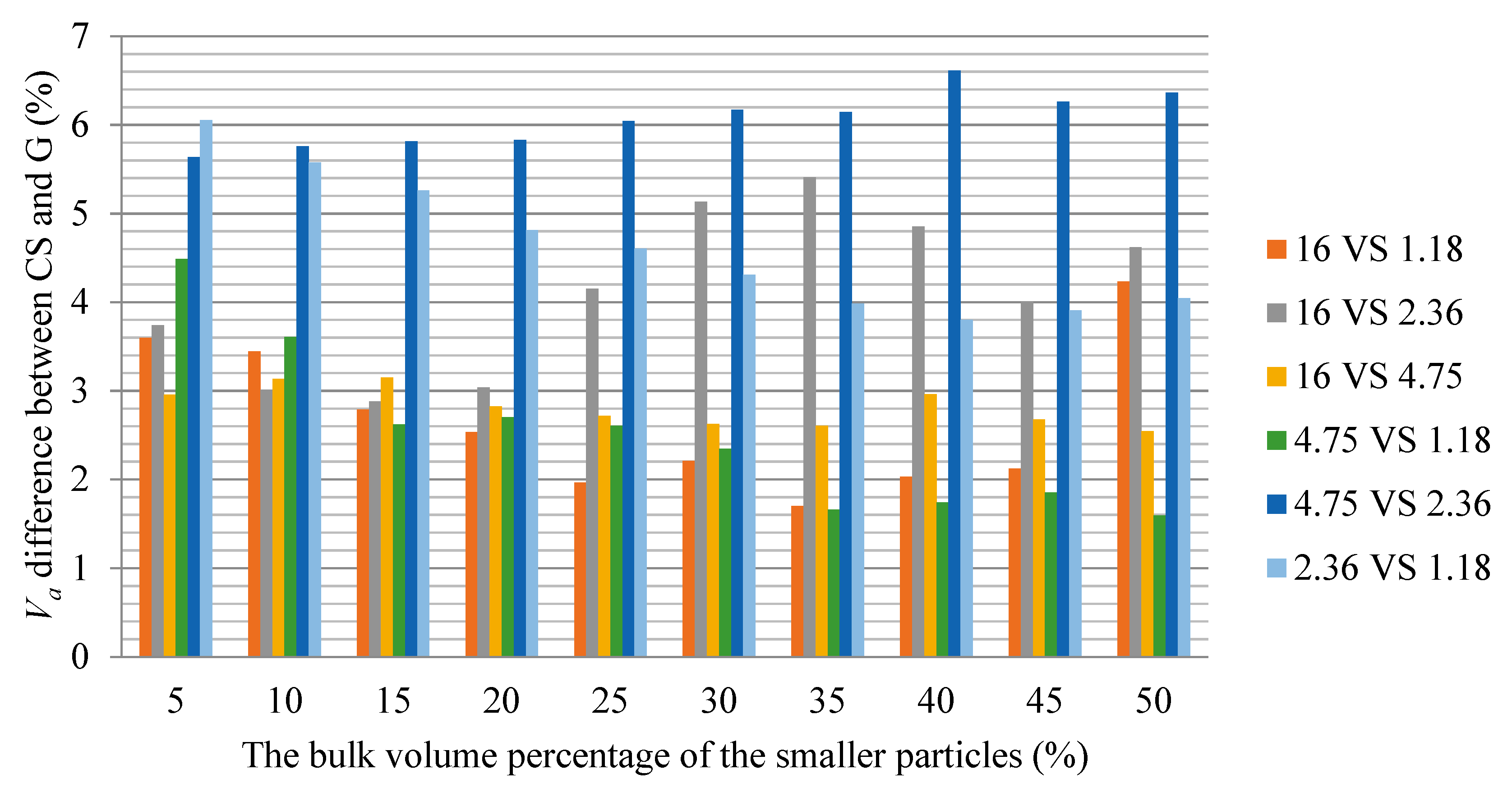
- Particle morphology has a significant effect on the Va of packed aggregate. Whether in the SSP or TSP test, the Va of crushed stone blend is significantly higher than that of gravel blend. In the SSP test, the biggest difference is for 4.75 mm particles in the loose packing test, where the Va of crushed stone blend is 16.64% higher than that of gravel blend. The smallest is for 1.18 mm particles in the loose packing test, where the Va of crushed stone blend is 5.27% higher than that of gravel.
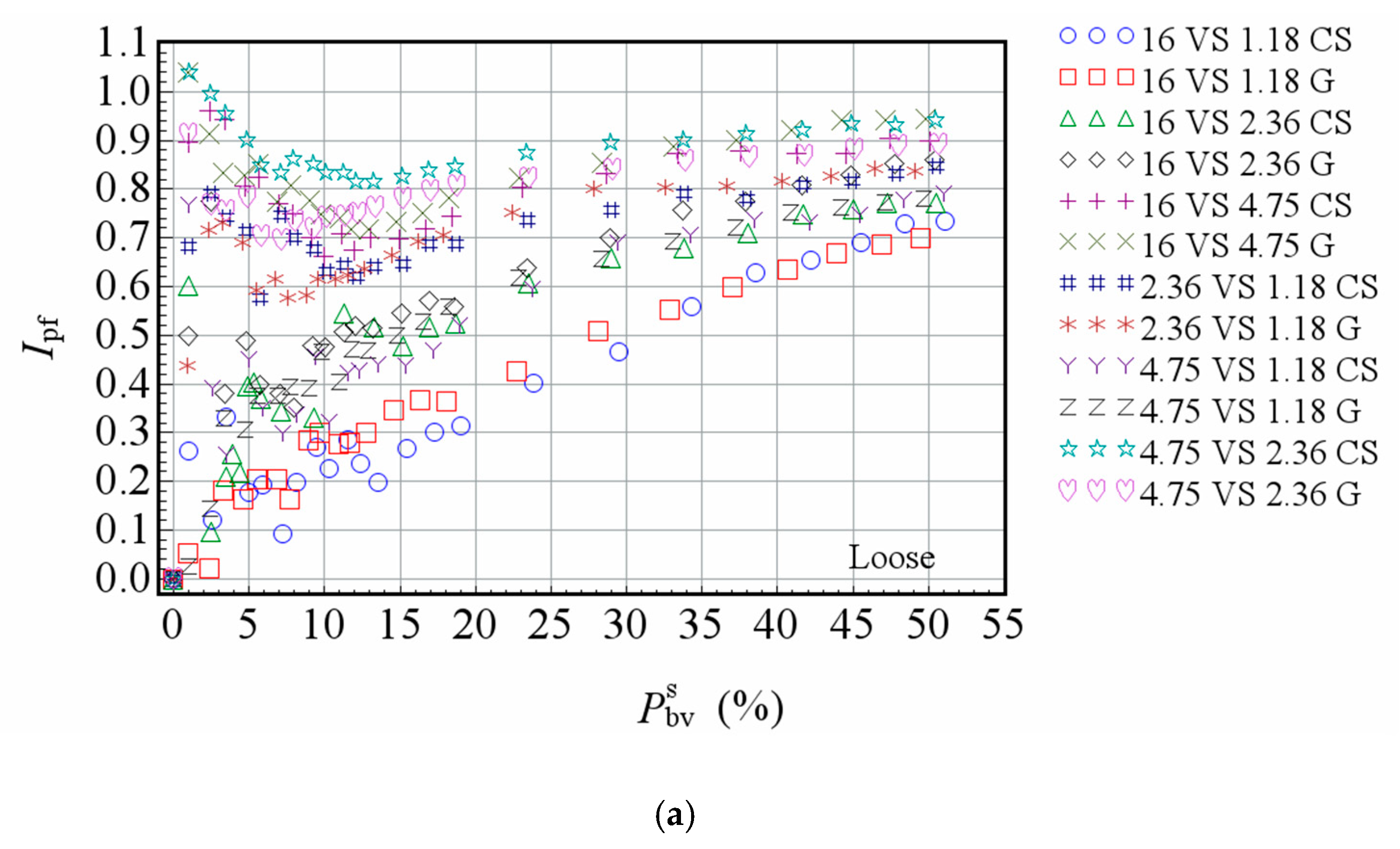
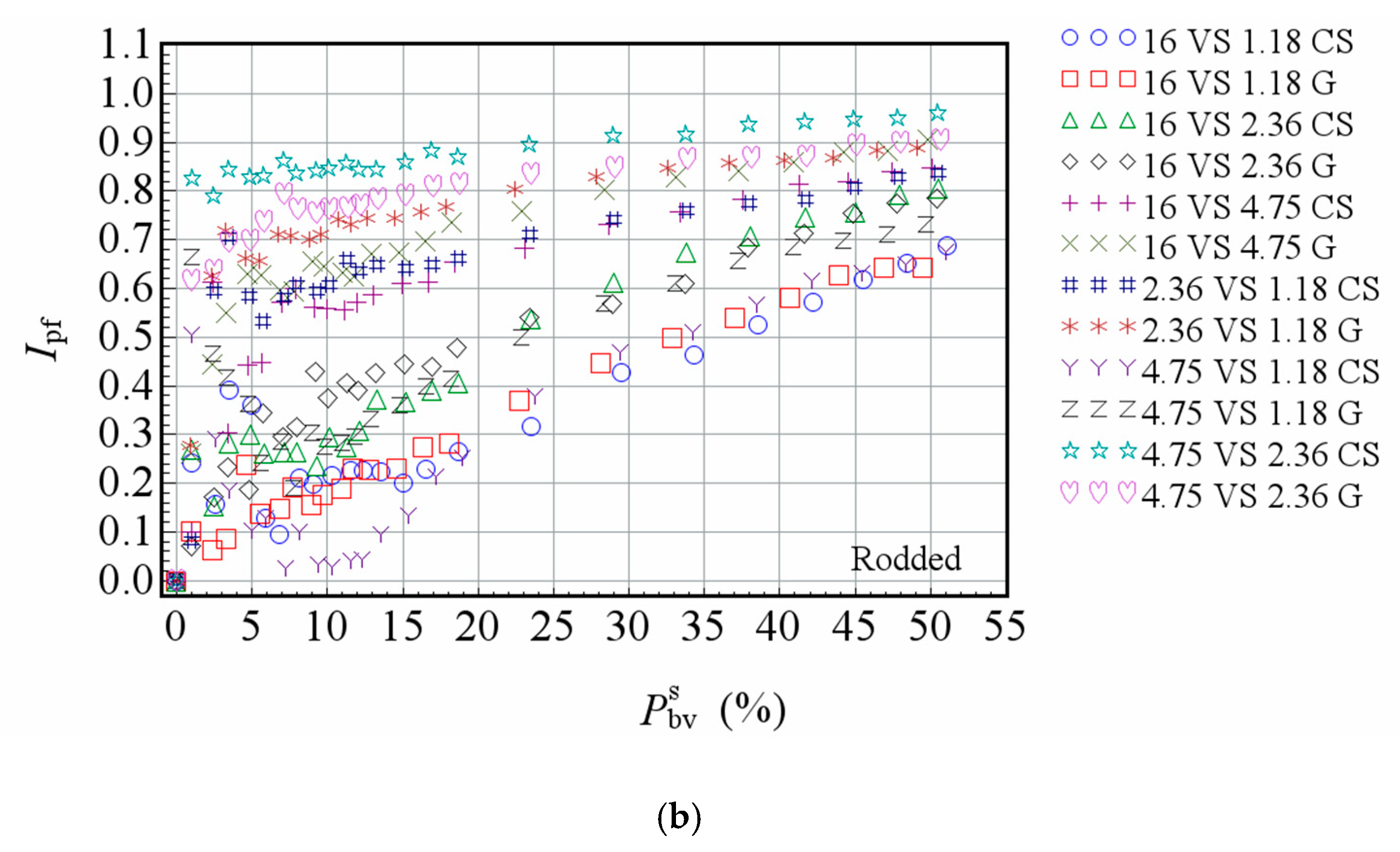
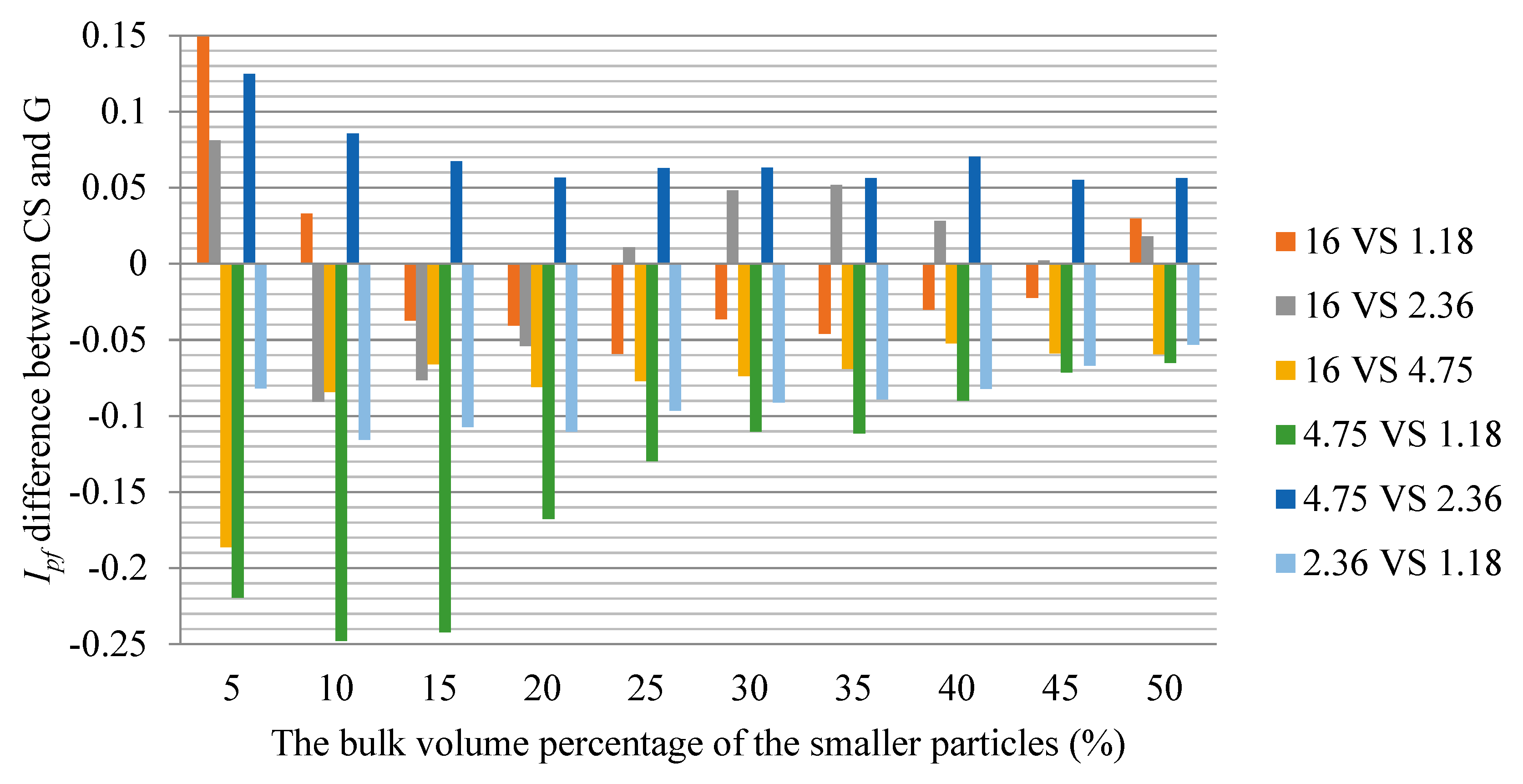
- The Ipf can be used to quantitatively distinguish the skeleton building and air void filling functions of smaller size particles in the TSP test. The Ipf is between 0 and 1, where 1 indicates that smaller size particles plays the same skeleton role as larger size particles in the blend, and 0 indicates that smaller size particles only fills air voids in the blend.
- The function of particles cannot be simply divided into skeleton building and air void filling. Particles in a mixture have the above two functions in varying degrees. Even in the combination of 16 VS 1.18 (size ratio is only 0.074), the Ipf of smaller particle size is not zero.
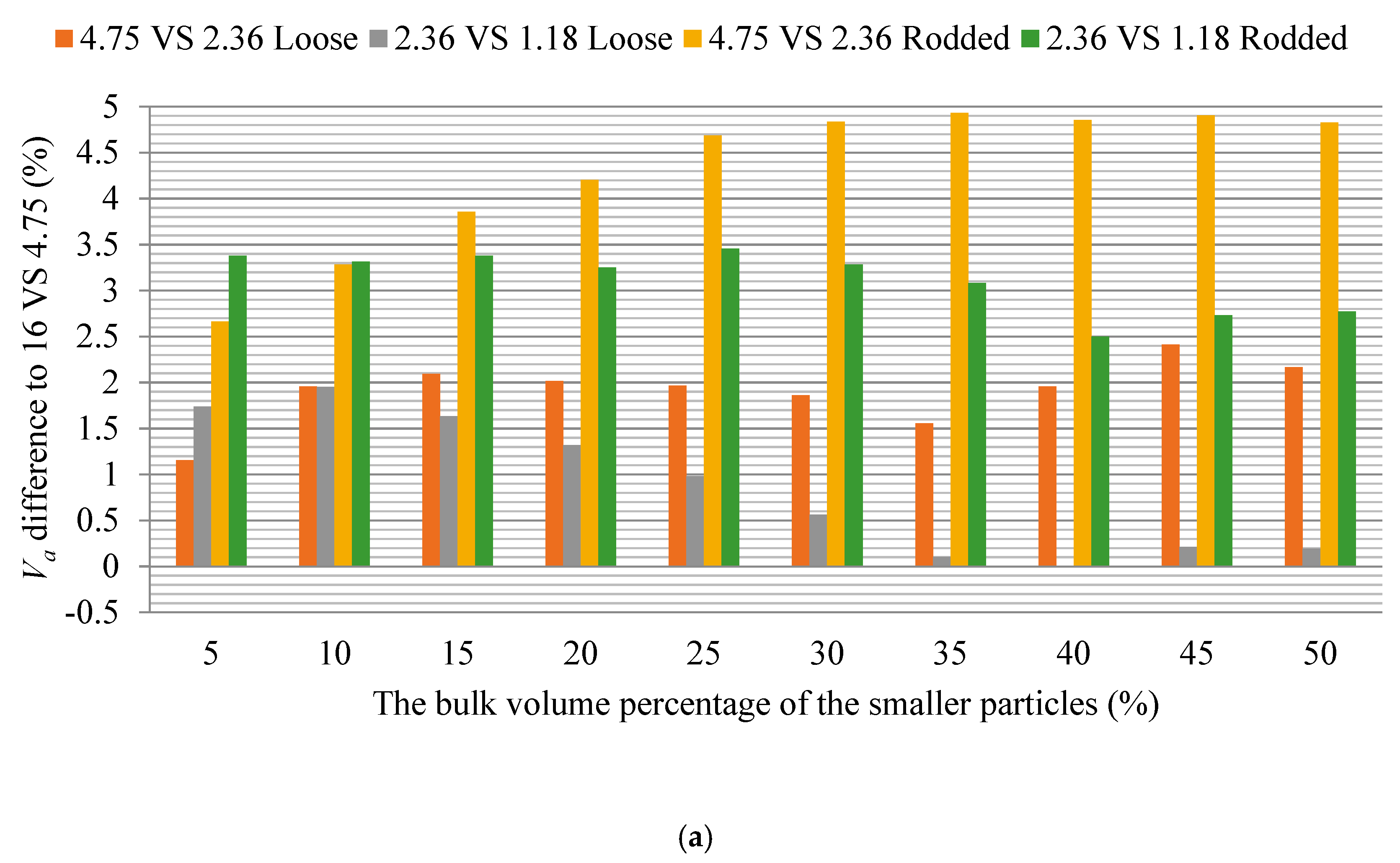
- The function of particles changes with respect to different particle size compositions. In the same combination, Ipf of smaller particles increases with the increasing of its proportion. The larger the particle size ratio in the mixture, the larger the increase of Ipf with the addition of smaller particles. The change of Ipf with the proportion of smaller size particles indicates that the function of particles is closely related to the specific composition of different size particles, and cannot be simply distinguished according to the relationship between particle sizes.
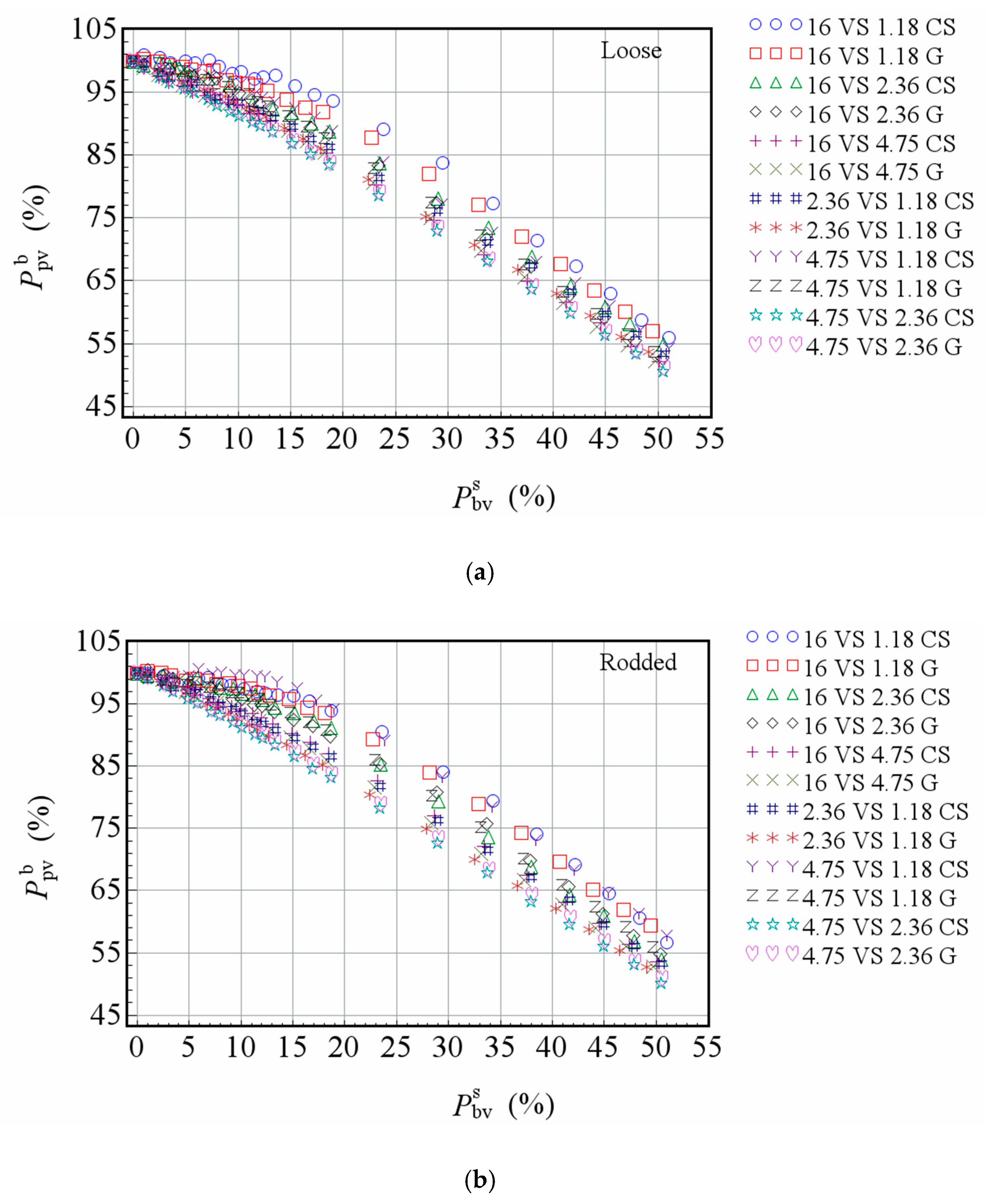
- Particle size has a significant impact on the packing characteristics of aggregates. For the SSP test, there is a significant difference in Va between packed aggregates with different sizes. For the TSP test, under the same particle size ratio and the same volume ratio, there are significant differences in Va and Ipf of smaller size particles among the combinations with different maximum particle size, where the change trend is complex and still needs further study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Christensen, D.W.; Bonaquist, R.F. Volumetric Requirements for Superpave Mix Design; NCHRP Report 573; Transportation Research Board of the National Academies: Washington, DC, USA, 2006. [Google Scholar]
- Cooper, S.B.; William, M.K.; Sharear, K. Testing and Analysis of LWT and SCB Properties of Asphalt Concrete Mixtures; No. Final Report 536; Louisiana Transportation Research Center: Baton Rouge, LA, USA, 2016. [Google Scholar]
- Das, P.K.; Björn Birgisson Jelagin, D.; Kringos, N. Investigation of the asphalt mixture morphology influence on its ageing susceptibility. Mater. Struct. 2013, 48, 1–14. [Google Scholar] [CrossRef]
- Zaumanis, M.; Poulikakos, L.D.; Partl, M.N. Performance-based design of asphalt mixtures and review of key parameters. Mater. Des. 2018, 141, 185–201. [Google Scholar] [CrossRef]
- Jenks, C.W.; Jencks, F.E.; Harrigan, T.; Adcock, M.; Delaney, E.P.; Freer, H. A Manual for Design of Hot Mix Asphalt with Commentary; NCHRP Report 673; Transportation Research Board, National Academy of Sciences: Washington, DC, USA, 2011. [Google Scholar]
- Vavrik, W.R.; Pine, W.J.; Huber, G.; Carpenter, S.H.; Bailey, R. The Bailey Method of Gradation Evaluation: The Influence of Aggregate Gradation and Packing Characteristics on Voids in the Mineral Aggregate. J. Assoc. Asph. Paving Technol. 2001, 70, 132–175. [Google Scholar]
- Yideti, T.F. Packing Theory-Based Framework for Performance Evaluation of Unbound Granular Materials; Royal Institute of Technology: Stockholm, Sweden, 2014. [Google Scholar]
- Li, S.; Zhao, J.; Lu, P.; Meng, L.; Li, T.; Jin, W. Research Progress on the Densest Packing of Basic 3D Objects. In Proceedings of the National Conference on Computational Mechanics of Granular Materials (CMGM-2012), Hunan, China, 16–18 September 2012. [Google Scholar]
- Meng, L.; Jiao, Y.; Li, S. Maximally dense random packings of spherocylinders. Powder Technol. 2016, 292, 176–185. [Google Scholar] [CrossRef]
- Meng, L.; Li, S. Disordered packing density of binary and polydisperse mixtures of curved spherocylinders. Particuology 2017, 32, 73–81. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Wu, K.; Wang, D. The CAVF method of asphalt mixture composition design. Highway 2001, 12, 17–21. [Google Scholar]
- Zhang, Y.M.; Chen, S.F.; Hu, G.W. Coarse aggregate gradation design of asphalt mixture by gradually filling test. J. Wuhan Univ. Technol. 2011, 33, 44–48. [Google Scholar]
- Chen, Z.; Yuan, W.; Gao, C. Research on Design Method of Multilevel Dense Built-in Gradation. China J. Highw. Transp. 2006, 19, 32–37. [Google Scholar]
- Miao, Y.; Wang, S.; Guo, L.; Li, J. A method for quantifying the packing function of particles in packed aggregate blend. Constr. Build. Mater. 2018, 188, 607–614. [Google Scholar] [CrossRef]
- Wang, L. An Evaluation of the Microstructure and the Macro-Behavior of Unbounded and Bounded Granular Materials; Georgia Institute of Technology: Atlanta, Georgia, 1998. [Google Scholar]
- Wang, L.B.; Frost, J.D.; Shashidhar, N. Microstructure study of WesTrack mixes from X-ray tomography images. Transp. Res. Rec. 2001, 1767, 85–94. [Google Scholar] [CrossRef]
- Moon, K.H.; Falchetto, A.C.; Jeong, J.H. Microstructural analysis of asphalt mixtures using digital image processing techniques. Can. J. Civ. Eng. 2014, 41, 74–86. [Google Scholar] [CrossRef]
- Wang, L.B.; Frost, J.D.; Lai, J.S. Three-dimensional digital representation of granular material microstructure from X-ray tomography imaging. J. Comput. Civ. Eng. 2004, 18, 28–35. [Google Scholar] [CrossRef]
- Al-Raoush, R. Microstructure characterization of granular materials. Phys. A Stat. Mech. Appl. 2007, 377, 545–558. [Google Scholar] [CrossRef]
- Lu, Y.; Garboczi, E.J. Bridging the Gap between Random Microstructure and 3D Meshing. J. Comput. Civ. Eng. 2014, 28, 4014007. [Google Scholar] [CrossRef]
- Stroeven, P.; Stroeven, M. Assessment of packing characteristics by computer simulation. Cem. Concr. Res. 1999, 29, 1201–1206. [Google Scholar] [CrossRef]
- Sobolev, K.; Amirjanov, A. Application of genetic algorithm for modeling of dense packing of concrete aggregates. Constr. Build. Mater. 2010, 24, 1449–1455. [Google Scholar] [CrossRef]
- Shen, S.; Yu, H. Characterize packing of aggregate particles for paving materials: Particle size impact. Constr. Build. Mater. 2011, 25, 1362–1368. [Google Scholar] [CrossRef]
- Xu, W.X.; Chen, H.S. Numerical investigation of effect of particle shape and particle size distribution on fresh cement paste microstructure via random sequential packing of dodecahedral cement particles. Comput. Struct. 2013, 114, 35–45. [Google Scholar] [CrossRef]
- Xu, W.X.; Lv, Z.; Chen, H.S. Effects of particle size distribution, shape and volume fraction of aggregates on the wall effect of concrete via random sequential packing of polydispersed ellipsoidal particles. Phys. A Stat. Mech. Appl. 2013, 392, 416–426. [Google Scholar] [CrossRef]
- Liu, L.; Shen, D.J.; Chen, H.S.; Xu, W.X. Aggregate shape effect on the diffusivity of mortar: A 3D numerical investigation by random packing models of ellipsoidal particles and of convex polyhedral particles. Comput. Struct. 2014, 144, 40–51. [Google Scholar] [CrossRef]
- Boler, H.; Qian, Y.; Tutumluer, E. Influence of Size and Shape Properties of Railroad Ballast on Aggregate Packing Statistical Analysis. Transp. Res. Rec. 2014, 94–104. [Google Scholar] [CrossRef]
- Han, D.; Zhu, J.H.; Li, L.; Pang, H.P. Verification and application of two-dimensional slice identification method in three-dimensional mesostructure under different aggregate gradations and packing algorithms. Constr. Build. Mater. 2016, 102, 843–851. [Google Scholar] [CrossRef]
- Ma, H.; Xu, W.; Li, Y. Random aggregate model for mesoscopic structures and mechanical analysis of fully-graded concrete. Comput. Struct. 2016, 177, 103–113. [Google Scholar] [CrossRef]
- Xiao, Y.; Tutumluer, E. Gradation and Packing Characteristics Affecting Stability of Granular Materials: Aggregate Imaging-Based Discrete Element Modeling Approach. Int. J. Geomech. 2017, 17. [Google Scholar] [CrossRef]
- Xu, H.; Xing, C.; Zhang, H.; Li, H.; Tan, Y. Moisture seepage in asphalt mixture using X-ray imaging technology. Int. J. Heat Mass Transf. 2019, 131, 375–384. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, J.; Dong, Q.; Tan, Y. Characterization of moisture vapor diffusion in fine aggregate mixtures using Fickian and non-Fickian models. Mater. Des. 2017, 124, 108–120. [Google Scholar] [CrossRef]
- Yu, B.; Gu, X.; Ni, F.; Gao, L. Microstructure characterization of cold in-place recycled asphalt mixtures by X-ray computed tomography. Constr. Build. Mater. 2018, 171, 969–976. [Google Scholar] [CrossRef]
- Gu, F.; Ma, W.; West, R.C.; Taylor, A.J.; Zhang, Y. Structural performance and sustainability assessment of cold central-plant and in-place recycled asphalt pavements: A case study. J. Clean. Prod. 2019, 208, 1513–1523. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Qian, G.; Zheng, J.; Zhang, Y. Three-Dimensional Simulation of Aggregate and Asphalt Mixture Using Parameterized Shape and Size Gradation. J. Mater. Civ. Eng. 2019, 31. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Gu, F.; Xu, T.; Wang, H. Impact of minerals and water on bitumen-mineral adhesion and debonding behaviours using molecular dynamics simulations. Constr. Build. Mater. 2018, 171, 214–222. [Google Scholar] [CrossRef]
- Dong, Q.; Yuan, J.; Chen, X.; Ma, X. Reduction of moisture susceptibility of cold asphalt mixture with Portland cement and bentonite nanoclay additives. J. Clean. Prod. 2018, 176, 320–328. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B.; Shu, X. Rubber modified concrete improved by chemically active coating and silane coupling agent. Constr. Build. Mater. 2013, 48, 116–123. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, H.; Shi, C.; Wei, C. Rheological performance investigation and sustainability evaluation of asphalt binder with thermochromic powders under solar radiation. Sol. Energy Mater. Sol. Cells 2019, 191, 175–182. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.; Xu, G.; Shi, C. Evaluation of aging behaviors of asphalt binders through different rheological indices. Fuel 2018, 221, 78–88. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Shi, C. Investigation of aging performance of SBS modified asphalt with various aging methods. Constr. Build. Mater. 2017, 145, 445–451. [Google Scholar] [CrossRef]
- Miao, Y.; Song, P.; Gong, X. Fractal and Multifractal Characteristics of 3D Asphalt Pavement Macrotexture. J. Mater. Civ. Eng. 2014, 26. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Digital Terrain Analysis; Science Press: Beijing, China, 2006. [Google Scholar]
- Ministry of Transport China. Test Methods of Aggregate for Highway Engineering (JTG E42-2005); China Communications Press: Beijing, China, 2005.
- Dullien, F. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]





| Size (mm) | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 |
| Crushed stone | 2.799 | 2.802 | 2.796 | 2.79 | 2.737 | 2.68 |
| Gravel | 2.546 | 2.538 | 2.581 | 2.565 | 2.501 | 2.594 |
| Bigger Particle | Smaller Particle | Combination Name | Size Ratio | ||
|---|---|---|---|---|---|
| Size (mm) | Size Range (mm) | Size (mm) | Size Range (mm) | ||
| 16 | 16–19 | 4.75 | 4.75–9.5 | 16 VS 4.75 | 0.297–0.5 |
| 16 | 16–19 | 2.36 | 2.36–4.75 | 16 VS 2.36 | 0.147–0.25 |
| 16 | 16–19 | 1.18 | 1.18–2.36 | 16 VS 1.18 | 0.074–0.124 |
| 4.75 | 4.75–9.5 | 2.36 | 2.36–4.75 | 4.75 VS 2.36 | 0.5 |
| 4.75 | 4.75–9.5 | 1.18 | 1.18–2.36 | 4.75 VS 1.18 | 0.25 |
| 2.36 | 2.36–4.75 | 1.18 | 1.18–2.36 | 2.36 VS 1.18 | 0.5 |
| Size (mm) | Type | Va (%) | ||||
|---|---|---|---|---|---|---|
| Loose | Dry-Rodded | Loose | Dry-Rodded | |||
| 16 | CS | 45.47 | 40.41 | 11.13 | 11.55 | 11.00 |
| G | 40.22 | 35.97 | 10.58 | |||
| 13.2 | CS | 44.18 | 40.18 | 9.05 | 8.30 | 13.04 |
| G | 40.51 | 34.94 | 13.75 | |||
| 9.5 | CS | 47.21 | 42.93 | 9.06 | 14.89 | 15.17 |
| G | 40.18 | 36.42 | 9.36 | |||
| 4.75 | CS | 46.52 | 41.91 | 9.90 | 16.64 | 15.37 |
| G | 38.78 | 35.47 | 8.53 | |||
| 2.36 | CS | 47.47 | 42.52 | 10.44 | 12.22 | 10.83 |
| G | 41.67 | 37.91 | 9.03 | |||
| 1.18 | CS | 47.92 | 44.11 | 7.95 | 5.27 | 7.25 |
| G | 45.40 | 40.91 | 9.89 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Y.; Liu, X.; Hou, Y.; Li, J.; Wu, J.; Wang, L. Packing Characteristics of Aggregate with Consideration of Particle size and Morphology. Appl. Sci. 2019, 9, 869. https://doi.org/10.3390/app9050869
Miao Y, Liu X, Hou Y, Li J, Wu J, Wang L. Packing Characteristics of Aggregate with Consideration of Particle size and Morphology. Applied Sciences. 2019; 9(5):869. https://doi.org/10.3390/app9050869
Chicago/Turabian StyleMiao, Yinghao, Xin Liu, Yue Hou, Juan Li, Jiaqi Wu, and Linbing Wang. 2019. "Packing Characteristics of Aggregate with Consideration of Particle size and Morphology" Applied Sciences 9, no. 5: 869. https://doi.org/10.3390/app9050869
APA StyleMiao, Y., Liu, X., Hou, Y., Li, J., Wu, J., & Wang, L. (2019). Packing Characteristics of Aggregate with Consideration of Particle size and Morphology. Applied Sciences, 9(5), 869. https://doi.org/10.3390/app9050869






