Nonlinear Modeling and Flight Validation of a Small-Scale Compound Helicopter

Abstract

The compound configuration is a good option for helicopters to break through speed limitation and improve maneuverability. However, the compound configuration applied on the small-scale helicopter has not been investigated in detail. In this study, an 11-state nonlinear dynamics model of a small-scale compound helicopter was established with the help of first physical principles and linear modification method. The ducted fan, free-rotate wing and horizontal stabilizer were considered in the compound configurations. To validate the accuracy of the model, high-quality flight data were obtained in hover and forward flights from 15 m/s to 32 m/s. Results show that the overall responses of the developed nonlinear model matched the hover data. In forward flight, it was proved that the nonlinear model has high accuracy in agreement with trim results and time-domain simulations. The wing model works well below 27 m/s. Furthermore, the effectiveness of the elevator and aileron in high speed was also verified in the simulation of a coordinated turn.

1. Introduction

Conventional helicopters use the rotor as the main lift component. In high-speed forward flight, the main rotor is operated in a complex mode. It provides forward thrust while providing the upward lift. This working mode suffers from disadvantages. Helicopters have notably good low-speed characteristics and can vertically take off and land (VTOL), which minimizes the requirements for a landing field. The helicopter can complete many rescue missions and heavy transport missions. In contrast, the fixed-wing aircraft offers excellent performance in the high-speed range. In a high-speed flight condition, the fixed-wing aircraft, which has a pure lift generator (wing) and a pure thrust generator (propeller), is much more efficient than a helicopter.

Aviation pioneers have attempted to combine fixed wing components with the helicopter to design a better configuration since the mid-20th century. For attack demands, many compound configurations were created to achieve better speed performance, enhanced cruise efficiency and higher altitude characteristics for aircraft such as the AH-56A Cheyenne, the Piasecki X-49A Speedhawk of 2007, the Sikorsky X2 demonstrator of 2008 and the Eurocopter X3 of 2010. The cruise speed of the compound helicopter exceeded 250 knots [1], which is a truly impressive result. The strategies of these existing products vary but the common point is that they all use propellers to create extra thrust and a wing is required to unload the rotor, except for the X2, which makes use of coaxial rotors. A fundamental compound helicopter configuration [2] uses a wing to unload the rotor and a propeller to create forward thrust in forward flight.

There is some research that focuses on the application of full-scale compound helicopters. In References [3] and [4], the authors investigated the trim results and the dynamic behaviors of the compound configurations similar to X2 and X3. It was discovered that the compound configuration demonstrates higher maneuverability in certain special maneuvers. In References [5,6,7], the NASA Heavy Lift Rotorcraft System Investigation program gave a comprehensive analysis on multiple compound helicopter configurations. CAMRAD II program was adopted to conduct overall design and optimization. NDARC (NASA Design and Analysis of Rotorcraft) software was utilized to design a slow-rotor, which can reduce aerodynamic drag in high speed. In Reference [8], a software was designed to optimize and visualize a multi-dimensional compound helicopter design problem. In Reference [9], a compound helicopter modified based on the GENHEL UH-60A model was considered for control optimization design. However, the algorithm was time-consuming for recent practical applications. Since the volume of research into compound helicopters is small and the existing compound products are military demonstrator types, the available flight data is quite limited and additional work is required in the practical domain. Meanwhile, with the rapid development of the unmanned helicopter nowadays, the great potential of compound helicopter miniaturization cannot be denied [10]. More practical research into compound helicopters can be conducted in the small-scale domain.

In the small-scale domain, some experience has been accumulated upon modeling methods. [11,12] gave linear dynamics models of CMU (Carnegie Mellon University) R-50 helicopter under hover and 15 m/s forward flight condition. The models were obtained by using system identification method in CIFER (developed by NASA Ames Research Center, CA, USA) software [13]. Similarly, in Reference [14], the hover and 9 m/s models of 5 kg Raptor 50 helicopter were identified from CIFER. [15] established the nonlinear model of a 10 kg helicopter based on first physical principles. The whole model proved to have good accuracy up to 15 m/s. Unfortunately, it is difficult to find more research that focuses on small-scale helicopters above 15 m/s forward speed. Apart from modeling by first physical principles, nonlinear models can also be obtained by nonlinear identification [16,17,18]. In the modeling, about 10~30 unknown parameters were selected for identification. Prediction error method (PEM) [17] or genetic convergent algorithm [16] can be adopted for searching the optimal values of the unknown parameters. However, these methods also need flight data of multiple operating conditions. In addition to the small-scale helicopter modeling, there is little research about the small-scale compound helicopters. Therefore, huge research potential can be explored in this domain.

This study intends to establish a reliable nonlinear mathematical model for a small-scale compound helicopter. The modeling method is meaningful not only for this particular prototype model but also for the compound research on multiple small-scale helicopter platforms, such as Yamaha R-50 [11], AF25B [17], MIT X-cell [11,12,19], NUS Raptor 90 SE HeLion [15,20], Raptor 50 [14] and so forth. In the study, three compound configurations were considered: (1) the general helicopter carried the ducted fan; (2) the general helicopter carried the ducted fan and free-rotate wing; (3) the general helicopter carried the ducted fan, free-rotate wing and horizontal stabilizer. In the modeling, components were established separately at first and were assembled together. The full model was modified by combining the system identification results. Flight data were obtained from hover condition to 32 m/s forward flight condition. The nonlinear model was validated using the trim results and the time-domain responses data. Furthermore, the validated model was expanded to calculate a coordinated turn route. The elevator and aileron work efficiently in the simulation. The study gives deep insight into small-scale helicopter dynamics over a wider speed range.

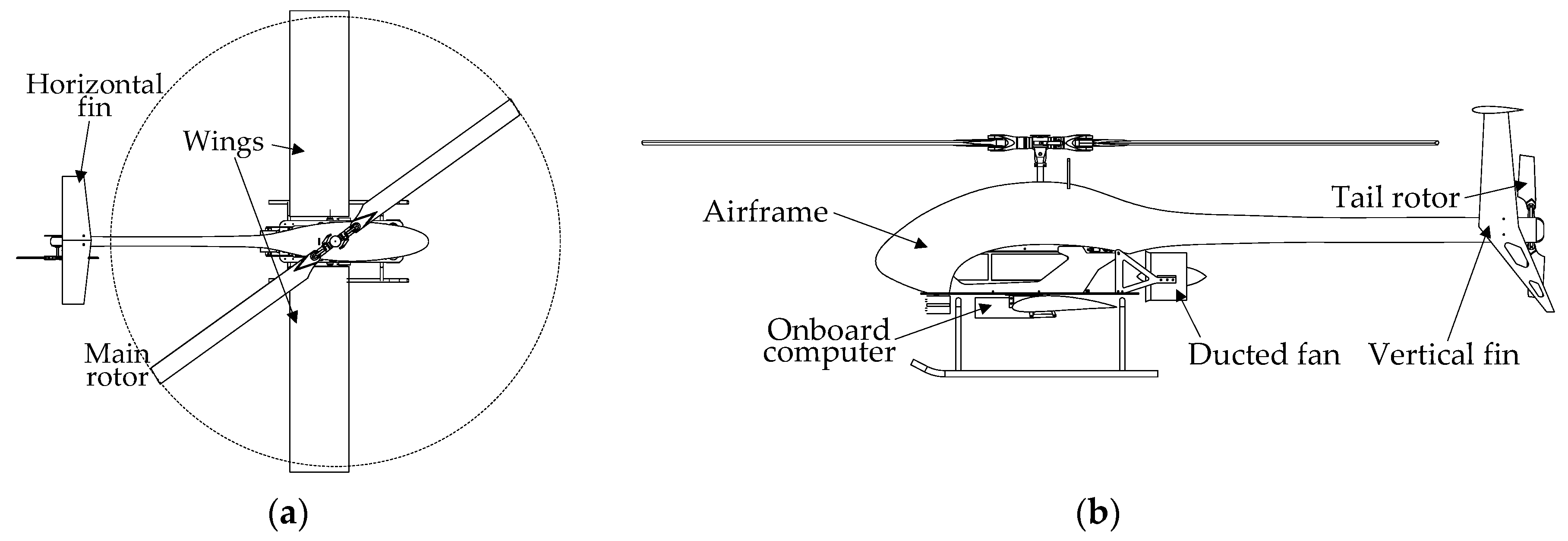
2. Small-Scale Compound Helicopter (SCH) Illustration

The small-scale compound helicopter (SCH) prototype model is shown in Figure 1. According to our previous experience, SCH greatly increased the maximum speed in forward flight from the original 25 m/s to 32 m/s due to the effect of the compound components on a general helicopter. Meanwhile, SCH improved the flight performance in high speed conditions. For SCH, there are two configurations that have been realized in the real flights (see Figure 1):

• Configuration D: general helicopter + ducted fan.
• Configuration WD: general helicopter + ducted fan + wings.

In addition, one more configuration is considered for simulation purpose (see Figure 2a,b):

• Configuration WDH: general helicopter + ducted fan + wings (work also as ailerons) + elevator (on the horizontal stabilizer).

In the following sections, the design of the SCH and the method of parameter collection will be introduced in a detailed manner.

2.1. General Helicopter Components

The FORZA 700 helicopter was used as the main component in SCH prototype model. This version is an electric type, motor powered. It does not have a stabilizer bar. To obtain all of the parameters needed for analysis, five steps can be used: direct measurement, ground experiment, aerodynamic coefficient gathering, flight testing and fine-tuning [20]. Now the first two steps will be expanded.

The size parameters were directly measured and the blade moment of inertia was calculated. The center of gravity (CG) was measured using the suspension method. High-quality photos were captured at each suspension position and the intersection point (CG) of the suspension lines was found by photo post-processing. The measured parameters are shown in

Table 1. Parameters from direct measurement.

Parameter	Value	Meaning
$I_{\mathrm{mr}}$	0.0715 $\mathrm{kg}\cdot {\mathrm{m}}^2$	Main rotor blade moment of inertia related to the hub
$R_{\mathrm{mr}}$	0.767 $\mathrm{m}$	Main rotor disc radius
$R_{tr}$	0.137 $\mathrm{m}$	Tail rotor disc radius
$c_{mr}$	0.065 $\mathrm{m}$	Main rotor blade chord length
$c_{tr}$	0.031 $\mathrm{m}$	Tail rotor blade chord length
$l_f$	1.332 $\mathrm{m}$	Airframe length
$D_{tr}$	0.963 $\mathrm{m}$	Tail rotor hub location behind the CG
$H_{tr}$	0.025 $\mathrm{m}$	Tail rotor hub location above the CG
$H_{mr}$	0.214 $\mathrm{m}$	Main rotor hub location above the CG
$g$	9.8015 $\mathrm{N}\cdot {\mathrm{kg}}^{-1}$	Acceleration due to gravity
$\rho$	1.225 $\mathrm{kg}/{\mathrm{m}}^3$	Air density
${\Omega }_{mr}$	1700 $\mathrm{rpm}$	Main rotor rotation speed
${\Omega }_{tr}$	360.2 $\mathrm{rpm}$	Tail rotor rotation speed

:

The swashplate of the helicopter was controlled by three servo actuators. The fourth servo controlled the tail rotor. ${\theta }_0$, ${\theta }_{1c}$ and ${\theta }_{1s}$ (deg) are the main rotor pitch components, which represent collective pitch, lateral cyclic pitch and longitudinal cyclic pitch, respectively. ${\theta }_T$ (deg) is the tail rotor collective pitch. The four control angles can be decided based on the pitch linkage and swashplate geometry as below:

$$\{\begin{array}{c}{\theta }_0=K_1\left(\frac{{\theta }_{A1}+{\theta }_{A2}+{\theta }_{A3}}{3}\right)+{\theta }_{00}\\ {\theta }_{1\mathrm{c}}=K_2\left(\frac{{\theta }_{A1}-{\theta }_{A2}}{2}\right)+{\theta }_{1\mathrm{c}0}\\ {\theta }_{1s}=K_3\left(\frac{{\theta }_{A1}+{\theta }_{A2}}{3}-\frac{2{\theta }_{A3}}{3}\right)+{\theta }_{1\mathrm{s}0}\\ {\theta }_T=K_4{\theta }_{A4}+{\theta }_{\mathrm{T}0}\end{array}$$

(1)

where $\left({\theta }_{00},{\theta }_{1c0},{\theta }_{1s0},{\theta }_{\mathrm{T}0}\right)$ correspond to the mid-point of the pitch angle ranges; $\left({\theta }_{A1},{\theta }_{A2},{\theta }_{A2},{\theta }_{A2}\right)$ are the control signals of the four servo actuators (normalized to [−0.5,0.5]). The three swashplate actuators are equispaced as shown in Figure 3. All the linkage gains can be obtained by identification tests on the ground, shown in

Table 2. Linkage gains.

Parameter	Value
$K_1$	22.67
$K_2$	16.06
$K_3$	14.64
$K_4$	64.70

. After $\left({\theta }_0,{\theta }_{1c},{\theta }_{1s},{\theta }_T\right)$ were obtained, the variables were normalized to [−0.5,0.5], marked as $\left({\delta }_{col},{\delta }_{lat},{\delta }_{lon},{\delta }_{ped}\right)$, respectively denoting collective, lateral cyclic, longitudinal cyclic and pedal control inputs.

2.2. Compound Components

In the early stage of the research, the basic FORZA 700 helicopter (Manufacturer: JRPROPO - Japan Remote Control Co,. Ltd, Tokyo, Japan) was tested in automatic flight. It was found that above 20 m/s the helicopter showed generally bad flight performance, such as large negative pitch angle, large collective pitch and high power consumption. It was hypothesized that, by combining features of ducted fan and wing, the maximum speed of the helicopter could be increased and the flight quality at high speed will be improved. A target for realization of 30 m/s forward speed in SCH was set. The size of the compound components was decided as follows.

For the wing component, the lift of the wing was expected to produce 80~90% of the total lift needed for the whole helicopter, from 20 m/s to the highest speed. The wingspan was chosen equal to $R_{mr}$, with an 11% cut at the root by the airframe. The lift was predicted by using CFD method. NACA4415 airfoil was selected due to its higher lift-to-drag ratio and sufficient thickness. For the ducted fan, similarly, the thrust was expected to create 80~90% of the total forward force. The choice of the ducted fan also took into consideration the weight and capacity of the batteries. In addition, the horizontal stabilizer was designed for balancing the pitching moments and exercising pitch control at high speed. The horizontal stabilizer was placed on the top of the T-tail, relatively clear of the rotor wake, as shown in Figure 2. The elevator occupied 36% of the stabilizer’s chord and its span equals to that of the stabilizer. Finally, the parameters of compound components are shown in

Table 3. Compound component parameters.

Parameter	Value	Meaning
$b_w$	0.75 m	Half wingspan
$c_w$	0.204 m	Wing chord
$D_w$	0.015 m	Wing hub location behind the CG
$H_w$	0.08 m	Wing hub location below the CG
$b_{hf}$	0.3 m	Horizontal stabilizer span
$c_{ele}$	0.03 m	Elevator chord
$S_{hf}$	0.025 m2	Horizontal stabilizer area
$D_{ht}$	0.967 m	Horizontal stabilizer location behind the CG
$H_{ht}$	0.276 m	Horizontal stabilizer location above the CG
$H_{dt}$	0.01 m	Ducted fan shaft location below the CG
$T_{df\_\max }$	3.4 kg	90 mm Ducted fan maximum thrust

.

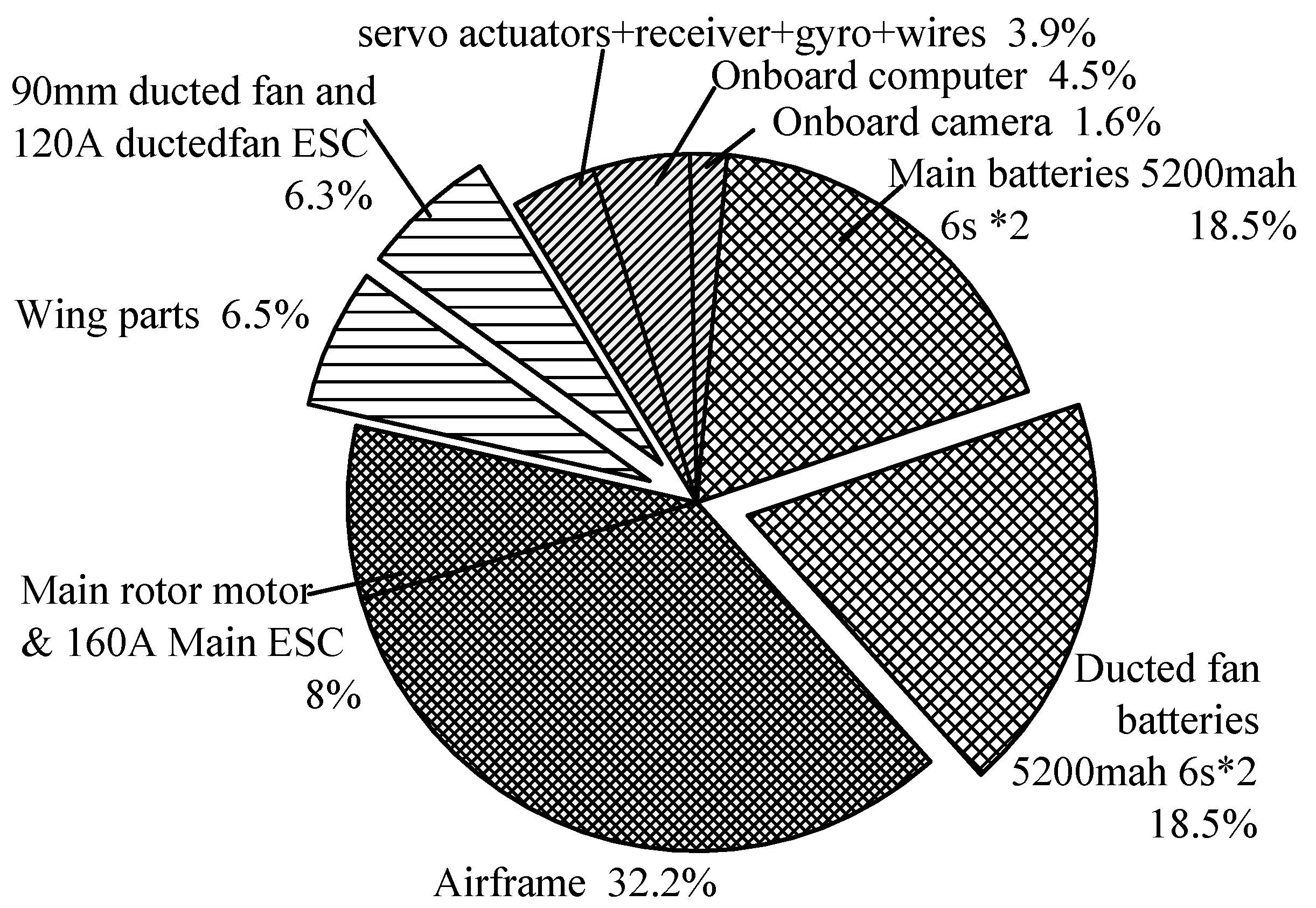
2.3. Overall Parameters

After assembling all components, the first item was the measurement of the CG (described above). Then, the work moved on to the moment of inertia of the helicopter. The moment of inertia can be obtained by physical experiments using the trifilar pendulum method [18]. In this method, a frame was built and was suspended by three ropes. The helicopter was placed on the frame centered at the CG and the oscillation period was recorded to calculate the 3-axis moment of inertia.

The weight distribution of Configuration WD is shown in Figure 4. All the data were collected from the real prototype model. The compound components accounted for 31.3% of the entire weight. The total weight $m$ was 9.5 kg. This total weight was the same between Configuration D and Configuration WD. In Configuration D, the model had extra weight installed to replace the wing. The onboard computer was suspended under the airframe board. It sent control signals to the actuators and recorded the flight data into a SD card.

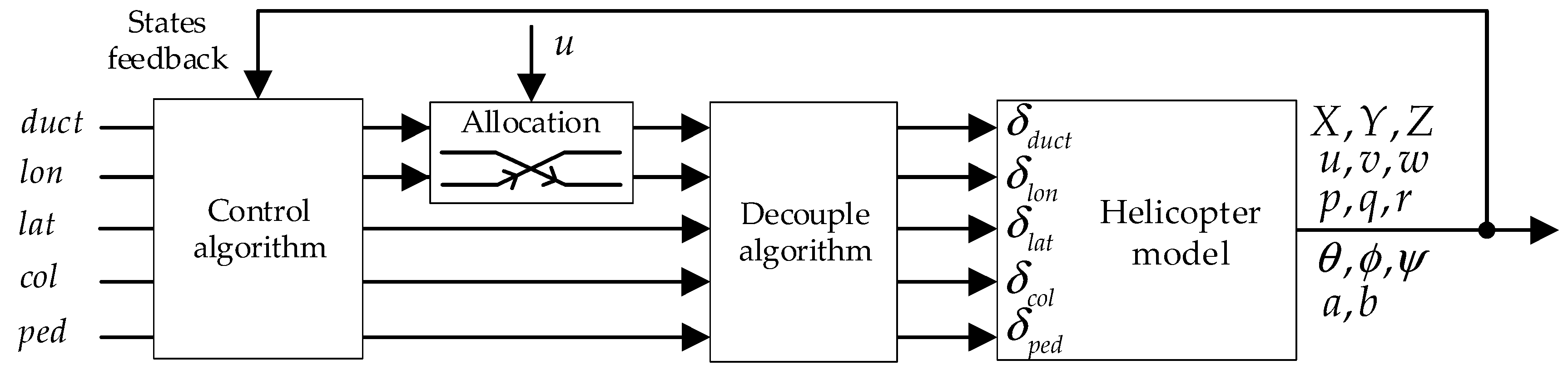
3. SCH Nonlinear Mathematical Model (NMM)

3.1. Modeling According to First Physical Principles

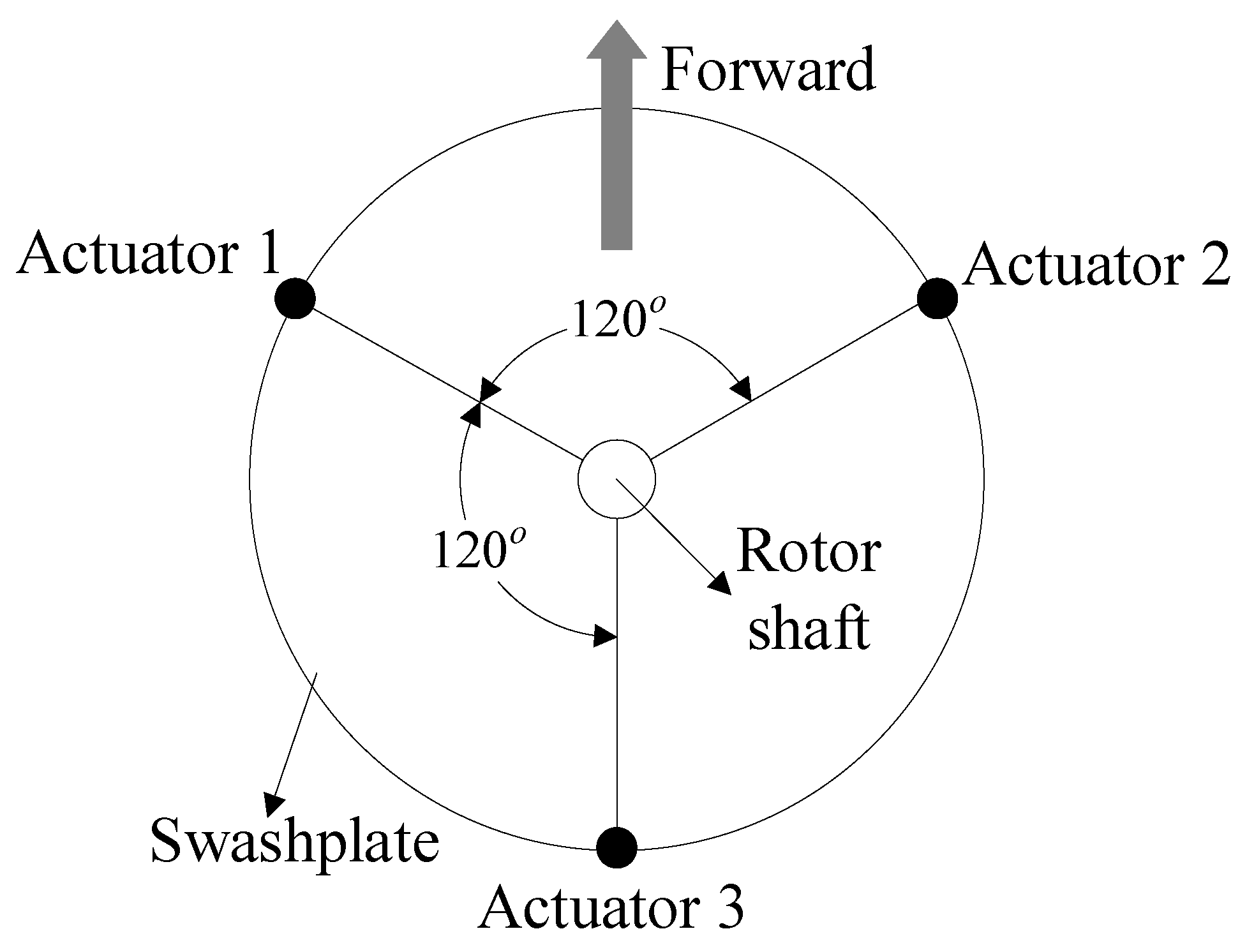
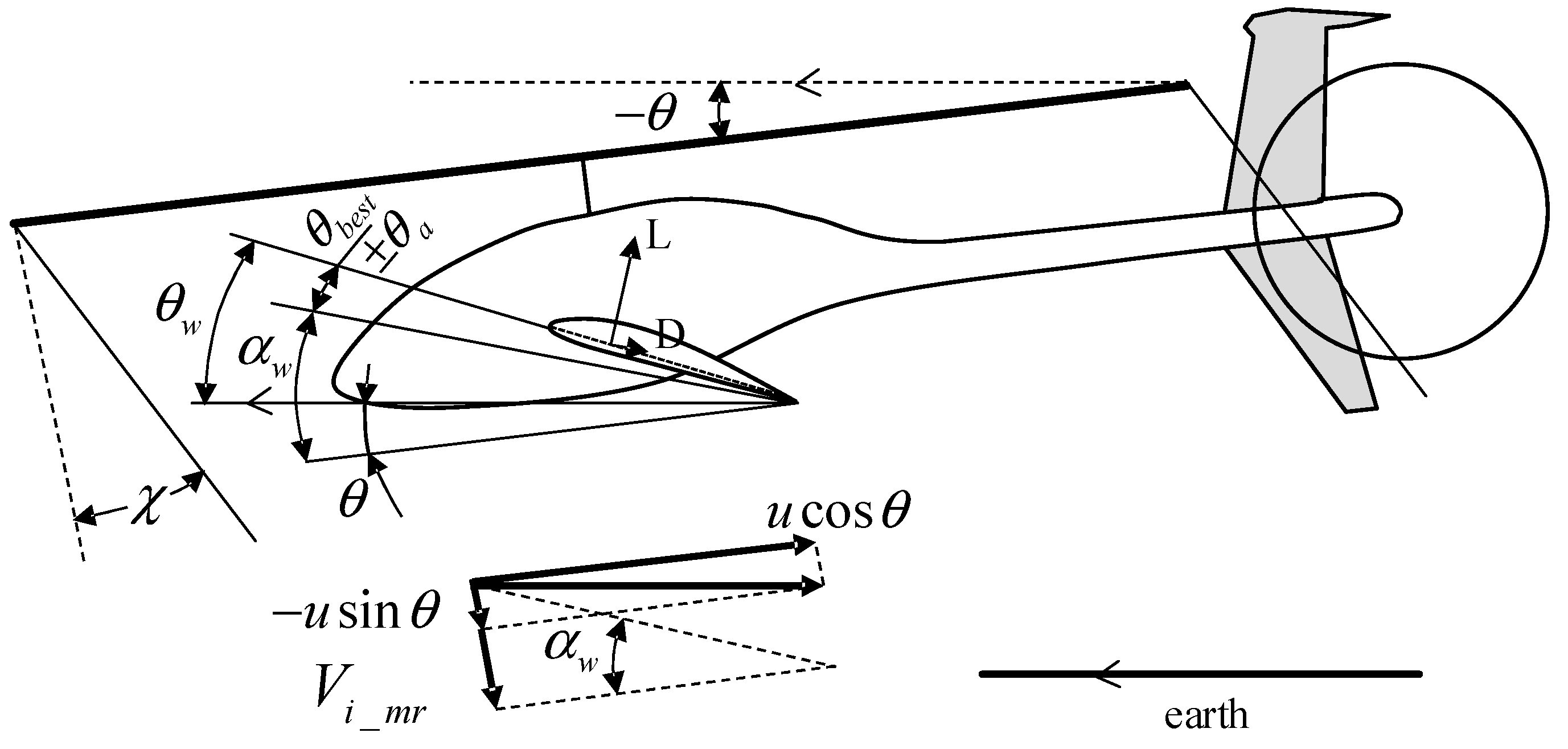
3.1.1. Main Rotor Model

To build a whole dynamics model, a method with suitable complexity must be chosen. For this 2-blade single-rotor small-scale helicopter, the complex rotor dynamics can be simplified while maintaining sufficient accuracy. First, a uniform inflow model was adopted and the induced velocity $v_{imr}$ was iteratively computed with the rotor lift [21]. A coupled first-order tip-path-plane (TPP) equation in roll and pitch motions was applied [12]:

$$\begin{gathered} {\tau }_f\dot{a}=-a-{\tau }_{f}q-\frac{1}{{\Omega }_{mr}}p+\frac{8}{\gamma {\Omega }_{mr}^2}\frac{K_{\beta }}{I_{\beta }}b+{\theta }_{1s} \\ {\tau }_f\dot{b}=-b-{\tau }_{f}p-\frac{1}{{\Omega }_{mr}}q+\frac{8}{\gamma {\Omega }_{mr}^2}\frac{K_{\beta }}{I_{\beta }}a+{\theta }_{1c} \end{gathered}$$

(2)

where ${\tau }_f$ is the rotor time constant, $\gamma$ is the rotor Lock number, $K_{\beta }$ is the spring constant of the flapping configuration and $I_{\beta }$ is the blade moment of inertia about the flapping hinge. $a$ and $b$ are the longitudinal and lateral flap angles.

$${\tau }_f=\frac{16}{\gamma {\Omega }_{mr}}$$

(3)

$$\gamma =\frac{\rho c_{mr}{a}_0{R}_{mr}^4}{I_{\beta }}$$

(4)

where $a_0$ is the lift coefficient slope of blade. In hover condition, $\gamma$ can be corrected for the inflow effects [13]. The effective Lock number ${\gamma }_{eff}$ is

$${\gamma }_{eff}=\frac{\gamma }{1+a_{0}s/16{\lambda }_i}$$

(5)

where $s$ is the rotor solidity and ${\lambda }_i$ is the non-dimensional inflow ratio, ${\lambda }_i=\sqrt{C_T/2}$. The rotor force and moment can be simplified using the TPP equation.

$$\begin{gathered} X_{mr}=-T_{mr}\sin a\cos b \\ {Y}_{mr}=T_{mr}\sin b\cos a \\ {Z}_{mr}=-T_{mr}\cos a\cos b \\ {L}_{mr}=(H_{mr}{T}_{mr}+K_{\beta })\sin b \\ {M}_{mr}=(H_{mr}{T}_{mr}+K_{\beta })\sin a \\ {P}_{mr}=-N_{mr}{\Omega }_{mr} \end{gathered}$$

(6)

where $X$, $Y$ and $Z$ are forward force, side force and upward force, respectively. $L$, $M$ and $N$ are roll moment, pitch moment and yaw moment, respectively. $T_{mr}$ is the rotor thrust, calculated by the blade element method. This simplification (Equation (6)) is credible for $\mu <0.3$ (equivalent to $u<42.7\mathrm{m}/\mathrm{s}$ for SCH) [21]. According to our flight condition, the simplification is trustworthy. The rotor rotation speed ${\Omega }_{mr}$ was fixed by the Krosmik ESC to 1700 rpm during the flights. $N_{mr}$ was calculated by the integration of blade elements’ drag [22].

3.1.2. Airframe Model

The form of the helicopter airframe was irregular. Even if the fairing was installed, the airframe can produce notably little moment. The forces can be expressed by drag area and velocities [20]:

$$X_f=\{\begin{array}{c}-\frac{\rho }{2}{S}_{fx}{u}_b{v}_{imr}\begin{array}{cc},& \end{array}if\left|u_b\right|\le v_{imr}\\ -\frac{\rho }{2}{S}_{fx}{u}_b\left|u_b\right|\begin{array}{cc},& \end{array}if\left|u_b\right|>v_{imr}\end{array}$$

(7)

$$Y_f=\{\begin{array}{c}-\frac{\rho }{2}{S}_{fy}{v}_b{v}_{imr}\begin{array}{cc},& \end{array}if\left|v_b\right|\le v_{imr}\\ -\frac{\rho }{2}{S}_{fy}{v}_b\left|v_b\right|\begin{array}{cc},& \end{array}if\left|v_b\right|>v_{imr}\end{array}$$

(8)

$$Z_f=-\frac{\rho }{2}{S}_{fz}(w_b-v_{imr})\left|w_b-v_{imr}\right|$$

(9)

where $u$, $v$ and $w$ are the 3-axis velocities. The subscript ${}_b$ represents the airframe coordinate system [23]. $S_{fx}$, $S_{fy}$ and $S_{fz}$ represent the airframe effective drag area in three axes. These drag areas can be obtained by measuring the projected areas of three axes on a 3D CATIA helicopter model.

3.1.3. Tail Model

The tail rotor model is similar to that of the main rotor but simpler. In this section, the flapping of tail rotor was neglected. The velocity field was influenced by the induced velocity from the main rotor. The function of the tail rotor is to balance the anti-torque and produce a yaw moment. Thus, the yaw moment created by the tail must be equal to the torque of the main rotor at the steady condition. The induced velocity of the tail rotor can be iteratively computed in a manner similar to that used on the main rotor. The tail rotor had only one control parameter, ${\delta }_{ped}$. The thrust $T_{tr}$ was calculated by the blade element method. Then,

$$Y_{tr}=-T_{tr}$$

(10)

$$L_{tr}=Y_{tr}{H}_{tr}$$

(11)

$$N_{tr}=-Y_{tr}{D}_{tr}$$

(12)

In the steady condition,

$$N_{tr}=-N_{mr}$$

(13)

3.1.4. Vertical Fin Model

Most of the time, the vertical fin had a safety-related function rather than a stability function for this helicopter. There was no rudder on the vertical fin. Yaw control in real flights totally relied on the tail rotor. When the speed increased, the force and moment of this small fin would be enlarged.

$$Y_{vf}=\{\begin{array}{c}-\frac{1}{2}\rho a_{0vf}{S}_{vf}{v}_{vf}\left|u_b\right|,\hspace{1em}\hspace{1em}if\left|\frac{v_{vf}}{u_b}\right|\le \tan {\alpha }_s\\ -\frac{1}{2}\rho S_{vf}{v}_{vf}\left|v_{vf}\right|,\hspace{1em}\hspace{1em}if\left|\frac{v_{vf}}{u_b}\right|>\tan {\alpha }_s\end{array}$$

(14)

$$L_{vf}=Y_{vf}{H}_{vf}$$

(15)

$$N_{vf}=-Y_{vf}{D}_{vf}$$

(16)

where ${\alpha }_s$ is the stall angle of vertical fin, $v_{vf}$ is the side velocity at the position of the vertical fin and $a_0{}_{vf}$ is the lift coefficient slope.

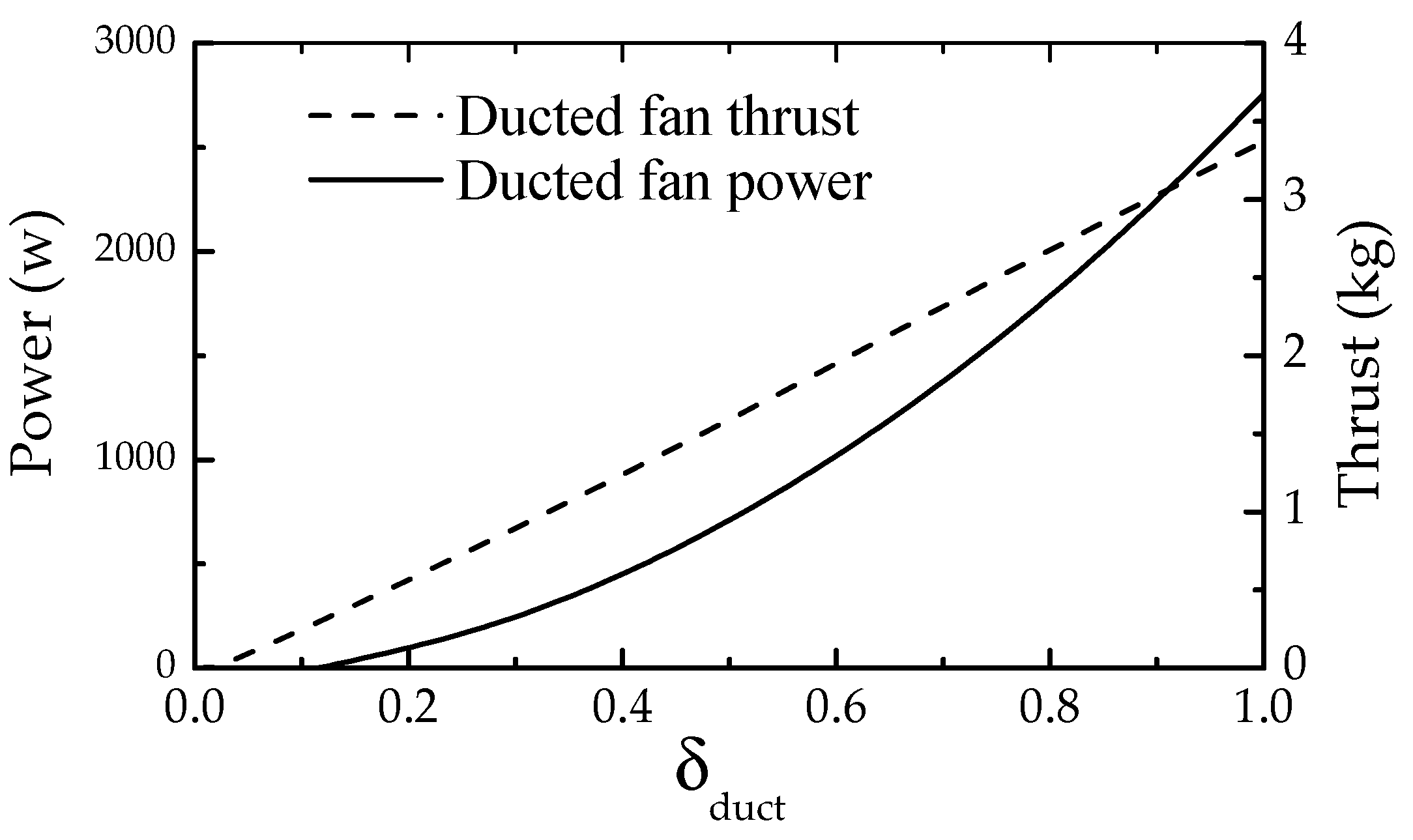
3.1.5. Ducted Fan Model

The static thrust and power data of the ducted fan were obtained from ground experiments. The results are shown in Figure 5. The ducted fan can produce an x-direction force $X_{duct}$ and y-axis moment $M_{duct}$. The delay of the force action was estimated as 0.4 s. The control signal ${\delta }_{duct}$ was normalized to [0,1].

3.1.6. Wing Model

In the previous research such as in Speedhawk compound helicopter, for reducing the cost of drag under hover condition, a large area of flap was partitioned on the wing. Apart from the drag in hover, problems arise during a transition flight when the angle of attack (AoA) is influenced by the airframe pitch angle. To solve these problems, a free-rotate wing was designed and installed on the test model. The wings on both sides of the airframe can rotate around its pitch axis controlled by servo actuators. The wing angle can change from $-20°$ to $90°$, which meets the demand of the VTOL inflow condition. Different input signals in each half of the wing also made the aileron control possible. The innovative wing solved the interference problem to a simple one. When in hover, the wing rotated to vertical orientation and in forward flight, the wing rotated to level orientation. During forward flight, the influence of the airframe pitch angle on the wings was balanced automatically.

$$\mathrm{Mode}1\mathrm{Hover}:{\theta }_w={\theta }_{best}$$

(17)

$$\mathrm{Mode}2\mathrm{Forward}\mathrm{flight}:{\theta }_w={\theta }_{best}-\theta (1-e^{-s{t}_w})\pm {\theta }_a\begin{array}{cc},& \end{array}\left({\theta }_w+\theta \right)\in \left[-20°,90°\right]$$

(18)

$${\theta }_{best}=\{\begin{array}{c}90°\begin{array}{ccc},& \mathrm{while}& \mathrm{Mode}1\end{array}\\ 5°\begin{array}{ccc},& \mathrm{while}& \mathrm{Mode}2\end{array}\end{array}$$

(19)

In the mode illustrations, $\theta$ is the pitch angle of helicopter. ${\theta }_a$ is the maneuver signals of aileron differential angles on each half of the wing. $t_w$ is the delay of the pitch control. ${\theta }_w$ is the pitch angle of the wing with respect to the helicopter’s body-fixed axes. During hover, ${\theta }_{best}$ was set to ${90}^{\mathsf{o}}$ and the wing was in vertical position for reducing drag. In forward flight, ${\theta }_{best}$ was selected for a greater ratio of lift-to-drag coefficient with consideration of a suitable moment. In the experiments, ${\theta }_{best}$ was set to $5^{\mathsf{o}}$ in mode 2. The angles mentioned above are shown in Figure 6.

In the modeling, to reduce the complexity, the interference from the main rotor to the wing was simplified by a linear interference assumption: First, calculate $\chi$, the wake skew angle of main rotor.

$$\tan \chi =\frac{\mu }{\lambda }=\frac{u\cos \theta }{v_{imr}-u\sin \theta }$$

(20)

With the aid of the CATIA helicopter model, it is known that when $\chi <70°$, the wing was located inside the wake of the rotor. In this condition, $v_{imr}$ should be considered. When $\chi >70°$, the wing was clear from the rotor wake and thus $v_{imr}$ should not be a factor. Then a linear change of $v_{imr}$ between $\chi \in \left[0°,70°\right]$ was assumed. The forces of the wings can be decided and the lift and drag in mode 2 can be written as:

$$dL=\frac{1}{2}\rho v_y^2{c}_y{C}_{l}dy$$

(21)

$$dD=\frac{1}{2}\rho v_y^2{c}_y{C}_{d}dy$$

(22)

$$Z=\sin {\alpha }_w{\displaystyle \int dD}-\cos {\alpha }_w{\displaystyle \int dL}$$

(23)

$$X=-\cos {\alpha }_w{\displaystyle \int dD}-\cos {\alpha }_w{\displaystyle \int dL}$$

(24)

$$C_l=f_l({\theta }_w)\begin{array}{cc},& \end{array}{C}_d=f_d({\theta }_w)$$

(25)

where $y$ is the distance to the rotor shaft. The subscript ${}_y$ represents the value of variables at the position $y$. $c$ is the wing chord. $C_l$ and $C_d$ are the lift and drag coefficients, respectively. ${\alpha }_w$ represents the inflow angle.

3.1.7. Horizontal Stabilizer Model

The horizontal stabilizer improves the pitch stability at high speed. When the speed increases, the stabilizer acts as a small wing that produces forces under the action of flow. Suppose ${\alpha }_{ht}$ is the effective AoA of the horizontal stabilizer. The pitch moment $M_{ht}$ and lift $T_{ht}$ produced by the stabilizer can be expressed as below:

$$M_{ht}=-T_{ht}{H}_{ht}$$

(26)

$$T_{ht}=\frac{1}{2}\rho u_b^2{S}_{ht}{C}_{L.ht}=\frac{1}{2}\rho u_b^2{S}_{ht}{C}_{L{\alpha }_{ht}.ht}{\alpha }_{ht}$$

(27)

where $C_{L{\alpha }_{ht}.ht}$ is the lift coefficient slope of horizontal stabilizer.

The horizontal stabilizer had an elevator on it. When the elevator deflected, it produced a lift increment $\Delta T_{ht}$ to the horizontal stabilizer. The lift increment caused a pitch moment increment $\Delta M_{ht}$ to the entire helicopter.

$$\Delta M_{ht}=-\Delta T_{ht}{H}_{ht}=-\frac{1}{2}\rho u_b^2{S}_{ht}{H}_{ht}{C}_{L{\theta }_e.ht}{\theta }_e$$

(28)

In Equation (28), ${\theta }_e$ is the elevator deflection angle. $C_{L{\theta }_e.ht}$ is the lift coefficient slope of ${\theta }_e$, where $C_{L{\theta }_e.ht}=\partial C_{L.ht}/\partial {\theta }_e$. $C_{L.ht}$ is the lift coefficient of horizontal stabilizer. According to [24], the coefficient of efficiency ${\eta }_e$ can be expressed as follows:

$${\eta }_e=\frac{C_{L{\theta }_e.ht}}{C_{L{\alpha }_{ht}.ht}}=\sqrt{\frac{S_e}{S_{ht}}}$$

(29)

Thus,

$$\Delta M_{ht}=-\Delta T_{ht}{H}_{ht}=-\frac{1}{2}\rho u_b^2{S}_{ht}{H}_{ht}{C}_{L{\alpha }_{ht}.ht}{\eta }_e{\theta }_e$$

(30)

3.1.8. Full Dynamics Model

After establishing the mathematical models of all components, an 11-state nonlinear SCH simulation model is assembled. The model has seven inputs: four command signals of general helicopter $\left({\delta }_{col},{\delta }_{lat},{\delta }_{lon},{\delta }_{ped}\right)$ and three command signals of compound components $\left({\delta }_{duct},{\theta }_a,{\theta }_e\right)$.

To simulate the helicopter responses under the control signals, the rigid-body motion of equations is written in the Newton-Euler form:

$$\dot{v}=\frac{1}{m}\stackrel{⌢}{F}-\omega \times v$$

(31)

$$\dot{\omega }=I^{-1}\stackrel{⌢}{M}-I^{-1}(\omega \times I\omega )$$

(32)

$$\dot{\theta }=\Phi (\theta )\omega$$

(33)

The states in this motion of equations are: linear velocity $\mathrm{v}={[\begin{array}{ccc}u& v& w\end{array}]}^T$, angular velocity $\mathsf{\omega }={[\begin{array}{ccc}p& q& r\end{array}]}^T$ and Euler angles $\mathsf{\theta }={[\begin{array}{ccc}\varphi & \theta & \psi \end{array}]}^T$. Consider the flap angles $a$ and $b$, the full nonlinear model is 11-state. $\stackrel{⌢}{F}=[X,Y,Z]$ and $\stackrel{⌢}{M}=[L,M,N]$ are the external force and moment vectors. The moment of inertia is defined by $I=dia{g}_{3\times 3}(\begin{array}{ccc}{I}_{xx},& I_{yy},& I_{zz}\end{array})$. $\mathsf{\Phi }$ is the velocity transformation matrix from body coordinate system [23] to ground coordinate system.

3.2. Nonlinear Model Modification

The advantage of a nonlinear model is that it contains dynamic features of a wider flight envelope. However, the accuracy of pure nonlinear modeling of helicopters is always unsatisfied. On the contrary, the linear models obtained from system identification method can provide more accurate results but only under the particular test conditions. Therefore, in this study, a linear modification method was designed to improve whole-model performances. The method extracted several essential nonlinear parameters and modified them with reference to system identification results.

In this section, the identification results adopt previous experience on SCH in References [25,26]. The procedure was conducted in frequency domain, assisted of CIFER software [13] (developed by NASA Ames Research Center).

Table 4. Main parameters from linear identification model (IDM).

Hover				30 m/s Configuration D		30 m/s Configuration WD
Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
${\tau }_f$	0.05560	$A_{{\delta }_{lat}}$	−0.03270	${\tau }_f$	0.0510	$X_u$	−0.328
$X_u$	−0.06020	$A_{{\delta }_{lon}}$	−0.4568	$L_b$	331.2	$L_p$	−3.09
$Y_v$	−0.1420	$B_{{\delta }_{lat}}$	0.5046	$B_{{\delta }_{lat}}$	0.2680	$L_{{\theta }_a}$	3.53
$Z_w$	−1.714	$B_{{\delta }_{lon}}$	−0.05330	$X_u$	−0.297
$M_a$	448.4	$Z_{{\delta }_{col}}$	−45.87	$Y_v$	−0.115
$L_b$	740.9	$N_{{\delta }_{ped}}$	75.28
$N_r$	−1.084
Cost value	39.9078			Cost value	47.7424	Cost value	58.1301

gathers the main identified parameters from CIFER and Figure 7 plots the frequency comparisons with flight results. As shown in Figure 7, the frequency responses of the linear identification model (IDM) matches the flight data in high quality. The cost value quantifies the matching quality. The smaller the cost value, the higher the matching degree in frequency domain. According to CIFER, a cost value lower than 100 can reflect a good quality of the identification results [13]. In Table 4, the cost values meet the requirement. In the following section, the modification will be conducted firstly in hover condition and then in forward flight condition.

3.2.1. Hover Modification

In hover condition, Configuration D model was applied in the tests. According to the previous analysis, the coupled roll pitch TPP equations (Equation (2)) were in a linear form, which can be easily modified using IDM results by

$$\begin{gathered} {\tau }_f\dot{a}=-a-{\tau }_{f}q-A_{b}b+A_{{\delta }_{lon}}{\delta }_{lon}+A_{{\delta }_{lat}}{\delta }_{lat} \\ {\tau }_f\dot{b}=-b-{\tau }_{f}p-B_{a}a+B_{{\delta }_{lat}}{\delta }_{lat}+B_{{\delta }_{lon}}{\delta }_{lon}. \end{gathered}$$

(34)

The flap equations in NMM were replaced entirely by Equation (34). The yaw dynamics contained a strong head-lock control law (in a 3-axis gyro component), which was linear too. It can be decided entirely by the identified gyro model [25], which contains the parameters $N_r$ and $N_{{\delta }_{ped}}$ in Table 4. Apart from these two directions, there are six essential derivatives to be discussed:

1.  Heave damping derivative $Z_w$ and heave maneuver derivative $Z_{col}$:

Because, the main rotor dominated the heave direction throughout the flight envelope [19]. $Z_w$ and $Z_{col}$ can be expressed as:

$$Z_w=a_0\cdot \frac{\rho ({\Omega }_{mr}{R}_{mr})\pi R_{mr}^2}{m}\cdot \frac{4s{\lambda }_i}{16{\lambda }_i+a_{0}s}$$

(35)

$$Z_{{\delta }_{col}}=a_0{K}_{col}\cdot \frac{8}{3}\frac{\rho {({\Omega }_{mr}{R}_{mr})}^2\pi R_{mr}^2}{m}\frac{s{\lambda }_i}{16{\lambda }_i+a_{0}s}$$

(36)

where $K_{col}$ is the scaling paraments to transform ${\theta }_{col}(rad)$ to ${\delta }_{col}([-0.5,0.5])$. In the above equations, $(\rho {({\Omega }_{mr}{R}_{mr})}^2\pi R_{mr}^2/m)$ was a constant value. Assume ${\lambda }_i$ and $s$ were estimated correctly, then the two nonlinear parameters $a_0$ and $K_{col}$ can be updated by $Z_w$ and $Z_{{\delta }_{col}}$ from IDM.

2.  Pitch damping derivative $M_a$ and roll damping derivative $L_b$:

Similarly, the main pitch and roll moments were mainly decided by the main rotor in an approximate form:

$$M_a=-(N_b\frac{K_{\beta }}{2}+T_{mr}{H}_{mr})/I_{xx}$$

(37)

$$L_b=-(N_b\frac{K_{\beta }}{2}+T_{mr}{H}_{mr})/I_{yy}$$

(38)

where $N_b$ is the blade number. $(T_{mr}{H}_{mr})$ was a small value. Assume $(T_{mr}{H}_{mr})$ was estimated correctly, then the nonlinear parameters $K_{\beta }$, $I_{xx}$ and $I_{yy}$ can be corrected by $M_a$ and $L_b$ from IDM.

3.  Forward velocity derivative $X_u$ and lateral velocity derivative $Y_v$:

The forward velocity derivative was influenced mainly by main rotor and airframe.

$$X_u=X_{umr}+X_{uf}$$

(39)

where $X_{uf}$ depends on $S_{fx}$ (the forward effective drag area of airframe). The x-force in the nonlinear model can be modified by using the following equations:

$$\Delta X_u=X_u{(}_{IDM})-X_u{(}_{NMM})$$

(40)

$$X{(}_{NMM})=X{(}_{NMM\_original})+m\cdot \Delta X_u\cdot u$$

(41)

For example, from Table 4 and

Table 5. Key modified parameters.

Parameter	Previous	Updated	Parameter	Previous	Updated
$a_0$	6.28	5.75	$\Delta X_u$ (hover)	0	−0.041
$K_{col}$	0.3011	0.2932	$\Delta Y_v$ (hover)	0	0.0485
$K_{\beta }$	157.54	160.57	$\Delta X_u$ (30 m/s D)	0	0.0102
$I_{xx}$	0.412	0.396	$\Delta X_u$ (30 m/s WD)	0	0.0291
$I_{yy}$	0.676	0.653	$\xi$	1	0.8762

, we can get $\Delta X_u=-0.041$. Then according to Equation (41), the updated x-force $X=X{(}_{NMM})-0.041\cdot m\cdot u$. If we linearize this equation and calculate the updated forward velocity derivative $\Delta X_u{(}_{NMM})$, the updated $\Delta X_u{(}_{NMM})$ = −0.0192 − 0.041 = −0.0602 $=\Delta X_u{(}_{IDM})$. Therefore, the updated $\Delta X_u{(}_{NMM})$ coincides with $\Delta X_u{(}_{IDM})$ in hover condition. This method guarantees a good accuracy of x-force modification in hover, while the high-speed features should be checked in the following validations.

The lateral direction was influenced by three parts: main rotor, airframe and tail rotor.

$$Y_v=Y_{vmr}+Y_{vf}+Y_{vtr}$$

(42)

Then, the y-force was modified as:

$$\Delta Y_v=Y_v{(}_{IDM})-Y_v{(}_{NMM})$$

(43)

$$Y{(}_{NMM})=Y{(}_{NMM\_original})+m\cdot \Delta Y_v\cdot v$$

(44)

3.2.2. Forward Flight Modification

There are two kinds of parameters that play an important role in high speed. One is the airframe drag, the other is the aerodynamic coefficient of the wing. These two aspects have a great impact on the following parameters: $X_u$, $L_p$, and $L_{{\theta }_a}$. Other parameters do not change greatly from hover to 32 m/s, which means the hover modification is still valid. In high speed, $X_u$ can be modified in a similar way in Equations (40) and (41) according to $X_u$(IDM).

But the lateral derivatives are different. Primarily, suggest that the dynamic model of the helicopter components was accurate in high speed. Then the error of lateral derivatives was mainly caused by the error of prediction on the wing part. During lateral control and rolling, the actual inflow of the wing was poorly estimated due to the interference of airframe and rotor. Thus, modifying the actual inflow angle of the wing proportionally was the best and most efficient way to correct these lateral derivatives in NMM by using $L_p$(IDM) and $L_{{\theta }_a}$(IDM).

For example, in a roll movement, the change of the effective inflow angle $a$ at different lateral position $y$ can be approximately expressed as $\Delta a(y)=py/u$ [24]. If we introduce a proportion parameter $\xi$ in the inflow angle, then $\Delta a(y)=\xi py/u$. Consequently, $L_p$ will be changed with respect to the value of $\xi$. Similarly, in aileron maneuver, $\Delta a\approx \xi {\theta }_a$. It is discovered that, by defining one $\xi$, both $L_p$ and $L_{{\theta }_a}$ can approximately fit the IDM results.

Finally, 10 mentioned modified parameters are gathered in Table 5. Both the previous values and the updated values are shown in the table. In

Table 6. Hover eigenvalues in the updated NMM compared with IDM.

Mode	IDM	NMM
Pitch	[0.4261, 21.6214]	[0.4812, 20.2831]
Roll	[0.3288, 26.9422]	[0.3695, 27.8265]
Yaw	[0.5045, 19.8832]	[0.5100, 23.1020]
Heave	(−1.7136)	(−1.7101)

, the eigenvalues of the linearized-modified NMM model at hover are compared with the IDM results. The eigenvalues in $[{\zeta }_e,{\omega }_e]$ denotes the second-order system and $({\sigma }_e)$ represents for first-order system. ${\zeta }_e$ is the damping ratio, ${\omega }_e$ (rad/s) is the natural frequency and ${\sigma }_e$ is the real part of the complex eigenvalue. From the table, we can see the eigenvalues of NMM at hover are close to the IDM’s, which indicates a credible performance of the updated NMM. In the following sections, “NMM” indicates the results from the updated NMM.

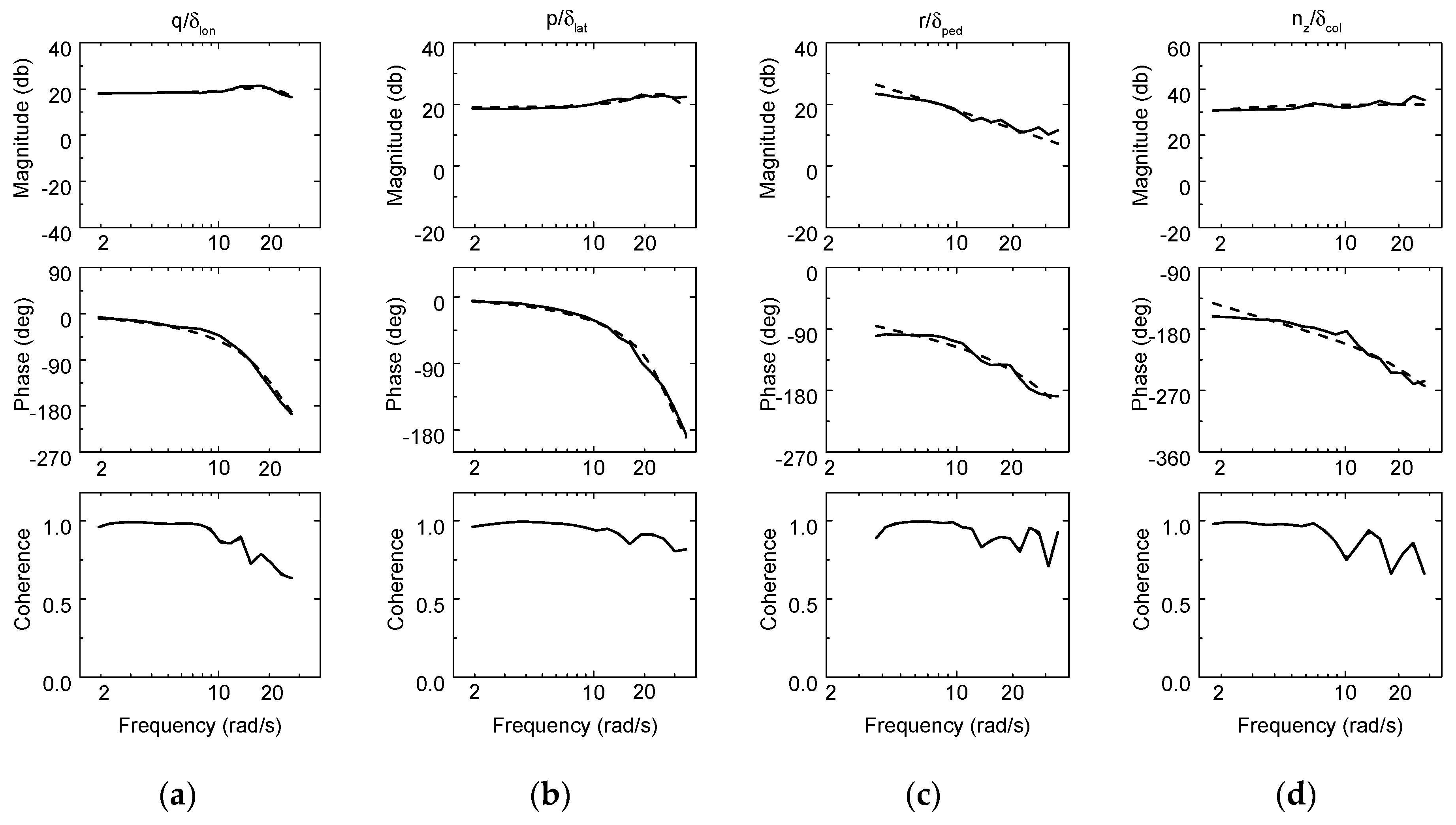
4. Flight Experiments

In hover flight, sweep-motions were manually conducted on Configuration D in longitudinal direction, lateral direction and yaw direction. Time duration was 10 s~15 s. The input control signals and output responses were recorded by the onboard computer. The output responses are angular velocities, linear accelerations, Euler angles, power and so forth.

In high speed condition, the compound flights were difficult to conduct manually. Thus, Configuration D and Configuration WD were realized in automatic flights. The control algorithm written in the onboard computer made the helicopter fly at a constant height following a route. Figure 8 shows the control logic in the tests. The helicopter performed an acceleration from hover to the target forward speed and maintained the target speed in straight and level status. In the allocation algorithm, from low speed to high speed, the ducted fan gradually replaced the action of the longitudinal cyclic pitch ${\delta }_{lon}$ to control the forward speed. In general configuration, the helicopter needs to maintain a $-{10}^{\mathsf{o}}$ pitch angle at 25 m/s to provide necessary forward thrust. But after installing the ducted fan in Configuration D, it only needs a constant $-2^{\mathsf{o}}$ pitch angle at 25 m/s and the ducted fan dominated the forward-direction control. In the experiment of Configuration WD, ${\theta }_a$ was set to zero and the lateral control still relied on the lateral cyclic pitch of the main rotor. The T-style vertical and horizontal stabilizer were not installed in these validation experiments. From the forward flight data, 5 s~10 s period of stable speed section at different target speeds were extracted. The criteria of selecting the stable speed sections were: error of forward speed $\left|\Delta u\right|\le \begin{array}{cc}0.3& \mathrm{m}/\mathrm{s}\end{array}$, error in height $\left|\Delta H\right|\le \begin{array}{cc}2& \mathrm{m}\end{array}$, error in pitch angle $\left|\Delta \theta \right|\le 2^{\mathsf{o}}$ and error in roll angle $\left|\Delta \varphi \right|\le 2^{\mathsf{o}}$. Trim results can be obtained by the mean values of these stable section data.

5. Results and Discussion

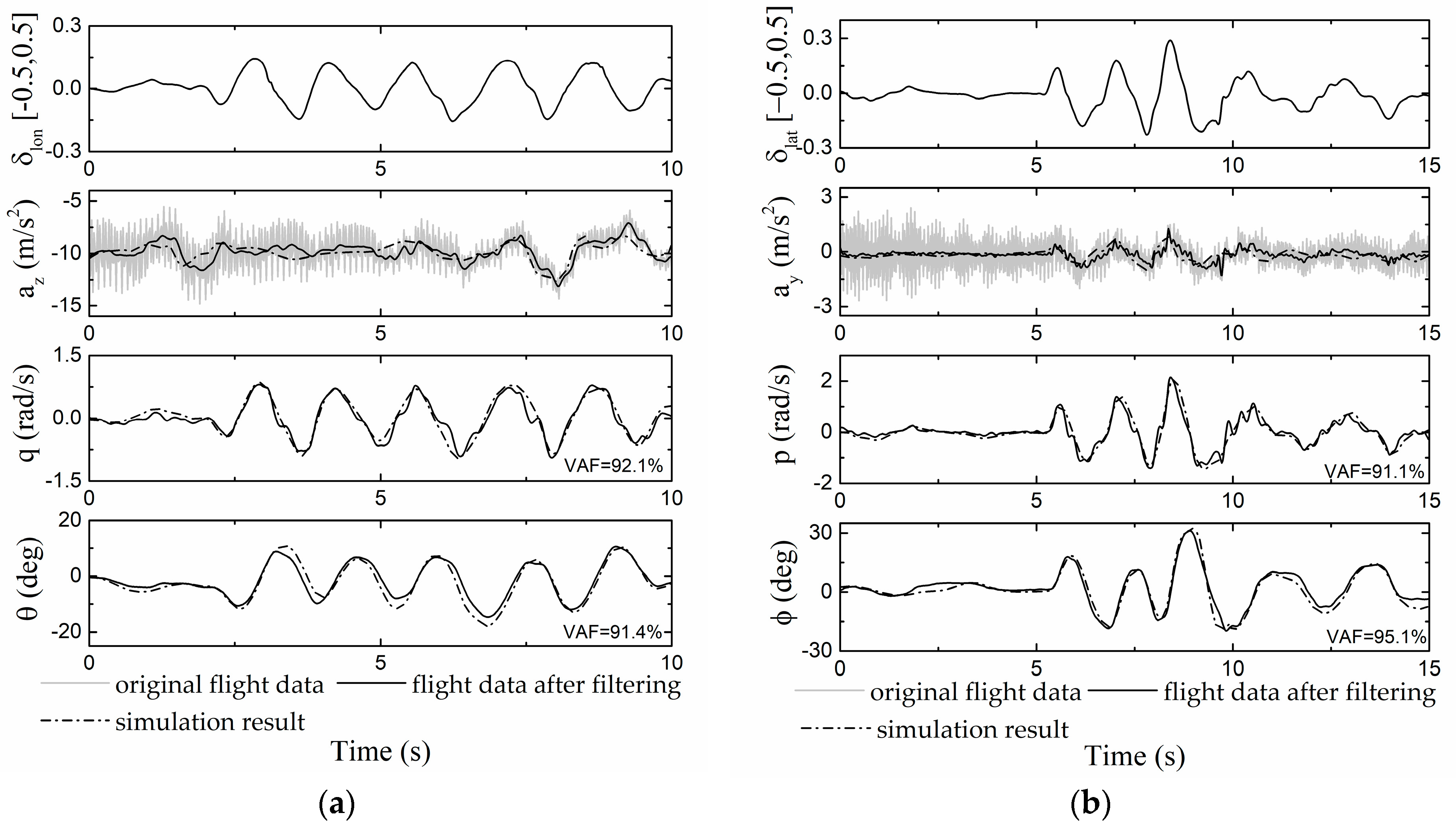
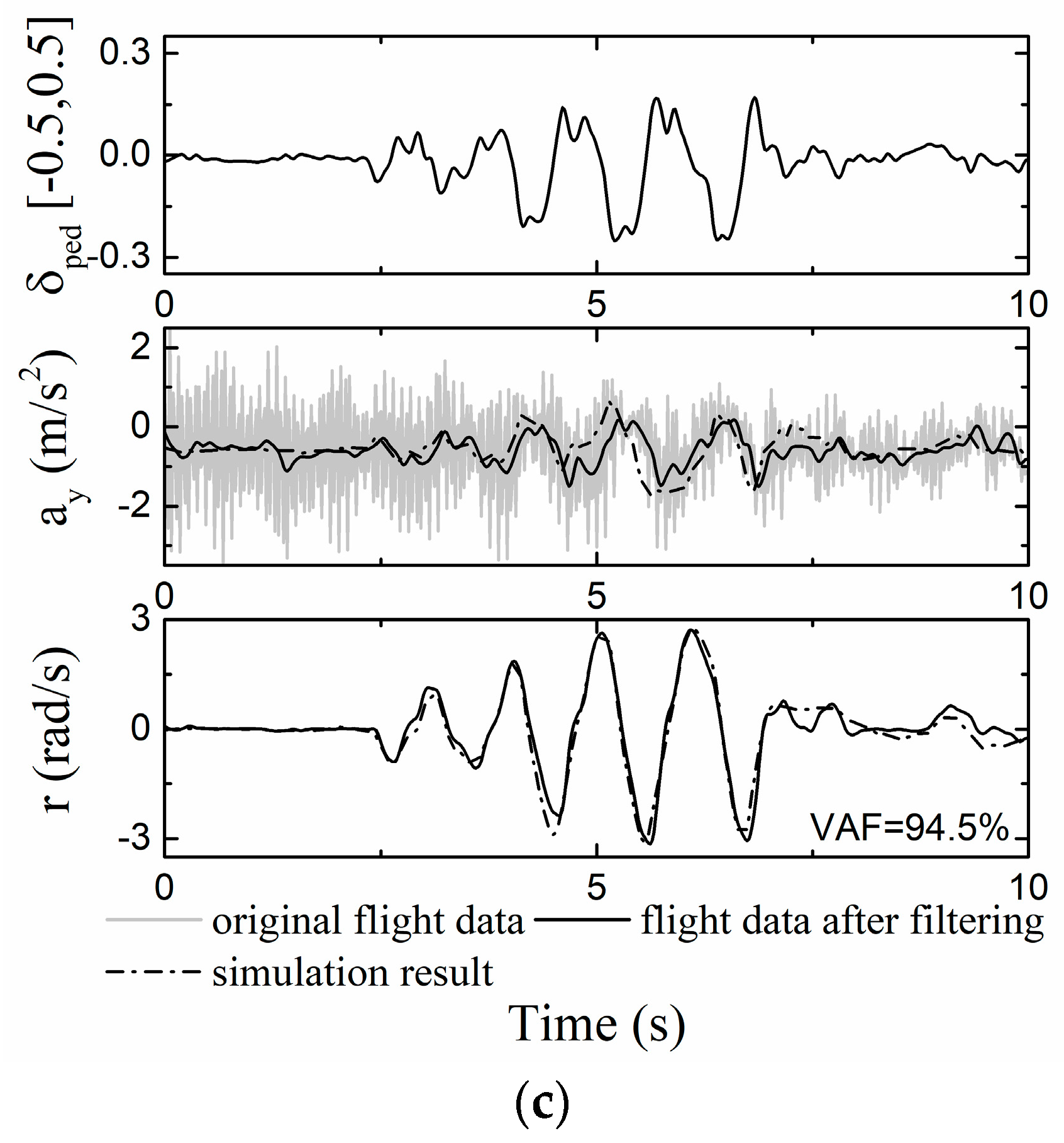
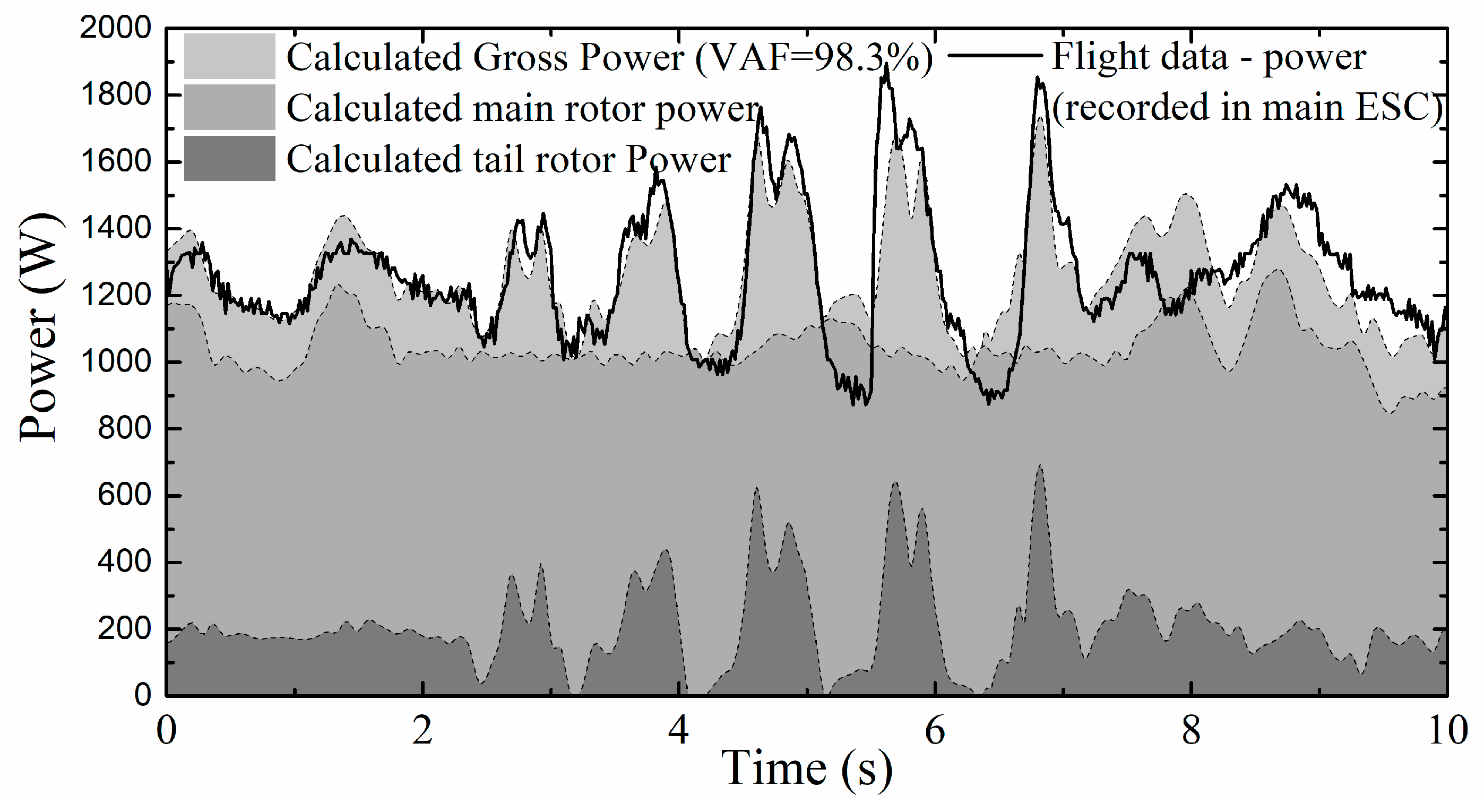
5.1. Hovering Validation

In hover validation, three directions were tested by sweep inputs under Configuration D. In Figure 9, the simulation results are compared with the helicopter responses in real flights. As observed from the comparisons, the calculations of the three directions follow the flight data well. Variance Accounted For (VAF) was calculated to verify the correctness of the model. All VAF are higher than 91%. The VAF of $\theta$ and $\varphi$ are in similar range with $q$ and $p$, indicating good predictions in hover. Compared with the IDM results in Reference [26], the correctness got from NMM are slightly lower then IDM. For example, in Figure 9a, $q$ VAF = 92.1%, while in IDM, VAF = 93.4%; In Figure 9b, $p$ VAF = 91.1%, while in IDM, VAF = 92.9%. Although in hover condition, NMM might not be as accurate as IDM, it is good enough for later research.

In addition, a large fluctuation in total power was found in the yaw excitation test. The main ESC had notably good functions and was able to record the motor and main battery parameters into a SD card during flights. Using the actual voltage and current of the battery output, the power dissipation of the entire helicopter in flights were obtained. In the simulation, the main rotor power and tail rotor power were calculated separately. The power simulations compared with flight data are shown in Figure 10. It is observed that the calculation of gross power matches well with the recorded power. In hover flight, the main rotor and tail rotor are the main power-consuming components. According to the calculations, the power of main rotor occupied approximately 85% of the gross power. During a yaw maneuver flight, the tail rotor power varied, making the gross power change from 1 kW to 1.7 kW, while power of main rotor was more stable.

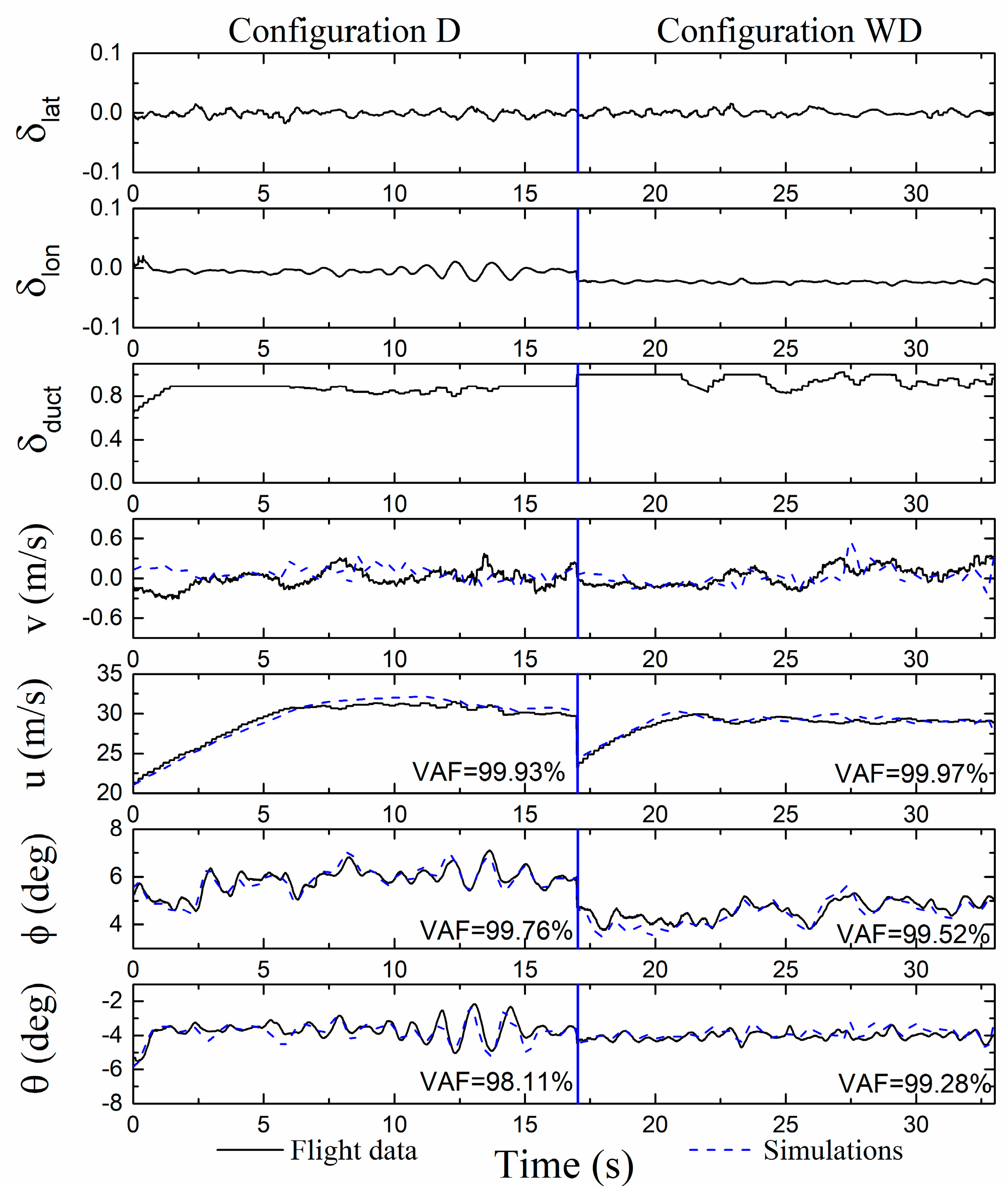
5.2. Forward Flight Validation

For verifying the reliability of the established nonlinear model in high-speed forward flights, the simulation results from NMM are compared with the trim data.

As shown in Figure 11, the solid points and hollow points represent the trim results in the stable speed sections. One data point represents one flight. The NMM predictions are presented by lines. In Configuration D, the maximum speed from experiments is 32 m/s, while in Configuration WD, the maximum speed is 30.7 m/s.

Figure 11a shows the only one compound control signal ${\delta }_{duct}$. ${\delta }_{duct}$ reached its highest value in Configuration D 32 m/s. Due to the fact that Configuration WD had greater drag then Configuration D, ${\delta }_{duct}$ in Configuration WD reached the highest point at 27 m/s. Subsequently, above 27 m/s, the pitch angle (Figure 11e) presented greater negative value and the helicopter showed worse overall performance relative to the optimal. In the pitch angle simulation (Figure 11e), the nonlinear model gives very good agreement with data for both conditions. In Figure 11b,h there are some underestimates on the collective pitch and the total power in Configuration WD above 27 m/s. It is because a greater interference from the rotor wake under a large negative pitch angle cannot be captured accurately by NMM.

In Figure 11c,d the trim values of ${\delta }_{lat}$ and ${\delta }_{lon}$ all focused around zero, which represents a balanced moment condition. In the roll angle calculation (Figure 11f), the nonlinear model fits the trim results of Configuration D closely. In Configuration WD, the simulation of the roll angle shows a lower estimation. The flight data of roll angle in Configuration WD was more scattered. This is because the Configuration WD carried a large wing component, which was more sensitive to the influence of lateral wind.

Figure 11g,h show the overall characteristics of the compound helicopter. $\zeta$ is a defined ratio, named the forward thrust ratio:

$$\zeta =\frac{X_{duct}/mg}{X_{duct}/mg+\sin (-\theta )}$$

(45)

where $\sin (-\theta )$ represents the projection of main rotor lift on the x-axis, $X_{duct}/mg$ represents the contribution of forward thrust by the ducted fan. This ratio is simple measure of the contribution of the ducted fan to net forward propulsive force. In the designing process, the expectation of the ratio in forward speed above 25 m/s is 80~90%. The real $\zeta$ (Figure 11g) of Configuration D was exactly in 80~90%, which meets the expectation. In $\zeta$ calculations, the nonlinear model predicts closely to the real data in both conditions. Figure 11h shows the total power recorded by the main ESC. In Configuration D, the nonlinear model predicts the power in high accuracy and in Configuration WD below 27 m/s, the power calculation shows credible results around the flight results.

Additionally, in Figure 12, groups of time-domain data were extracted for simulation. The data contain part of the accelerate section and the stable speed section. Two sets of data are presented in the figure: one is Configuration D under reference speed of 30.5 m/s, the other is Configuration WD under reference speed of 30 m/s. The blue dash lines show the NMM responses following the real control signals. The calculated $v$ focuses around zero, similar to the flight results. In $u$ calculations, the acceleration rate and the target speed value are captured accurately. That is to say the aerodynamic drags in these high-speed periods are well evaluated. $\theta$ and $\varphi$ smoothly fluctuated following the control signals. Unlike the sweep signals in the hover identification, the fluctuations of $\theta$ and $\varphi$ in Figure 12 were well controlled within $2^{\mathsf{o}}$. The calculation of NMM has high quality and VAF are close to 100% from the results.

In summary, the nonlinear model has high accuracy over a large speed range, which guarantees the effectiveness of later analysis. In this validation, it is proved that the 2-mode controlled wing can work effectively, and the wing model based on the linear interference assumption is credible below 27 m/s. The ducted fan is efficient in providing forward thrust and unloading the main rotor. The nonlinear model with modification is successful in predicting the whole-helicopter dynamics.

5.3. Configuration WDH Simulation

In this section, the study expands the research of SCH nonlinear model. A comprehensive investigation is conducted in a new simulation route by considering the elevator and aileron in Configuration WDH. The newly added components have been introduced in Section 3, such as the T-style vertical/horizontal stabilizer, the elevator on the horizontal stabilizer and the aileron function in wing component. The coordinated turn is a systematic control route. The turn should coordinate elevator control, aileron control and yaw control to perform a perfect turning circle. The structured $H_{\infty }$ control method was adopted in the simulation. The control requirements were:

$$\{\begin{array}{c}w=0\\ v_b=0\\ u_b=\mathrm{constant}\\ \varphi =\mathrm{constant}\\ r_b=\frac{g}{u}\tan \varphi \\ q_b=\mathrm{constant}\end{array}$$

(46)

where $\varphi$ was controlled by aileron. $r$ was still controlled by tail rotor collective pitch. $q$ was controlled by the elevator on the horizontal stabilizer. The simulation was conducted on $u_b=20 \mathrm{m}/\mathrm{s}$.

In the simulation, as shown in Figure 13, the Configuration WDH performs a perfect coordinated turn in a semi-circle. The error of height is less than 2 m. In Figure 14, variations of multiple variables during the turn are plotted. The control of ${\theta }_a$ and ${\theta }_e$ is effective with small oscillation and overshoot to obtain the target attitude. Such as in Figure 14a, a 3 degree ${\theta }_a$ can produce 0.6 rad/s roll angular velocity $p$ (Figure 14d). Then the helicopter reaches $-{20}^{\mathsf{o}}$ roll angle $\varphi$ (Figure 14e) within 2 s and performs little overshoot and fluctuation. The control of aileron and elevator consumes small amount of power in this process. However, in the real flights, the helicopter needed longer time to stable during the turning point under main rotor control and large amount of power was consumed. The control performance of main rotor cannot be as good as the performance by ${\theta }_a$ and ${\theta }_e$ in Configuration WDH. The Configuration WDH benefits from a clear flow condition of the wings. It is noteworthy that during the lateral control of aileron, the main rotor also produces a damping moment ($L_{main rotor}$). This is a symbol of stability but it indeed lowers the maneuver efficiency. The main rotor reacts more like a burden in this high-speed flight. In addition, an extra $q_b$ helps to make the helicopter fly at a stable height.

The simulation in coordinated turn proves the feasibility of the elevator component and the differential maneuver of the aileron-wing. The simulation confirms the effectiveness of SCH nonlinear model in a wider route setting.

6. Conclusions

This article offers a detailed analysis of the nonlinear mathematical model of an innovative small-scale compound helicopter. Three compound configurations were studied. An 11-state nonlinear simulation model was established, considering a free-rotate wing, ducted fan model, horizontal stabilizer model and so forth. Apart from the linear coupled roll pitch dynamics and the linear yaw dynamics, 10 main parameters in the nonlinear model were modified with the help of system identification results. Flight data of large flight envelope from hover to 32 m/s forward flight were prepared in verification database. Conclusions can be drawn as follows:

(1)

Compared with the hover data, the nonlinear dynamics model has high accuracy in simulating the sweep responses, especially in the calculations of pitch and roll angles. The power of main rotor occupied 85% of the gross power. Tail rotor made the gross power vary from 1 kW to 1.7 kW in yaw maneuver.

(2)

In forward flight comparisons, the predictions of the nonlinear model are in good agreement with the trim results from the real flights, especially in Configuration D and in Configuration WD below 27 m/s. The interference between the wing and main rotor should be treated more carefully under a large negative pitch angle in speed above 27 m/s. The nonlinear model with modification is successful in predicting the time-domain responses in forward speed around 30 m/s.

(3)

In the coordinated turn simulation, the elevator and aileron work efficiently. The control fluctuations decrease greatly in 2 s. The control performance in Configuration WDH has smaller oscillation and overshot than the control in the real flights. The main rotor creates stable damping in roll movement during the turn simulation.