An Optimal Fuzzy PID Controller Design Based on Conventional PID Control and Nonlinear Factors

Abstract

This paper proposes an optimal fuzzy proportional–integral–derivative (PID) controller design based on conventional PID control and nonlinear factors. With the equivalence between fuzzy logic controllers (FLCs) and conventional PID controllers, a conventional PID controller design can be rapidly transformed into an equivalent FLC by defining the operating ranges of the input/output of the controller. The proposed nonlinear factors can further tune the nonlinearity of the membership functions (MFs) distributed in the operating ranges. In this manner, a fuzzy PID controller can be developed with less parameters and optimized by using the genetic algorithm (GA). In addition, the aforementioned equivalent FLC can act as one individual in the initial population of GA, and significantly enhances the GA efficiency. Simulation results demonstrate the feasibility of this technique. This resulted in an optimal fuzzy PID controller design with only eight parameters with a concise controller structure, and most importantly, the optimal fuzzy PID controller design is now more systematic.

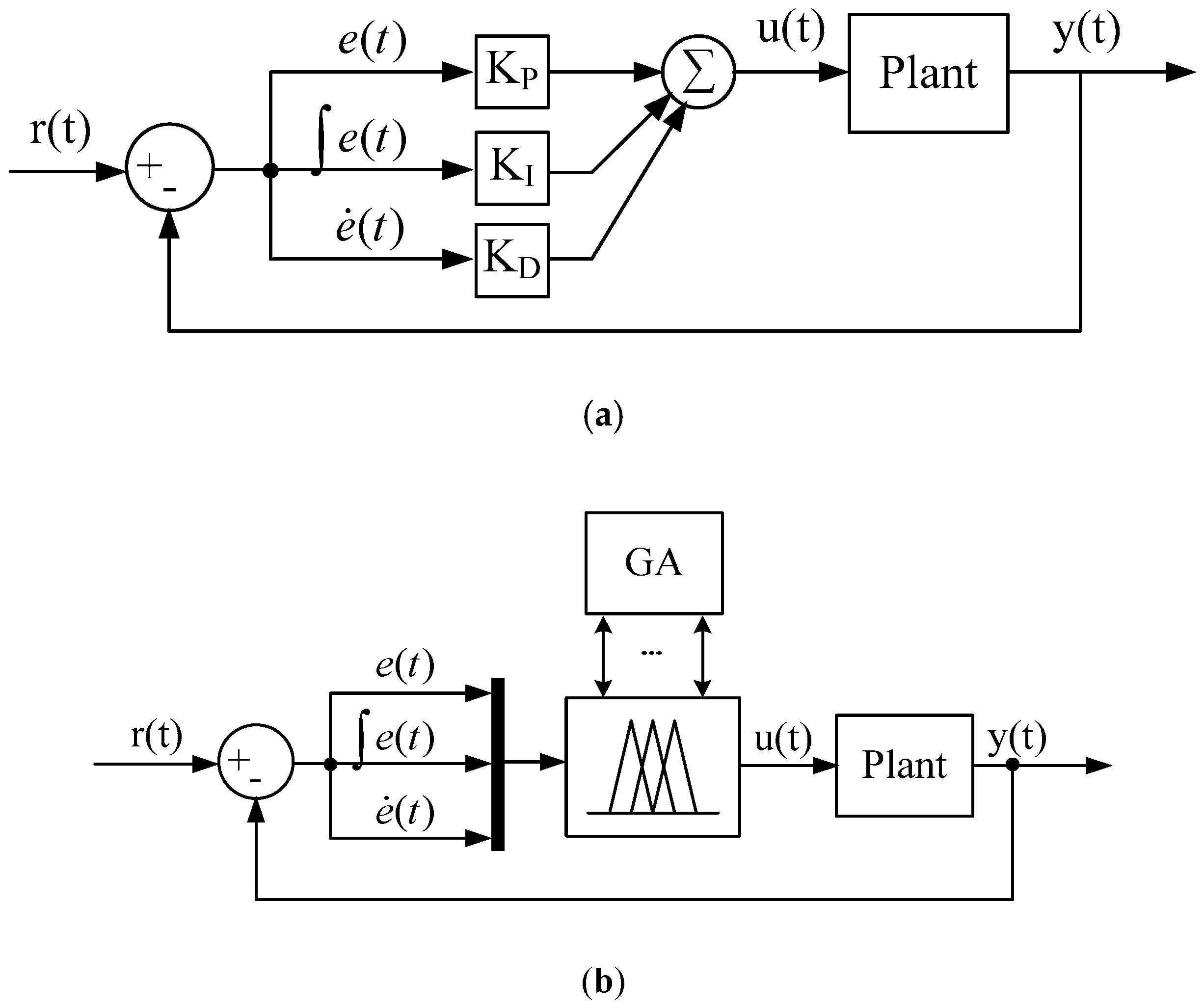
1. Introduction

The well-known proportional–integral–derivative (PID) controllers are still widely employed in industrial process control even though many kinds of control theories have been developed. The popularity of a PID controller can be attributed to its good performance and functional simplicity. The three-mode controller contains a proportional (P), an integral (I), and a derivative (D) term to make a system yield a desirable response in settling time, steady-state error, and overshoot. An engineer can efficiently tune the three gains through experience or some simple principles, such as the classical tuning rules proposed by Ziegler-Nichols [1]. Moreover, a simplified PI or PD controller is also popular for a multitude of practical applications.

A fuzzy logic controller (FLC) is based on fuzzy rules and fuzzy inference. The fuzzy rules can reflect human experience or knowledge, and exhibit nonlinearity to control more complex plants, which can be linear or nonlinear. Like conventional PI or PD controllers, FLCs also have PI-type or PD-type controllers. Essentially, a FLC design includes the type of FLC, the number and shape of membership functions (MFs), and the fuzzy rules [2]. The genetic algorithm (GA) is employed to determine the optimal parameters of a system. Since the design techniques of conventional linear PID controllers have matured, it is advantageous to use the GA to optimize fuzzy PID controller design. Researchers have introduced an analytical design for an optimal fuzzy PID controller [3], which has a simple structure, but uses complicated procedures. Another optimal fuzzy PID controller combining a fuzzy PI controller with a fuzzy D controller was proposed [4], but this device is actually a conventional PID controller with an adaptive control capability with complicated analytic formulas. An optimal fuzzy PID controller can also be built by combining a fuzzy PI controller and a fuzzy PD controller in parallelism [5] with optimal tuning of scaling factors and MFs. The conventional PID controller can also be directly put in the optimal design for fuzzy controllers [6], where the PID control is the master controller, and the fuzzy control is the slave control to enhance the master one.

The controller structure should be the primary consideration for a fuzzy PID controller design. As for the fuzzy control rules, in principle, they should follow conventional PID control. Then the problem of tuning the MFs in order to improve system performance must be solved [7]. The shape of MFs can be defined by chromosome bits and optimized by the GA [8,9] to improve the system responses, such as speed and precision of control [9,10]. On the other hand, each fuzzy variable MF is usually set to a symmetrical shape. The adjustment of a MF from symmetrical [11] to asymmetrical can also obtain improvements in system performance [12]. Moreover, some researchers use scaling factors to normalize the operating ranges and tune scaling factors to finish optimization [13]. In this paper, we choose to tune the operating ranges, which are important parameters for defining the equivalent FLC from a conventional PID controller.

In recent decades, many evolutionary algorithms have been developed, such as the particle swarm algorithm (PSO), cuckoo search (CS), and so on. Evolutionary programming (EP) claims that the traditional GA will not only have a premature convergence, but may also be trapped in the local optima. A fuzzy PID controller design using a novel PSO-EP based hybrid algorithm has been found in [14]. Furthermore, it is shown that a FLC + EP based PID controller provides a more rapid response than a FLC + GA based PID controller [15]. In this paper, we will still apply GA, and give each optimized parameter its own crossover point in the GA process to enhance the GA’s efficiency.

As most optimal fuzzy PID controller designs with complex structures or a large number of tuning parameters, this study developed an optimal fuzzy PID controller with less parameters and a concise controller structure. Based on our previous work, the equivalence between fuzzy PID controllers and conventional PID controllers is shown in [16]. Nonlinear factors are further proposed to represent the nonlinearity of the MFs distributed in the operating ranges. For each MF itself, it will exhibit an asymmetrical shape. In the proposed optimal fuzzy PID controller, there will be only a total of eight adjusted parameters. Moreover, if a conventional PID controller design can be obtained in advance, an equivalent FLC in the initial GA design can be used and this can potentially speed up the optimization process. Pelusi previously researched designing optimal control systems through GA and neuro-fuzzy techniques [17,18,19], and the results can be utilized as a benchmark to compare with the proposed design. Furthermore, the proposed optimal fuzzy PID controller is also applied to the motor control system [20], and the simulation results indicate speed control with good performance and the capability of disturbance rejection [21].

This study presents the optimal fuzzy PID controller design (Section 2), followed by the simulation results of Matlab/Simulink for verifying the proposed design (Section 3). Finally, the concluding remarks are discussed (Section 4).

2. The Proposed Optimal Fuzzy PID Controller Design

The conventional PID controllers have been widely applied in industrial applications. The common equation is expressed as follows:

$$u(t)=K_{P}e(t)+K_I{\displaystyle \int e(t)}dt+K_D\frac{de(t)}{dt},$$

(1)

where the controller provides a proportional term, an integration term, and a derivative term. In the next section, we will describe the proposed optimal fuzzy PID controller design.

2.1. The Equivalent FLC from a Conventional PID Controller

For a conventional PID controller in Equation (1), the output $u(t)$ and the three inputs $e(t)$, ${\displaystyle \int e(t)}$, and $\dot{e}(t)$ can be thought of as fuzzy variables in the FLC design. It is assumed that the operating ranges for $u(t)$, $e(t)$, ${\displaystyle \int e(t)}$, and $\dot{e}(t)$ are $O{R}_u=[-a_u,a_u]$, $O{R}_e=[-a_e,a_e]$, $O{R}_i=[-a_i,a_i]$, and $O{R}_d=[-a_d,a_d]$, respectively. In this subsection, some important results from our previous work [16] on the equivalence between fuzzy PID controllers and conventional PID controllers are excerpted to clarify the parameter definitions and notations.

For input fuzzy variables $e(t)$, ${\displaystyle \int e(t)}$, and $\dot{e}(t)$, each variable is represented by equally-spaced and triangular-shaped $m$ fuzzy sets, as shown in Figure 1. As for the output fuzzy variable $u(t)$, it is fuzzified by $3m-2$ singleton MFs.

With the overall fuzzy rules represented by the sliced cube fuzzy associative memory (FAM), as shown in Figure 2, and each fuzzy rule defined as:

$$IFe(t)\mathrm{is}{E}_i\mathrm{and}{\displaystyle \int e(t)\mathrm{is}{I}_j\mathrm{and}\dot{e}(t)}\mathrm{is}{D}_{k}THENu(t)\mathrm{is}{U}_l,l=i+j+k-2,$$

(2)

and the crisp output $u(t)$ of the corresponding equivalent fuzzy logic controller is given by:

$$u(t)=\frac{a_u}{3a_e}e(t)+\frac{a_u}{3a_i}{\displaystyle \int e(t)}dt+\frac{a_u}{3a_d}\frac{de(t)}{dt},$$

(3)

which implies a linear PID controller with:

$$K_P=\frac{a_u}{3a_e},K_I=\frac{a_u}{3a_i},\mathrm{and}{K}_D=\frac{a_u}{3a_d}.$$

(4)

We can find that Equation (4) has no relation with $m$, and it is worth mentioning that the fuzzy inference and defuzzification processes should be limited to some specific operations [16]. Moreover, for the equivalent fuzzy PID Controller corresponding to a conventional PID controller, there are four parameters $[a_e,a_i,a_d,a_u]$ in all for tuning.

2.2. The Nonlinear Factor for Tuning MFs

In the previous subsection, the fuzzy sets representing input/output the fuzzy variables $e(t)$, ${\displaystyle \int e(t)}$, $\dot{e}(t)$, and $u(t)$ are equally-spaced, which is one of the reasons the results show a linear FLC. To exhibit the nonlinearity of a FLC, we proposed a nonlinear factor $\gamma$ to tune MFs. Without losing its generality, let us take fuzzy variables $e(t)$ and $u(t)$ as an example. To illustrate the concept of nonlinear factor $\gamma$, $e(t)$ is supposed to have $m$ = 7 fuzzy sets, and $u(t)$ has $3m-2$ = 19 fuzzy singletons, as shown in Figure 3. It is noted that the variable $m$ should be an odd number. In this paper, we use $p_k$, $k\ge 0$, to represent the center of fuzzy sets $E_{k+\frac{m+1}{2}}$ or $U_{k+\frac{3m-1}{2}}$. The nonlinear factor $\gamma$ is defined as:

$$\gamma =\frac{P_k-P_{k-1}}{P_{k-1}-P_{k-2}},\gamma >0.$$

(5)

It can be observed that the nonlinear factor $\gamma$ represents the center distance ratio of the MFs before and after.

In Figure 3a, it is the linear case with nonlinear factor $\gamma$ = 1. Figure 3b shows the case of $\gamma$ < 1, where the closer the MF is to the zero, the wider the MF will be. On the contrary, if $\gamma$ > 1, the closer MF to the zero will have a narrower shape, as shown in Figure 3c. With the definition of nonlinear factors, each MF itself can exhibit an asymmetrical shape and influence the system response.

From Equation (4) in Section 2.1, we get four parameters for tuning a linear FLC. Adding the nonlinear factor for each fuzzy variable in this subsection, there will be a total of eight parameters, $[a_e,a_i,a_d,a_u,{\gamma }_e,{\gamma }_i,{\gamma }_d,{\gamma }_u]$, which need to be adjusted for an optimal fuzzy PID controller design.

2.3. The Efficient Genetic Algorithm

The GA is employed to find the optimal parameter set for a fuzzy PID controller. Basically, the GA includes some major components, such as encoding schemes, fitness evaluations, parent selection, crossover operators, and a mutation operator. This study applied binary coding and adopted the integrated absolute error (IAE) as the performance index [22], shown in Equation (6):

$$IAE={\displaystyle \sum _{i=1}^n\left|e[n]\right|}.$$

(6)

The fitness value will be the inverse value of the performance index, i.e., the smaller absolute sum of errors will obtain a larger fitness value.

In this paper, we hope to enhance the GA efficiency, and discuss the crossover operation in GA computation. In some GA codes, the bits of different parameters will be concatenated into a large long string of bits. Afterwards, the crossover operation was done with only one crossover point. This will simplify the programming considerably, but may reduce GA efficiency due to the possible damage to good genes. In the proposed improved scheme, each parameter has its own crossover point, as illustrated in Figure 4. In this manner, good genes will not be easily destroyed by the crossover operation. Moreover, we will increase genetic diversity by enlarging the mutation rate. Simulation results show an efficient GA for optimal fuzzy PID controller design.

3. Simulation Results

This section evaluates the performance of the proposed optimal fuzzy PID controller by considering a two-order plant and motor control systems. The simulation is verified by use of Matlab/Simulation.

Simulation 1: A Two-Order Plant

A two-order controlled plant is shown below with transfer function [19]:

$$G(s)=\frac{2}{{{\displaystyle s}}^2+12s+24}.$$

(7)

First, the unit feedback control structure is adopted, as shown in Figure 5. A preliminary conventional PID controller design with ${{\displaystyle K}}_P=50$, ${{\displaystyle K}}_I=250$, and ${{\displaystyle K}}_D=1.5$ can be obtained through some basic traditional techniques. Experiments to verify the proposed design approach can be seen in the following section.

Subsequently, we built the equivalent FLC for the above conventional PID controller design through the procedure shown below, which will satisfy Equation (4).

• ${{\displaystyle OR}}_e$ is set as $[-{{\displaystyle a}}_e,{{\displaystyle a}}_e]=[-1.33,1.33]$, which is the range for $e(t)$.
• ${{\displaystyle OR}}_u$ is set as $[-{{\displaystyle a}}_u,{{\displaystyle a}}_u]=[-199.5,199.5]$ to satisfy ${{\displaystyle K}}_P=50$.
• ${{\displaystyle OR}}_i$ is set as $[-{{\displaystyle a}}_i,{{\displaystyle a}}_i]=[-0.266,0.266]$ to satisfy ${{\displaystyle K}}_I=250$.
• ${{\displaystyle OR}}_d$ is set as $[-{{\displaystyle a}}_d,{{\displaystyle a}}_d]=[-44.33,44.33]$ to satisfy ${{\displaystyle K}}_D=1.5$.

The parameter $m$ is set as 5, resulting in 5 fuzzy sets for each input variable of the FLC. Figure 6 shows the settings of all the MFs in the Matlab environment. The linearity of the equivalent fuzzy PID controller can be verified by the control surface view shown in Figure 7, which is similar to the plan surface shown in [23]. The resulting equivalent fuzzy PID controller has almost the same system response as the conventional PID controller.

With the conventional PID controller design and the corresponding equivalent FLC, we finally have a basic understanding about the operating ranges of fuzzy I/O variables for a FLC. We can then add additional nonlinear factors and enlarge the operating ranges to find the optimal fuzzy PID controller through GA.

For the GA optimization, we use an 11-bit binary coding for each variable, and each generation contains 20 individuals. The search domains are confined to ${{\displaystyle 0<a}}_e\le 10$, ${{\displaystyle 0<a}}_i\le 50$, ${{\displaystyle 0<a}}_d\le 100$, ${{\displaystyle 0<a}}_u\le 5000$ and ${{\displaystyle 0.01<\gamma }}_{(e,i,d,u)}\le 7$.

Moreover, the mutation rate is set as 0.1, and the elitism is applied to keep the best two individuals across generations. It is required to initialize a population with randomly generated individuals and evaluate the fitness value of each individual for the first step of GA. In this stage, our first attempt is taking the above equivalent FLC design, $[a_e,a_i,a_d,a_u,{\lambda }_e,{\lambda }_i,{\lambda }_d,{\lambda }_u]$ = [1.33, 0.266, 44.33, 199.5, 1, 1, 1, 1], as one individual in the population of the first generation. Figure 8 shows the performance of GAs across generations, where the optimal design with initial equivalent FLC may yield faster convergence with higher quality than the optimal design without initial equivalent FLC.

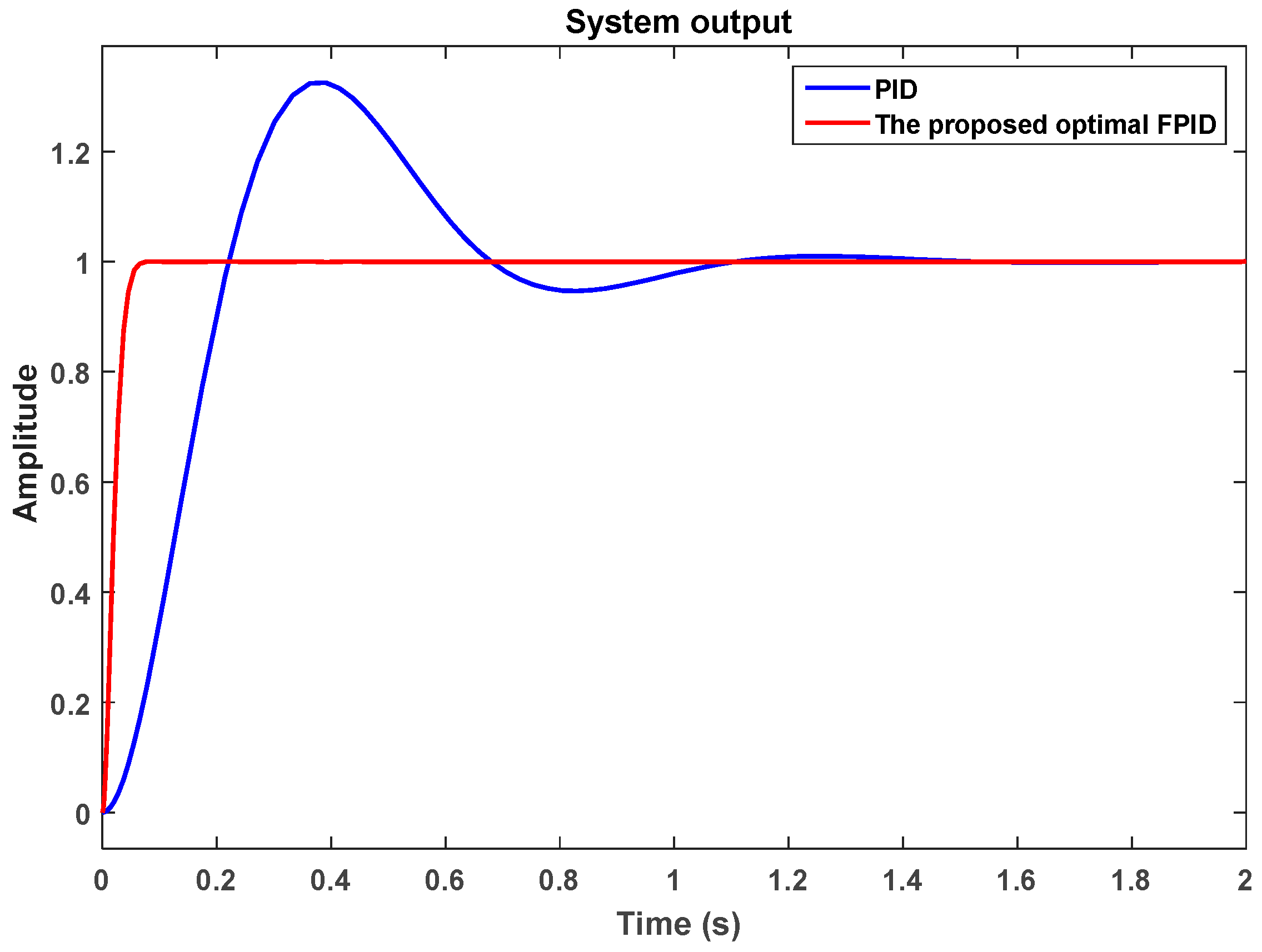
The step responses with the conventional PID controller (${{\displaystyle K}}_P=50$, ${{\displaystyle K}}_I=250$, ${{\displaystyle K}}_D=1.5$) and the proposed optimal fuzzy PID controller (with initial equivalent FLC) are shown in Figure 9. The resulting eight optimized parameters are shown in

Table 1. The eight optimized parameters.

Optimized Operating Ranges				Optimized Nonlinear Factors
$a_e$	$a_i$	$a_d$	$a_u$	${{\displaystyle \gamma }}_e$	${{\displaystyle \gamma }}_i$	${{\displaystyle \gamma }}_d$	${{\displaystyle \gamma }}_u$
5.3053	26.3556	99.4626	3009.3	4.1275	5.5227	0.8344	0.2872

. Furthermore,

Table 2. Response performance of different controllers.

Controller	Tr (s) 10–90%	$\mathit{Ts}\left(\mathbf{s}\right)\pm 2\%$	P.O. (%)	Ess
Pelusi’s GNFC [19]	0.153	0.276	0	0.917
The proposed optimal FPID	0.047	0.059	1.73	0

summarizes the response performance, including the rise time (Tr), the settling time (Ts), the percentage overshoot (P.O.), and the steady-state error (E_ss), of Pelusi’s GNFC optimized controller [19] and the proposed optimal fuzzy PID controller. Pelusi has provided many kinds of controllers, such as the genetic fuzzy controller (GFC), the neuro fuzzy controller (NFC), and the genetic neuro fuzzy controller (GNFC), but the GNFC has the best performance. Compared with Pelusi’s design, the proposed optimal FPID has smaller Tr and Ts, but a very small overshoot occurred at peak time t = 0.08 s with amplitude 1.0173, as shown in Figure 9. On the other hand, Pelusi’s GNFC controller belongs to a PD-type FLC, so E_ss cannot be eliminated.

Figure 10 shows the MFs of the fuzzy I/O variables in the proposed optimal fuzzy PID controller, and the control surface view under ${\displaystyle \int e}(t)=26.3556$ is shown in Figure 11.

Simulation 2: DC Motor Speed Control

High-performance motor drives are very important in many industrial applications. Based on the design procedure in Simulation 1, a separately excited dc motor with the physical parameters listed in

Table 3. DC motor parameters [20].

Parameter/Specification	Value	Unit
$R_a$ (Armature resistance)	1	Ohm
$L_a$ (Armature inductance)	0.5	H
$J_r$ (Rotor inertia)	0.01	Kg·m2
$K_b$ (Back EMF constant)	0.01	Volt·s/rad
$K_t$ (Torque constant)	0.01	N·m/A
$K_f$ (Mechanical damping factor)	0.1	N·m·s/rad
Rated speed	1200	r.p.m

is used as the controlled plant [20], and Figure 12 shows the constructed model in Simulink.

This is a speed control problem with the desired speed at 1200 rpm [20]. The control structure is shown in Figure 13 for both the PID controller and the proposed optimal fuzzy PID controller. The resulting speed responses of the initial conventional PID controller design with ${{\displaystyle K}}_P=50$, ${{\displaystyle K}}_I=60$, and ${{\displaystyle K}}_D=3$, and the proposed optimal fuzzy PID controller are shown in Figure 14. The search domains of the operating ranges for this case are confined to ${{\displaystyle 0<a}}_e\le \mathrm{20,000}$, ${{\displaystyle 0<a}}_i\le \mathrm{50,000}$, ${{\displaystyle 0<a}}_d\le \mathrm{200,000}$, ${{\displaystyle 0<a}}_u\le \mathrm{5,000,000}$, and ${{\displaystyle 0.01<\gamma }}_{(e,i,d,u)}\le 7$.

The resulting eight optimized parameters are shown in

Table 4. The eight optimized parameters.

Optimized Operating Ranges				Optimized Nonlinear Factors
$a_e$	$a_i$	$a_d$	$a_u$	${{\displaystyle \gamma }}_e$	${{\displaystyle \gamma }}_i$	${{\displaystyle \gamma }}_d$	${{\displaystyle \gamma }}_u$
5061.1	12,946	122,030	3,556,400	2.7357	0.8036	0.6253	0.1661

, and

Table 5. Response performance of different controllers.

Controller	Tr (s) 10–90%	$\mathit{Ts}\left(\mathbf{s}\right)\pm 2\%$	P.O. (%)
Singh’s Fuzzy GA controller [20]	0.1	0.121	5.8466
The proposed optimal FPID	0.044	0.054	2.23

summarizes some response parameters of Singh’s optimized fuzzy-GA controller [20] and the proposed optimal fuzzy PID controller. It shows that the proposed design has smaller Tr and Ts than Singh’s design. Finally, Figure 15 shows all the resulting MFs of the fuzzy I/O variables.

Simulation 3: DC Motor Speed Control with Load Disturbance

To further verify the feasibility and disturbance rejection capability of the proposed design, a DC motor speed control example with load disturbance [21] is adopted.

Table 6. DC motor parameters [21].

Parameter/Specification	Value	Unit
$R_a$ (Armature resistance)	2.25	Ohm
$L_a$ (Armature inductance)	4.65 × 10−2	H
$J_r$ (Rotor inertia)	7 × 10−2	Kg·m2
$K_b$ (Back EMF constant)	1.1	Volt·s/rad
$K_t$ (Torque constant)	1.1	N·m/A
$K_f$ (Mechanical damping factor)	2 × 10−3	N·m·s/rad

shows the DC motor parameters, and Figure 16 and Figure 17 illustrate the desired speed command and load disturbance at t = 3 s, respectively.

In this case, the sample-and-hold unit and the zero-order hold unit, which can be used to model A/D (analog-to-digital) and D/A (digital-to-analog) converters, are added to make a discretized FLC, as shown in Figure 18. It must be noted that the gain (K) in the “discrete-time integrator” and “discrete derivative” is set as 1 [16]. The system input and the resulting responses are shown in Figure 19, with sampling period ts set as 0.1 ms. The system responses in Figure 19 include the initial conventional PID controller design (${{\displaystyle K}}_P$ = 0.42, ${{\displaystyle K}}_I$ = 25.127, ${{\displaystyle K}}_D$ = 0.012), and the proposed optimal fuzzy PID controller design. Furthermore, since we cannot obtain the response waveform of Al-Maliki’s design [21], we run a similar response to Al-Maliki’s design by the proposed FPID.

Table 7. The eight optimized parameters.

	Optimized Operating Ranges				Optimized Nonlinear Factors
	$a_e$	$a_i$	$a_d$	$a_u$	${{\displaystyle \gamma }}_e$	${{\displaystyle \gamma }}_i$	${{\displaystyle \gamma }}_d$	${{\displaystyle \gamma }}_u$
The proposed optimal FPID	11,412	3346.4	183,980	3,251,100	6.5110	5.9331	0.4719	2.5169
The proposed FPID with a similar response to Al-Maliki’s results	1000	137	117,000	264,180	2.3145	2.1590	5.9060	3.1692

shows the eight optimized parameters of the proposed FPID design. The search domains of the operating ranges are confined to ${{\displaystyle 0<a}}_e\le \mathrm{20,000}$, ${{\displaystyle 0<a}}_i\le \mathrm{50,000}$, ${{\displaystyle 0<a}}_d\le \mathrm{200,000}$, ${{\displaystyle 0<a}}_u\le \mathrm{5,000,000}$, and ${{\displaystyle 0.01<\gamma }}_{(e,i,d,u)}\le 7$. Then the performance comparison between Al-Maliki’s Fuzzy PID with KF (Kalman Filter) [21] and the proposed optimal FPID is summarized in

Table 8. Response performance of different controllers.

Controller	Tr (s) 10–90%	$\mathit{Ts}\left(\mathbf{s}\right)\pm 2\%$	P.O. (%)
Al-Maliki’s FLC-PID with KF [21]	~0.15	0.257	0.5
The proposed optimal FPID	0.0409	0.0516	1.38
The proposed FPID with a similar response to Al-Maliki’s results	0.14	0.254	0

. Simulation results demonstrate that the proposed optimal FPID has smaller Tr and Ts than Al-Maliki’s design, but has a larger overshoot. Furthermore, the proposed design has good performance in disturbance rejection.

Finally, Figure 20 shows all the resulting MFs of the fuzzy I/O variables of the proposed optimal FPID, and the control surface view under ${\displaystyle \int e}(t)=3346.4$ is shown in Figure 21.

There is another main reason for us to run a system response which is similar to Al-Maliki’s design [21], as shown in Figure 19. As we also hope to compare the responses of the controller outputs, which will indicate the power consumption of the implemented controllers, and this is very important to help us understand the transient behaviors of the system. For a separately excited DC motor, the speed is controlled by varying the source voltage to armature. Figure 22 shows the controller outputs of the proposed optimal FPID and the proposed FPID with similar response to Al-Maliki’s design. The controller output of the proposed optimal FPID has a higher peak than Al-Maliki’s design.

To summarize of the above simulation examples, the proposed optimal fuzzy PID controller has quicker responses with smaller rising time and settling time. However, we still cannot claim that the proposed optimal FPID has outperformed other methods. In order to compare it with other approaches, we used the same IAE performance index, shown in Equation (6), but it is not practical to only consider the error signal without considering the energy or the power consumption of the controller output. The proposed optimal FPID design features a simple controller structure and a straightforward design approach based on conventional PID control and only eight nonlinear factors.

Table 9. Number of tuning parameters for different controllers.

Model Name	Number of Tuning Parameters
Pelusi’s Fuzzy PD [19]	69
Singh’s Fuzzy GA database [20]	21
Al-Maliki’s FLC-PID with KF [21]	20 (FLC-PD:10 & FLC-PI:10)
The proposed optimal FPID	8

shows comparisons with the number of tuning parameters for different controllers.

4. Conclusions

Based on the equivalence between fuzzy PID controllers and conventional PID controllers, this paper proposed an optimal fuzzy PID controller design with each fuzzy variable’s MFs tuned by a nonlinear factor. Firstly, for a controlled plant, one can make a preliminary conventional PID controller design by some traditional techniques. Then the conventional PID controller design can be transformed into an equivalent FLC with four parameters defining the operating ranges of the I/Os. Subsequently, for each fuzzy I/O variable, one nonlinear factor is used for tuning the nonlinearity of MFs. Thus, there will be a total of eight parameters needed to be optimized by GA for an optimal fuzzy PID controller. To enhance the GA efficiency, each parameter must be given a crossover point. Finally, we set the aforementioned equivalent FLC to be one individual in the first generation of GA. This can yield quick and global convergence. In fact, we also found that in some simulations it made no significant difference if we did not take the equivalent FLC to act as one individual in the initial population of GA. This implies that the GA programming in this paper is really efficient. In conclusion, the proposed design approach makes an optimal fuzzy PID controller design more straightforward, and the controller structure more concise. This is quite advantageous for designers because they will have a clearer concept about the operating ranges of fuzzy I/O variables. As a result, we can now simply and appropriately increase the searching space for the optimal fuzzy PID controller design.