Compensation of Frequency Drift in Frequency-Sweep Polarization-Modulation Ranging System

Featured Application

Absolute distance measurement.

Abstract

In frequency-sweep polarization-modulation ranging, distance is determined by the frequency of modulated waves and the corresponding wavelength multiple when emitted and returned waves are in phase. However, measurement of the frequency and the wavelength multiple is affected by thermally induced phase delay of the polarized wave. In this article we systematically discuss the principle of the ranging method and analyze the influences of thermally induced phase delay. New approaches to measurement are proposed to eliminate the impact on frequency and the wavelength multiple. Theoretical analysis and experimental results proved the efficiency and applicability of the methods.

1. Introduction

Absolute distance measurement (ADM) technologies are of significant application in scientific and engineering fields such as large equipment manufacturing, spacecraft fabrication, and general-purpose coordinate measurements [1,2,3]. Various methods of ADM have been developed over the past decades, such as phase shift-based ranging [4,5,6], frequency scanning interferometry-based ranging [7,8,9,10], multi-wavelength interference-based ranging [11,12,13,14], and femtosecond optical comb-based ranging [10,15,16,17]. In recent years, the latter three technologies have achieved great accuracy in laboratory, but the systems are complex and their performance needs to be enhanced in an industrial setting. The phase shift ranging method is a common technology in industry, in which the phase differences between continuous emitted and reference waves are compared. However, in phase shift ranging systems, the performance of phase discrimination is influenced by parasitic parameters in the circuit, and as a result ranging precision is limited.

The frequency-sweep polarization-modulation (FSPM) method is another phase ranging method in which modulation frequency is scanned and searched when emitted and returned waves are in phase, thus avoiding the environmental disturbance as well as shortage of phase discrimination [18,19,20]. It was proposed by Kern & Co. Ltd. and first applied in the commercial distance meter ME5000 [21,22,23]. Due to its simple structure and high resolution, the FSPM ranging technique has the potential for small size and high performance. However, in the FSPM ranging system, the frequency is vulnerable to phase delay variation due to the sensitivity of crystals (e.g., LiNbO₃) in the electro-optic modulator (EOM) to temperature disturbance. The heat dissipation of electronic components and laser irradiation will accelerate the temperature variation [24], thus leading to distance measurement errors.

In order to investigate this problem, a theoretical model was developed for the FSPM ranging systems. Based on the model, a correction approach for diminishing the thermally-induced errors in the system was proposed. A reciprocating sweeping method and multi-frequency interval method were respectively proposed to improve the measurement accuracy of frequency and the corresponding wavelength multiple. The validity of the method was proved by theoretical analysis and experiments. The article is organized as follows: In Section 2, the principle of the FSPM-based system is introduced, measurement errors due to phase delay are discussed, and the compensation methods are proposed. In Section 3, experiments are conducted to prove the effectiveness of the methods. Finally, a brief conclusion is given in Section 4.

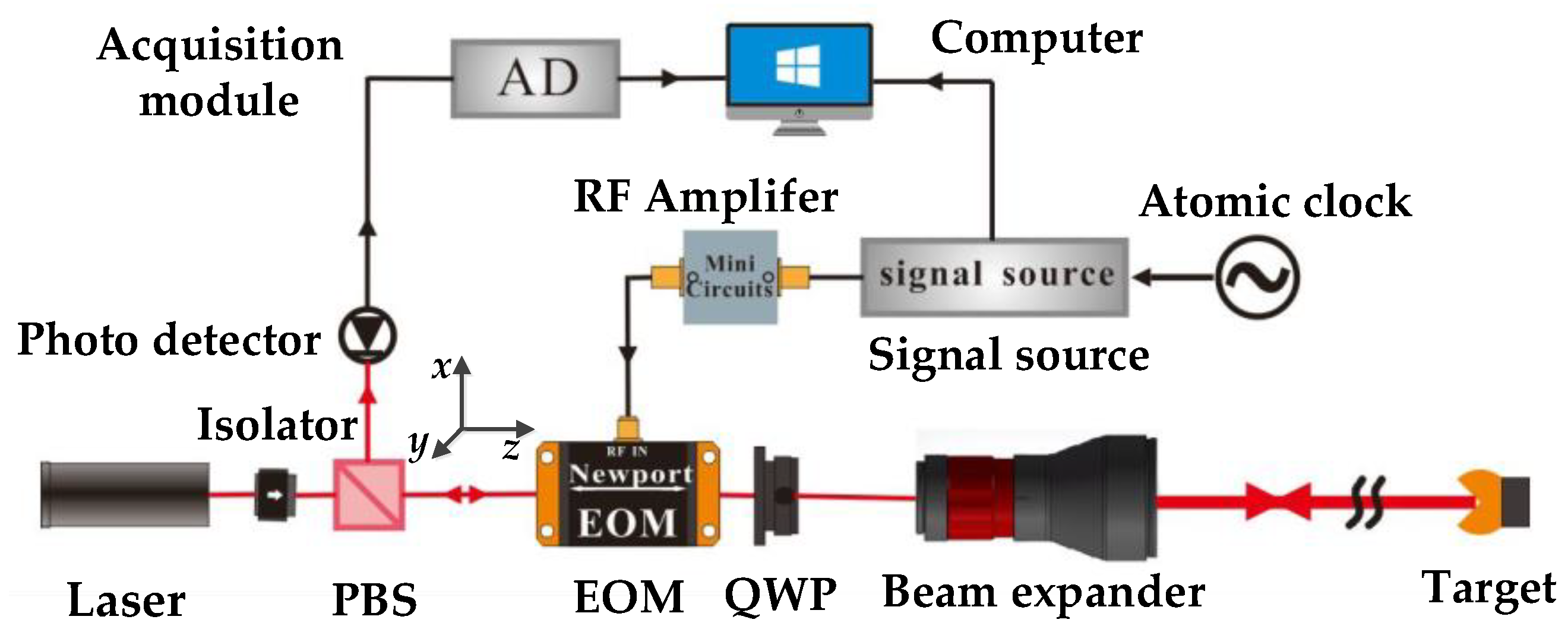
2. Principle and Method

2.1. The Principle and Model

The frequency-sweep polarization-modulation ranging system consists of a continuous wave laser, an isolator, a polarizing beam splitter (PBS), an EOM, a quarter wave plate (QWP), a beam expander (EXP) and the target, as shown in Figure 1.

To illustrate the working principle of the FSPM ranging method, a Cartesian coordinate system is established. The z-axis represents the direction of wave propagation, while the x-axis is the polarization direction of linearly polarized light generated by the laser. In the system, continuous polarized light emitted by the laser travels through an isolator and a PBS tipped 45 degrees from the x-axis, so equal amplitude of polarization components in the x-axis and y-axis is achieved when light travels into the EOM. The EOM generates phase retardation between the two components in a sinusoidal manner with linearly changed frequency. The QWP has a fast axis oriented at 45 degrees to the x-axis, so the light travels to the target and returns by the same path, to then be demodulated by the EOM. The phase difference between the polarization components when light transmits through the EOM successively can be respectively described as:

$$\begin{array}{l}{\phi }_1=k\sin \left(\omega t\right),\\ {\phi }_2=k\sin \left(\omega t+\phi \right){+\delta }_{\mathrm{T}},\end{array}$$

(1)

where ω is the modulation frequency, k represents the modulation depth, ${\delta }_{\mathrm{T}}$ represents the additional phase delay between the polarization components, φ is the phase shift of the modulation signal during the round-trip time, and φ = 4πf(t)nl/c, where f(t) is the modulation frequency, c represents the speed of light in vacuum, n is the refractive index of the air, and l is the distance to be measured. Note that in the equation, $0<k\le 1$ for linear modulation and ${\delta }_{\mathrm{T}}$ is small, typically less than π/2. With the amplitude of x and y components normalized, the intensity of light received by the detector can be written as:

$$\mathrm{I}=1-\cos \left({\phi }_1{-\phi }_2\right)=1-\cos \left(2k\cos \frac{2\omega t+\phi }{2}\sin \frac{\phi }{2}\right)·{\cos \delta }_{\mathrm{T}}+\sin \left(2k\cos \frac{2\omega t+\phi }{2}\sin \frac{\phi }{2}\right)·{\cos \delta }_{\mathrm{T}}.$$

(2)

After simplification and filtering the high-frequency components, the equation can be rewritten as:

$$\mathrm{I}=1-\left(1-\frac{k^2}{2}+\frac{k^2}{2}\cos \phi \right)·{\cos \delta }_{\mathrm{T}}.$$

(3)

Obviously, if ${\cos \delta }_{\mathrm{T}}$ is constant, there exists a cosine relationship between intensity and modulation frequency. Minimums of the equations By obtaining the corresponding frequencies f_x, f_x+1 (k∈N) at adjacent minima, the distance can be determined by:

$$l =\mathrm{N}·\frac{\mathrm{c}}{{2\mathrm{n}f}_x},\mathrm{in}\mathrm{which} \mathrm{N}=\left[\frac{f_x}{f_{x+1}{-f}_x}\right],$$

(4)

where, N is the wavelength multiple, [ ] is the rounding operation, f_x/(f_x+1 − f_x) is the initial value of the wavelength multiple, which comprises an integer and a fraction part, so the rounding operation is necessary. For convenience in the manuscript, The frequencies f_x and f_x+1 will be defined as “in phase” frequency. Value of difference of adjacent in-phase frequencies i.e., f_x+1 − f_x will be defined as frequency interval f_b, which is ideally a constant when distance is invariant.

2.2. Influence of Thermally Induced Phase Delay and Traditional Correction Method

In a transverse modulator configuration, the effects of temperature variation on modulation characteristics are mainly as follows: first, due to the thermo-optic effect of the crystal, the refractive index of the crystal changes with temperature. More concretely, the change in the refractive index along the direction of light transmission causes the optical path variation of light, and the change in refractive index perpendicular to the direction of light transmission results in an additional phase delay of the polarization [25]. Second, due to the elasto-optical effect of the crystal, the stress caused by the thermal expansion of the crystal also changes the refractive index and the longitudinal length of the crystal. As a result, the thermally induced phase delay can be expressed as follows:

$${\delta }_T=\frac{2\mathsf{\pi }}{\mathsf{\lambda }}\Delta {\mathrm{n}}_{t}l+\frac{2\mathsf{\pi }}{\mathsf{\lambda }}{\mathrm{n}}_t\Delta l,$$

(5)

where λ represents wavelength of light, n_t is the initial value of natural birefringence in the direction perpendicular to light transmission, and$\Delta {\mathrm{n}}_t$ is the thermally induced birefringence variation. l represents the initial value of the length of the crystal, and $\Delta l$ is the thermally induced variation of the crystal length.

Several techniques have been applied to compensate for the thermally induced phase delay in the applications of EOM. An example of this is connecting a compensate crystal that has the same size and performance with the modulate crystal, with the optical axes of the crystals perpendicular to each other so that the phase delay in the two identical crystals are complementary [26]. Another way is to make the two crystals in series, with one half-wave plate placed in the middle of them to make the polarization plane of the polarized light rotate by λ/2 [24]. In these methods, crystals with exactly the same parameters and their perfect assembly are the key to compensation, but that is difficult to achieve. In the FSPM ranging system, a quarter-wave plate is placed between the crystal and the target so that when light passes through the quarter-wave plate during emitting and returning, the plane of polarization can be rotated by λ/2 to achieve the complementation [27,28]. In this structure, the adjustment is simpler and the compensation is better. However, in the FSPM ranging system, a mismatch of polarizing devices and reflection of polarized light are inevitable and lead to the additional rotation of the polarization plane of light. Even a very small mismatch of polarization devices or any reflection in the system will result in the rotation of the polarization plane, and produce residual thermally induced phase delay.

In our experiment, the residual thermally induced phase delay was tested first. Since thermally induced phase delay varies slowly, it can be measured through a polarization analysis system (Thorlabs, PAX5710). At the same time, the temperature in the modulator chamber was tested with a high-precision temperature controller (Wavelength, Tc_lab), with results shown in Figure 2. As is shown, with the increase of temperature, the phase delay slowly increased, accompanied by periodic oscillation, and when temperature growth slowed down, the oscillation speed also decreased.

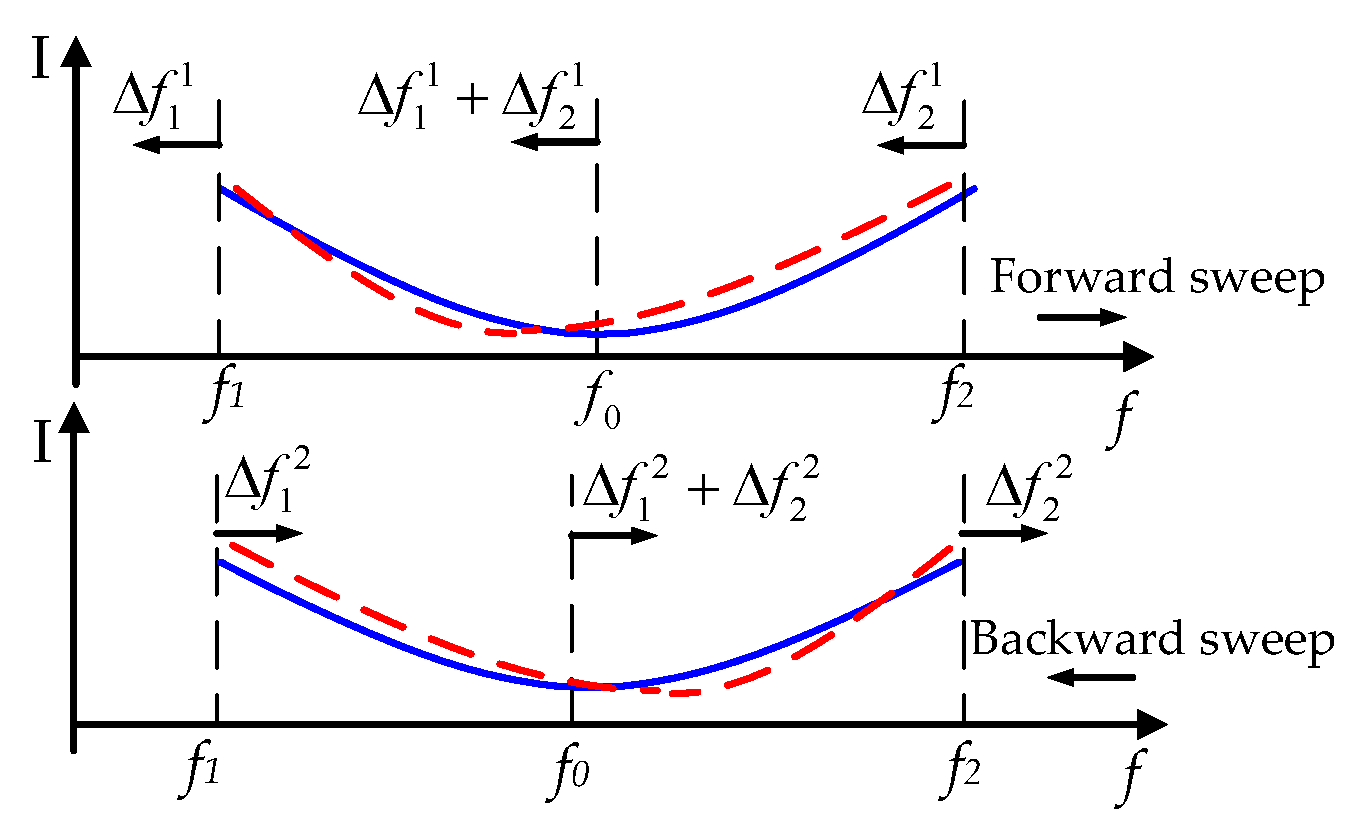
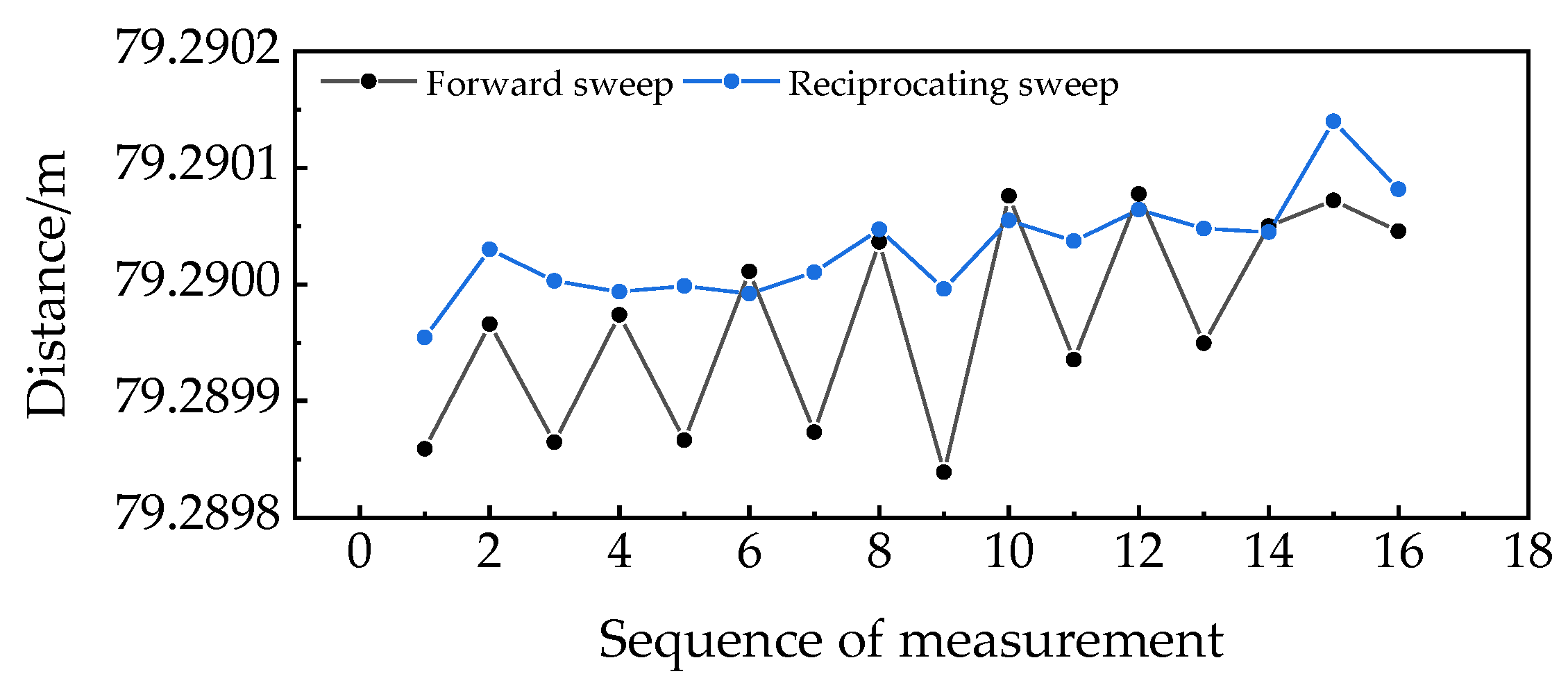
2.3. Reciprocating Sweeping-Based Measurement of “in Phase” Frequency

The change of additional phase delay accelerates or decelerates the polarization variation when the wave is modulated across the “in phase” frequency, thus destroying the symmetry of the intensity curve, leading to the shift of minima. The shift can be manifested in variation of the curve slope. Through the derivation of Equation (3), the slope of the intensity curve at the ideal minimum ${\phi }_0$ can be written as:

$${\mathrm{I}}^{\prime }\left({\phi }_0\right)=\underset{\Delta \phi \to 0}{\lim }\frac{I\left({\phi }_0+\Delta \phi \right)-I\left({\phi }_0-\Delta \phi \right)}{2\Delta \phi }=\underset{\Delta \phi \to 0}{\lim }\frac{-\left(1-\frac{k^2}{2}+\frac{k^2}{2}\cos \Delta \phi \right)\left({\sin \delta }_0\sin \Delta \delta \right)}{\Delta \phi },$$

(6)

where ${\delta }_0$ is the thermally induced phase delay when${\phi =\phi }_0,$ Δ$\phi$ is the increment on point of ${\phi }_0$, Δδ is the increment on point of δ₀. According to the above equation, ${\mathrm{I}}^{\prime }\left({\phi }_0\right)$ is a result of interaction between modulation depth, frequency scanning, and phase delay variation. Large modulation depths and frequency sweep speed are beneficial for eliminating the effect of thermally induced phase delay. However, modulation depth and sweep speed are often limited owing to equipment limitations, and a larger modulation depth requires a larger microwave voltage, thus aggravating the heating problem of the modulation circuit. Interestingly, we found that Equation (6) is an odd function about φ, so the orientation of the frequency shift can be controlled through frequency sweep directions. When modulation frequency is swept forward (i.e., from the lower frequency to the higher frequency), Δφ(t) > 0, otherwise, Δφ(t) < 0. Therefore, during the forward and backward sweep, the minimum drifts in opposite directions. Through averaging of such reciprocating sweeping, the drift errors can be diminished and frequency measurement stability can be improved. The method is further analyzed below.

Suppose the ideal frequency under test is f₀. f₁ and f₂ are frequencies very close to f₀ and satisfy the equations f₁ = f₀ − δf and f₂ = f₀ + δf. If the system is not affected by thermally induced phase delay, obviously we get the equation I(f₁) = I(f₂), then the exact value of f₀ can be worked out through: f₀ = (f₁ + f₂)/2. However, due to thermally induced phase delay, during the forward sweeping, f₁ and f₂ respectively moves $\Delta f_1^1$ and $\Delta f_2^1$ towards lower frequency, then in the backward sweeping, f₁ and f₂ respectively moves $\Delta f_1^2$ and $\Delta f_2^2$ towards the opposite side, as shown in Figure 3.

Taking random measurement errors $\upsilon$ into account, the extremum of the measurements are respectively expressed as:

$$\begin{array}{c}{f}_0^1=\frac{\left(f_1-\Delta f_1^1\pm \left|{\upsilon }_1^1\right|\right)+\left(f_2-\Delta f_2^1\pm \left|{\upsilon }_2^1\right|\right)}{2},\\ f_0^2=\frac{\left(f_1+\Delta f_1^2\pm \left|{\upsilon }_1^2\right|\right)+\left(f_2+\Delta f_2^2\pm \left|{\upsilon }_2^2\right|\right)}{2}.\end{array}$$

(7)

Through n times of such sweeps, the frequency can be obtained by:

$$f_0=\frac{2\mathrm{n}\left(f_1+f_2\right)+{{\displaystyle \sum }}_{i=1}^n\left(\Delta f_1^{2n} -\Delta f_1^{2n-1}\right)+{{\displaystyle \sum }}_{i=1}^n\left(\Delta f_2^{2\mathrm{n}} -\Delta f_2^{2\mathrm{n}-1}\right)\pm {{\displaystyle \sum }}_{i=1}^{2n}\left|{\upsilon }_1^n\right|\pm {{\displaystyle \sum }}_{i=1}^{2n}\left|{\upsilon }_2^n\right|}{4n}.$$

(8)

During the time of reciprocating sweeping, variation of δ is small so items of ${{\displaystyle \sum }}_{i=1}^n\left(\Delta f_1^{2n}-\Delta f_1^{2n-1}\right)$ and ${{\displaystyle \sum }}_{i=1}^n\left(\Delta f_2^{2\mathrm{n}}-\Delta f_2^{2\mathrm{n}-1}\right)$can be diminished to some extent, and the random measurement error of frequency can be compensated by averaging.

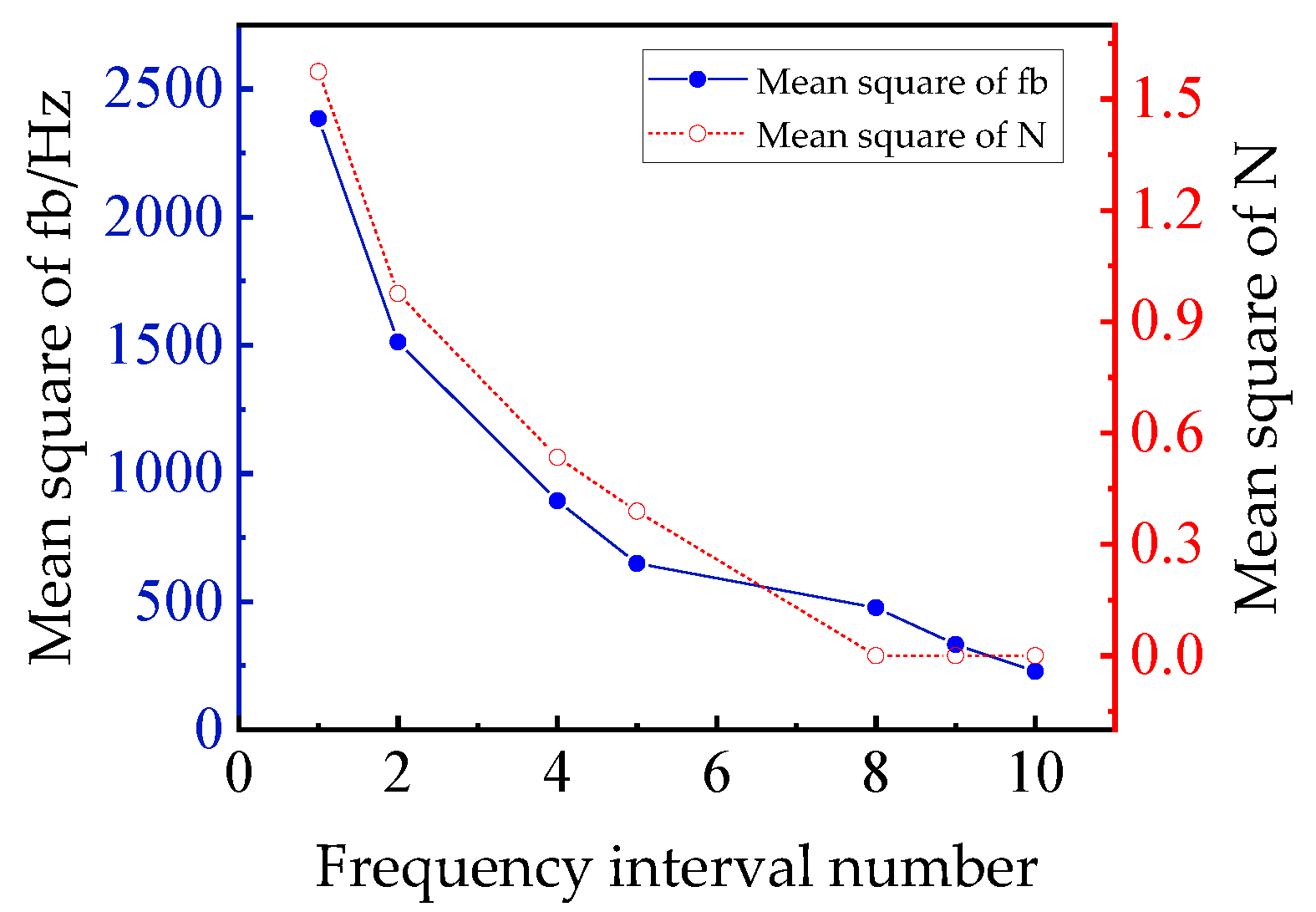
2.4. Multi-Frequency Interval-Based Measurement of Frequency Interval

Although frequency error can be partially eliminated through the reciprocating sweeping method, measurement of N requires a higher accuracy of frequency. The measurement error of N can be expressed as:

$$\Delta \mathrm{N}=\left[\frac{\Delta f_x}{f_x}-\frac{\Delta f_{\mathrm{b}}·f_x}{f_{\mathrm{b}}^2}\right]=\left[-\frac{\Delta f_{\mathrm{b}}·f_x}{f_{\mathrm{b}}^2}\right].$$

(9)

The above equation indicates that the absolute error of N is determined by the relative error of f_b. However, in the FSPM method, the impact of relative error of f_b is often 2N times larger than the relative error of f_x, which means the accuracy of f_x may not meet the accuracy requirement of f_b. If f_x is around 2.5 GHz, l is about 100 m, a frequency measurement error of 2500 Hz only contributes a ranging error of 100 μm, but the resulting relative error of f_b contributes a ranging error of 0.36 m. To ensure the accuracy of N, Δf_b should be less than 90 Hz, which cannot be satisfied by the reciprocating sweeping method.

In order to reduce the measurement error of f_b, we used the characteristic of equal spacing of the “in phase” frequencies in our multi-frequency interval-based approach. For example, f_b can be expressed as follows:

$$f_b=\frac{\left(f_{x+u} {-f}_x\right)}{u},$$

(10)

where f_x is an arbitrary “in phase” frequency in sweeping band, f_x+u is the uth “in phase” frequency on its upper side. Therefore, N can be rewritten as:

$$\mathrm{N}=\left[\frac{f_x}{f_b}\right]=\left[\frac{u·f_x}{f_{x+u}{-f}_x}\right].$$

(11)

Hence, taking the frequency drift and random measurement error into account, the multi-frequency interval can be expressed as:

$$f_{x+u}{-f}_x=u·f_b\pm \Delta f_u\pm \left(\left|{\upsilon }_{x+u}\right|+\left|{\upsilon }_x\right|\right),$$

(12)

where $\Delta f_u$ represents the frequency drift. The measurement error of the wavelength multiple can be expressed as:

$$\Delta \mathrm{N}=\left[\frac{\Delta f_x}{f_{\mathrm{b}}}-\frac{f_x·\Delta \left(f_{x+u}{-f}_x\right)}{u·f_{\mathrm{b}}^2}\right]\approx \left[-\frac{f_x·\Delta \left(f_{x+u}{-f}_x\right)}{u·f_b^2}\right]=\left[-\frac{f_x\Delta \left(\pm \Delta f_u\pm \left(\left|{\upsilon }_{x+u}\right|+\left|{\upsilon }_x\right|\right)\right)}{u·f_b^2}\right].$$

(13)

Therefore, errors caused by frequency drift and random measurement error are u times narrower than the general method.

In the above method, u can be determined by the following equation:

$$u\left[\frac{f_{x+u} {-f}_x}{f_{x+1} {-f}_x}\right].$$

(14)

According to the expression of $\Delta u$:

$$\Delta u=\left[\frac{\Delta \left(f_{x+u}-f_x\right)}{f_b}-\frac{\Delta \left(f_{x+1}{-f}_x\right)}{u·f_b} \right]=\left[-\frac{\pm \Delta f_u\pm \left(\left|{\upsilon }_{x+u}\right|+\left|{\upsilon }_x\right|\right)}{f_b}-\frac{\pm \Delta f_1\pm \left(\left|{\upsilon }_{x+1}\right|+\left|{\upsilon }_x\right|\right)}{u·f_b}\right].$$

(15)

The items are small quantities, that is, $\pm \Delta f_u\pm \left(\left|{\upsilon }_{x+u}\right|+\left|{\upsilon }_x\right|\right)/f_b\ll 1$, $\pm \Delta f_1\pm \left(\left|{\upsilon }_{x+1}\right|+\left|{\upsilon }_x\right|\right)/\left({uf}_b\right)\ll 1$, so u can be accurately acquired.

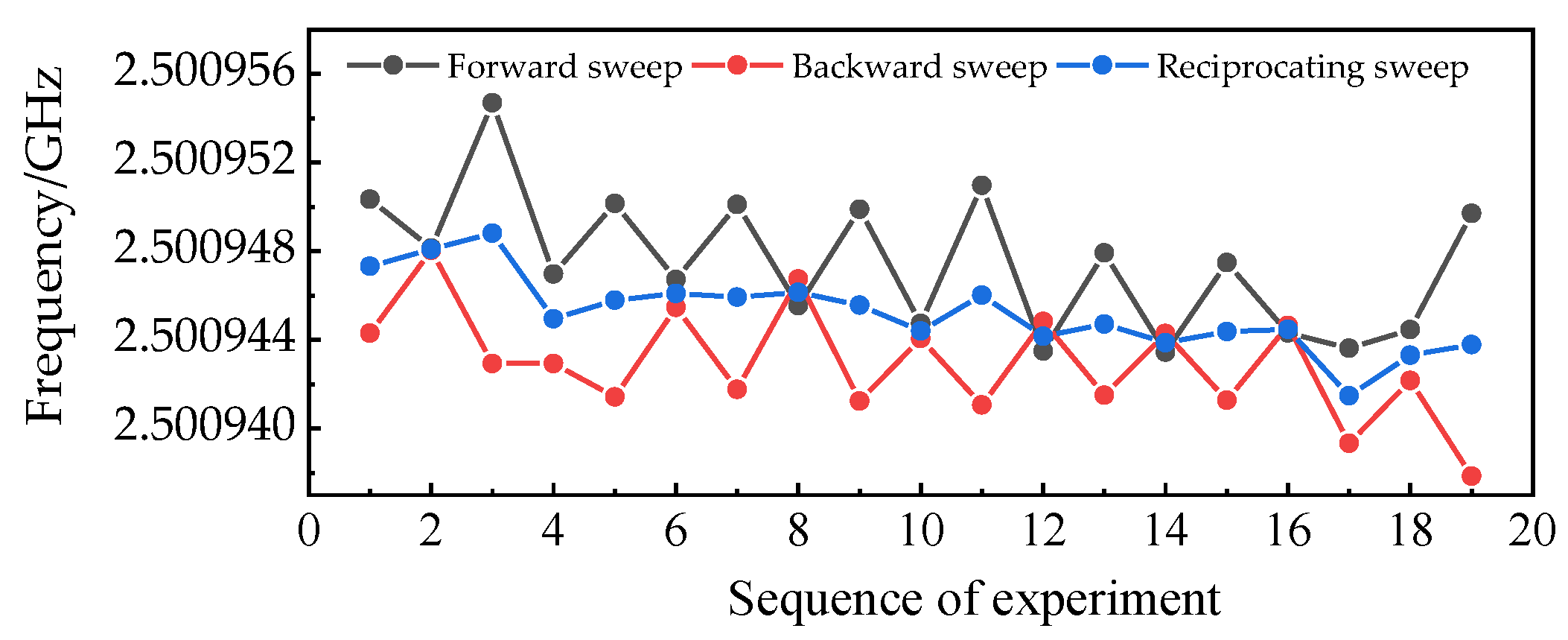
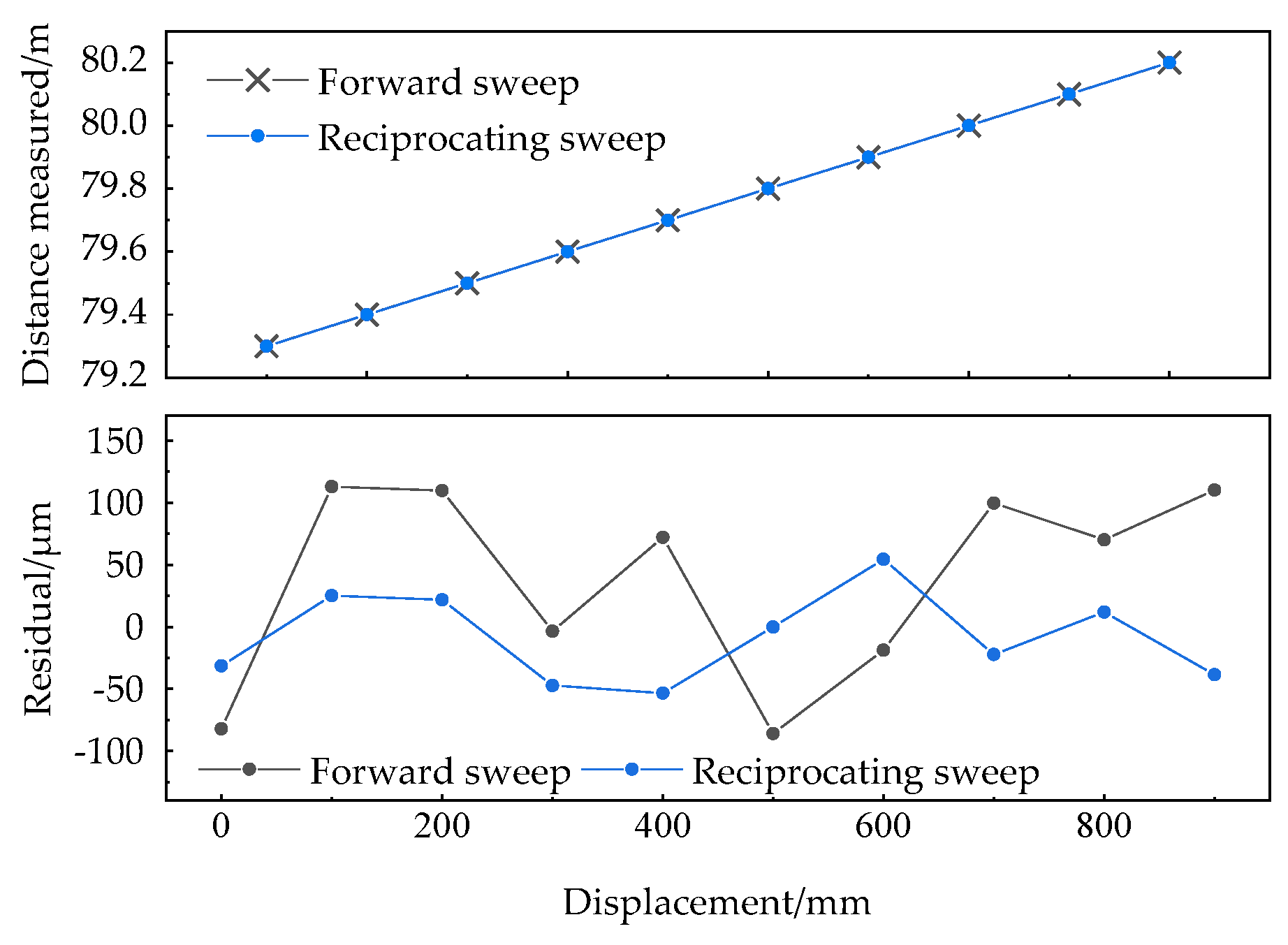
3. Experimental Results and Discussion

In order to verify the effectiveness of above methods, the experimental system shown in Figure 1 was established and several experiments were conducted. In the system, a He-Ne laser (Newport R-32734) served as the light source, a high-frequency phase modulator (Newport, 4431, V_π is 40 V) served as the modulator, a signal generator (Keysight, N5171B) provided the modulation signal, the preset sweeping range was set from 2.500 to 2.520 GHz, with a sweep step size of 1 kHz. The residence time at each frequency was 20 ms. An avalanche detector (Thorlabs, APD410A) was used for the photoelectric conversion. A PXI oscilloscope (NI, 5171R) served as the acquisition and processing module. The target was approximately 80 m away from the crystal.

To evaluate the method of reciprocating sweep in compensation of thermally induced phase delay, an “in phase” frequency was obtained by different methods and results are shown in Figure 4. In the figure, black and red dots respectively denote the results obtained through forward and backward sweep, and blue dots denote the average of measurement results obtained by the reciprocating sweep. Results obtained through forward and backward sweeps drifted in opposite directions, and the forward sweeps had a larger statistical average than that of the backward sweeps. Through reciprocating sweeps, the results had a repeatability of 1727 Hz, which was much smaller than that of forward sweep (3130 Hz) and backward sweep (2503 Hz).

To validate our measurement method of N, N was tested with multi-frequency intervals. The “in phase” frequency f_x near the lower edge of band was first obtained in the reciprocating sweep method, then, the uth “in phase” frequency on its upper side was obtained, and f_b and N were respectively determined according to Equations (10) and (11). u was set to change from 1 to 10 in seven groups of tests, each group of tests contained 10 independent measurements; the statistical results are shown in Figure 5. In the single-frequency interval method, the mean squares of f_b and N were 2384 Hz and 1.5, respectively. As u increased from 1 to 8, the mean square of f_b was reduced to 332 Hz, and the mean square of N was reduced to 0. Further increase of u would result in further reduction of the standard deviation of f_b, but in our experiment, the frequency interval number of 8 was sufficient for an accurate measurement of N.

With the accurate measurement of N, distance could be determined through the “in phase” frequency and the corresponding N; results are shown in Figure 6. The statistical average of the forward sweeps was 6 µm larger than the backward sweeps. The statistical uncertainties of the forward sweeps and reciprocating sweeps were 87.1 µm and 44.1 µm, respectively.

Finally, an uncertainty test was conducted using a dual-frequency laser interferometer. The target retroreflector was moved from 79.29 to 80.29 m by ten steps at an increment of 100 mm. A commercial heterodyne interferometer (5519, Keysight) was used to measure the displacement of the target. By the application of linear fitting, the residual error between the reference displacement and the measured distance could be obtained as shown in Figure 7. The residual error of the forward sweep was from −85.9 to 113 μm. With the reciprocating sweep method, the max residual error was 54.4 μm. The relative error was attributed to the random measurement error of frequency, the temperature dependence of crystal properties, the air-path distance variation, and the instability of frequency reference. The random measurement error of frequency could be further reduced by reducing the sweep step size and increasing the signal-to-noise ratio of the system. The temperature dependence of crystal property included the refractive index and the length change on the optical path, and air-path distance variation was mainly caused by the variation of the air refractive index.

4. Conclusions

We systematically discussed the principle of the FSPM based ranging method and the impact of thermally induced phase delay on “in phase” frequency and wavelength multiple. To eliminate the frequency drift caused by the phase delay, a measurement method based on a reciprocating sweep was proposed. To obtain an accurate wavelength multiple, a multi-frequency interval approach was proposed according to the equal interval distribution of “in phase” frequencies. The results of our experiment proved the efficiency and applicability of the methods. The maximum deviation of the measured results between the FSPM-based system and the interferometer was 54.4 μm.