Mitigating the Impact of Mask Absorber Error on Lithographic Performance by Lithography System Holistic Optimization
Abstract
1. Introduction
2. Modeling of DUV Lithography
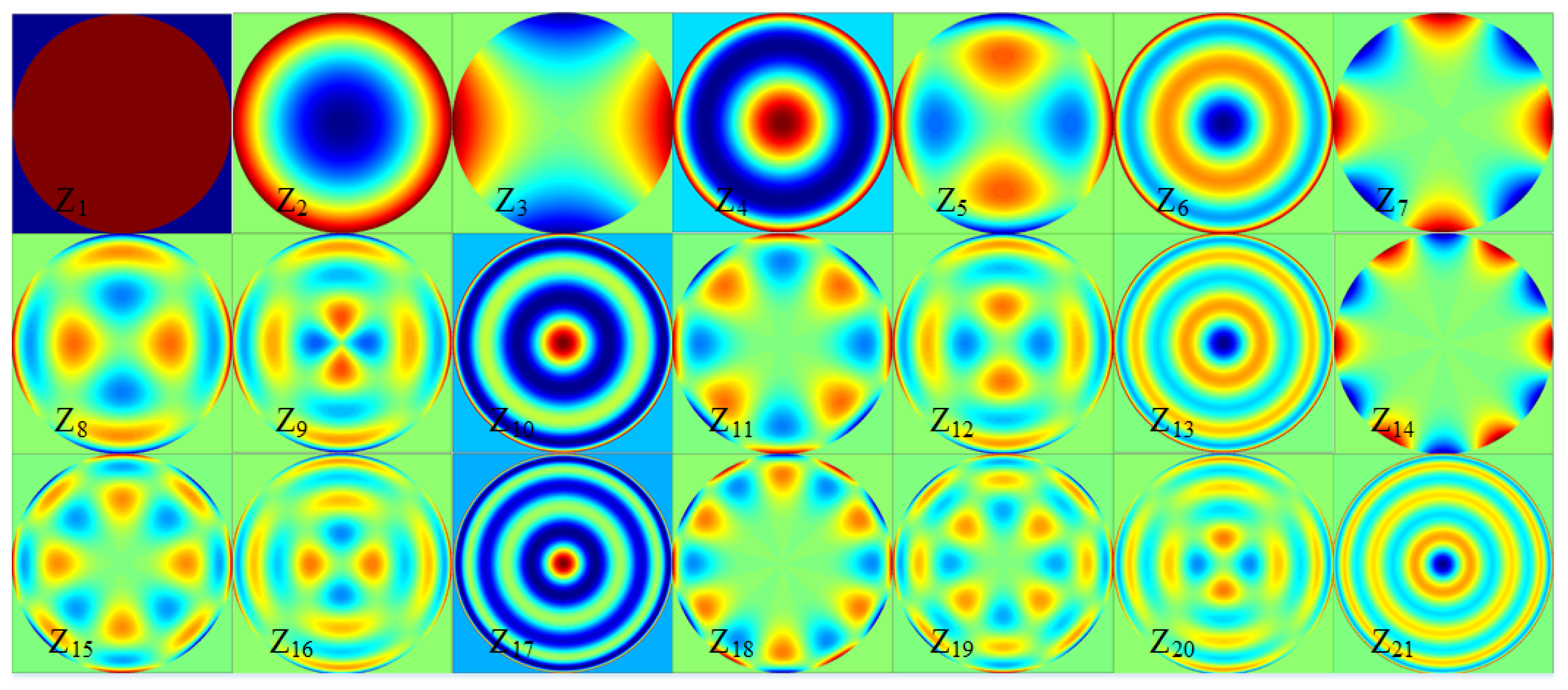
2.1. Source Pattern Representation
2.2. Mathematical Modeling
3. SNPCO Method for DUV Lithography System
4. Optimization Results
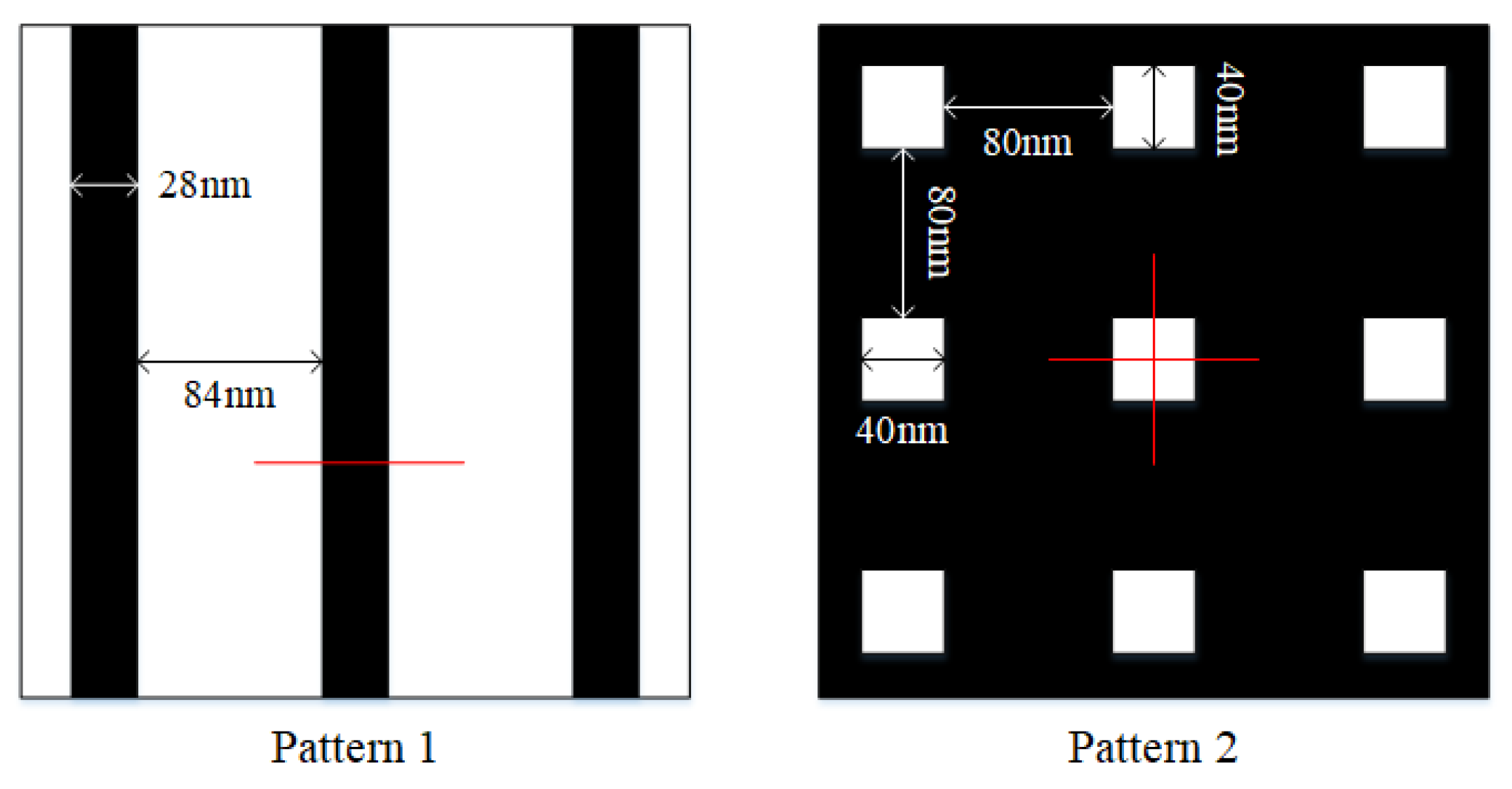
4.1. Simulation Conditions
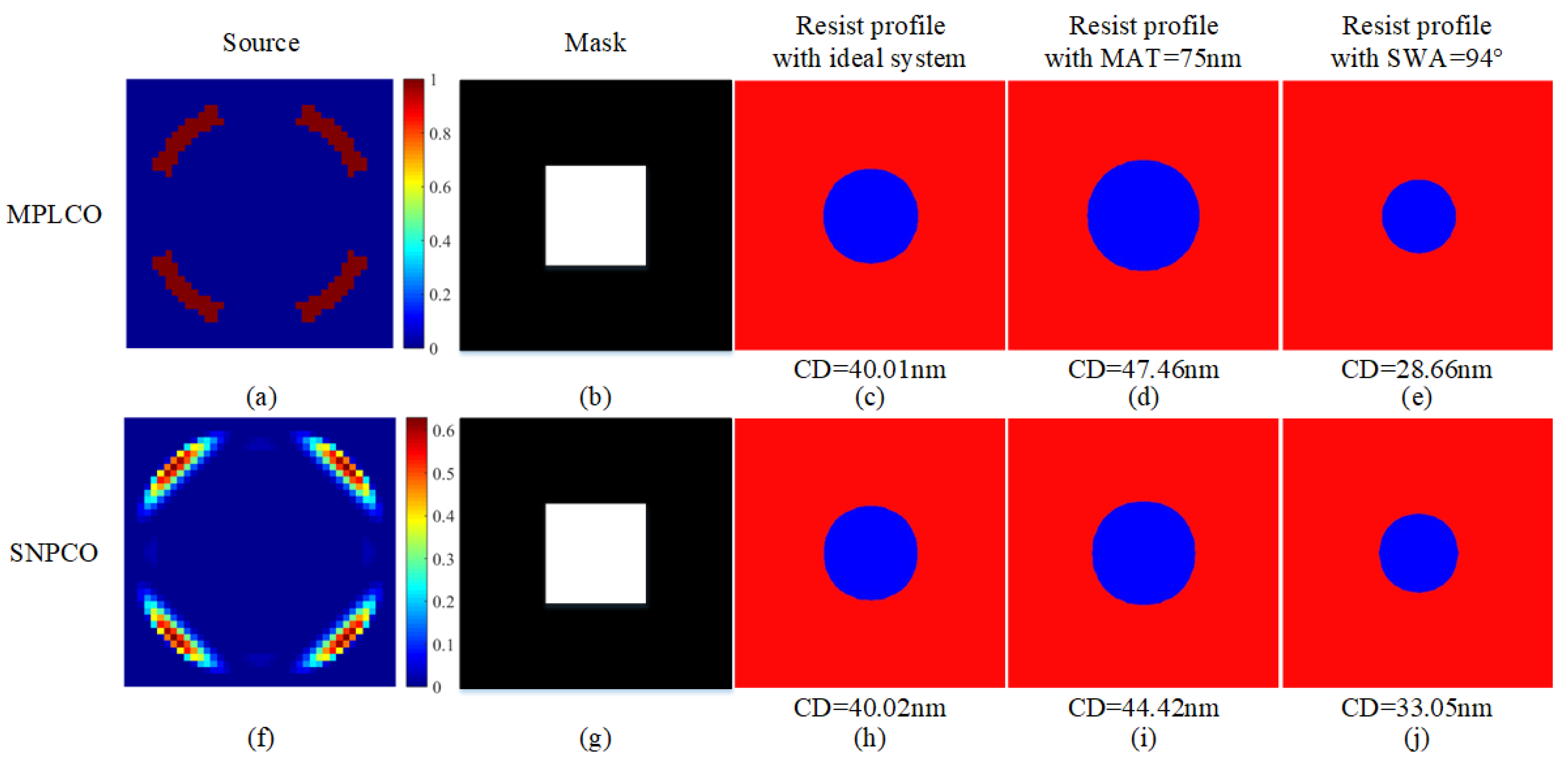
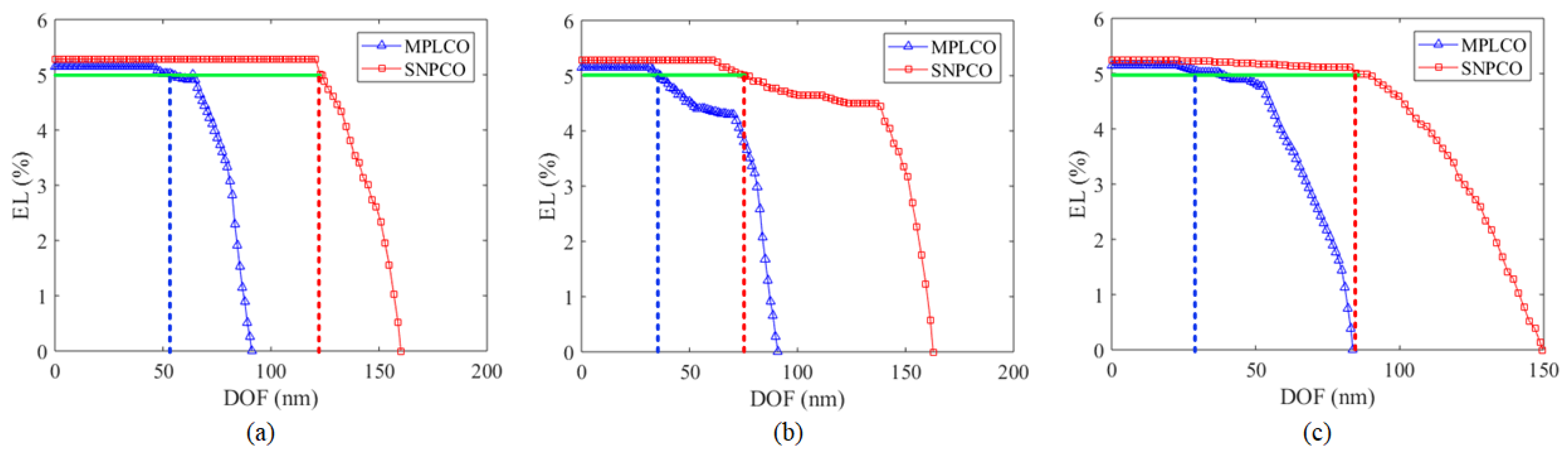
4.2. Simulation Results
4.2.1. Line Space Pattern
4.2.2. Contact Hole Pattern
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rothschild, M. A roadmap for optical lithography. Opt. Photonic News 2010, 21, 26–31. [Google Scholar] [CrossRef]
- Azpiroz, J.T.; Burchard, P.; Yablonovitch, E. Boundary layer model to account for thick mask effects in photolithography. In Proceedings of the SPIE 5040, Optical Microlithography XVI, Santa Clara, CA, USA, 26 June 2003. [Google Scholar]
- Bai, M.; Melvin, L.S., III; Yan, Q.; Shiely, J.P.; Falch, B.J.; Fu, C.; Wang, R. Approximation of three dimensional mask effects with two dimensional features. In Proceedings of the SPIE 5751, Emerging Lithographic Technologies IX, Bellingham, WA, USA, 6 May 2005. [Google Scholar]
- Sturtevant, J.; Tejnil, E.; Lin, T.; Schulze, S. Impact of 14-nm photomask uncertainties on computation lithography solutions. J. Micro/Nanolithogr. MEMS MOMES 2014, 13, 011004. [Google Scholar] [CrossRef]
- Yoshizawa, M.; Philipsen, V.; Leunissen, L. Optimizing absorber thickness of attenuating phase shifting Masks for Hyper-NA Lithography. In Proceedings of the SPIE 6154, Optical Microlithography XIX, San Jose, CA, USA, 13 March 2006. [Google Scholar]
- Liu, P. Accurate prediction of 3D mask topography induced best focus variation in full-chip photolithography applications. In Proceedings of the SPIE 8166, Photomask Technology, Monterey, CA, USA, 13 October 2011. [Google Scholar]
- Yu, T.; Lio, E.; Chen, P.; Wei, C.; Chen, Y.; Peng, M.; Chou, W.; Yu, C. UDOF direct improvement by modulating mask absorber thickness. In Proceedings of the SPIE 9985, Photomask Technology, San Jose, CA, USA, 3 October 2016. [Google Scholar]
- Finders, J.; Winter, L.; Last, T. Mitigation of mask three-dimensional induced phase effects by absorber optimization in ArFi and extreme ultraviolet lithography. J. Micro/Nanolithogr. MEMS MOMES 2016, 15, 021408. [Google Scholar] [CrossRef]
- Bouma, A.; Miyazaki, J.; Veen, M.V.; Finders, J. Impact of mask absorber and quartz over-etch on mask 3D induced best focus shifts. In Proceedings of the SPIE 9231, 30th European Mask and Lithography Conference, Dresden, Germany, 17 October 2014. [Google Scholar]
- Cho, J.; Baek, S.; Nam, K. Fogging and pattern loading effect by writing strategy. In Proceedings of the SPIE 4754, Photomask and Next Generation Lithography Mask Technology IX, Yokohama, Japan, 1 August 2002. [Google Scholar]
- Jia, N.; Yang, S.-H.; Kim, S.; Choi, J. Study of lens heating behavior and thick mask effects with a computational method. In Proceedings of the SPIE 9052, Optical Microlithography XXVII, San Jose, CA, USA, 31 March 2014. [Google Scholar]
- Plumhoff, J.; Constantine, C.; Shin, J.; Rausa, E. Improvements in MoSi EAPSM CD bias and iso-dense linearity plasma etch results utilizing design of experiments process optimization of Gen III ICP plasma source. In Proceedings of the SPIE 4754, Photomask and Next-Generation Lithography Mask Technology IX, Yokohama, Japan, 1 August 2002. [Google Scholar]
- Mueller, M.; Komarov, S.; Baik, K.-H. High-Resolution Etching of MoSi using Electron Beam patterned chemically amplified resist. In Proceedings of the SPIE 5130, Photomask and Next Generation Lithography Mask Technology X, Yokohama, Japan, 28 August 2003. [Google Scholar]
- Sturtevant, J.; Buck, P.; Schulze, S.; Fryer, D. 14-nm photomask simulation sensitivity. In Proceedings of the SPIE 9231, 30th European Mask and Lithography Conference, Dresden, Germany, 17 October 2014. [Google Scholar]
- Rudolph, O.H.; Evanschitzky, P.; Erdmann, A.; Bär, E.; Lorenz, J. Rigorous electromagnetic field simulation of the impact of photomask line-edge and line-width roughness on lithographic processes. J. Micro/Nanolithogr. MEMS MOMES 2012, 11, 013004. [Google Scholar] [CrossRef]
- Wistrom, R.; Sakamoto, Y.; Panton, J.; Faure, T.; Isogawa, T.; McGuire, A. Controlling the sidewall angle of advanced attenuated phase-shift photomasks for 14nm and 10nm lithography. In Proceedings of the SPIE 8880, Photomask Technology, Monterey, CA, USA, 9 September 2013. [Google Scholar]
- Ko, K.; Moon, Y.; Jeong, C.; Kim, H.; Jeon, C.; Oh, H. Influence of a non-ideal sidewall angle of extreme ultra-violet mask absorber for 1×-nm patterning in isomorphic and anamorphic lithography. Microelectron. Eng. 2017, 181, 1–9. [Google Scholar] [CrossRef]
- Sears, M.K.; Bekaert, J.; Smith, B.W. Lens wavefront compensation for 3D photomask effects in subwavelength optical lithography. Appl. Opt. 2013, 52, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Fühner, T.; Evanschitzky, P.; Erdmann, A. Mutual source, mask and projector pupil optimization. In Proceedings of the SPIE 8326, Optical Microlithography XXV, San Jose, CA, USA, 13 March 2012. [Google Scholar]
- Li, J.; Lam, E.Y. Robust source and mask optimization compensating for mask topography effects in computational lithography. Opt. Express 2014, 22, 9471–9485. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Li, Y.; Dong, L.; Ma, X.; Guo, X. Inverse pupil wavefront optimization for immersion lithography. Appl. Opt. 2014, 53, 6861–6871. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Li, Y.; Dong, L.; Liu, L. Co-optimization of the mask, process, and lithography-tool parameters to extend the process window. J. Micro/Nanolithogr. MEMS MOMES 2014, 13, 013015. [Google Scholar] [CrossRef]
- Aluizio Prata, J.; Rusch, W.V.T. Algorithm for computation of Zernike polynomials expansion coefficients. Appl. Opt. 1989, 28, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Liu, S.; Li, J.; Lam, E. Efficient source mask optimization with Zernike polynomial functions for source representation. Opt. Express 2014, 22, 3925–3937. [Google Scholar] [CrossRef] [PubMed]
- Lv, W.; Liu, S.; Wu, X.; Lam, E. Illumination source optimization in optical lithography via derivative-free optimization. J. Opt. Soc. Am. A 2014, 31, B19–B26. [Google Scholar] [CrossRef] [PubMed]
- Plagianakos, V.P.; Magoulas, G.D.; Vrahatis, M.N. Learning rate adaptation in stochastic gradient descent. In Advances in Convex Analysis and Global Optimization, Nonconvex Optimization and Its Applications; Hadjisavvas, N., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2001; Volume 54, pp. 433–444. [Google Scholar]
- Han, C.; Li, Y.; Ma, X.; Liu, L. Robust hybrid source and mask optimization to lithography source blur and flare. Appl. Opt. 2015, 54, 5291–5302. [Google Scholar] [CrossRef] [PubMed]
- International Technology Roadmap for Semiconductors. Available online: http://www.itrs2.net/ (accessed on 4 March 2019).
- Owa, S.; Wakamoto, S.; Murayama, M.; Yaegashi, H.; Oyama, K. Immersion lithography extension to sub-10 nm nodes with multiple patterning. In Proceedings of the SPIE 9052, Optical Microlithography XXVII, San Jose, CA, USA, 31 March 2014. [Google Scholar]




| Source optimization procedure |
| 1. Initialization: Assign the coefficient vector c of the starting source, source optimization step size , the increment of c for derivative calculation, the weighting coefficients of the objective functions, maximum source iteration number , initial source iteration number , initial alternate loop count , and the maximum alternate loop count . 2. Update the source pattern: If ; While ; Randomly generate the absorber errors and ; Calculate the search direction at the current iteration point using the Equation (13); Update the Zernike coefficient vector: . end Else: Terminate the SNPCO method, and output the source pattern and the numerical aperture (NA) and process parameters. 3. Output the optimized source pattern into the NA and process parameters optimization procedure. |
| NA and process parameters optimization procedure |
| 1. Initialization: Assign the NA and process parameters vector x, the parameters optimization step size , the increment of x for derivative calculation , maximum NA and process parameters iteration number , initial process and lithography-tool iteration number . 2. Normalize the optimization parameters using Equation (12); 3. Update the NA and process parameters: While ; Randomly generate the absorber errors and ; Calculate the search direction at the current iteration point using Equation (14); Update the NA and process parameters vector: . End 4. Return the optimized NA and process parameters to the source optimization procedure. |
| Parameters | Min. | Max. |
|---|---|---|
| Hotplate duration (s) | 10 | 100 |
| Transition duration (s) | 2 | 20 |
| Chill plate duration (s) | 10 | 60 |
| Development time (s) | 5 | 60 |
| NA | 1 | 1.35 |
| Pattern | Parameters | MPLCO Results | SNPCO Results |
|---|---|---|---|
| Line space | Hotplate duration (s) | 62 | 31 |
| Transition duration (s) | 12 | 10 | |
| Chill plate duration (s) | 28 | 21 | |
| Development time (s) | 34 | 46 | |
| NA | 1.34 | 1.23 |
| Pattern | Parameters | MPLCO Results | SNPCO Results |
|---|---|---|---|
| Contact hole | Hotplate duration (s) | 64 | 61 |
| Transition duration (s) | 12 | 9 | |
| Chill plate duration (s) | 35 | 29 | |
| Development time (s) | 40 | 32 | |
| NA | 1.35 | 1.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, N.; Li, E.; Sun, Y.; Li, T.; Li, Y.; Wei, P.; Liu, L. Mitigating the Impact of Mask Absorber Error on Lithographic Performance by Lithography System Holistic Optimization. Appl. Sci. 2019, 9, 1275. https://doi.org/10.3390/app9071275
Sheng N, Li E, Sun Y, Li T, Li Y, Wei P, Liu L. Mitigating the Impact of Mask Absorber Error on Lithographic Performance by Lithography System Holistic Optimization. Applied Sciences. 2019; 9(7):1275. https://doi.org/10.3390/app9071275
Chicago/Turabian StyleSheng, Naiyuan, Enze Li, Yiyu Sun, Tie Li, Yanqiu Li, Pengzhi Wei, and Lihui Liu. 2019. "Mitigating the Impact of Mask Absorber Error on Lithographic Performance by Lithography System Holistic Optimization" Applied Sciences 9, no. 7: 1275. https://doi.org/10.3390/app9071275
APA StyleSheng, N., Li, E., Sun, Y., Li, T., Li, Y., Wei, P., & Liu, L. (2019). Mitigating the Impact of Mask Absorber Error on Lithographic Performance by Lithography System Holistic Optimization. Applied Sciences, 9(7), 1275. https://doi.org/10.3390/app9071275





