Wavelet Transform Application for/in Non-Stationary Time-Series Analysis: A Review

Abstract

Non-stationary time series (TS) analysis has gained an explosive interest over the recent decades in different applied sciences. In fact, several decomposition methods were developed in order to extract various components (e.g., seasonal, trend and abrupt components) from the non-stationary TS, which allows for an improved interpretation of the temporal variability. The wavelet transform (WT) has been successfully applied over an extraordinary range of fields in order to decompose the non-stationary TS into time-frequency domain. For this reason, the WT method is briefly introduced and reviewed in this paper. In addition, this latter includes different research and applications of the WT to non-stationary TS in seven different applied sciences fields, namely the geo-sciences and geophysics, remote sensing in vegetation analysis, engineering, hydrology, finance, medicine, and other fields, such as ecology, renewable energy, chemistry and history. Finally, five challenges and future works, such as the selection of the type of wavelet, selection of the adequate mother wavelet, selection of the scale, the combination between wavelet transform and machine learning algorithm and the interpretation of the obtained components, are also discussed.

1. Introduction

The time series (TS) analysis is the study of a sequence of data collected through time. It is an effective approach for investigating the variability of variables, and thus widely used in many areas of science and engineering. Mathematically, TS ($y_t$) is stationary if, for all t [1]:

$$E(y_t)=E\left[(y_{t-1})\right]=\mu ,$$

(1)

$$Var(y_t)={\gamma }_0<\infty ,$$

(2)

$$Cov(y_t,y_{t-k})=y_t,$$

(3)

where $E(.)$ is the expected value defined as the ensemble average of the quantity, and $Var(.)$ and $Cov(.)$ are, respectively, the variance and the covariance functions.

Stationarity in the wide sense is also known as weak stationarity, covariance stationarity or second-order stationarity [2]. If these constraint conditions are violated, the TS would exhibit non-stationary characteristics, which is a major challenge for several fields (e.g., remote sensing, finance, medicine, engineering and hydrology). For this reason, several approaches are developed in order to analyze the non-stationary characteristics. These approaches can be classified into two main types: time methods (e.g., Auto-Correlation Analysis method, Regression method, Seasonal Auto-Regressive Integrated Moving Average, Break for Additive Trend and Season) and Spectro-Temporal methods [3].

Spectro-Temporal methods allow for the characterization of frequency variations. A brief survey of the methods available for processing non-stationary data, such as Short Time-Frequency Transformer (STFT), Wigner–Ville Distribution (WVD), Empirical Mode Decomposition (EMD) and Wavelet Transformation (WT), will be presented. For time-frequency analysis, Gabor [4] introduced the STFT, also called a windowing technique, which maps the signal into a two-dimensional function of time and frequency. This technique uses a fixed amount of time for all frequencies which restrict flexibility. However, it allows for obtaining information with a limited precision. This is why Russell et al. [5] introduced the WVD approach as a quadratic time-frequency representation. In fact, WVD is defined as a Fourier transform (FT) of the central covariance. The limitation of this method lies in the cross-term interference problem indicated by the existence of negative power for some frequency ranges. Additionally, Huang et al. [1] developed the EMD method which is suitable for processing non-stationary TS. This method decomposes the data ‘modes’, i.e., Intrinsic Mode Functions (IMFs), without leaving the time domain. However, it is purely empirical and lacks a theoretical basis. Comparatively, WT becomes a widely used tool for signal analysis. One of the main advantages of WT is that it may decompose a signal directly according to the frequency and represents it in the frequency domain distribution state in the time domain. As for the wavelet transformation, both time and frequency information of the signal are retained. It is thus a more powerful transformation for time-frequency analysis.

This paper reviews the related studies on the development and applications of WT for different fields over the period between 2004 and 2018. The different references, the used data, the objective behind using WT, the mother wavelet and its performance are all summarized. The purpose of this paper is to provide researchers and engineers with a deeper comprehensive knowledge of the theory and application of the WT method for non-stationary TS. In fact, the primary research questions considered in this survey are:

• Q1: What are the different types of WT for non-stationary time-series analysis?
• Q2: What are the uses of WT in different fields?
• Q3: Considering those different fields, what are the limits of the WT method?
• Q4: What are the future perspectives of WT for non-stationary time-series analysis?

The remainder of this paper is organized into five parts, starting with the Introduction section (Figure 1). Section 2 presents a brief introduction of the theoretical background of WT, including the mostly used wavelets. Then, Section 3 reviews the application of WT in several fields. Afterwards, further discussions of the new WT trends and some concluding remarks are given in Section 4 and Section 5, respectively.

2. Theoretical Background of Wavelet Transforms

The WT decomposes a signal at different timescales. It is defined as a set of basic functions ${\psi }_{a,b}(t)$ that can be generated by translating and scaling the so-called mother wavelet as follows [6]:

$${\psi }_{a,b}=\frac{1}{\sqrt{a}}\psi (\frac{t-b}{a});a>0,-\infty <b<\infty ,$$

(4)

where a is the scale parameter and b determines the location of the wavelet. In this paper, we describe the mostly used WT in the literature. In practice, there are different WT types where many mother wavelets are used. They are summarized as follows.

2.1. Continuous Wavelet Transform (CWT)

The CWT is used for mapping the changing properties of non-stationary signals. However, CWT is a time-frequency representation of a signal $f(t)$ that can be defined by the following equation:

$$W_f(a,b)={\int }_{-\infty }^{\infty }f(t){\psi }_{a,b}^{*}(t)dt=\frac{1}{\sqrt{a}}{\int }_{-\infty }^{\infty }{\psi }_{a,b}^{*}(\frac{t-b}{a})f(t)dt,$$

(5)

where ${\psi }_{a,b}^{*}$ is the mother wavelet conjugate [7]. The wavelet coefficients $W_f(a,b)$ are obtained by continuously varying the scale parameter and the position parameter in order to select the different portions of the signal and analyze the different scale variations [8,9]. The constituent wavelets of the original signal are obtained by multiplying each coefficient by the appropriate scaled and shifted wavelet. The mostly used mother wavelet for CWT is the “Morlet” function which extracts features with equal variance in time and frequency.

2.1.1. Cross-Wavelet Transform (XWT)

The XWT measures the similarity between two waveforms (W). It is defined by

$$W^{XY}=W^X{W}^{Y*},$$

(6)

where X and Y refer to two TSs and * is the complex conjugation. Torrence and Compo [10] defined the theoretical distribution of the cross-wavelet power of two TSs, as follows:

$$D(\frac{|w_n^x(s)w_n^{y*}(s)|}{{\sigma }_x{\sigma }_y}<p)=\frac{z_v(p)}{v}\sqrt{P_k^x{P}_k^y},$$

(7)

where $P_k^x$ and $P_k^y$ describe the power spectra background, s is the scale, and $z_v(p)$ is the confidence level associated with the probability p.

2.1.2. Wavelet Coherency (WTC)

WTC is the measurement of the coherency of the XWT in the time-frequency space. Torrence and Webster [11] defined the WTC of two TS by

$$R^2(s)=\frac{|S(s^{-1}{W}_n^{XY}(s)){|}^2}{S(s^{-1}|W_n^X{(s)|}^2.S(s^{-1}|W_n^Y(s){|}^2)},$$

(8)

where s is the scale and S is a smoothing operator.

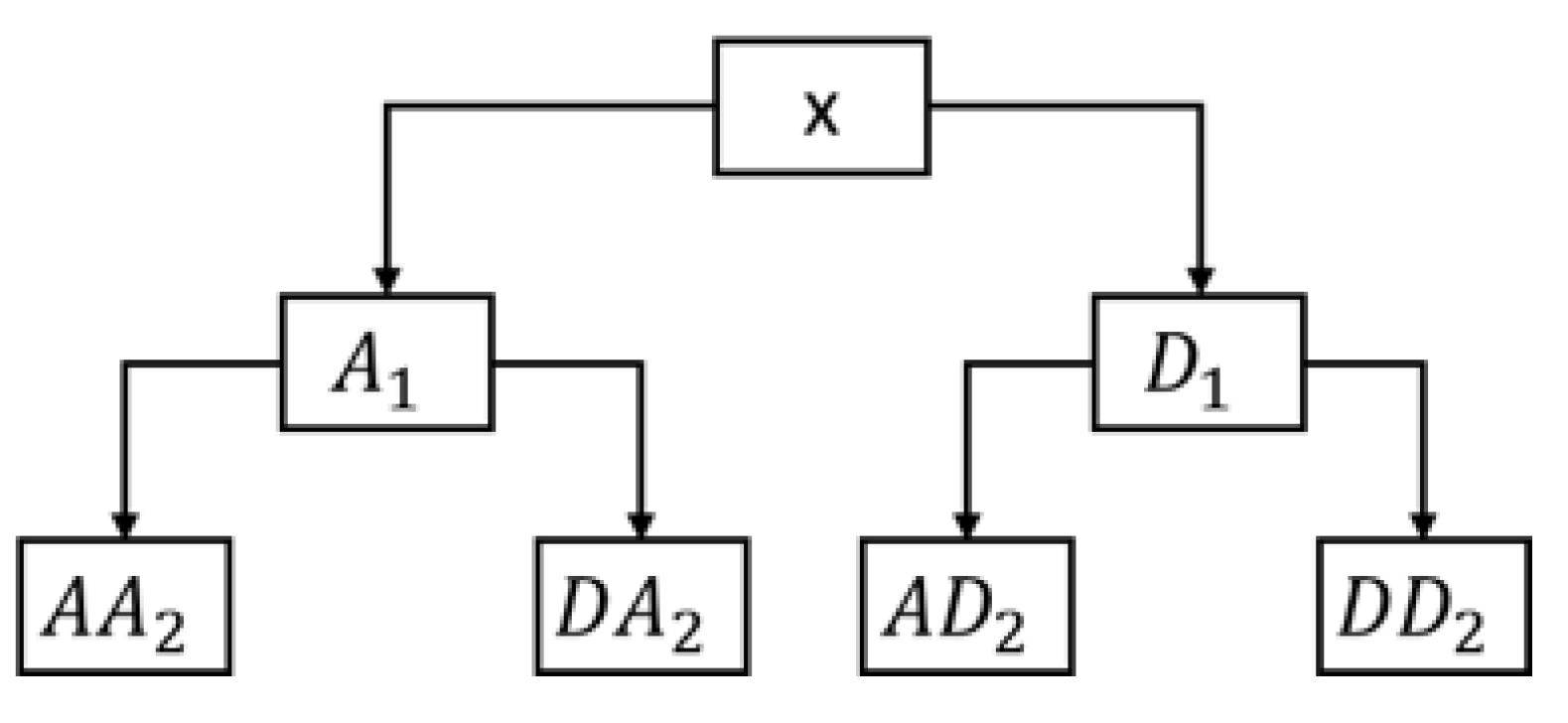
2.2. Discrete Wavelet Transform (DWT)

The DWT is a discrete set of the wavelet scales and translations. It is specially adapted for the sampled value [6]. However, this transform decomposes the signal into a mutually orthogonal set of wavelets. This specificity represents the main difference between DWT and CWT. In fact, the DWT employs a dyadic grid, where the mother wavelet is scaled by power two ($a=2^j$) and translated by an integer ($b=k{2}^j$ ), where k is a location index running from 1 to $2^{-j}N$ (N is the number of observations) and j runs from 0 to J (J is the total number of scales).

The DWT is expressed by the following equation:

$${\psi }_{j,k}(t)=2^{-j/2}\psi (2^{-j}t-k).$$

(9)

The DWT coefficients are obtained from the following expression:

$$W_{j,k}=W(2^j,k{2}^j)=2^{-j/2}{\int }_{-\infty }^{\infty }f(t)\overline{\psi (2^{-j}t-k)}dt.$$

(10)

The means of the Inverse Discrete Wavelet Transform (IDWT) is calculated in order to reconstruct the original signal (or its parts) from the wavelet coefficients $W_{j,k}$, such that:

$$f(t)=\sum _{j=-\infty }^{\infty }\sum _{k=-\infty }^{\infty }{W}_{j,k}{\psi }_{j,k}(t).$$

(11)

The DWT supports different mother wavelets, such as Harr, Daubechies, Biorthogonal, Symlet, Meyer and Coiflets. The Haar wavelet is the first and simplest mother wavelet, whereas the Daubechies wavelet is a family of orthogonal wavelets. In the literature, there are 20 functions for this family, namely from Daubechies $N=1$ to Daubechies $N=20$, where N refers to the number of wavelets and scaling parameter used for decomposing the signal. If $N=1$, Daubechies is similar to Haar wavelet. The Symlet and Coiflet are defined as a modified version of Daubechies wavelets. However, Symlet is a Daubechies wavelet with increased symmetry. The difference between Daubechies and Coiflet is the vanishing moment of the scaling function. In addition, the Coiflet wavelet uses six scaling and wavelet function coefficients, which makes the analysis smoother. Finally, Biorthogonal wavelet deals with semi-orthogonal, biorthogonal or non-orthogonal wavelet bases. This family supports symmetric wavelets and uses two different wavelet functions and two scaling functions that may generate a different multi-resolution analysis.

2.3. Multi-Resolution Analysis (MRA)

The MRA, also well known as a pyramid algorithm, is defined as a hierarchical representation of DWT [12]. It is based on decomposing the original signal into m level by successively translating and convolving the mother wavelet using low-pass (LP) and high-pass (HP) filters. These filters retain the detail (D) and approximation (A) components. The signal can be reconstructed by the sum of the last approximation component and all the detail components, as illustrated in Figure 2.

2.4. Wavelet Packet Decomposition (WPD)

The WPD was introduced by Coifman, Meyer and Wickenhauser [13,14,15]. This method is a generalization of wavelet decomposition that offers a richer signal analysis. However, a level-by-level transformation of a signal is provided from the time domain into the frequency domain. The DWT decomposes the approximation components at each level, whereas the WPD decomposes both the approximation and detail components [16], as shown in Figure 3. This characteristic delivers a better frequency resolution. To reconstruct the original signal, the combination of the various decomposition levels is used.

2.5. Maximal Overlap Discrete Wavelet Transform (MODWT)

MODWT, also called stationary wavelet transform (SWT), is an extended DWT representation using the “a trous” algorithm proposed by [17,18]. Compared to DWT, the MODWT is designed to overcome the lack of translation-invariance. In fact, the MODWT is invariant to circular shifting of the time series under analysis, while the DWT is not. Using MODWT, filters are up-sampled at each level. For this reason, MODWT is considered as a redundant wavelet because the same number of samples is presented in each set of coefficients.

The MODWT can handle samples of any size N, while the DWT restricts the sample size to a multiple of $2^j$, where J is the level of the decomposition; Furthermore, while both the DWT and MODWT can be used for an analysis of variance based on wavelet and scaling coefficients, the MODWT wavelet variance estimator can be shown to be asymptotically more efficient than the same estimator based on DWT [17,18,19,20,21].

2.6. Empirical Wavelet Transform (EWT)

The EWT is an adaptive method combining the WT and EMD which decomposes the signal into amplitude and frequency-modulated components called IMFs. As introduced in [22], the EWT is defined in three steps. First, the FT method is used to obtain the frequency spectrum of the analyzed signal in the frequency range $[0,\pi ]$. Then, the frequency spectrum is segmented into N number of contiguous segments using the EWT boundary detection method. Finally, the empirical scaling and wavelet functions are defined in each segment as the set of band-pass filters. The EWT is discussed in more details in [22].

3. Wavelet Transformation for Non-Stationary Time-Series: State-of-the-Art

This section reviews the applications of WT in different fields. The wavelet applications are summarized in

Table 1. Details of the surveyed papers, including year of publication, authors, the field, the data, the selected WT, the application of WT and the performance. MSE: Mean Squared Error, MRE: Mean Relative Error, RE: Relative Error, RMSE: Root Mean Square Error, MAPE: Mean Absolute Percentage Error, ACF: Autocorrelation Function, EVI: Enhanced Vegetation Index, MODIS: Moderate-Resolution Imaging Spectroradiometer, NDVI: Normalized Vegetation Index, AGC: Apparent Green Cover, LAI: Leaf Area Index, AVHRR: Advanced Very High-Resolution Radiometer, EEG: Electroencephalography, ECG: Electrocardiogram, LST: Land Surface Temperature, MCSA: Motor Current Signature Analysis, SNR: Signal-to-Noise-Ratio, CR: Compression Ratio, PRD: Percent Root Mean Square Difference, FBSE: Fourier Bessel Series Expansion and PV: Solar Photovoltaic, SD: Standard Deviation, DJIA:the Dow Jones Industrial Average, NHST: Northern Hemisphere Surface Temperature, MJO: Madden Julian Oscillation, ENSO: EL Nino Southern Oscillation, SST: Sea Surface Temperature, NAO: North Atlantic Oscillation, BMI: Maximum annual Ice extent in the Baltic Sea.

Representative References	Data	Application of Wavelet	Wavelet Transform	Performance
Geo-sciences and Geophysics
[23,24,25,26,27,28,29,30]	Deep-sea sediment record TS monthly NHST MJO and ENSO TS the standardized time series of winter The standardized BMI percentile time series Atmospheric and Oceanic dataset SST and NAO TS	trend analysis correlation and coherency cross-spectral analysis wavelet based spatial verification	CWT, DWT, XWT, MODWT, Foster’s wavelet, Morlet, Meyer
Remote sensing:Vegetation
[7,31,32,33,34,35,36,37,38,39,40]	NDVI MODIS data EVI MODIS TS NDVI eight day, MODIS LAI eight-day and MODIS Albedo 16-day composite data AVHR/NDVI data in Spain area 1 Km AGC spot vegetation data Landsat NDVI TS and LST MODIS EVI data coupled with quality assessment science data Simulated NDVI TS	Multi-scale analysis Wavelet-based denoising Wavelet-based feature Trend analysis	MODWT DWT CWT MRA Coiflets Daubechies Symlet Haar Meyer Morlet	RMSE
Engineering
[41,42,43,44,45]	Cutting strain in tool holder and motor current Different simulated single-degree-of-freedom systems and one experimental system. Simulated data experienced by MCSA Electricity TS data of 30s	Denoising Feature extraction Time frequency analysis Parameter identification Prediction	CWT DWT MRA WPD Daubechies Symlet Coiflet Morlet
Hydrology
[46,47,48,49,50,51]	Monthly Annual and monsoon precipitation series in 7 zones of India Annual precipitation Annual runoff Streamflow times series in nine stations for the Black Sea region of Turkey	Multi-temporal scale analysis Deterministic component identification Denoising Complexity quantification Cross-correlation analysis Simulation and forecasting Cross-correlation analysis Forecasting Wavelet-based variability	CWT DWT XWT WTC Daubechies Coiflets Meyer BiorSplines RverseBior Morlet	MRE RE P10: percentage pace rate of RE $<10\%$ P20: percentage pace rate of RE $<20\%$ Maximum RE Minimum RE SD of RE RMSE Thiel inequality coefficient
Finance
[19,21,52,53,54,55,56,57,58,59,60,61]	Sunspot, stock exchange and IBM stock price series Original and return data of US stock market: Dow Jones Index U.S gross domestic product TS Monthly Home price in 12 US cites dataset DJIA stock price index and the industrial production index for the US Daily Eurozone stock market	Forecasting Denoising Wavelet-based test Multi-temporal scale analysis Spectral analysis Multi-scale analysis wavelet variance wavelet cross-correlation	MRA DWT CWT MODWT Haar WTC, XWT Daubechies Symmlet Coiflet Meyer Least Asymmetric	MSE MAPE ACF
Medicine
[62,63,64,65,66]	ECG signal EEG signal	Time-frequency analysis Denoising Data compression Classification Prediction	DWT CWT EWT WPD	CR PRD Sensitivity Specificity Accuracy MSE SNR
Ecology
[67,68,69]	Simulated and real data Real TS Population TS (Lemming) Climate TS	Multi-scale analysis Wavelet coherency Wavelet power spectrum	CWT DWT Morlet
Renewable Energy
[70]	Solar irradiation Historic PV data	Prediction	SWT
History and Social Science
[71,72]	Roman Empire and the European Union TS nineteenth century French GNP series	Forecasting	CWT Haar Morlet
Chemistry
[73]	Different oil samples	Multi-scale analysis	Daubechies

. The related studies are compared in terms of field, data, the mother wavelet used, the application of WT types and the performance.

3.1. Application of WT in Geo-Sciences and Geophysics

The WT was investigated in several applications related to the climate, meteorology, oceanography, geo-sciences and geophysics [10,11]. Kumar and Foufoula-Georgiou [74] discussed the advantage of WT in geophysics due to their unique properties for the analysis of natural phenomena. In fact, the WT originated in geophysics in the early 1980s for the analysis of seismic signal. After a decade of significant mathematical formalism, they are now also being exploited for the analysis of several other geophysical processes such as atmospheric turbulence, space-time rainfall, ocean wind waves, seafloor bathymetry, geologic layered structures, climate change, among others. In addition, Kumar and Foufoula-Georgiou [75] introduced the power of wavelets for analysis of non-stationary processes that contain multi-scale features, detection of singularities, analysis of transient phenomena, fractal and multi-fractal processes, and signal compression.

Farge [23] reviewed the applications for the turbulences analysis. In the first step, the CWT, DWT and their properties were introduced. They concluded that WT is a very suitable method for turbulence analysis. Additionally, Meyer [9] presented the CWT. The usefulness of the WT in oceanography and meteorology was discussed by examining the dispersion of Yanai waves. Lau and Weng [24] applicated the CWT in order to analyze two climate TS. The first TS was the 2.5 million year (Myr) deep-sea sediment record in the North Atlantic, which provides information on the variation of global ice volume. However, the second is the monthly NHST for the period January, 1854–July, 1993. The Morlet wavelet was used to study the trend for both TS. In addition, the basic concept of WT, compared with similar concepts used in music, was also provided. The WT was applied in [25] to analyze the relationship between two atmospheric phenomena interact: the MJO and the ENSO events. Their method was based on the cross-spectral analysis and MODWT to analyze the variance, covariance and the wavelet subseries of the daily measurements. Furthermore, Grinsted et al. [26] applicated the CWT and XWT in order to analyze the coherency between two times series: the standardized TS of winter (DJF) and the standardized BMI percentile TS. In fact, the mechanistic models of physical relationships between the TS was tested. In addition, the phase angle statistics that can be used to gain confidence in causal relationships was demonstrated. Finally, the Monte Carlo method was used to assess the statistical significance against the red noise background. Witt and Schumann [27] investigated the WT in order to analyze the Holocene climate variability. The Foster’s wavelet analysis algorithm was applied in order to determine the different records in Greenland ice cores. Then, Liu et al. [76] used the wavelet power spectra to solve the bias problem for atmospheric and oceanic data sets. In fact, the study was based on the definition of the energy of the wavelet power spectrum which make a substantial improvement in the spectral estimate, allowing for a comparison of the spectral peaks across scales. The results were validated with an artificial TS and a real coastal sea level record. Moreover, Polanco et al. [28] used the wavelet spectral analysis in order to analyze the SST and the NAO pattern. In fact, the XWT was applied to investigate the environmental effects (SST, NAO) on octopus abundance fluctuations measured as capture per unit of effort (CPUE) from 1989 to 2007 in the waters of the Canary Islands. Recently, Weniger et al. [29] reviewed the application of wavelet based spatial verification techniques in order to develop a high-resolution numerical weather prediction model. They concluded that the MRA was principally used in order to analyze the meteorological applications. Particularly, the Point-Measure Enhancements (PME), the Intensity-Scale Skill Score (ISS) and the Wavelet Coefficient Score (WCS) were developed. Polanco-Martínez and Faria [30] used the wavelet transform in order to analyze the oxygen isotope ratio of the GISP2 deep ice core (Greenland) data. In fact, to evaluate the statistical significance of the Foster’s wavelet spectrum, a non-parametric computing-intensive test was developed based on the Monte Carlo simulations.

3.2. Application of WT in Remote Sensing in Vegetation Analysis

In the remote sensing field, WT has been widely used to analyze vegetation TS. However, several applications are developed to ameliorate the quality of forecasting and to detect the land change as well as crop phenology.

On the one hand, WT has been used as a filter for denoising TS in several research works. For example, Sakamoto et al. [31] used the EVI from the MODIS TS to detect the phenological stages of paddy rice. First, the abnormal data affected by clouds was removed. Then, the DWT (Equation (9)) was applied as a filter to denoise the EVI TS using several types of mother wavelets, such as the Coiflets, Daubechies and Symlet. Finally, the phenological stages were specified. To prove the effectiveness of the proposed approach, the RMSE of the estimated phenological date and growing period against the statistical data (e.g., growing period, planning date, heading date and harvesting date) was calculated. Moreover, Bruce et al. [32] drew a comparison between wavelet-based and Fourier-based features. The authors proved that the result of a classification was better than Fourier when using a 3-level Haar wavelet as a denoising method in the original data. Different methods for denoising, such as median filtering, moving average filtering and wavelet denoising, were applied. Then, two classifiers were used, namely Nearest Mean (NM) and Nearest Neighbour (NN). Additionally, Lu et al. [33] analyzed three types of vegetation from MODIS data (e.g., 8-day NDVI/LAI and 16-day MODIS albedo): the deciduous broadleaf forest, evergreen broadleaf forest and double-cropping rice. As a first step, the control information was used. The blue band of MODIS data was exploited as an indicator to detect the small cloud and to overcome the drawbacks using the inverse weighted interpolation. Finally, the Daubechies SWT was applied to remove the noise in TS. To prove the effectiveness of the proposed approach in comparison with the Fourier-based fitting method, the Savitzky–Golay filter and Best Index Slope Extraction (BISE) algorithm were both applied [33].

On the other hand, the WT has been widely used for multi-temporal scale analysis. For example, Percival et al. [7] applied the WT to analyze the NDVI data for four vegetation groups (boreal, temperate, tundra and frost) based on the modified Köppen classification system. In addition, the authors studied the variance across different scales as well as the correlation structure of TS, and applied the Haar MODWT (Section 2.5) to analyze the multi-temporal scale. Martínez and Gilabert [34] used the Meyer wavelet into the MRA (introduced in Section 2.3) to capture and describe both inter- and intra-annual vegetation changes of AVHRR NDVI TS. The intra-annual change was associated with the seasonal change to define several key features in relation to the vegetation phenology, such as the minimum NDVI and the amplitude of the phenological cycle. The inter-annual change was calculated to detect the abrupt and subtle changes by trend analysis where the Mann–Kendall test was applied. This approach was tested on AVHR/NDVI data in Spain over the period between 1989 and 2002 and used the precipitation data to analyze the climatic influences in some regions. Moreover, Martínez et al. [35] investigated the Meyer wavelet along with the MRA to examine the land condition of a dry land region in Senegal from 2001 to 2009 using 1-km AGC SPOT vegetation data. The vegetation seasonality was studied from the denoised TS, whereas the temporal variability of the inter-annual component was studied using the Mann–Kendall test. Campos and Di Bella [36] applied the Meyer WT-MRA to analyze the land cover change. Four MODIS TS from 2000 to 2010 were used. These TS expressed different changes, such as inundation in Cambodia and Vietnam, fire in Spain, farming in Argentina and urbanization in China. In addition, two Landsat-TM images were analyzed to characterize different change levels in the spatial dimension. Afterwards, Piao et al. [37] detected change using the MODIS NDVI TS from five different regions located in the Chinese Mainland from 2001 to 2010. While the inter-annual change was analyzed using the Morlet CWT, a detailed change in certain regions was detected using the combination between wavelet and region growing. As for Rathinasamy et al. [38], they have applied WT to investigate the temporal variability of the scaling characteristic of Landsat NDVI TS and LST in a heterogeneous area in India. Using MRA DWT, three detail fields, i.e., horizontal, diagonal and vertical, have been produced for each level of decomposition. Then, the linear regression and the slope test have been calculated to analyze the different components. In addition, several mother wavelets, such as Haar, Symmlet and Daubechies, have been applied to understand how the scaling analysis depends on the chosen mother wavelet function. Additionally, Priyadarshi et al. [39] have deployed the WT for land cover change and trend analysis using MODIS EVI coupled with quality assessment science data for the period from 2005 to 2014. In addition, the Daubechies DWT has been applied to detect trends in the EVI TS. The trend has been analyzed using the Mann–Kendall and Sen’s slope tests. Recently, Ben Abbes et al. [40] have compared three satellite image time-series decomposition methods, namely Break for Additive Season and Trend (BFAST), MRA-WT, and Seasonal Trend Loess (STL), for vegetation change detection. Four simulated NDVI TS have been used to test the proposed approach. While the Meyer MRA has been selected to decompose the TS, the RMSE has been calculated to compare the three methods. Finally, the authors have proved that MRA-WT is more informative due to the multi-level decomposition.

3.3. Application of WT in Engineering

The wavelet analysis has been usefully applied to a variety of pertinent problems in engineering, such as vibration modes, the condition monitoring of rotating machinery, machine diagnostics, etc. For example, Peng and Chu [42] presented a review about the different applications of WT in machine fault diagnostics. The WT applications over the last ten years were divided into six categories, namely time-frequency analysis of signals, fault features extraction, singularity detection, denoising and extraction of weak signals, vibration signal compression, as well as system and parameter identification. Pal et al. [41] used the WPD approach (presented in Section 2.4) to decompose the cutting strain in the tool holder and motor current. To do so, several mother wavelets, such as Daubechies, Symlet and Coiflets, were employed. Finally, the obtained features were analyzed using the radial basis neural network and back-propagation neural networks for the prediction of machine performance. Moreover, Staszewski and Wallace [43] developed a wavelet-based frequency response function (FRF). The main objective was to analyze the vibration system with time-varying parameters. The Morlet wavelet was applied to present the data in the time-frequency domain. Finally, to extract and visualize data from the wavelet, the wavelet ridge algorithm was exploited.

Two years later, the WT was presented by Kompella et al. [44] to detect the bearing faults. The simulated data experienced by the induction machine using the motor current signature analysis were used. At first, the noise was removed using an adaptive Wiener filter. Then, the spectral analysis was performed using Daubechies DWT. The fault severity was estimated using the standard deviation and energy of wavelet coefficients. In addition, the power spectral density of the wavelet was calculated to elevate the fault index parameter. Recently, Islam et al. [45] have applied WT to predict the timing and class of a fluctuation event. For this reason, the frequency TS has been first decomposed using the Morlet wavelet. Then, the data have been divided into regions according to high and low wavelet coefficients. After that, the Kruskal–Wallis ANOVA test has been applied at the 5% significant level to measure the variations for the different regions.

3.4. Application of WT in Hydrology

Several approaches have been proposed to analyze the hydrology process due to its important impacts on the ecosystem and the varieties of TS. However, the observed hydrologic series are usually complex and show non-stationary and multi-temporal scale characteristics in daily, monthly, annual, inter-annual, decadal and larger scales [3,77,78]. To deal with this problem, the WT has been widely applied in several fields of hydrology which were reviewed by Sang [46]. The paper classified the wavelet applications into six categories, namely multi-temporal scale characteristics (i.e., CWT), wavelet aided deterministic component identification, wavelet entropy, wavelet-based denoising, cross-correlation analysis, and forecasting.

As for Pandey et al. [47], they have studied trend analysis using a Daubechies DWT (from db5 to db10) based on monthly, annual and monsoon precipitation data in seven areas in India to identify the seasonal variation and the long- and short-term fluctuation. Firstly, a linear regression test has been applied to detect the linear trend. Then, some statistical analyses along with the Sequential Mann–Kendall (SQMK) test for the seasonal and annual precipitation series have been calculated. The selection of the mother wavelet has been made using the MRE and RE criteria of the z value of the Mann–Kendall test. In addition, the maximum level of decomposition for the different mother wavelets has been calculated. Finally, the SQMK has been analyzed for the combination of approximations, detailed series and visualised events at different thresholds.

In addition, Tamaddun et al. [48] have deployed a wavelet decomposition to evaluate the correlation between U.S. snow water equivalent and two major oceano-atmospheric indices. A Morlet CWT has been used to evaluate the variability of the data. The XWT and the WTC, which were respectively introduced in Section 2.1.1 and Section 2.6 as two derivatives of CWT, have been also used to illustrate and quantify the associations between the different parameters o 56-year TS obtained from 323 Snow Telemetry (SNOTEL) sites. Potocki et al. [49] have presented an overview of the different wavelet applications for discharge and suspend sediment analysis. Four different objectives have been presented in their study: wavelet-based multi-temporal scale, trend analysis, forecasting, and wavelet-aided simulation of synthetic series. The wavelet-based hybrid black box model has been introduced for forecasting.

Recently, Wang et al. [50] have used WT for a forecasting task. The proposed approach is based on WT for denoising coupled with Rank-set Pair analysis (RSPA). The authors have affirmed that the quality of denoising is related to the selection of the threshold value (T) and the suitable mother wavelet. They have first compared the Coif3-RSPA (Coiflets wavelet), bior 2.4-RSPA (BiorSplines wavelet), Artificial Neural Network (ANN) and Autoregressive Method (AR) using annual runoff TS at the Huayuanku station and lower Yellow River. Then, the bior2.4-RSPA compared with RSPA has been tested for different thresholds (T = 4, 5, 6) for the same data. In addition, the RSPA, AR, ANN, db6-RSPA (Daubechies wavelet) and dmey-RSPA (DMeyer wavelet) have been compared for different thresholds (T = 4, 5, 6) in Sanmenxia Station and Middle Yellow River annual runoff in the second case and at the Beijing station annual precipitation in the fourth case. Finally, in the third case, the RSPA, AR, ANN, db9-RSPA (Daubechies wavelet) and rbio3.5-RSPA (ReverseBior wavelet) have been applied for different thresholds (T = 4, 5, 6) in Zhengzhou Station and lower Yellow River annual precipitation time-series. To evaluate the performance of some models (e.g., the RE and the RMSE) in all cases, nine error metrics have been calculated. Santos et al. [51] have recently studied the changes of streamflow times series in nine stations in the Black Sea region of Turkey. First, the Morlet and Paul CWT have been used to analyze the periodicity and variability of the precipitation data over the period between 1964 and 2007. Second, the scale-average wavelet power has been applied to carry out the cluster analysis. Then, the correlation distance between the different stations together with 16 statistics, such as the geometric mean, the standard deviation and the kurtosis, have been calculated.

3.5. Application of WT in Finance

Wavelet analysis has been investigated in several financial and economics time series. This is due to its capacity of studying a number of concepts such as non-stationarity, multiresolution and approximate decorrelation emerge from wavelet filters [17,18,79,80]. In fact, several applications were developed in order to study the such as the co-movement among international stock market, analysis of the evolution of the oil, commodity price, etc.

In the state of the art, several works were developed in order to study the interaction and co-movement in the international stock market. For example, Pinho et al. [59] used the DWT, MODWT and cross wavelet power in order to study eleven stock indices. In addition, Shik Lee [56] applicated the DWT and MRA in order the investigate the dynamics and the protentional interaction in the international stock market. Two basic time series were used: the daily stock market market indices of the KOSPI (Korea Composite Stock Price Index) and the DJIA (Dow Jones industrial average), which cover the period January 1995 to August 2000. Principally, the Haar wavelet was applied as a basic wavelet function. Finally, to study the spill over effects and the interaction between the USA and Korea market, the regression and slope coefficient were calculated. Furthermore, the MODWT was applied in [21] in order to study the relationship between real stock returns and outputs growth. In the first step, the scaling properties of the DJIA stock price index and the industrial production index for the US over the period 1961–2006 were used. Then, the lead/lag relationship between stock returns and real economic activity was analyzed applying wavelet correlation and cross-correlation analyzes to wavelet coefficient. Rua and Nunes [57] analyzed the major developed economies, namely, Germany, Japan, United Kingdom and the United States over the last four decades using wavelet squared coherency. First, they calculated the standard deviation, skewness and kurtosis to get information for the different data. Then, the wavelet transform was applied for the analysis of the time- and frequency varying co-movement. Tiwari et al. [81] used the CWT in order to analyze the level of co-movements, contagion and rolling correlation between the stock markets of the PIIGS (Portugal, Italy, Ireland, Greece and Spain) and of the largest European stock market (UK) and Germany. First, using the wavelet power spectrum, the evolution of the stock market returns series, their volatility and jumps, which appear in different crisis moments were analyzed. Then, the wavelet coherence was applied to analyze the stock markets’ co-movements, and the phase-differences in order to identify the lead-lag situations.

Additionally, the wavelet transform was applicated to analyze the evolution of the oil. Aguiar-Conraria and Soares [60] used cross wavelet analysis to decompose the time–frequency effects of oil price changes on the macroeconomy. They applicated the Morlet wavelet in order to analyze the relation between oil prices and industrial production. Benhmad [61] used the MRA wavelet in order to study the linear and nonlinear Granger causality between the real oil price and the real effective U.S. Dollar exchange rate. In the first step, the data into macroeconomic variables were decomposed at various scales. Then, the relationships among the decomposed series on a scale by scale basis were studied. More recently, Jia et al. [82] studied the evolution feature of the world crude oil market integration and diversification from the perspective of the interdependent structural relationship of global oil prices. The wavelet based complex network was developed. In fact, this latter is based on the MODWT analysis to extract multi-period characteristics of original oil prices, the grey relation analysis (GRA analysis) to measure the interdependent relationship of oil prices and constructing the multi-period network model of the global oil price co-movement. Finally, two critical reference indexes, namely the reference decision-making cycle and the target regional market, were proposed for decision makers to better adjust their strategies. Furthermore, a novel multivariate, dynamic approach—the wavelet local multiple correlation (WLMC)—was proposed recently by [83] and this tool was firstly applied to analyze the relationship between oil time series in the time-scale domain [84]. This approach is suitable for use with energy data of any kind that change over time and involve heterogeneous agents who make decisions across different time horizons and operate on different time scales. The different approach to study the crude oil energy resources worldwide were reviewed in [85]. In fact, the different work that analyzes the behavior of oil spot and future prices and their determinants during periods of market uncertainty, particularly in the context of economic and financial crises, were studied.

Aguiar-Conraria et al. [58] investigated the cross-wavelet in order to study the monetary policy variables (money aggregates and interest rates) and macroeconomic variables (industrial production and inflation). The Morlet wavelet was chosen as the optimal joint time-frequency concentration. Gallegati [86] used the MODWT in order to test whether contagion occurred during the US subprime crisis of 2007. In fact, the wavelet was applied to decompose macroeconomic time series, and data in general, into their time-scale components, and to provide an alternative representation of the variability and association structure of certain stochastic processes on a scale-by-scale basis. To handle multivariate time series, Fernández-Macho [19] used the MODWT in order to analyze a daily Eurozone stock market returns during a recent period. In fact, two statistical tools were studied to determine the overall correlation for the whole multivariate set on a scale-by-scale basis. Ranta [87] investigated the MODWT to examine contagion among the major world markets during the last 25 years. In addition, the wavelet coherency was used in order to analyze the correlation structure between co-movements at different time scales. Recently, Polanco-Martínez et al. [20] analyzed EU peripheral (so-called PIIGS) stock market indices and the S&P Europe 350 index (SPEURO), as a European benchmark market, over the pre-crisis (2004–2007) and crisis (2008–2011) periods. In the first step, they decomposed the daily log returns for the two time intervals (pre-crisis and 90 crisis periods) applying the MODWT with a Daubechies least asymmetric (LA) wavelet. Then, they computed the MODWT wavelet correlation in order to analyze the relationships among the five daily log returns of the PIIGS. Finally, they applied a nonlinear Granger causality test to the wavelet decomposition coefficients of these stock market returns.

In addition, Dghais and Ismail [52] studied the financial time-series using DWT. First, the unit root test was used to check the stationarity of the daily price of the Dow Jones Index (DJIA30) series from 2004 to 2012. Therefore, the original and return data were decomposed into different components based on five wavelet families, namely Haar, Daubechies, Symmlet, Coiflets and a discrete approximation of the Meyer wavelet. In addition, the ACF and the ANOVA table were applied to compare the five wavelets. Finally, the authors determined the best mother wavelet for decomposition in order to reduce noise from the original and return data. Moreover, a bootstrap wavelet-based hypothesis test was proposed by Bašta [53]. The proposed approach was tested using the yearly U.S Gross Domestic Product (GPD) TS from 1929 to 2014. The Haar MODWT was also applied (Section 2.5). First, the robust filtering and modified cross-validation were used to smooth the squared MODWT wavelet in order to study the variability of the series. Then, several statistical tests, such as the standard deviation, were performed to get more information on the variability and non-stationarity of the series. Finally, the bootstrap was used to approximate the distribution of the test statistics under the null hypothesis. Masset [54], in turn, studied the frequency domain methods to analyze the TS. The utilities of the WT for decomposing the original TS into trend and seasonality were also studied. Meanwhile, the MODWT and DWT were applied to analyze the variance of the scaling coefficient using the monthly Home price dataset in 12 US cites from 1987 to 2012. As a practical issue, several mother wavelets, such as Haar, Daubechies and Least-Asymmetric, were tested, and the gain function of each type was illustrated. In addition, the variance and the autocorrelation between the original return data and the wavelet smooth series were calculated. Finally, the distribution of the wavelet variance was measured across scales.

Finally, a useful overview of the applications of WT in finance was provided by Chakrabarty et al. [55]. The available literature on WT applications is divided into four broad categories: horizon heterogeneity, denoising, structural features and development of the test. This review is basically concentrated on the study of the first category due to the complexity of heterogeneous financial TS, which results in risks and correlation.

3.6. Application of WT in Medicine

In this subsection, the WT is presented in the analysis of bio-signals. In fact, two types of data, namely ECG and EEG signals, were basically studied. While EEG is a measure of the electrical activity associated with the heart, ECG is a graphical measure of the electrical activities in the human heart muscles. Both signals are non-stationary [80].

Addison [62] presented a review of the WT of the ECG signal. Several applications based on DWT and CWT, such as the detection of localized abnormality, ECG morphology, distortion and noise, were discussed. In addition, the authors concentrated on the heart rate variability and the cardiac arrhythmias. After 2005, there were a few works—for example, Alyasseri et al. [66] have applied the WT for denoising the EEG signal. Then, the CWT has been coupled with $\beta$-Hill climbing in order to find the optimal wavelet parameters when calculating the minimum MSE between the original and denoised ECG signals. To evaluate the performance of the proposed approach, the PRD and SNR have been calculated.

In addition, the WT was investigated in several works to analyze the electroencephalography signals. For example, Bhattacharyya et al. [63] analyzed the EEG signal of the focal and non-focal groups to detect the epileptogenic area. The proposed approach was based on the empirical wavelet technique to decompose the original signal and to detect different rhythms. The Central Tendency Measure (CTM) parameter was used to estimate the area measured for various reconstructed phase spaces obtained from the rhythms. Finally, the least square support vector machine (LS-SVM) was used to classify the focal and non-focal groups of the EEG signal. Moreover, Bhattacharyya et al. [65] have used the wavelet-based filter bank in order to represent the multi-component synthetic signals and real EEG signals in the time-frequency domain. The method has been divided into four steps. First, the FBSE has been employed to represent the multi-component signal in the spectral domain. Then, to estimate the accuracy of the boundary frequency, the scale-based boundary detection method has been used. In addition, the WT has been applied to decompose the signal into narrow-band components. Finally, the MSE has been used to compare the proposed approach to the EWT and Hilbert–Huang Transform (HHT). Recently, Alickovic et al. [64] have used different WT types in order to automatically detect and predict the seizure onset. The EEG data has been used with two datasets: Freiburg (intracranial EEG) and CHB-MIT (scalp EEG). The first step consists of denoising the EEG signal using the multiscale principal component analysis. Then, the EMD, DWT and WPD have been used to extract features from the denoised signal. After that, several classifiers, such as Random Forest (RF), Support Vector Machine (SVM), Multi-Layer Perceptron (MLP) and k-Nearest Neighbour (K-NN), have been tested for prediction purposes. Finally, several performance criteria, such as sensitivity, specificity and accuracy, have been used to calculate the performance of the different cases.

3.7. Application of WT in Other Fields

In some few works, the wavelet decomposition was also applied in other fields. For example, Mi et al. [67] introduced the CWT to analyze the ecological time-series. The authors also applied the Monte Carlo assessment for statistical significance test of WT and compared the Morlet and Mexican hat wavelets using simulated and real ecological data. In addition, Cazelles et al. [68] also used the CWT in order to analyze ecological TS for the red grouse population in northeast Scotland. They discussed the choice of the Morlet mother wavelet and drew a comparison between EMD and DWT in order to prove the effectiveness of the CWT in analysing ecological non-stationary TS. As for Kausrud et al. [69], they used a wavelet-based spectrum in order to analyze the relation between the Lemming cycles and the climate change. A Lemming distribution and a climate data from 1970 to 2005 were used. Chiang et al. [70] have introduced a stationary WT for forecasting a solar photovoltaic (PV) system power. The proposed approach has been divided into two steps: training and prediction. A hybrid method based on a wavelet and random forest technique has been also presented. Finally, to minimize the prediction error, a bias compensation technique has been proposed. Baubeau and Cazelles [72] used the Morlet CWT for the nineteenth century French GNP series analysis. The wavelet-based spectrum was used in order to add some new details to measure the accuracy. In fact, they separated the accuracy of a series into amplitude and time variations. Yaroshenko et al. [71] applied the WT for forecasting TS in the Roman Empire and the European Union. First, the TS were decomposed using Haar and Morlet wavelet. Then, the sign change of the spectrum of Lyapunov exponents was analyzed. These steps allow the analysis and detection of the instability of a state during wars and crises. Finally, the artificial neural network was used to quantitatively determine and forecast the stability of a state. Some other works used wavelets in chemistry. For example, Rios et al. [73] investigated the corrosion of steel in crude oil using a wavelet analysis of electrochemical noise. The Daubechies WT and energy distribution were applied to separate the contributions of two types of corrosions in oil samples with different compositions and to analyze the effect of those variables on the changes that occurred during 55 days of immersion in the experiment. This approach was adopted for different oil samples: the corrosion process of AISI 1020 in crude oil, naphthenic acid (500 and 3000 ppm), and H2S (50 and 1000 ppm).

4. Discussion

Several representative literature sources about the applications of WT in different fields were reviewed above. However, all the publications seem to be virtually impossible to be reviewed. A summary of the WT applications in different fields will be described below, followed by a discussion of the actual challenges and the future perspectives of WT. In geo-sciences and geophysics, different basic wavelet transforms are used such as the DWT, CWT, MODWT and XWT [23,25,76]. Principally the WT are used for trend analysis, correlation and coherency between two time series, cross-spectral analysis and wavelet based spatial verification, whereas there are limited applications concerning forecasting. In remote sensing fields, different types of WT were applied, namely CWT, MODWT, DWT-MRA to NDVI and EVI TS. Principally, the MRA-DWT proved its effectiveness in several works [34,35,38,40]. Compared to other methods, Ben Abbes et al. [40] proved that WT is faster than the BFAST method and is more informative. To our knowledge, the presented applications of WT in remote sensing in vegetation concentrate on wavelet denoising and multi-scale analysis, whereas there are limited applications concerning trend analysis and forecasting. In hydrology, both DWT and CWT are considered as the mostly used methods. The CWT was especially used to localize non-stationary variability, whereas DWT was used for denoising and the identification of true components. Compared with other statistical methods, WT has the advantage of identifying the nonstationary variability of hydrologic variables at multi-time scales, which is important to understand the hydrologic variability and to make mid-to-long-term predictions. In the future, wavelet de-noising, wavelet-aided complexity description and wavelet cross-correlation analyses should be further investigated in order to understand the hydrologic process. In medicine, WT was used in several applications, such as denoising, compression, frequency analysis and forecasting, in order to analyze the EEG and ECG data. The main advantage of WT in this field is flexibility in the local spectral and temporal information received from a signal. In fact, short duration, high frequency, longer duration, and lower frequency information can be captured simultaneously. Generally, several parameters such as the mother wavelet and the scale are tested in order to improve the performance of the related methods [88]. The choice of one or more parameter is made using different statistical tests, such as MSE, CR and PRD. In addition, several types of WT, such as DWT, EWT, and WPD, were investigated. Alikovic et al. [64] have recently proved that WPD gives a better performance than DWT. However, the CWT has not been well investigated in this field. A research study on CWT can be conducted to analyze medicine TS and can yield good results in several applications. In finance, the DWT, MODWT and XWT are the principal used types [52,59], where the main advantage is the ability to conserve time information. Future research prospects in this field will be forecasting the financial behaviour in stock market and study the mitigation of agency cost. In engineering, different data were used for TS denoising, prediction, feature extraction, etc. Several types of wavelets, such as DWT, CWT, and WPD, were tested. In this field, DWT coefficients are particularly useful for signal compression problems, whereas CWT is favoured when a high temporal resolution is required at all scales. Compared to other temporal methods, WT has the ability of multi-scale analysis and time–frequency features extraction. In the future, the analysis of two or more signals simultaneously must be more investigated in order to find the relationship between the different TS. In addition, both in geo-sciences and finance, the wavelet cross-correlation was well investigated. Recently, a multi variate wavelet transform version was developed in order to analyze more than two time series. For example, Soon et al. [89] used the multiple cross-wavelet transform algorithm to analyze the Holocene solar and climatic variations. Then, Herrera et al. [90] developed a generalisation of the XWT in order to study the solar activity records. In addition, Aguiar-Conraria and Soares [91] used the multivariate version of the CWT and Fernández-Macho [83] investigated the extended (multivariate version) version of the wavelet correlation via MODWT in order to analyze the correlation between financial time series.

As a result, WT has proved its effectiveness in the different fields. It can be considered as a noise reduction approach by eliminating the detail components of the first level. In addition, WT extracts more information due to the hierarchical strategy of multiple frequency dynamics within the TS. In fact, different types of WT have been used (e.g., CWT, DWT, stationary WT, EWT, XWT and WPD) and several mother wavelets have been selected (e.g., Meyer, Morlet, Daubechies, Symlet, Haar, Coiflets). This variety and availability of different functions is considered as a key advantage of WT due to the possibility of choosing the most appropriate for the signal under investigation. However, the application of WT has not achieved a standard status yet. The different challenges of wavelet decomposition which were not extensively dealt with in this review will be discussed.

• Selection of WT type: First, a general methodology for selecting the adequate WT (DWT, CWT, WPD, MODWT, XWT, WTC, EWT) is still missing. In addition, only some articles, such as Sang et al. [92], discussed the advantages and disadvantages of DWT and CWT. In fact, all the methods have different superiorities. For example, the CWT is superior in determining the scale contents and the variety in time. However, the DWT is well-known for decomposing the series into sub-signals given the proper wavelet and temporal scale. Additionally, the experimental results are principally used in order to choose the adequate wavelet, as introduced in Chakrabarty et al. [55] and Tamaddun et al. [48].
• Choice of mother wavelet: The second challenge is the choice of the proper mother wavelet. In fact, the quality of the obtained results is affected by the wavelet function. Generally, a mother wavelet has the following properties, namely orthogonality, compact size, support, symmetry, and vanishing moment [93]. However, the same properties can exist in different mother wavelets. To overcome this drawback, it should be admitted that the choice of wavelet is related to the type of application and the used TS. Sang et al. [92] have proposed that the wavelet properties and the composition of the series are the principal criteria for selecting the adequate mother wavelet. The different properties introduced by Sang are summarized as follows: (1) the wavelet should have the progressive and linear phase; (2) the wavelet should exhibit a good localization both in time and frequency domains; (3) the wavelet should be adapted to the trade-off between time and scale resolutions; and (4) the wavelet should also meet the orthogonal condition. Recently, Wijaya et al. [94] have used a statistical test in order to compare 38 mother wavelets. The information Quality Ratio has been tested for seven different TS as a new statistical metric for mother wavelet selection. In addition, some other works have also dealt with this empirical problem [31,47].
• Selection of the timescale: The selection of the range scales used in the WT is an ignored problem. In fact, the scales that are out of range result in meaningless information, thus misleading the signal analysis. Yang et al. [95] have examined the influence of the level of decomposition on the forecasting task. The majority of solutions to this problem are qualitative and empirical. However, objective and operable methods are much more needed.
• Combination with machine learning: To our knowledge, the present applications such as forecasting cannot be made using WT alone. At present, many machine learning methods, such as K-NN, MLP, Random Forest (RF), SVM, ANN, and deep learning, are combined with WT for TS analysis. Several works have demonstrated that these hybrid methods have the best performance due to their complementarity [50,63,64,70]. As a future work, we propose to develop a hybrid method based on WT and deep learning for non-stationary TS forecasting.
• Components interpretation: Finally, in our opinion, the most important and difficult problem is to find the significant evaluation of the components from the original time series. For example, the MRA-DWT decomposes the signal into approximation and detail components. All of these components are stationary signals corresponding to the original non-stationary signal. As a result, the signification of each sub-signal is still missing.

5. Conclusions

In this review, several applications of WT are summarized in order to analyze non-stationary TS. All applications are divided into seven applied sciences fields, including the geo-sciences and geophysics, the remote sensing, engineering, hydrology, finance and medicine. The WT applications in other fields, such as history, ecology and chemistry, are also discussed. In addition, some challenges and future works on the use of WT for non-stationary TS are analyzed in order to provide insights to the relevant studies. In fact, we have discussed the influence of the type of the wavelet, the mother wavelet and the scale for the TS analysis. Furthermore, the combination of wavelet and machine learning have been successfully employed in recent years. In addition, the interpretation of the different components after the decomposition was discussed. In conclusion, the WT will continue to be one of the most appealing techniques that dominate the different fields.