Experimental Study on Hysteretic Behavior of the Overlapped K-Joints with Concrete Filled in Chord
Abstract
:Featured Application
Abstract
1. Introduction
2. Experimental Study
2.1. Test Specimens
2.2. Material Properties
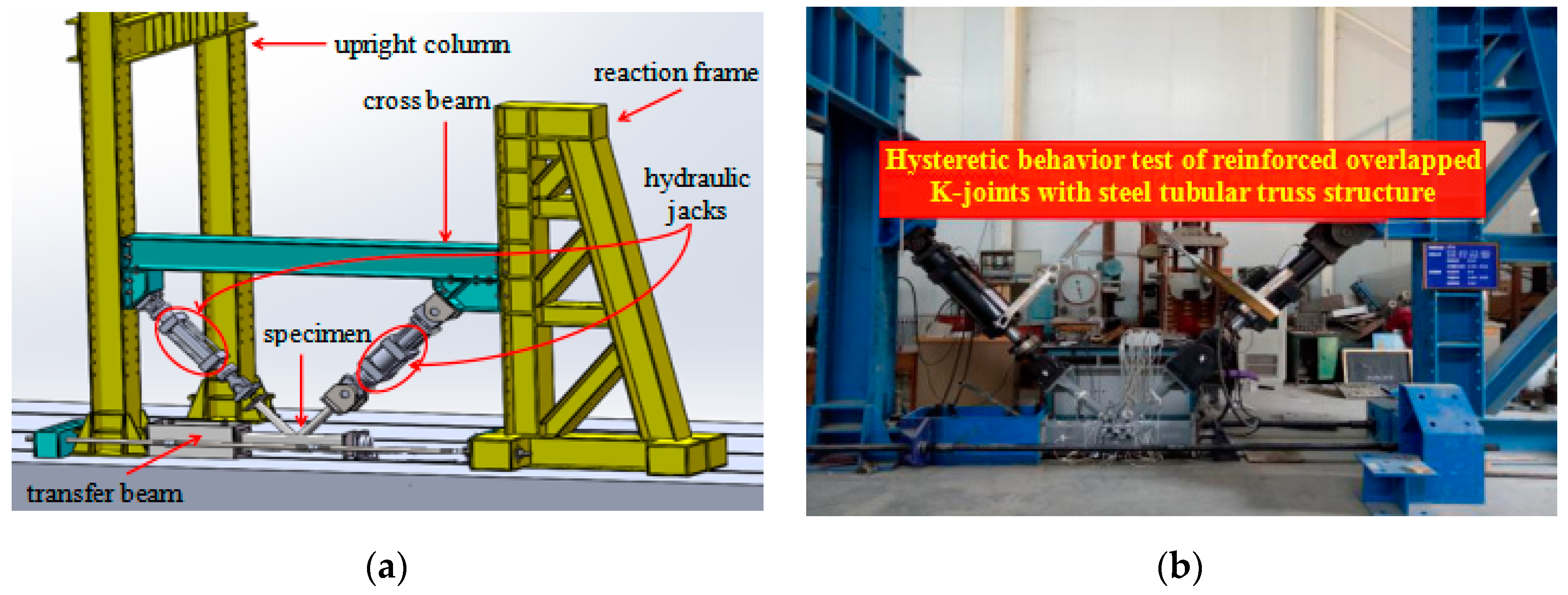
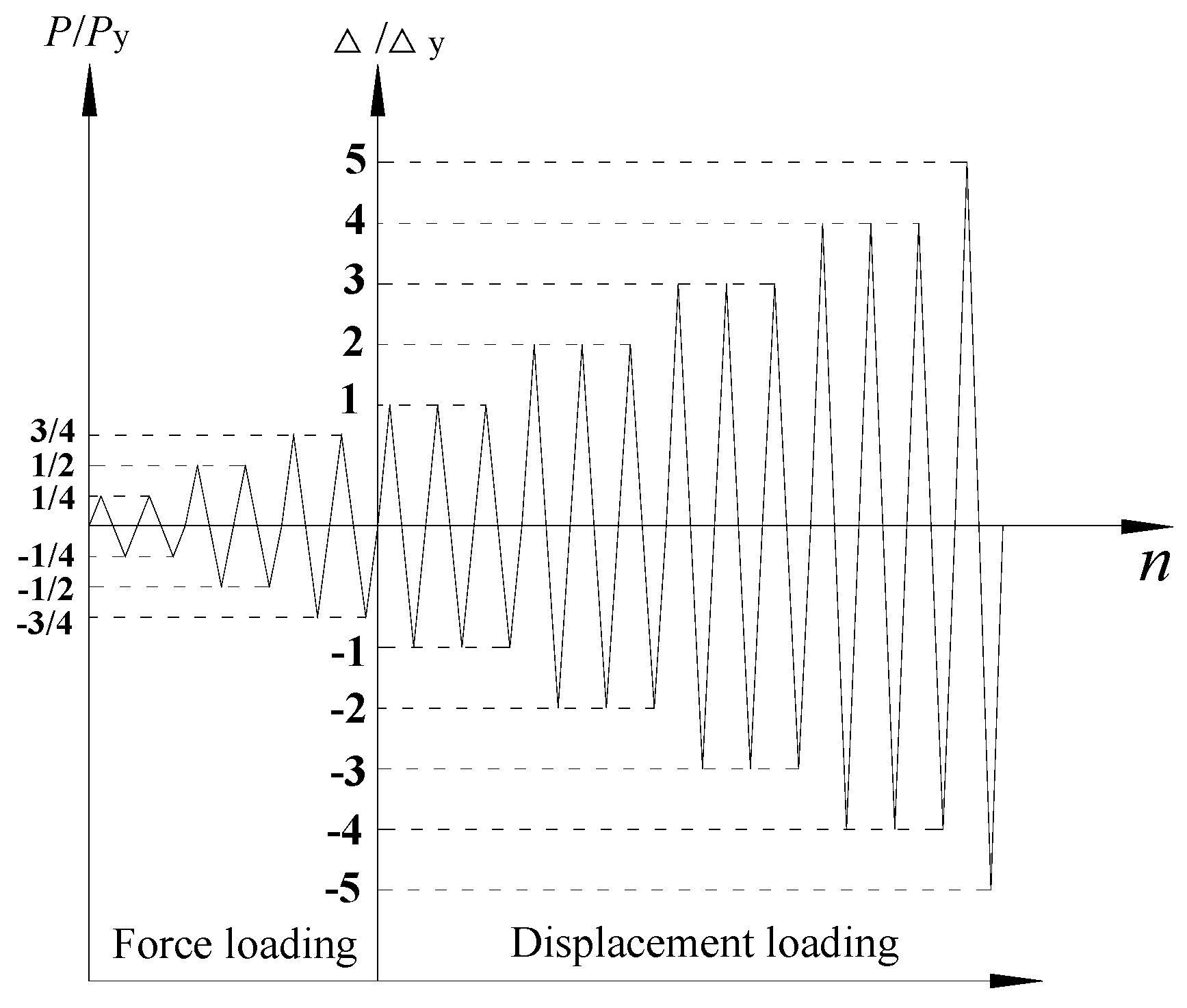
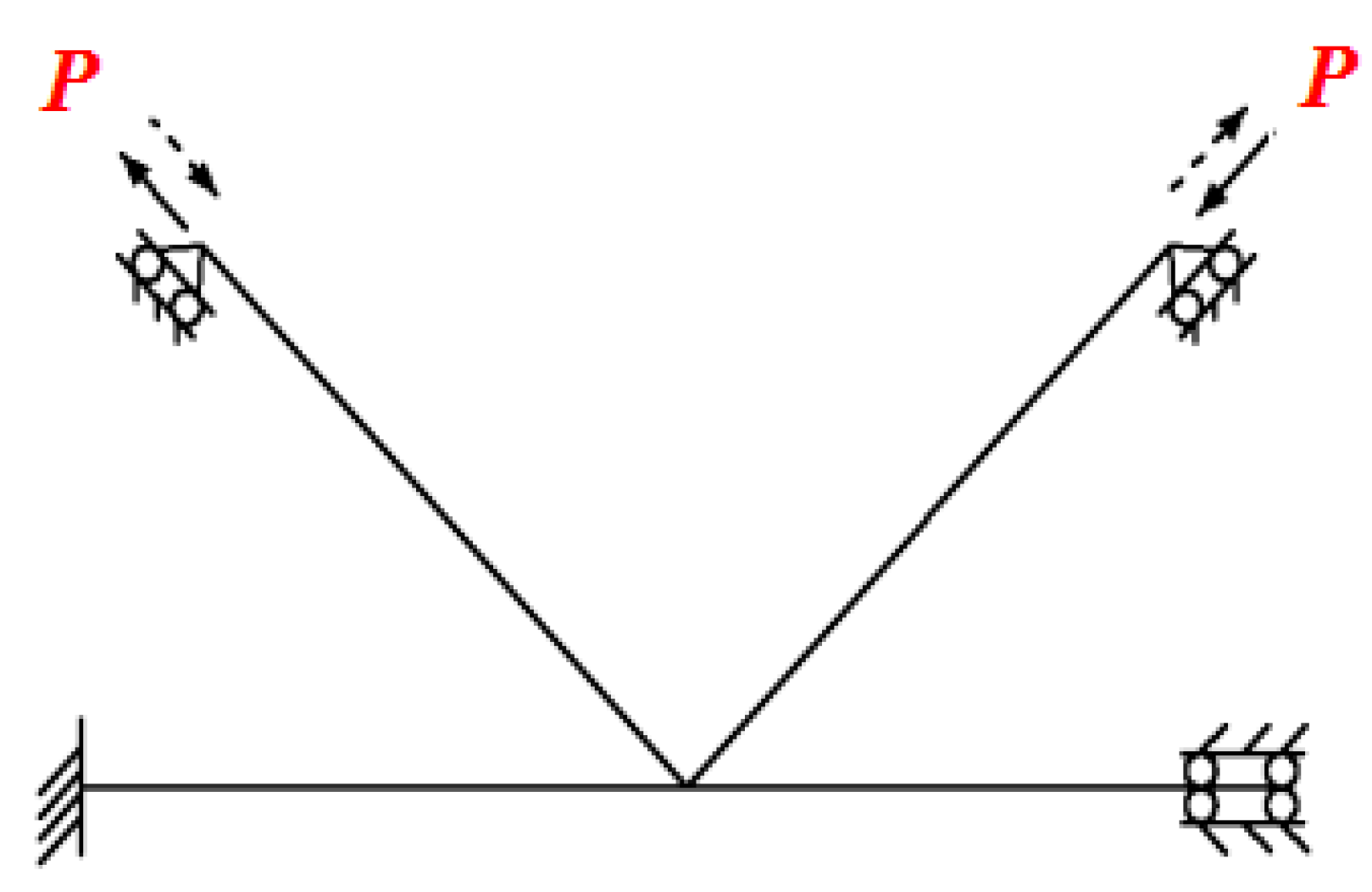
2.3. Loading Scheme and Test Program
3. Test Results
3.1. Failure Modes
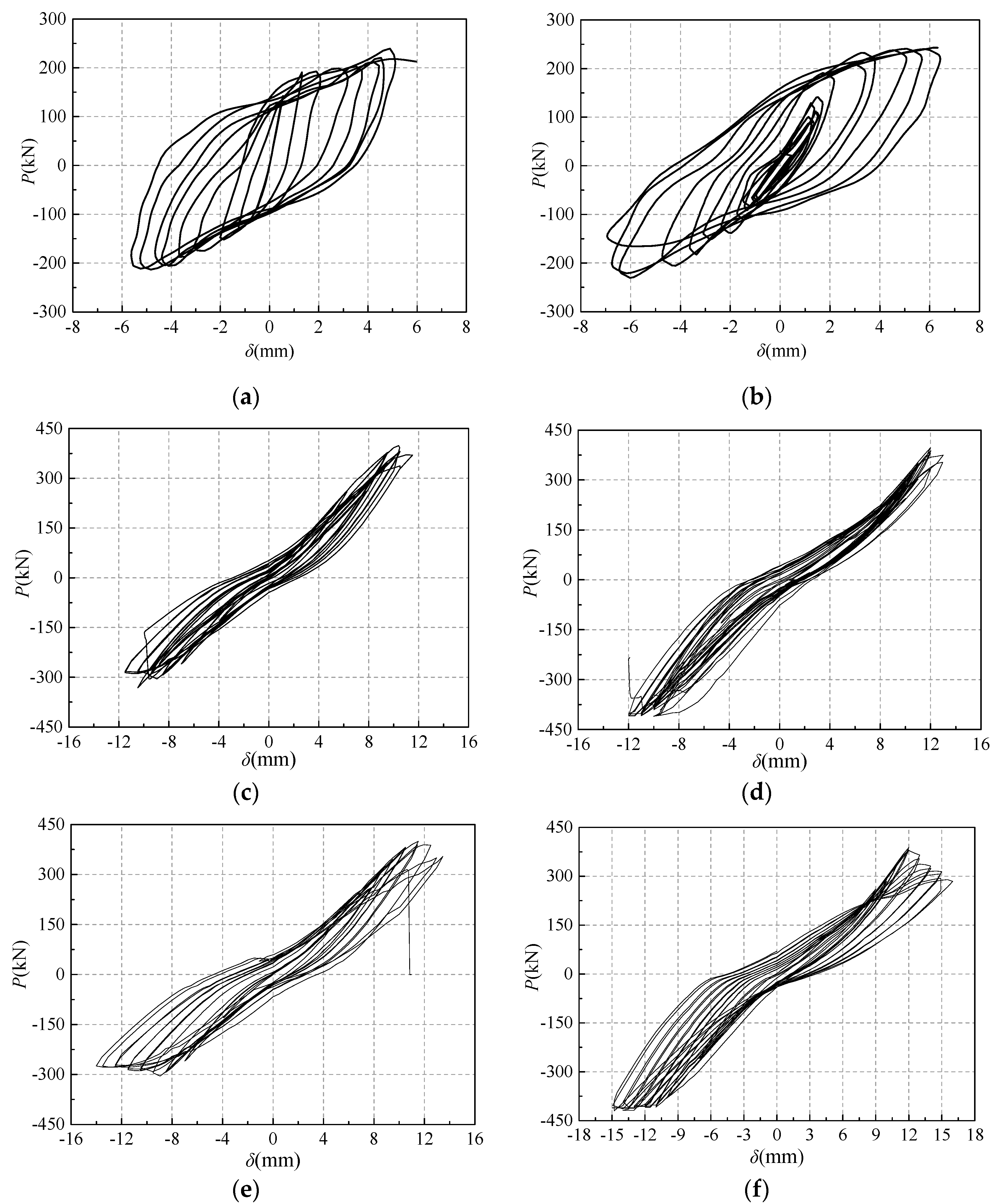
3.2. Load-Displacement Hysteretic Curve
3.3. Skeleton Curve and Ductility Coefficient
3.4. Energy Dissipation Analysis
4. Finite Element Analysis
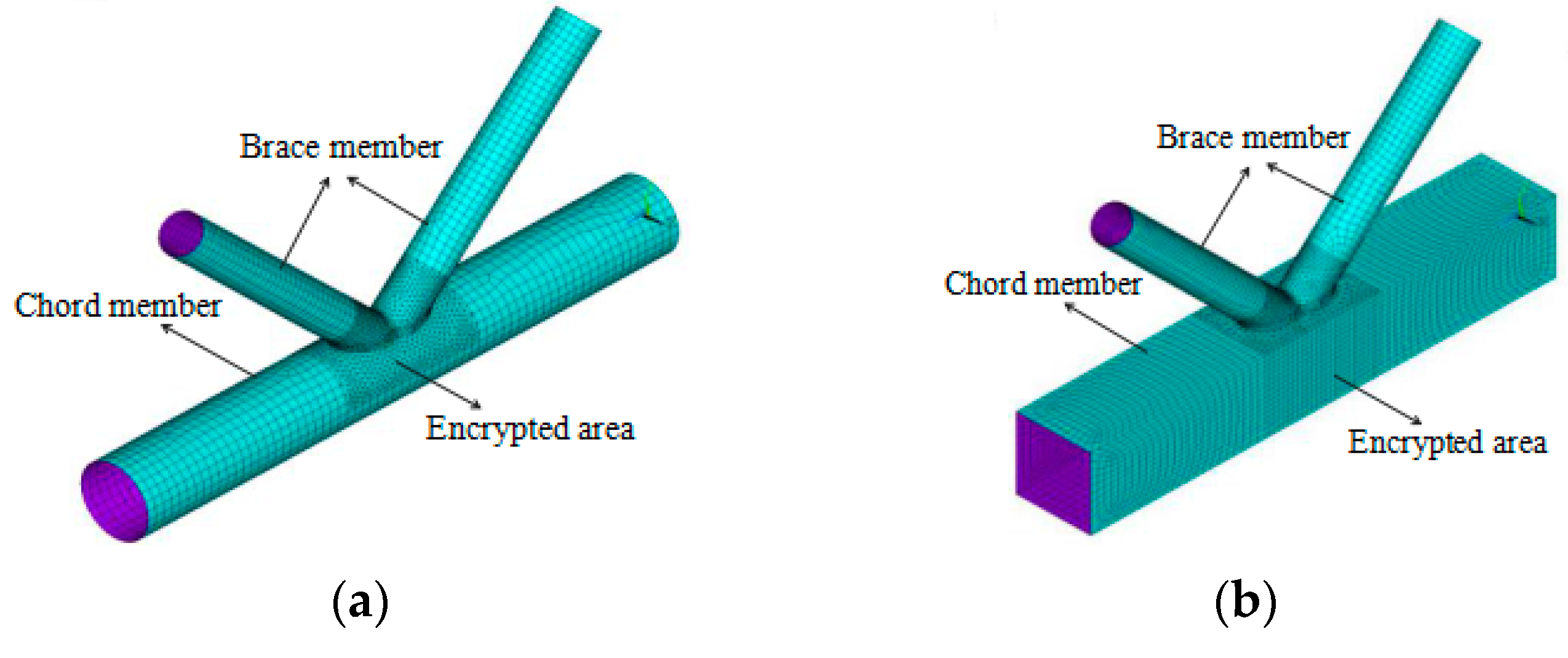
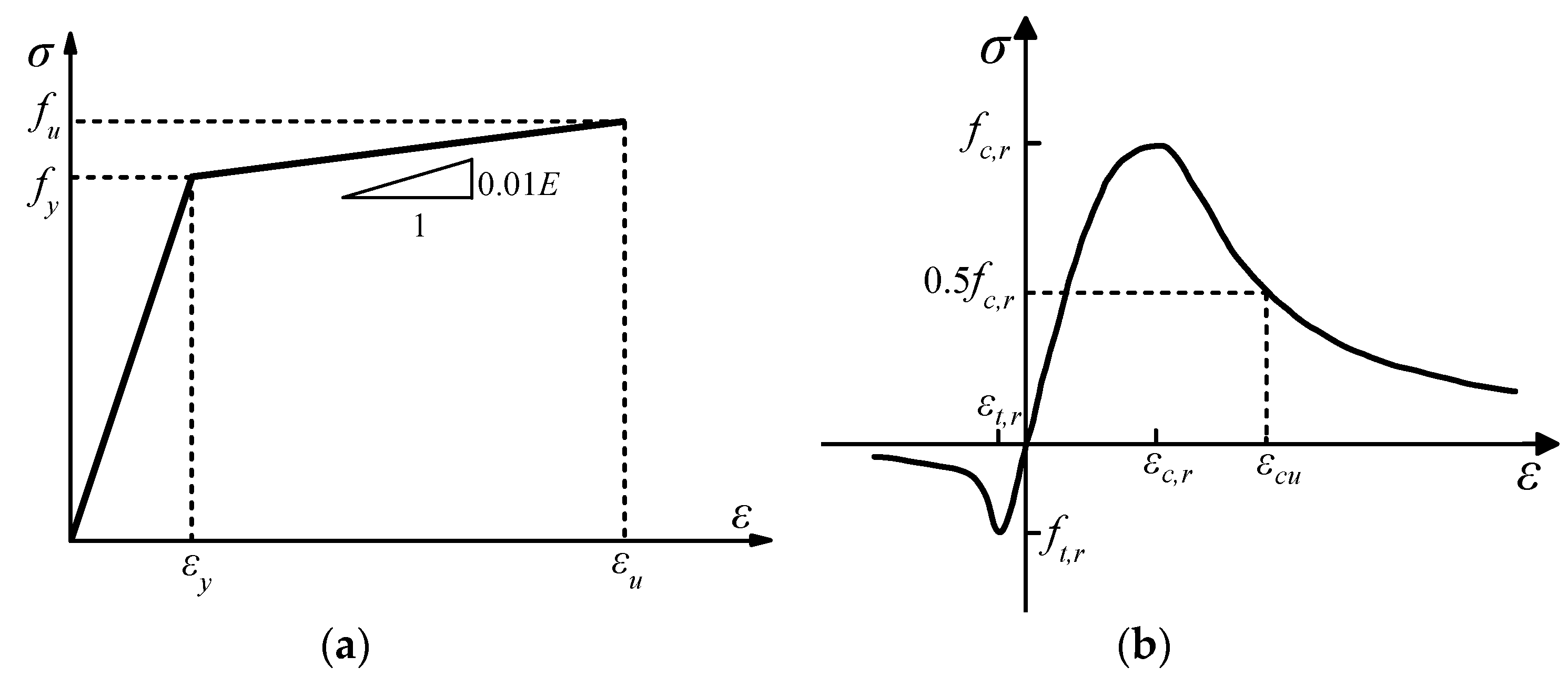
4.1. Establishment of a Finite Element Model
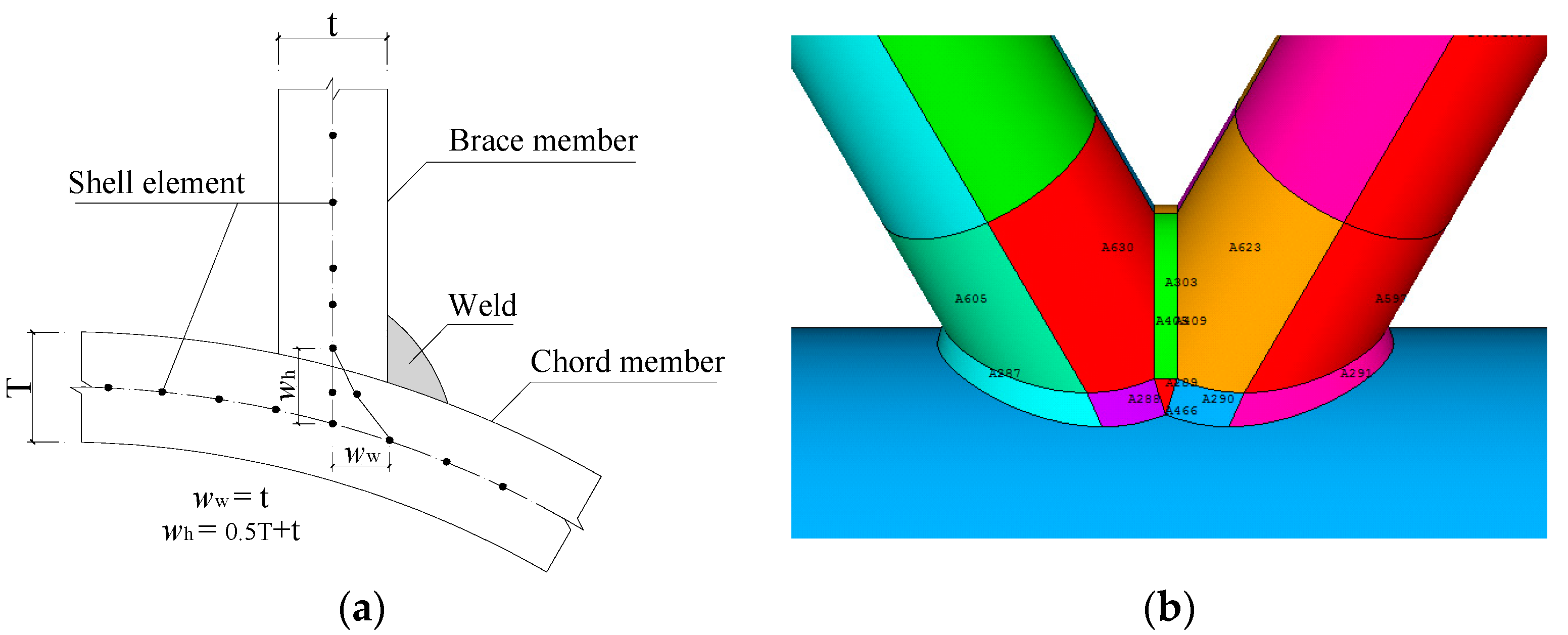
4.2. Weld Modeling
4.3. The Result Analysis of test and finite element
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, T.; Wu, Q.; Wang, L.; Huo, L.; Song, G. Monitoring of Bolt Looseness-induced Damage in Steel Truss Arch Structure using Piezoceramic Transducers. IEEE Sens. J. 2018, 18, 6677–6685. [Google Scholar] [CrossRef]
- Tiainen, T.; Mela, K.; Jokinen, T.; Heinisuo, M. The effect of steel grade on weight and cost of warren-type welded tubular trusses. Proc. Inst. Civ. Eng. Struct. Build. 2017, 170, 855–873. [Google Scholar] [CrossRef]
- Gillman, A.; Fuchi, K.; Buskohl, P.R. Truss-based nonlinear mechanical analysis for origami structures exhibiting bifurcation and limit point instabilities. Int. J. Solids Struct. 2018, 147, 80–93. [Google Scholar] [CrossRef]
- Wardenier, J.; Packer, J.A.; Zhao, X.L.; Van der Vegte, G.J. Hollow Sections in Structural Applications; CIDECT: Geneva, Switzerland, 2010. [Google Scholar]
- Han, L.-H. Some recent developments of concrete filled steel tubular (CFST) structures in China. In Proceedings of the 4th International Conference on Steel & Composite Structures 2010, Sydney, Australia, 21–23 July 2010; pp. 43–54. [Google Scholar]
- Wu, Q.; Yoshimura, M.; Takahashi, K.; Nakamura, S.; Nakamura, T. Nonlinear seismic properties of the Second Saikai Bridge: A concrete filled tubular (CFT) arch bridge. Eng. Struct. 2006, 28, 163–182. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Xu, X.; Sivakumaran, K.S.; Chen, Y. Hysteretic behaviour of overlapped tubular k-joints under cyclic loading. J. Constr. Steel Res. 2018, 145, 397–413. [Google Scholar] [CrossRef]
- Wang, X.L.; Yang, W.W.; Zou, L. Finite Element Analysis for Unstiffened Overlapped CHS K-Joints Welded in Different Ways. Adv. Mater. Res. 2011, 163–167, 299–306. [Google Scholar]
- Wang, X.L.; Chen, P.; Yang, W.W. Finite Element Analysis for Unstiffened Overlapped CHS KK-Joints Welded in Different Ways. Adv. Mater. Res. 2011, 446–449, 533–536. [Google Scholar] [CrossRef]
- Yang, W.; Wang, X. Numerical analysis of hysteretic behavior of unstiffened overlapped CHS K-Joints in steel pipe structures by finite element method. J. Lanzhou Univ. Technol. 2012, 33, 009. [Google Scholar]
- Yang, W.; Wang, X. Experimental research on seismic behavior of unstiffened overlapped CHS K-Joints. J. Build. Struct. 2013, 34, 85–92. [Google Scholar]
- Zhang, L.; Li, Z.; Cheng, M. Concrete-Filled Steel Tubular Truss Girders as Bridge Structures; People Communication Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Chen, B.; Wang, T.-L. Overview of concrete filled steel tube arch bridges in China. Practice periodical on structural design and construction. ASCE 2009, 14, 70–80. [Google Scholar]
- Song, G.; Vlattas, J.; Johnson, S.E.; Agrawal, B.N. Active vibration control of a space truss using a lead zirconate titanate stack actuator. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2001, 215, 355–361. [Google Scholar] [CrossRef]
- Han, L.H.; Zheng, L.Q.; He, S.H.; Tao, Z. Tests on curved concrete filled steel tubular members subjected to axial compression. J. Constr. Steel Res. 2011, 67, 965–976. [Google Scholar] [CrossRef]
- Xue, J.Q.; Briseghella, B.; Chen, B.C. Effects of debonding on circular CFST stub columns. J. Constr. Steel Res. 2012, 69, 64–76. [Google Scholar] [CrossRef]
- Ding, F.X.; Luo, L.; Wang, L.; Cheng, S.; Yu, Z.W. Pseudo-static tests of terminal stirrup-confined concrete-filled rectangular steel tubular columns. J. Constr. Steel Res. 2018, 144, 135–152. [Google Scholar] [CrossRef]
- Qian, X.D.; Choo, Y.S.; Liew, J.Y.R.; Wardenier, J. Static Strength of Thick-Walled CHS X-Joints Subjected to Brace Moment Loadings. J. Struct. Eng. 2007, 133, 1278–1287. [Google Scholar] [CrossRef]
- Patel, V.I.; Hassanein, M.F.; Thai, H.T.; Al Abadi, H.; Elchalakani, M.; Bai, Y. Ultra-high strength circular short CFST columns: Axisymmetric analysis, behaviour and design. Eng. Struct. 2019, 179, 268–283. [Google Scholar] [CrossRef]
- Du, G.; Zhang, J.; Zhang, J.; Song, G. Experimental Study on Stress Monitoring of Sand-Filled Steel Tube during Impact Using Piezoceramic Smart Aggregates. Sensors 2017, 17, 1930. [Google Scholar] [CrossRef]
- Du, G.; Li, Z.; Song, G. A PVDF-Based Sensor for Internal Stress Monitoring of a Concrete-Filled Steel Tubular (CFST) Column Subject to Impact Loads. Sensors 2018, 18, 1682. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, B.; Li, B.; Song, G.; Teng, J. Monitoring for Large Cross-Section CFSTs of a Super High-Rise Building with Piezoceramic Actuators and Sensors. Adv. Mater. Res. 2011, 163–167, 2553–2559. [Google Scholar] [CrossRef]
- International Institute of Welding (IIW). Static Design Procedure for Welded Hollow Section Joints-Recommendations, Doc. XV-1402-12, 3rd ed.; International Institute of Welding: Paris, France, 2012. [Google Scholar]
- Zhao, X.Z.; Chen, Y.; Chen, Y.Y.; Wang, G.N.; Xu, L.X.; Zhang, R.Q. Experimental study on static behavior of unstiffened overlapped CHS K-joints. J. Build. Struct. 2006, 27, 23–29. (In Chinese) [Google Scholar]
- Sakai, Y.; Hosaka, T.; Isoe, A.; Ichikawa, A.; Mitsuki, K. Experiments on concrete filled and reinforced tubular K-joints of truss girder. J. Constr. Steel Res. 2004, 60, 683–699. [Google Scholar] [CrossRef]
- Xu, W.; Han, L.-H.; Tao, Z. Flexural behaviour of curved concrete filled steel tubular trusses. J. Constr. Steel Res. 2014, 93, 119–134. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, R.; Xiong, L. Experimental and numerical investigations on double-skin CHS tubular X-joints under axial compression. Thin-Walled Struct. 2016, 106, 268–283. [Google Scholar] [CrossRef]
- Hou, C.; Han, L.-H.; Mu, T.-M. Behaviour of CFDST chord to CHS brace composite K-joints: Experiments. J. Constr. Steel Res. 2017, 135, 97–109. [Google Scholar] [CrossRef]
- Feng, R.; Young, B. Tests of concrete-filled stainless steel tubular T-joints. J. Constr. Steel Res. 2008, 64, 1283–1293. [Google Scholar] [CrossRef]
- Feng, R.; Chen, Y.; Wei, J.; He, K.; Fu, L. Behaviour of grouted stainless steel tubular X-joints with CHS chord under axial compression. Thin-Walled Struct. 2018, 124, 323–342. [Google Scholar] [CrossRef]
- Lesani, M.; Bahaari, M.; Shokrieh, M. Detail investigation on un-stiffened T/Y tubular joints behavior under axial compressive loads. J. Constr. Steel Res. 2013, 80, 91–99. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, D. Nonlinear finite element analysis of the ultimate strength of tubeangle combo tower K-joints. Strength Mater. 2015, 47, 355–361. [Google Scholar] [CrossRef]
- Lv, B.H.; Chen, Z.Q.; Li, H.; Guan, S.Q.; Li, X.L.; Zhang, L. Research on the ultimate bearing capacity for steel tubular transmission tower’s joints with annular plate. Appl. Mech. Mater. 2012, 166–169, 379–384. [Google Scholar] [CrossRef]
- Rong, Z.J.; Wang, X.M.; Lv, B.H.; Zhang, X.Y.; Zhang, L. Theoretical analysis on the ultimate bearing capacity for steel tubular transmission tower’s joints with annular plate. Appl. Mech. Mater. 2014, 664, 175–181. [Google Scholar] [CrossRef]
- Qian, X.; Zhang, Y.; Choo, Y.S. A load-deformation formulation for CHS X-and K-joints in push-over analyses. J. Constr. Steel Res. 2013, 90, 108–119. [Google Scholar] [CrossRef]
- Yin, Y.; Han, Q.H.; Bai, L.J.; Yang, H.D.; Wang, S.P. Experimental Study on hysteretic behaviour of tubular N-joints. J. Constr. Steel Res. 2009, 65, 326–334. [Google Scholar] [CrossRef]
- Xu, F.; Chen, J.; Jin, W.L. Experimental investigation of SCF distribution for thin-walled concrete-filled CHS joints under axial tension loading. Thin-Walled Struct. 2015, 93, 149–157. [Google Scholar] [CrossRef]
- Qian, X.; Jitpairod, K.; Marshall, P.; Swaddiwudhipong, S.; Ou, Z.; Zhang, Y.; Pradana, M.R. Fatigue and residual strength of concrete-filled tubular X-joints with full capacity welds. J. Constr. Steel Res. 2014, 100, 21–35. [Google Scholar] [CrossRef]
- Tong, L.W.; Xu, G.W.; Yang, D.L.; Mashiri, F.R.; Zhao, X.L. Fatigue behavior and design of welded tubular T-joints with CHS brace and concrete-filled chord. Thin-Walled Struct. 2017, 120, 180–190. [Google Scholar] [CrossRef]
- Lee, M.M.K.; Llewelyn-Parry, A. Strength prediction for ring-stiffened DT-joints in offshore jacket structures. Eng. Struct. 2005, 27, 421–430. [Google Scholar] [CrossRef]
- Xia, J.; Chang, H.; Goldsworthy, H.; Bu, Y.; Lu, Y. Axial hysteretic behavior of doubler-plate reinforced square hollow section tubular T-joints. Mar. Struct. 2017, 55, 162–181. [Google Scholar] [CrossRef]
- Shao, Y.B.; Li, T.; Seng, T.L.; Chiew, S.P. Hysteretic behaviour of square tubular T-joints with chord reinforcement under axial cyclic loading. J. Constr. Steel Res. 2011, 67, 140–149. [Google Scholar] [CrossRef]
- Chinese Code. GB/50017-2017 Standard for Design of Steel Structures; Standards Press of China: Beijing, China, 2017. [Google Scholar]
- Chinese Code. Jgj81-2002 Technical Specification for Welding of Steel Structure of Building; Standards Press of China: Beijing, China, 2003. [Google Scholar]
- Chinese Code. Gb/T 228-2002 Metallic Materials-Tensile Testing at Ambient Temperature; Standards Press of China: Beijing, China, 2002. [Google Scholar]
- Chinese Code. Gb/T50081-2002 Test Method of Mechanical Properties on Ordinary Concrete; Standards Press of China: Beijing, China, 2003. [Google Scholar]
- ANSYS-Inc. ANSYS Structural Analysis Guide. 2004. Available online: http://www.ansys.stuba.sk/html/guide_55/g-str/GSTRToc.htm (accessed on 1 November 2018).
- Vegte, G.J.V.D. The Static Strength of Uniplanar and Multiplanar Tubular T- and X-Joints; Delft University Press: Delft, The Netherlands, 1995. [Google Scholar]
- Peng, J.; Hu, S.; Zhang, J.; Cai, C.S.; Li, L.Y. Influence of cracks on chloride diffusivity in concrete: A five-phase mesoscale model approach. Constr. Build. Mater. 2019, 197, 587–596. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Zhou, H.; Gu, H. Multiple cracks detection in pipeline using damage index matrix based on piezoceramic transducer-enabled stress wave propagation. Sensors 2017, 17, 1812. [Google Scholar] [CrossRef]
- Li, W.; Xu, C.; Ho, S.; Wang, B.; Song, G. Monitoring concrete deterioration due to reinforcement corrosion by integrating acoustic emission and FBG strain measurements. Sensors 2017, 17, 657. [Google Scholar] [CrossRef]
- Kong, Q.; Robert, R.; Silva, P.; Mo, Y. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Xu, K.; Ren, C.; Deng, Q.; Jin, Q.; Chen, X. Real-time monitoring of bond slip between GFRP bar and concrete structure using piezoceramic transducer-enabled active sensing. Sensors 2018, 18, 2653. [Google Scholar] [CrossRef]
- Luo, M.; Li, W.; Hei, C.; Song, G. Concrete Infill Monitoring in Concrete-Filled FRP Tubes Using a PZT-Based Ultrasonic Time-of-Flight Method. Sensors 2016, 16, 2083. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Du, G.; Song, G. Damage Detection of L-Shaped Concrete Filled Steel Tube (L-CFST) Columns under Cyclic Loading Using Embedded Piezoceramic Transducers. Sensors 2018, 18, 2171. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, M.; Hei, C.; Song, G. Quantitative evaluation of compactness of concrete-filled fiber-reinforced polymer tubes using piezoceramic transducers and time difference of arrival. Smart Mater. Struct. 2017, 27, 035023. [Google Scholar] [CrossRef]
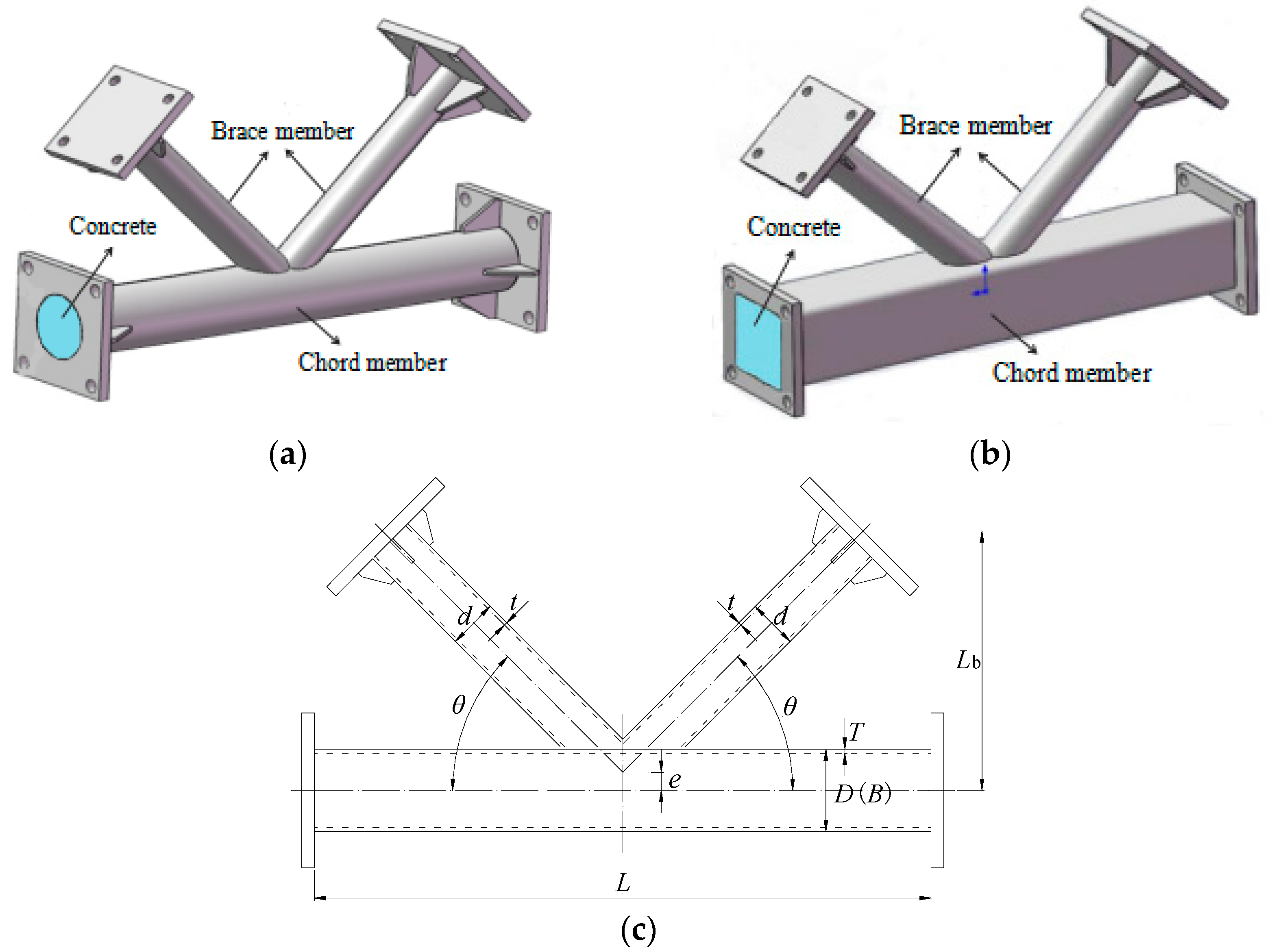






| Specimens | L (mm) | Lb (mm) | E (mm) | D(B) (mm) | T (mm) | D (mm) | T (mm) | θ | Strengthened Measures |
|---|---|---|---|---|---|---|---|---|---|
| K-CC | 1200 | 450 | 35 | 159 | 6 | 89 | 5 | 45° | unstrengthened |
| K-CCC1 | 1200 | 450 | 35 | 159 | 6 | 89 | 5 | 45° | ordinary concrete |
| K-CCC2 | 1200 | 450 | 35 | 159 | 6 | 89 | 5 | 45° | fly ash concrete |
| K-RC | 1200 | 450 | 55 | 200 | 8 | 95 | 5 | 45° | unstrengthened |
| K-RCC1 | 1200 | 450 | 55 | 200 | 8 | 95 | 5 | 45° | ordinary concrete |
| K-RCC2 | 1200 | 450 | 55 | 200 | 8 | 95 | 5 | 45° | fly ash concrete |
| Specification | fy (MPa) | fu (MPa) | E (GPa) | εy = fy/E | fu/fy | δ (%) |
|---|---|---|---|---|---|---|
| ☐ 200 × 200 × 8 | 391.1 | 533.0 | 226.2 | 0.0017 | 1.36 | 45.3 |
| φ95 × 5 | 377.6 | 515.6 | 214.6 | 0.0017 | 1.37 | 37.1 |
| φ159 × 6 | 386.5 | 531.5 | 222.4 | 0.0017 | 1.38 | 41.9 |
| φ89 × 5 | 373.1 | 510.1 | 210.2 | 0.0018 | 1.37 | 38.3 |
| Specimens | δu (mm) | δy (mm) | μ |
|---|---|---|---|
| K-CC | 6.20 | 1.68 | 3.68 |
| K-CCC1 | 11.89 | 3.56 | 3.34 |
| K-CCC2 | 12.52 | 3.62 | 3.46 |
| K-RC | 6.73 | 1.74 | 3.87 |
| K-RCC1 | 12.47 | 3.61 | 3.45 |
| K-RCC2 | 13.06 | 3.66 | 3.57 |
| Specimens | U (kN·m) | Usum (kN·m) | η |
|---|---|---|---|
| K-CC | 2.08 | 9.95 | 13.68 |
| K-CCC1 | 2.22 | 15.54 | 5.89 |
| K-CCC2 | 3.62 | 23.22 | 7.55 |
| K-RC | 2.24 | 9.66 | 13.46 |
| K-RCC1 | 2.38 | 18.02 | 4.48 |
| K-RCC2 | 3.46 | 26.71 | 6.58 |
| Specimens | Test Result (kN) | FEA Result (kN) | Error |
|---|---|---|---|
| K-CC | 232.38 | 228.65 | 1.61% |
| K-CCC1 | 398.72 | 405.93 | 1.82% |
| K-CCC2 | 389.36 | 424.73 | 9.08% |
| K-RC | 235.36 | 230.28 | 2.16% |
| K-RCC1 | 408.69 | 412.27 | 0.88% |
| K-RCC2 | 404.37 | 413.48 | 2.25% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Yan, R.; Suo, Y.; Zhang, G.; Huang, B. Experimental Study on Hysteretic Behavior of the Overlapped K-Joints with Concrete Filled in Chord. Appl. Sci. 2019, 9, 1456. https://doi.org/10.3390/app9071456
Yang W, Yan R, Suo Y, Zhang G, Huang B. Experimental Study on Hysteretic Behavior of the Overlapped K-Joints with Concrete Filled in Chord. Applied Sciences. 2019; 9(7):1456. https://doi.org/10.3390/app9071456
Chicago/Turabian StyleYang, Wenwei, Ruhao Yan, Yaqi Suo, Guoqing Zhang, and Bo Huang. 2019. "Experimental Study on Hysteretic Behavior of the Overlapped K-Joints with Concrete Filled in Chord" Applied Sciences 9, no. 7: 1456. https://doi.org/10.3390/app9071456
APA StyleYang, W., Yan, R., Suo, Y., Zhang, G., & Huang, B. (2019). Experimental Study on Hysteretic Behavior of the Overlapped K-Joints with Concrete Filled in Chord. Applied Sciences, 9(7), 1456. https://doi.org/10.3390/app9071456





