IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving
Abstract
:1. Introduction
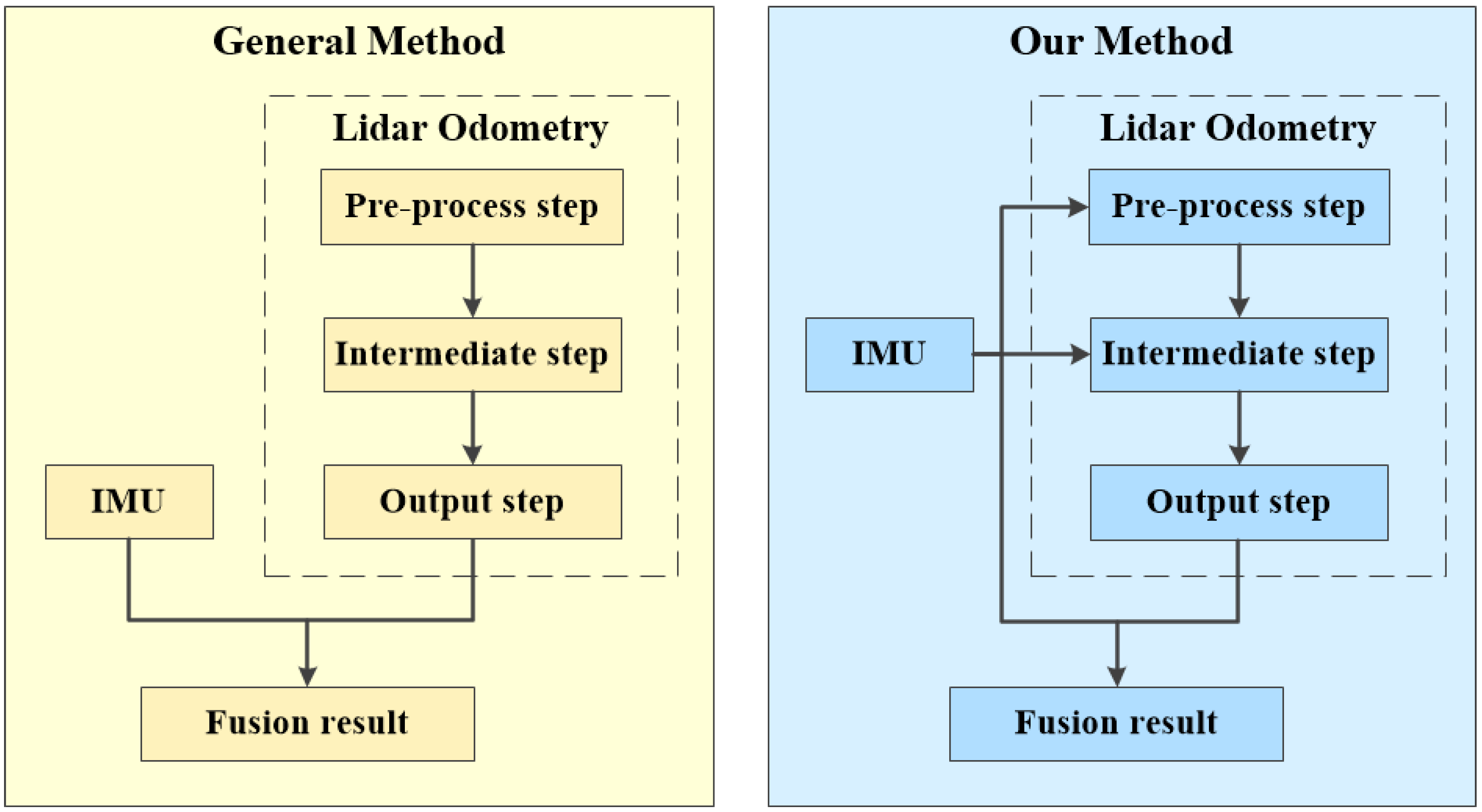
- We propose an efficient method for hand–eye calibration between the IMU and the lidar, which is a pre-requisite for making good use of the IMU.
- In the pre-processing step of the lidar odometry algorithm, we emphasize that the intra-frame correction is equivalent to inter-frame registration, and propose an efficient method for utilizing the IMU information to rectify the distorted point clouds.
- In the intermediate step, we use IMU to obtain the initial guess for the lidar odometry algorithm, and compare this approach with previous methods which usually use the registration results from the previous two scans as the initial guess.
- By combining the lidar odometry with the IMU information, we obtain a complete localization system which can output stable, accurate, and high-frequency localization results at a frequency of around 40 Hz.
2. Related Works
3. The Proposed Approach
3.1. Coordinate Systems and Notations
- World Coordinate System . In , we define the coordinates of a point by latitude, longitude, and altitude, the x-axis points to the east, the y-axis points to the north, and the z-axis points to the sky, following the right-hand rule. This coordinate system is defined in a global scale and will never change.
- Body Coordinate System . This coordinate is fixed with the IMU, which is installed in the center of two rear wheels of the vehicle. The x-axis points to the right, the y-axis points to the forward, and the z-axis points to the upward, following the right-hand rule.
- Lidar coordinate system . The lidar is mounted on top of the vehicle, and the origin of is located at the center of the lidar. The three axes of this coordinate system are the same as in .
3.2. Motion Prior from IMU and Wheel Encoder
3.3. Pre-Processing Step 1: Lidar-IMU Hand–Eye Calibration
- To avoid the intra-frame distortion caused by the vehicle’s own movement, the frames should be chosen when the vehicle is stationary.
- The relative rotation angle of the two frames needs to be greater than 90 degrees, and the relative translation distance should be small.
- The rotational axes for these multiple transformation pairs should not be parallel.
3.4. Pre-Processing Step 2: Intra-Frame Correction
3.4.1. Rectification with the Aid of IMU
3.4.2. Rectification by Previous Registration Results
3.4.3. Rectification by Registering Two Distorted Point Clouds
3.5. Intermediate Step: Inter-Frame Registration
3.6. Output Step: Fusion in an EKF Framework
3.6.1. Basic Concepts
3.6.2. System Model
3.6.3. Measurement Model
| Algorithm 1: The fusion framework of our system. |
input: The history pose set and pose at time from the IMU; pose at time from the lidar odometry; previous pose output: Current pose  |
4. Experimental Results
4.1. Experiments on Hand–Eye Calibration
4.2. Experiments on Intra-Frame Correction
4.3. Experiments on Inter-Frame Registration
4.3.1. Tests with Different Methods of Assigning Initial Guess
4.3.2. Tests with Different Lidar Odometry Algorithms
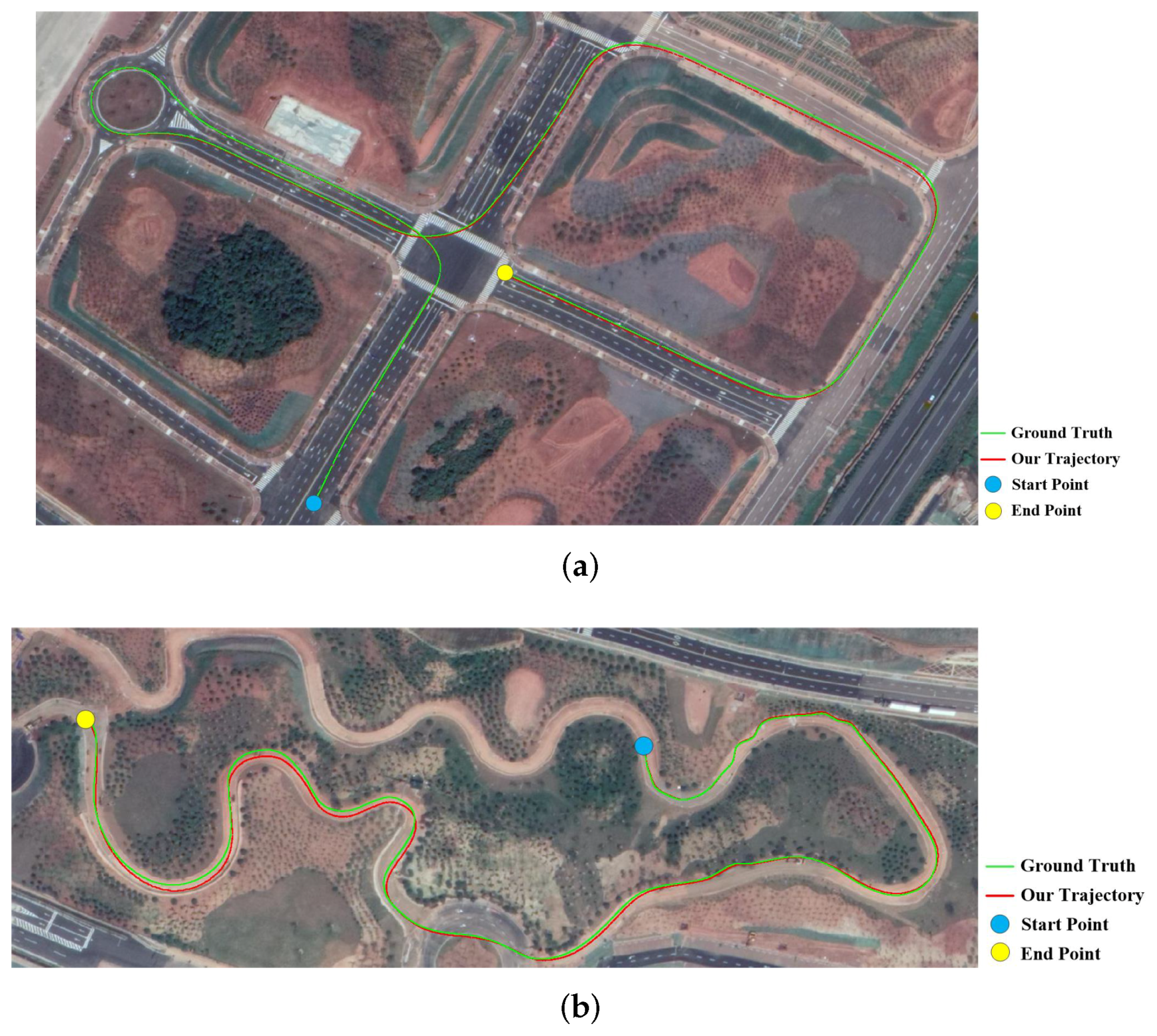
4.3.3. Tests in Both Urban and Off-Road Environments
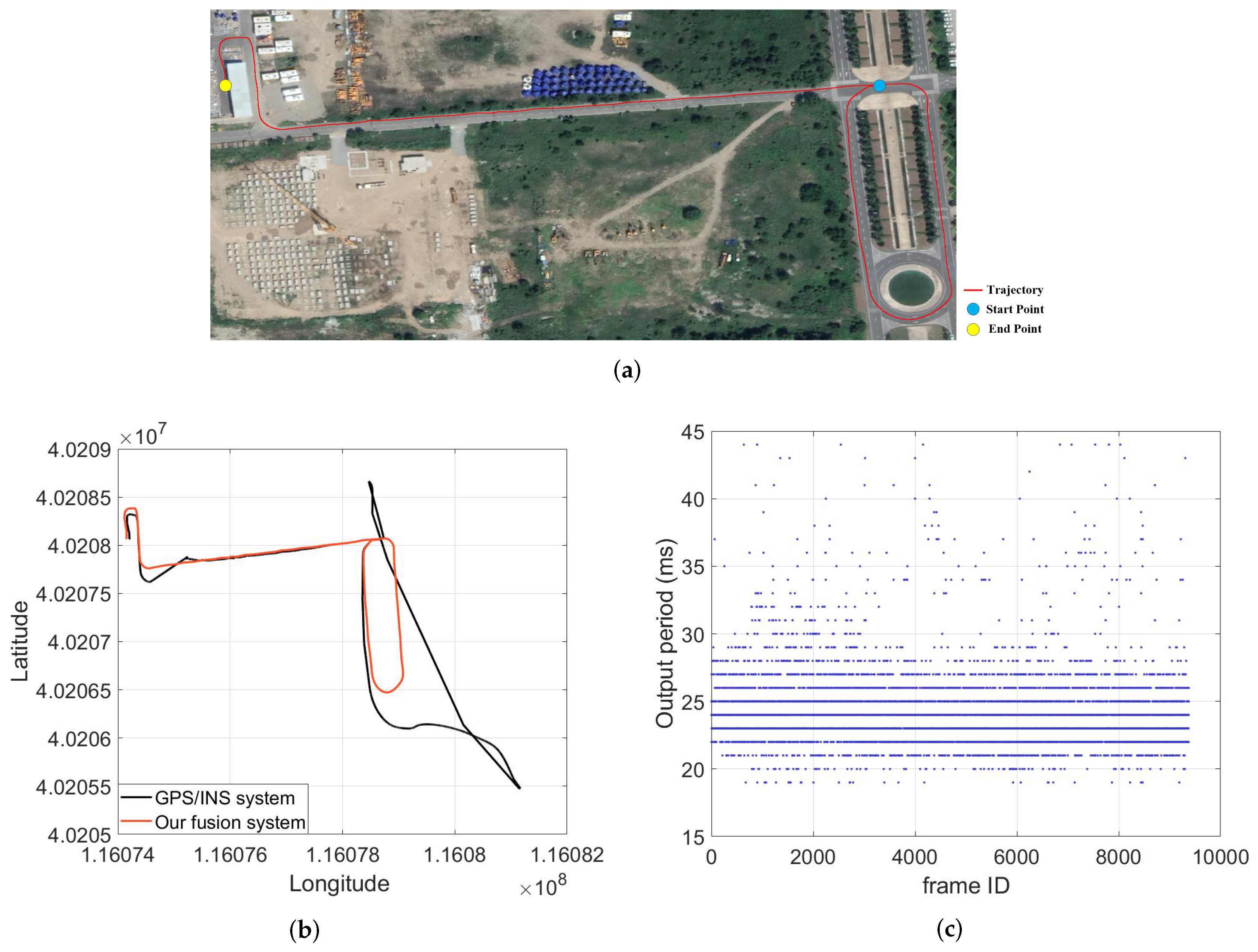
4.4. Experiments in GNSS-Denied Environment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kos, T.; Markezic, I.; Pokrajcic, J. Effects of multipath reception on GPS positioning performance. In Proceedings of the Elmar-2010, Zadar, Croatia, 15–17 September 2010; pp. 399–402. [Google Scholar]
- Kohlbrecher, S.; von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable SLAM system with full 3D motion estimation. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar]
- Gao, Y.; Liu, S.; Atia, M.M.; Noureldin, A. INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm. Sensors 2015, 15, 23286–23302. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Chen, Y.; Niu, X.; Wang, L.; Chen, L.; Liu, J.; Shi, C.; Hyyppä, J. LiDAR scan matching aided inertial navigation system in GNSS-denied environments. Sensors 2015, 15, 16710–16728. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Atia, M.M.; Gao, Y.; Givigi, S.; Noureldin, A. An inertial-aided LiDAR scan matching algorithm for multisensor land-based navigation. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014; pp. 2089–2096. [Google Scholar]
- Ye, H.; Liu, M. LiDAR and Inertial Fusion for Pose Estimation by Non-linear Optimization. arXiv, 2017; arXiv:1710.07104. [Google Scholar]
- Pierzchala, M.; Giguere, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R.; Magnenat, S. Comparing ICP variants on real-world data sets. Auton. Robots 2013, 34, 133–148. [Google Scholar] [CrossRef]
- Stoyanov, T.; Magnusson, M.; Andreasson, H.; Lilienthal, A.J. Fast and accurate scan registration through minimization of the distance between compact 3D NDT representations. Int. J. Robot. Res. 2012, 31, 1377–1393. [Google Scholar] [CrossRef]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.; Gachter, S.; Martinelli, A.; Tomatis, N.; Siegwart, R. A comparison of line extraction algorithms using 2D range data for indoor mobile robotics. Auton. Robots 2007, 23, 97–111. [Google Scholar] [CrossRef]
- Aghamohammadi, A.; Taghirad, H. Feature-Based Laser Scan Matching for Accurate and High Speed Mobile Robot Localization. In Proceedings of the EMCR, Freiburg, Germany, 19–21 September 2007. [Google Scholar]
- Furukawa, T.; Dantanarayana, L.; Ziglar, J.; Ranasinghe, R.; Dissanayake, G. Fast global scan matching for high-speed vehicle navigation. In Proceedings of the 2015 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), San Diego, CA, USA, 14–16 September 2015; pp. 37–42. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; pp. 109–111. [Google Scholar]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robots 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Hemann, G.; Singh, S.; Kaess, M. Long-range GPS-denied aerial inertial navigation with LIDAR localization. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1659–1666. [Google Scholar]
- Wan, G.; Yang, X.; Cai, R.; Li, H.; Zhou, Y.; Wang, H.; Song, S. Robust and Precise Vehicle Localization Based on Multi-Sensor Fusion in Diverse City Scenes. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4670–4677. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017; pp. 231–234. [Google Scholar]
- Kepper, J.H.; Claus, B.C.; Kinsey, J.C. A Navigation Solution Using a MEMS IMU, Model-Based Dead-Reckoning, and One-Way-Travel-Time Acoustic Range Measurements for Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2018, 1–19. [Google Scholar] [CrossRef]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual–Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef]
- Wu, L.; Ren, H. Finding the Kinematic Base Frame of a Robot by Hand-Eye Calibration Using 3D Position Data. IEEE Trans. Autom. Sci. Eng. 2017, 14, 314–324. [Google Scholar] [CrossRef]
- Shah, M.; Eastman, R.D.; Hong, T. An overview of robot-sensor calibration methods for evaluation of perception systems. In Proceedings of the Workshop on Performance Metrics for Intelligent Systems, College Park, MD, USA, 20–22 March 2012; pp. 15–20. [Google Scholar]
- Tsai, R.Y.; Lenz, R.K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- Dornaika, F.; Horaud, R. Simultaneous robot-world and hand-eye calibration. IEEE Trans. Robot. Autom. 1998, 14, 617–622. [Google Scholar] [CrossRef] [Green Version]
- Huang, K.; Stachniss, C. On Geometric Models and Their Accuracy for Extrinsic Sensor Calibration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–9. [Google Scholar]
- Scherer, S.; Rehder, J.; Achar, S.; Cover, H.; Chambers, A.; Nuske, S.; Singh, S. River mapping from a flying robot: State estimation, river detection, and obstacle mapping. Auton. Robots 2012, 31, 189–214. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]










| Rectification Methods | Average Processing Time (ms) |
|---|---|
| By previous registration | 2.565 |
| By registering two distorted point clouds | 68.504 |
| By IMU data | 4.546 |
| Rectification Methods | Mean Relative Position Error |
|---|---|
| Method 1 | 0.79% |
| Method 2 | 0.94% |
| Method 3 | 0.57% |
| Without Rectification | 2.28% |
| Speed (km/h) | Methods of Assigning Initial Guess | Mean Relative Position Error |
|---|---|---|
| 25 | IMU | 0.31% |
| Previous regist | 0.46% | |
| 60 | IMU | 0.57% |
| Previous regist | 1.32% |
| Lidar Odometry Methods | Mean Relative Position Error |
|---|---|
| ICP | 6.28% |
| NDT | 3.85% |
| LOAM | 0.31% |
| Environment | Distance (km) | Mean Relative Position Error |
|---|---|---|
| Urban | 1.097 | 0.31% |
| Off-road | 0.983 | 0.93% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Fu, H.; Dai, B. IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving. Appl. Sci. 2019, 9, 1506. https://doi.org/10.3390/app9071506
Xue H, Fu H, Dai B. IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving. Applied Sciences. 2019; 9(7):1506. https://doi.org/10.3390/app9071506
Chicago/Turabian StyleXue, Hanzhang, Hao Fu, and Bin Dai. 2019. "IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving" Applied Sciences 9, no. 7: 1506. https://doi.org/10.3390/app9071506
APA StyleXue, H., Fu, H., & Dai, B. (2019). IMU-Aided High-Frequency Lidar Odometry for Autonomous Driving. Applied Sciences, 9(7), 1506. https://doi.org/10.3390/app9071506





