Two-Dimensional Constellation Shaping in Fiber-Optic Communications

Abstract

Constellation shaping has been widely used in optical communication systems. We review recent advances in two-dimensional constellation shaping technologies for fiber-optic communications. The system architectures that are discussed include probabilistic shaping, geometric shaping, and hybrid probabilistic-geometric shaping solutions. The performances of the three shaping schemes are also evaluated for Gaussian-noise-limited channels.

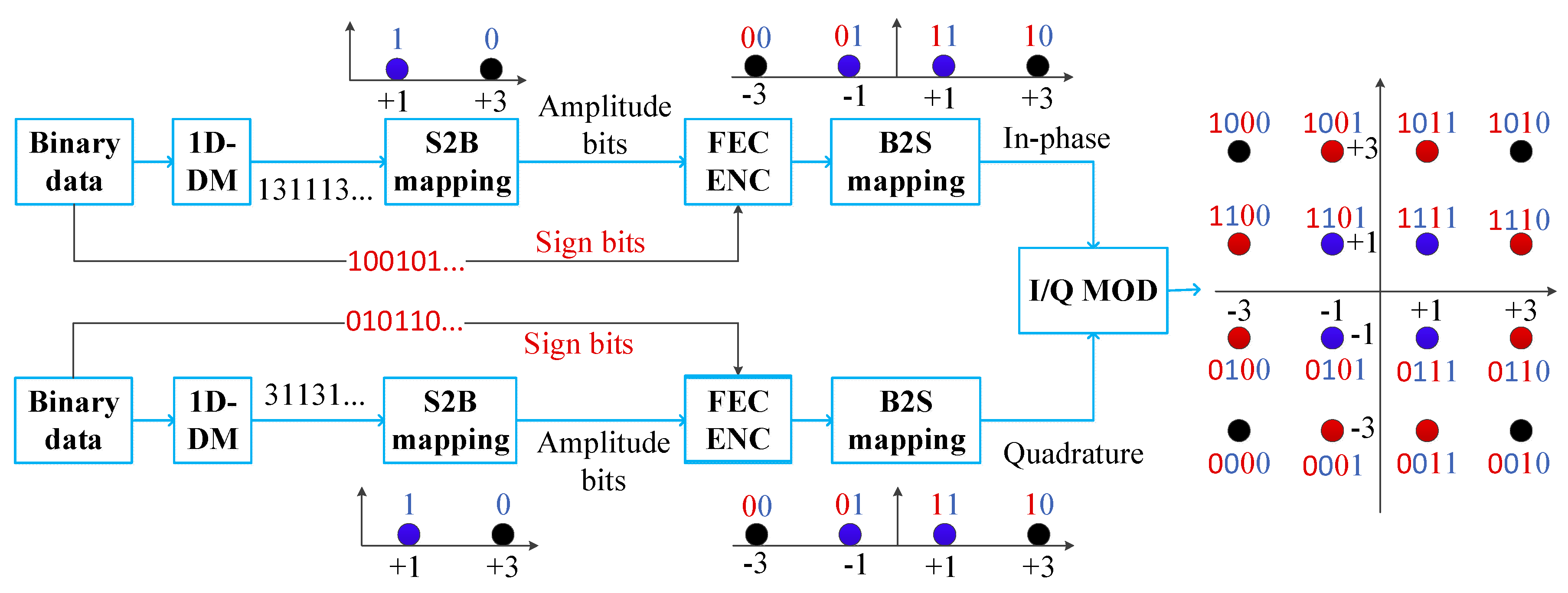
1. Introduction

The advances in photonics integrated circuit [1,2], software-defined networking [3,4], application-oriented fibers [5,6], and optical amplifiers [7,8], have been greatly pushing forward development and commercialization of optical communications. In the modern optical transport systems, especially in terrestrial and transoceanic fiber-optic communications, advanced modulation formats have been overwhelmingly implemented in optical transceivers [9,10,11,12,13,14], thanks to the ever-cheaper optical frontend and powerful digital signal processing (DSP) chips with smaller size and lower power consumption. Traditional quadrature amplitude modulation (QAM) formats have been applied extensively to realize high-capacity and long-reach optical communications, and we have witnessed numerous two-dimensional QAM (2D-QAM)-based hero experiments in recent years to explore the highest possible system capacity and longest transmission distance [15,16,17].

Due to the loss profile of the standard single mode fiber (SSMF) and gain profile of commercial Erbium-doped fiber amplifiers (EDFAs), C-band window (1530–1565 nm) is mostly used for data loading [18]. However, the capacity bottleneck becomes more visible for the traditional QAM-based C-band optical transmissions [19]. In order to meet the increasing bandwidth requirements, in particular the upcoming 5G infrastructure, more advanced solutions are expected to be introduced to optical infrastructures. We can roughly divide the promising solutions into two categories: coded modulation [20,21,22,23,24,25,26,27] and extended multiplexing [17,28,29,30,31]. The idea of coded modulation is increasing information bits per channel use, including higher-order 2D modulation formats, like 1024QAM [22], multidimensional QAM formats, like 4D optimized constellations [23], and constellation shaping techniques [24,25,26], like probabilistic shaping (PS)-64QAM [25]. Alternatively, extended multiplexing is a more straightforward solution, which mainly contains C+L band wavelength multiplexing [17,28] and space-division multiplexing [29,30,31]. All the solutions come with the trade-off choice between optical complexity and electrical complexity. In order to implement C+L band wavelength multiplexing, C-band EDFAs and L-band EDFAs should be used together to simultaneously amplify the channel loss per span [17]. Raman amplifier may be another option [32], but the telecom industry is not in favor of it because of its high cost. Space-division multiplexing based on few-mode fiber or multi-core fiber is an efficient way to directly boost the aggregate capacity. However, it seems to have been put at the bottom of the to-do list, because (i) it will be quite challenging to replace and rebuild the current fiber links, (ii) space-division-multiplexing-based optical amplifiers are too expensive for commercial applications, and (iii) complex multi-input multi-output (MIMO) channel equalization may be required to compensate channel crosstalk [33]. The telecom industry always chooses the most cost-efficient way to upgrade their communication systems. Therefore, extended multiplexing solution is barely found in the roadmap of optical communications, especially in the field of long-reach optical communications. On the contrary, coded modulation seems to be a more attracting solution. Higher modulation formats are more common now, but they have more stringent requirements on optical signal-to-noise ratio (OSNR), digital-to-analog converter/analog-to-digital converter (DAC/ADC), and DSP recovery. Multidimensional QAM solution can further enlarge the minimum Euclidean distance between constellation points, but it requires powerful DSP technology to recover signals. What is more, such performance optimization can come at a price of less information bits per channel use [34].

In traditional QAM formats, the constellation points are located on a uniform grid. Such uniform QAM formats are easy for generation and recovery but suffer a 1.53-dB asymptotic loss towards the Shannon limit. In order to close the gap, constellation shaping was introduced to optical communications. Constellation shaping, including PS [25,35,36,37], geometric shaping (GS) [26,38,39,40,41], and hybrid probabilistic-geometric shaping (HPGS) [42,43,44,45], is used to mimic a Gaussian distribution with limited constellation points. Although target at approaching Gaussian distribution, PS and GS have completely different generation and detection implementations. GS-QAM is obtained by optimizing some metrics, like mutual information (MI) [40] and generalized MI (GMI) [41], which will relocate the constellation point in geometric space. PS-QAM is applied on a uniform grid, but the constellation points will be transmitted with different probabilities. HPGS can optimize the performance in both geometric space and probabilistic space which should, in principle, provide the optimal performance.

In this paper, we review recent advances on 2D constellation shaping in fiber-optic communications. Section 2 gives an overview of PS, GS, and HPGS. Section 3 discusses the performance of PS, GS, and HPGS in Gaussian-noise-limited channels. Finally, the concluding remarks are given in Section 4.

2. Typical Constellation Shaping Schemes

2.1. Probabilistic Shaping

In a Gaussian-noise-limited channel, PS-QAM yielding a Maxwell–Boltzmann (M–B) distribution is recognized as the optimal format to maximize the channel capacity [46]. In general, the low-amplitude constellation points are sent with a higher probability than the high-amplitude ones. Besides, the constellation points under the same amplitude layer are sent equally likely. Therefore, the average symbol power will be decreased, but at a cost of lower source entropy.

The first PS scheme was proposed by Gallager, which is based on many-to-one mapping [47]. Complex forward error correction (FEC) coding is required to be implemented to recover the original bits from the systematic errors after many-to-one demapping. The recently proposed arithmetic coding-based constant composition distribution matcher (CCDM) is an invertible fix-to-fix length distribution matcher, enabling maximum information rate asymptotically in the block-length [48]. Later, there are some methods proposed to further reduce the complexity of CCDM, like multiset-partition distribution matching [49] and streaming distribution matching [50]. The first PS-based coded modulation was probabilistic amplitude shaping (PAS) [51], which could seamlessly combine the binary FEC coding and CCDM in a square M-QAM format.

The proposed PAS enables capacity approaching fiber-optic communications, but also brings some issues. Firstly, CCDM and the modified CCDM architectures are hard to be implemented in commercial optical transceivers. Secondly, more bit-to-symbol (B2S) mapping and symbol-to-bit (S2B) mapping modules are required to be implemented at the transceivers, leading to extra complexity. Thirdly, there will be an entropy loss by shaping on a given M-ary signal constellation format. Fourthly, intrablock error propagation will loom over the dematching procedure once the FEC coding cannot totally correct all bit errors. Fifthly, the applicable FEC code rate is limited, which will be lower-bounded by $[{\log }_2\left(M\right)-2]/{\log }_2\left(M\right)$. Sixthly, DSP circuit will be under a higher pressure to recover Gaussian-like constellation diagrams. Thereafter, more pilot-tones are essential to be used for signal recovery. Last but not least, although could be used for reach extension, PAS-MQAM suffers more from the modulation-dependent noise in long-haul fiber-optic communications [52].

In a square MQAM format, the coordinate of each constellation can be represented by the Cartesian product of two pulse-amplitude modulation (PAM) coordinates, namely,

$$X=\left\{\pm 1, \pm 3,\dots , \pm \left(\sqrt{M}-1\right)\right\}$$

(1)

The well-known M–B distribution is defined by

$$P_{X_v}\left(x\right)=e^{-v{\left|x\right|}^2}/{{\displaystyle \sum }}_{x^{\prime }\in X}{e}^{-v{\left|x^{\prime }\right|}^2}$$

(2)

where $v$ is a non-negative scaling factor. If $v$ is 0, the PAM format follows a uniform distribution.

The capacity of PAS-MQAM format can be defined as [51]

$$C=H\left(p\right)-m\left(1-R\right)$$

(3)

where $H\left(p\right)$ is the entropy of the PAS-MQAM format, $R$ is the FEC code rate, and $m={\log }_2\left(M\right)$.

Figure 1 shows the conceptual diagram of PAS-MQAM generation, where 16QAM is used as an illustrative example. In such scheme, the 1D amplitude symbols labeled by 1-3-1-1-1-3…, will be probabilistically shaped according to the M–B distribution (the probabilities of Symbol-1 and Symbol-3 are indicated by the blue and black colors, respectively), and the sign bits labeled by 1-0-0-1-0-1…, will be used to carry the uniformly distributed parity-check bits. The S2B mapping is used to map the Symbol-1 and Symbol-3 to amplitude bits, i.e., Bit-1 and Bit-0, respectively. In the FEC encoder, the party-check bits will be appended to the sign bits, and combine with the amplitude bits. Such encoded bits are remapped to PAM-4 symbols (00→−3, 01→−1, 11→+1, 10→+3). Therefore, after FEC coding, the M–B distribution will not be changed, and Gray-mapping rule is still applicable.

2.2. Geometric Shaping

GS-QAM is generated by optimizing certain criterion under a given signal-to-noise ratio (SNR). Such criteria can be maximizing MI [40], maximizing GMI [41], maximizing constellation figure of merit [53], or minimizing mean-square error of Gaussian distribution [54], etc. Typically, the lower-amplitude constellation points will be more concentrated around the origin. Generalized cross constellations and Voronoi constellations were proposed decades ago [38,39]. GMI-optimized constellations have also been proposed recently to enhance the capacity in a binary FEC coding featured fiber-optic communication systems.

GS could potentially simplify the process to generate Gaussian-like constellations, but it also brings several issues. Firstly, due to the unavailability of Gray-mapping in most cases, GMI performance hardly approach MI performance. Although nonbinary FEC coding is a solution to close such gap, the high complexity hinders its commercial development [55]. Secondly, the common asymmetry of the constellations may result in more complex PAM constellations in both in-phase and quadrature branches. Therefore, the ADC/DAC is required to be implemented with higher resolutions. Thirdly, the DSP circuits to recover GS-MQAM formats are not compatible with the ones to recover regular-MQAM. As a result, new DSP algorithms are suggested to be developed to efficiently recover the GS-MQAM signals. Fourthly, it is hard to reach standard agreements between optical transceiver manufacturers due to the variety of GS-QAM formats and the matched DSP algorithms.

Figure 2 shows the conceptual diagram of a GS-QAM-based communication system. If binary FEC coding is used, the suboptimal B2S mapping table has to be found to minimize the gap between GMI and MI, in order to minimize the Non-Gray mapping penalty. Brutal force algorithm may be used to find such mapping rule at a cost of high computational complexity. Alternatively, binary data can be mapped to the GS-QAM symbols through any B2S look-up table, followed by a reasonable complexity nonbinary FEC encoder to sustain reliable communications [56].

Figure 3 shows 16/32/64QAM formats generated by maximizing constellation figure of merit [53], minimizing mean-square error of Gaussian distribution [57], and maximizing GMI [41], respectively. The GS-16QAM constellation shown in Figure 3a is obtained by maximizing the minimum Euclidean distance under the same average power of the 16-ary constellation.

The GS-32QAM constellation shown in Figure 3b can be obtained by the following steps.

• Choosing 2D Gaussian distribution as the optimal source distribution, and select the uniformly distributed regular-32QAM as the initial constellation.
• Generating a symbol sequence following the Gaussian distribution.
• Distributing the symbols into 32 clusters, where the decision is made as per the minimum Euclidean distance from the 32QAM constellation points obtained in previous iteration.
• Finding the average central positions from the symbols labeled by each cluster. Such 32 points located on the central positions are used as the new MQAM constellation points.
• Iterating over Steps 2 and 4 until convergence.

The GS-64QAM constellation shown in Figure 3b is designed with the constraint of Gray mapping, which can maximize the GMI. Due to the Gray mapping constraint, such scheme cannot fully explore the 2D space, but it can also reduce capacity gap towards the Shannon limit.

It is an open question about the optimal GS solution, since it depends on lots of implementation scenarios. When the amount of the constellation points is more than 64, GS may suffer more implementation penalties than PS.

2.3. Hybrid Probabilistic-Geometric Shaping

When more flexible constellation formats are required, especially multi-dimensional QAM formats, HPGS may be an enabling technique, since each constellation point during the optimization process will not be limited to equal probability or uniform-grid locations. Figure 4 shows HPGS-5QAM and HPGS-9QAM formats based on Huffman coding [58,59]. The probability of each symbol is predetermined by the corresponding Huffman tree, and the coordinates of the symbols can be obtained by optimizing the MI.

As an illustrative example, the generation process of HPGS-9QAM constellation can be found below:

• Parsing the binary source into nine blocks labeled by unique bit sets {00, 010, 110, 011, 100, 1110, 1111, 1010, 1011}. If the binary sequence is sufficiently long, the resulting blocks should be generated with the probabilities of {P(00) = 1/4, P(010) = 1/8, P(011) = 1/8, P(100) = 1/8, P(1110) = 1/16, P(1111) = 1/16, P(1010) = 1/16, P(1011) = 1/16}. Thereafter, the entropy is 3, i.e., there is no entropy loss.
• Mapping the 9-block sequence to any 9-QAM symbols with the constraints: (i) The 9-ary constellation points with the same probability are uniformly located in the same power layer, (ii) The constellation points with higher probabilities are located at higher power layers. In other words, such 9-ary constellation should be featured with three power layers and 1, 4, and 4 points are equally spaced in each power layer, respectively.
• Maximizing the MI by iterating over all amplitude ratios and phase differences of such 9-ary constellation.

Huffman coding can be treated as a variable-length and prefix-free PS scheme, which can also be uniquely decodable, but it cannot provide flex rate.

There are four major problems for this HPGS scheme. Firstly, it is quite challenging to implement Huffman coding when the amount of symbols increase. Secondly, as any other variable-length coding technology, Huffman coding will also suffer from the overflow or underflow problems. Thirdly, the higher-complexity nonbinary FEC coding is required. Fourthly, error propagation may occur if unexpected symbol errors remained after FEC decoding.

A more efficient and practical way to generate HPGS-QAM is based on universal probabilistic shaping scheme and GMI-optimized GS scheme [44,60]. Figure 5 shows the constellation formats for HPGS-32QAM, as well as the regular/PS-32QAM.

The constellation diagram of the HPGS-32QAM shown in Figure 5a is generated by the generalized pairwise optimization algorithm. The objective function is maximizing GMI under the constraints of zeros mean amplitude and normalized average power. The two constraints can be expressed as

$$p_i{x}_i=-A-p_j{x}_j$$

(4)

$${\left|p_j{x}_j+b\right|}^2+\frac{p_j}{p_i{}^2}{\left|x_j\right|}^2=1-B$$

(5)

where ($x_i, x_j$) is one pair of the M-ary constellation ($M=32$ in this case), $p_i$ is the probability of $x_i$, $A={\displaystyle \sum }_{k=1,k\ne i,k\ne j}^M{p}_k{x}_k$, and $B={\displaystyle \sum }_{k=1,k\ne i,k\ne j}^M{p}_k{\left|x_k\right|}^2$. The objective of maximizing GMI will be searching the ($x_i, x_j$) pair over a hypersphere with the center and radius determined by the other $M-2$ constellation points. Such generalized pairwise optimization algorithm can converge to the final steady state after iterating all $M\left(M-1\right)/2$ pairs. As a rule of thumb, we suggest start the iteration with the regular-32QAM, and the optimal HPGS-32QAM shown in Figure 5a can be obtained within 1000 iterations.

Such HPGS constellation could provide the trade-off between the number of nearest symbols and their Hamming distance. Any constellation format shown in Figure 5 does not belong to the square QAM category. As a result, the well-known PAS scheme cannot be used for the PS purpose.

Figure 6 shows the modified probabilistic fold shaping and universal probabilistic shaping schemes [60]. Probabilistic fold shaping can be used for shaping any F-fold rotationally symmetric constellation, like regular-32QAM, as shown in Figure 6a. In such kind of constellations, the bits determining the fold index yield uniform distribution, which can be used to carry the parity-check bits. There is a major difference between PAS and probabilistic fold shaping. PAS is a 1D shaping scheme, which uses the single bit determining the positive or negative amplitude to carry the parity-check bit and shapes the 1D-PAM with a 1D M–B distribution. On the contrary, probabilistic fold shaping is a 2D shaping scheme, which uses the ${\log }_2\left(F\right)$ bits determining the fold indexes to carry the parity-check bits, and shapes the 2D constellation points in one fold with a 2D M–B distribution. As an illustrative example, the 32QAM shown in Figure 6a is featured with four-fold rotational symmetry. The 8-ary constellation points in one fold are firstly shaped with a 2D M–B distribution, where different colors indicate different probabilities. The bit sets {11,01,00,10} determining the fold indexes will carry the parity-check bit after FEC encoding and rotate the 8-ary constellation by 0°, 90°, 180°, 270°, respectively. Therefore, 2D M–B distribution can be applied to the constellation points in one fold, and the selection of the fold-index can be performed by the parity-check bits. The target distribution will not be changed after the binary FEC coding.

The universal probabilistic shaping scheme shown in Figure 6b can be applied to shape any QAM format. The MQAM symbols generated from the CCDM may not yield a M–B distribution. The binary bits generated after the bit labeling block are used to carry the uniformly distributed parity-check bits. During the process of B2S mapping, the parity-check bits will be uniformly mapped to partial MQAM symbols, i.e., N-ary QAM (NQAM) symbols, where N is the largest power of 2 to contain the MQAM constellation points with the desirable probabilities of >$\left(1-R\right)/M$. Assuming that the desirable probability distribution of the MQAM symbols is $P_M\left(x\right)$, the probability distribution of the MQAM symbols after the CCDM is $P_D\left(x\right)$, and probability distribution of the NQAM symbols is given by $P_N\left(y\right)=1/N$. The final relationship can be written as $P_M\left(x\right)=\left[R{P}_D\left(x\right)/{\log }_2\left(M\right)+(1-R)P_N\left(y\right)/{\log }_2\left(N\right)\right]/[R/{\log }_2\left(M\right)+\left(1-R)/{\log }_2\left(N\right)\right]$. In such a way, any desirable distribution of the HPGS-MQAM symbols can be obtained.

3. Performance Comparison in Gaussian-Noise-Limited Channels

As a rule of thumb, HPGS-MQAM cannot show clear performance improvement over PS-MQAM and GS-MQAM when M < 32. In addition, if M ≥ 64, PS-MQAM could closely approach the Shannon limit, thus it is not necessary to apply HPGS to higher order QAM formats. In this paper, we performed Monte Carlo simulations in MATLAB. The block-length of the CCDM was chosen more than 5000, so the normalized divergence of the encoder output and the desired distribution is negligible. The awgn function provided by MATLAB was used to add white Gaussian noise to the 2D-MQAM signals. All the results were averaged over 1000 trials.

In a numerical simulation, as shown in Figure 7, we compared the MI performances of the minimizing mean-square error of Gaussian-distribution-based GS-8/16/32QAM, CCDM-based PS-8/16/32QAM, and regular-8/16/32QAM. Figure 7a1,a2,b1,b2,c1,c2 show the constellation diagrams of PS/GS-8/16/32QAM. Here we chose MI as the metric for performance comparison, because MI can be measured without the consideration of the FEC coding performance. Given that most of the current nonbinary FEC coding and binary FEC coding schemes may vary in performance and implementation penalty, MI instead shows the upper limit of the capacity obtained with the “ideal” FEC coding scheme [61]. In order to easily describe the PS-MQAM with an entropy of A b/s, we adopt the notation of PS-MQAMA. For example, we use PS-8QAM2.3 to denote the PS-8QAM with an entropy of 2.3 b/s. As we can see from Figure 7a,b, the best MI performances can be obtained by GS-8/16QAM. GS-8/16QAM can always outperform regular-8/16QAM. PS-8QAM can have comparable performance over GS-8QAM when the SNR is less than 6.2 dB; the performances of PS-16QAM and GS-16QAM are quite similar when the SNR is less than 11.7 dB. In the region of high SNR region, PS-8/16QAM cannot bring better MI performance. In Figure 7c, we find that the best performance can be achieved by PS/GS-32QAM separately. In addition, GS-32QAM is always better than regular-32QAM in terms of MI performance. When the SNR is more than 15.7 dB, GS-32QAM has the best performance, while PS-32QAM formats can maximize the MI performance when the SNR is less than 15.7 dB.

Although PS-256QAM and PS-1024QAM have been investigated over fiber links [62], we still believe that PS-64QAM is expected to be the most promising solution for high-order QAM-based fiber-optic communications, at least for the upcoming 400 G/800 G Ethernet. It is mainly because that PS-64QAM has near-capacity-approaching performance, and its implementation penalty may also be well reduced to an acceptable level in the near future. While, unfortunately, regular-64QAM and PS-64QAM have been suffering a large implementation penalty so far. Here we compare the performances of PAS-64QAM and GMI-optimized HPGS-32QAM (referred to as opti-32QAM in this paper).

In another numerical simulation, Figure 8 shows the post-FEC bit error rate (BER) versus SNR performances of PAS-64QAM, opti-32QAM, PS-32QAM, and regular-32QAM. DVB-S2 irregular low-density parity-check (LDPC) codes were applied for FEC coding. The performance comparisons were executed under the same capacity levels, i.e., C = 3.33 b/s and C = 4 b/s.

Table 1. The parameters used in the post-forward error correction (FEC) bit error rate (BER) analysis under the same capacity.

C [b/s]	H/R	R-32QAM	Opti-32QAM	PS-32QAM	PAS-64QAM
3.33	$H\left(p\right)$	5	5	4.33	4.53
	$R$	2/3	2/3	4/5	4/5
4	$H\left(p\right)$	5	5	4.55	5.2
	$R$	4/5	4/5	8/9	4/5

lists the parameters used in the post-FEC BER analysis under the capacity levels of 3.33 b/s and 4 b/s. In Figure 8a, the performance of PS-32QAM is slightly better than opti-32QAM, but worse than PAS-64QAM by 0.2 dB. Opti-32QAM shows a 0.8-dB performance improvement over regular-32QAM in case of C = 3.33 b/s. In Figure 8b, the performance of opti-32QAM is better than PS-32QAM by 0.2 dB, better than regular-32QAM by 0.8 dB when the capacity is 4 b/s. However, PAS-64QAM is also shown to outperform opti-32QAM by 0.4 dB. It is reasonable to find that PAS-64QAM always has the best post-FEC performance over shaped 32QAM. While in a realistic communication system, we believe that the performance of HPGS-32QAM (opti-32QAM) should be similar to that of PAS-64QAM, due to the higher implementation penalties that PAS-64QAM may suffer.

4. Concluding Remarks

Constellation shaping will play an increasingly important role in fiber-optic communications in the wake of the booming 5G era. In this paper, we focused on the performance of 2D constellation shaping in Gaussian-noise-limited channels. We have discussed three key constellation shaping schemes, i.e., PS, GS, and HPGS, and analyzed their pros and cons in terms of performance and implementation complexity. We also introduced two modified CCDM-based shaping schemes, i.e., probabilistic fold shaping and universal PS, which could enable applying PS on any 2D modulation format. We found that GS-8QAM and GS-16QAM could outperform PS/regular-8QAM and PS-regular-16QAM, respectively, in terms of MI performance. In addition, the best MI performance of 32-ary QAM format could be reached by PS-32QAM and GS-32QAM separately. We compared the post-FEC BER performances of HPGS/PS/regular-32QAM and PAS-64QAM under the same capacity.

The performances of HPGS/PS-32QAM were shown to be similar, and better than regular-32QAM. What is more, PAS-64QAM could still have 0.2–0.4 dB performance gains over HPGS/PS-32QAM.

For a commercial CCDM-based PS implementation, the power consumption is mainly determined by the block length and the entropy of the CCDM, as well as FEC coding selection. GS-QAM formats will cost more power consumption than regular-QAM formats, because of that a higher complexity DSP circuit is required to be used for GS-QAM-based transceivers to recover the signal from the received data with Gaussian-like distribution. Although the best performance can be theoretically achieved by HPGS-QAM, the extra power consumption arising from PS and GS schemes is nontrivial. Considering that both PS and GS can closely approach the Shannon limit and only limited margin can be reached by HPGS, HPGS may not be in favor by the industry due to the low benefit–cost ratio.