Addressing Complete New Item Cold-Start Recommendation: A Niche Item-Based Collaborative Filtering via Interrelationship Mining
Abstract
:1. Introduction
- Different from current related approaches that only utilize attribute values [15,16,17,18,19,20,21,22,23,24], the proposed approach extends the binary relations between each pair of attributes using interrelationship mining and extracts new binary relations to construct interrelated attributes that can reflect the interrelationship between each pair of attributes. Furthermore, some significant properties of interrelated attributes are presented, and theorems for the number of interrelated attributes as well as a detailed process of proof are given in this paper.
- Unlike most related works that can enhance either accuracy or diversity of recommendations, but not in both [15,16,17,18,19,20,21,22,23,24], the proposed approach can provide new item recommendations with satisfactory accuracy and diversity simultaneously, and the experimental results in Section 4 confirm this.
2. Background and Related Work
2.1. Traditional IBCF Approach and the Associated CNICS Problem
2.2. Interrelationship Mining Theory
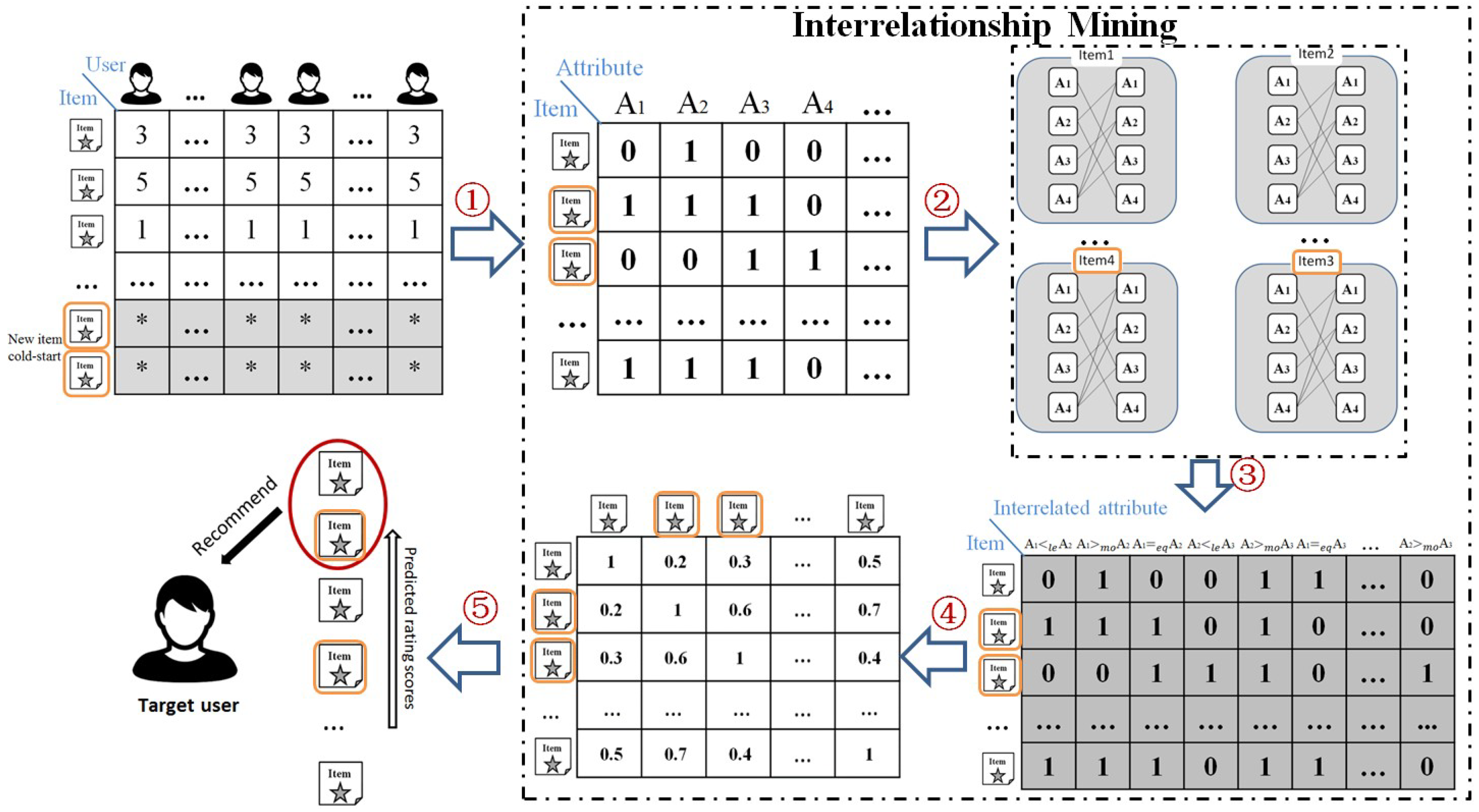
3. Proposed Approach: IBCF Approach based on Interrelationship Mining
3.1. Motivation of the Proposed Approach
- A user prefers attribute a of movies more than attribute b,
- The significance of attribute a is identical to the attribute b.
3.2. Construction of Interrelated Attributes
3.3. Number of Interrelated Attributes
3.4. JAC based on Interrelated Attributes
- Both items and have attributes .
- Item also has all attributes but item does not have any of these attributes.
- Item also has all attributes but item does not have any of these attributes.
- Both items and do not have attributes ,
3.5. Example of Proposed Approach in CNICS Problem
- Both and have attribute .
- There is no attribute that has but does not have, so .
- has attribute but does not have that.
- Both and do not have attribute .
| Algorithm 1 Proposed approach | |
| Input: User-item matrix RM, item-attribute matrix AM, and a target user . | |
| Output: Recommended items for the target user . | |
| : The set of items’ attributes. | |
| : The set of interrelated attributes. | |
| : Neighborhood of the target item . | |
| L: Number of items in the neighborhood of the target item . | |
| N: Number of items recommended to the target user . | |
| : The set of items that the target user has not rated. | |
| : Rating prediction of target item for the target user . | |
| 1: | |
| 2: | For each pair of attributes do |
| 3: | Obtain the three interrelated attributers: |
| 4: | End for |
| 5: | For each interrelated attribute do |
| 6: | For each item do |
| 7: | Set the attribute value of by Equations (8)–(10) |
| 8: | End for |
| 9: | End for |
| 10: | For each pair of items do |
| 11: | Compute the similarity between and according to interrelated attributes |
| 12: | End for |
| 13: | For each target item do |
| 14: | Find the L most similar items of target item to comprise neighborhood |
| 15: | Predict rating score of target item from the items in |
| 16: | End for |
| 17: | Recommend the top N target items having the highest predicted rating scores to the target user |
4. Experiments and Evaluation
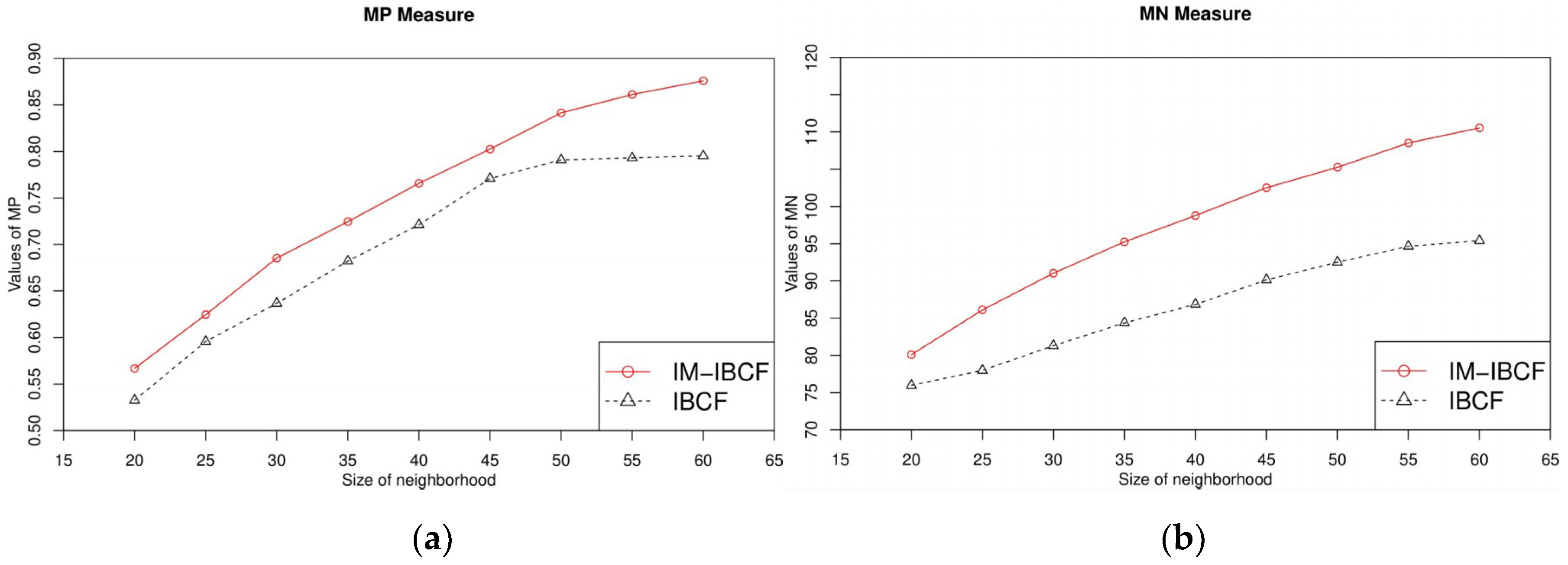
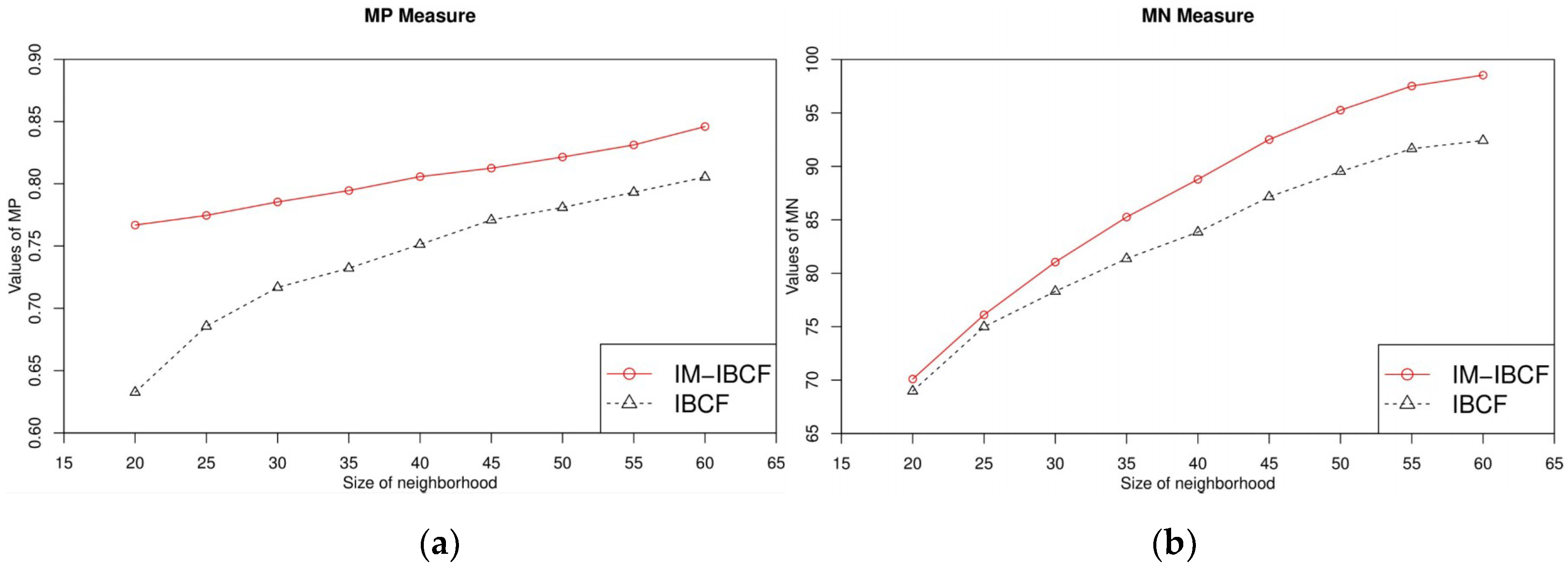
4.1. Experimental Setup and the Evaluation Metrics
4.2. Experimental Results and Analysis
5. Conclusions and Future Work
Author Contributions
Conflicts of Interest
References
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F. Recommender system survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Lu, J.; Wu, D.; Mao, M.; Wang, W.; Zhang, W. Recommender system application developments: A survey. Decis. Support Syst. 2015, 74, 12–32. [Google Scholar] [CrossRef]
- Zhang, Z.; Kudo, Y.; Murai, T. Neighbor selection for user-based collaborative filtering using covering-based rough sets. Ann. Oper. Res. 2017, 256, 359–374. [Google Scholar] [CrossRef]
- Rosaci, D. Finding semantic associations in hierarchically structured groups of Web data. Form. Asp. Comput. 2015, 27, 867–884. [Google Scholar] [CrossRef]
- De Meo, P.; Fotia, L.; Messina, F.; Rosaci, D.; Sarné, G.M. Providing recommendations in social networks by integrating local and global reputation. Inf. Syst. 2018, 78, 58–67. [Google Scholar] [CrossRef]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithm. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Chen, T.; Sun, Y.; Shi, Y.; Hong, L. On sampling strategies for neural network-based collaborative filtering. In Proceedings of the 23th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 767–776. [Google Scholar]
- Thakkar, P.; Varma, K.; Ukani, V.; Mankad, S.; Tanwar, S. Combing user-based and item-based collaborative filtering using machine learning. Inf. Commun. Technol. Intell. Syst. 2019, 107, 173–180. [Google Scholar]
- Guo, G.; Zhang, J.; Yorke-Smith, N. TrustSVD: Collaborative filtering with both the explicit and implicit influence of user trust and of item ratings. In Proceedings of the 29th AAAI Conference on Artificial Intelligence, Texas, TX, USA, 25–30 February 2015; pp. 123–129. [Google Scholar]
- Deshpande, M.; Karypis, G. Item-based top-n recommendation algorithms. ACM Trans. Inf. Syst. 2004, 22, 143–177. [Google Scholar] [CrossRef]
- Lika, B.; Kolomvatsos, K.; Hadjiefthymiades, S. Facing the cold start problem in recommender systems. Expert Syst. Appl. 2014, 41, 2065–2073. [Google Scholar] [CrossRef]
- Wei, J.; He, J.; Chen, K.; Zhou, Y.; Tang, Z. Collaborative filtering and deep learning based recommendation system for cold start items. Expert Syst. Appl. 2017, 69, 29–39. [Google Scholar] [CrossRef]
- Said, A.; Jain, B.J.; Albayrak, S. Analyzing weighting schemes in collaborative filtering: Cold start, post cold start and power users. In Proceedings of the 27th Annual Symposium on Applied Computing, Trento, Italy, 26–30 March 2012; pp. 2035–2040. [Google Scholar]
- Ahn, H.J. A new similarity measure for collaborative filtering to alleviate the new user cold-starting problem. Inf. Sci. 2008, 178, 37–51. [Google Scholar] [CrossRef]
- Basilico, J.; Hofmann, T. Unifying collaborative and content-based filtering. In Proceedings of the 21th International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; pp. 9–26. [Google Scholar]
- Cohen, D.; Aharon, M.; Koren, Y.; Somekh, O.; Nissim, R. Expediting exploration by attribute-to-feature mapping for cold-start recommendations. In Proceedings of the 7th ACM Conference on RecSys, Como, Italy, 27–31 August 2017; pp. 184–192. [Google Scholar]
- Koutrika, G.; Bercovitz, B.; Garcia-Molina, H. FlexRecs: Expressing and combining flexible recommendations. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; pp. 745–758. [Google Scholar]
- Schein, A.I.; Popescul, A.; Ungar, L.H.; Pennock, D.M. Generative models for cold-start recommendations. In Proceedings of the 2001 SIGIR Workshop Recommender Systems, New Orleans, LA, USA, September 2001; Volume 6. [Google Scholar]
- Stern, D.H.; Herbrich, R.; Graepel, T. Matchbox: Large scale online bayesian recommendations. In Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 111–120. [Google Scholar]
- Gantner, Z.; Drumond, L.; Freudenthaler, C.; Rendle, S.; Schmidt-Thieme, L. Learning Attribute-to-Feature Mappings for Cold-Start Recommendations. In Proceedings of the 10th IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 176–185. [Google Scholar]
- Kula, M. Metadata embeddings for user and item cold-start recommendations. In Proceedings of the 2nd CBRecSys, Vienna, Austria, 16–20 September 2015; pp. 14–21. [Google Scholar]
- Mantrach, A.; Saveski, M. Item cold-start recommendations: Learning local collective embeddings. In Proceedings of the 8th ACM Conference on RecSys, Foster City, Silicon Valley, CA, USA, 6–10 October 2014; pp. 89–96. [Google Scholar]
- Sahoo, N.; Krishnan, R.; Duncan, G.; Callan, J. The halo effect in multicomponent ratings and its implications for recommender systems: The case of yahoo! movies. Inf. Syst. Res. 2013, 23, 231–246. [Google Scholar] [CrossRef]
- Kudo, Y.; Murai, T. Indiscernibility relations by interrelationships between attributes in rough set data analysis. In Proceedings of the IEEE International Conference on Granular Computing, Hangzhou, China, 11–13 August 2012; pp. 220–225. [Google Scholar]
- Kudo, Y.; Murai, T. Decision logic for rough set-based interrelationship mining. In Proceedings of the IEEE International Conference on Granular Computing, Beijing, China, 13–15 December 2013; pp. 172–177. [Google Scholar]
- Kudo, Y.; Murai, T. Interrelationship mining from a viewpoint of rough sets on two universes. In Proceedings of the IEEE International Conference on Granular Computing, Noboribetsu, Japan, 22–24 October 2014; pp. 137–140. [Google Scholar]
- Kudo, Y.; Murai, T. A Review on Rough Set-Based Interrelationship Mining; Fuzzy Sets, Rough Sets, Multisets and Clustering; Springer: Milano, Italy, 2017; pp. 257–273. [Google Scholar]
- Yao, Y.Y.; Zhou, B.; Chen, Y. Interpreting low and high order rules: A granular computing approach. In Proceedings of the Rough Sets and Intelligent Systems Paradigms (RSEISP), Warsaw, Poland, 28–30 June 2007; pp. 371–380. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An algorithmic framework for performing collaborative filtering. In Proceedings of the 22th International ACM Conference Research and Development in Information Retrieval, Berkeley, CA, USA, 15–19 August 1999; pp. 230–237. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Riedl, J. An empirical analysis of design choices in neighborhood-based collaborative filtering algorithms. Inf. Retr. 2002, 5, 287–310. [Google Scholar] [CrossRef]
- Gan, M.; Jiang, R. Constructing a user similarity network to remove adverse influence of popular objects for personalized recommendation. Expert Syst. Appl. 2013, 40, 4044–4053. [Google Scholar] [CrossRef]
| u1 | u2 | u3 | u4 | u5 | u6 | u7 | … | |
|---|---|---|---|---|---|---|---|---|
| i1 | 3 | 2 | 3 | 5 | 2 | 2 | 3 | … |
| i2 | 4 | 1 | 4 | 2 | 3 | 1 | 5 | … |
| i3 | 2 | 1 | * | * | * | * | * | … |
| i4 | 4 | 5 | 1 | 3 | * | * | * | … |
| i5 | * | * | * | * | * | * | * | … |
| i6 | * | * | * | * | * | * | * | … |
| u1 | u2 | u3 | u4 | |
|---|---|---|---|---|
| i1 | 3 | 2 | 4 | 2 |
| i2 | 5 | 4 | 5 | 4 |
| i3 | 4 | 5 | 1 | 3 |
| i4 | 1 | 3 | 1 | 1 |
| i5 | 2 | 4 | 2 | 5 |
| iti1 | * | * | * | * |
| iti2 | * | * | * | * |
| at1 | at2 | at3 | |
|---|---|---|---|
| i1 | 1 | 0 | 0 |
| i2 | 1 | 1 | 1 |
| i3 | 1 | 0 | 1 |
| i4 | 0 | 0 | 1 |
| i5 | 0 | 1 | 0 |
| iti1 | 0 | 1 | 1 |
| iti2 | 1 | 1 | 0 |
| at1>leat2 | at1>leat2 | at1>leat2 | at1=eqat2 | at1=eqat2 | at1=eqat2 | at1<moat2 | at1<moat2 | at1<moat2 | |
|---|---|---|---|---|---|---|---|---|---|
| i1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| i3 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| i5 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| iti1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| iti2 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| i1 | i2 | i3 | i4 | i5 | iti1 | iti2 | |
|---|---|---|---|---|---|---|---|
| i1 | 1 | 0 | 0.25 | 0 | 0 | 0 | 0.25 |
| i2 | 0 | 1 | 0.20 | 0 | 0 | 0.20 | 0.20 |
| i3 | 0.25 | 0.20 | 1 | 0.25 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0.25 | 1 | 0 | 0.25 | 0 |
| i5 | 0 | 0 | 0 | 0 | 1 | 0.25 | 0.25 |
| iti1 | 0 | 0.20 | 0 | 0.25 | 0.25 | 1 | 0 |
| iti2 | 0.25 | 0.20 | 0 | 0 | 0.25 | 0 | 1 |
| #Recommended Items | Recommendation Approach | #Neighborhood | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | L = 45 | L = 50 | L = 55 | L = 60 | ||
| N = 2 | IM-IBCF | 0.478 | 0.479 | 0.480 | 0.476 | 0.473 | 0.468 | 0.462 | 0.473 | 0.500 |
| IBCF | 0.474 | 0.524 | 0.526 | 0.475 | 0.417 | 0.434 | 0.450 | 0.447 | 0.444 | |
| N = 4 | IM-IBCF | 0.261 | 0.266 | 0.270 | 0.274 | 0.278 | 0.273 | 0.270 | 0.273 | 0.276 |
| IBCF | 0.273 | 0.286 | 0.289 | 0.255 | 0.236 | 0.233 | 0.237 | 0.229 | 0.222 | |
| N = 6 | IM-IBCF | 0.196 | 0.199 | 0.209 | 0.211 | 0.214 | 0.207 | 0.204 | 0.198 | 0.191 |
| IBCF | 0.234 | 0.221 | 0.222 | 0.219 | 0.216 | 0.201 | 0.193 | 0.189 | 0.186 | |
| N = 8 | IM-IBCF | 0.164 | 0.197 | 0.187 | 0.164 | 0.203 | 0.195 | 0.188 | 0.186 | 0.185 |
| IBCF | 0.207 | 0.166 | 0.169 | 0.201 | 0.161 | 0.157 | 0.153 | 0.147 | 0.141 | |
| #Recommended Items | Recommendation Approach | #Neighborhood | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | L = 45 | L = 50 | L = 55 | L = 60 | ||
| N = 2 | IM-IBCF | 0.235 | 0.238 | 0.237 | 0.242 | 0.239 | 0.235 | 0.233 | 0.236 | 0.241 |
| IBCF | 0.231 | 0.239 | 0.238 | 0.239 | 0.240 | 0.232 | 0.230 | 0.232 | 0.239 | |
| N = 4 | IM-IBCF | 0.251 | 0.249 | 0.251 | 0.258 | 0.263 | 0.265 | 0.261 | 0.269 | 0.273 |
| IBCF | 0.246 | 0.257 | 0.259 | 0.262 | 0.257 | 0.256 | 0.254 | 0.259 | 0.265 | |
| N = 6 | IM-IBCF | 0.273 | 0.264 | 0.271 | 0.281 | 0.278 | 0.279 | 0.284 | 0.285 | 0.289 |
| IBCF | 0.268 | 0.269 | 0.279 | 0.277 | 0.273 | 0.280 | 0.281 | 0.283 | 0.287 | |
| N = 8 | IM-IBCF | 0.286 | 0.283 | 0.290 | 0.286 | 0.297 | 0.311 | 0.308 | 0.307 | 0.303 |
| IBCF | 0.281 | 0.287 | 0.285 | 0.288 | 0.290 | 0.293 | 0.297 | 0.304 | 0.301 | |
| #Recommended Items | Recommendation Approach | #Neighborhood | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | L = 45 | L = 50 | L = 55 | L = 60 | ||
| N = 2 | IM-IBCF | 0.374 | 0.373 | 0.375 | 0.379 | 0.371 | 0.369 | 0.367 | 0.364 | 0.361 |
| IBCF | 0.372 | 0.375 | 0.376 | 0.374 | 0.368 | 0.366 | 0.364 | 0.362 | 0.360 | |
| N = 4 | IM-IBCF | 0.288 | 0.290 | 0.293 | 0.297 | 0.295 | 0.291 | 0.292 | 0.294 | 0.296 |
| IBCF | 0.289 | 0.291 | 0.287 | 0.286 | 0.284 | 0.282 | 0.280 | 0.284 | 0.288 | |
| N = 6 | IM-IBCF | 0.217 | 0.216 | 0.213 | 0.210 | 0.218 | 0.216 | 0.214 | 0.211 | 0.210 |
| IBCF | 0.215 | 0.218 | 0.219 | 0.213 | 0.213 | 0.212 | 0.210 | 0.207 | 0.202 | |
| N = 8 | IM-IBCF | 0.186 | 0.187 | 0.191 | 0.187 | 0.185 | 0.182 | 0.181 | 0.180 | 0.177 |
| IBCF | 0.182 | 0.189 | 0.188 | 0.185 | 0.184 | 0.183 | 0.180 | 0.179 | 0.176 | |
| #Recommended Items | Recommendation Approach | #Neighborhood | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | L = 45 | L = 50 | L = 55 | L = 60 | ||
| N = 2 | IM-IBCF | 0.128 | 0.131 | 0.133 | 0.130 | 0.129 | 0.122 | 0.118 | 0.119 | 0.115 |
| IBCF | 0.089 | 0.126 | 0.129 | 0.132 | 0.112 | 0.123 | 0.115 | 0.112 | 0.109 | |
| N = 4 | IM-IBCF | 0.159 | 0.164 | 0.165 | 0.166 | 0.169 | 0.158 | 0.155 | 0.148 | 0.142 |
| IBCF | 0.149 | 0.121 | 0.122 | 0.125 | 0.128 | 0.131 | 0.133 | 0.135 | 0.136 | |
| N = 6 | IM-IBCF | 0.166 | 0.169 | 0.171 | 0.177 | 0.181 | 0.172 | 0.165 | 0.157 | 0.153 |
| IBCF | 0.162 | 0.166 | 0.174 | 0.179 | 0.171 | 0.168 | 0.164 | 0.156 | 0.151 | |
| N = 8 | IM-IBCF | 0.176 | 0.186 | 0.194 | 0.203 | 0.205 | 0.196 | 0.191 | 0.184 | 0.188 |
| IBCF | 0.178 | 0.179 | 0.181 | 0.183 | 0.186 | 0.187 | 0.189 | 0.186 | 0.184 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-P.; Kudo, Y.; Murai, T.; Ren, Y.-G. Addressing Complete New Item Cold-Start Recommendation: A Niche Item-Based Collaborative Filtering via Interrelationship Mining. Appl. Sci. 2019, 9, 1894. https://doi.org/10.3390/app9091894
Zhang Z-P, Kudo Y, Murai T, Ren Y-G. Addressing Complete New Item Cold-Start Recommendation: A Niche Item-Based Collaborative Filtering via Interrelationship Mining. Applied Sciences. 2019; 9(9):1894. https://doi.org/10.3390/app9091894
Chicago/Turabian StyleZhang, Zhi-Peng, Yasuo Kudo, Tetsuya Murai, and Yong-Gong Ren. 2019. "Addressing Complete New Item Cold-Start Recommendation: A Niche Item-Based Collaborative Filtering via Interrelationship Mining" Applied Sciences 9, no. 9: 1894. https://doi.org/10.3390/app9091894
APA StyleZhang, Z.-P., Kudo, Y., Murai, T., & Ren, Y.-G. (2019). Addressing Complete New Item Cold-Start Recommendation: A Niche Item-Based Collaborative Filtering via Interrelationship Mining. Applied Sciences, 9(9), 1894. https://doi.org/10.3390/app9091894





