Abstract
Robotics is a highly developed field in industry, and there is a large research effort in terms of humanoid robotics, including the development of multi-functional empathetic robots as human companions. An important function of a robot is to find an optimal coverage path planning, with obstacle avoidance in dynamic environments for cleaning and monitoring robotics. This paper proposes a novel approach to enable robotic path planning. The proposed approach combines robot reasoning with knowledge reasoning techniques, hedge algebra, and the Spiral Spanning Tree Coverage (STC) algorithm, for a cleaning and monitoring robot with optimal decisions. This approach is used to apply knowledge inference and hedge algebra with the Spiral STC algorithm to enable autonomous robot control in the optimal coverage path planning, with minimum obstacle avoidance. The results of experiments show that the proposed approach in the optimal robot path planning avoids tangible and intangible obstacles for the monitoring and cleaning robot. Experimental results are compared with current methods under the same conditions. The proposed model using knowledge reasoning techniques in the optimal coverage path performs better than the conventional algorithms in terms of high robot coverage and low repetition rates. Experiments are done with real robots for cleaning in dynamic environments.
1. Introduction
Mobile robots are categorized in both classical and heuristic methods in Coverage Path Planning (CPP). These methods can be divided subcategories such as analytical methods, evolutionary methods, enumerative methods, and meta-heuristic methods [1]. In real-world applications, these methods are highly dependent on the ability to optimize coverage path planning with minimized obstacles in a dynamic environment [1]. In mobile robots, Coverage Path Planning (CPP) algorithms have been implemented in many ‘real-world’ applications in dynamic environments; examples include domestic robots, such as cleaning and monitoring robots, automatic lawn mowers, inspection robots, painting robots, and industrial robots [1,2,3]. There are generally two types of motion planning approaches for a cleaning robot. These are (according to the behavior of obstacles) off-line (or static) and on-line (or dynamic) motion planning [1,4]. In the case of stationary obstacles, robot routing uses a predefined decision.
Such a use-case motion planning is called offline decision making or static motion planning. When the obstacles are not static (that is, they are moving or dynamic obstacles), motion planning is termed as on-line or dynamic motion planning [1,2,5,6,7,8,9].
In an investigation by František et al. [6], the authors address the identification of obstacles and path coverage. The sampling-based method employs metrics, collision checking, heuristics, post processing and local planning, addressing the situations covered with an optimal path to attempt to prevent robot collisions. In a dynamic environment, research by Duchon et al. [7] has attempted to improve the A* (A-star) algorithms for mobile robot navigation based on a grid map. The research uses heuristics to optimize time, coverage and distance traveled. However, the approach does not address obstacles in a dynamic environment.
Recently, algorithms have been developed using an on-line coverage-based approach, the ‘boustrophedon division’ algorithm, typically the BA* algorithm [9,10,11,12]. The BA* algorithm performs a search using a backtracking mechanism to ensure that all regions are found, and the workspace of the robot is covered completely. In a known environment, the cleaning robot applies to model a graph-based representation, based on the known environmental information; The BA* algorithm then uses the method of graph traversal for coverage path planning. In an unknown environment, the learning robot employs a sensing system to explore and identify the environment [9,10,11,12]. The approach uses modeling, and generates a graph based on the identified environmental information in the coverage path planning.
A major approach is the decomposition of the working environment into smaller, simpler, and non-overlapping areas; the robot covers each small area by a primitive motion, such as the ‘boustrophedon’ (or zig-zag) move. The Spiral-STC algorithm proposed by Gabriely & Rimon [13] divides the map into ‘megacells’, then a spanning tree is generated to connect all ‘megacells’ to provide coverage by following the spanning tree. In multiple tasks, Manuel, et al. have investigated how a robot locally finds the best paths and coverage actions to keep the desired coverage level over the environmental dynamic [5]. The investigation of a robot proposed an on-line coverage algorithm in grid environments, in order to find an optimal way in simulations [13]. In machine learning approaches, some studies have been concerned with K-mean clustering [12], neural networks [14] and genetic algorithms [15] for finding the coverage path of a mobile robot. In monitoring industry robot applications [15,16,17,18,19], these robots applied the approaches of the cluttered environment with limited onboard energy for robot monitoring [15] and cleaning robot in the control for coverage path [16].
These investigations have considered the CPP problem. In this paper, we have addressed two fundamental scientific questions related to mobile robotic systems: (i) how can a robot form a high-level probabilistic representation of an operating space (the environment), and (ii) how can a robot understand and reason about the operating environment. The first issue is related to feature extraction (the obstacles), the second issue can be viewed in terms of special recognition (modeling the operating environment). The paper aims to propose a new approach, which combines robot reasoning (hedge algebra integrated and knowledge reasoning techniques) with the Spiral Spanning Tree Coverage (STC) algorithm for a cleaning and monitoring robot operating in a dynamic environment. This approach is used to apply knowledge inference and hedge algebra with a Spiral STC algorithm to enable autonomous robot control with obstacle avoidance and optimal coverage path planning.
The remainder of this paper is structured as follows: An introduction to the coverage path planning problem is provided in Section 2. Robot reasoning and applied hedge algebra, the process of robot movement, robot sensing in dynamic environments, and the rules with knowledge-based reasoning, are introduced in this section. The proposed model for CPP is presented in Section 3 with the path planning processing algorithm. Evaluation is addressed in Section 4. The experimental results and discussions are proposed in Section 5. Concluding observations and potential future work are given in Section 5 as well.
2. Robot Reasoning Combined with Its Hedge Algebras
2.1. The Robot Coverage Path Planning Problem
CPP for a cleaning robot is the problem of finding a path that the robot needs to follow to pass through all of the points in its working environment. Also, the robot should be able to avoid all obstacles while following the path. CPP can be applied for several types of robot application, which may include: Vacuum cleaning robots, demining robots, inspection robots, painting robots, and lawn mowers. The characteristics and requirements for CPP have been defined in earlier research addressing CPP, and these characteristics and requirements may be summarized as follows:
- The coverage is complete: The robot must travel through all nodes in its working area;
- The overlapping area is minimized: In the ideal case, robot’s trajectory must contain no overlapping between different moves in the same working session. However, when the working area is made up of complicated shapes, overlapping is usually unavoidable to ensure a complete coverage. Also, no part of the trajectory should be repeated;
- The path is viable for a robot: The robot must be able to follow the path in a sequential and continuous manner, based upon simple primitive motions, such as going straight, turning left or right;
- Robots must be able to avoid all of the obstacles that they may encounter during their working session;
- Under the conditions experienced by the robot, achieving the optimal path is expected.
The CPP problem is related to some other well-known planning problems, such as the traveling salesman, cleaning watchmen problems and the art gallery problems. The traveling salesman problem relates to the identification of the shortest path while visiting a set of points (i.e., a salesman must visit a number of cities or neighborhoods within cities). The art gallery problem finds the minimum number of guards, and the placement of these guards in a polygonal gallery, so that the guards can cover the whole area of the gallery. The cleaning watchmen problem focuses on finding the shortest cyclic route in a workplace, so that the watchmen can cover the whole working place area when it follows the path. All of the above problems are known as NP hard.
2.2. Robot Reasoning in Dynamic Environments
2.2.1. Robot Sensing in Dynamic Environments
The robot is equipped with sensors directed on the left side, right side, to the rear, and to the front (i.e., the robot sensing is implemented in four directions). All of the sensors have the same range, and are capable of recognizing a free cell, a cell containing an obstacle, or a cell bounded by a wall (possibly on two sides of a cell). As the robot moves perpendicular to the wall, whenever it meets an obstacle and the wall, both sensors should be ON, and this will notify the robot that there is an irregular obstacle. The robot may not move to any cell if the robot is faced with four obstacles.
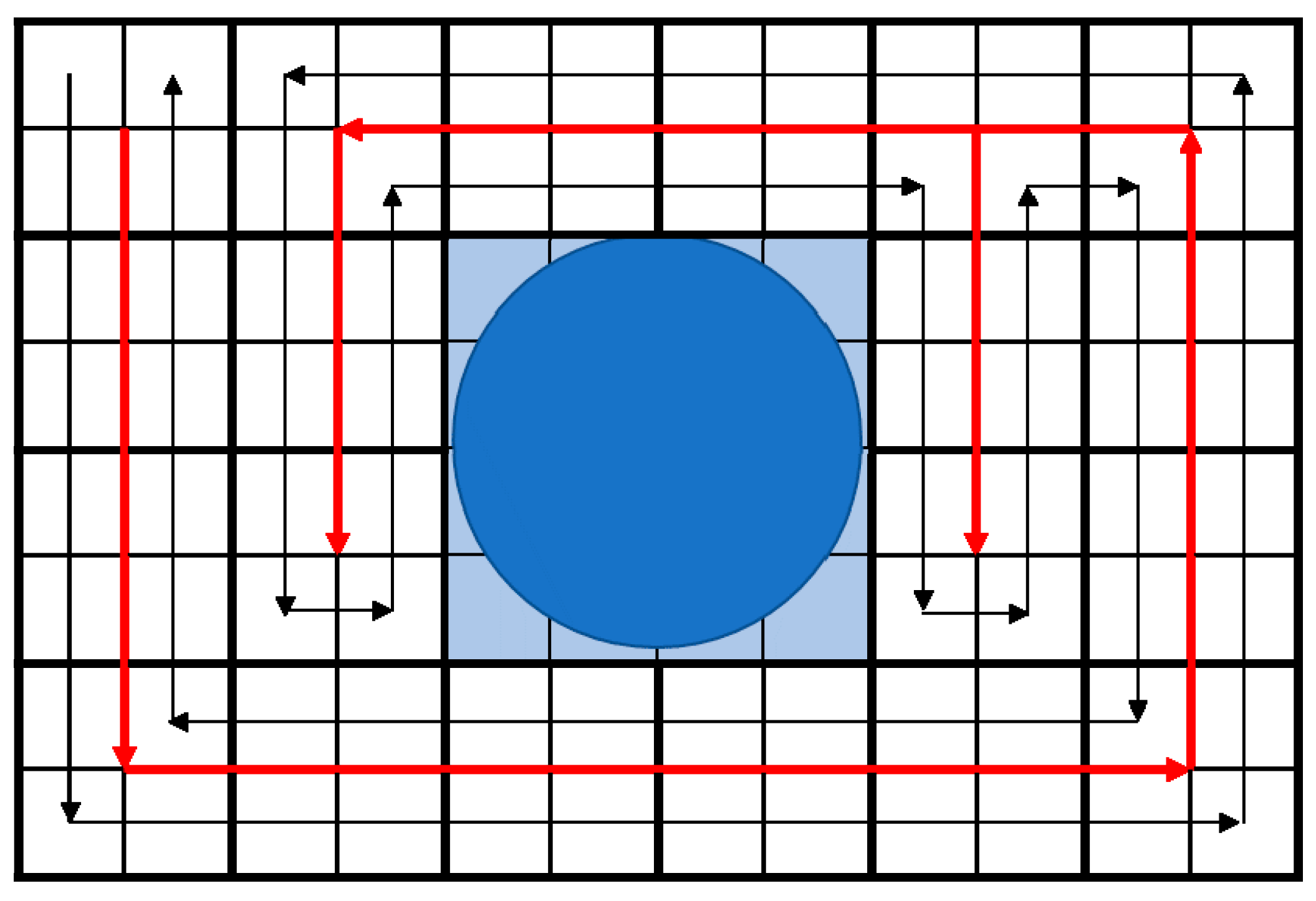
In Figure 1, the obstacle is at the center, and cells marked with blue color are considered part of the obstacle, so a robot will not cover these cells. The starting point is the top left cell. The spanning tree is shown with dark arrows. Furthermore, the expansion of the spanning tree is shown with red arrows. And the actual trajectory of the robot is represented by the thin, black arrows.
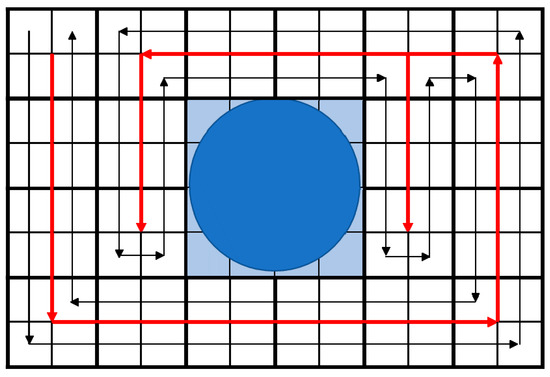
Figure 1.
Coverage Path Planning with Spiral Spanning Tree Coverage (STC).
2.2.2. Applied Hedge Algebra for Robot Sensing in Dynamic Environments
For the robot, camera vision and linguistics are used in robot sensing to realize cognition in the location process; this process can be used to detect results in an optimal robot decision. The fundamental factors related to a location are both the identification of potential paths and the selection of the optimal decision in the range of appropriate alternative options. Additionally, a robot reasoning can be incorporated in linguistic elements and reasoning things to describe robots in coverage path [16], While the robot characteristics of linguistic variables and the meaning of hedges in natural language are used to quantify robot sense. Figure 2 shows a robot sensing in dynamic environments.

Figure 2.
A cleaning robot for using Coverage Path Planning in Big C supermarket.
In real-world applications of Turkey and Vietnam, a robotic vacuum cleaner in Big C in experiments can be applied automatically to clean a variety of areas in the supermarket through a vacuum cleaning in dynamic environments, as shown in Figure 2. The robot avoids obstacles consisting of moving or dynamic obstacles. Robot operation is generally based on a simple obstacle avoidance approach, using infrared sensors, while utilizing laser mapping techniques. These sensors and a range finder camera are embedded to hedge algebra for robot sensing in the dirty cleaning and collision avoidance approach.
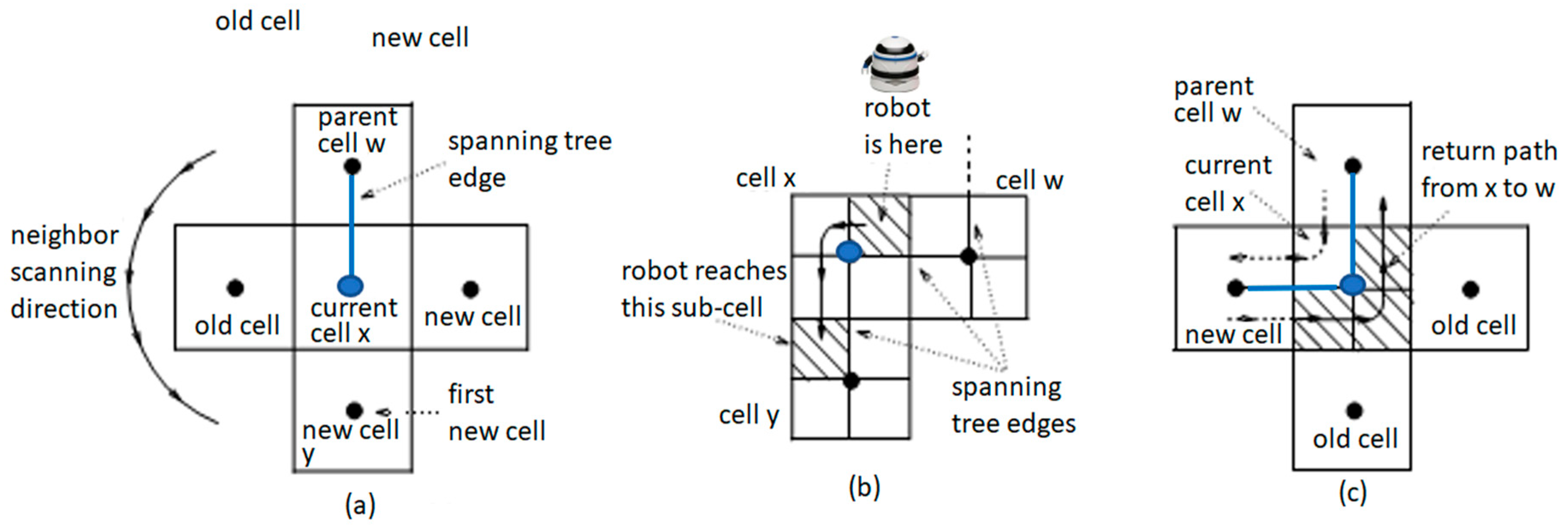
The movement of a robot at the current cell is shown in Figure 3.
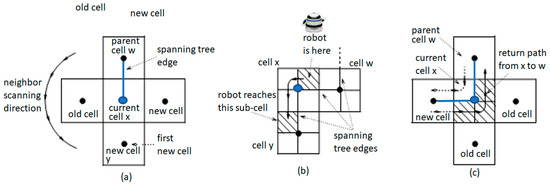
Figure 3.
(a) Counterclockwise scanning of four neighbors. (b) a move from x to a new cell y. (c) a return from x to a parent cell w.
Concept of Hedge Algebra (HA)
(1) Hedge Algebra (HA)
The Hedge Algebra (HA) are defined by formula AX = (X, G, C, H, ), where, G = {c+, c−} represents primary generators, in which c+ and c− are, respectively, represents a linguistic variable in positive X, C = {0, 1, W} is a constant of sets, consisting of elements in X. H which is a set of hedges, “” is semantics in the relation in order on X. For each x X in HA, H(x) is representative of terms u X generated from x by applying the hedges of H and u = hn, …, h1x, with hn, …, h1 H. H = H+ H−, in which H− presents a set of negative hedges, and H+ presents a set of all positive hedges of X. It is assumed that H− = {h−1 < h−2 <, …, < h−q} and H+ = {h1 < h2 <, …, < hp} [15,20].
(2) Definition 1
Transformation of numerical values to linguistic values in the range of value [0,1]. In function is considered as follows:
If and then we have , with in domain of language Ai.
If then we have with is domain of language Ai
(3) Definition 2
Let be a linear algebra with its complete and of a measurement of the opacity . Mapping is called fuzzy based on if it is constructed as inductively with the length x as follows:
- Let : We construct fuzzy space and , with , so that they form a differential range of [0,1], and are derived from the order of the parts and in which we have .
- Assume that fuzzy space with has been constructed with . Let f be a subset of , in which they arise from the sequence between elements in
Let as the opacity of the x, and denote as the fuzzy set of . For being a positive integer, we set .
(4) Relevant Robot Senses Using Hedge Algebra
To set a linguistic variable for a Robot of truth variable SUCCESS, dom(SUCESS) = {successful, fault, very successful, very fault, more successful, more fault, little successful, little fault…}, dom{SUCESS} be presented as an algebra structure AT = (T(X), G, H, ≤) where:
- : the set values linguistic (;
- : a set of elements (;
- : a set hedge (very, more, little);
- : the semantic relation(s) on words (a fuzzy concept). The semantic relations are the order relations obtained from the natural meaning (false ≤ success, more success ≤ very success, very false ≤ more success, possible success ≤ success, little false ≤ false,)
In the example of the cleaning robot, the structure of such algebras can be described in either possibly clean or dirty values T = {clean, dirty, very clean, very dirty, approximately clean, possibly clean, approximately clean or possibly clean, approximately clean and possibly clean, etc.}. It can be expressed by “approximately clean” ∪ “possibly clean”, and it equals to “clean” in the structure of extended hedge algebra of the linguistic truth variable.
2.2.3. Rules Considered by Robot Direction in Knowledge-Based
The rules of robot direction used in the knowledge-based reasoning techniques direct the movement(s) of the robot. Consider the rules applied in reasoning to direct the movement(s) of the robot; the rules are in the form as shown in Rule i:
where and the conditions of Rule i satisfy robot actions . In typical rules, a robot can be considered in the inference combined with events as follows:
- IF (Conditions) THEN (apply the actions with these automated rules)
- ELSE find a new rule in KB.
3. The Proposed Model
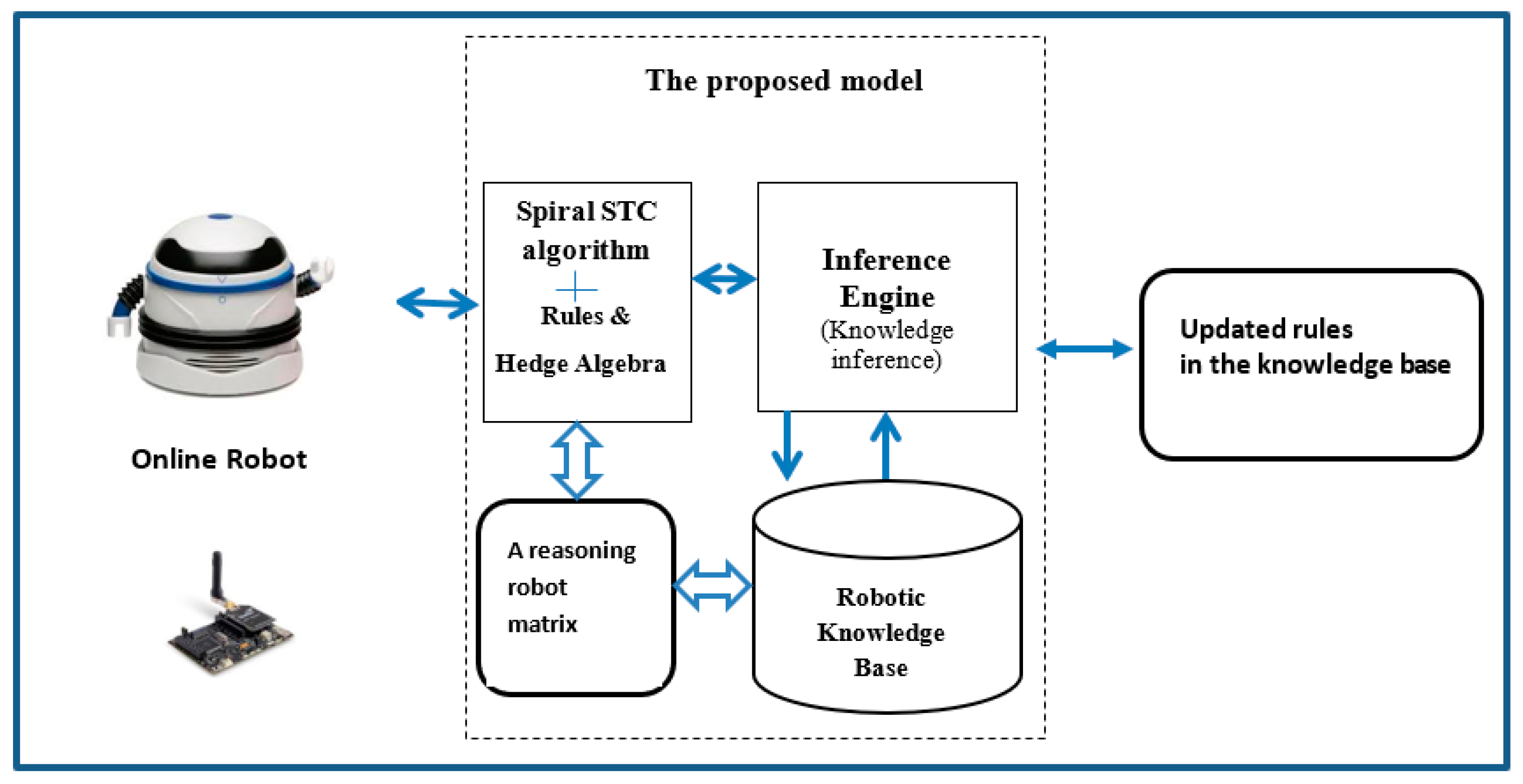
The proposed Hybrid Spiral Spanning Tree Coverage-Hedge Algebras model in Knowledge Reasonings for Robot Coverage Path Planning is designed to achieve improvements to the Spiral STC algorithm, combined with fuzzy rules in order to find optimal CPP areas. To find an optimal path, avoid obstacles, and maximize coverage, a robot can apply its rules in the knowledge base. The proposed model for Robot Coverage Path Planning is as shown in Figure 4.
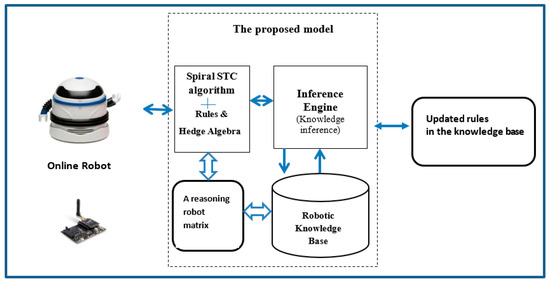
Figure 4.
The proposed model.
In the proposed model, before releasing the robot in the operating space, the rules and the hedge algebra are programmed into the robot in order to quantify the robot sensing and reasoning in CPP problems. The proposed model consists of five steps: Step 1 creates a matrix for robot knowledge reasonings in order to consider a robot direction based on robot stages. All data sets quantified by hedge algebras, together with reasoning techniques. Step 2 considers an average vector from the robot reasoning matrix, in order to find the best directions. To cover all path planning, Step 3 can be applied as the STC algorithm for the optimal robot coverage path. To use the rules in knowledge-base to find an optimal path while avoiding fixed and moving obstacles, the robot applies forward chaining approach with updated rules to the knowledge base. For the similar conditions in the case study of robot simulations and real robot experiments, the robot applies existing rules with good behaviors in reasonings for coverage path planning.
The rules (in the knowledge-base) are created existent rules, and are updated by experts to find the optimal approach for cleaning. The rules are applied as follows: (i) The robot traverses the operating space, visiting all the nodes, (ii) the robot must complete all the nodes in the operating space, such as obstacle(s), bounded walls, without repeating or overlapping paths (i.e., to enable the identification of the optimal coverage path), (iii) the robot must avoid all obstacles (static and moving objects); (iv) the robot will find the ‘optimal path’ including the uncertainties (a dynamic operating space) with its motion trajectories.
The proposed algorithm is described as follows:
Step 1. Create a matrix for robot knowledge reasonings
Let } be a set of robot stages (after a robot visited each node in the path) that is used to show robot directions in its knowledge reasoning, where m is the number of robot stages in an environment T. To consider robot direction in an environment T, its robot stage weight represented by the i-th robot direction of the j-th robot reasoning, considered by the t-th robot case study in the past (quantified historical data sets in the reasoning robot), where n is the number of robot directions. A reasoning robot matrix can be constructed as follows:
Note that an initial robot weight is zero value for a robot matrix. As considering hedge algebras discussed in Section B1, it can be quantified to input the reasoning robot matrix. A robot direction can be used in Step 2 using the robot reasoning matrix.
Step 2. Consider a vector average from the reasoning robot matrix.
For each direction of a robot, n directions of a controlled robot can be represented by the vector as follows:
To calculate the vector, we have a result of the vector as follows:
where ; the output of V* is the average vector of considered robot directions.
Step 3. Apply STC algorithm for optimal robot coverage path by using Procedure STC(w, x) to create a spanning tree coverage
| Procedure. While is a root contained a starting cell, is a main cell. |
|
| End of while. |
|
| End of Procedure |
Step 4. Use the rules in knowledge-base to find an optimal path while avoiding fixed and moving obstacles
| These steps of the proposed algorithm will be completed while the grid lines have been scanned where, |
|
| { |
| Temp = GT; Vet = 0; |
| Obstacle = Loc(Temp,R); |
| while ((Obstacle ≠ 0) and (KL ⊄ GT)) do |
| r ← Get(Obstacle) // r: left → q |
| Vet = Vet ∪ {r}; R = R \ {r}; |
| Temp = Temp ∪ {q}; |
| Obstacle = Loc(Temp, R); |
| end while |
| if (KL ⊂ Temp) then |
| exit(‘ Robot passed the obstacles’); |
| else exit (‘Robot could not be successful’); |
| } |
The output of Step 4 shows an optimal path to the robot, using the rules of forward chaining, while avoiding fixed and moving obstacles.
Step 5. To update and manage the rules in the knowledge base
The rules of a set: where rule is the production rule implemented to enable the robot to avoid obstacles and dead-end paths, and where:
Note: Repeat Step 1 to 4 until the robot visits the coverage path completely.
4. Experimental Result and Evaluation
4.1. Experimental Results
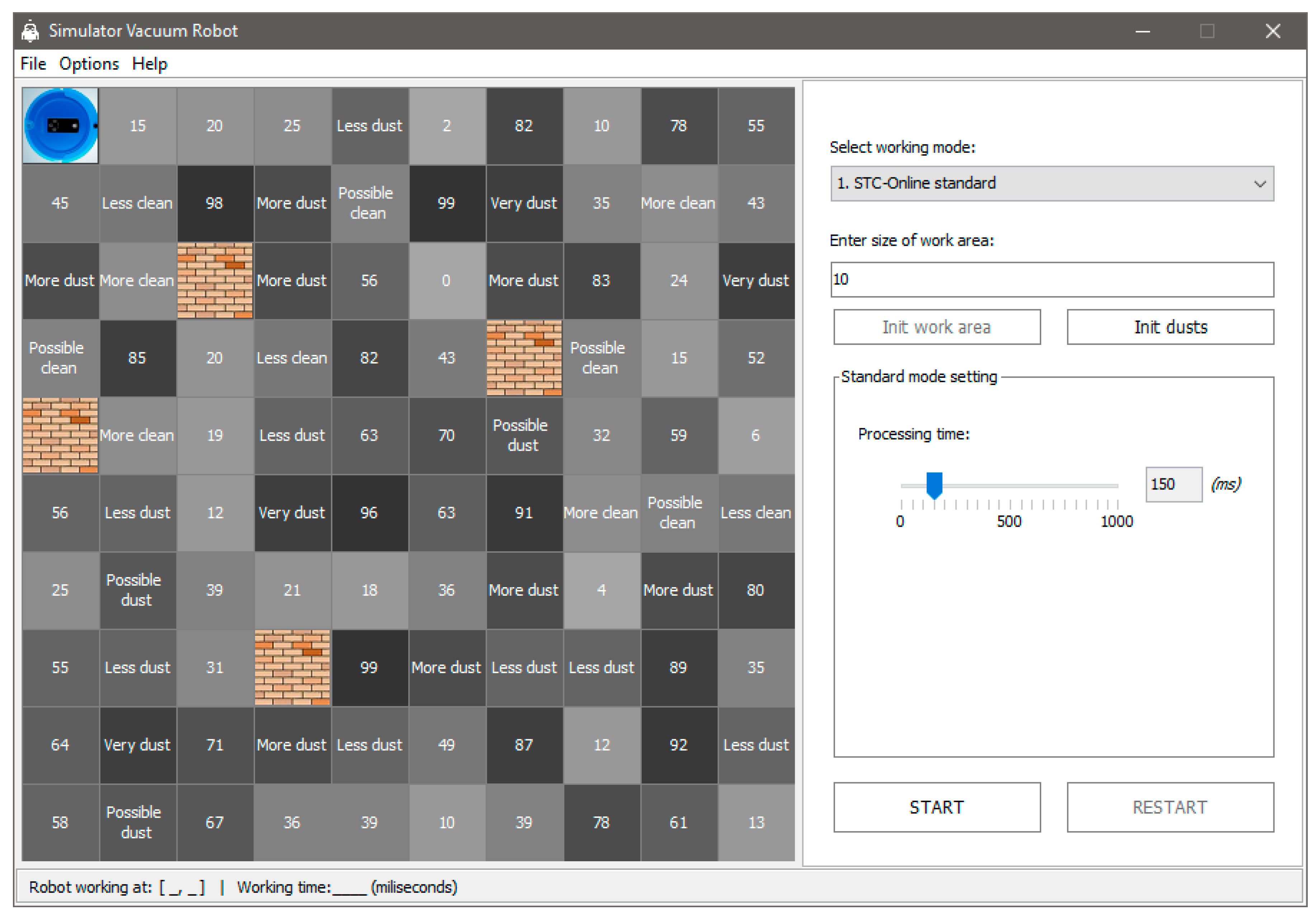
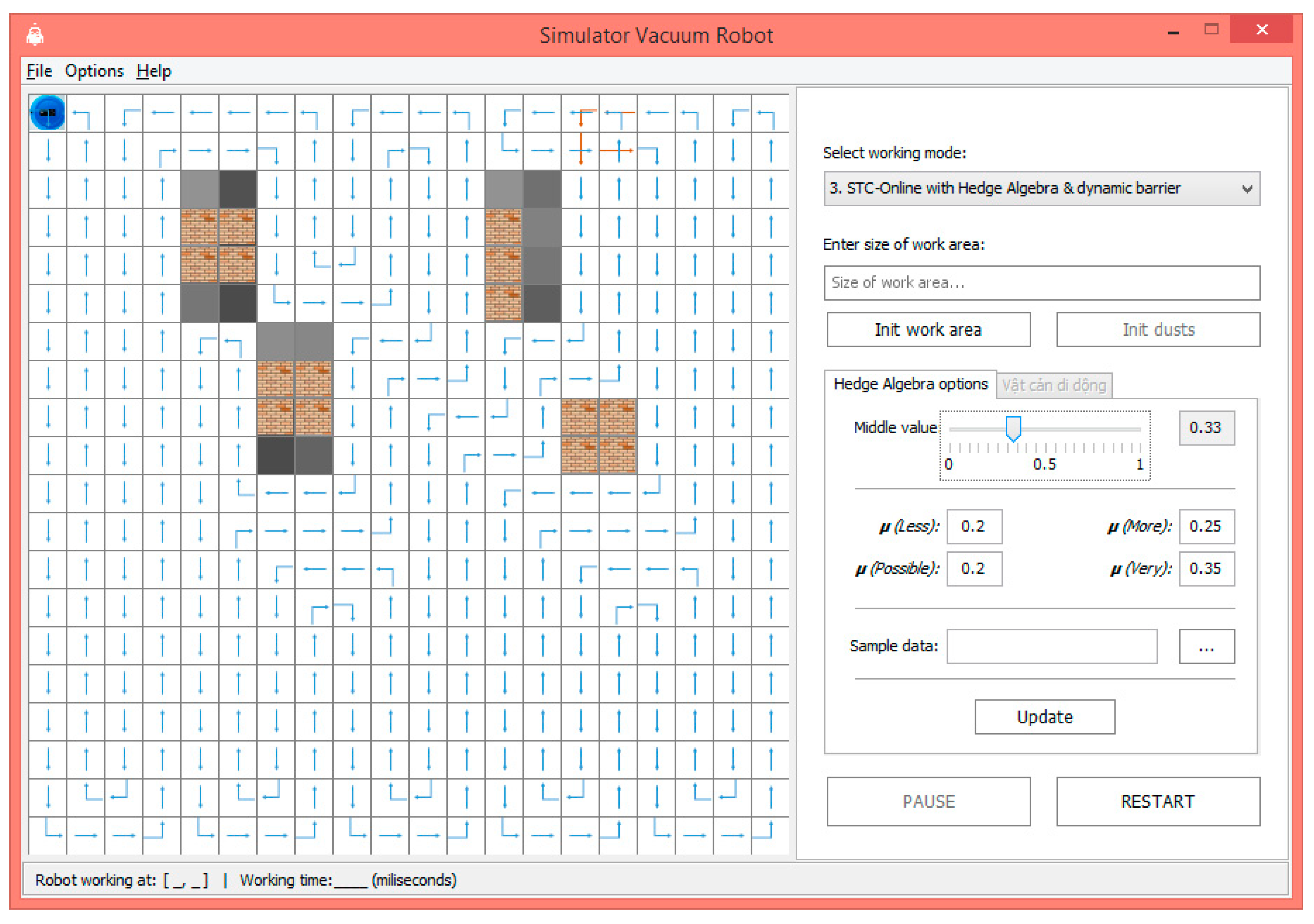
In our experimental evaluation of the proposed model, we have evaluated a number of path planning case studies in both experimental simulation results and real robot. Our proposed model has been applied to the same conditions and mapping in the range of cell numbering nodes (80–450). In simulation results, we can adjust the numbers of nodes that the robot traveled, and the considered rules when a robot faces moving and static obstacles. The interface of the algorithms has been tested in simulations, as shown in Figure 5, Figure 6 and Figure 7. Figure 5 shows the beginning of an experimental interface. Figure 6 shows the robot path visited for the proposed model with static obstacles, where there are no moving obstacles. Figure 7 shows the robot path visited for the proposed model where there are moving obstacles.
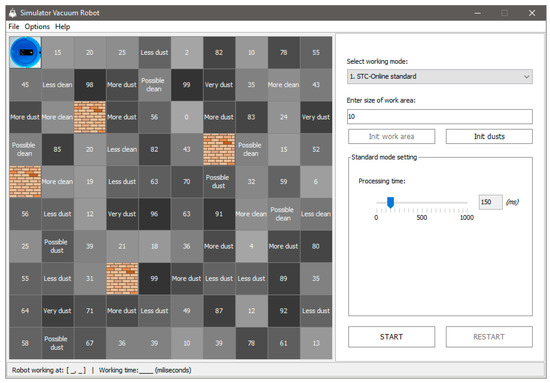
Figure 5.
The interface for the experimental robot setting (the operating environment).
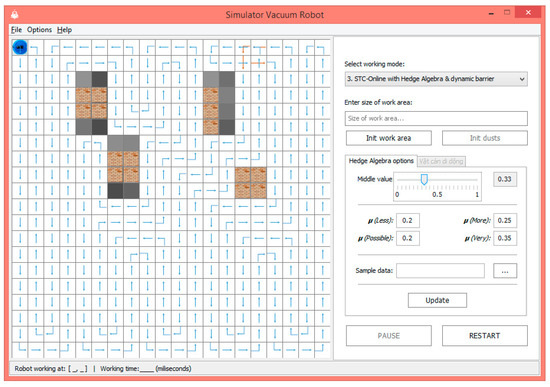
Figure 6.
The proposed model showing the robot path visited with no moving obstacles.
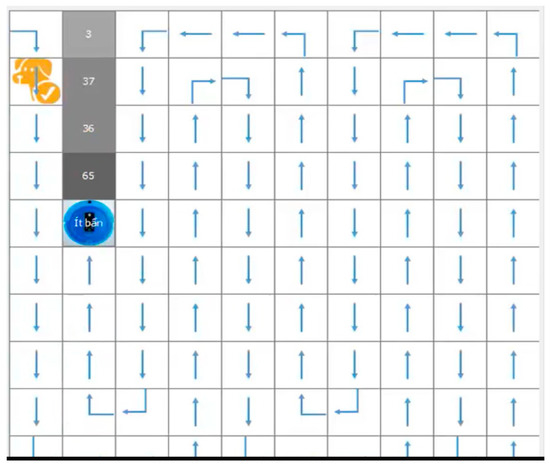
Figure 7.
The proposed model showing the robot path visited with moving obstacles.
4.2. Experimental Results in a Real Case Study of Robot Coverage Path Planning
We have tested the experiments for a cleaning robot which senses a dirty floor. Considering hedge algebras, we have the hedge algebras as follows:
- (1)
- (2)
- (3)
- (4)
- (5)
In vacuum robot senses, the structure of such algebras can be described in either possibly clean or dirty values T = {clean, dirty, very clean, very dirty, approximately clean, possibly clean, approximately clean or possibly clean, approximately clean and possibly clean, etc.}
Let = {, ,…,} be a set of robot stages that use to show robot directions in its knowledge reasoning, where m is the number of robot stages in an environment T, as shown in Table 1.

Table 1.
The robot stages on the importance of degrees using Hedge Algebras.
For each direction of a robot, n directions of a controlled robot can be represented by the vector as follows:
Note that V* is the average vector of considered robot directions.
The rules of a robot are in the form in Rule i as follows:
Table 2 shows a sample of Rule i satisfy robot actions .

Table 2.
Rules present in robot reasonings to find optimal directions.
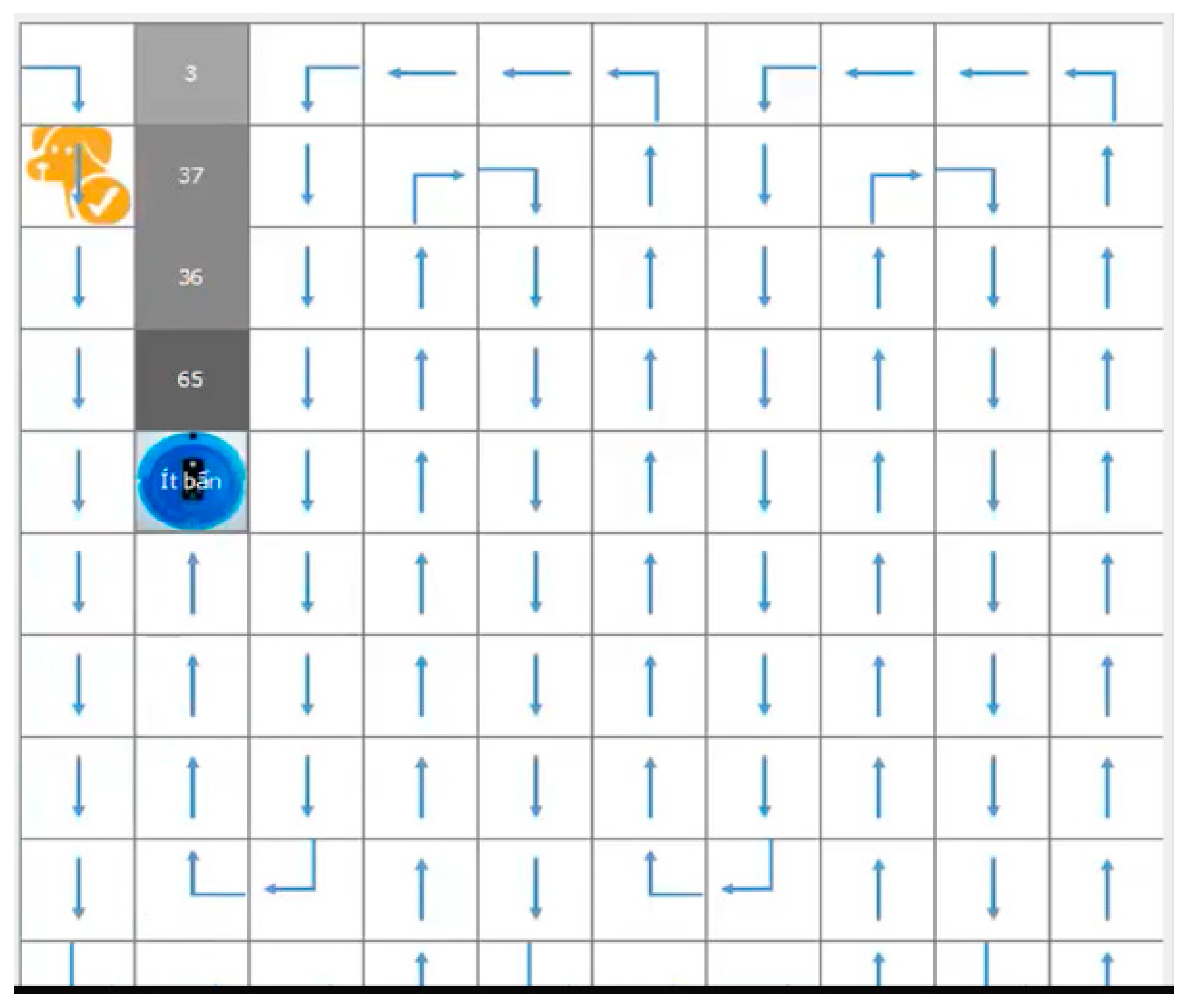
The real robot in experiments successfully completed the pilot tests for controlling the vacuum robot in CIST Robot laboratory under the same conditions and environments, as shown in Figure 8 and Figure 9. We have tested in a case study of a real robot that supports to control the robot which is integrated with its software components of the mechanical device. The robot knows how to clean with its performance in the coverage path. Robot software is embedded to control the autonomous tasks of a robot in its coverage path planning. In dirty floors, the robotic can process automation to allow the robot to achieve significant operational efficiency, using sensors that provide the same range, and are capable of recognizing a free cell, a cell containing an obstacle, or a cell bounded by a wall (possibly on two sides of a cell). As the robot moves perpendicular to the wall, whenever it meets an obstacle and the wall, both sensors should be ON, and this will notify the robot that there is an irregular obstacle. The robot may not move to any cell if the robot is faced with static and moving obstacles.

Figure 8.
A sample of a vacuum robot faced with regular and irregular obstacles.

Figure 9.
A sample of a monitoring robot with multiple directions in regular and irregular obstacles at the CIST Lab.
To consider dirt in the floors, the degree of importance of the function, corresponding to the means of cleaning approaches in Hedge algebras, based on the dirt that is shown in how the robot can start working on the identified and mapped directions, helps the robot to move quickly.
To consider robot directions (moved straightway, left, right, stop, …, etc.), rules considered by experts are obtained from historical data that can be applied in optimal robot path planning. In the case study of experiments, we used 50 rules for considered robots in dynamic environments to avoid complex obstacles.
4.3. Evaluation
To evaluate the overall performance of the proposed model, the performance was compared with the methods such as Mobile robot navigation (MRN) [4], BA*: An Online Complete Coverage Algorithm for Cleaning Robots (BA*) [9] and Complete Coverage Path Planning Algorithms based on A* Algorithms (A*-CPP) [21]. The repetition rate of methods is used to compare the performance of methods. It is indicated that the results in simulations is to consider the robot in traveling overlaps when it has completed a coverage path. Further testing these methods of a robot were evaluated in repetition rate in robot coverage path planning with moving obstacles.
The robot coverage rate percentage can be calculated in Equation (2) [4]:
where
- ▪
- At is the total nodes of the environment
- ▪
- Ao is the total area of the obstacles and Ap is the total area covered by the robot’s path.
4.3.1. A Comparison of the Repetition Rate for Evaluation of the Methods
In testing of robots in dynamic environments, the robot visits multiple-static obstacles in complex situations such as regular, irregular, multiple regular, and multiple irregular obstacles. Note that a regular obstacle can be defined a common object in frequently appeared basic obstacles. The testing experiment was in the range between 80–150 nodes (cells), with the performance of the robot coverage path about 90–100%. In the experimental results, the repetition rate for the proposed approach is lower than those of the MRN, BA* and A*-CPP methods, with respect to simple regular and irregular obstacle environments, as depicted in Table 3.

Table 3.
The repetition rate in experimental result simulations in various environments.
As shown in Table 3, the repetition rate of the proposed model is lower than achieved for the MNR, BA* and A*-CPP methods in regular obstacles, irregular obstacles, multiple obstacles and multiple irregular obstacles.
To do a similar scenario in the simulation experiment, a real robot was applied in the complex obstacles during the coverage path planning process. The complete CPP performance for the methods in terms of the repetition rate in the real robot are as follows: Regular obstacles, irregular obstacles, multiple obstacles, and multiple irregular obstacles, as depicted in Table 4.

Table 4.
Experimental results in a real robot.
As shown in Table 4, experimental results of the real robot show that our proposed model achieves the highest coverage rate with a low repetition rate when compared to the MNR, BA* and A*-CPP methods evaluated. The proposed model has achieved complete coverage of the environmental area (the operational space) with a low repetitive coverage rate.
4.3.2. Comparison of Repetition Rate and Duration in Robot Coverage Path Planning with Moving Obstacles
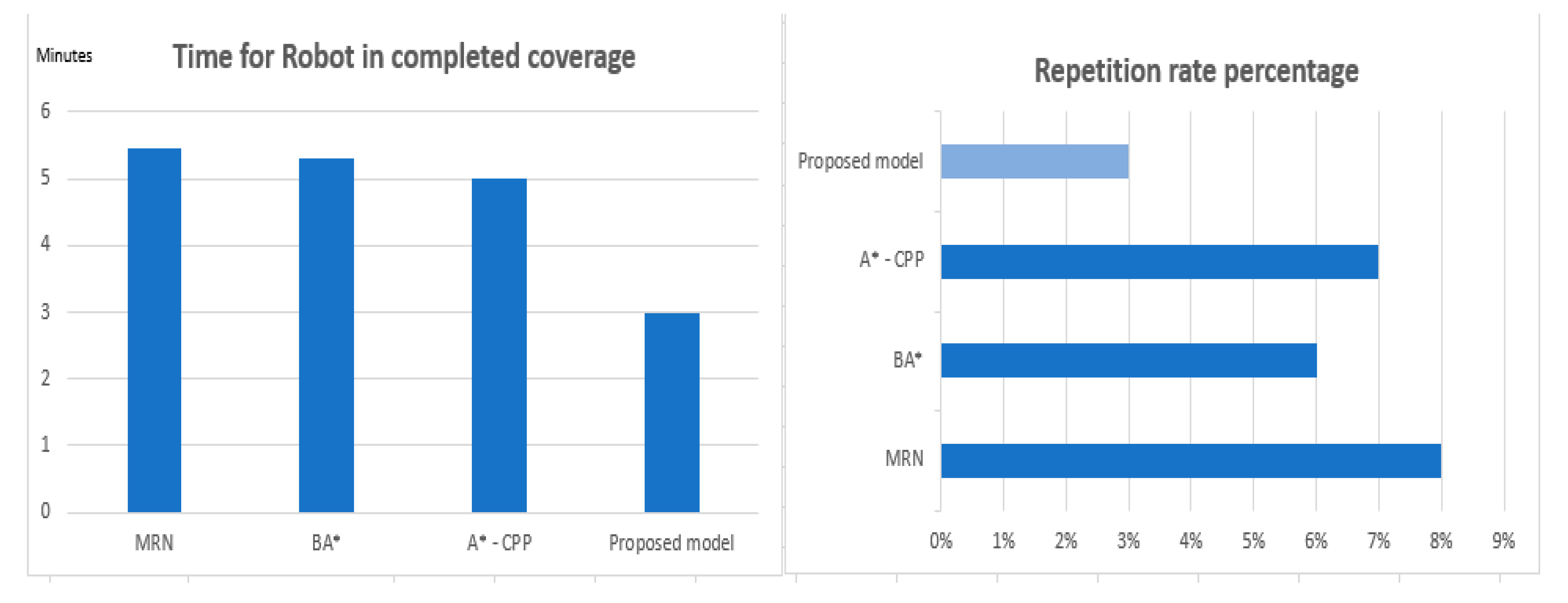
In the experimental testing, we compared the proposed model with the other latest methods considered, these methods were: MNR, BA* and A*-CPP methods. The evaluation compared, when a robot faces with moving obstacles: (i) The duration, awareness, and ability [of the robot] to cover both static and dynamic environments, and (ii) the repetition rate where a robot faces obstacles in uncertain and dynamic operating environments. The tests evaluated in the operating environment with moving obstacles, which are randomly running in simulations. The experiments are done with the numbers of nodes (cells) in the range (200–550), the average results derived from the experiments are shown in Figure 10.
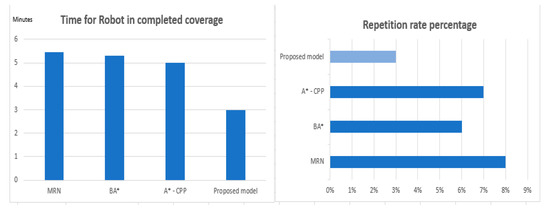
Figure 10.
The duration times and repetition rate for robot visits in dynamic environments.
From Figure 10 it may be seen that in terms of the duration times and repetition rate (for a robot to traverse an operating environment effectively the search space), our proposed model outperforms lower than those of the MNR, BA* and A*-CPP methods.
Further testing simulations for a robot faced with moving obstacles, of these methods in terms of the repetition rate of a robot (100–250 nodes), together with static obstacles are as follows: Regular obstacles, irregular obstacles, multiple obstacles, and multiple irregular obstacles. Table 5 demonstrates the reduction in duration time (in seconds) achieved using our proposed model over the alternative methods for all types of operating environment and obstacle type.

Table 5.
A comparative analysis of the duration time to visit the operational environment.
Table 6 shows that the repetition rate (a robot to traverse an operating environment—effectively the search space) for our proposed model under all operating environments, massively outperforms the alternative methods considered; this is evidenced by the ability of the proposed method to achieve complete coverage of the operational environment with a very low repetitive coverage rate in the range 2% to 7%.

Table 6.
A comparative analysis of the repetition rate in traversing the operational environment.
4.3.3. Result Discussions
The experimental results evaluated in the operating environment with static/moving obstacles which are randomly running in simulations. The experiments of the proposed model are done with the numbers of nodes (cells) in the range of (80–550).
The average results derived from the experiments of the proposed model with the number of nodes in the range of 80 to 200 reaches a 90–100% coverage path rate with static obstacles. When the number of nodes increased from 200 to 550, the robot coverage path rate was about 90–98%. The rules considered in the knowledge base can be influenced with a coverage rate about 100%, however, the repetition rate can be increased. To address the problems, the weights of these rules should be considered to be matching the rules of a robot with its various situations in regular, irregular, multiple regular, and multiple irregular obstacles while running the simulations. In further testing results, a repetition rate of the proposed model in the experiment is about 2% with regular, 4% with irregular, multiple regular, and 7% with multiple irregular obstacles. Knowledge of experts has a significant role of enhancing the rule quality, which updates the knowledge base. It can reduce the repetition rate, while experts update the matched rules in the knowledge base. It is possible to optimize the cover path, repetition rate and running time, mostly based on the rules considered. We can create an objective function to adjust suitable parameters influenced by the robot cover path, repetition rate and running time.
5. Concluding Observations
In this paper, we have presented a new robot control method to enable a cleaning robot to traverse an operating space characterized by both static and dynamic obstacles. The proposed approach has been shown to be capable of moving around static and dynamic operating spaces effectively and efficiently.
In conclusion, our proposed model provides for the shortest duration (operational environment traverse time) with the lowest repetition rate (the duplication of cells within the operational environment). The experimental results indicate that the effectiveness of the proposed model in terms of the repetition and time traveled in uncertain environments (moving obstacles and static obstacles).
Further investigations in the future work extend the rule-based in pattern learning approaches, combined with rules considered from experts to address complex situations in moving obstacles when the robot visits an optimal coverage path.
Author Contributions
Investigation, H.V.P. & F.A.; Literature review, H.V.P., I.K. & N.A.; Methodology, H.V.P. & F.A.; Project administration, I.K. & N.A.; Software & Testing, H.V.P., F.A. & I.K.; Supervision, H.V.P.; and all of the authors wrote the paper.
Funding
This research is funded by the Hanoi University of Science and Technology (HUST) under project number T2018-PC-018.
Acknowledgments
This research is funded by the Hanoi University of Science and Technology (HUST) under project number T2018-PC-018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Zafar, M.N.; Mohanta, J.C. Methodology for Path Planning and Optimization of Mobile Robots: A Review. Procedia Comput. Sci. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Gayathri, R.; Uma, V. Ontology based knowledge representation technique, domain modeling languages and planners for robotic path planning: A survey. ICT Express 2018, 4, 69–74. [Google Scholar]
- Šelek, A.; Seder, M.; Petrović, I. Mobile robot navigation for complete coverage of an environment. IFAC PapersOnLine 2018, 51, 512–517. [Google Scholar] [CrossRef]
- Palacios-Gasós, J.M.; Talebpour, Z.; Montijano, E.; Sagüés, C.; Martinoli, A. Optimal path planning and coverage control for multi-robot persistent coverage in environments with obstacles. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1321–1327. [Google Scholar]
- František, D.; Andrej, B.; Martin, K.; Peter, B.; Martin, F.; Tomáš, F.; Ladislav, J.; Path, P. Modified a Star Algorithm for a Mobile Robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar]
- Vasudevan, S.; Gächter, S.; Nguyen, V.; Siegwart, R. Cognitive maps for mobile robots—An object-based approach. Robot. Auton. Syst. 2007, 55, 359–371. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Cheng, S.; Xie, Y. Double Heuristic Optimization Based on Hierarchical Partitioning for Coverage Path Planning of Robot Mowers. In Proceedings of the 12th International Conference on Computational Intelligence and Security (CIS), Wuxi, China, 16–19 December 2016; pp. 186–189. [Google Scholar]
- Viet, H.H.; Dang, V.H.; Laskar, M.N.U.; Chung, T. BA*: An Online Complete Coverage Algorithm for Cleaning Robots. Appl. Intell. 2013, 39, 217–235. [Google Scholar] [CrossRef]
- Viet, H.H.; An, S.H.; Chung, T. Dyna-Q based Vector Direction for Path Planning Problem of Autonomous Mobile Robots in Unknown Environments. Adv. Robot. 2013, 27, 159–173. [Google Scholar] [CrossRef]
- Viet, H.H.; Choi, S.; Chung, T. Dyna-QUF: Dyna-Q based Univector Field Navigation for Autonomous Mobile Robots in Unknown Environments. J. Central South Univ. 2013, 20, 1178–1188. [Google Scholar] [CrossRef]
- Laskar, M.N.U.; Viet, H.H.; Chung, T. EKF and K-means to Generate Optimized Paths of a Mobile Robot. Int. J. Control Autom. 2013, 6, 53–64. [Google Scholar]
- Gabriely, Y.; Rimon, E. Spiral-stc: An on-line coverage algorithm of grid environments by a mobile robot. In Proceedings of the IEEE International Conference Robotics and Automation ICRA’02, Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 954–960. [Google Scholar]
- Chen, K.; Liu, Y. Optimal complete coverage planning of wall-climbing robot using improved biologically inspired neural network. In Proceedings of the IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 587–592. [Google Scholar]
- Nguyen, C.H.; Tran, T.S.; Pham, D.P. Modeling of a semantics core of linguistic terms based on an extension of hedge algebra semantics and its application. Knowl. Based Syst. 2014, 67, 244–262. [Google Scholar] [CrossRef]
- Prabakaran, V.; Elara, M.R.; Pathmakumar, T.; Nansai, S. Floor cleaning robot with reconfigurable mechanism. Autom. Constr. 2018, 91, 155–165. [Google Scholar] [CrossRef]
- Gomez, J.I.V.; Melchor, M.M.; Lozada, J.C.H. Optimal Coverage Path Planning Based on the Rotating Calipers Algorithm. In Proceedings of the International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Morelos, México, 21–24 November 2017; pp. 140–144. [Google Scholar]
- Bouzid, Y.; Bestaoui, Y.; Siguerdidjane, H. Quadrotor-UAV optimal coverage path planning in cluttered environment with a limited onboard energy. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 979–984. [Google Scholar]
- Yakoubi, M.A.; Laskri, M.T. The path planning of cleaner robot for coverage region using Genetic Algorithms. J. Innov. Digit. Ecosyst. 2016, 3, 37–43. [Google Scholar] [CrossRef]
- Ho, N.C.; van Long, N. Fuzziness measure on complete hedge algebras and quantifying semantics of terms in linear hedge algebras. Fuzzy Sets Syst. 2007, 158, 452–471. [Google Scholar] [CrossRef]
- Cai, Z.; Li, S.; Gan, Y.; Zhang, R.; Zhang, Q. Research on Complete Coverage Path Planning Algorithms based on A* Algorithms. Open Cybern. Syst. J. 2014, 8, 418–426. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).