Electrochemical Characterization and Simulation of Ion Transport in Anion Exchange Membranes for Water Treatment Applications
Abstract
1. Introduction
2. Experimental Methods
2.1. Materials and Reagents
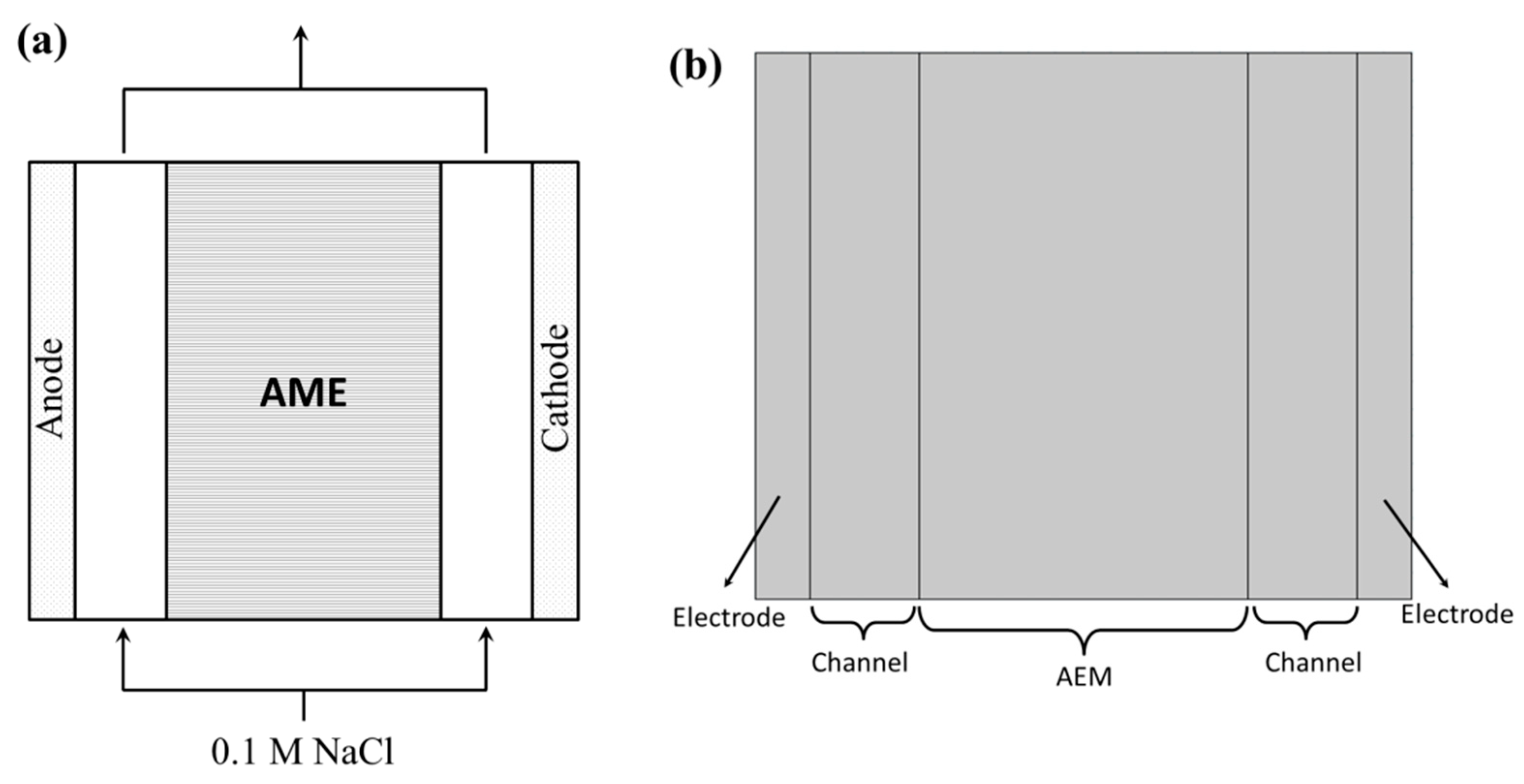
2.2. Apparatus
2.3. Electrochemical Characterization Methods
3. Simulation Methods
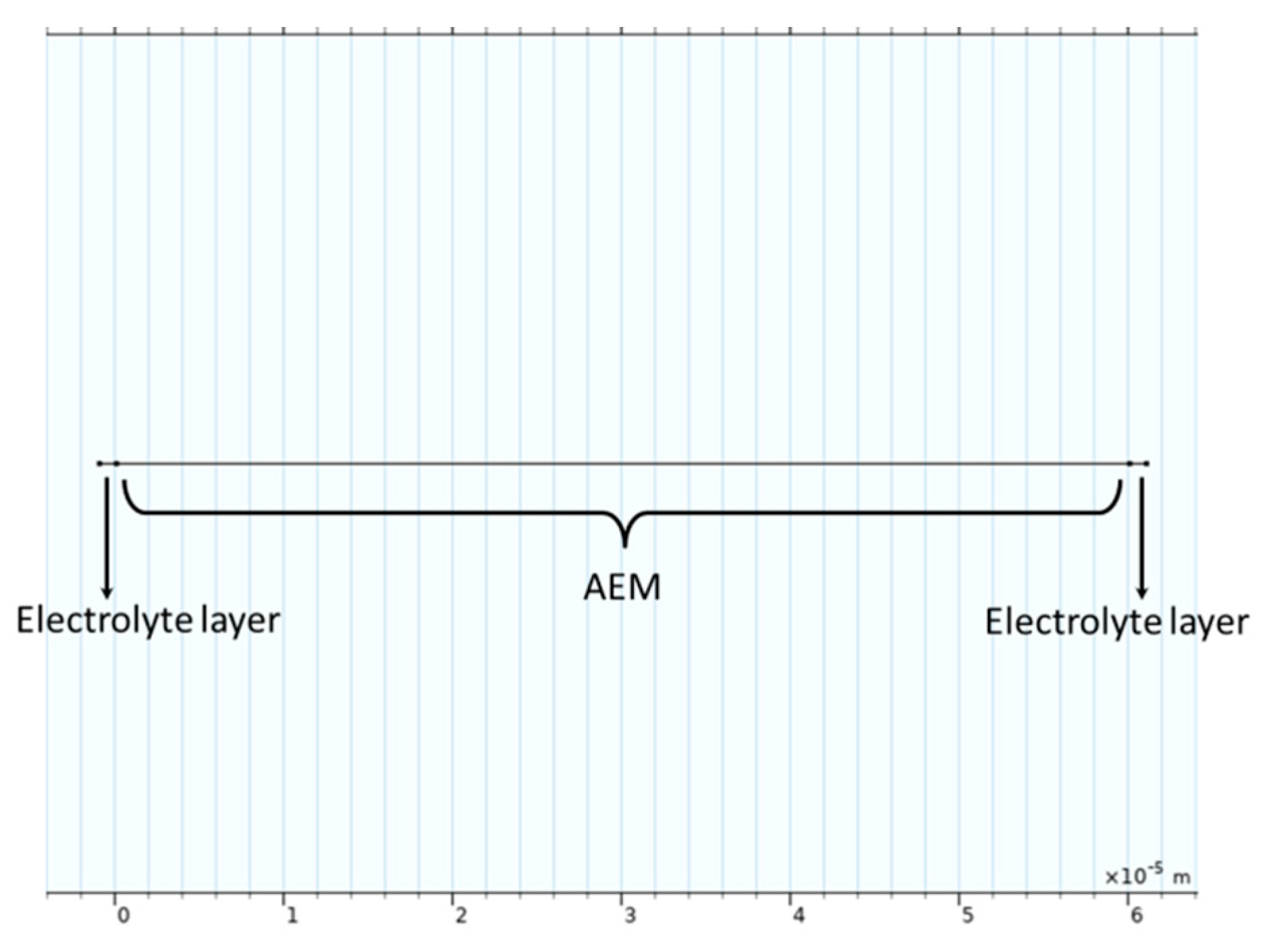
3.1. Modeling Details
3.1.1. Setting Details for Chronopotentiometry and I–V Curve Modeling
3.1.2. Setting Details for EIS Modeling
3.2. Governing Equations
3.3. Boundary Conditions
3.3.1. Boundary Conditions for Chronopotentiometry and I–V Curve Modeling
3.3.2. Boundary Conditions for EIS Modeling
4. Results and Discussion
4.1. Chronopotentiometry Tests and Simulation Results
4.2. Current–Voltage (I–V) Tests and Simulation Results
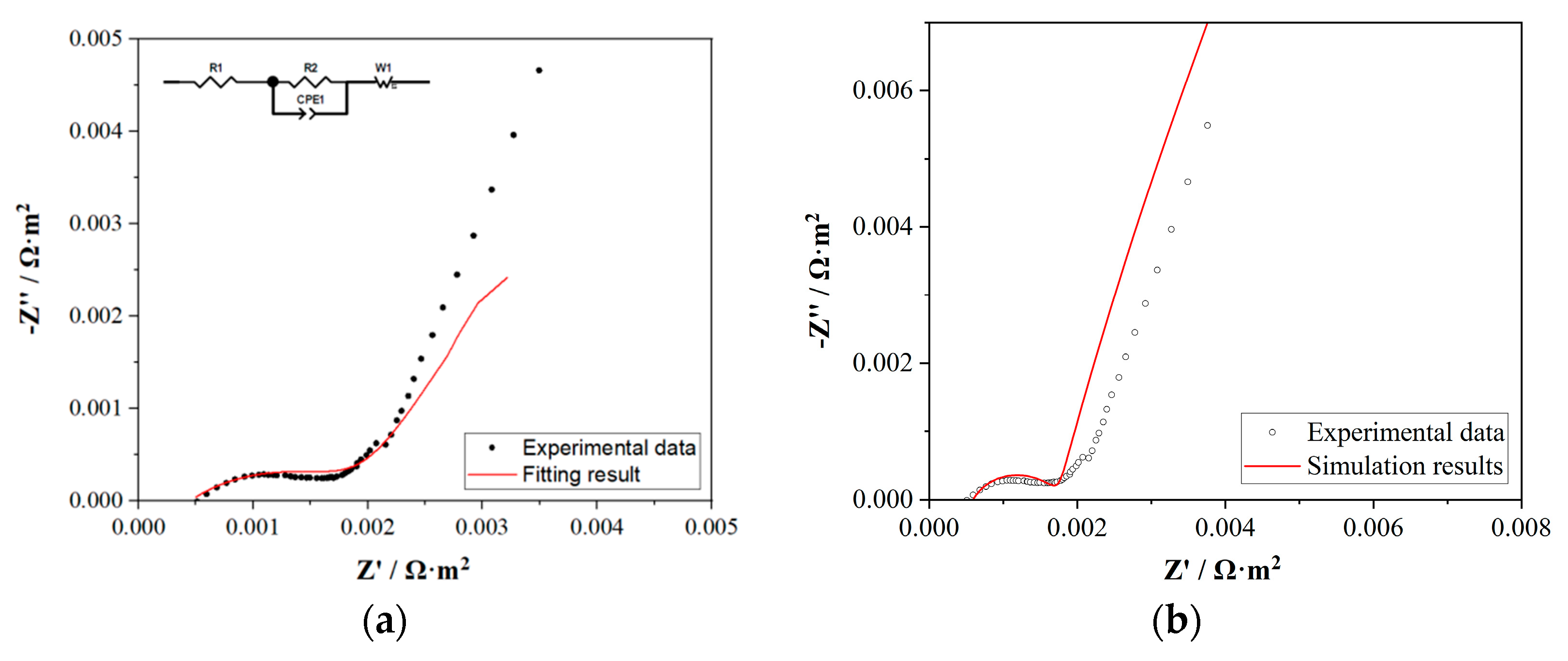
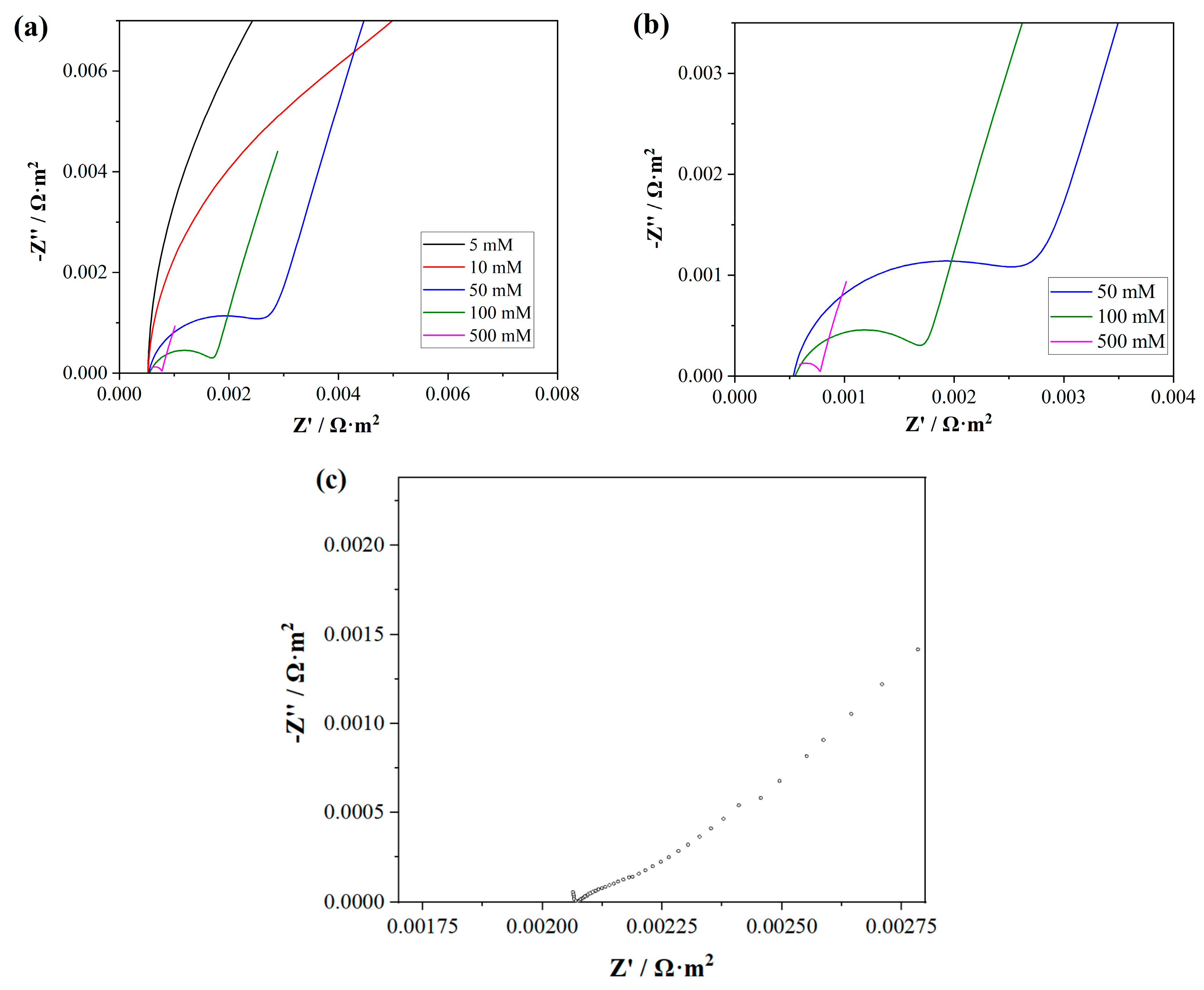
4.3. Electrochemical Impedance Spectroscopy (EIS) Tests and Simulation Results
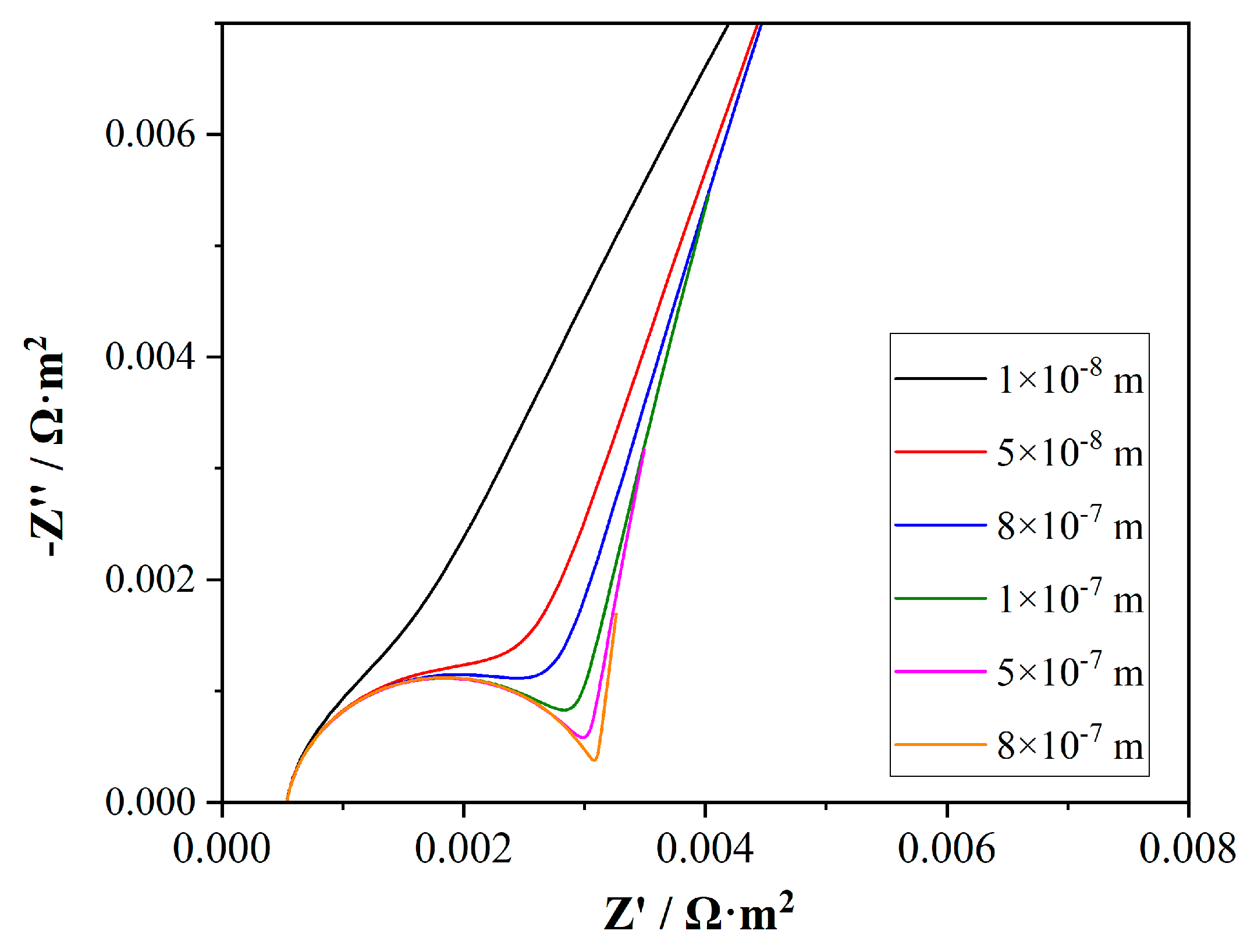
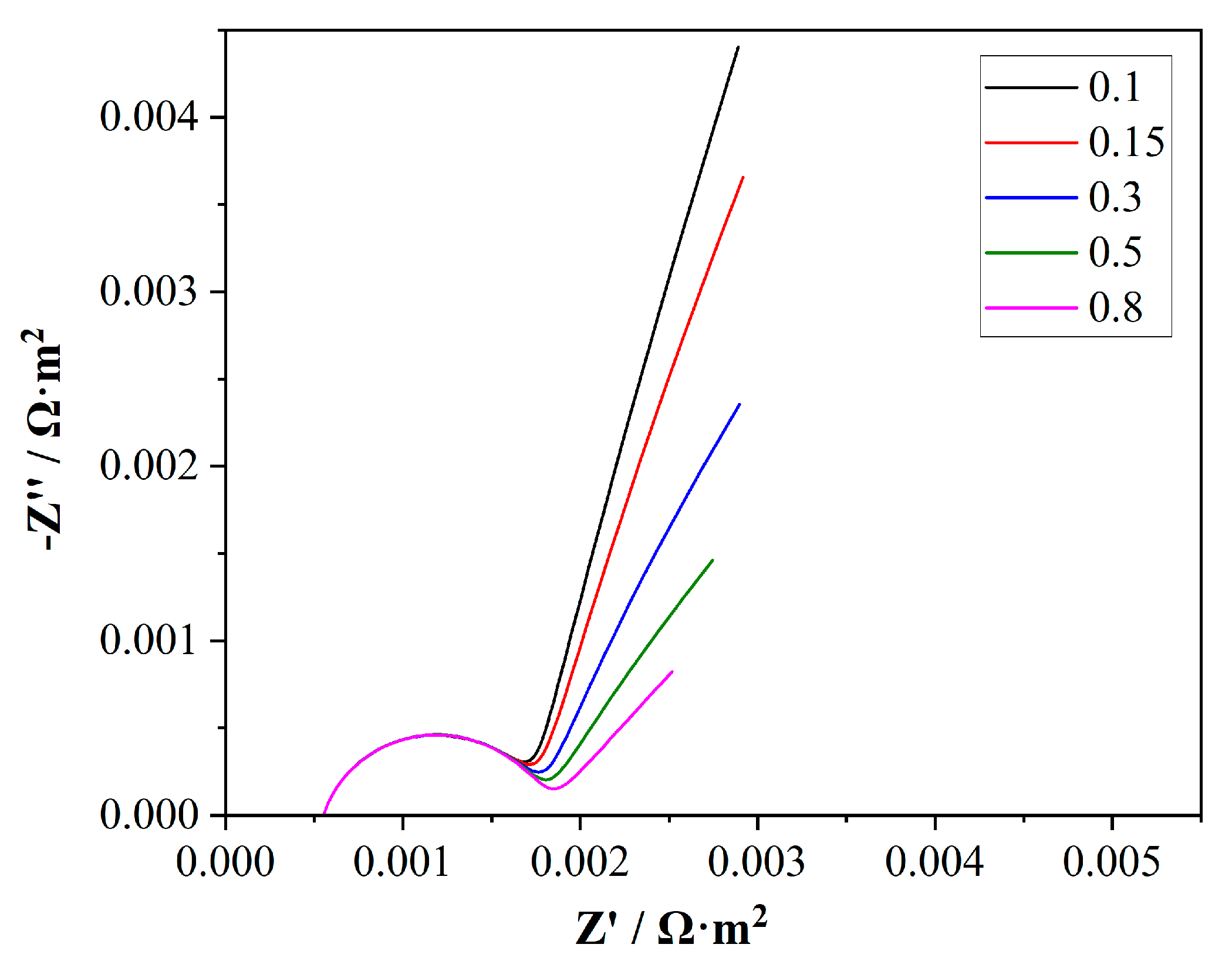
4.4. Effect of Electrolyte Properties on EIS Simulation Results
4.4.1. Effect of Electrolyte Layer Thickness
4.4.2. Effect of Bulk Solution Concentration
4.5. Effect of Membrane Electrolyte Volume Fraction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, T.W. Ion exchange membranes: State of their development and perspective. J. Membr. Sci. 2005, 263, 1–29. [Google Scholar] [CrossRef]
- Liu, L.; Ma, H.Y.; Khan, M.; Hsiao, B.S. Recent Advances and Challenges in Anion Exchange Membranes Development/Application for Water Electrolysis: A Review. Membranes 2024, 14, 85. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Y.; Qin, Z.B.; Deng, Y.D.; Wu, Z.; Hu, W.B. Development and Challenges of Biphasic Membrane-Less Redox Batteries. Adv. Sci. 2022, 9, 2105468. [Google Scholar] [CrossRef] [PubMed]
- Ramaswamy, N.; Mukerjee, S. Alkaline Anion-Exchange Membrane Fuel Cells: Challenges in Electrocatalysis and Interfacial Charge Transfer. Chem. Rev. 2019, 119, 11945–11979. [Google Scholar] [CrossRef]
- Al-Amshawee, S.; Yunus, M.Y.B.; Azoddein, A.A.M.; Hassell, D.G.; Dakhil, I.H.; Abu Hasan, H. Electrodialysis desalination for water and wastewater: A review. Chem. Eng. J. 2020, 380, 122231. [Google Scholar] [CrossRef]
- Zuo, P.P.; Ran, J.; Ye, C.C.; Li, X.Y.; Xu, T.W.; Yang, Z.J. Advancing Ion Selective Membranes with Micropore Ion Channels in the Interaction Confinement Regime. ACS Nano 2024, 18, 6016–6027. [Google Scholar] [CrossRef]
- Alabi, A.; AlHajaj, A.; Cseri, L.; Szekely, G.; Budd, P.; Zou, L.D. Review of nanomaterials-assisted ion exchange membranes for electromembrane desalination. NPJ Clean Water 2018, 1, 10. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Swanckaert, B.; Geltmeyer, J.; Rabaey, K.; De Buysser, K.; Bonin, L.; De Clerck, K. A review on ion-exchange nanofiber membranes: Properties, structure and application in electrochemical (waste)water treatment. Sep. Purif. Technol. 2022, 287, 120529. [Google Scholar] [CrossRef]
- Takagi, R.; Vaselbehagh, M.; Matsuyama, H. Theoretical study of the permselectivity of an anion exchange membrane in electrodialysis. J. Membr. Sci. 2014, 470, 486–493. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Besha, A.T.; Tsehaye, M.T.; Aili, D.; Zhang, W.J.; Tufa, R.A. Design of Monovalent Ion Selective Membranes for Reducing the Impacts of Multivalent Ions in Reverse Electrodialysis. Membranes 2020, 10, 7. [Google Scholar] [CrossRef]
- Kotoka, F.; Merino-Garcia, I.; Velizarov, S. Surface Modifications of Anion Exchange Membranes for an Improved Reverse Electrodialysis Process Performance: A Review. Membranes 2020, 10, 160. [Google Scholar] [CrossRef]
- Ghalloussi, R.; Chaabane, L.; Larchet, C.; Dammak, L.; Grande, D. Structural and physicochemical investigation of ageing of ion-exchange membranes in electrodialysis for food industry. Sep. Purif. Technol. 2014, 123, 229–234. [Google Scholar] [CrossRef]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Ahmed, M. Characterization and applications of ion-exchange membranes and selective ion transport through them: A review. J. Appl. Electrochem. 2023, 53, 1537–1562. [Google Scholar] [CrossRef]
- Barros, K.S.; Martí-Calatayud, M.C.; Scarazzato, T.; Bernardes, A.M.; Espinosa, D.C.R.; Pérez-Herranz, V. Investigation of ion-exchange membranes by means of chronopotentiometry: A comprehensive review on this highly informative and multipurpose technique. Adv. Colloid Interface Sci. 2021, 293, 102439. [Google Scholar] [CrossRef]
- Eniola, J.O.; Kujawa, J.; Nwokoye, A.; Al-Gharabli, S.; Avornyo, A.K.; Giwa, A.; Amusa, H.K.; Yusuf, A.O.; Okolie, J.A. Advances in electrochemical membranes for water treatment: A comprehensive review. Desalin. Water Treat. 2024, 319, 100450. [Google Scholar] [CrossRef]
- Le, X.T.; Viel, P.; Tran, D.P.; Grisotto, F.; Palacin, S. Surface Homogeneity of Anion Exchange Membranes: A Chronopotentiometric Study in the Overlimiting Current Range. J. Phys. Chem. B 2009, 113, 5829–5836. [Google Scholar] [CrossRef]
- Mareev, S.A.; Butylskii, D.Y.; Pismenskaya, N.D.; Nikonenko, V.V. Chronopotentiometry of ion-exchange membranes in the overlimiting current range. Transition time for a finite-length diffusion layer: Modeling and experiment. J. Membr. Sci. 2016, 500, 171–179. [Google Scholar] [CrossRef]
- El Sayed, A.M.; Etoh, B.; Yamauchi, A.; Yang, W.K. Effect of anionic and cationic exchange polymeric layers on current-voltage curves and chronopotentiometry of a charged composite membrane. Desalination 2008, 229, 109–117. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nikonenko, V.V. A numerical experiment approach to modeling impedance: Application to study a Warburg-type spectrum in a membrane system with diffusion coefficients depending on concentration. Electrochim. Acta 2012, 81, 268–274. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kozmai, A.E. Electrical equivalent circuit of an ion-exchange membrane system. Electrochim. Acta 2011, 56, 1262–1269. [Google Scholar] [CrossRef]
- Sang, S.B.; Wu, Q.M.; Huang, K.L. A discussion on ion conductivity at cation exchange membrane/solution interface. Colloids Surf. A Physicochem. Eng. Asp. 2008, 320, 43–48. [Google Scholar] [CrossRef]
- Dunwell, M.; Yan, Y.S.; Xu, B.J. Understanding the influence of the electrochemical double-layer on heterogeneous electrochemical reactions. Curr. Opin. Chem. Eng. 2018, 20, 151–158. [Google Scholar] [CrossRef]
- Ito, M. Structures of water at electrified interfaces: Microscopic understanding of electrode potential in electric double layers on electrode surfaces. Surf. Sci. Rep. 2008, 63, 329–389. [Google Scholar] [CrossRef]
- Zhao, Y.; Duan, L. Research on Measuring Pure Membrane Electrical Resistance under the Effects of Salinity Gradients and Diffusion Boundary Layer and Double Layer Resistances. Membranes 2022, 12, 816. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Paddison, S.J. Perspective: Morphology and ion transport in ion-containing polymers from multiscale modeling and simulations. Front. Chem. 2022, 10, 981508. [Google Scholar] [CrossRef]
- Tu, B.; Chen, M.; Xie, Y.; Zhang, L.; Eisenberg, B.; Lu, B. A parallel finite element simulator for ion transport through three-dimensional ion channel systems. J. Comput. Chem. 2013, 34, 2065–2078. [Google Scholar] [CrossRef]
- Kuldeep; Manzanares, J.A.; Kauranen, P.; Mousavihashemi, S.; Murtomäki, L. Determination of Ionic Diffusion Coefficients in Ion-Exchange Membranes: Strong Electrolytes and Sulfates with Dissociation Equilibria. ChemElectroChem 2022, 9, e202200403. [Google Scholar] [CrossRef]
- Kali, R.; Milner, S.T. Simulations predict salt partitioning in nanostructured ion exchange membranes. J. Membr. Sci. 2024, 697, 122582. [Google Scholar] [CrossRef]
- Moya, A.A. Electrochemical impedance of ion-exchange membranes in asymmetric arrangements. J. Electroanal. Chem. 2011, 660, 153–162. [Google Scholar] [CrossRef]
- Moya, A.A.; Horno, J. Study of the linearity of the voltage-current relationship in ion-exchange membranes using the network simulation method. J. Membr. Sci. 2004, 235, 123–129. [Google Scholar] [CrossRef]
- Available online: https://www.comsol.com/ (accessed on 19 March 2024).
- Niroula, S.; Chaudhary, C.; Subedi, A.; Thapa, B.S. Parametric Modelling and Optimization of Alkaline Electrolyzer for the Production of Green Hydrogen. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1279, 012005. [Google Scholar] [CrossRef]
- Kaya, M.F.; Demir, N. Numerical Investigation of PEM Water Electrolysis Performance for Different Oxygen Evolution Electrocatalysts. Fuel Cells 2017, 17, 37–47. [Google Scholar] [CrossRef]
- Sand, H.J.S., III. On the concentration at the electrodes in a solution, with special reference to the liberation of hydrogen by electrolysis of a mixture of copper sulphate and sulphuric acid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 1, 45–79. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nebavskiy, A.V.; Nichka, V.S.; Urtenov, M.K.; Nikonenko, V.V. The nature of two transition times on chronopotentiograms of heterogeneous ion exchange membranes: 2D modelling. J. Membr. Sci. 2019, 575, 179–190. [Google Scholar] [CrossRef]
- Volodina, E.; Pismenskaya, N.; Nikonenko, V.; Larchet, C.; Pourcelly, G. Ion transfer across ion-exchange membranes with homogeneous and heterogeneous surfaces. J. Colloid Interface Sci. 2005, 285, 247–258. [Google Scholar] [CrossRef]
- Tanaka, Y. Water dissociation reaction generated in an ion exchange membrane. J. Membr. Sci. 2010, 350, 347–360. [Google Scholar] [CrossRef]
- Bellon, T.; Polezhaev, P.; Vobecká, L.; Svoboda, M.; Slouka, Z. Experimental observation of phenomena developing on ion-exchange systems during current-voltage curve measurement. J. Membr. Sci. 2019, 572, 607–618. [Google Scholar] [CrossRef]
- Fu, R.Q.; Xu, T.W.; Yang, W.H.; Pan, Z.X. A new derivation and numerical analysis of current-voltage characteristics for an ion-exchange membrane under limiting current density. Desalination 2005, 173, 143–155. [Google Scholar] [CrossRef]
- Vásquez-Garzón, M.L.; Bonotto, G.; Marder, L.; Ferreira, J.Z.; Bernardes, A.M. Transport properties of tartrate ions through an anion-exchange membrane. Desalination 2010, 263, 118–121. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation-exchange membranes. J. Chem. Soc. Faraday Trans. II 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Nikonenko, V.; Uzdenova, A.; Kovalenko, A.; Urtenov, M. Theoretical Study of the Influence of Electroconvection on the Efficiency of Pulsed Electric Field (PEF) Modes in ED Desalination. Membranes 2024, 14, 225. [Google Scholar] [CrossRef]
- Belashova, E.D.; Melnik, N.A.; Pismenskaya, N.D.; Shevtsova, K.A.; Nebavsky, A.V.; Lebedev, K.A.; Nikonenko, V.V. Overlimiting mass transfer through cation-exchange membranes modified by Nafion film and carbon nanotubes. Electrochim. Acta 2012, 59, 412–423. [Google Scholar] [CrossRef]
- Ahmad, M.; Ahmed, M.; Ali, A.; Wani, T.A.; Khalid, K.; Ali, I. Effect of the polyelectrolyte multilayers’ charge on water splitting, fluxes of ions, selectivities and current efficiencies in ion transport through membranes. Desalination 2024, 587, 117925. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, J.; Wang, P.; Wang, Z.; Shi, F.; Liu, H. Investigations on the interfacial capacitance and the diffusion boundary layer thickness of ion exchange membrane using electrochemical impedance spectroscopy. J. Membr. Sci. 2016, 502, 37–47. [Google Scholar] [CrossRef]
- Giner-Sanz, J.J.; Ortega, E.M.; Pérez-Herranz, V. Mechanistic equivalent circuit modelling of a commercial polymer electrolyte membrane fuel cell. J. Power Sources 2018, 379, 328–337. [Google Scholar] [CrossRef]
- Park, J.-S.; Choi, J.-H.; Woo, J.-J.; Moon, S.-H. An electrical impedance spectroscopic (EIS) study on transport characteristics of ion-exchange membrane systems. J. Colloid Interface Sci. 2006, 300, 655–662. [Google Scholar] [CrossRef]
- Moya, A.A. Low-frequency development approximations to the transmissive Warburg diffusion impedance. J. Energy Storage 2022, 55, 105632. [Google Scholar] [CrossRef]



| Technical Specifications | Units | Value |
|---|---|---|
| Ion Exchange Capacity | mmol·g−1 | 0.90–1.10 |
| Thickness (Wet) | μm | 60–80 |
| Water Content (25 °C) | wt % | 20–25 |
| Membrane Resistance | Ω·cm2 | 4.5–5.5 |
| Translation Number | - | ≥0.98 |
| Stability | pH | 1–14 |
| Parameters | Value | Description |
|---|---|---|
| Da | 1 × 10−9 m2/s | Diffusion coefficient of anion |
| Dc | 1 × 10−11 m2/s | Diffusion coefficient of cation |
| c_bulk | 100 mol/m3 | Bulk concentration |
| Cdl | 0.1 F/m2 | Double-layer interfacial capacitance |
| i0ref | 964.85 A/m2 | Reference exchange current density |
| freq_min | 1 Hz | Minimum frequency |
| freq_max | 10,000 Hz | Maximum frequency |
| L_m | 6 × 10−5 m | Membrane length |
| A_el | 1 × 10−4 m2 | Electrode area |
| V_app | 0.005 V | Applied perturbation potential |
| ε | 0.15 | Electrolyte volume fraction in membrane |
| L_s | 1 × 10−7 m | Electrolyte layer (space between membrane and electrode) length |
| Element | Value | Error (%) |
|---|---|---|
| R1 (Ω) | 4.476 | 0.10 |
| R2 (Ω) | 10.76 | 10.33 |
| CPE1-T (F) | 0.00019018 | 4.91 |
| CPE1-P | 0.49158 | 5.47 |
| W1-R (Ω) | 10.91 | 9.17 |
| W1-T (F) | 0.0064176 | 19.87 |
| W1-P | 0.40078 | 19.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, Q.; Liu, Y.; Guo, G.; Zhang, Y. Electrochemical Characterization and Simulation of Ion Transport in Anion Exchange Membranes for Water Treatment Applications. Membranes 2025, 15, 123. https://doi.org/10.3390/membranes15040123
Lang Q, Liu Y, Guo G, Zhang Y. Electrochemical Characterization and Simulation of Ion Transport in Anion Exchange Membranes for Water Treatment Applications. Membranes. 2025; 15(4):123. https://doi.org/10.3390/membranes15040123
Chicago/Turabian StyleLang, Qiaolin, Yang Liu, Gaojuan Guo, and Yang Zhang. 2025. "Electrochemical Characterization and Simulation of Ion Transport in Anion Exchange Membranes for Water Treatment Applications" Membranes 15, no. 4: 123. https://doi.org/10.3390/membranes15040123
APA StyleLang, Q., Liu, Y., Guo, G., & Zhang, Y. (2025). Electrochemical Characterization and Simulation of Ion Transport in Anion Exchange Membranes for Water Treatment Applications. Membranes, 15(4), 123. https://doi.org/10.3390/membranes15040123







