A Sensitivity Analysis of the SPACSYS Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Parameters and Simulated Outputs
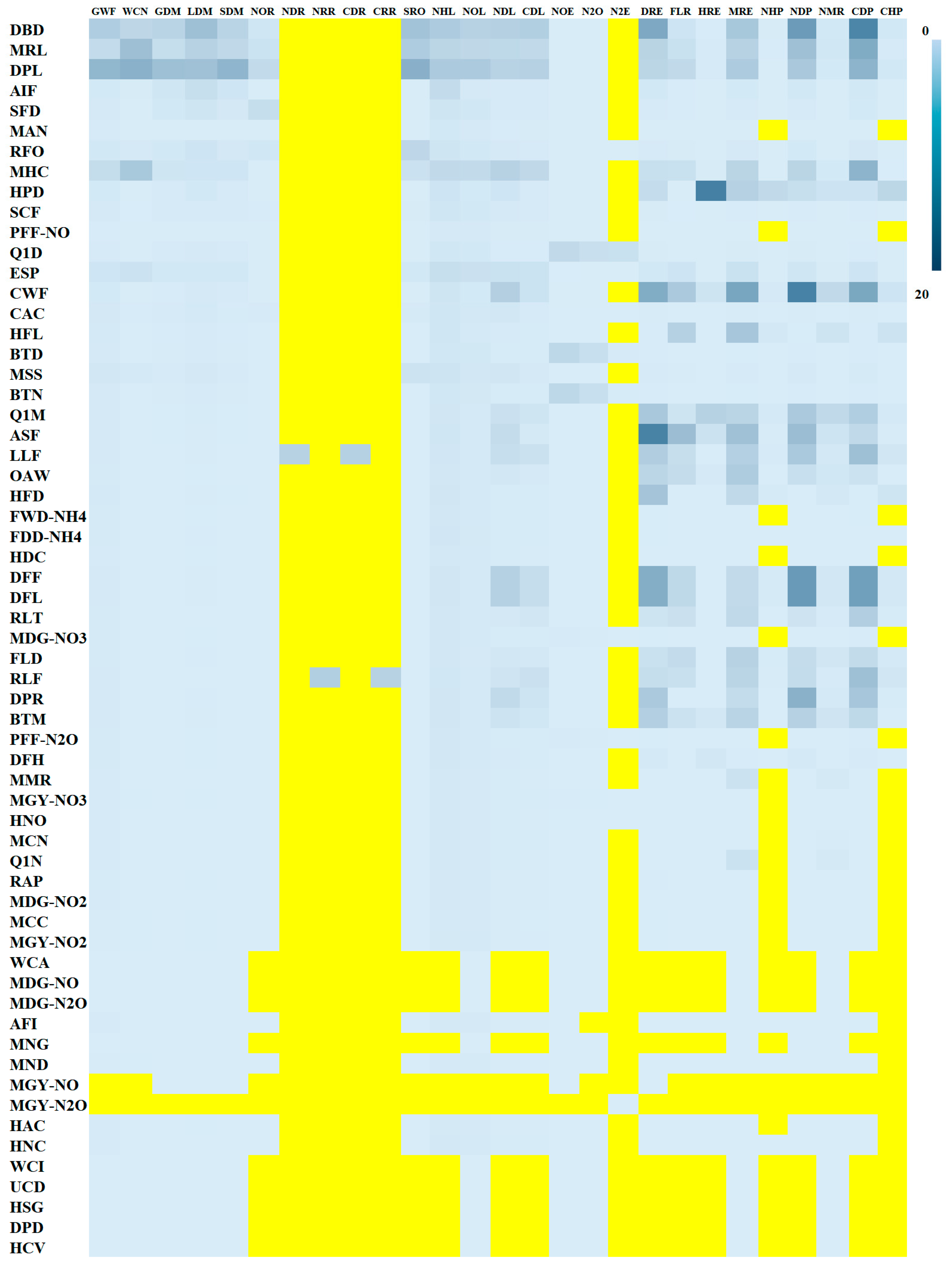
2.3. Sensitivity Analysis and Diagnostics
2.4. Simulated Climate and Soil Data
3. Results
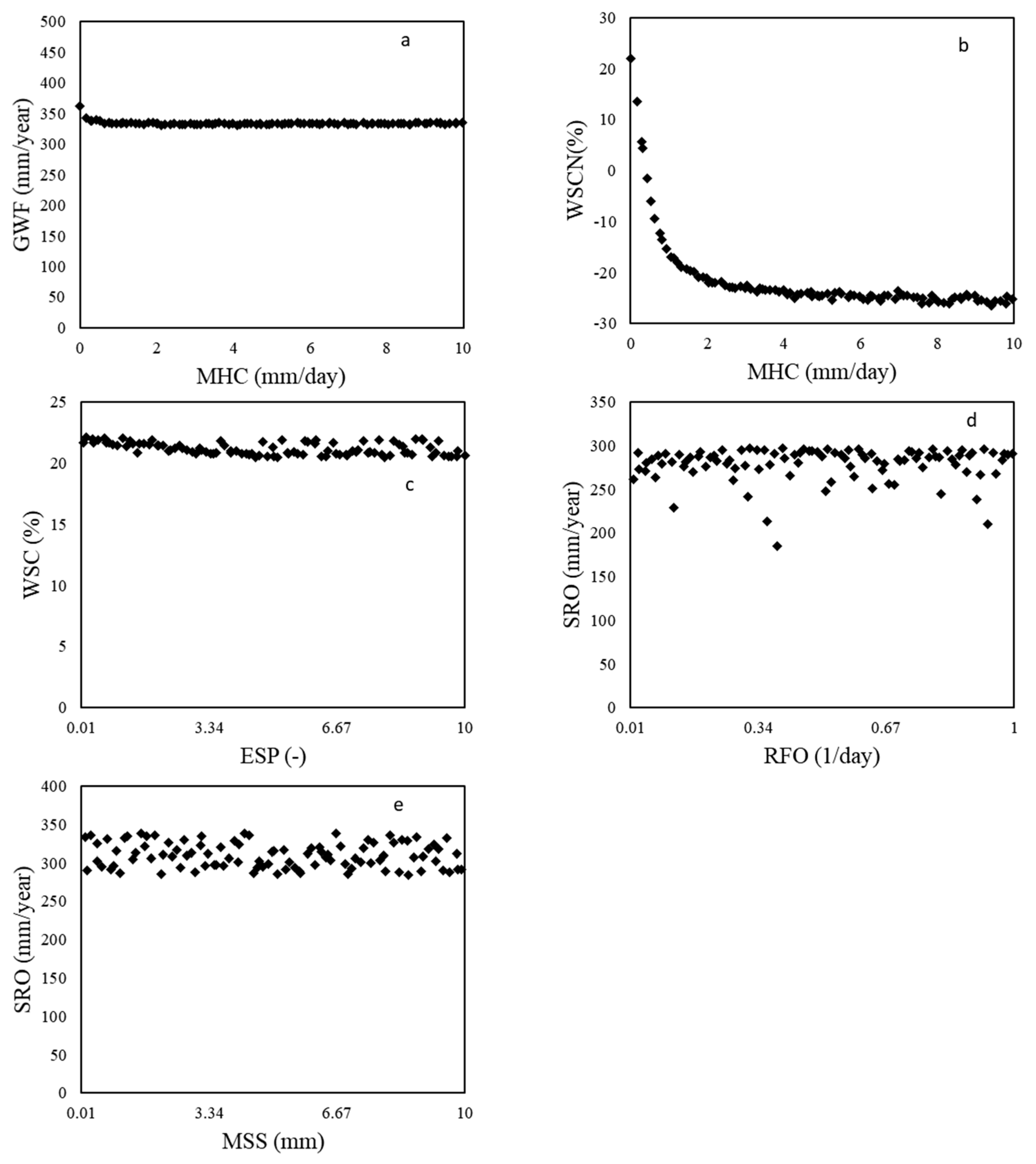
3.1. Soil Water Dynamics
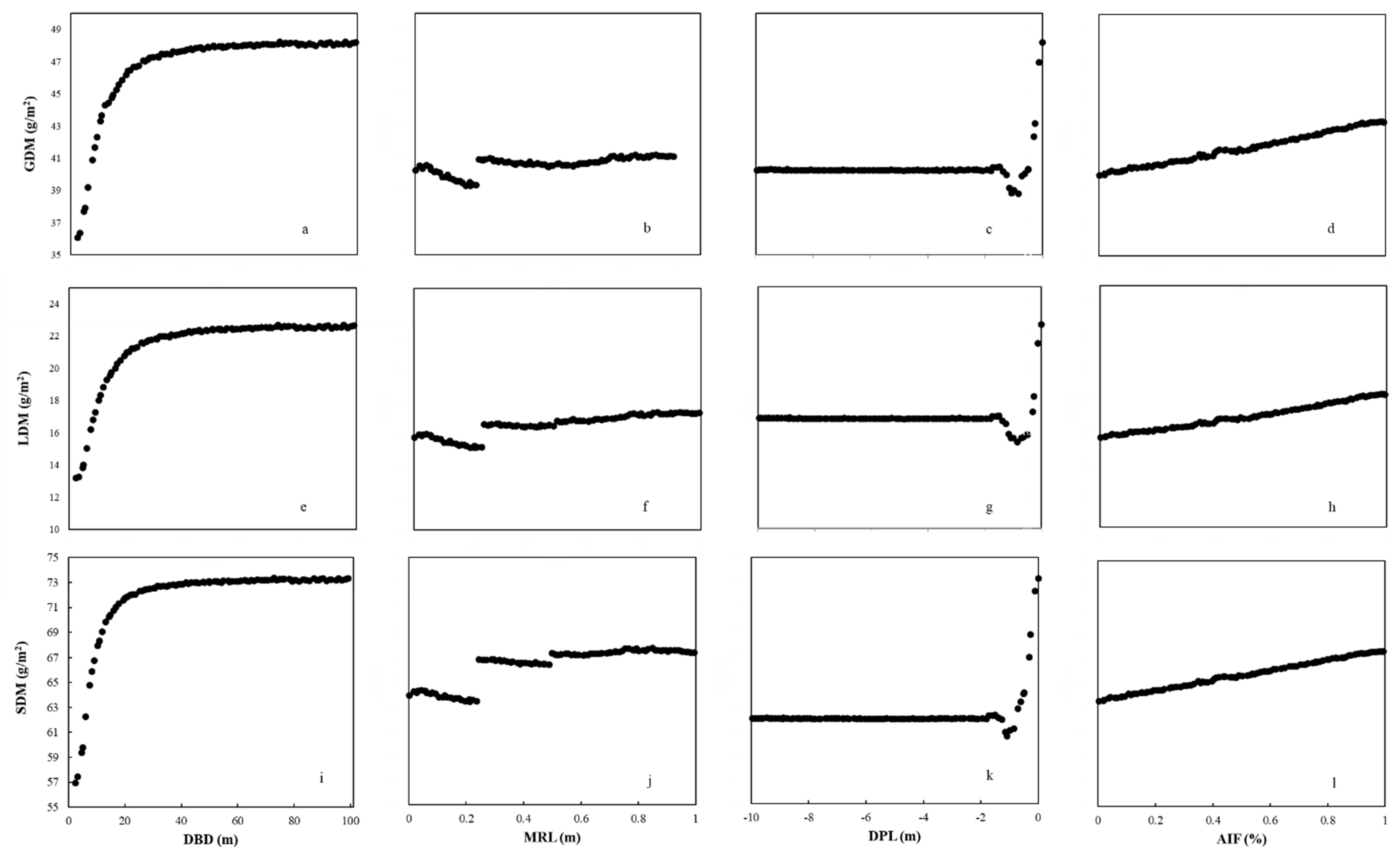
3.2. Dry Matter of Winter Wheat
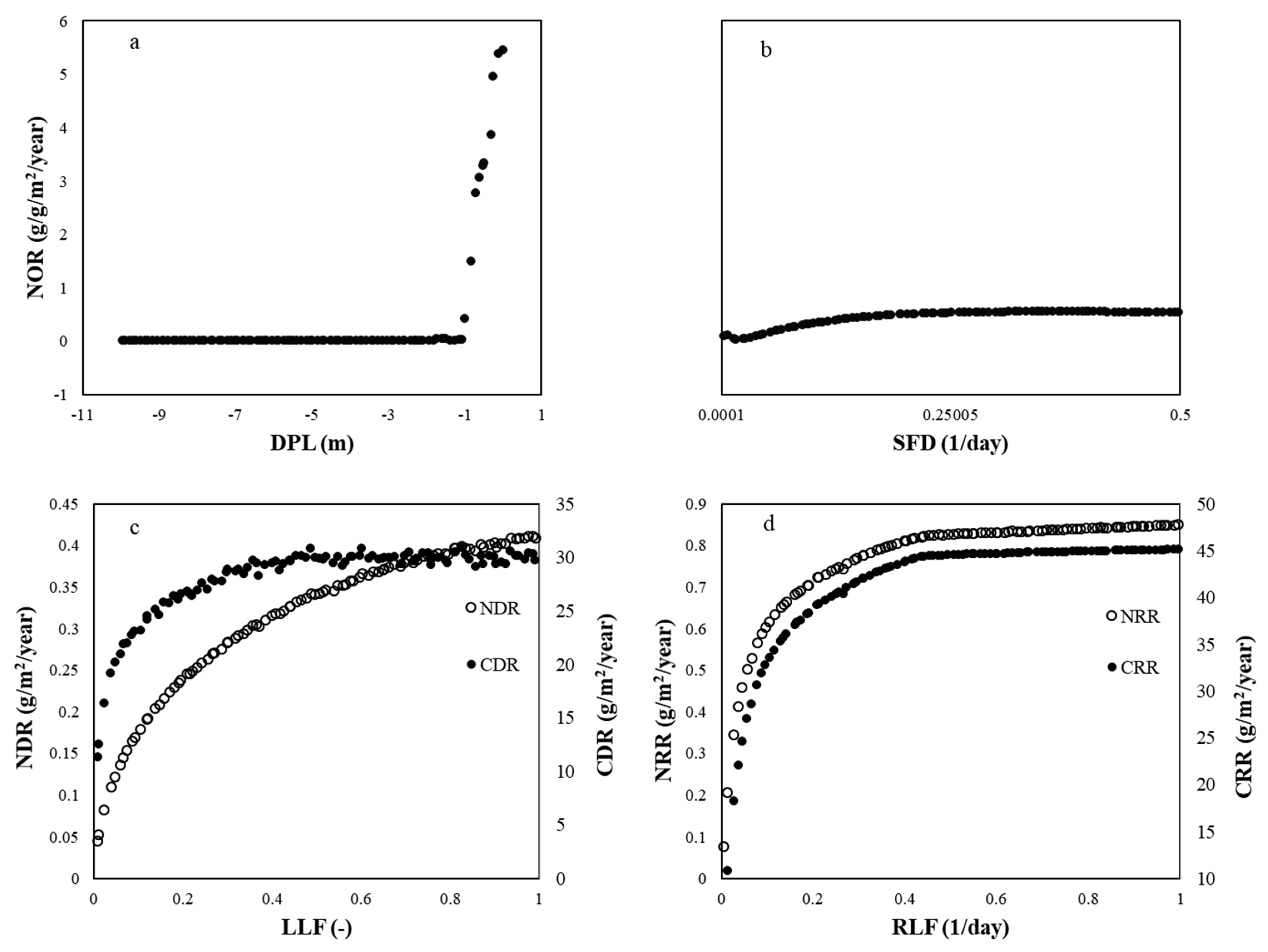
3.3. Nitrogen and Carbon Losses from Soil
3.3.1. Losses with Surface Runoff
3.3.2. Nitrogen and Carbon Leaching
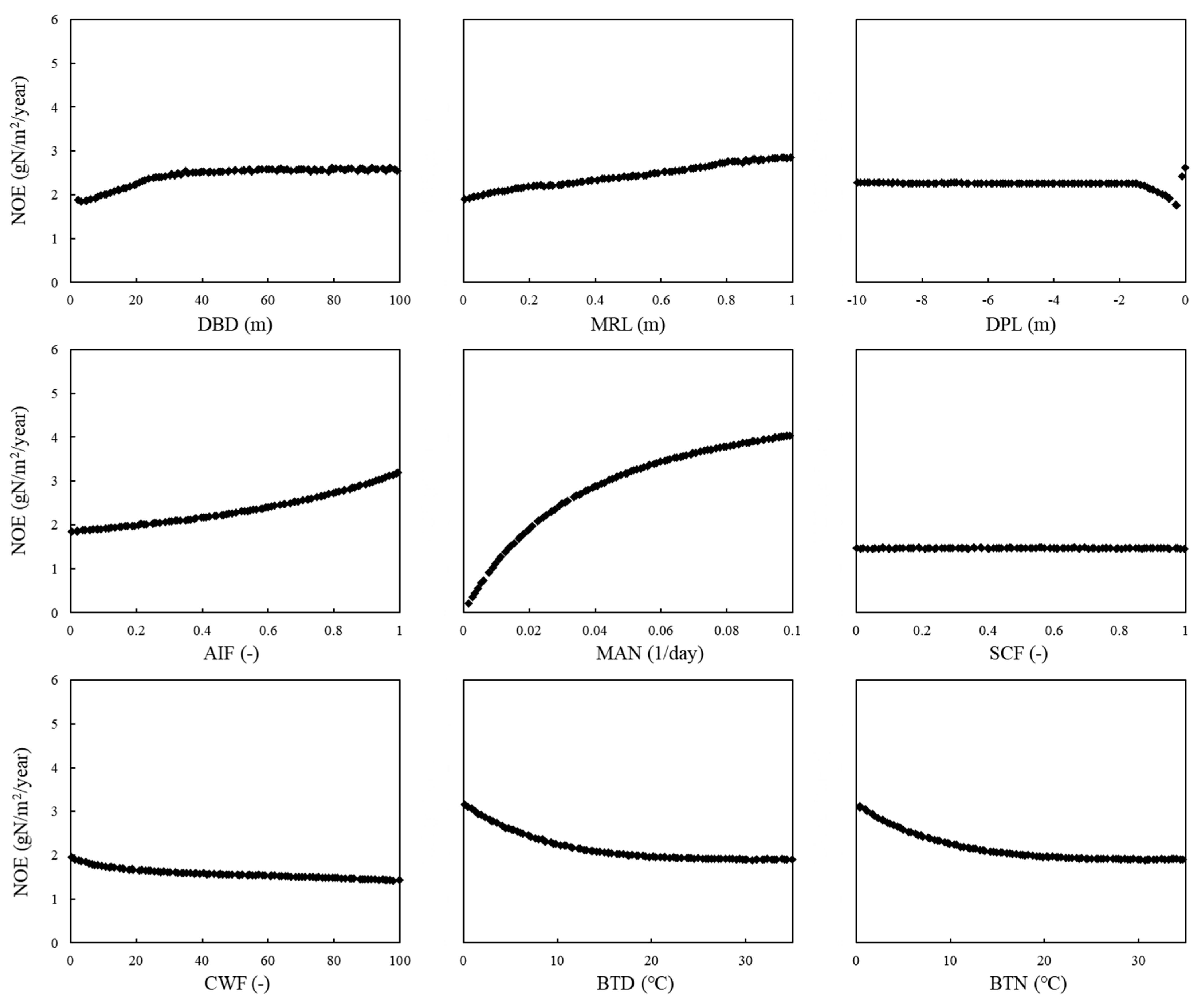
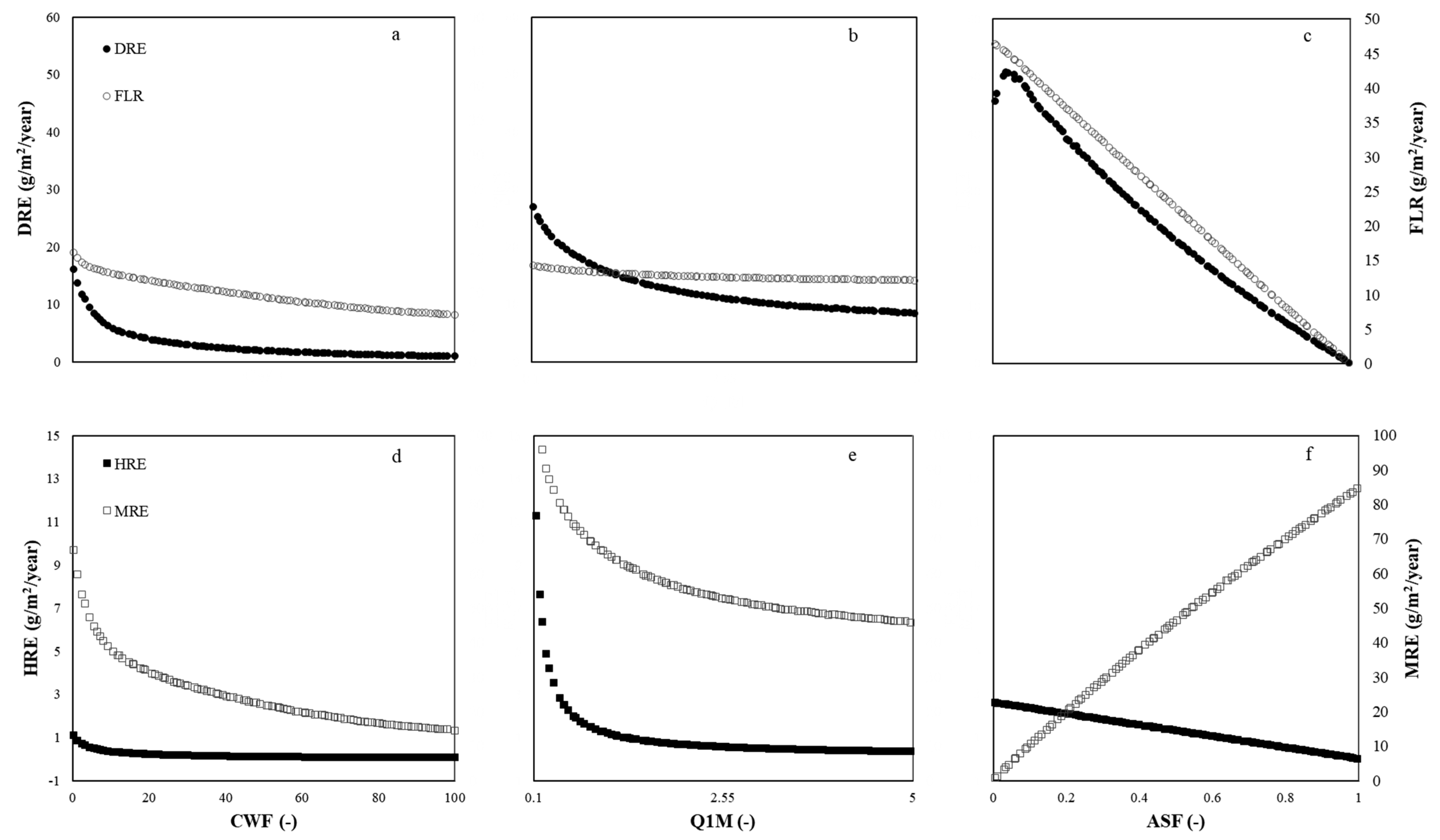
3.3.3. Gas Emissions
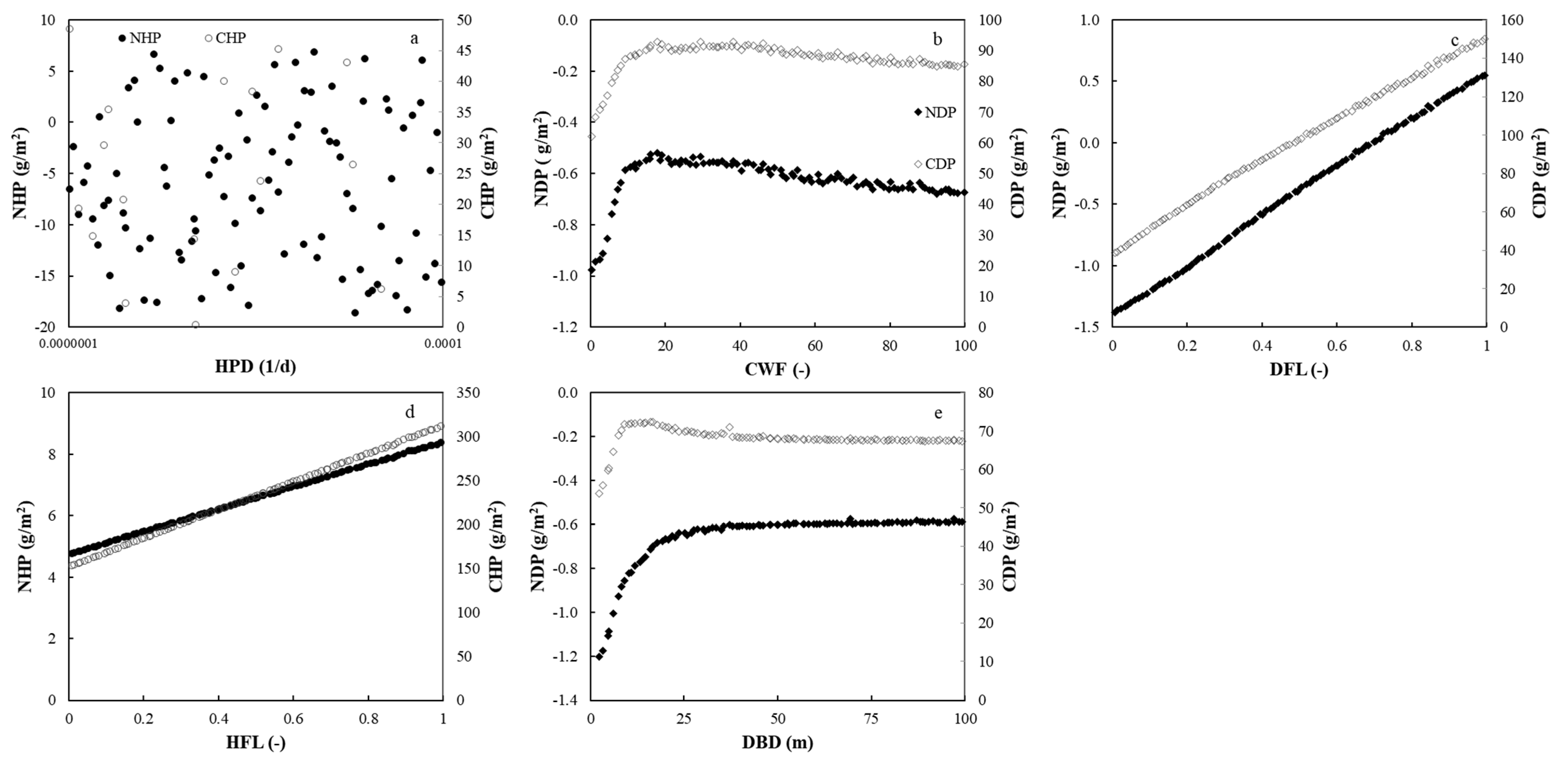
3.4. Changes of Soil C and N Pools
4. Discussion
4.1. Sensitive Parameters for Water Dynamics
4.2. Sensitive Parameters for Yield and Biomass
4.3. Sensitive Parameters for Losses from Soil
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Abbreviations | Variable Description | Unit | Min | Max |
|---|---|---|---|---|---|
| 1 | SFD | Specific fertiliser dissolution rate | 1/day | 0.0001 | 0.5 |
| 2 | Q1N | Coenzyme Q10 temperature coefficient for nitrification | - | 0.1 | 5 |
| 3 | Q1M | Coenzyme Q10 temperature coefficient for mineralization | - | 0.1 | 5 |
| 4 | Q1D | Coenzyme Q10 temperature coefficient for denitrification | - | 0.1 | 5 |
| 5 | PFF-NO | NO production fraction from nitrification | - | 0.00001 | 0.1 |
| 6 | PFF-N2O | N2O production fraction from nitrification | - | 0.000001 | 0.01 |
| 7 | MHC | Minimum hydraulic conductivity | mm/day | 0 | 10 |
| 8 | MMR | Microbial maintenance respiration rate | 1/day | 0.01 | 2 |
| 9 | MDG-NO3 | Maximum NO3 denitrifier growth rate | 1/day | 1 | 40 |
| 10 | MDG-N2O | Maximum N2O denitrifier growth rate | 1/day | 1 | 20 |
| 11 | MDG-NO2 | Maximum NO2 denitrifier growth rate | 1/day | 1 | 40 |
| 12 | MDG-NO | Maximum NO denitrifier growth rate | 1/day | 1 | 20 |
| 13 | MNG | Maximum nitrifier growth rate | 1/day | 0.1 | 15 |
| 14 | MND | Maximum nitrifier death rate | 1/day | 0.01 | 5 |
| 15 | MGY- NO3 | Maximum growth yield on NO3 | gC/gN | 0.01 | 1 |
| 16 | MGY- NO2 | Maximum growth yield on NO2 | gC/gN | 0.01 | 1 |
| 17 | MGY- NO | Maximum growth yield on NO | gC/gN | 0.01 | 3 |
| 18 | MGY- N2O | Maximum growth yield on N2O | gC/gN | 0.01 | 4 |
| 19 | MAN | Maximum autotrophic nitrification rate | 1/day | 0.001 | 0.1 |
| 20 | MCC | Maintenance coefficient on carbon in denitrification | 1/day | 0.0001 | 0.02 |
| 21 | HPD | Humus potential decomposition rate | 1/day | 0.0000001 | 0.001 |
| 22 | HFL | Partitioning fraction to humus from decomposed fresh litter | - | 0 | 1 |
| 23 | HFD | Partitioning fraction to humus from decomposed dissolved organic matter | - | 0 | 1 |
| 24 | HDC | Michaelis constant on dissolved organic carbon concentration | g/m3 | 1 | 40 |
| 25 | HAC | Michaelis constant on ammonium concentration | gN/m3 | 1 | 30 |
| 26 | HNO | Michaelis constant on NOx concentration | gN/m3 | 50 | 200 |
| 27 | FLD | Fresh litter potential decomposition rate | 1/day | 0.0001 | 0.1 |
| 28 | DBD | distance between drainpipes | m | 2 | 100 |
| 29 | DPR | Potential decomposition rate of dissolved organic matter | 1/day | 0.0001 | 0.1 |
| 30 | UCD | Unsaturated conductivity decrease | - | 0 | 10 |
| 31 | SCF | Soil cover fraction to prevent infiltration | - | 0 | 1 |
| 32 | RFO | Runoff first order rate coefficient | 1/day | 0.01 | 1 |
| 33 | MRL | Minimum roughness length | m | 0.001 | 1 |
| 34 | MSS | Maximum surface storage (no runoff) | mm | 0.01 | 10 |
| 35 | HSG | Half saturation global radiation intensity | J/m2/day | 0 | 10,000,000 |
| 36 | ESP | Empirical scale in pore shape | - | 0.01 | 10 |
| 37 | DPL | Drain pipe level, negative downwards | m | -10 | 0 |
| 38 | DPD | Drain pipe diameter | m | 1 | 10 |
| 39 | CAC | Corresponding water amount that the ground is fully covered | mm | 1 | 200 |
| 40 | RAP | Relative activity at porosity | - | 0 | 1 |
| 41 | WCI | Water content interval to unity | vol% | 1 | 15 |
| 42 | OAW | Optimal water content at which there is no adverse effect from soil moisture | vol% | 3 | 40 |
| 43 | CWF | Coefficient in the water function for decomposition | - | 0 | 100 |
| 44 | ASF | Assimilation factor | - | 0 | 1 |
| 45 | LLF | Unit loss fraction of litter with surface runoff | - | 0 | 1 |
| 46 | RLF | Unit loss fraction of residue with surface runoff | - | 0 | 1 |
| 47 | BTM | Reference temperature at which the reaction function is unity for mineralization | °C | 0 | 35 |
| 48 | RLT | A transferring fraction of residue to the litter pool | 1/day | 0 | 0.5 |
| 49 | DFH | A transferring fraction of decomposed humus pool to dissolved organic matter | - | 0 | 1 |
| 50 | DFF | A transferring fraction of decomposed fresh litter to dissolved organic matter | - | 0 | 1 |
| 51 | DFL | A transferring fraction of litter to dissolved organic matter | - | 0 | 1 |
| 52 | HNC | Michaelis constant on nitrate concentration | gN/m3 | 5 | 15 |
| 53 | BTN | Reference temperature at which the reaction function is unity for nitrification | °C | 0 | 35 |
| 54 | BTD | Reference temperature at which the reaction function is unity for denitrification | °C | 0 | 35 |
| 55 | WCA | Water content interval activity | vol% | 0 | 100 |
| 56 | FWD- NH4 | NH4 fraction in wet deposition | - | 0 | 1 |
| 57 | FDD- NH4 | NH4 fraction in dry deposition | - | 0 | 1 |
| 58 | AFI | Fraction of ammonium that cannot move freely with water | - | 0 | 1 |
| 59 | MCN | C:N ratio in microbial biomass | - | 5 | 15 |
| 60 | AIF | A fraction of ammonium that can be used for immobilisation | - | 0 | 1 |
| 61 | HCV | Vapour pressure deficit at which leaf stomata half closed |
| No. | Abbreviations | Output | Unit |
|---|---|---|---|
| 1 | GWF | Groundwater water flux | mm/year |
| 2 | WSC | Soil water content change in the soil profile | % |
| 3 | GDM | Grain dry matter | gDM/m2 |
| 4 | LDM | Leaf dry matter | gDM/m2 |
| 5 | SDM | Stem dry matter | gDM/m2 |
| 6 | NOR | NO3 loss with surface runoff | gN/m2/year |
| 7 | NDR | Dissolved N loss with surface runoff | gN/m2/year |
| 8 | NRR | Residue N loss with surface runoff | gN/m2/year |
| 9 | CDR | Dissolved C loss with surface runoff | gC/m2/year |
| 10 | CRR | Residue C loss with surface runoff | gC/m2/year |
| 11 | SRO | Surface runoff | Mm/year |
| 12 | NHL | NH4 leaching | gN/m2/year |
| 13 | NOL | NO3 leaching | gN/m2/year |
| 14 | NDL | N dissolved leach | gN/m2/year |
| 15 | CDL | C dissolved leach | gN/m2/year |
| 16 | NOE | NO emission rate | gN/m2/year |
| 17 | N2O | N2O emission rate | gN/m2/year |
| 18 | N2E | N2 emission rate | gN/m2/year |
| 19 | DRE | Dissolved release | gC/m2/year |
| 20 | FLR | Fresh litter release | gC/m2/year |
| 21 | HRE | Humus release | gC/m2/year |
| 22 | MRE | Microbial release | gC/m2/year |
| 23 | NHP | N in humus | gN/m2 |
| 24 | NDP | Dissolved N | gN/m2 |
| 25 | NMR | Mineralization rate | gN/m2/year |
| 26 | CDP | Dissolved C | gC/m2 |
| 27 | CHP | C in humus | gC/m2 |






References
- Krishnan, P.; Aggarwal, P. Global sensitivity and uncertainty analyses of a web based crop simulation model (web InfoCrop wheat) for soil parameters. Plant. Soil 2018, 423, 443–463. [Google Scholar] [CrossRef]
- Leolini, L.; Bregaglio, S.; Moriondo, M.; Ramos, M.C.; Bindi, M.; Ginaldi, F. A model library to simulate grapevine growth and development: Software implementation, sensitivity analysis and field level application. Eur. J. Agron. 2018, 99, 92–105. [Google Scholar] [CrossRef]
- Eitzinger, J.; Thaler, S.; Schmid, E.; Strauss, F.; Ferrise, R.; Moriondo, M.; Bindi, M.; Palosuo, T.; Rötter, R.; Kersebaum, K.C.; et al. Sensitivities of crop models to extreme weather conditions during flowering period demonstrated for maize and winter wheat in Austria. J. Agric. Sci. 2012, 151, 813–835. [Google Scholar] [CrossRef]
- Sommer, R.; Mukalama, J.; Kihara, J.; Koala, S.; Winowiecki, L.; Bossio, D. Nitrogen dynamics and nitrous oxide emissions in a long-term trial on integrated soil fertility management in Western Kenya. Nutr. Cycl. Agroecosyst. 2016, 105, 229–248. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhao, Y.C.; Shi, X.Z.; Liu, Y.; Wang, S.H.; Yu, D.S. Sensitivity and uncertainty analysis of CENTURY-modeled SOC dynamics in upland soils under different climate-soil-management conditions: A case study in China. J. Soils Sediments 2017, 17, 85–96. [Google Scholar] [CrossRef]
- Wu, R.; Lawes, R.; Oliver, Y.; Fletcher, A.; Chen, C. How well do we need to estimate plant-available water capacity to simulate water-limited yield potential? Agric. Water Manag. 2019, 212, 441–447. [Google Scholar] [CrossRef]
- Grassini, P.; van Bussel, L.G.J.; van Wart, J.; Wolf, J.; Claessens, L.; Yang, H.; Boogaard, H.; de Groot, H.; van Ittersum, M.K.; Cassman, K.G. How good is good enough? Data requirements for reliable crop yield simulations and yield-gap analysis. Field Crop. Res. 2015, 177, 49–63. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Dukes, M.D.; Hochmuth, G.J.; Jones, J.W.; Graham, W.D. Evaluation of sweet corn yield and nitrogen leaching with CERES-Maize considering input parameter uncertainties. Trans. ASABE 2011, 54, 1257–1268. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Specka, X.; Nendel, C.; Wieland, R. Analysing the parameter sensitivity of the agro-ecosystem model MONICA for different crops. Eur. J. Agron. 2015, 71, 73–87. [Google Scholar] [CrossRef]
- Jabloun, M.; Li, X.X.; Zhang, X.Y.; Tao, F.L.; Hu, C.S.; Olesen, J.E. Sensitivity of simulated crop yield and nitrate leaching of the wheat-maize cropping system in the North China Plain to model parameters. Agric. For. Meteorol. 2018, 263, 25–40. [Google Scholar] [CrossRef] [Green Version]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global sensitivity analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; McGechan, M.B.; McRoberts, N.; Baddeley, J.A.; Watson, C.A. SPACSYS: Integration of a 3D root architecture component to carbon, nitrogen and water cycling-model description. Ecol. Model. 2007, 200, 343–359. [Google Scholar] [CrossRef]
- Abalos, D.; Cardenas, L.M.; Wu, L.H. Climate change and N2O emissions from South West England grasslands: A modelling approach. Atmos. Environ. 2016, 132, 249–257. [Google Scholar] [CrossRef]
- Liang, S.; Li, Y.F.; Zhang, X.B.; Sun, Z.G.; Sun, N.; Duan, Y.H.; Xu, M.G.; Wu, L.H. Response of crop yield and nitrogen use efficiency for wheat-maize cropping system to future climate change in northern China. Agric. For. Meteorol. 2018, 262, 310–321. [Google Scholar] [CrossRef]
- Zhang, X.B.; Xu, M.G.; Sun, N.; Xiong, W.; Huang, S.M.; Wu, L.H. Modelling and predicting crop yield, soil carbon and nitrogen stocks under climate change scenarios with fertiliser management in the North China Plain. Geoderma 2016, 265, 176–186. [Google Scholar] [CrossRef]
- Zhang, X.B.; Sun, Z.G.; Liu, J.; Ouyang, Z.; Wu, L.H. Simulating greenhouse gas emissions and stocks of carbon and. nitrogen in soil from a long-term no-till system in the North China Plain. Soil Tillage Res. 2018, 178, 32–40. [Google Scholar] [CrossRef]
- Perego, A.; Wu, L.; Gerosa, G.; Finco, A.; Chiazzese, M.; Amaducci, S. Field evaluation combined with modelling analysis to study fertilizer and tillage as factors affecting N2O emissions: A case study in the Po valley (Northern Italy). Agric. Ecosyst. Environ. 2016, 225, 72–85. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Griffith, B.A.; Misselbrook, T.H. Sustainable grassland systems: A modelling perspective based on the North Wyke Farm Platform. Eur. J. Soil Sci. 2016, 67, 397–408. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Yang, J.Y.; Zhou, W.; Drury, C.F.; Yang, X.M.; Reynolds, W.D.; Wang, H.; He, P.; Li, Z.T. Sensitivity analysis of crop yields, soil water contents and nitrogen leaching to precipitation, management practices and soil hydraulic properties in semi-arid and humid regions of Canada using the DSSAT model. Nutr. Cycl. Agroecosystems 2016, 106, 201–215. [Google Scholar] [CrossRef]
- Zhao, G.; Bryan, B.A.; Song, X.D. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar, environmental, and management parameters. Ecol. Model. 2014, 279, 1–11. [Google Scholar] [CrossRef]
- Yan, W.-J.; Wan, H.-P.; Ren, W.-X. Analytical local and global sensitivity of power spectrum density functions for structures subject to stochastic excitation. Comput. Struct. 2017, 182, 325–336. [Google Scholar] [CrossRef]
- Ginot, V.; Gaba, S.; Beaudouin, R.; Aries, F.; Monod, H. Combined use of local and ANOVA-based global sensitivity analyses for the investigation of a stochastic dynamic model: Application to the case study of an individual-based model of a fish population. Ecol. Model. 2006, 193, 479–491. [Google Scholar] [CrossRef]
- Loosvelt, L.; Vernieuwe, H.; Pauwels, V.R.N.; de Baets, B.; Verhoest, N.E.C. Local sensitivity analysis for compositional data with application to soil texture in hydrologic modelling. Hydrol. Earth Syst. Sci. 2013, 17, 461–478. [Google Scholar] [CrossRef] [Green Version]
- Krishna, N.A.; Pennington, H.M.; Coppola, C.D.; Eisenberg, M.C.; Schugart, R.C. Connecting local and global sensitivities in a mathematical model for wound healing. Bull. Math. Biol. 2015, 77, 2294–2324. [Google Scholar] [CrossRef]
- Nguyen-Tuan, L.; Lahmer, T.; Datcheva, M.; Schanz, T. Global and local sensitivity analyses for coupled thermo–hydro–mechanical problems. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 707–720. [Google Scholar] [CrossRef]
- Link, K.G.; Stobb, M.T.; Di Paola, J.; Neeves, K.B.; Fogelson, A.L.; Sindi, S.S.; Leiderman, K. A local and global sensitivity analysis of a mathematical model of coagulation and platelet deposition under flow. PLoS ONE 2018, 13, e0200917. [Google Scholar] [CrossRef] [PubMed]
- Naves, J.; Rieckermann, J.; Cea, L.; Puertas, J.; Anta, J. Global and local sensitivity analysis to improve the understanding of physically-based urban wash-off models from high-resolution laboratory experiments. Sci. Total Environ. 2020, 709, 136152. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, Y.; Harris, P.; Sint, H.; Murray, P.J.; Lee, M.; Wu, L. Assessment of soil water, carbon and nitrogen cycling in reseeded grassland on the North Wyke Farm Platform using a process-based model. Sci. Total Environ. 2017, 603-604, 27–37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Li, Y.; Harris, P.; Cardenas, L.; Dunn, R.M.; Sint, H.; Murray, P.; Lee, M.; Wu, L. Modelling field scale spatial variation in water run-off, soil moisture, N2O emissions and herbage biomass of a grazed pasture using the SPACSYS model. Geoderma 2018, 315, 49–58. [Google Scholar] [CrossRef]
- Wu, L.; Rees, R.M.; Tarsitano, D.; Zhang, X.B.; Jones, S.K.; Whitmore, A.P. Simulation of nitrous oxide emissions at field scale using the SPACSYS model. Sci. Total Environ. 2015, 530, 76–86. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Shepherd, A. Special features of the SPACSYS modeling package and procedures for parameterization and validation. In Methods of Introducing System Models into Agricultural Research; Ahuja, L.R., Ma, L., Eds.; ASA, CSSA & SSSA: Madison, WI, USA, 2011; pp. 117–154. [Google Scholar]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Ballantine, D.J.; Tanner, C.C. Controlled drainage systems to reduce contaminant losses and optimize productivity from New Zealand pastoral systems. N. Z. J. Agric. Res. 2013, 56, 171–185. [Google Scholar] [CrossRef]
- Ritzema, H.P. Drain for gain: Managing salinity in irrigated lands—A review. Agric. Water Manag. 2016, 176, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Jouni, H.J.; Liaghat, A.; Hassanoghli, A.; Henk, R. Managing controlled drainage in irrigated farmers’ fields: A case study in the Moghan plain, Iran. Agric. Water Manag. 2018, 208, 393–405. [Google Scholar] [CrossRef]
- Tomic, F.; Kricka, T.; Simunic, I.; Petosic, D.; Voca, N.; Jukic, Z. Effect of drainage systems on the water release rate in the process of drying wheat and corn grain. Irrig. Drain. 2007, 56, 107–113. [Google Scholar] [CrossRef]
- Helmers, M.; Christianson, R.; Brenneman, G.; Lockett, D.; Pederson, C. Water table, drainage, and yield response to drainage water management in southeast Iowa. J. Soil Water Conserv. 2012, 67, 495–501. [Google Scholar] [CrossRef]
- Carstensen, M.V.; Poulsen, J.R.; Ovesen, N.B.; Børgesen, C.D.; Hvid, S.K.; Kronvang, B. Can controlled drainage control agricultural nutrient emissions? Evidence from a BACI experiment combined with a dual isotope approach. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–17. [Google Scholar] [CrossRef]
- Borin, M.; Bonaiti, G.; Giardini, L. Controlled drainage and wetlands to reduce agricultural pollution: A lysimetric study. J. Environ. Qual. 2001, 30, 1330–1340. [Google Scholar] [CrossRef] [PubMed]
- Mohammadzadeh-Habili, J.; Mostafazadeh-Fard, B. Hydraulic calculation of field drain pipe diameter: Using the theory of spatially-varied flow with increasing discharge. Biosyst. Eng. 2010, 106, 559–563. [Google Scholar] [CrossRef]
- Ma, J.M.; Daggupaty, S.M. Stability dependence of height scales and effective roughness lengths of momentum and heat transfer over roughness changes. Bound. Layer Meteorol. 1998, 88, 145–160. [Google Scholar] [CrossRef]
- Martinez-Agirre, A.; Alvarez-Mozos, J.; Lievens, H.; Verhoest, N.E.C. Influence of surface roughness measurement scale on radar backscattering in different agricultural soils. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5925–5936. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.G.; Li, X.; Han, X.J.; Jin, R. Estimation of surface soil moisture and roughness from multi-angular ASAR imagery in the Watershed Allied Telemetry Experimental Research (WATER). Hydrol. Earth Syst. Sci. 2011, 15, 1415–1426. [Google Scholar] [CrossRef] [Green Version]
- Moret-Fernández, D.; Latorre, B.; Giner, M.L.; Ramos, J.; Alados, C.L.; Castellano, C.; López, M.V.; Jimenez, J.J.; Pueyo, Y. Estimation of the soil hydraulic properties from the transient infiltration curve measured on soils affected by water repellency. CATENA 2019, 178, 298–306. [Google Scholar] [CrossRef]
- Fernandez-Galvez, J.; Pollacco, J.A.P.; Lassabatere, L.; Angulo-Jaramillo, R.; Carrick, S. A general Beerkan estimation of soil transfer parameters method predicting hydraulic parameters of any unimodal water retention and hydraulic conductivity curves: Application to the kosugi soil hydraulic model without using particle size distribution data. Adv. Water Resour. 2019, 129, 118–130. [Google Scholar] [CrossRef]
- Pinheiro, E.A.R.; van Lier, Q.D.; Simunek, J. The role of soil hydraulic properties in crop water use efficiency: A process-based analysis for some Brazilian scenarios. Agric. Syst. 2019, 173, 364–377. [Google Scholar] [CrossRef] [Green Version]
- Vereecken, H.; Kamai, T.; Harter, T.; Kasteel, R.; Hopmans, J.; Vanderborght, J. Explaining soil moisture variability as a function of mean soil moisture: A stochastic unsaturated flow perspective. Geophys. Res. Lett. 2007, 34, 6. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.Z.; Zhang, L.; Liang, Y.L.; Hu, X.T.; Cai, H.J.; Gu, B.J. Effects of limited irrigation on yield and water use efficiency of winter wheat in the Loess Plateau of China. Agric. Water Manag. 2002, 55, 203–216. [Google Scholar] [CrossRef]
- Lawless, C.; Semenov, M.A.; Jamieson, P.D. Quantifying the effect of uncertainty in soil moisture characteristics on plant growth using a crop simulation model. Field Crop. Res. 2008, 106, 138–147. [Google Scholar] [CrossRef]
- Gao, Y.J.; Li, Y.; Zhang, J.C.; Liu, W.G.; Dang, Z.P.; Cao, W.X.; Qiang, Q. Effects of mulch, N fertilizer, and plant density on wheat yield, wheat nitrogen uptake, and residual soil nitrate in a dryland area of China. Nutr. Cycl. Agroecosyst. 2009, 85, 109–121. [Google Scholar] [CrossRef]
- Raun, W.R.; Johnson, G.V. Improving nitrogen use efficiency for cereal production. Agron. J. 1999, 91, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Zorb, C.; Ludewig, U.; Hawkesford, M.J. Perspective on wheat yield and quality with reduced nitrogen supply. Trends Plant Sci. 2018, 23, 1029–1037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; He, X.; Williams, J.R.; Izaurralde, R.C.; Atwood, J.D. Sensitivity and uncertainty analyses of crop yields and soil organic carbon simulated with EPIC. Trans. ASAE 2005, 48, 1041–1054. [Google Scholar] [CrossRef]
- Ibrahim, M.; Cao, C.G.; Zhan, M.; Li, C.F.; Iqbal, J. Changes of CO2 emission and labile organic carbon as influenced by rice straw and different water regimes. Int. J. Environ. Sci. Technol. 2015, 12, 263–274. [Google Scholar] [CrossRef]
- Jugsujinda, A.; Delaune, R.D.; Lindau, C.W.; Sulaeman, E.; Pezeshki, S.R. Factors controlling carbon dioxide and methane production in acid sulfate soils. Water Air Soil Pollut. 1996, 87, 345–355. [Google Scholar] [CrossRef]
- Pires, C.V.; Schaefer, C.; Hashigushi, A.K.; Thomazini, A.; Filho, E.I.F.; Mendonca, E.S. Soil organic carbon and nitrogen pools drive soil C-CO2 emissions from selected soils in Maritime Antarctica. Sci. Total Environ. 2017, 596, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Hu, C.; Mohamed, I.; Wang, J.; Zhang, G.S.; Li, Z.G.; Chen, F. Soil CO2 emissions and drivers in rice-wheat rotation fields subjected to different long-term fertilization practices. Clean Soil Air Water 2016, 44, 867–876. [Google Scholar] [CrossRef]
- Oorts, K.; Merckx, R.; Gréhan, E.; Labreuche, J.; Nicolardot, B. Determinants of annual fluxes of CO2 and N2O in long-term no-tillage and conventional tillage systems in northern France. Soil Tillage Res. 2007, 95, 133–148. [Google Scholar] [CrossRef]
- Rodrigo, A.; Recous, S.; Neel, C.; Mary, B. Modelling temperature and moisture effects on C-N transformations in soils: Comparison of nine models. Ecol. Model. 1997, 102, 325–339. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Y.; Huang, M.; Harris, P.; Wu, L. A Sensitivity Analysis of the SPACSYS Model. Agriculture 2021, 11, 624. https://doi.org/10.3390/agriculture11070624
Shan Y, Huang M, Harris P, Wu L. A Sensitivity Analysis of the SPACSYS Model. Agriculture. 2021; 11(7):624. https://doi.org/10.3390/agriculture11070624
Chicago/Turabian StyleShan, Yan, Mingbin Huang, Paul Harris, and Lianhai Wu. 2021. "A Sensitivity Analysis of the SPACSYS Model" Agriculture 11, no. 7: 624. https://doi.org/10.3390/agriculture11070624
APA StyleShan, Y., Huang, M., Harris, P., & Wu, L. (2021). A Sensitivity Analysis of the SPACSYS Model. Agriculture, 11(7), 624. https://doi.org/10.3390/agriculture11070624








