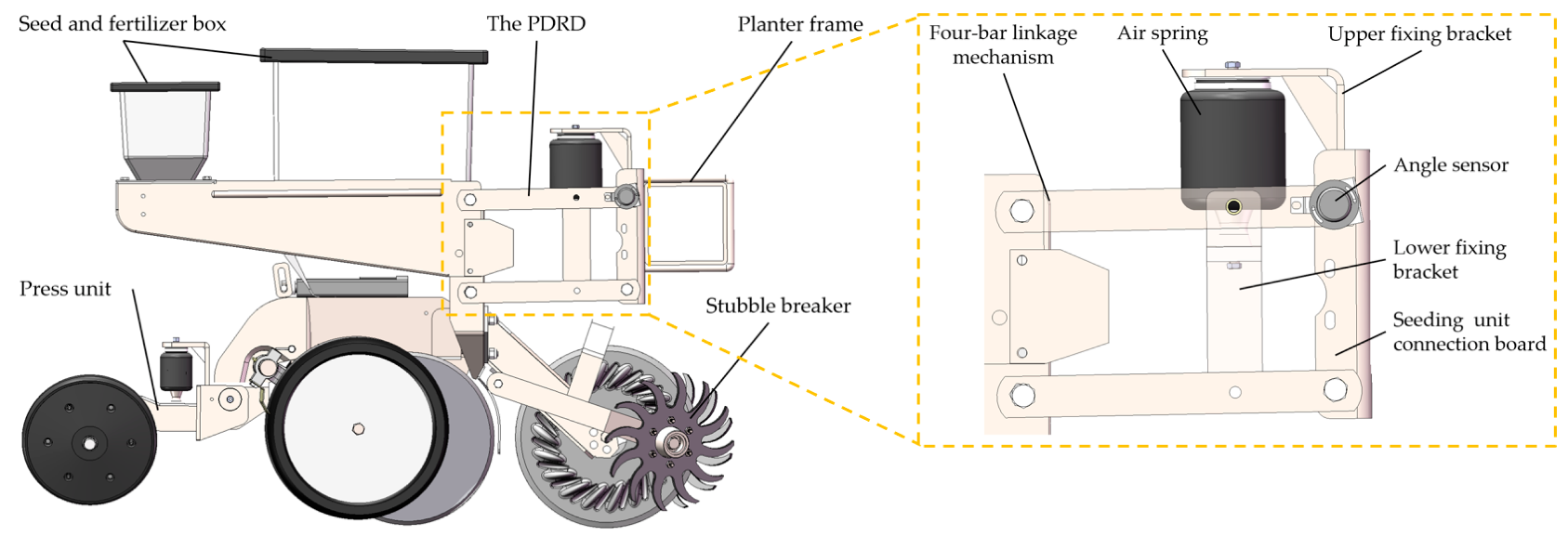
Design and Analysis of Pneumatic Downforce Regulating Device for No-Till Corn Planter
Abstract
:1. Introduction
2. Materials and Methods
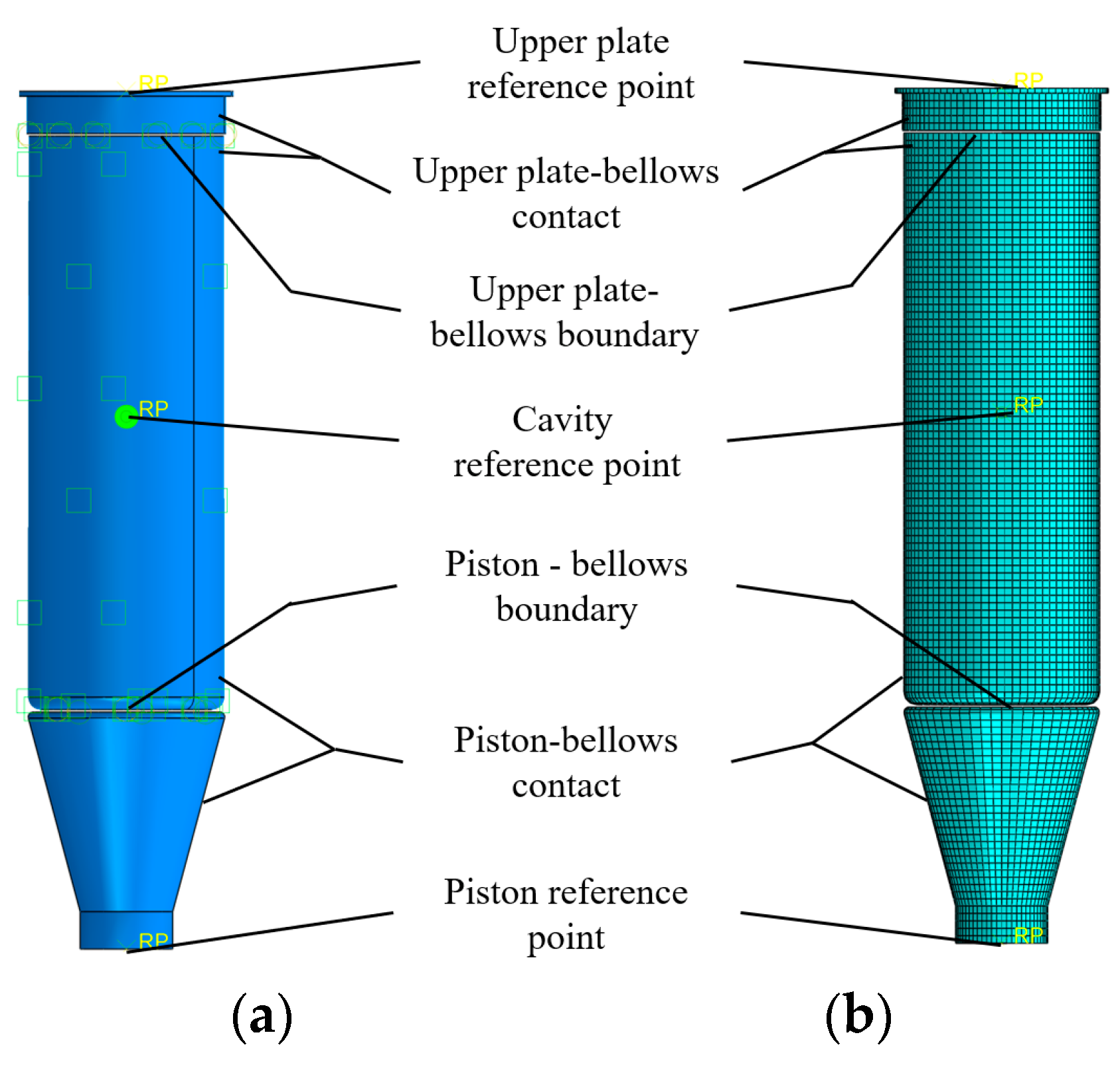
2.1. F E Model
2.1.1. Model Material
2.1.2. Contact and Boundary
2.1.3. Meshing and Step Definition
2.2. Test Design and Index Measurement
2.2.1. Test Factors
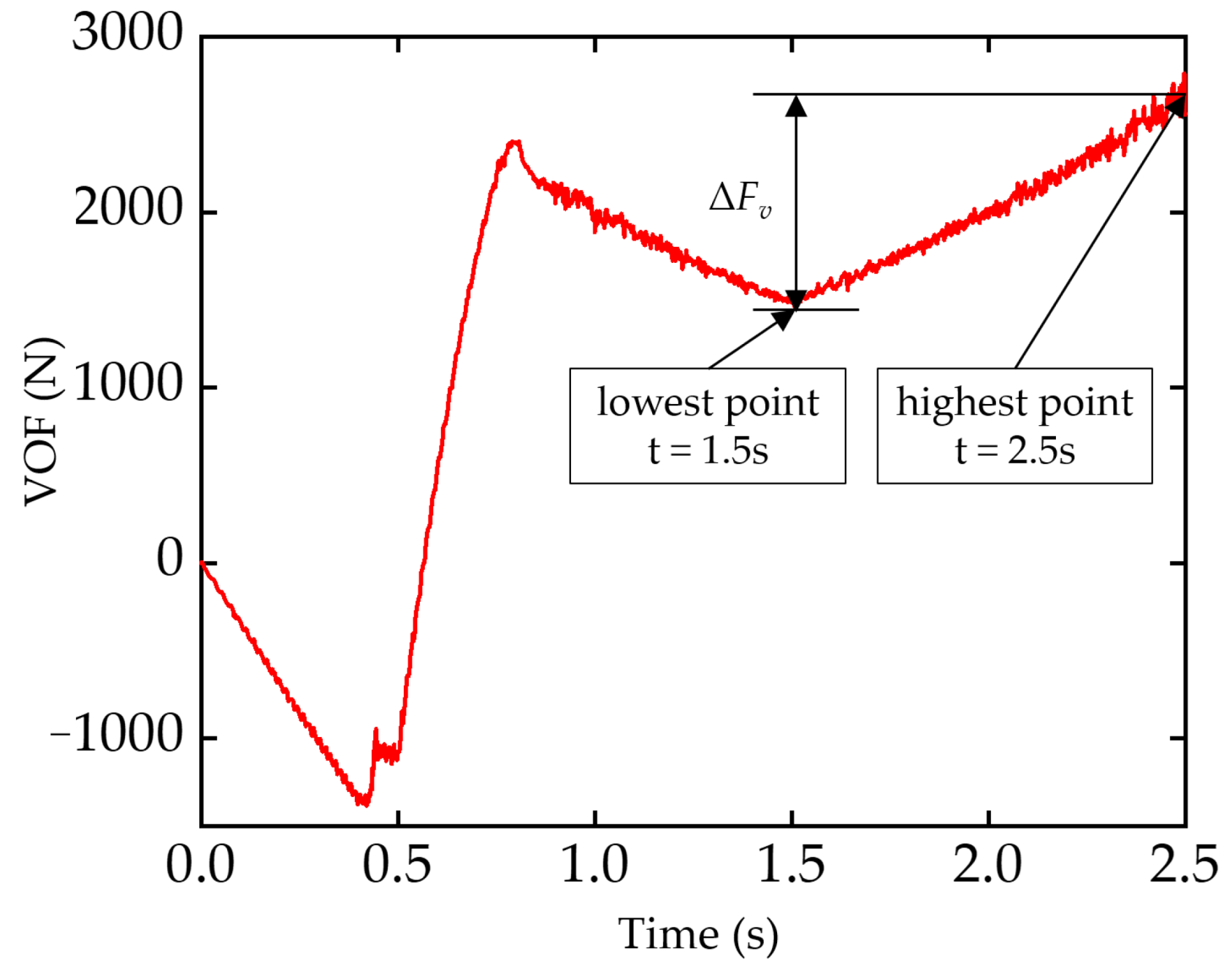
2.2.2. Data Collection and Processing
- 1.
- The Average VOF
- 2.
- The VS
- 3.
- Deformation Rate of Bellows
- 4.
- The Internal Pressure Difference
3. Results and Discussion
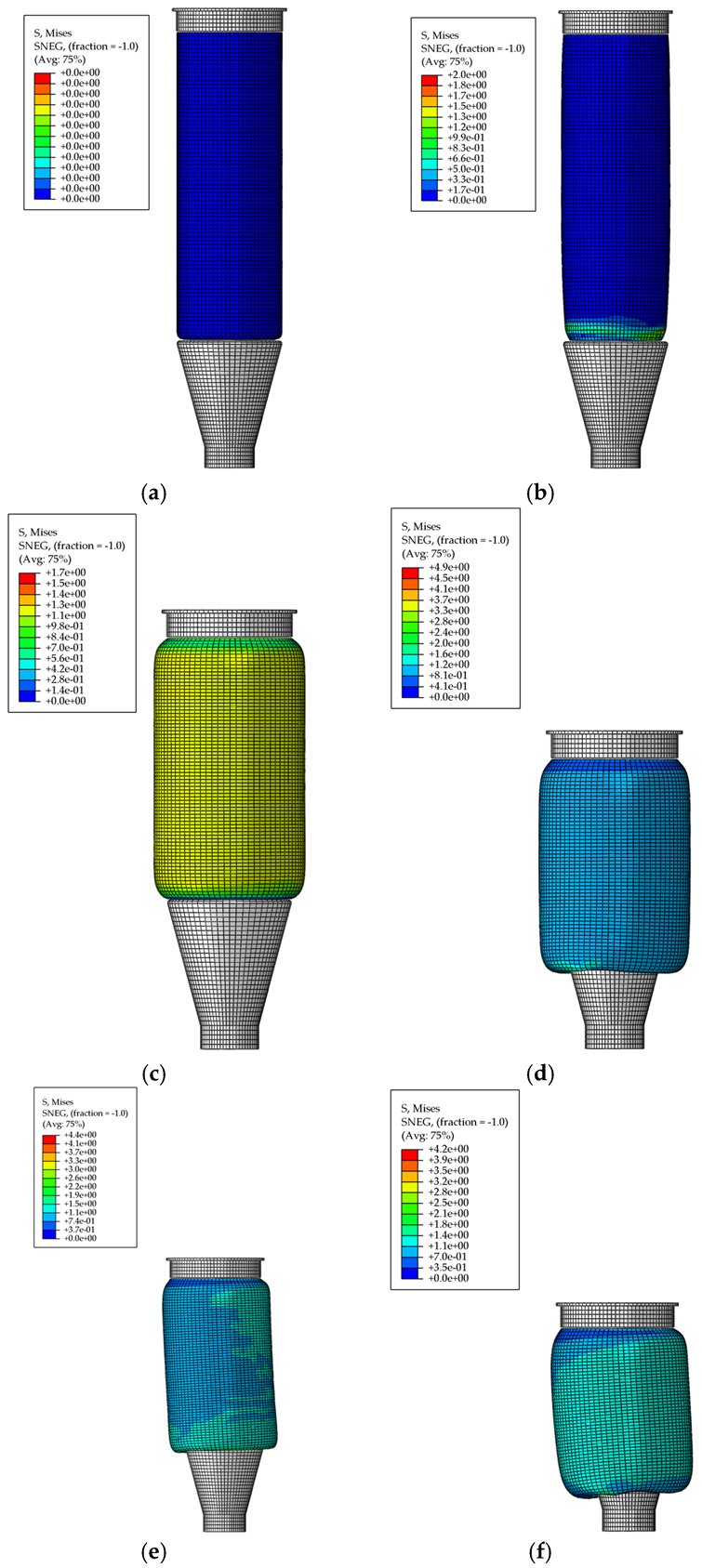
3.1. Experimental Verification of F E Model
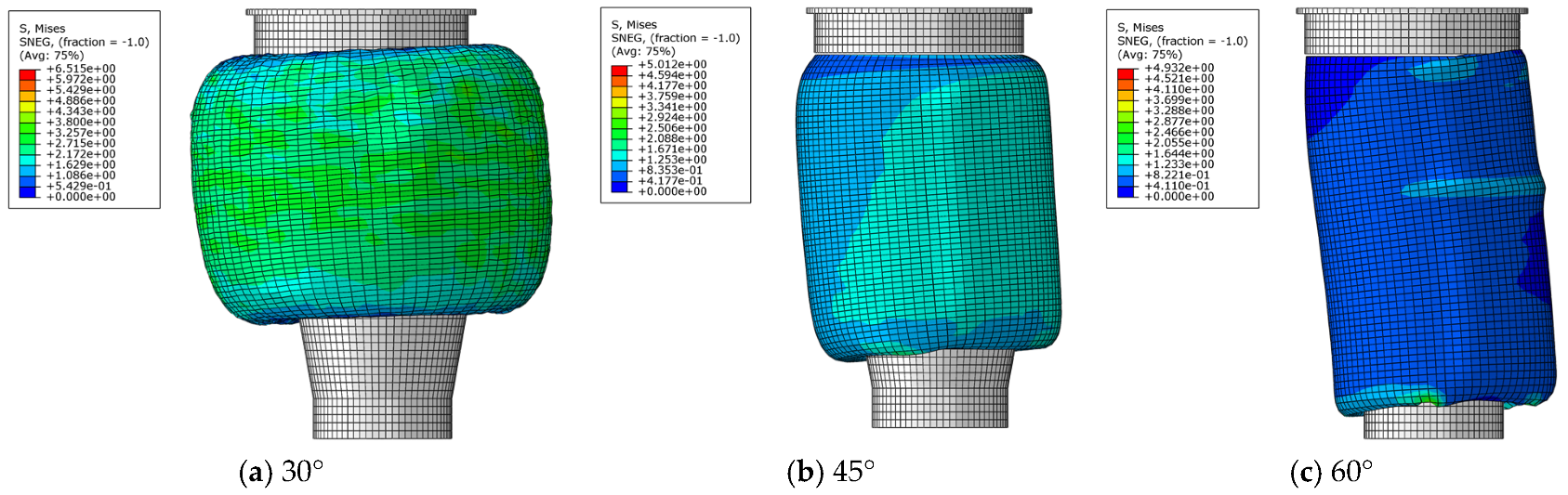
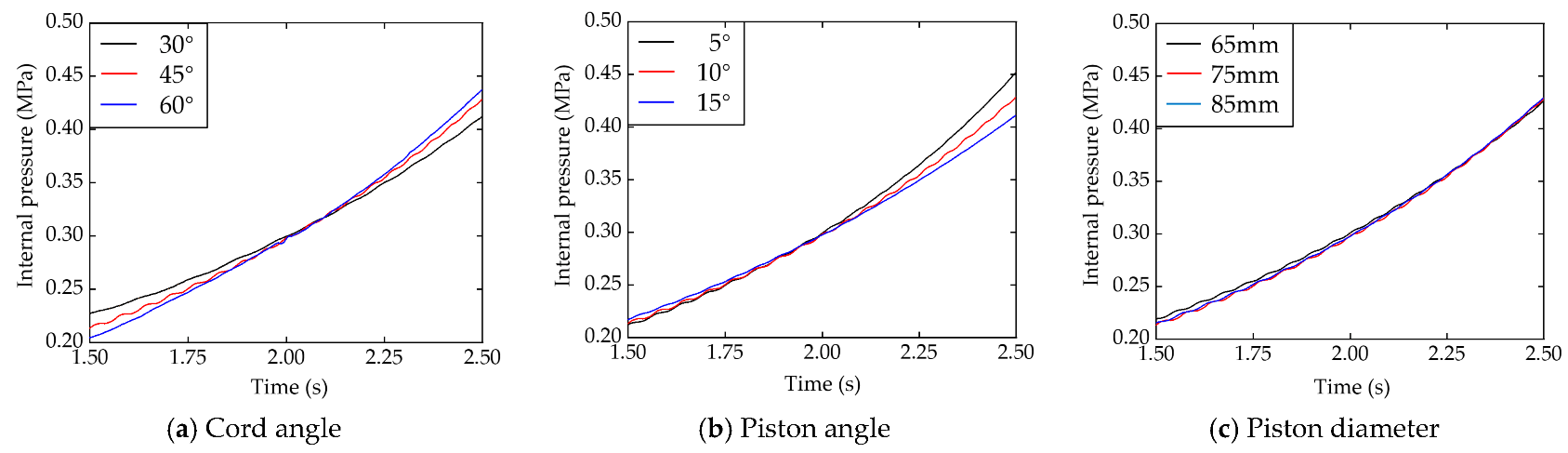
3.2. Impact Analysis of Experimental Factors
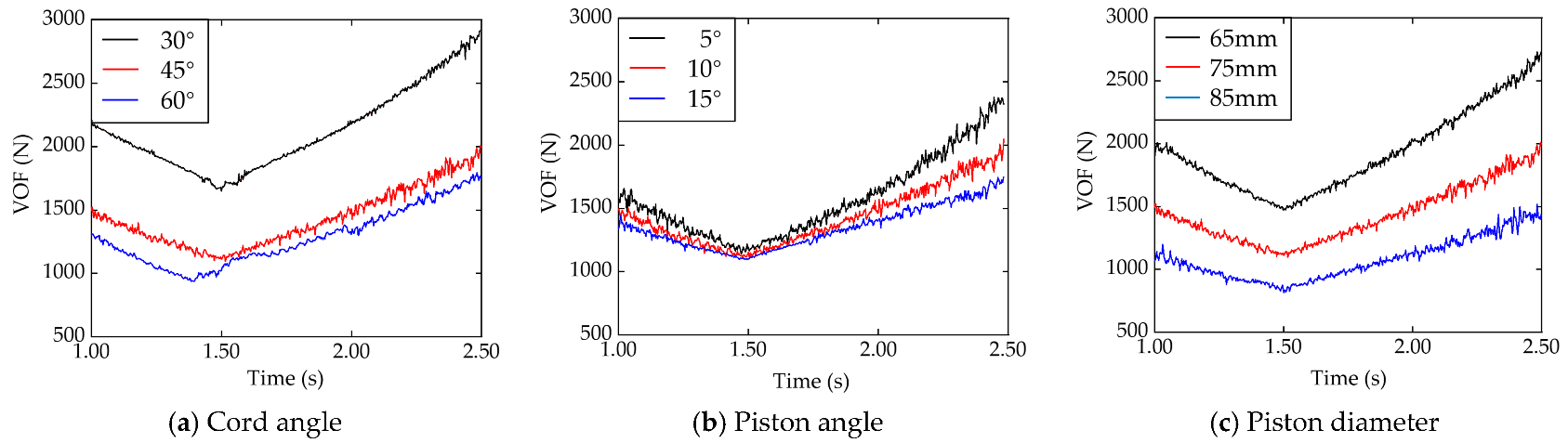
3.2.1. Impact Analysis of the VOF
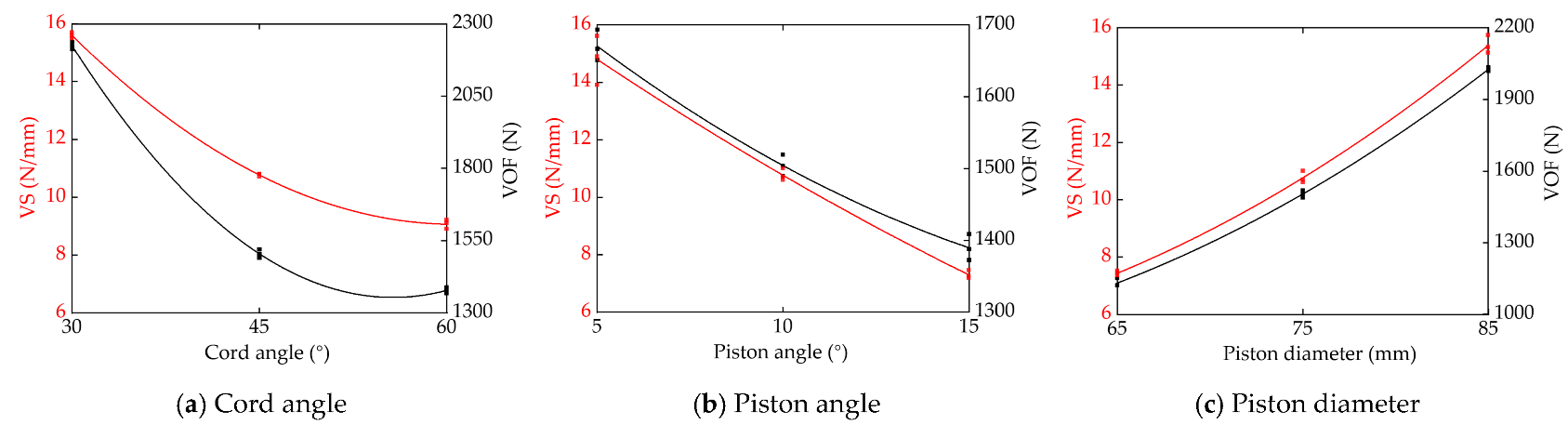
3.2.2. Impact Analysis of the VS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gratton, J.; Chen, Y.; Tessier, S. Design of a spring-loaded downforce system for a no-till seed opener. Can. Agric. Eng. 2003, 45, 29–35. [Google Scholar]
- Virk, S.S.; Porter, W.M.; Li, C.; Rains, G.C.; Snider, J.L.; Whitaker, J.R. On-farm evaluation of planter downforce in varying soil textures within grower fields. Precis. Agric. 2021, 22, 777–799. [Google Scholar] [CrossRef]
- Badua, S.A.; Sharda, A.; Strasser, R.; Ciampitti, I. Ground speed and planter downforce influence on corn seed spacing and depth. Precis. Agric. 2021, 22, 1154–1170. [Google Scholar] [CrossRef]
- Bai, W.; Sun, Z.X.; Zhang, L.Z.; Zheng, J.M.; Feng, L.S.; Cai, Q.; Xiang, W.Y.; Feng, C.; Zhang, Z. Furrow loose and ridge compaction plough layer structure optimizing root morphology of spring corn and improving its water use efficiency. Trans. Chin. Soc. Agric. Eng. 2019, 35, 88–97. [Google Scholar] [CrossRef]
- Hemmat, A.; Adamchuk, V.I. Sensor systems for measuring soil compaction: Review and analysis. Comput. Electron. Agr. 2008, 63, 89–103. [Google Scholar] [CrossRef]
- Lipiec, J.; Horn, R.; Pietrusiewicz, J.; Siczek, A. Effects of soil compaction on root elongation and anatomy of different cereal plant species. Soil Tillage Res. 2012, 121, 74–81. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H. Compaction and subsoiling effects on corn growth and soil bulk density. Soil Sci. Soc. Am. J. 2003, 67, 1213–1219. [Google Scholar] [CrossRef]
- Finlay, M.J.; Tisdall, J.M.; McKenzie, B.M. Effect of tillage below the seed on emergence of wheat seedlings in a hard setting soil. Soil Tillage Res. 1994, 28, 213–225. [Google Scholar] [CrossRef]
- Shi, D.J.; Yan, F.Y.; Fan, J.Z.; Zhong, C.S.; Lyu, J.Z. Effects of different sowing depths on seedling characters and yield of maize under no-tillage conditions. J. Hunan Agric. Univ. Nat. Sci. 2014, 2014, 19–21, 24. [Google Scholar] [CrossRef]
- Zhang, R. Study on Precision Depth-Control Mechanism of Corn No-Till Planter in Double-Cropping Area. Ph.D. Thesis, China Agricultural University, Beijing, China, 2016. [Google Scholar]
- Nielsen, S.K.; Munkholm, L.J.; Lamandé, M.; Nørremark, M.; Skou-Nielsen, N.; Edwards, G.T.C.; Green, O. Seed drill instrumentation for spatial coulter depth measurements. Comput. Electron. Agr. 2017, 141, 207–214. [Google Scholar] [CrossRef]
- The Keys to Consistent Emergence. Available online: https://www.precisionplanting.com/agronomy/research/the-keys-to-consistent-emergence (accessed on 20 July 2022).
- Liu, W.D.; Tollenaar, M.; Stewart, G.; Deen, W. Impact of planter type, planting speed, and tillage on stand uniformity and yield of corn. Agron. J. 2004, 96, 1668. [Google Scholar] [CrossRef]
- Virk, S.S.; Fulton, J.P.; Porter, W.M.; Pate, G.L. Row-crop planter performance to support variable-rate seeding of maize. Precis. Agric. 2020, 21, 603–619. [Google Scholar] [CrossRef]
- Jing, H.R.; Zhang, D.X.; Wang, Y.X.; Yang, L.; Fan, C.L.; Zhao, H.H.; Wu, H.L. Development and performance evaluation of an electro-hydraulic downforce control system for planter row unit. Comput. Electron. Agr. 2020, 172, 105073. [Google Scholar] [CrossRef]
- Huang, D.Y.; Zhu, L.T.; Jia, H.L.; Yu, T.T. Automatic control system of seeding depth based on piezoelectric film for no-till planter. Trans. Chin. Soc. Agric. Mach. 2015, 46, 1–8. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Wang, X.; Yang, S.; Zhao, X.G.; Dou, H.J.; Zhao, C.J. Design and test of pneumatic downforce control system for planting. Chin. Soc. Agric. Mach. 2019, 50, 19–29. [Google Scholar] [CrossRef]
- John Deere 1705 Twin Row Planter. Available online: https://www.deere.com/en/planting-equipment/1705-twin-row-planter/# (accessed on 19 July 2022).
- Precision Planting. Available online: https://www.precisionplanting.com/products/product/airforce (accessed on 19 July 2022).
- Kinze. Available online: https://www.kinze.com/planter-performance/down-force/pneumatic/ (accessed on 19 July 2022).
- Bester, T.; Oman, S.; Nagode, M. Determining influential factors for an air spring fatigue life. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 284–294. [Google Scholar] [CrossRef]
- Wang, H.Y.; He, F.; Zhao, J.; Cao, H. Study on mechanical properties of air spring with auxiliary chamber based on fluid-solid coupling. China Rubber Ind. 2012, 59, 300–303. [Google Scholar]
- Yuan, C.Y.; Zhou, K.K.; Wu, Q.L.; An, D.F.; Wang, G.L. Finite element method to analyze vehicle air spring. J. Mech. Eng. Sci. 2009, 45, 262–266. [Google Scholar] [CrossRef]
- Xu, Y.M.; Hao, W. Analysis on static mechanical properties of air spring based on ABAQUS. China Rubber Ind. 2015, 62, 41–44. [Google Scholar]
- Gao, Y.Y. Research on Monitoring and Control Method of Corn Sowing Depth and Seeding Downforce. Ph.D. Thesis, China Agricultural University, Beijing, China, 2020. [Google Scholar]
- Gao, Y.Y.; Wang, X.; Yang, S.; Zhai, C.Y.; Zhao, X.G.; Zhao, C.J. Development of CAN-based sowing depth monitoring and evaluation system. Chin. Soc. Agric. Mach. 2019, 50, 23–32. [Google Scholar] [CrossRef]
- Chen, J.J. Study on Modeling Methods and Dynamic Characteristics of Vehicular Air Damping Air Spring. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Chen, X.X.; Li, B.R.; Yang, G.; Du, J.M. Modeling and tests for load of a cystiform air spring. J. Shock Vib. 2014, 33, 80–84. [Google Scholar] [CrossRef]
- Lu, J. Design and Optimization of Heavy Truck Air Suspension System. Master’s Thesis, Qingdao University, Qingdao, China, 2020. [Google Scholar]
- Chen, D. The Analysis of Air-Spring’s Stiffness on Vehicle. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Hu, D.A.; Gan, L.L.; Ding, F.; He, X.W. Simulation of stiffness character of diaphragm air spring based on change piston contour. Comput. Simul. 2012, 29, 331–334+388. [Google Scholar]



| Composition | Materials | Model | Parameters | |
|---|---|---|---|---|
| Rubber layer | Rubber | Mooney–Rivlin | C10 (MPa) | C01 (MPa) |
| 0.5178 | 0.1426 | |||
| Cord layer | Cord | / | Young modulus (MPa) | Poisson’s ratio |
| 7200 | 0.3 | |||
| Number | Factor | Variable’s Value | Conditions |
|---|---|---|---|
| 1–3 | Cord angle α/° | 30,45,60 | β = 10° d1 = 75 mm |
| 4–6 | Piston angle β/° | 5,10,15 | α = 45° d1 = 75 mm |
| 7–9 | Piston diameter d1/mm | 65,75,85 | α = 45° β = 10° |
| Height /mm | Vertical Force | Pitch Diameter | Pressure | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Meas/N | Simu/N | Diff/% | Meas/mm | Simu/mm | Diff/% | Meas/MPa | Simu/MPa | Diff/% | |
| 240 | 1824.9 | 1892.0 | 3.55 | 93.5 | 94.5 | 1.08 | 0.205 | 0.213 | 3.98 |
| 220 | 1621.5 | 1683.9 | 3.71 | 94.3 | 95.6 | 1.34 | 0.235 | 0.250 | 6.18 |
| 200 | 1467.4 | 1561.7 | 6.04 | 95.1 | 95.7 | 0.66 | 0.276 | 0.298 | 7.47 |
| 180 | 1265.3 | 1297.1 | 2.46 | 95.8 | 96.4 | 0.66 | 0.340 | 0.354 | 4.01 |
| 160 | 1020.8 | 1111.8 | 8.18 | 96.8 | 96.9 | 0.09 | 0.413 | 0.429 | 3.74 |
| Object | Cord Angle | Piston Angle | Pitch Diameter | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 30 | 45 | 60 | 5 | 10 | 15 | 65 | 75 | 85 | |
| Average VOF FMv/N | 2224.3 | 1504.2 | 1377.6 | 1670.5 | 1504.2 | 1389.6 | 1131.6 | 1504.2 | 2025.9 |
| VS ks/N/mm | 15.6 | 10.8 | 9.1 | 14.8 | 10.8 | 7.3 | 7.4 | 10.8 | 15.4 |
| Deformation rate kD/% | 62.3 | 19.2 | 3.3 | 20.6 | 19.2 | 19.7 | 18.4 | 19.2 | 22.4 |
| Pressure difference Δp/MPa | 0.185 | 0.216 | 0.231 | 0.240 | 0.216 | 0.194 | 0.207 | 0.216 | 0.213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Wang, Q.; Xu, D.; Huang, S.; Wang, X.; Wang, L. Design and Analysis of Pneumatic Downforce Regulating Device for No-Till Corn Planter. Agriculture 2022, 12, 1513. https://doi.org/10.3390/agriculture12101513
Cao X, Wang Q, Xu D, Huang S, Wang X, Wang L. Design and Analysis of Pneumatic Downforce Regulating Device for No-Till Corn Planter. Agriculture. 2022; 12(10):1513. https://doi.org/10.3390/agriculture12101513
Chicago/Turabian StyleCao, Xinpeng, Qingjie Wang, Dijuan Xu, Shenghai Huang, Xiuhong Wang, and Longbao Wang. 2022. "Design and Analysis of Pneumatic Downforce Regulating Device for No-Till Corn Planter" Agriculture 12, no. 10: 1513. https://doi.org/10.3390/agriculture12101513
APA StyleCao, X., Wang, Q., Xu, D., Huang, S., Wang, X., & Wang, L. (2022). Design and Analysis of Pneumatic Downforce Regulating Device for No-Till Corn Planter. Agriculture, 12(10), 1513. https://doi.org/10.3390/agriculture12101513






