Abstract
The working environment of a picking robot is complex, and the motion-planning algorithm of the picking manipulator will directly affect the obstacle avoidance effect and picking efficiency of the manipulator. In this study, a time-optimal rapidly-exploring random tree (TO-RRT) algorithm is proposed. First, this algorithm controls the target offset probability of the random tree through the potential field and introduces a node-first search strategy to make the random tree quickly escape from the repulsive potential field. Second, an attractive step size and a “step-size dichotomy” are proposed to improve the directional search ability of the random tree outside the repulsive potential field and solve the problem of an excessively large step size in extreme cases. Finally, a regression superposition algorithm is used to enhance the ability of the random tree to explore unknown space in the repulsive potential field. In this paper, independent experiments were carried out in MATLAB, MoveIt!, and real environments. The path-planning speed was increased by , the path length was decreased by , and the number of collision detections was reduced by . The TO-RRT algorithm can be used to provide key technical support for the subsequent design of picking robots.
1. Introduction
Citrus is one of the most economically important crops in the world, and it is also the most cultivated fruit in southwestern China. Currently, citrus fruits are mainly picked manually, which is time-consuming, laborious, and expensive. According to a survey, the labor used in citrus picking operations accounts for of the whole production process. With the sharp decline in the number of rural employees in China, the development of the citrus industry has been severely restricted. To improve the efficiency of picking and enhance the competitiveness of China’s citrus industry, both the research and development of citrus-picking robots have become research hotspots at home and abroad, and the path planning of the picking manipulator is one of the most difficult technologies.
In recent years, a series of path-planning methods have been proposed. The artificial potential field (APF) can be used to prevent the manipulator from colliding with obstacles when approaching the target. However, the APF easily falls into a local minimum, and it easily falls into oscillation in a complex environment [1]. Compared to the APF, the rapidly-exploring random tree (RRT) is more adaptable, faster, and more variable, but it is difficult to find the best path when using this approach [2]. Bidirectional RRT and RRT-connect algorithms are used to generate two random trees at the initial node and the target node, respectively, which improves the search speed compared with the RRT algorithm, but the path is still not optimal [3,4]. The RRT-star (RRT*) algorithm is used to make the path gradually converge with the optimum in the search process by reselecting the parent node and rerouting, but its running time is longer than that of the RRT algorithm [5]. Mohammed et al. [6] defined a straight line connecting the initial node and the target node so that the generation probability of the random tree node was normally distributed with the distance from the straight line, preventing excessive searching and avoiding falling into local extreme values. However, the searching ability in a complex environment still needs to be improved. Akgun et al. [7] combined the bidirectional RRT and RRT* algorithms to optimize the search time. Jeong et al. [8] proposed an RRT*-Quick method, which caused the nodes to tend to share the same parent node in a circular (or spherical) neighborhood. While the path generated using this method was smoother than the path generated by the RRT* algorithm, the search time increased slightly. Jeong et al. [9] introduced an informed-RRT algorithm into the RRT*-quick method to limit the sampling space of the random tree and solve the problem of increased search time caused by expanding the search domain in the process of improving the quality of the solution. When the tree nodes reached the maximum, the RRT* Fixed Nodes (RRT*FN) algorithm was used to remove a weak node and add a high-performance node so that the generated tree node was much smaller than the one in the RRT* algorithm. However, this method had little performance gap with the RRT* algorithm before the tree nodes reached the maximum number of nodes [10].
The RRT* algorithm has a strong ability to optimize the path cost, but its search efficiency is low. Cao et al. [11] introduced the target gravity to the RRT algorithm, and the attraction generated by the random node and the attraction generated by the target node were used to jointly guide the generation of new nodes in the random tree. This method improved the search speed of the random tree, but it could not escape the obstacle area quickly when blocked by obstacles. Wang et al. [12] changed the sampling area and assigned node state values so that the random tree could only be expanded through boundary nodes to reduce the generation of invalid nodes, but many redundant nodes were generated near obstacles. Zhang et al. [13] screened new nodes based on a biased-RRT algorithm. If the distance between the new node and the parent node was greater than the distance between the new node and any other nearby node, the new node was discarded. This method can be used to prevent excessive searching of the space and reduce the total number of nodes. Gong et al. [14] made the search direction of the random tree always point to the target node and performed local path planning near the obstacles. Although this method could reduce excessive searching of the space, its escape speed was slow when the random tree was blocked by many large obstacles. Li et al. [15] put forward an adaptive RRT-connect (ARRT-connect), which allowed the random tree to still have good performance in a narrow environment, and path planning could still be completed in a short time. Gao et al. [16] proposed a planning method based on an independent potential field that made the manipulator explore the gradient direction when it was far away from the target and avoided obstacles through the random search. Wang et al. [17] selected tree nodes according to the geometric structure and position of obstacles so that a path with a lower cost could be quickly obtained, but the effect of avoiding obstacles with irregular shapes was poor.
In this paper, based on a citrus tree environment, taking the shortest time as the optimization goal, and taking the Franka manipulator as the experimental platform, the RRT algorithm is improved in multiple dimensions. Its main contributions are as follows:
- On the basis of the biased-RRT, the potential field function and the adaptive probability threshold are introduced, so that the random tree has corresponding growth strategies in different potential fields. The above strategies improve the directional search ability of random trees in the repulsive potential field and enhance the escape ability of random trees in the repulsive potential field;
- To solve the problem of “falling into a trap” in the repulsive potential field of random trees, a node-first search strategy is proposed, which makes the selection of extended nodes of random trees more purposeful;
- Proper step size is crucial to improve search ability. Using an attractive step size is helpful to reduce the number of collision detections and computational complexities outside the repulsive potential field. “Step-size dichotomy” solves the problem of random trees colliding with obstacles many times due to too large of step size in the repulsive potential field;
- By introducing a regression superposition algorithm, the random tree can avoid over-searching space in the repulsive potential field and enhance the escape ability.
The rest of this article is organized as follows: The basic principles of the RRT algorithm, as well as some improvement methods and the design process of the TO-RRT algorithm, including the adaptive probability threshold, the node-first search strategy, an attractive step size, “step-size dichotomy”, and a regression superposition algorithm are introduced in Section 2. In Section 3, the performance of various algorithms in MATLAB, MoveIt!, and the real environment are compared. The main contributions of the article and future work are discussed in Section 4. The full text is summarized in Section 5.
2. Materials and Methods
2.1. RRT Algorithm
The RRT algorithm, which is a spatial search algorithm based on random sampling, aims to generate a collision-free random tree connecting the first and the last positions [18,19].
Each time the grows, a random node is generated in the space. Then, the tree node closest to is found in the tree, and a new tree node is found in the direction of with a fixed step and is connected to as . If neither nor collide with obstacles, and are added to the random tree. After several expansions, if the distance between and is less than the given threshold, the finds a path connecting to , as shown in Algorithm 1.
| Algorithm 1. RRT Algorithm. |
| 1: |
| 2: for to do |
| 3: |
| 4: |
| 5: |
| 6: if then |
| 8: end if |
| then |
| 10: return |
| 11: end if |
| 12: end for |
2.2. Some Improvement Methods
The RRT algorithm can be used to effectively explore high-dimensional space, but the path cost is high, and the algorithm takes a long time to reach completion. The biased-RRT algorithm can be used to effectively solve the shortcomings of the RRT algorithm [20,21,22,23], as shown in Algorithm 2.
| Algorithm 2. Biased-RRT Algorithm. |
| 1: |
| 2: for to do |
| 3: if then |
| 4: |
| 5: else |
| 6: |
| 7: end condition |
| 8: |
| 9: |
| 10: if then |
| 11: |
| 12: end if |
| 13: if then |
| 14: return |
| 15: end if |
| 16: end for |
In Algorithm 2, is determined by the size between the random number, , and the probability threshold . If , takes any point in the space; otherwise, the target node is taken as the sampling point.
The biased-RRT algorithm is used to guide the growth of the random tree, increase the effectiveness of sampling points, and shorten the time of path planning. However, when obstacles obstruct the growth of random trees, the biased-RRT algorithm cannot escape the obstacles quickly. Therefore, some scholars have put forward corresponding solutions, as shown in Table 1.

Table 1.
Comparison of RRT improvement methods.
2.3. TO-RRT Algorithm
2.3.1. Adaptive Probability Threshold
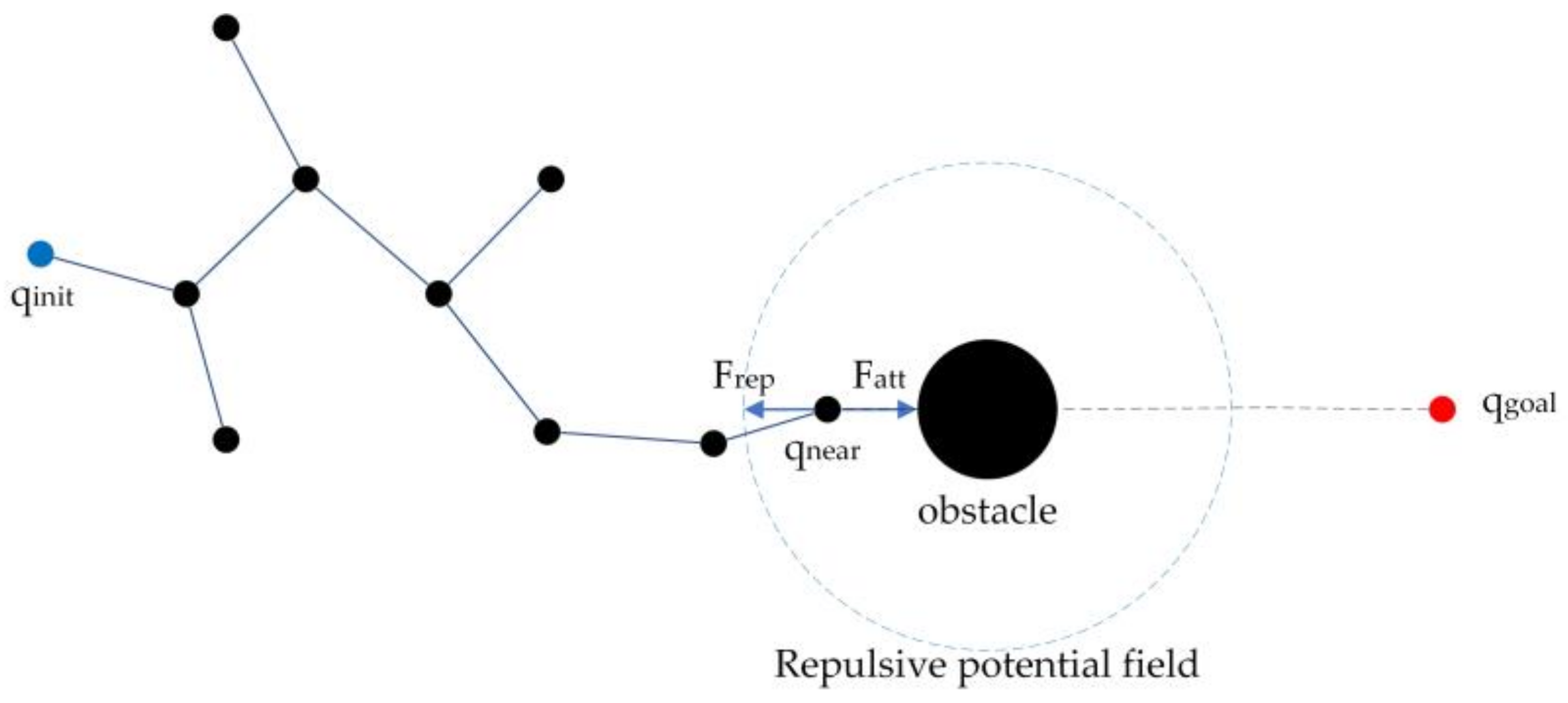
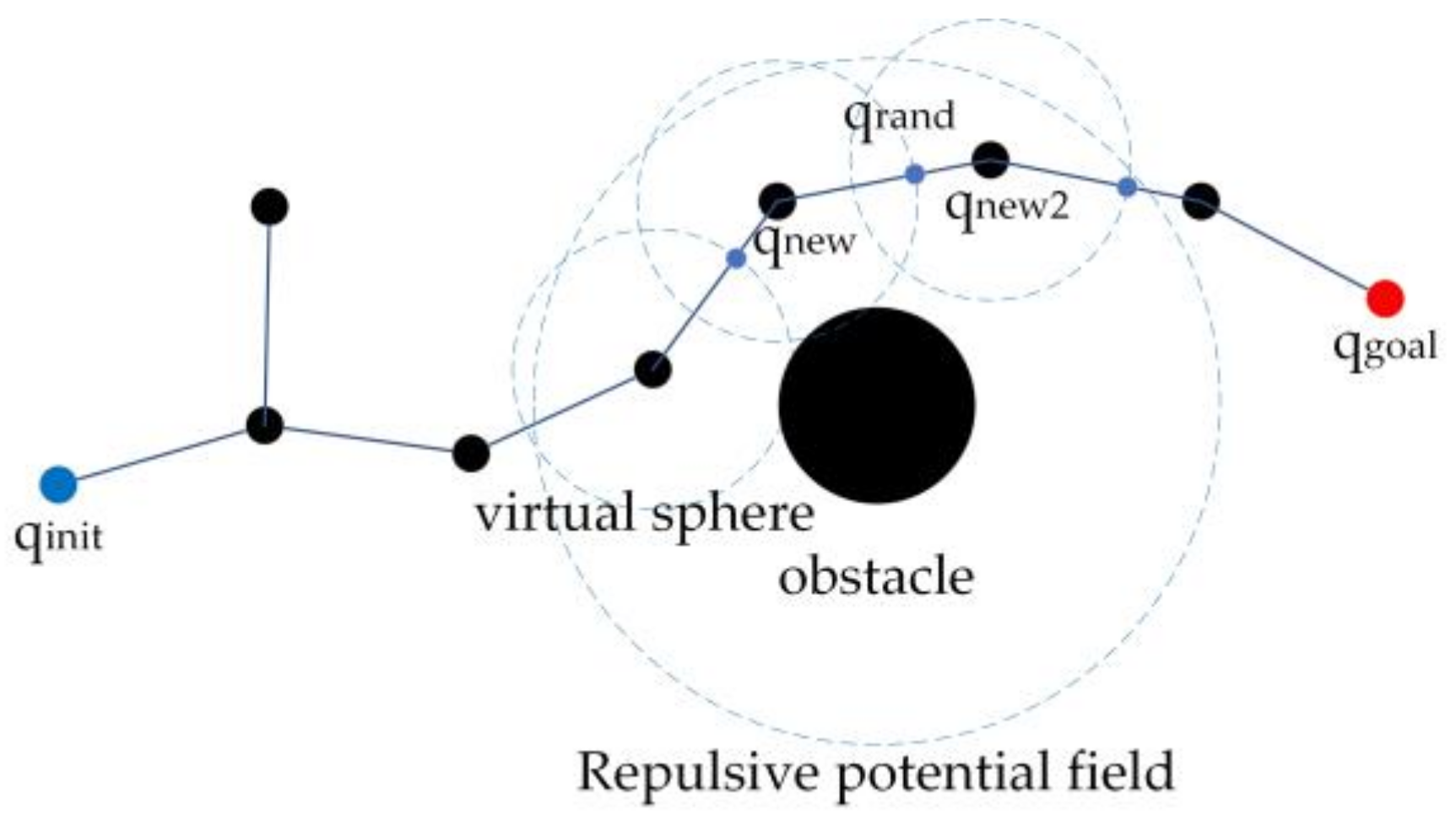
At present, some improved RRT algorithms have been used to add potential field functions to the target node , random nodes , and obstacles. The random tree changes its growth direction under the action of a combined potential field, which makes it expand to the target when avoiding obstacles [27,28,29,30,31,32,33]. This kind of algorithm improves the search efficiency of the random tree, but each expansion of the random tree requires several vector operations of the potential field force, which occupies a large amount of the system memory. In addition, if the repulsive potential field of the obstacles is considered, the algorithm may fall into a local minimum problem, as is common in APF, resulting in being unable to generate a new node , as shown in Figure 1.
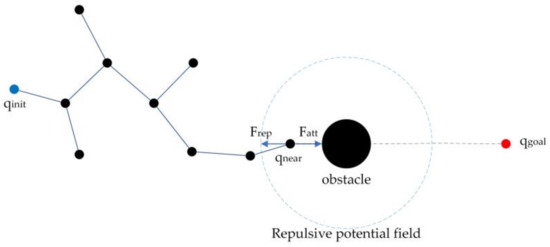
Figure 1.
The algorithm falls into a local minimum.
Considering the complexity and uncertainty of the above algorithm in different environments, an attractive potential field and a repulsive potential field for the target node and obstacle, respectively, based on the biased-RRT algorithm were established. Therefore, the probability threshold changed according to the different types of potential fields.
Similar to the APF algorithm, the range of the attractive potential field was the whole operating space, while the range of the repulsive potential field was limited to a certain distance around the obstacle. In the range of the repulsive potential field, if the random tree tended to search for the target node , the random tree had a strong ability to grow biased. At this time, if the obstacle blocked , multiple failed growth near obstacles could occur for the random tree, so it tended to search randomly within the repulsive potential field. When the random tree left the range of the repulsive potential field, it continued to tend to search for , as shown in Algorithm 3.
| Algorithm 3. Probability Threshold under the Control of Potential Field. |
| 1: if then |
| 2: |
| 3: else |
| 4: |
| 5: end if |
| 6: return |
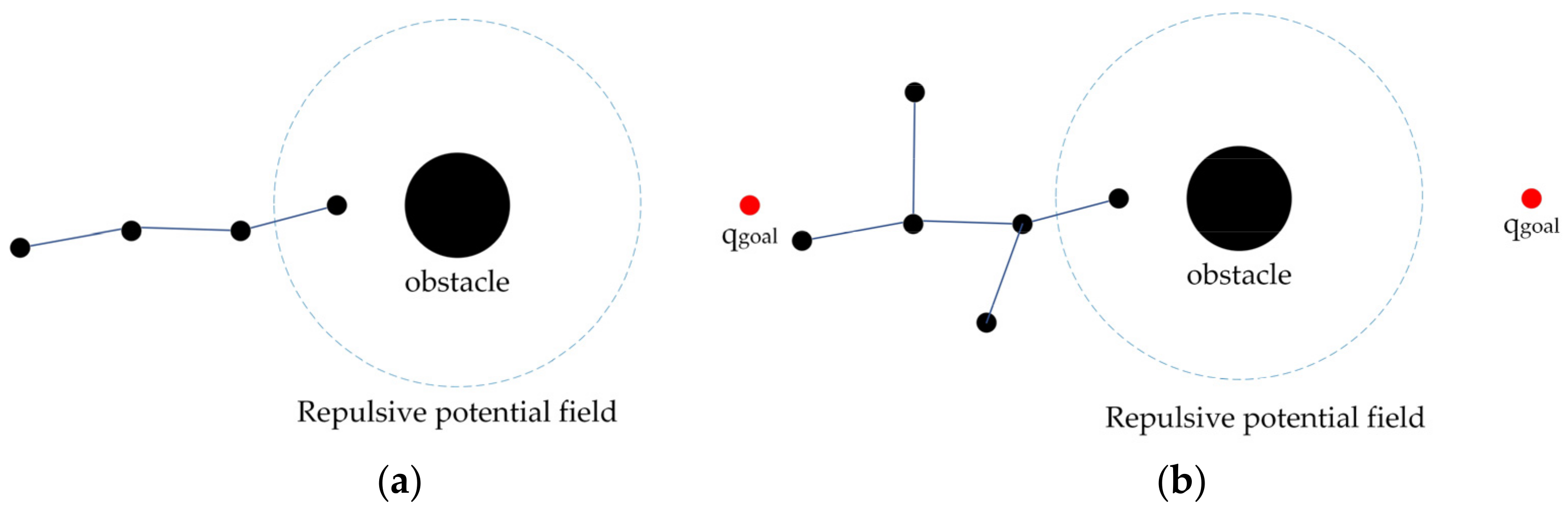
The growths of the random tree under both the control of the constant probability threshold and the adaptive probability threshold are shown in Figure 2a,b, respectively. Figure 2a shows that, if the random tree maintained a constant probability threshold during the search process, the obstacle did not affect the goal of random tree expansion. If the adaptive probability threshold was adopted, the random tree chose a better growth direction according to the location tendency of the new node. It was learned through many experiments that the probability threshold outside the scope of the repulsive potential field was 0.3, and the probability threshold inside the range of the repulsive field was 0.7.
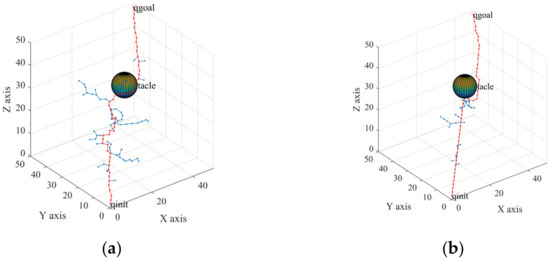
Figure 2.
Threshold comparison. (a) Constant probability threshold; (b) Adaptive probability threshold.
2.3.2. Node-First Search Strategy
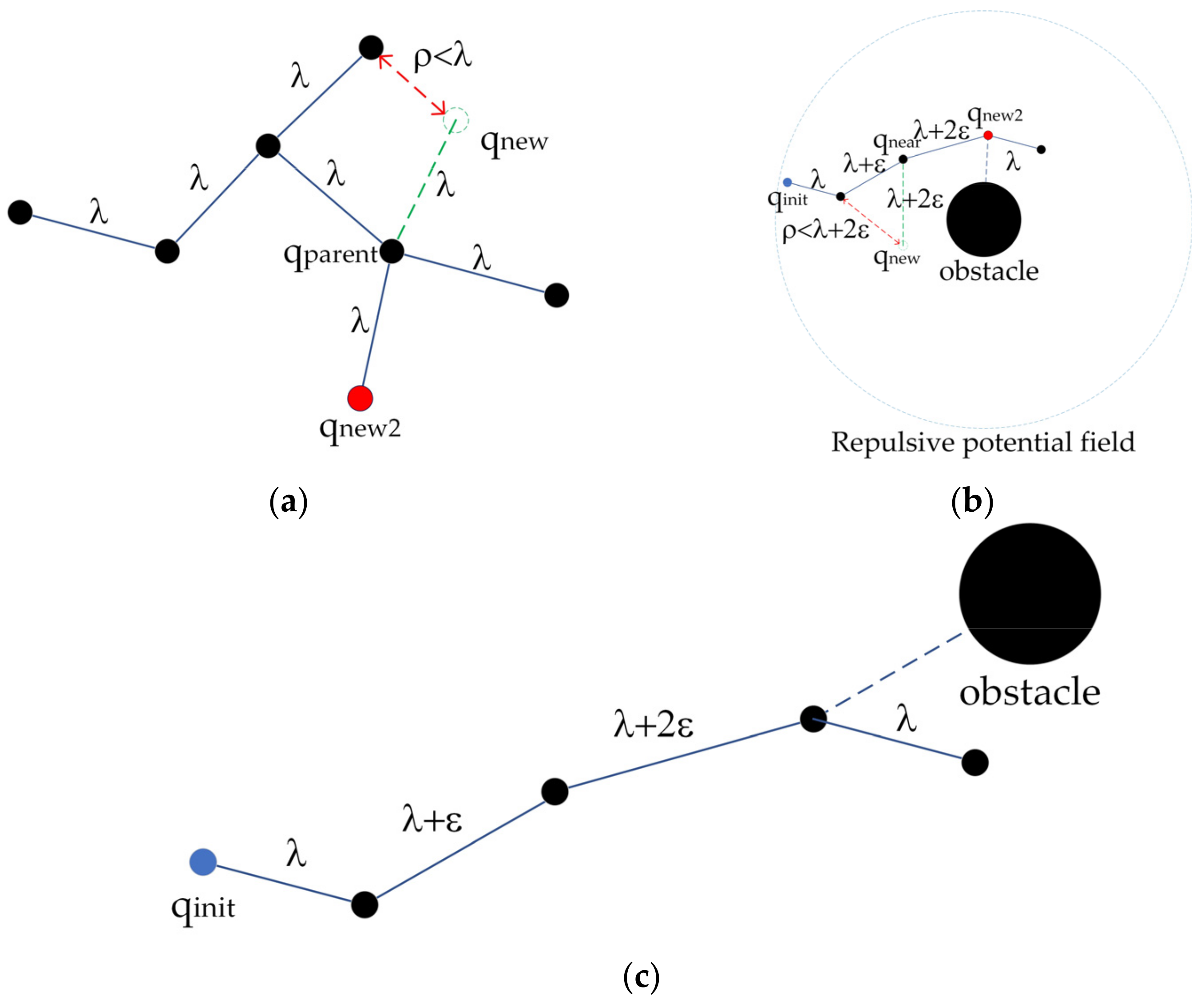
According to the biased-RRT algorithm, when , takes the coordinate value of and then selects the closest to in the random tree as the parent node of . If the random tree only expands to the target in each search round without considering the random search, then the new node in this search round will become the parent node of the new node in the next search round, and the random tree is a straight line segment connecting and .
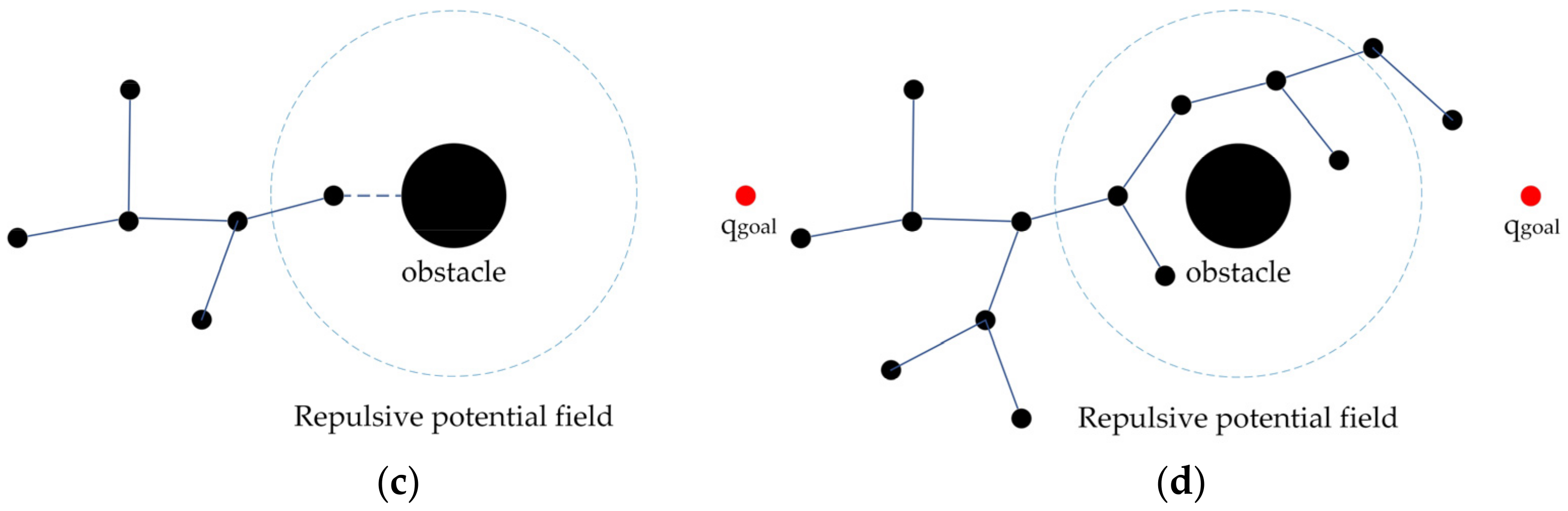
As in Section 2.3.1, when the end node of the random tree expands to the range of the repulsive potential field, the random tree tends to select any node in the space as in the next search selection, so the probability of random expansion of the end node is small. If the next round of search satisfies , since the end node of the random tree is closest to , will be expanded, causing the newly generated path to collide with the obstacle. To summarize, when , the end node collides with the obstacle; when , any node in the tree will be selected for expansion, which is no different from the traditional RRT algorithm. This phenomenon is called “falling into a trap”, as shown in Figure 3.
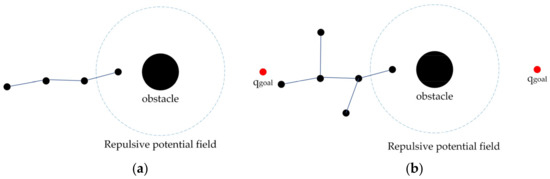
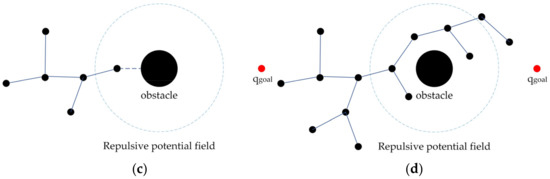
Figure 3.
The random tree falls into a trap in the repulsive potential field. (a) The random tree entering obstacle potential field; (b) The random tree begins to expand randomly; (c) The random trees collide with obstacles; (d) The random tree is expanded several times.
For this reason, a node-first search strategy was proposed in this paper, as shown in Algorithm 4. When the of the random tree grew into the range of the repulsive potential field of obstacles, a virtual spherical surface with a radius and center was generated. If was satisfied in the next round of search, point on the virtual spherical surface was preferentially selected, and was used as the parent node of the next round of search to generate a new node . If and the line segment did not collide with obstacles, the path and were kept. A new search round continued until the end node of the random tree was separated from the obstacles, as shown in Figure 4.
| Algorithm 4. Node-First Search Algorithm. |
| 1: if then |
| 2: if then |
| 3: |
| 4: else |
| 5: |
| 6: end if |
| 7: else |
| 8: |
| 9: end if |
| 10: return |
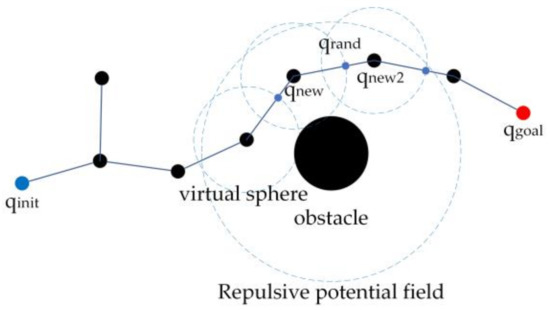
Figure 4.
Schematic diagram of the node-first search strategy.
2.3.3. Attractive Step Size and Step-Size Dichotomy
From the above description, the node-first search strategy was used to prevent the random tree “falling into a trap” within the range of the repulsive potential field. Since the random tree has a certain probability of random search outside the range of the repulsive potential field of obstacles, more iterations will be generated. An appropriate step size can effectively reduce the iterations of the random tree. In the case that the length of the path is determined, a small step size will cause more collision detections and distance calculations, and a large step size will often make the random tree collide with obstacles. Therefore, the step size should be expanded as much as possible on the premise of reducing the number of collisions [34,35].
According to the APF algorithm, the attractive force of acts on the whole operating space and is proportional to the distance between the end joints of the manipulator, which is beneficial to control the growth step of the RRT. If obstacles are not considered, the random tree should increase the step size when it is far away from to quickly expand to . When the random tree is closer to , if it continues to maintain a large step size, a large number of redundant nodes will be generated at , as shown in Figure 5a. Therefore, the random tree should gradually approach with small step sizes, as shown in Figure 5b.
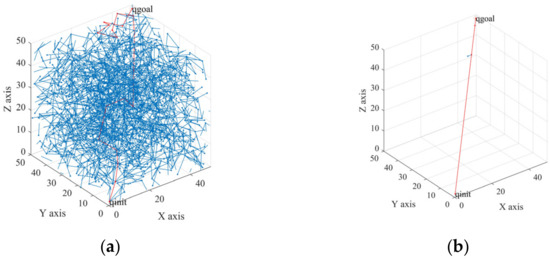
Figure 5.
Fixed step size and attractive step size. (a) Fixed step size; (b) Attractive step size.
For this reason, an attractive step size was proposed, which was defined as:
where represents the attractive step size, and is the attractive parameter.
If obstacles are considered, the step size of the random tree in the random search is fixed, and an attractive step size is taken when growing toward . This method ensures that the random tree grows toward as soon as possible outside the range of the repulsive potential field and avoids collisions with obstacles due to excessive steps within the range of the repulsive potential field.
The parameters of the potential field function of the manipulator are different in different operating spaces. For example, when the attractive parameter is too large, will increase accordingly. If , will collide with obstacles. In addition, the end nodes tend to grow toward outside the range of the repulsive potential field. Therefore, the random tree still has a high probability of colliding with obstacles in the next round of search.
For this reason, a “step-size dichotomy” was introduced to solve the problem of excessive step size. When grew toward and there were obstacles between them, the distance between and the obstacles was calculated. If , the was shortened to the original value of , and the sizes of and were compared again until ; see Algorithm 5.
| Algorithm 5. Step-size Dichotomy. |
| 1: if then |
| 2: while do |
| 3: |
| 4: end while |
| 5: else |
| 6: |
| 7: end if |
| 8: return |
2.3.4. Regression Superposition Algorithm
From Section 2.3.3, if the random tree grows within the range of the obstacle repulsive potential field, a large number of redundant nodes will be generated on the surface of the obstacle due to the high probability of the random search, as shown in Figure 6a. As a result, a regression superposition algorithm is proposed in this section to adaptively select extended nodes and change the step size of the random search, as shown in Figure 6b.
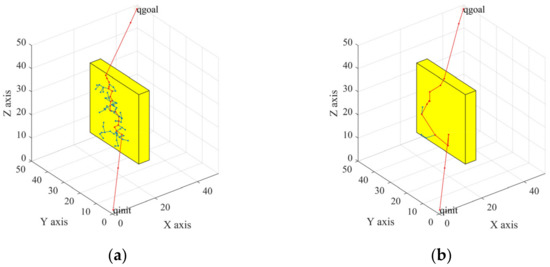
Figure 6.
Differences before and after improvement. (a) The random trees generated a large number of nodes on the surface of obstacles; (b) The random tree had fewer nodes on the obstacle surface.
The regression superposition algorithm consists of a regression algorithm [36] and a step-size superposition algorithm. In the regression algorithm, if the distance between and was larger than the distance between and any node in the random tree except , it was considered to meet the regression conditions:
If Formula (2) was satisfied, was regarded as a regression node. The regression node would not become the tree node of the random tree, but it was removed until a new node that did not meet the regression condition was found, as shown in Figure 7a.
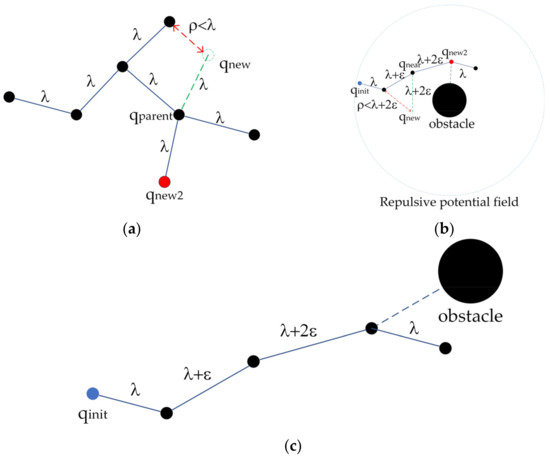
Figure 7.
Regression superposition algorithm. (a) Regression algorithm; (b) Regression superposition algorithm; (c) Step-size superposition algorithm. Note: , the initial step size; , the step size of superposition; , the distance between and any node.
To further reduce the number of tree nodes, the step-size superposition algorithm was incorporated based on a regression algorithm. When the random tree was searched randomly, the initial step size was set to , and the step size was increased by after each round of the random search until the extended branches of the random tree collided with obstacles. Then, the search step size of the next round was returned to the initial step size , and the step size was superimposed again until the random tree searched toward , as shown in Figure 7c.
The random tree used an attractive step size when searching toward to reduce the generation of redundant nodes. During the random search of the random tree, the regression superposition algorithm was used to enhance the ability of the random tree to search the unknown space, as shown in Figure 7b.
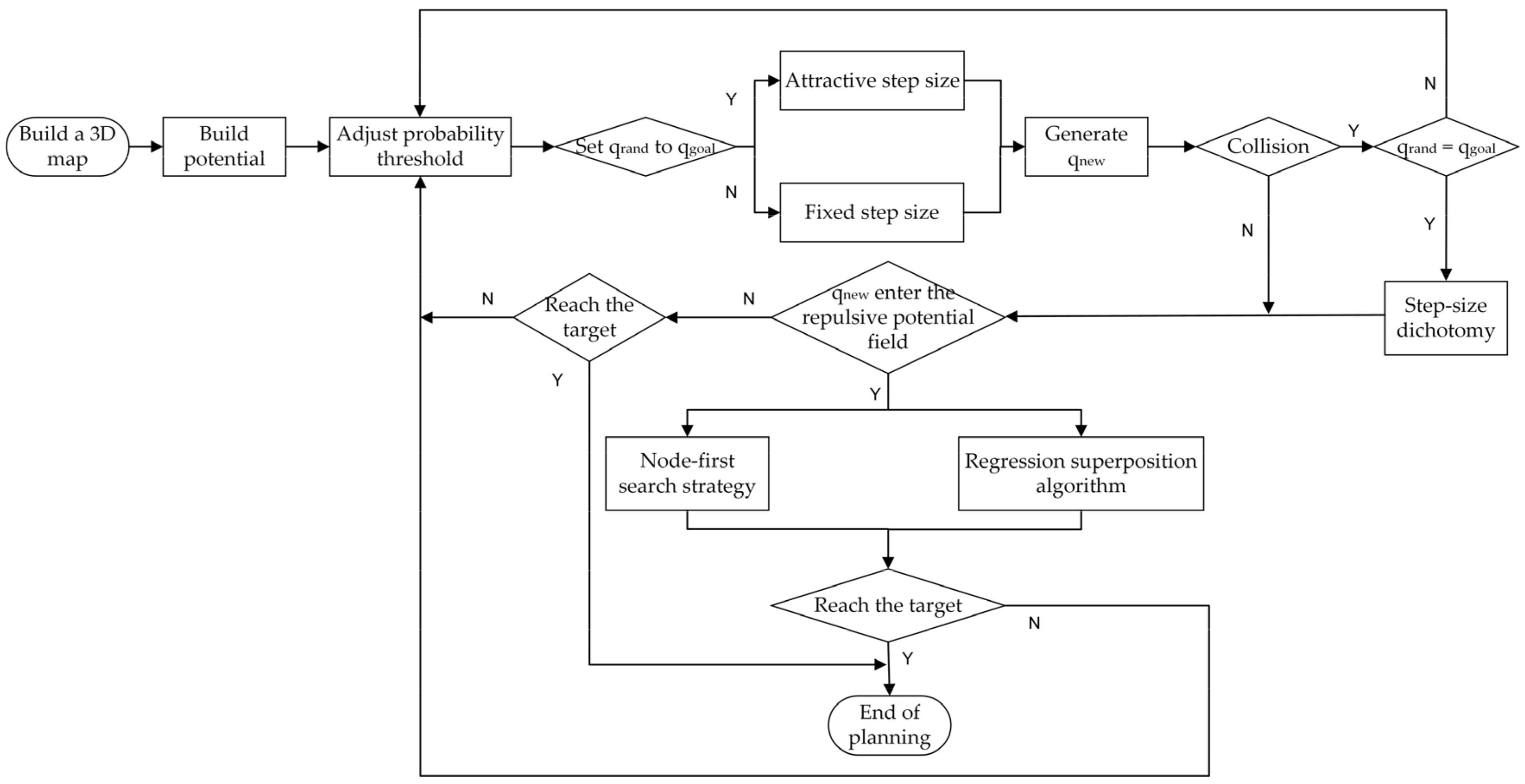
The TO-RRT algorithm was used to dynamically adjust the growth direction of the random tree by the probability threshold controlled by the potential field and to define two different growth methods according to the different growth directions. Therefore, the random tree could quickly grow to the target outside the range of the repulsive potential field and quickly determine the escape path within the range of the repulsive potential field. The algorithm flow chart is shown in Figure 8.
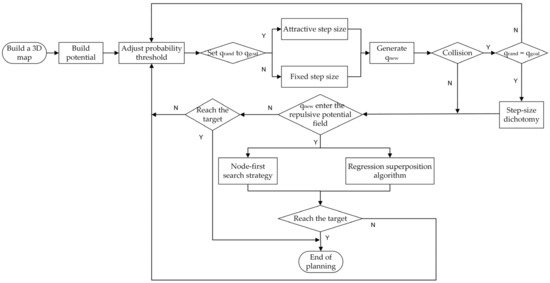
Figure 8.
Flowchart of the TO-RRT algorithm. Note: A, yes; N, no.
3. Results
3.1. Comparative Experiment of Path Planning in a Complex Environment
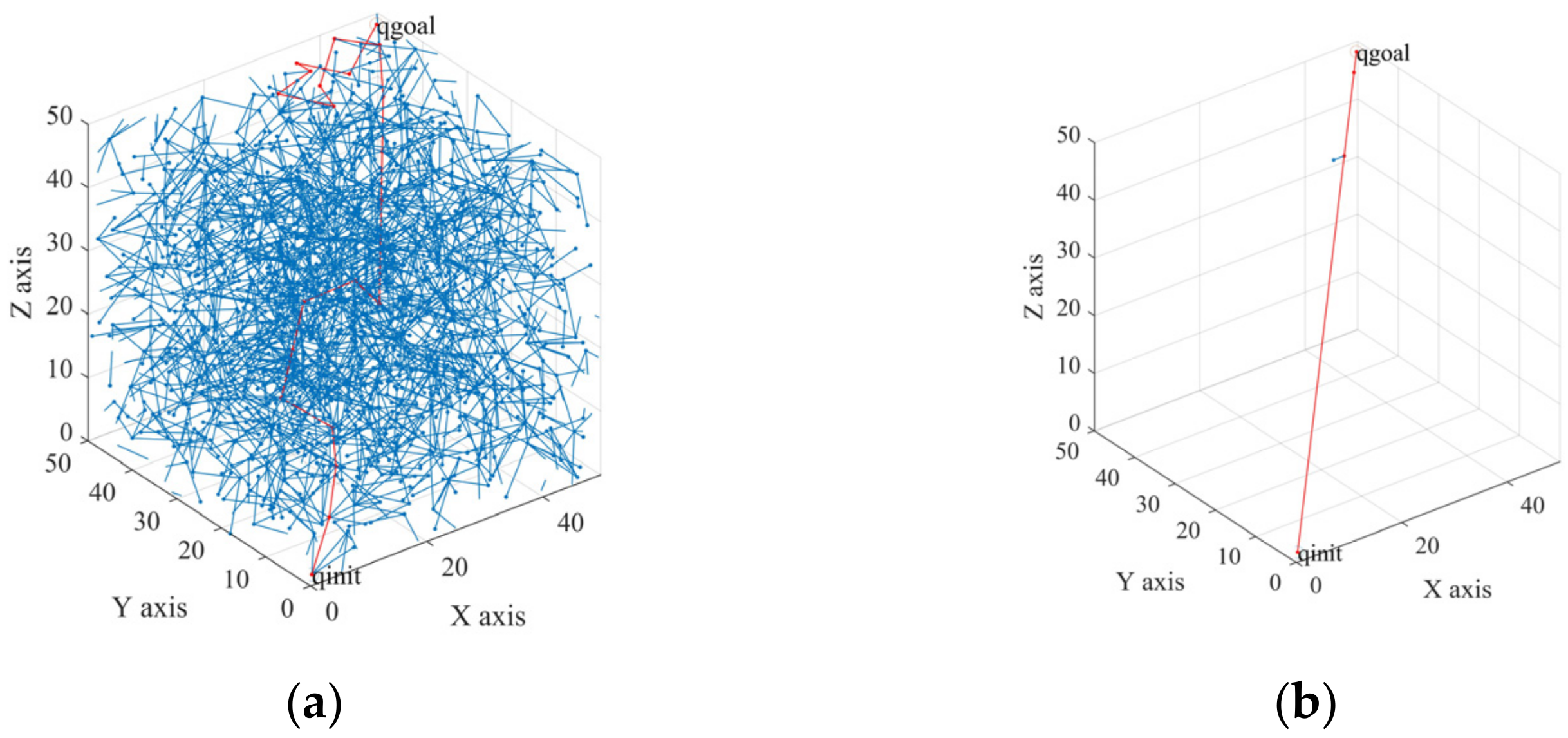
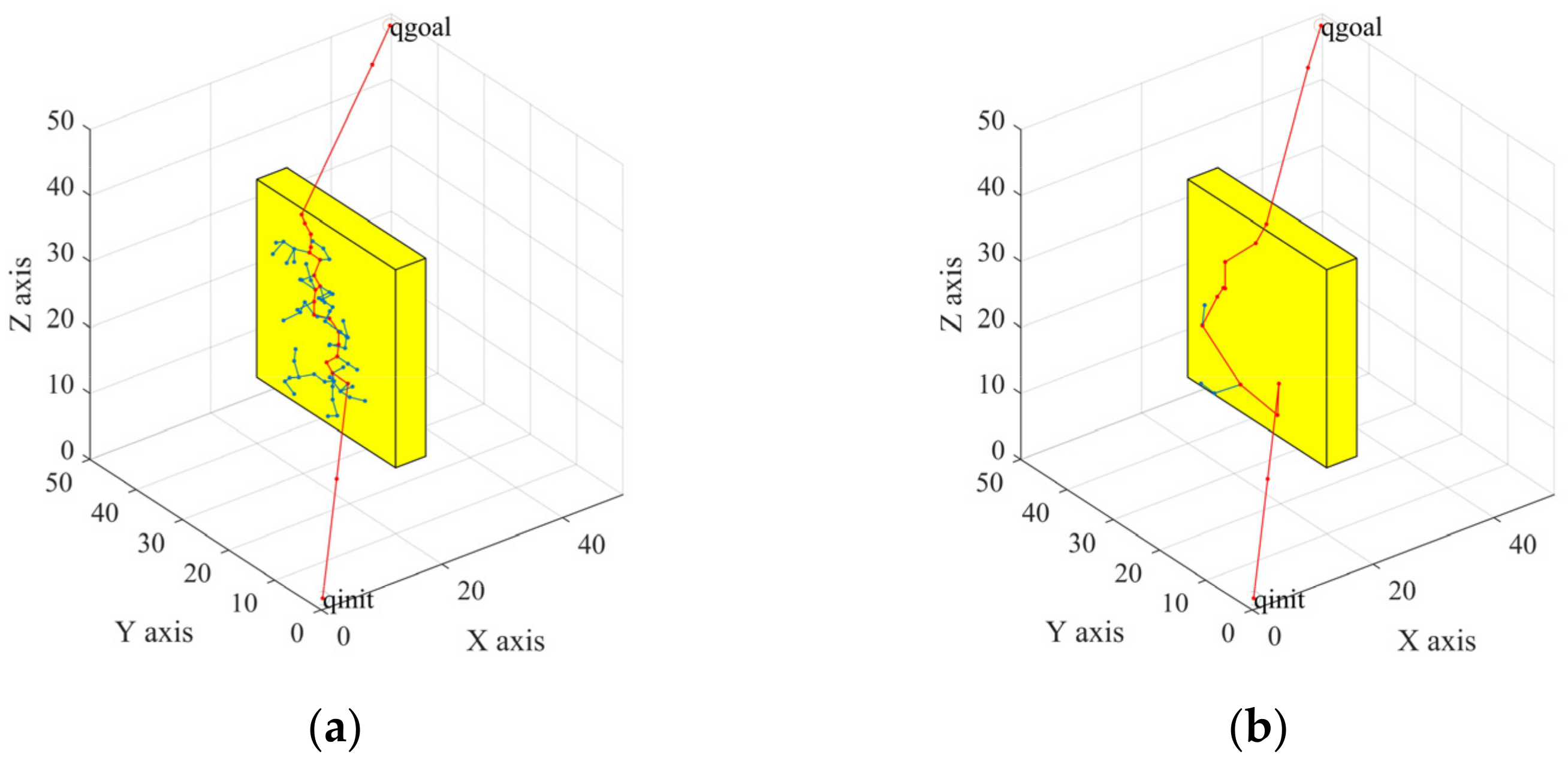
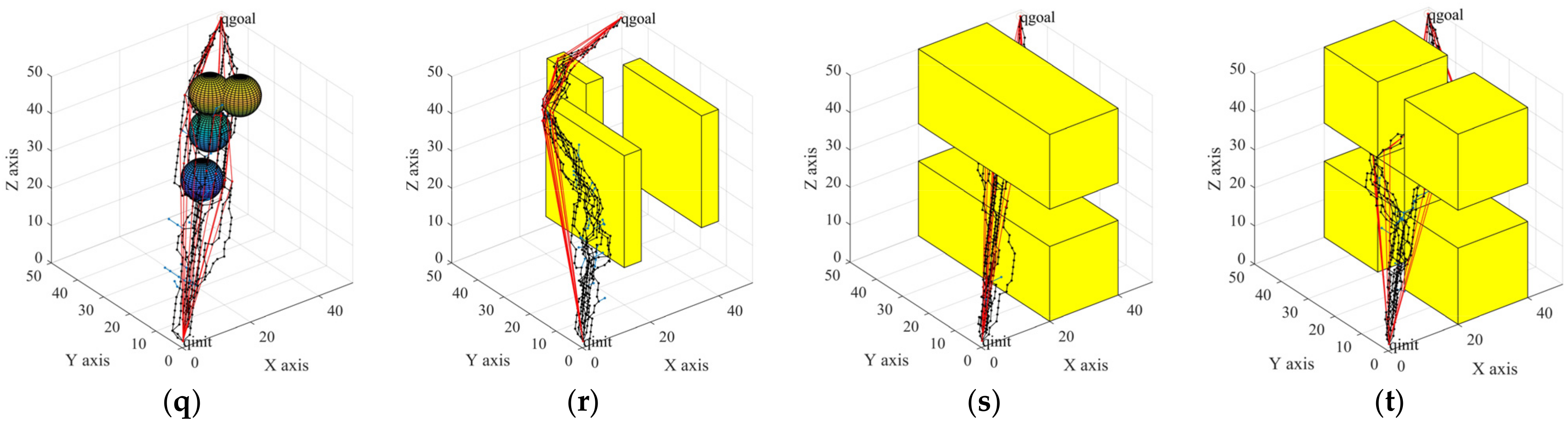
To verify the speed, stability, and low path cost of the TO-RRT algorithm, the RRT algorithm, the biased-RRT algorithm with a target offset probability of , the TO-RRT algorithm, the RRT-BCR algorithm, and the NC-RRT algorithm are compared in this section using complex environments (i.e., a multi-sphere environment, a multi-rectangle environment, a single-channel environment, and a multi-channel environment).
In the simulation experiment, the initial step size was 2, the maximum number of failed growth times was 100,000, the map size was , the starting point was (1, 1, 1), and the target point was (49, 49, 49). The blank area in the map represented the obstacle-free area, other colors represented the obstacle area, the blue path represented the random tree, the black path represented the collision-free path from the starting point to the target point, and the red path represented the path optimized by the greedy algorithm.
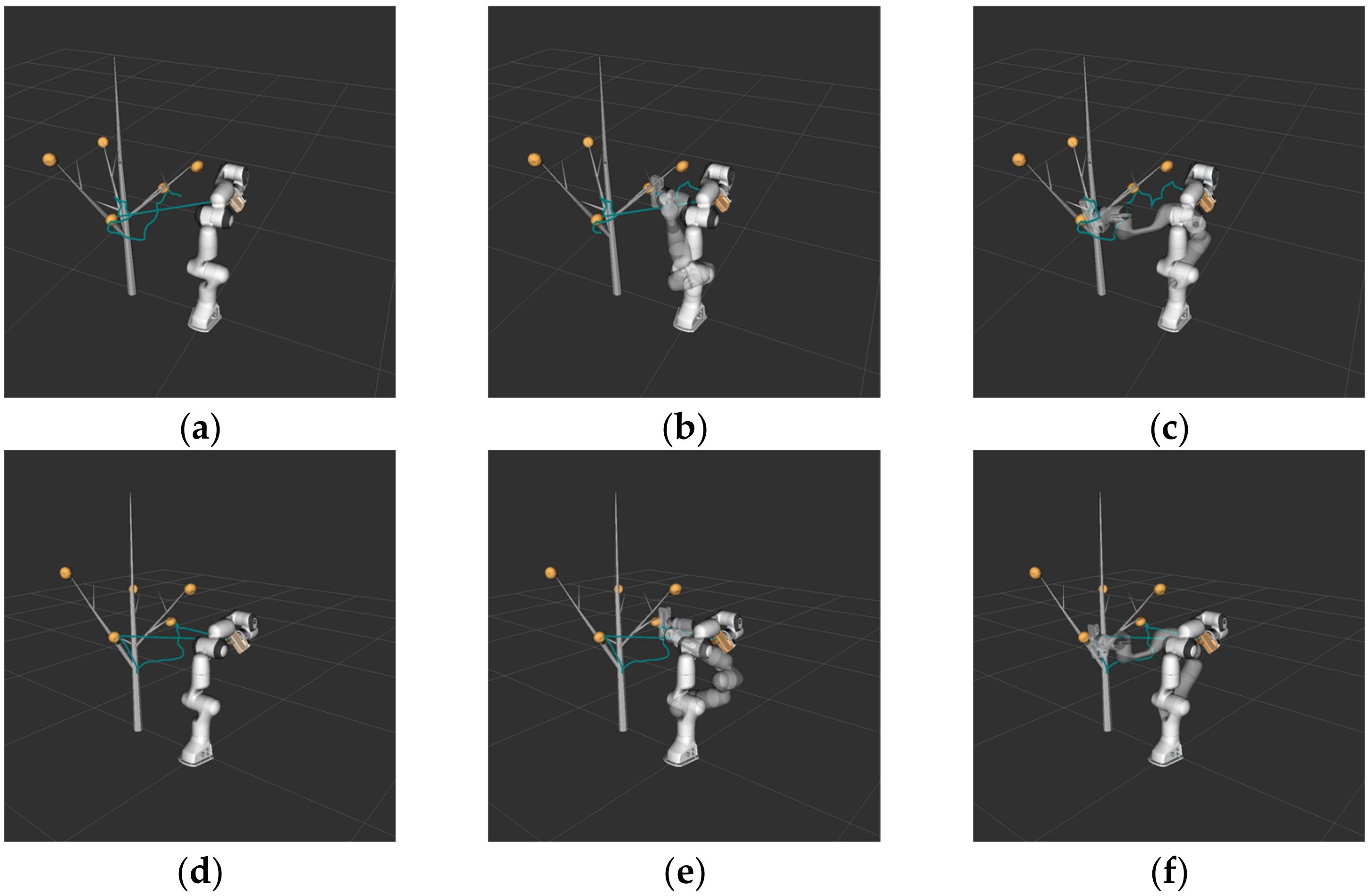
Figure 9a,e,i,m,q show that, although the RRT algorithm can be used to find a collision-free path from the initial point to the target point, the whole space was searched, so that the highest amount path nodes were generated. Compared with the RRT algorithm, the biased-RRT algorithm did not search too much invalid space, so there were fewer path nodes. When using the RRT-BCR algorithm and the NC-RRT algorithm, the sizes of the random trees were reduced through a regression mechanism and an adaptive sampling area, respectively. The TO-RRT algorithm was used to greatly reduce the number of nodes in the space, and its complexity was the lowest. Figure 9b,f,j,n,r show that the RRT algorithm still searched the whole space. Although the biased-RRT algorithm generated fewer nodes than the RRT algorithm, the search tree generated a large number of nodes on the surface of obstacles, which increased the number of iterations. The NC-RRT algorithm made the random tree tend to expand through boundary nodes through the node control mechanism, so it had fewer redundant nodes. It can be seen from Figure 9c,d,g,h,k,l,o,p,s,t that the RRT algorithm and the biased-RRT algorithm could not quickly find the “escape channel”. Although the RRT-BCR algorithm limited the expansion of nodes that were prone to collision, it increased the expansion times of other nodes. Due to the regression superposition algorithm and node-first search strategy introduced into the TO-RRT algorithm, the random tree could quickly search the nearby area to find the “escape channel” in the repulsive potential field.
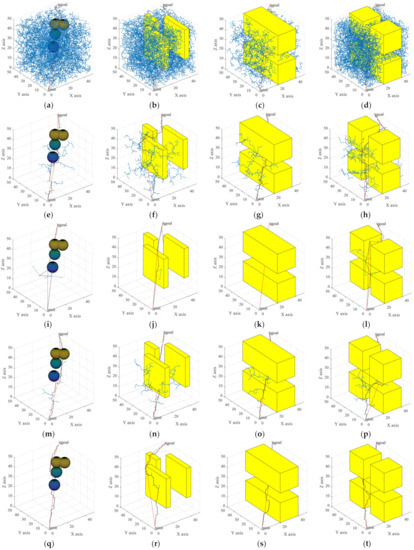
Figure 9.
The performances in different environments of: the RRT algorithm (a–d); the biased-RRT algorithm with a target offset probability of (e–h); the TO-RRT algorithm (i–l); the RRT-BCR algorithm (m–p); and the NC-RRT algorithm (q–t).
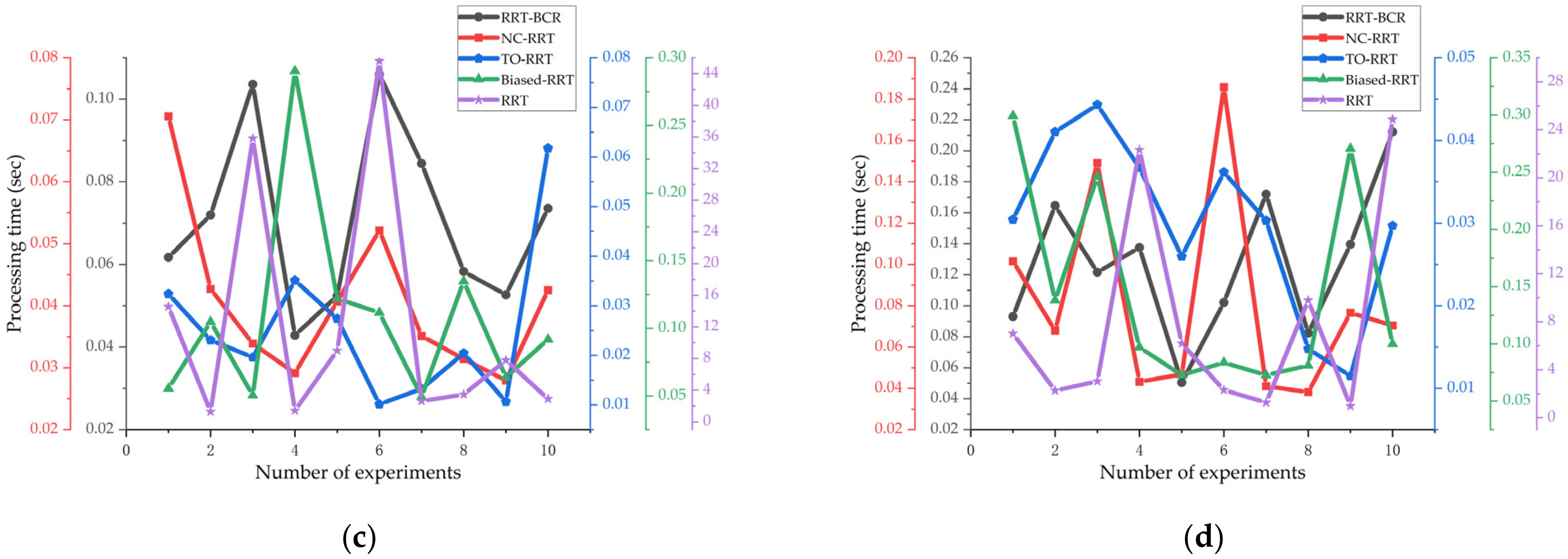
There are certain errors and contingencies in a single experiment. To better reflect a real situation, 10 simulation experiments were carried out in the same environment as described above, shown in Figure 10.
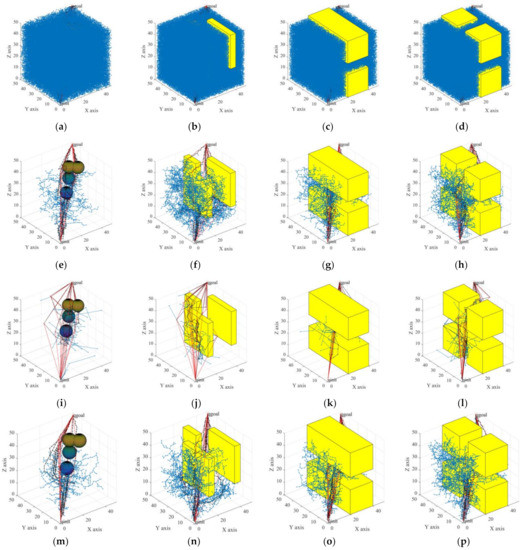
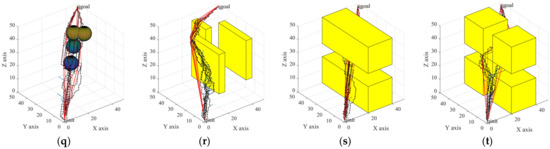
Figure 10.
Ten experiments each of: the RRT algorithm (a–d); the biased-RRT algorithm with a target offset probability of (e–h); the TO-RRT algorithm (i–l); the RRT-BCR algorithm (m–p); and the NC-RRT algorithm (q–t).
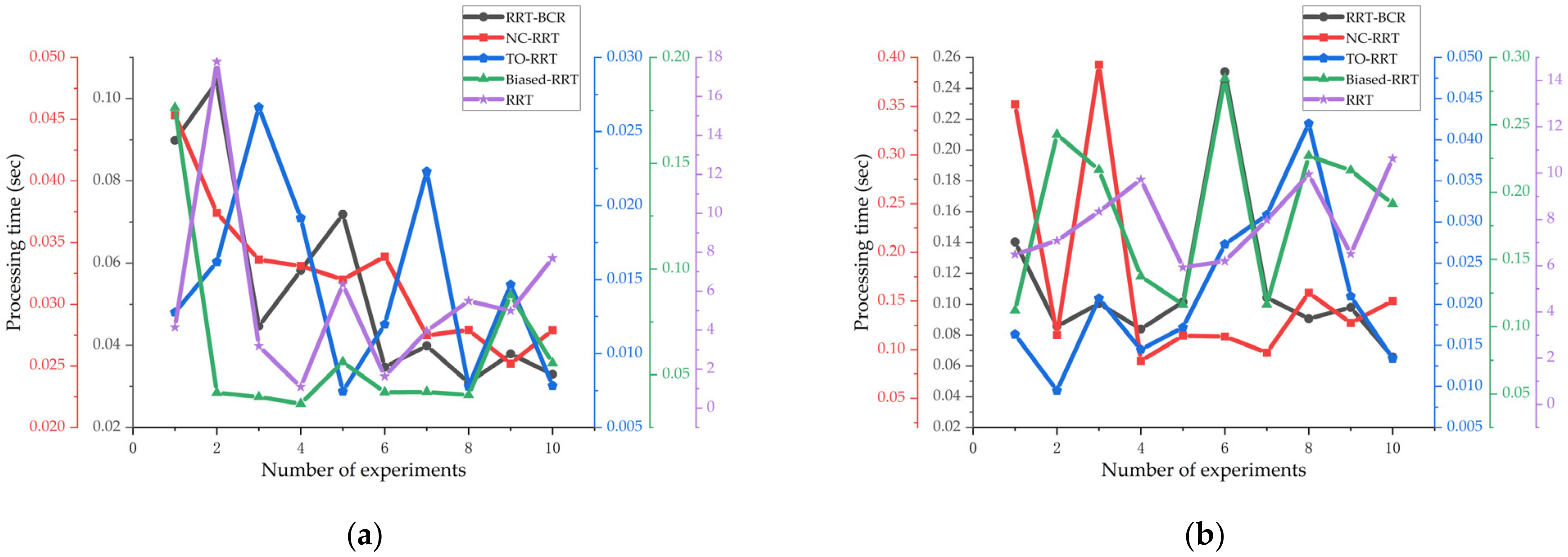
Figure 10 shows that the TO-RRT algorithm maintained strong stability in 10 experiments and did not traverse the whole space due to being blocked by obstacles, while the RRT algorithm and the biased-RRT algorithm both generated a large number of nodes in the space. In addition, the RRT-BCR algorithm had fewer path nodes than the biased-RRT algorithm, and in the NC-RRT algorithm, there was little difference in the path in each search. The comparison of the running times of the three algorithms in different environments is shown in Figure 11. Figure 11 shows that the RRT algorithm had the longest running time and poor running-time stability, especially in a single-channel environment, with the longest running time at 45.6057 s and the shortest running time at 1.2880 s. Compared with the RRT algorithm, the biased-RRT algorithm had a much shorter running time and strong running-time stability, but the search time in a complex environment was longer. The longest running times of the TO-RRT algorithm in the four environments were 0.0225 s, 0.0420 s, 0.0618 s, and 0.0443 s, and the shortest running times were 0.0056 s, 0.0134 s, 0.0101 s, and 0.0115 s. The difference between the longest search time and the shortest search time in a single environment did not exceed 0.06 s, which not only indicated a short search time but also a strong and stable running time. The NC-RRT algorithm performed poorly in a multi-rectangle environment, with a difference of 4.44 times between the longest running time and the shortest running time, while the RRT-BCR algorithm was only 3.82 times.
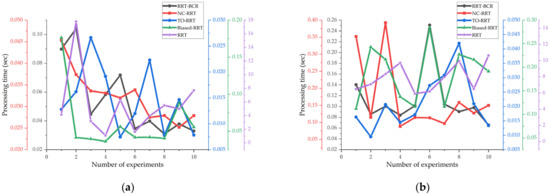
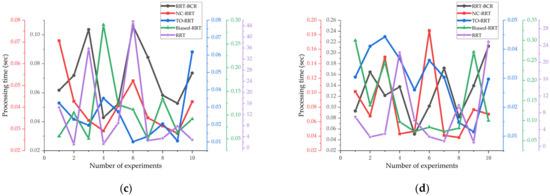
Figure 11.
The running times of the RRT algorithm, the biased-RRT algorithm with a target offset probability of , the TO-RRT algorithm, the RRT-BCR algorithm, and the NC-RRT algorithm. (a) Multi-sphere environment; (b) Multi-rectangle environment; (c) Single-channel environment; (d) Multi-channel environment.
Table 2 shows the average values of each index of the 3 algorithms over 10 experiments (biased-RRT represents the biased-RRT algorithm with a target offset probability of ). In the multi-sphere environment, the TO-RRT algorithm had a running time that was less than the RRT algorithm, which was mainly because the number of collision detections and the number of failed node growths of the former were reduced by and , respectively, compared with the latter. In addition, compared with the RRT algorithm, the number of path nodes in the TO-RRT algorithm was reduced by , which shortened the length of its search path by . When the random tree encountered a large area of obstacles, the TO-RRT algorithm was used to reflect the advantages in the search time more than the RRT algorithm. For example, the number of tree nodes and the number of failed growths of nodes of the RRT algorithm in the multi-rectangle environment reached 17,358.3 and 3144.8, respectively, resulting in a running time of 7.8822 s, while the running time of the TO-RRT algorithm was only 0.0213 s. In addition, the RRT-BCR algorithm performed better than the NC-RRT algorithm in a multi-rectangle environment, and its running time was shortened by compared with the NC-RRT algorithm because the RRT-BCR algorithm removed nodes that collided many times when facing obstacles with large occlusion areas. The biased-RRT algorithm produced too much failure growth when encountering obstacles with large areas. For example, in a multi-channel environment, the node failure growth rate of the biased-RRT algorithm was , while the RRT algorithm and TO-RRT algorithm had node failure growth rates of only and , respectively. Therefore, the biased-RRT algorithm was not ideal in a complex environment. Since the NC-RRT algorithm always took the area between the configuration point and the target as the sampling radius and tended to use boundary nodes for expansion, it could not produce valid nodes when the obstacle was between the configuration point and the target. For example, in multi-channel and multi-rectangle environments, the collision detection times of the NC-RRT algorithm were 21,487 times and 55,077 times. In summary, compared with the other algorithms, the TO-RRT algorithm had significant advantages in searching speed and the number of nodes in the random tree.

Table 2.
Experimental results of each algorithm in different environments.
3.2. Obstacle Avoidance Test Based on the Robotics Toolbox
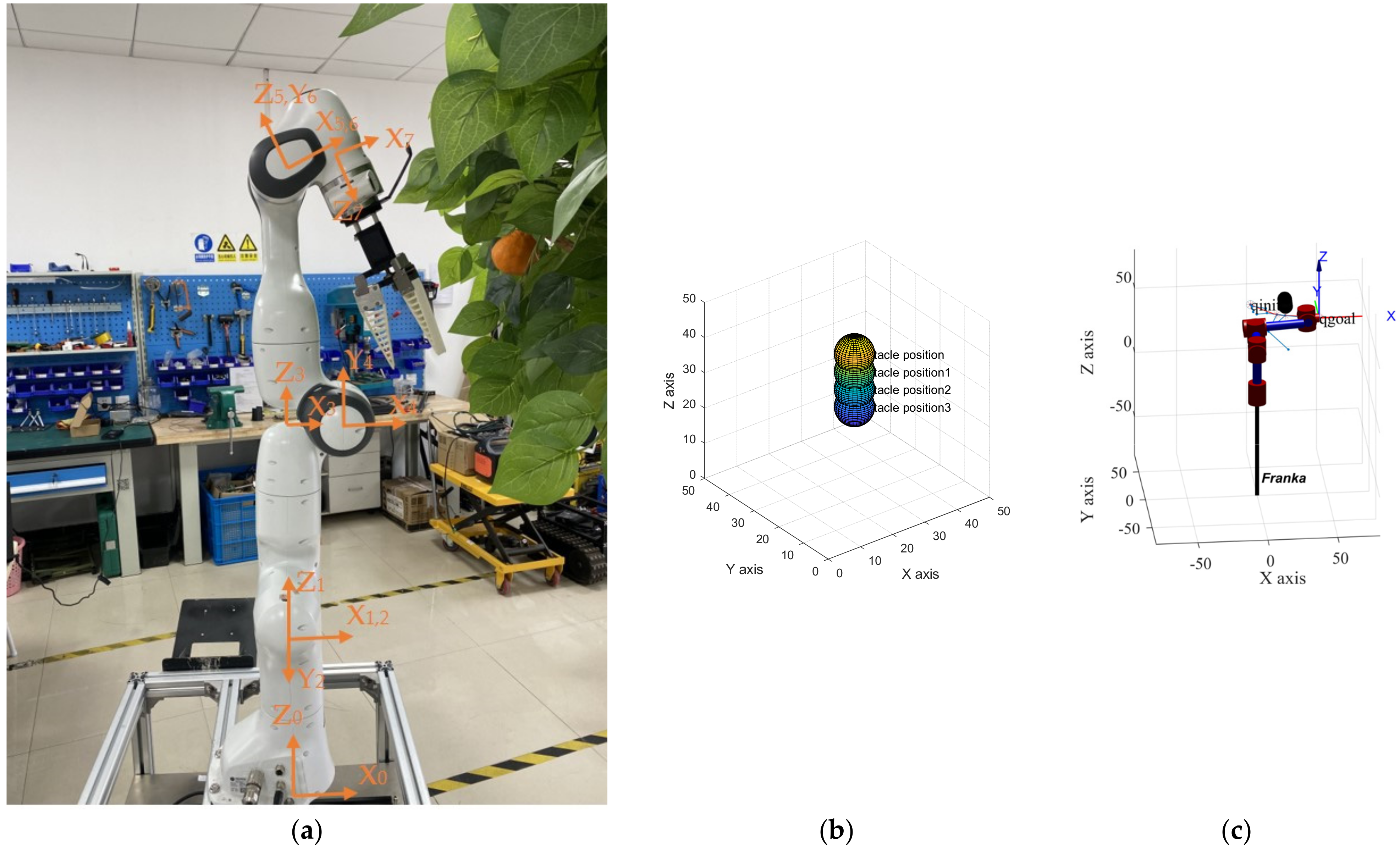
To verify the feasibility of the TO-RRT algorithm on the manipulator, Robotics Toolbox 10.2 in MATLAB was used to model the Franka manipulator. Franka is a 7-DOF robot with high precision and fast response. Its payload is 3 kg, and the maximum contact area is 855 mm. The Franka manipulator can realize two-way communication between itself and the workstation through the Franka Control Interface (FCI) and an Ethernet connection. Therefore, complete real-time control can be achieved with a sampling frequency of 1 kHz. In terms of picking performance, Franka’s pose repeatability is within 0.1 mm. Even at the highest speed of 2 m/s, the path deviation can be ignored, which provides good working conditions for fruit picking. The physical object of the Franka manipulator and its D-H parameters are shown in Figure 12a and Table 3, respectively.
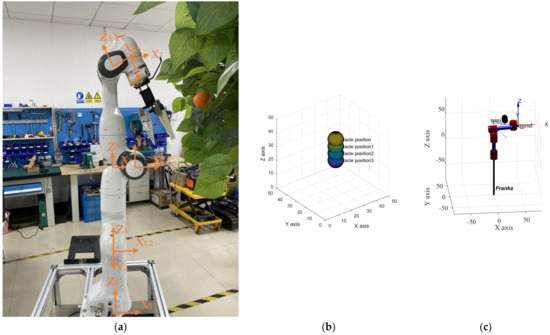
Figure 12.
Materials and results of simulation experiments based on using Robotics Toolbox. (a) The physical object of the Franka manipulator; (b) Trunk model; (c) The Franka manipulator avoids obstacles.

Table 3.
D-H parameters.
To simplify the trunk and improve the operation speed of the TO-RRT algorithm, the trunk was regarded as a combination of spheres [29], as shown in Figure 12b and Table 4. To judge whether the manipulator collided with obstacles, the shortest distance from the center of the sphere to the origin of the coordinate system of adjacent links of the manipulator was used. The three-dimensional coordinates of each joint of the manipulator were obtained through a forward kinematics solution, and if the manipulator did not collide with the tree trunk, the following conditions must be met:

Table 4.
Obstacle parameters.
In the formula, is the radius of the obstacle ball, and is the radius of the cylinder.
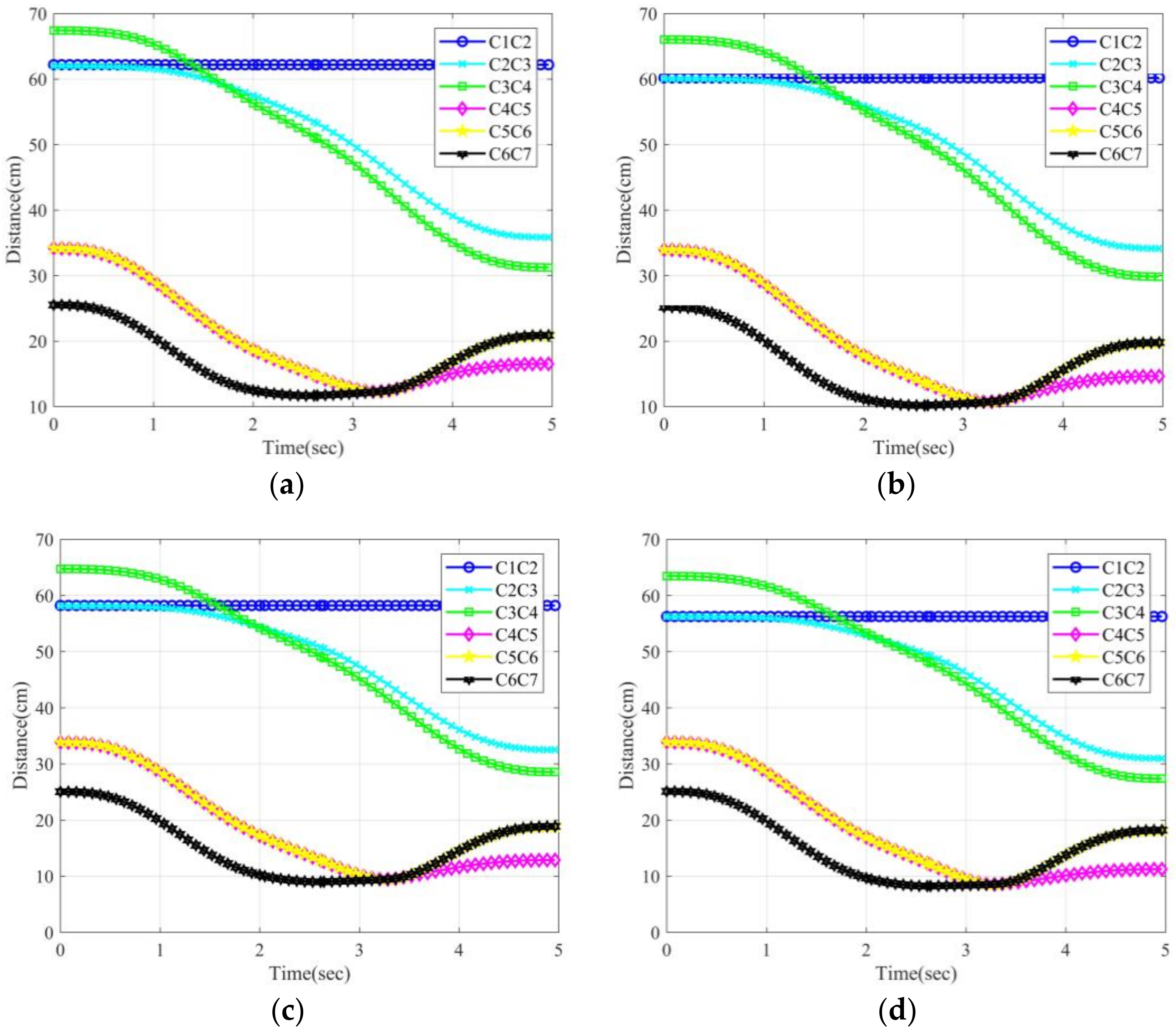
Figure 12c shows the Franka manipulator using the TO-RRT algorithm to plan its path, and the minimum-snap trajectory optimization algorithm was used to smooth the trajectory of the manipulator [37,38]. Figure 13 shows the shortest distance.
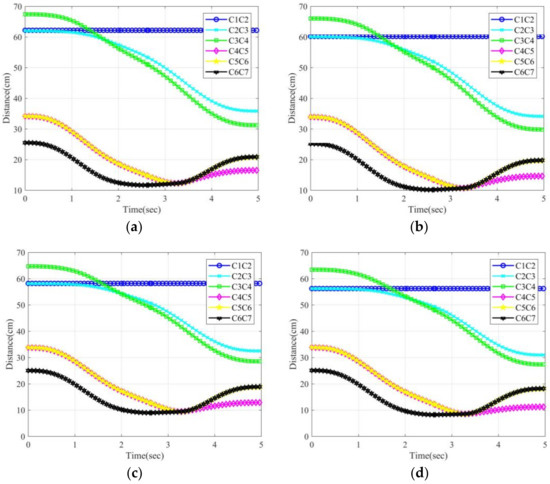
Figure 13.
The shortest distance from the center of the sphere to the origin of the coordinate system of adjacent links of the manipulator. (a) Obstacle with coordinates (25,55,48); (b) Obstacle with coordinates (25,53,47); (c) Obstacle with coordinates (25,51,46); (d) Obstacle with coordinates (25,49,45). represents the distance between the line segment between coordinate system i and coordinate system i + 1 and the center of the sphere.
3.3. Comparative Experiments in a Virtual Picking Environment
The motion-planning experiment of the Franka manipulator was initially realized through Robotics toolbox, which proved that the TO-RRT algorithm was feasible in the motion of the manipulator. MoveIt! was used in this section to build a virtual picking environment and to conduct comparative experiments on different algorithms in this environment. The experimental parameters are shown in Table 5.

Table 5.
Experimental parameters.
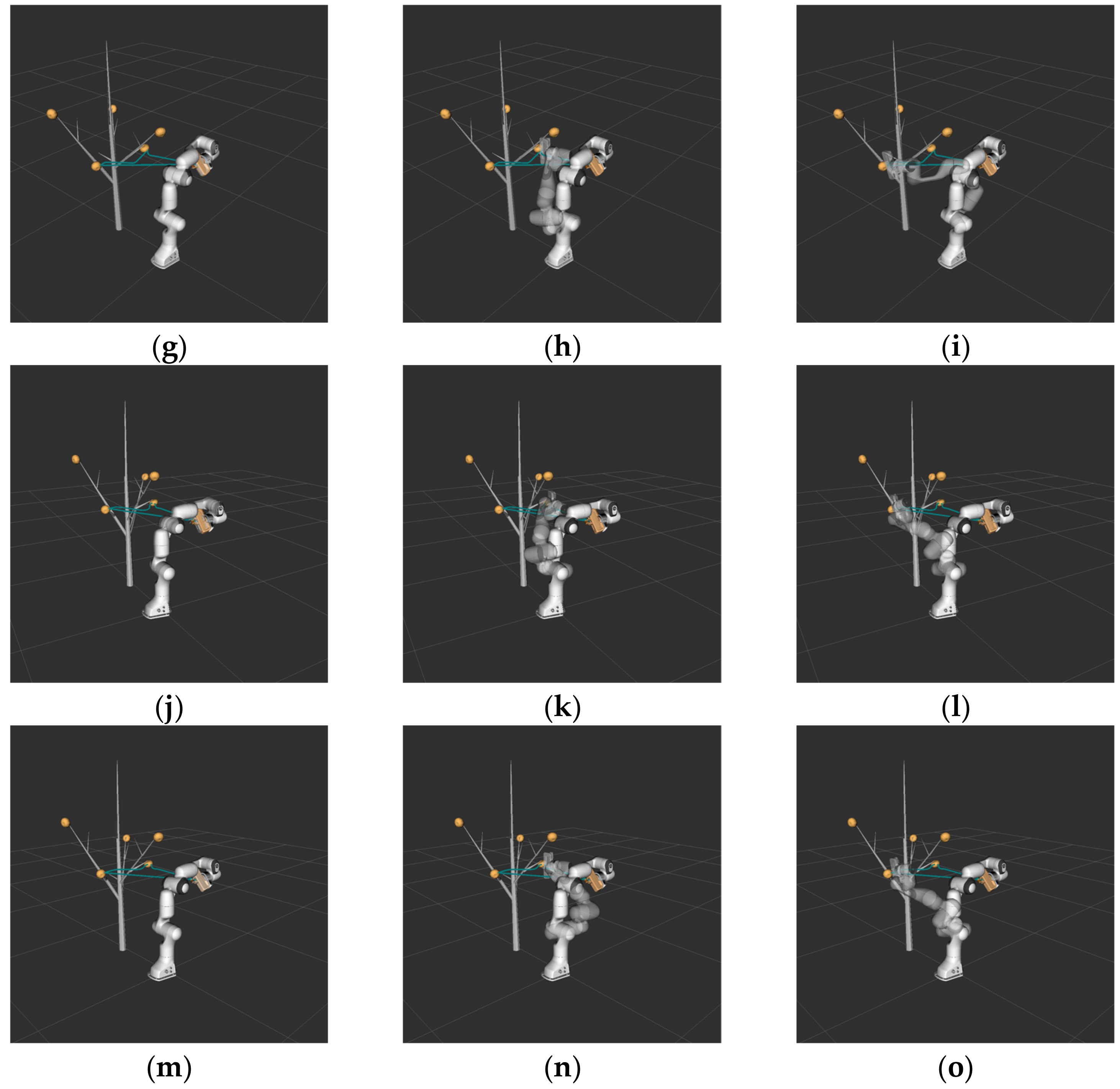
During the experiment, the maximum search time was 10 min, the maximum number of failed searches was 10,000, and the search domain was . Due to the large number of sampling points generated, the global search time of the RRT algorithm was 243.322451 s. Compared with the RRT algorithm, the search time of the biased-RRT algorithm was only 3.720342 s. However, affected by the nature of obstacles and the probability threshold, the collision-free path generated by the biased-RRT algorithm was less smooth. In contrast, since the NC-RRT algorithm controlled the sampling interval, its trajectory was the smoothest among all the algorithms. Compared with the previous algorithms, the TO-RRT search time and path length were only 0.074915 s and 0.63548128 m, respectively, due to the generation of smaller random trees. The simulation results are shown in Table 6 and Figure 14.

Table 6.
Experimental data using MoveIt!.
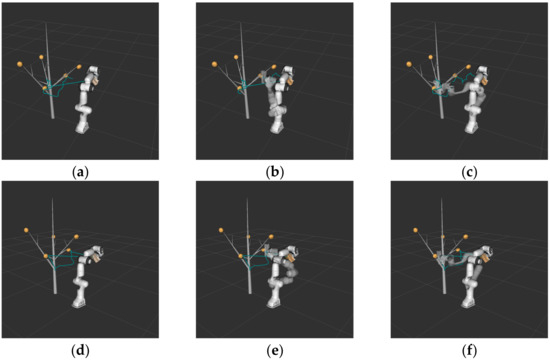
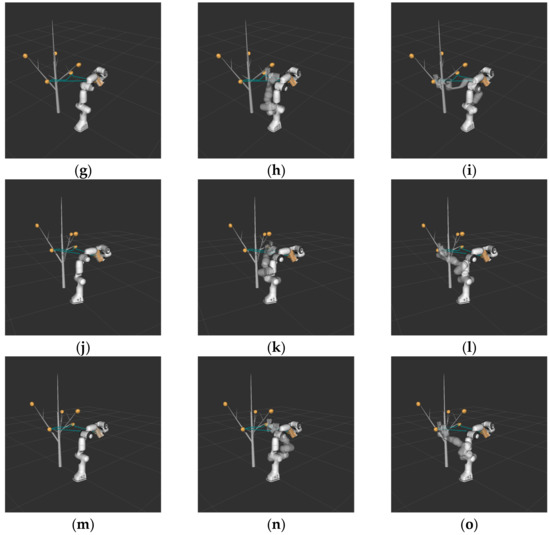
Figure 14.
The use of MoveIt! with: the RRT algorithm (a–c); the biased-RRT algorithm with a target offset probability of (d–f); the TO-RRT algorithm (g–i); the RRT-BCR algorithm (j–l); and the NC-RRT algorithm (m–o).
3.4. Contrastive Experiments in Real Environments
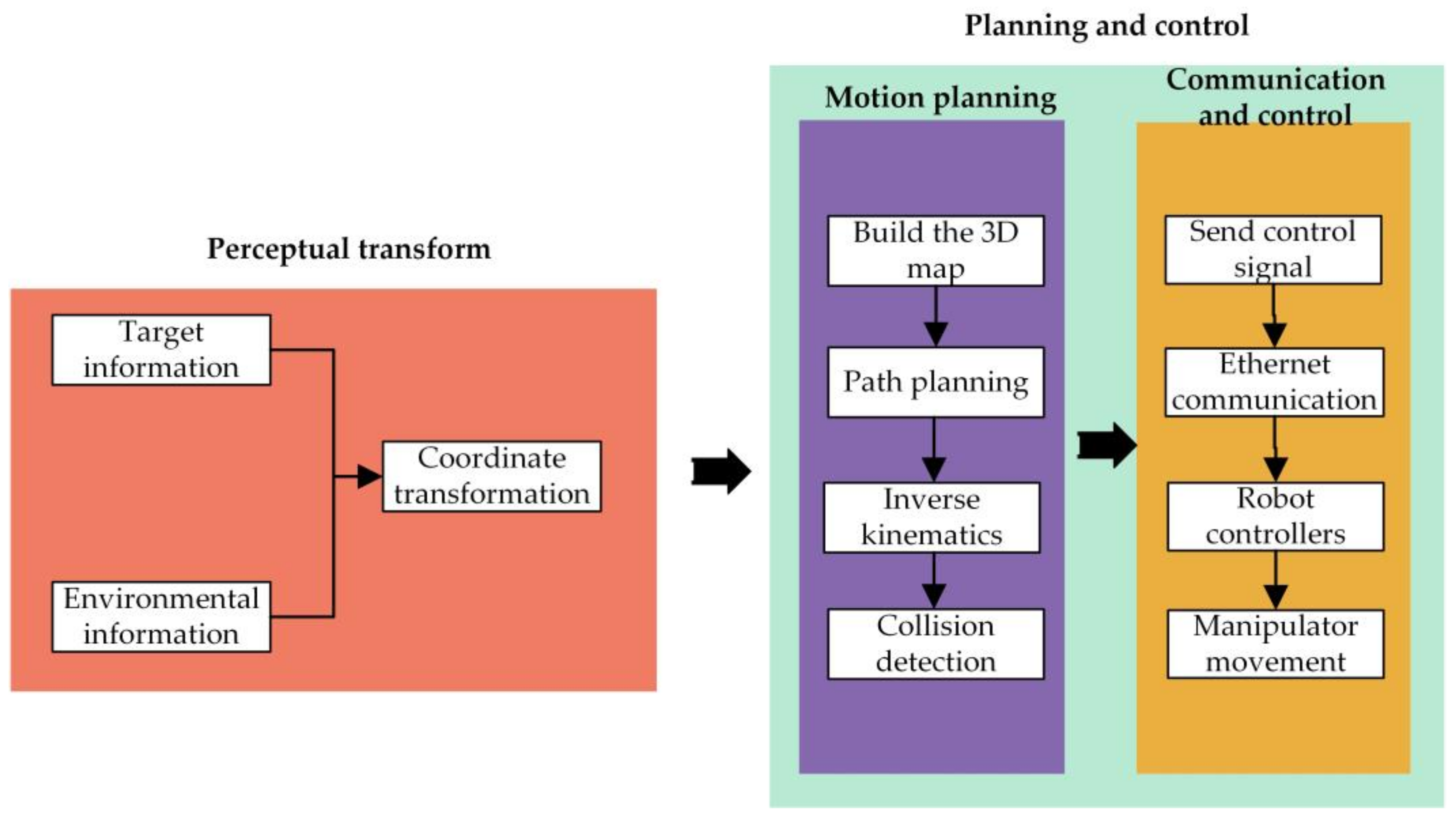
To test the performance of TO-RRT in actual picking, the Franka manipulator was taken as the moving object, the citrus as the operation object, and the tree trunk as the obstacle avoidance object to construct a multi-objective citrus-picking environment. The environmental parameters are shown in Table 7 and Table 8. First, the manipulator adjusted its pose to the initial state, and its joint angle was . Second, the three-dimensional coordinates of the citrus, the parameter information of obstacles, and the picking pose of the manipulator were transmitted to the planning thread, and the continuous and collision-free trajectory was obtained through inverse kinematics. Finally, MoveIt! published the trajectory through moveit_commander to move_group and transmitted the control signal to the robot controllers to complete the picking action. The control block diagram is shown in Figure 15. The experimental results showed that the TO-RRT algorithm could be used to effectively reduce the nodes, shorten the planning time, and reduce the movement time of the manipulator, as shown in Figure 16 and Table 9.

Table 7.
Obstacle information.

Table 8.
Target information.
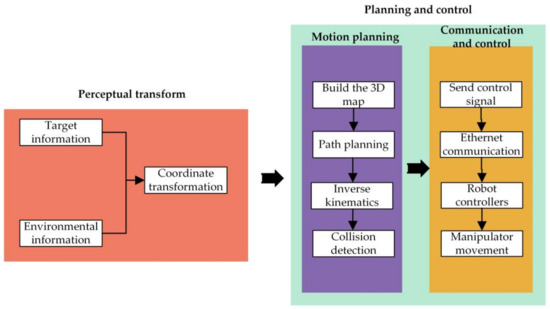
Figure 15.
Control block diagram.

Figure 16.
The manipulator reached Citrus 1 and Citrus 2 and avoided the branches. (a) Initial state of manipulator; (b) The manipulator reaches the first citrus; (c) Obstacle avoidance of the manipulator; (d) The manipulator reaches the second citrus.

Table 9.
Comparison of the planning time and movement time.
4. Discussion
4.1. Analysis
From Figure 10a–d, since the RRT algorithm did not consider the effect of target offset probability, the entire workspace was searched in all environments. The above problems led to the huge scale of the random tree and caused more collision detection times. Therefore, the path length and movement time of the manipulator were the longest among all the algorithms, as shown in Table 6 and Table 9. From Table 2, the biased-RRT algorithm avoided redundant searching through heuristic guidance, effectively reducing the number of tree nodes and collision detection times. From the average index in Table 2, since the RRT-BCR algorithm removed nodes that collided multiple times, its node failure growth rate was very low. However, this approach took a considerable amount of computation time, only 0.0112 s less than the biased-RRT algorithm, as shown in Table 9. From the average index in Table 2, the path length of the NC-RRT algorithm was the shortest, and the running time was second only to the TO-RRT algorithm. As can be seen from the multi-rectangle environment in Table 2, the NC-RRT algorithm had to continuously expand its sampling space when facing obstacles with large occlusion areas, resulting in 55,077 collision detections (which was the highest among all the algorithms). From Table 2, the TO-RRT algorithm reduced the numbers of path nodes and collision detections through an attractive step size, reduced the number of node failure growth through the node-first search strategy, and, finally, enhanced the escape ability through the regression superposition algorithm. However, the TO-RRT algorithm produced larger steps near obstacles, which led to a slightly longer path length than the other improved algorithms, as shown in Table 6.
4.2. Future Work
Industry 5.0 is a new generation of the industrial revolution representing “personalization”, in which personalized products and services are created for humans by using the creativity of human experts to interact with efficient, intelligent, and precise machines. The key technologies of Industry 5.0, such as human–computer interaction, collaborative robots, and edge computing (EC), can provide ideas and technical support for Agriculture 5.0 [39].
As the number of China’s aging population increases by the year, the number of rural employees has dropped sharply, and original agricultural production methods can no longer meet the development needs of the current citrus industry. Through the high integration of artificial intelligence and mechanical equipment, the transformation and upgrade of the production mode of China’s agricultural industry can be realized. The improved method proposed in this paper can be used in the fields for picking robots and pruning robots and for the path planning of orchard patrol robots [40,41,42]. By analyzing the characteristics of a citrus tree environment, the work presented in this paper aimed to optimize the time required and improve it on the basis of a traditional algorithm to greatly shorten the planning time of the manipulator and reduce the movement time of the manipulator to a certain extent. However, the detection of obstacles is an objective challenge faced by this method.
In recent years, path planning through deep reinforcement learning (DRL) has become a research hotspot. A robot senses environmental information through sensors and trains the samples in the process of continuous interaction with the environment to complete an efficient, accurate, and low-environment-dependence path-planning method. The fusion of deep reinforcement learning and traditional path-planning algorithms has gradually become a research trend. For example, LM-RRT determines the selection probability of extension and connection trees based on reinforcement learning and guides the trees to pass through narrow channels quickly [43]. Based on this, the research on improving the TO-RRT algorithm by reinforcement learning will be discussed in the next stage.
5. Conclusions
A time-optimal RRT algorithm based on the characteristics of the complex environment of citrus trees was proposed in this paper. The constructed algorithm had an attractive potential field and a repulsive potential field for the target node and obstacle, respectively. In addition, dynamic adjustment of the probability threshold under the action of the superimposed potential field was achieved, and a node-first search strategy was used to solve the “falling into a trap” problem. In addition, an attractive step size and a “step-size dichotomy” were introduced in this algorithm so that the random tree could expand the step size as much as possible on the premise of reducing the number of collisions. Finally, a regression superposition algorithm was used to improve the search efficiency of the random tree in the range of the obstacle repulsive potential field. The TO-RRT algorithm was simulated in complex environments, and the motion-planning of the Franka manipulator was carried out using Robotics Toolbox and MoveIt! It can be seen from the simulation results that the TO-RRT algorithm had fewer tree nodes, collision detection times, and failed growth times, so this algorithm had a shorter planning time than the RRT algorithm, the biased-RRT algorithm, the RRT-BCR algorithm, and the NC-RRT algorithm, especially when the random tree faced a large obstacle area. To obtain the performance of the algorithm in real work, we built a real picking environment indoors. Through the performance evaluation of various indicators of the different algorithms, it was proved that the TO-RRT algorithm still had a good performance in movement time.
Author Contributions
Conceptualization, C.L., L.X. and Q.F.; methodology, C.L., L.X. and Q.F.; software, C.L., Z.T. and X.W.; writing—original draft preparation, C.L. and L.X.; writing—review and editing, C.L., L.X. and Q.F.; visualization, C.L., Z.T., J.G. and X.W.; supervision, L.X. and Q.F.; funding acquisition, L.X. and Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Science and Technology Plan Project: Z201100008020009; Key R&D project of Science and Technology Department of Sichuan Province: 2020YFN0025; Key Projects of Innovation and Entrepreneurship of Sichuan Science and Technology Department: 2021JDRC0091; Chengdu Technology Innovation R&D Project: 2021-YF05-01744-SN.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 396–404. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. 1998. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.35.1853&rep=rep1&type=pdf (accessed on 10 March 2022).
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. Proceedings 2000 ICRA. Millennium Conference. In Proceedings of the IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 995–1001. [Google Scholar] [CrossRef] [Green Version]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. In Proceedings of the Robotics Science and Systems 2010, Zaragoza, Spain, 27 June 2010; Volume 104. Available online: http://www.roboticsproceedings.org/rss06/p34.pdf (accessed on 15 March 2022). [CrossRef]
- Mohammed, H.; Romdhane, L.; Jaradat, M.A. RRT* N: An efficient approach to path planning in 3D for Static and Dynamic Environments. Adv. Robot. 2021, 35, 168–180. [Google Scholar] [CrossRef]
- Akgun, B.; Stilman, M. Sampling heuristics for optimal motion planning in high dimensions. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2640–2645. [Google Scholar] [CrossRef]
- Jeong, I.B.; Lee, S.J.; Kim, J.H. RRT*-quick: A motion planning algorithm with faster convergence rate. In Robot Intelligence Technology and Applications 3; Intelligent Systems and Computing: Cham, Switzerland, 2015; pp. 67–76. [Google Scholar] [CrossRef]
- Jeong, I.B.; Lee, S.J.; Kim, J.H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Adiyatov, O.; Varol, H.A. Rapidly-exploring random tree based memory efficient motion planning. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 4–7 August 2013; pp. 354–359. [Google Scholar] [CrossRef]
- Cao, X.; Zou, X.; Jia, C.; Chen, M.; Zeng, Z. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Wang, X.; Luo, X.; Han, B.; Chen, Y.; Liang, G.; Zheng, K. Collision-free path planning method for robots based on an improved rapidly-exploring random tree algorithm. Appl. Sci. 2020, 10, 1381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, Y.; Zheng, J.; Yu, J. Path planning of industrial robot based on improved RRT algorithm in complex environments. IEEE Access 2018, 6, 53296–53306. [Google Scholar] [CrossRef]
- Gong, H.; Yin, C.; Zhang, F.; Hou, Z.; Zhang, R. A path planning algorithm for unmanned vehicles based on target-oriented rapidly-exploring random tree. In Proceedings of the 2017 11th Asian Control Conference (ASCC), Gold Coast, QLD, Australia, 17–20 December 2017; pp. 760–765. [Google Scholar] [CrossRef]
- Li, B.; Chen, B. An Adaptive Rapidly-Exploring Random Tree. IEEE/CAA J. Autom. Sin. 2021, 9, 283–294. [Google Scholar] [CrossRef]
- Gao, X.; Wu, H.; Zhai, L.; Sun, H.; Jia, Q.; Wang, Y.; Wu, L. A rapidly exploring random tree optimization algorithm for space robotic manipulators guided by obstacle avoidance independent potential field. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418782240. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Meng, M.Q.H. An improved RRT algorithm incorporating obstacle boundary information. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 625–630. [Google Scholar] [CrossRef]
- Veras, L.G.; Medeiros, F.; Guimaraes, L. Systematic literature review of sampling process in rapidly-exploring random trees. IEEE Access 2019, 7, 50933–50953. [Google Scholar] [CrossRef]
- Zu, W.; Fan, G.; Gao, Y.; Ma, H.; Zhang, H.; Zeng, H. Multi-UAVs Cooperative Path Planning Method based on Improved RRT Algorithm. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1563–1567. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Wang, M.; Dan, T. Design and implementation of improved RRT algorithm for collision free motion planning of high-dimensional robot in complex environment. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012; pp. 1391–1397. [Google Scholar] [CrossRef]
- Kang, G.; Kim, Y.B.; You, W.S.; Lee, Y.H.; Oh, H.S.; Moon, H.; Choi, H.R. Sampling-based path planning with goal oriented sampling. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 1285–1290. [Google Scholar] [CrossRef]
- Ahmadyan, S.N.; Kumar, J.A.; Vasudevan, S. Goal-oriented stimulus generation for analog circuits. In Proceedings of the 49th Annual Design Automation Conference, New York, NY, USA, 3 June 2012; pp. 1018–1023. [Google Scholar] [CrossRef]
- Wang, J.; Wu, S.; Li, H.; Zou, J. Path planning combining improved rapidly-exploring random trees with dynamic window approach in ROS. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1296–1301. [Google Scholar] [CrossRef]
- Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Trans. Ind. Electron. 2020, 68, 7244–7251. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, W.; Liu, G.; Pan, X.; Liu, X. A heuristic rapidly-exploring random trees method for manipulator motion planning. IEEE Access 2019, 8, 900–910. [Google Scholar] [CrossRef]
- Wen, N.; Zhang, R.; Liu, G.; Wu, J.; Qu, X. Online planning low-cost paths for unmanned surface vehicles based on the artificial vector field and environmental heuristics. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420969076. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Ayaz, Y. Potential functions based sampling heuristic for optimal path planning. Auton. Robot. 2016, 40, 1079–1093. [Google Scholar] [CrossRef] [Green Version]
- Zaid, T.; Qureshi, A.H.; Yasar, A.; Raheel, N. Potentially guided bidirectionalized rrt* for fast optimal path planning in cluttered environments. Robot. Auton. Syst. 2018, 108, 13–27. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, J.; Zheng, Y.; Huang, Q. Obstacle Avoidance Path Planning of Manipulator of Forestry Felling & Cultivation Machine. Sci. Silvae Sin. 2021, 57, 179–192. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H.; Liu, X.; Xu, Y. An Improved RRT Industrial Robot Path Avoidance Planning Algorithm. Inf. Control 2021, 50, 235–246. [Google Scholar] [CrossRef]
- Liu, C.; Han, J.; An, K. Dynamic Path Planning Based on an Improved RRT Algorithm for RoboCup Robot. Robot 2017, 39, 8–15. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. Cooperative Path Planning of Dual-arm Robot Based on Attractive Force Self-adaptive Step Size RRT. Robot 2020, 42, 606–616. [Google Scholar] [CrossRef]
- Ruan, X.; Zhou, J.; Zhang, J.; Zhu, X. Robot goal guide RRT path planning based on sub-target search. Control Decis. 2020, 35, 2543–2548. [Google Scholar] [CrossRef]
- Lin, N.; Zhang, Y. An adaptive RRT based on dynamic step for UAVs route planning. In Proceedings of the 2014 5th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 27–29 June 2014; pp. 1111–1114. [Google Scholar] [CrossRef]
- Wang, C.; Meng, Q.H. Variant step size RRT: An efficient path planner for UAV in complex environments. In Proceedings of the 2016 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Angkor Wat, Cambodia, 6–10 June 2016; pp. 555–560. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Jiang, L.; Meng, J.; Xie, Y. Motion Planning of Mobile Manipulator Based on RRT with Sparse Nodes. China Mech. Eng. 2020, 32, 9. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar] [CrossRef]
- Richter, C.A.; Bry, A.P.; Roy, N. Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments. In Robotics Research; Springer Tracts in Advanced Robotics; Springer: Cham, Switzerland, 23 April 2016; Volume 114, pp. 649–666. [Google Scholar] [CrossRef]
- Reddy, P.; Pham, Q.V.; Prabadevi, B.; Deepa, N.; Dev, K.; Gadekallu, T.; Ruby, R.; Liyanage, M. Industry 5.0: A survey on enabling technologies and potential applications. J. Ind. Inf. Integr. 2021, 26, 100257. [Google Scholar] [CrossRef]
- Gadekallu, T.R.; Rajput, D.S.; Reddy, M.P.K.; Lakshmanna, K.; Bhattacharya, S.; Singh, S.; Jolfaei, A.; Alazab, M. A novel PCA–whale optimization-based deep neural network model for classification of tomato plant diseases using GPU. J. Real-Time Image Process. 2021, 18, 1383–1396. [Google Scholar] [CrossRef]
- Li, T.; Feng, Q.; Qiu, Q.; Xie, F.; Zhao, C. Occluded Apple Fruit Detection and Localization with a Frustum-Based Point-Cloud Processing Approach for Robotic Harvesting. Remote Sensing. 2022, 14, 482. [Google Scholar] [CrossRef]
- Li, T.; Qiu, Q.; Zhao, C. Task planning of multi-arm harvesting robots for high-density dwarf orchards. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Zuo, L.; Xu, X. A learning-based multi-RRT approach for robot path planning in narrow passages. J. Intell. Robot. Syst. 2018, 90, 81–100. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).